Neuronale Netze leicht gemacht (Teil 91): Vorhersage durch Frequenzbereiche (Frequency Domain Forecasting, FreDF)
Einführung
Die Vorhersage von Zeitreihen zukünftiger Preise ist in verschiedenen Finanzmarktszenarien von entscheidender Bedeutung. Die meisten der derzeit existierenden Methoden beruhen auf einer gewissen Autokorrelation in den Daten. Mit anderen Worten, wir nutzen das Vorhandensein von Korrelationen zwischen Zeitschritten, die sowohl in den Eingabedaten als auch in den vorhergesagten Werten bestehen.
Zu den Modellen, die an Popularität gewinnen, gehören diejenigen, die auf der Transformer-Architektur basieren und Selbstaufmerksamkeits-Mechanismen (Self-Attention) für die dynamische Autokorrelationsschätzung verwenden. Außerdem ist ein zunehmendes Interesse an der Verwendung von Frequenzanalysen in Prognosemodellen zu beobachten. Die Darstellung der Sequenz von Eingabedaten im Frequenzbereich hilft, die Komplexität der Beschreibung der Autokorrelation zu vermeiden und verbessert die Effizienz verschiedener Modelle.
Ein weiterer wichtiger Aspekt ist die Autokorrelation in der Abfolge der vorhergesagten Werte. Natürlich sind die vorhergesagten Werte Teil einer größeren Zeitreihe, die die analysierten und vorhergesagten Sequenzen umfasst. Daher erhalten die vorhergesagten Werte die Korrelation der analysierten Daten. Dieses Phänomen wird jedoch bei modernen Prognosemethoden häufig ignoriert. Moderne Methoden verwenden vor allem das Paradigma der Direktprognose (DF), die gleichzeitig mehrstufige Prognosen erstellt. Dabei wird implizit davon ausgegangen, dass die Schritte in der Abfolge der vorhergesagten Werte unabhängig sind. Diese Diskrepanz zwischen Modellannahmen und Datenmerkmalen führt zu einer suboptimalen Prognosequalität.
Eine der Lösungen für dieses Problem wurde in der Publikation „FreDF: Learning to Forecast in Frequency Domain“ vorgeschlagen. Die Autoren des Papiers schlugen eine direkte Vorhersagemethode mit Frequenzverstärkung (FreDF) vor. Es verdeutlicht das DF-Paradigma, indem es die vorhergesagten Werte und die Abfolge der Kennzeichen (labels) im Frequenzbereich abgleicht. Beim Wechsel in den Frequenzbereich, wo die Basen orthogonal und unabhängig sind, wird der Einfluss der Autokorrelation wirksam reduziert. So bekämpft FreDF die Inkonsistenz zwischen der Annahme über DF und der Existenz von Autokorrelation von Kennzeichen, während die Vorteile von DF erhalten bleiben.
Die Autoren der Methode testeten ihre Wirksamkeit in einer Reihe von Experimenten, die die deutliche Überlegenheit des vorgeschlagenen Ansatzes gegenüber modernen Methoden zeigten.
1. FreDF-Algorithmus
Das DF-Paradigma verwendet ein Modell mit mehreren Ausgängen ɡθ zur Erstellung von T-Schritt-Prognosen Ŷ = ɡθ(X). Yt sei die Stufe t von Y, und Yt(n) sei die n-te Stichprobenbeobachtung. Die Modellparameter θ werden durch Minimierung des mittleren quadratischen Fehlers (MSE) optimiert:
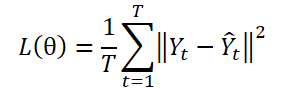
Beim DF-Paradigma wird der Vorhersagefehler bei jedem Schritt unabhängig berechnet, wobei jedes Element der Sequenz als separate Aufgabe behandelt wird. Bei diesem Ansatz wird jedoch die Autokorrelation innerhalb von Y übersehen, was im Widerspruch zum Vorhandensein einer Autokorrelation der Labels steht. Dies führt zu einer verzerrten Wahrscheinlichkeit und einer Abweichung vom Maximum-Likelihood-Prinzip bei der Modellbildung.
Eine Strategie zur Überwindung dieser Einschränkung besteht darin, die Abfolge der Kennzeichen in einem transformierten Bereich darzustellen, der aus orthogonalen Basen besteht. Dies kann insbesondere durch die Fourier-Transformation erreicht werden, bei der die Sequenz auf orthogonale Basen projiziert wird, die mit unterschiedlichen Frequenzen verbunden sind. Durch die Umwandlung der Kennzeichenfolge in den orthogonalen Frequenzbereich kann die Abhängigkeit von der Autokorrelation der Kennzeichen wirksam reduziert werden.

wobei i die imaginäre Einheit ist, die als √(-1) definiert ist,
exp(•) ist die mit der Frequenz k verbundene Fourier-Basis, die für verschiedene k-Werte orthogonal ist.
Aufgrund der Orthogonalität der Basis umgeht die Darstellung der Kennzeichenfolge im Frequenzbereich die Abhängigkeit, die sich aus der Autokorrelation im Zeitbereich ergibt. Dies verdeutlicht das Potenzial des Lernens von Vorhersagen im Frequenzbereich.
Bei der klassischen Anwendung von DF-Ansätzen wird zu einem gegebenen Zeitpunkt n die historische Folge Xn in das Modell eingegeben, um T-Schritt-Prognosen zu generieren, bezeichnet als Ŷn=ɡθ(Xn). Der Prognosefehler im Zeitbereich Ltmp wird berechnet.
Zusätzlich zum klassischen Ansatz schlagen die Autoren der FreDF-Methode vor, vorhergesagte Werte und Kennzeichensequenzen in den Frequenzbereich zu transformieren. Dann wird der Vorhersagefehler im Frequenzbereich mit der folgenden Formel berechnet:

Hier ist jeder Term der Summation eine Matrix aus komplexen Zahlen A; |A| bezeichnet die Operation der Berechnung und Summierung des Moduls jedes Elements in der Matrix. In diesem Fall wird der Modulus einer komplexen Zahl a = ar + i ai als √(ar^2 + ai^2) berechnet.
Bitte beachten Sie, dass die Autoren der FreDF-Methode aufgrund der unterschiedlichen numerischen Eigenschaften der Kennzeichensequenz im Frequenzbereich nicht die quadratische Verlustform (MSE) verwenden, wie sie für die Berechnung von Verlustfehlern im Zeitbereich typisch ist. Insbesondere haben verschiedene Frequenzkomponenten oft sehr unterschiedliche Größenordnungen, wobei niedrige Frequenzen im Vergleich zu höheren Frequenzen um mehrere Größenordnungen höhere Volumina aufweisen, was die quadratischen Verlustmethoden instabil macht.
Die Vorhersagefehler im Zeit- und Frequenzbereich werden mit dem Koeffizienten α im Wertebereich [0,1] kombiniert, der die relative Stärke der Entzerrung im Frequenzbereich steuert:
![]()
FreDF umgeht den Effekt der Autokorrelation der Zielwerte, indem es die generierten vorhergesagten Werte und die Abfolge der Kennzeichen im Frequenzbereich abgleicht. Außerdem bleiben die Vorteile von D.F. erhalten, wie z.B. die effiziente Ausgabe und die Multitasking-Fähigkeit. Die Besonderheit von FreDF ist seine Kompatibilität mit verschiedenen Prognosemodellen und Transformationen. Diese Flexibilität erweitert den möglichen Anwendungsbereich des FreDF erheblich.
Im Folgenden wird die Visualisierung der Methode durch den Autor vorgestellt.
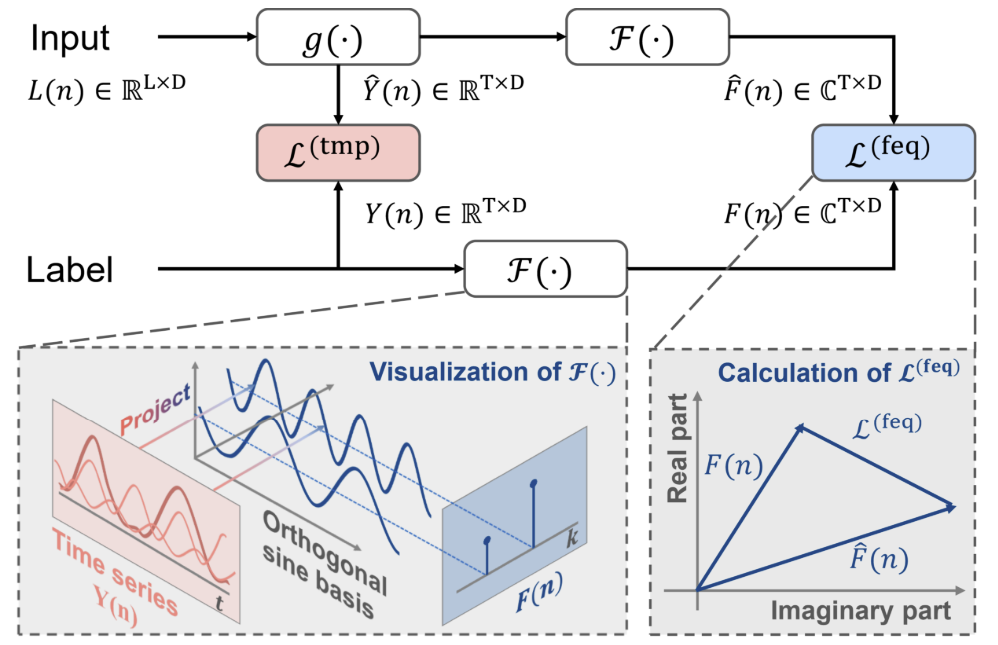
2. Implementierung in MQL5
Nachdem wir uns mit den theoretischen Aspekten der vorgeschlagenen FreDF-Methode beschäftigt haben, kommen wir nun zum praktischen Teil unseres Artikels, in dem wir unsere Vision des Ansatzes umsetzen werden. Aus der oben dargestellten theoretischen Beschreibung lässt sich schließen, dass der vorgeschlagene Ansatz keine besonderen Designmerkmale in die Modellarchitektur einführt. Außerdem hat sie keinen Einfluss auf den eigentlichen Betrieb des Modells. Seine Wirkung ist nur während des Modelltrainings zu erkennen. Wahrscheinlich kann die vorgeschlagene FreDF-Methode mit einer komplexen Verlustfunktion verglichen werden. Wir werden sie also verwenden, um das Modell zu trainieren, dessen Zielmarken nach unserem a priori Wissen Autokorrelationsabhängigkeiten aufweisen.
Bevor wir mit dem Aufbau eines neuen Objekts für die Umsetzung der vorgeschlagenen Ansätze beginnen, ist es erwähnenswert, dass die Autoren der Methode die Fourier-Transformation verwendet haben, um Daten aus einer Zeitreihe in einen Frequenzbereich zu transformieren. Es muss gesagt werden, dass die FreDF-Methode recht flexibel ist. Sie funktioniert auch gut in Kombination mit anderen Methoden zur Transformation von Daten in den orthogonalen Bereich. Die Autoren der Methode haben eine Reihe von Experimenten durchgeführt, um ihre Wirksamkeit bei der Verwendung anderer Transformationen zu beweisen. Die Ergebnisse dieser Versuche werden im Folgenden vorgestellt.

Wie man sehen kann, zeigen die Modelle, die die Fourier-Transformation verwenden, bessere Ergebnisse.
Ich möchte Ihre Aufmerksamkeit auf den Koeffizienten α lenken. Sein Wert von etwa 0,8 scheint aufgrund der Versuchsergebnisse optimal zu sein. Es ist anzumerken, dass die Modellgenauigkeit nach den Ergebnissen derselben Experimente abnimmt, wenn die Vorhersage nur im Frequenzbereich durchgeführt wird (mit α gleich 1).
Daraus können wir schließen, dass der Trainingsprozess sowohl den Zeit- als auch den Frequenzbereich des untersuchten Signals umfassen sollte, um ein optimales Zeitreihenvorhersagemodell zu erhalten. Unterschiedliche Darstellungen ermöglichen es uns, mehr Informationen über das Signal zu erhalten und dadurch ein effizienteres Modell zu trainieren.
Aber kommen wir zurück zu unserer Umsetzung. Nach den Ergebnissen der von den Autoren der Methode durchgeführten Experimente ermöglicht die Fourier-Transformation das Training von Modellen mit einem geringeren Vorhersagefehler. Im vorherigen Artikel haben wir bereits die direkte und umgekehrte, schnelle Fourier-Transformation implementiert. Wir können diese Entwicklungen in unserer neuen Implementierung nutzen.
Um die FreDF-Ansätze zu implementieren, erstellen wir eine neue Klasse CNeuronFreDFOCL, die die Hauptfunktionalität von der Basisklasse CNeuronBaseOCL der neuronalen Schicht erbt. Die Struktur der neuen Klasse ist unten dargestellt.
class CNeuronFreDFOCL : public CNeuronBaseOCL { protected: uint iWindow; uint iCount; uint iFFTin; bool bTranspose; float fAlpha; //--- CBufferFloat cForecastFreRe; CBufferFloat cForecastFreIm; CBufferFloat cTargetFreRe; CBufferFloat cTargetFreIm; CBufferFloat cLossFreRe; CBufferFloat cLossFreIm; CBufferFloat cGradientFreRe; CBufferFloat cGradientFreIm; CBufferFloat cTranspose; //--- virtual bool FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false); virtual bool Transpose(CBufferFloat *inputs, CBufferFloat *outputs, uint rows, uint cols); virtual bool FreqMSA(CBufferFloat *target, CBufferFloat *forecast, CBufferFloat *gradient); virtual bool CumulativeGradient(CBufferFloat *gradient1, CBufferFloat *gradient2, CBufferFloat *cummulative, float alpha); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) { return true; } virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); public: CNeuronFreDFOCL(void) {}; ~CNeuronFreDFOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint count, float alpha, bool need_transpose = true, ENUM_OPTIMIZATION optimization_type = ADAM, uint batch = 1); virtual bool calcOutputGradients(CArrayFloat *Target, float &error); //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual int Type(void) const { return defNeuronFreDFOCL; } virtual void SetOpenCL(COpenCLMy *obj); };
Die vorgestellte Struktur der neuen Klasse weist zwei bemerkenswerte Merkmale auf:
- Interne Objekte werden nur durch Datenpuffer dargestellt und es gibt keine internen Schichten.
- Die Methode calcOutputGradients wird außer Kraft gesetzt.
Ein weiteres implizites Merkmal kann hier erwähnt werden: Dieses Objekt enthält keine trainierbaren Parameter, was ziemlich selten ist. All diese Merkmale hängen mit dem Zweck der Klasse zusammen: Wir erstellen eine Klasse mit einer komplexen Verlustfunktion, nicht eine trainierbare neuronale Schicht. Und die calcOutputGradients-Methode in unserer neuronalen Schichtenarchitektur ist für die Berechnung der Abweichungen der vorhergesagten Werte von den Zielwerten zuständig. Bei der Implementierung der Methoden werden wir uns mit dem Zweck der internen Objekte und Variablen vertraut machen.
Alle Objekte werden statisch deklariert, sodass wir den Konstruktor und Destruktor der Klasse „leer“ lassen können. Alle Vorgänge im Zusammenhang mit der Freigabe des Speichers werden vom System selbst durchgeführt.
Klassenobjekte werden in der Init-Methode initialisiert. Wie üblich übergeben wir in den Parametern dieser Methode die wichtigsten Konstanten, die die Architektur der Klasse definieren. Hier haben wir:
- window, ein Fenster, das ein Element der Eingabedaten beschreibt,
- count für die Anzahl der Elemente in der Sequenz,
- alpha der Koeffizient für die Ausgleichskraft des Frequenz- und Zeitbereichs,
- need_transpose, das Flag, das anzeigt, dass die Daten für die Frequenzumwandlung transponiert werden müssen.
Dieses Objekt wird bei der Ausgabe des Modells verwendet. Die Eingabe sind also die von unserem Modell erzeugten Vorhersagewerte. Die Daten müssen in einem Format bereitgestellt werden, das mit den angestrebten Ergebnissen übereinstimmt. Die Parameter window und count entsprechen sowohl den vorhergesagten als auch den Zielwerten. Wir bieten dem Nutzer auch die Möglichkeit, Daten in den Frequenzbereich in einer anderen Ebene zu transformieren. Aus diesem Grund haben wir das Flag need_transpose eingeführt.
Ich möchte hier die Ergebnisse einiger anderer Experimente zitieren, die von den Autoren der Methode durchgeführt wurden. Sie testeten die Leistung der Modelle beim Vergleich von Frequenzcharakteristika in einheitlichen Zeitreihen einer multivariaten Sequenz (T), in Bezug auf einzelne Zeitschritte(D) und für die gesamte Sequenz (2D).

Die besten Ergebnisse lieferte das Modell, das die Häufigkeitscharakteristik der allgemeinen Aggregatabfolge darstellt. Als Außenseiter des Experiments erwies sich der Vergleich von Frequenzverläufen einzelner Zeitschritte. Die Analyse der Häufigkeitscharakteristika von uniformen Zeitreihen war die zweitbeste, knapp hinter dem Spitzenreiter.
In unserer Implementierung bieten wir dem Nutzer die Möglichkeit, die Messung für die Frequenzumwandlung auszuwählen, indem er den Wert des entsprechenden Flags need_transpose angibt. Um 2-dimensionale Frequenzmerkmale zu vergleichen, geben wir die Größe der gesamten Sequenz im Parameter window an und verwenden die folgenden Werte für die übrigen Parameter:
- count: 1,
- need_transpose: false.
bool CNeuronFreDFOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint count, float Alpha, bool need_transpose = true, ENUM_OPTIMIZATION optimization_type = ADAM, uint batch = 1) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * count, optimization_type, batch)) return false;
Im Methodenrumpf rufen wir zunächst die entsprechende gleichnamige Methode der Elternklasse auf und überprüfen das Ergebnis der Operationen. Auch hier implementiert die übergeordnete Klasse die erforderlichen Steuerelemente, einschließlich der Größe der zu erstellenden neuronalen Schicht. Für die Größe der Ebene geben wir das Produkt aus den Variablen window und count an. Wenn wir nur in einem dieser Felder einen Nullwert angeben, wird das gesamte Produkt gleich „0“ sein, und die Methode der übergeordneten Klasse schlägt fehl.
Nach erfolgreicher Ausführung der Methode der übergeordneten Klasse speichern wir die erhaltenen Werte in lokalen Variablen.
bTranspose = need_transpose; iWindow = window; iCount = count; fAlpha = MathMax(0, MathMin(Alpha, 1)); activation = None;
Wie wir bereits gesehen haben, benötigen wir für die schnelle Fourier-Transformation Puffer mit einer Größe von einer Potenz von 2. Berechnen wir die Größe der Datenpuffer:
//--- Calculate FFTsize uint size = (bTranspose ? count : window); int power = int(MathLog(size) / M_LN2); if(MathPow(2, power) != size) power++; iFFTin = uint(MathPow(2, power));
Der nächste Schritt ist die Initialisierung der internen Datenpuffer. Zunächst initialisieren wir die Frequenzgangpuffer der vorhergesagten Werte. Wir verwenden ein Design mit 2 Datenpuffern. Ein Puffer wird für die Aufzeichnung der Daten der realen Komponente verwendet, der zweite für die imaginäre Komponente.
//--- uint n = (bTranspose ? iWindow : iCount); if(!cForecastFreRe.BufferInit(iFFTin * n, 0) || !cForecastFreRe.BufferCreate(OpenCL)) return false; if(!cForecastFreIm.BufferInit(iFFTin * n, 0) || !cForecastFreIm.BufferCreate(OpenCL)) return false;
Als Nächstes erstellen wir ähnliche Puffer für die Frequenzmerkmale der Zielwerte:
if(!cTargetFreRe.BufferInit(iFFTin * n, 0) || !cTargetFreRe.BufferCreate(OpenCL)) return false; if(!cTargetFreIm.BufferInit(iFFTin * n, 0) || !cTargetFreIm.BufferCreate(OpenCL)) return false;
Wir schreiben den Vorhersagefehler in die Puffer cLossFreeRe und cLossFree:
if(!cLossFreRe.BufferInit(iFFTin * n, 0) || !cLossFreRe.BufferCreate(OpenCL)) return false; if(!cLossFreIm.BufferInit(iFFTin * n, 0) || !cLossFreIm.BufferCreate(OpenCL)) return false;
Bitte beachten Sie, dass es wichtig ist, beide Komponenten der Frequenzmerkmale zu vergleichen. Für eine korrekte Vorhersage von Zeitreihen sind sowohl die Amplituden als auch die Phasen der Frequenzmerkmale der Zeitreihen wichtig.
Außerdem müssen Puffer für die Erfassung von Fehlergradienten auf der Ebene der vorhergesagten Zeitreihenwerte angelegt werden:
if(!cGradientFreRe.BufferInit(iFFTin * n, 0) || !cGradientFreRe.BufferCreate(OpenCL)) return false; if(!cGradientFreIm.BufferInit(iFFTin * n, 0) || !cGradientFreIm.BufferCreate(OpenCL)) return false;
Um Speicher zu sparen, können wir die Puffer cGradientFreeRe und cGradientFreeIm ausschließen. Sie können leicht ersetzt werden, zum Beispiel durch die Puffer cForecastFreeRe und cForecastFreeIm. Aber ihr Vorhandensein macht den Code besser lesbar. Außerdem ist die Menge an Speicher, die sie in unserem Fall verwenden, nicht kritisch.
Schließlich erstellen wir einen temporären Puffer, um die transponierten Werte zu schreiben, falls erforderlich:
if(!cTranspose.BufferInit(iWindow * iCount, 0) || !cTranspose.BufferCreate(OpenCL)) return false; //--- return true; }
Nach der Dateninitialisierung erstellen wir in der Regel eine Methode für den Vorwärtsdurchgang. Es wurde bereits gesagt, dass ein Objekt dieser Klasse während des Betriebs keine Operationen mit Daten durchführt. Wie Sie wissen, beschreibt die Methode für den Vorwärtsdurchgang die Arbeitsweise des Modells. Wir könnten die Methode für den Vorwärtsdurchgang mit einem „Dummy“ umdefinieren, aber wie würden wir dann Daten übertragen? Wie immer möchten wir den Prozess des Kopierens von Daten minimieren, da das Datenvolumen unterschiedlich sein kann und die Prozessorganisation zusätzliche „Overhead-Kosten“ verursacht. In diesem Zusammenhang machen wir die Methode für den Vorwärtsdurchgang so einfach wie möglich. Bei dieser Methode wird nur die Übereinstimmung der Zeiger auf die Ergebnispuffer in der aktuellen und der vorherigen Schicht überprüft. Falls erforderlich, ersetzen wir den Zeiger in der aktuellen Ebene durch den Ergebnispuffer der vorherigen Ebene.
bool CNeuronFreDFOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL || !NeuronOCL.getOutput()) return false; if(NeuronOCL.getOutput() != Output) { Output.BufferFree(); delete Output; Output = NeuronOCL.getOutput(); } //--- return true; }
Wir ersetzen also den Zeiger auf einen Puffer, anstatt die Daten unabhängig von ihrem Volumen zu übertragen. Bitte beachten Sie, dass die Kontrolle bei jedem Durchlauf durchgeführt wird und die Datenpuffer nur beim ersten Durchlauf ersetzt werden.
Wir implementieren die Hauptfunktionen der Klasse für den Rückwärtsdurchgang. Lassen Sie uns zunächst ein wenig Vorbereitungsarbeit leisten. Um die erforderliche Funktionalität vollständig zu implementieren, werden wir 2 kleine Kernel auf der Programmseite von OpenCL erstellen.
Die Autoren der FreDF-Methode empfehlen die Verwendung von MAE als Verlustfunktion bei der Schätzung von Abweichungen im Frequenzbereich. Sie stellen außerdem fest, dass die Stabilität des Trainings bei der Verwendung von MSE abnimmt. Ich möchte Sie daran erinnern, dass unsere grundlegende neuronale Schichtklasse CNeuronBaseOCL tatsächlich MSE verwendet, um den Fehlergradienten zu bestimmen. Wir müssen also einen Kernel erstellen, um den Vorhersagefehlergradienten mit Hilfe von MAE zu bestimmen. Mathematisch gesehen ist dies ganz einfach: Wir müssen nur den Vektor der vorhergesagten Werte vom Vektor der Zielkennzeichen subtrahieren.
__kernel void GradientMSA(__global float *matrix_t, __global float *matrix_o, __global float *matrix_g ) { int i = get_global_id(0); matrix_g[i] = matrix_t[i] - matrix_o[i]; }
Nach der Bestimmung des Fehlergradienten im Frequenz- und Zeitbereich müssen wir die Fehlergradienten mit Hilfe des Temperaturkoeffizienten kombinieren. Lassen Sie uns diese Funktionalität in den Kernel CumulativeGradient implementieren, der, so denke ich, recht einfach zu verstehen sein sollte.
__kernel void CumulativeGradient(__global float *gradient_freq, __global float *gradient_tmp, __global float *gradient_out, float alpha ) { int i = get_global_id(0); gradient_out[i] = alpha * gradient_freq[i] + (1 - alpha) * gradient_tmp[i]; }
Ich möchte daran erinnern, dass wir für die Umwandlung von Daten vom Zeitbereich in den Frequenzbereich und zurück den Algorithmus der schnellen Fourier-Transformation verwenden, den wir im vorigen Artikel eingeführt haben. Dieser Artikel enthält eine Beschreibung des verwendeten Algorithmus und der Methode zur Platzierung des Kernels in der Ausführungswarteschlange.
Die Algorithmen für die Platzierung der Kernel in der Ausführungswarteschlange werden jetzt nicht weiter betrachtet. Sie folgen alle demselben Verfahren, das bereits mehrfach in den Artikeln dieser Reihe vorgestellt wurde, auch im vorigen Artikel.
Betrachten wir die Methode CNeuronFreDFOCL::calcOutputGradients, die die Hauptfunktionalität unserer Klasse implementiert. Wie Sie wissen, ermittelt diese Methode entsprechend der Struktur unserer Modelle die Abweichung der vorhergesagten Werte von den Zielkennzeichen. In den Methodenparametern erhalten wir einen Zeiger auf den Puffer mit den Zielwerten. Nach der Durchführung der Methodenoperationen müssen wir den Fehlergradienten in den entsprechenden Puffer der aktuellen Schicht speichern.
bool CNeuronFreDFOCL::calcOutputGradients(CArrayFloat *Target, float &error) { if(!Target) return false; if(Target.Total() < Output.Total()) return false;
Im Methodenrumpf prüfen wir die Korrektheit des empfangenen Zeigers auf den Zielwertpuffer. Außerdem muss seine Größe mindestens so groß sein wie der Ergebnissensor des Modells.
Da der empfangene Puffer möglicherweise keine Kopie seiner selbst auf der Kontextseite von OpenCL hat, müssen wir ihn dort für spätere Berechnungen erstellen. Um jedoch die Kontextressourcen von OpenCL sparsamer zu nutzen, werden wir die gewonnenen Daten in den bereits erstellten Gradientenpuffer übertragen.
if(Target.Total() == Output.Total()) { if(!Gradient.AssignArray(Target)) return false; } else { for(int i = 0; i < Output.Total(); i++) { if(!Gradient.Update(i, Target.At(i))) return false; } } if(!Gradient.BufferWrite()) return false;
Hier gibt es 2 mögliche Entwicklungen. Wenn die Größe des Puffers der Zielkennzeichen und des Puffers für den vorhergesagten Wert gleich sind, wird die bestehende Kopiermethode verwendet. Andernfalls verwenden wir eine Schleife, um die erforderliche Anzahl von Werten zu übertragen. In jedem Fall werden die Daten nach dem Kopieren in den OpenCL-Kontextspeicher übertragen.
Die gewonnenen Daten werden dann zur Berechnung der Abweichungen sowohl im Zeit- als auch im Frequenzbereich verwendet. Bitte beachten Sie, dass bei der Berechnung von Abweichungen im Zeitbereich der Fehlergradientenpuffer unserer Schicht mit den berechneten Abweichungen überschrieben wird, während die ermittelten Zielwerte vollständig verloren gehen. Daher müssen wir vor der Berechnung der Abweichungen im Zeitbereich zumindest die erhaltenen Zeitreihen der Zielkennzeichen in Frequenzkomponenten zerlegen.
Eine Zeitreihe kann in Frequenzmerkmale in zwei Dimensionen zerlegt werden. Die zu verwendende Methode wird durch den Wert des Flags bTranspose bestimmt. Wenn das Flag auf true gesetzt ist, wird zunächst der Ergebnispuffer des Modells transponiert und dann in Frequenzgänge zerlegt:
if(bTranspose) { if(!Transpose(Output, GetPointer(cTranspose), iWindow, iCount)) return false; if(!FFT(GetPointer(cTranspose), NULL, GetPointer(cForecastFreRe), GetPointer(cForecastFreIm), false)) return false;
Wir führen ähnliche Operationen für den Tensor der Zielkennzeichen durch:
if(!Transpose(Gradient, GetPointer(cTranspose), iWindow, iCount)) return false; if(!FFT(GetPointer(cTranspose), NULL, GetPointer(cTargetFreRe), GetPointer(cTargetFreIm), false)) return false; }
Wenn das Flag bTranspose false ist, dann führen wir die Zerlegung der Ziel- und vorhergesagten Werte in die entsprechenden Frequenzmerkmale ohne vorherige Transposition durch:
else { if(!FFT(Output, NULL, GetPointer(cForecastFreRe), GetPointer(cForecastFreIm), false)) return false; if(!FFT(Gradient, NULL, GetPointer(cTargetFreRe), GetPointer(cTargetFreIm), false)) return false; }
Sobald die Frequenzcharakteristiken bestimmt sind, können wir die Abweichungen sowohl im Zeit- als auch im Frequenzbereich berechnen, ohne dass wir uns um den Verlust von Zielwerten sorgen müssen.
if(!FreqMSA(GetPointer(cTargetFreRe), GetPointer(cForecastFreRe), GetPointer(cLossFreRe))) return false; if(!FreqMSA(GetPointer(cTargetFreIm), GetPointer(cForecastFreIm), GetPointer(cLossFreIm))) return false; if(!FreqMSA(Gradient, Output, Gradient)) return false;
Beachten Sie, dass wir im Frequenzbereich Abweichungen sowohl im reellen als auch im imaginären Teil des Frequenzgangs ermitteln. Denn der Wert der Phasenverschiebung ist nicht weniger wichtig als die Signalamplitude. Allerdings können wir die Gradienten der Fehler im Zeit- und Frequenzbereich nicht direkt approximieren. Offensichtlich sind die Daten nicht vergleichbar. Daher müssen wir zunächst die Gradienten des Frequenzgangfehlers in den Zeitbereich zurückführen. Dazu verwenden wir die inverse Fourier-Transformation.
if(!FFT(GetPointer(cLossFreRe), GetPointer(cLossFreIm), GetPointer(cGradientFreRe), GetPointer(cGradientFreIm), true)) return false;
Die Fehlergradienten des Zeit- und Frequenzbereichs wurden in eine vergleichbare Form gebracht. Nun hängt die Messung der Frequenzkennlinienextraktion vom Wert des Flags bTranspose ab. Daher müssen wir den Fehlergradienten im Frequenzbereich entsprechend dem Flag-Wert transformieren. Erst dann können wir den kumulativen Fehlergradienten unseres Modells bestimmen.
if(bTranspose) { if(!Transpose(GetPointer(cGradientFreRe), GetPointer(cTranspose), iCount, iWindow)) return false; if(!CumulativeGradient(GetPointer(cTranspose), Gradient, Gradient, fAlpha)) return false; } else if(!CumulativeGradient(GetPointer(cGradientFreRe), Gradient, Gradient, fAlpha)) return false; //--- return true; }
Vergessen wir nicht, die Ergebnisse bei jedem Schritt zu kontrollieren. Der logische Wert der Operationen wird an den Aufrufer zurückgegeben.
Nachdem wir den Fehlergradienten am Modellausgang bestimmt haben, müssen wir ihn an die vorherige Schicht weitergeben. Wir implementieren diese Funktionalität in der Methode CNeuronFreDFOCL::calcInputGradients, die in ihren Parametern einen Zeiger auf das Objekt der vorherigen neuronalen Schicht erhält.
Beachten Sie, dass unsere Schicht keine trainierbaren Parameter enthält. Während des Feedforward-Durchlaufs haben wir den Datenpuffer ersetzt und zeigen die Werte der vorherigen Schicht als Ergebnisse an. Was ist der Zweck dieser Methode? Es ist ganz einfach. Wir müssen lediglich den oben berechneten kumulativen Fehlergradienten an die Aktivierungsfunktion der vorherigen Schicht anpassen.
bool CNeuronFreDFOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false; //--- return DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), Gradient, NeuronOCL.Activation()); }
Da unsere Klasse keine trainierbaren Parameter enthält, definieren wir die Methode updateInputWeights mit einem sogenannten „empty stub“ neu.
Das Fehlen von übertragbaren Parametern in der Klasse wirkt sich auch auf die Datei-Operationsmethoden aus. Denn wir brauchen keine irrelevanten internen Objekte zu speichern. Daher rufen wir beim Speichern von Daten nur die gleichnamige Methode der Elternklasse auf.
bool CNeuronFreDFOCL::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false;
Wir speichern die Werte der Variablen, die die Gestaltungsmerkmale des Objekts beschreiben:
if(FileWriteInteger(file_handle, int(iWindow)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iCount)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iFFTin)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(bTranspose)) < INT_VALUE) return false; if(FileWriteFloat(file_handle, fAlpha) < sizeof(float)) return false; //--- return true; }
Der AlgorithmusLoad zur Wiederherstellung eines Objekts aus einer Datendatei sieht ein wenig komplizierter aus. Hier stellen wir zunächst die Elemente der übergeordneten Klasse wieder her:
bool CNeuronFreDFOCL::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false;
Dann laden wir die variablen Daten in der Reihenfolge, in der sie gespeichert wurden, und vergessen dabei nicht zu prüfen, wann das Ende der Datei erreicht ist:
if(FileIsEnding(file_handle)) return false; iWindow = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iCount = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iFFTin = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; bTranspose = bool(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; fAlpha = FileReadFloat(file_handle);
Dann müssen wir die verschachtelten Objekte entsprechend den geladenen Parametern der Klassenarchitektur initialisieren. Objekte werden ähnlich wie der Algorithmus zur Initialisierung einer neuen Klasseninstanz initialisiert:
uint n = (bTranspose ? iWindow : iCount); if(!cForecastFreRe.BufferInit(iFFTin * n, 0) || !cForecastFreRe.BufferCreate(OpenCL)) return false; if(!cForecastFreIm.BufferInit(iFFTin * n, 0) || !cForecastFreIm.BufferCreate(OpenCL)) return false; if(!cTargetFreRe.BufferInit(iFFTin * n, 0) || !cTargetFreRe.BufferCreate(OpenCL)) return false; if(!cTargetFreIm.BufferInit(iFFTin * n, 0) || !cTargetFreIm.BufferCreate(OpenCL)) return false; if(!cLossFreRe.BufferInit(iFFTin * n, 0) || !cLossFreRe.BufferCreate(OpenCL)) return false; if(!cLossFreIm.BufferInit(iFFTin * n, 0) || !cLossFreIm.BufferCreate(OpenCL)) return false; if(!cGradientFreRe.BufferInit(iFFTin * n, 0) || !cGradientFreRe.BufferCreate(OpenCL)) return false; if(!cGradientFreIm.BufferInit(iFFTin * n, 0) || !cGradientFreIm.BufferCreate(OpenCL)) return false; if(bTranspose) { if(!cTranspose.BufferInit(iWindow * iCount, 0) || !cTranspose.BufferCreate(OpenCL)) return false; } else { cTranspose.BufferFree(); cTranspose.Clear(); } //--- return true; }
Damit ist die Beschreibung der Methoden unserer neuen Klasse CNeuronFreDFOCL abgeschlossen. Den vollständigen Code dieser Klasse finden Sie in der Anlage.
Nach der Konstruktion der Methoden der neuen Klasse gehen wir in der Regel dazu über, die Architektur des trainierbaren Modells zu beschreiben. Aber in diesem Artikel haben wir eine eher ungewöhnliche neuronale Schicht gebaut. Wir haben eine komplexe Verlustfunktion in Form einer neuronalen Schicht implementiert. Wir können also das oben erstellte Objekt zu einem der Modelle hinzufügen, die wir zuvor trainiert haben, es erneut trainieren und sehen, wie sich die Ergebnisse ändern. Für meine Experimente habe ich das Modell FEDformer gewählt, dessen Architektur hier beschrieben wird hier. Fügen wir ihr eine neue Ebene hinzu.
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- ........ ........ //--- layer 17 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Nachdem ich eine Weile darüber nachgedacht hatte, beschloss ich, das Experiment auszuweiten. Die Autoren der FreDF-Methode haben einen eigenen Algorithmus zur Nutzung der Abhängigkeiten in den vorhergesagten Ergebnissen vorgeschlagen. Tatsächlich gibt es auch eine Abhängigkeit zwischen den einzelnen Parametern der Ergebnisse unseres Akteurs. Zum Beispiel schließen sich die Volumina von Kauf- und Verkaufsgeschäften gegenseitig aus, da wir zu jedem Zeitpunkt nur in einer Richtung eine offene Position haben. Stop-Loss- und Take-Profit-Parameter bestimmen die Stärke der höchstwahrscheinlich bevorstehenden Bewegung. Daher sollte der Take-Profit einer Long-Position bis zu einem gewissen Grad mit dem Stop-Loss einer Short-Position korreliert sein und umgekehrt. Ähnliche Überlegungen lassen sich anstellen, um Abhängigkeiten bei den vorhergesagten Critic-Werten zu erkennen. Warum also nicht das Experiment auf die genannten Modelle ausweiten? Gesagt, getan. Hinzufügen einer neuen Ebene zu den Modellen „Akteur“ und „Kritiker“:
bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; } //--- Actor ......... ......... //--- layer 17 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NActions; descr.count = 1; descr.step = int(false); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- Critic ......... ......... //--- layer 17 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NRewards; descr.count = 1; descr.step = int(false); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
Bitte beachten Sie, dass wir in diesem Fall die Häufigkeitscharakteristiken der gesamten Ergebnisfolge analysieren und nicht die einzelner unitäre Reihen.
Unsere Implementierung der von der FreDF-Methode vorgeschlagenen Ansätze erfordert keine Anpassungen der für das Modelltraining und die Interaktion mit der Umwelt verwendeten Expert Advisors. Das bedeutet, dass wir zum Testen der erzielten Ergebnisse zuvor erstellte Expert Advisors und Trainingsdatensätze verwenden können.
3. Tests
Wir haben viel Arbeit investiert, um die von den Autoren von FreDF vorgeschlagenen Ansätze mit MQL5 umzusetzen. Jetzt kommen wir zur letzten Phase unserer Arbeit: Schulung und Tests.
Wie bereits erwähnt, werden wir die Modelle mit dem zuvor erstellten Expert Advisor und den zuvor gesammelten Trainingsdaten trainieren. In unseren Artikeln trainieren wir Modelle auf den historischen Daten des EURUSD-Instruments mit dem H1-Zeitrahmen für das Jahr 2023.
Zunächst trainieren wir das Modell des Umgebungszustands, den Encoder. Das Modell wird so trainiert, dass es künftige Zustände der Umwelt über einen durch die Konstante NForecast bestimmten Planungshorizont vorhersagt. In meinem Experiment habe ich 12 aufeinander folgende Kerzen verwendet. Die Prognose wird im Zusammenhang mit allen analysierten Parametern erstellt, die den Zustand der Umwelt beschreiben.
#define NForecast 12 //Number of forecast
Beim Training des Encoders ist eine Verringerung des Vorhersagefehlers im Vergleich zu einem ähnlichen Modell ohne Verwendung von FreDF-Ansätzen zu erkennen. Wir haben jedoch keinen grafischen Vergleich der Prognoseergebnisse durchgeführt. Daher ist es schwierig, die tatsächliche Qualität der Prognosewerte zu beurteilen. An dieser Stelle ist anzumerken, dass unser Ziel nicht darin besteht, die genauesten Prognosen für alle analysierten Indikatoren zu erhalten, so seltsam es auch erscheinen mag. Das Akteursmodell nutzt den latenten Raum des Encoders, um über optimale Aktionen zu entscheiden. Das Ziel der ersten Trainingsphase ist es, den informativsten latenten Raum des Encoders zu erhalten, der die wahrscheinlichste bevorstehende Preisbewegung kodiert.
Wie zuvor analysiert das Encoder-Modell nur die Preisbewegung, sodass wir in der ersten Phase des Trainings die Trainingsmenge nicht aktualisieren müssen.
In der zweiten Phase unseres Lernprozesses suchen wir nach der optimalen Handlungsstrategie des Akteurs. Hier führen wir ein iteratives Training der Modelle von Akteur und Kritiker durch, das sich mit der Aktualisierung des Trainingsdatensatzes abwechselt.
Als Ergebnis mehrerer Iterationen des Trainings der Akteurspolitik ist es uns gelungen, ein Modell zu entwickeln, das Gewinne erwirtschaften kann. Wir haben die Leistung des trainierten Modells im MetaTrader 5 Strategietester mit realen historischen Daten für Januar 2024 getestet. Die Testparameter stimmten vollständig mit den Parametern des Trainingsdatensatzes überein, einschließlich des Instruments, des Zeitrahmens und der Parameter der analysierten Indikatoren. Die Testergebnisse sind in den folgenden Screenshots dargestellt.
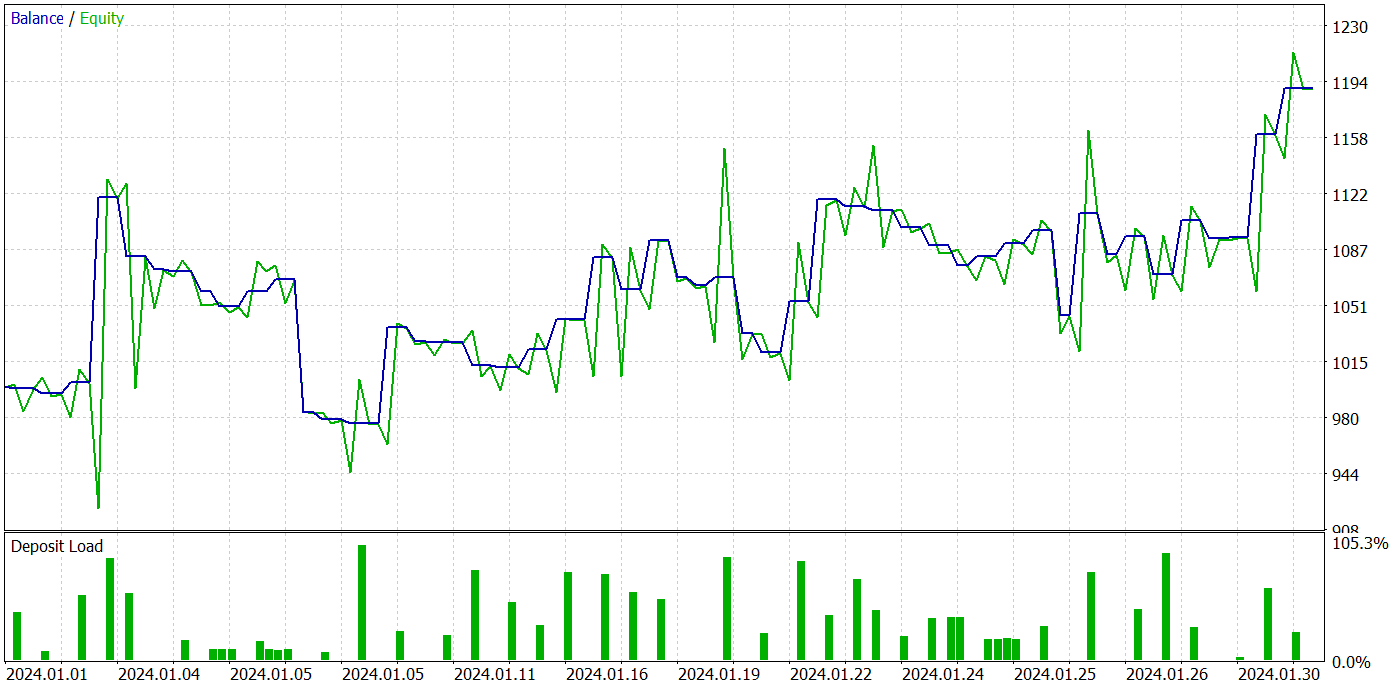
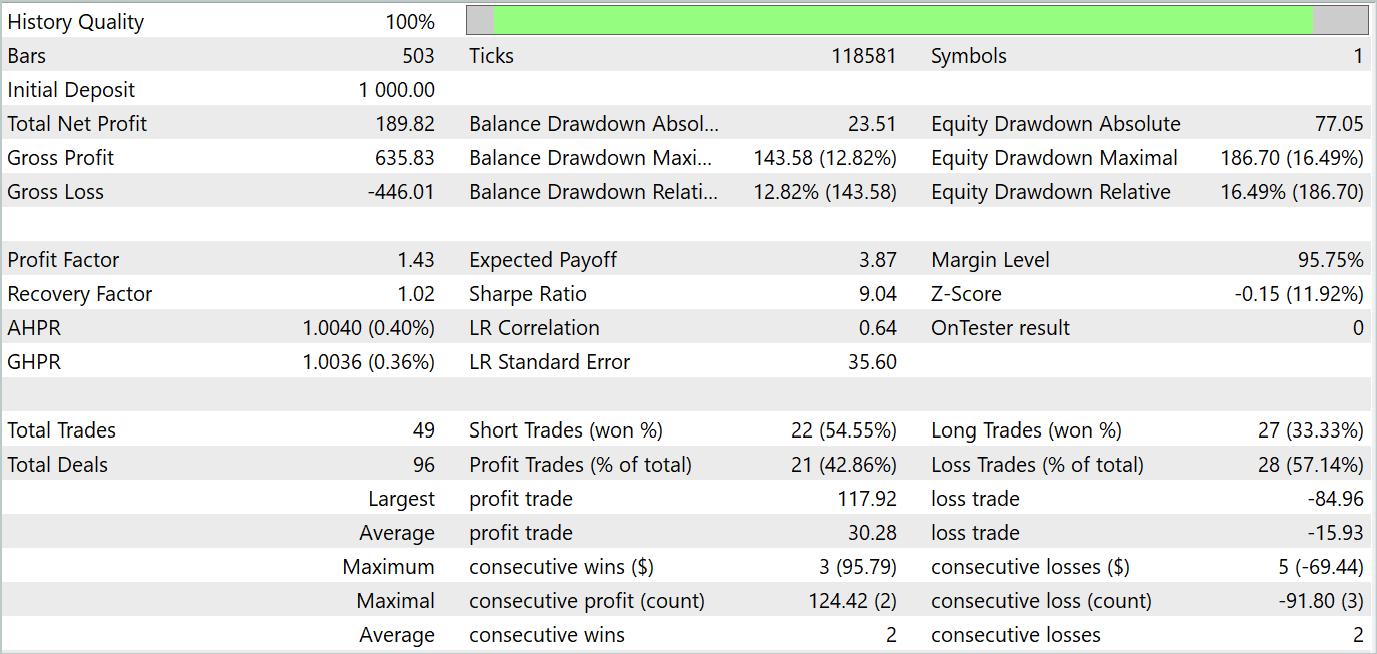
Anhand der Testergebnisse lässt sich ein klarer Trend zur Erhöhung des Kontostands erkennen. Während des Testzeitraums führte das Modell 49 Handelsgeschäfte aus, von denen 21 mit Gewinn abgeschlossen wurden. Ja, weniger als die Hälfte der Positionen waren rentabel. Allerdings ist der durchschnittlich gewinnbringende Handel fast 2-mal so groß wie der durchschnittliche Verlusthandel. Im Ergebnis beträgt der Gewinnfaktor des Modells im Testdatensatz 1,43 und das Gesamteinkommen für den Monat etwa 19 %.
Schlussfolgerung
In diesem Artikel haben wir die Methode FreDF erörtert, die darauf abzielt, die Zeitreihenprognose zu verbessern. Die Autoren der Methode haben empirisch nachgewiesen, dass die Vernachlässigung der Autokorrelation in der markierten Sequenz zu einer Verzerrung der Wahrscheinlichkeit und einer Verschlechterung der Qualität der Prognosen im derzeitigen DF-Paradigma führt. Sie präsentierten eine einfache, aber wirksame Modifikation des derzeitigen DF-Paradigmas, die die Autokorrelation berücksichtigt, indem sie Vorhersage- und Markierungssequenzen im Frequenzbereich aneinander anpasst. Die FreDF-Methode ist mit verschiedenen Prognosemodellen und Transformationen kompatibel, was sie flexibel und vielseitig macht.
Im praktischen Teil des Artikels haben wir unsere Vision der vorgeschlagenen Ansätze in der Sprache MQL5 umgesetzt. Wir ergänzten das zuvor erstellte FEDformer-Modell um die vorgeschlagenen Ansätze und führten ein Training durch. Dann haben wir das trainierte Modell getestet. Die Testergebnisse deuten auf die Wirksamkeit der vorgeschlagenen Ansätze hin, da die Hinzufügung von FreDF die Effizienz des Modells erhöht hat, wenn alle anderen Faktoren gleich bleiben.
Ich möchte auf die Flexibilität der FreDF-Methode hinweisen, die es ermöglicht, sie mit einer Vielzahl von bestehenden Modellen effektiv zu nutzen.
Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Beispielsammlung EA |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | StudyEncoder.mq5 | Expert Advisor | Encode Training EA |
| 5 | Test.mq5 | Expert Advisor | Trainings-EA für das Model |
| 6 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 7 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 8 | NeuroNet.cl | Code Base | Die Bibliothek des Programmcodes von OpenCL |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/14944
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Entwicklung eines Replay Systems (Teil 51): Die Dinge werden kompliziert (III)
Entwicklung eines Replay Systems (Teil 51): Die Dinge werden kompliziert (III)
 PSAR, Heiken Ashi und Deep Learning gemeinsam für den Handel nutzen
PSAR, Heiken Ashi und Deep Learning gemeinsam für den Handel nutzen
 Neuronale Netze leicht gemacht (Teil 92): Adaptive Vorhersage im Frequenz- und Zeitbereich
Neuronale Netze leicht gemacht (Teil 92): Adaptive Vorhersage im Frequenz- und Zeitbereich
 Wie man die automatische Optimierung in MQL5 Expert Advisors implementiert
Wie man die automatische Optimierung in MQL5 Expert Advisors implementiert
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.