Neuronale Netze leicht gemacht (Teil 74): Trajektorienvorhersage mit Anpassung

Einführung

Die Entwicklung einer Handelsstrategie ist untrennbar mit der Analyse der Marktsituation und der Vorhersage der wahrscheinlichsten Entwicklung eines Finanzinstruments verbunden. Diese Bewegung korreliert häufig mit anderen Finanzanlagen und makroökonomischen Indikatoren. Dies ist vergleichbar mit dem Transportwesen, bei dem jedes Fahrzeug sein eigenes Ziel verfolgt. Ihre Handlungen im Straßenverkehr sind jedoch bis zu einem gewissen Grad miteinander verknüpft und werden durch die Verkehrsregeln streng geregelt. Auch aufgrund der individuellen Wahrnehmung der Straßensituation durch die Fahrzeugführer verbleibt ein Teil der Stochastik auf den Straßen.

Auch in der Welt der Finanzen unterliegt die Preisbildung bestimmten Regeln. Die von den Marktteilnehmern erzeugte Stochastizität von Angebot und Nachfrage führt jedoch zu einer Stochastizität der Preise. Dies könnte der Grund dafür sein, dass viele der in der Schifffahrt verwendeten Methoden zur Vorhersage der Trajektorie bei der Vorhersage künftiger Preisbewegungen gut funktionieren.

In diesem Artikel möchte ich Ihnen eine Methode zur effektiven gemeinsamen Vorhersage der Trajektorien aller Agenten der Umgebung mit dynamischem Lernen von Gewichten ADAPT vorstellen, die vorgeschlagen wurde, um Probleme im Bereich der Navigation von autonomen Fahrzeugen zu lösen. Diese Methode wurde zuerst in dem Artikel „ADAPT: Efficient Multi-Agent Trajectory Prediction with Adaptation“ vorgestellt.

1. ADAPT-Algorithmus

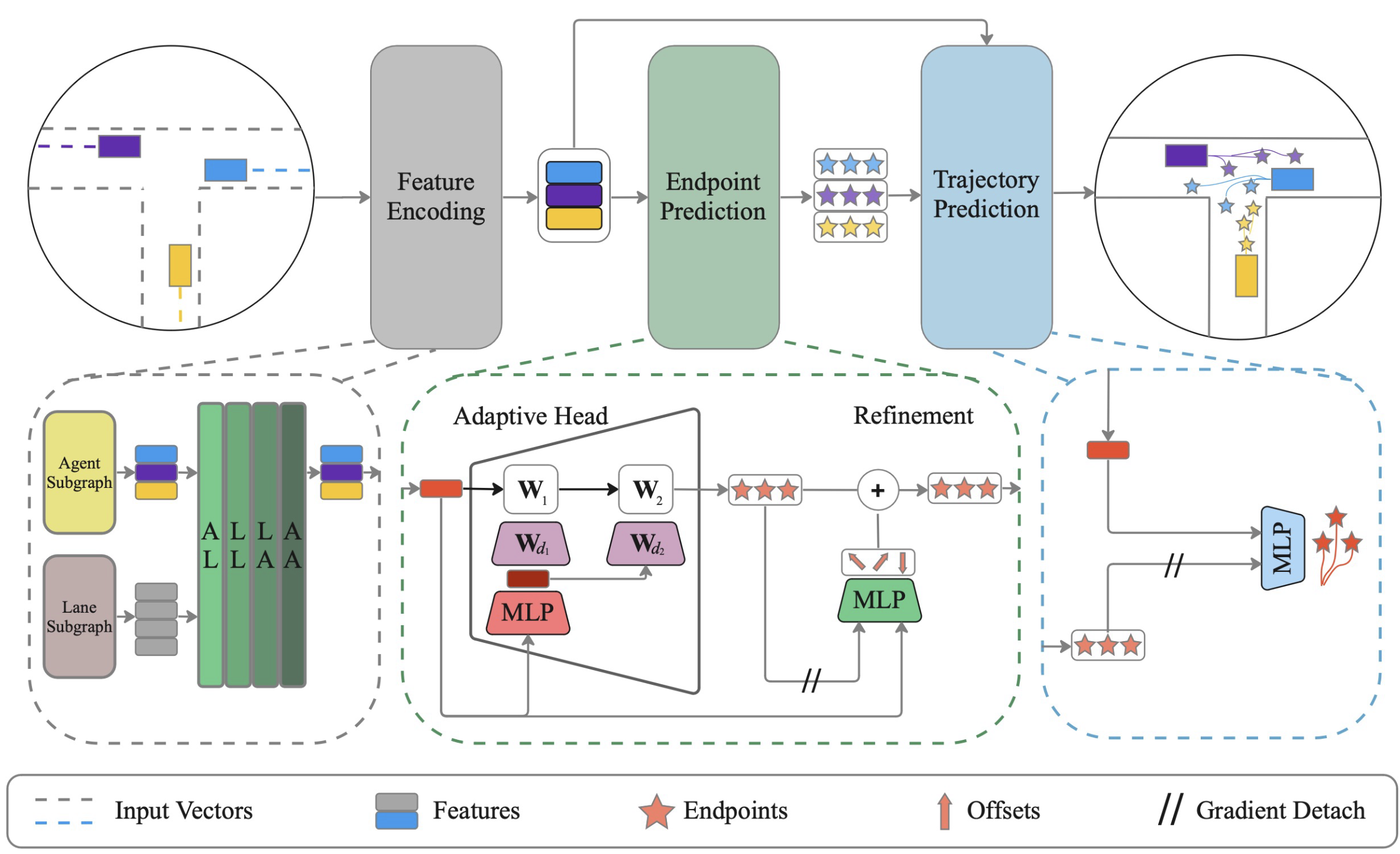
Die Methode ADAPT analysiert die vergangenen Trajektorien aller Agenten in der Umgebungskarte und sagt ihre zukünftigen Trajektorien voraus. Eine vektorisierte Umgebungsdarstellung modelliert verschiedene Arten von Interaktionen zwischen Agenten und der Karte, um die bestmögliche Darstellung der Agenten zu erhalten. Ähnlich wie bei den Zielsetzungsansätzen sagt der Algorithmus zunächst eine mögliche Menge von Endpunkten voraus. Jeder Endpunkt wird dann verfeinert, um die Verschiebung des Agenten in der Umgebung zu berücksichtigen. Danach wird die gesamte an den Endpunkten ermittelte Trajektorie vorhergesagt.

Die Autoren der Methode stabilisieren das Modelltraining durch die Trennung von Endpunkt- und Trajektorienvorhersage mit Gradientenstopp. Das von den Autoren vorgestellte Modell verwendet kleine mehrschichtige Perceptrons zur Vorhersage von Endpunkten und Trajektorien, um die Modellkomplexität gering zu halten.

Die von den Autoren vorgeschlagene Methode verwendet eine vektorisierte Darstellung, um die Karte und die Agenten auf strukturierte Weise zu kodieren. Bei dieser Darstellung wird für jedes Umgebungselement unabhängig voneinander ein zusammenhängender Graph erstellt, wobei die vergangenen Trajektorien der Agenten und die Umgebungskarte berücksichtigt werden. Die Autoren der Methode schlagen vor, zwei getrennte Teilgraphen für Agenten und Kartenobjekte zu verwenden.

ADAPT ermöglicht es Ihnen, verschiedene Arten von Interaktionen zwischen Umgebungnelementen zu simulieren. Die Autoren schlugen vor, vier Arten von Beziehungen zu modellieren:agent-to-lane (AL), lane-to-lane (LL), lane-to-agent (LA) und agent-to-agent (AA).

Interdependenzen werden ähnlich wie bei AutoBots durch mehrköpfige Aufmerksamkeitsblöcke analysiert. Die Selbstaufmerksamkeitsblöcke (self-attention blocks, AA, LL) werden jedoch mit Hilfe eines Cross-Attention-Encoders durch Kreuz-Beziehungsblöcke (AL, LA) ergänzt. Jede Interaktion wird nacheinander modelliert, und der Prozess wird L-mal wiederholt.

Auf diese Weise können die Zwischenmerkmale bei jeder Iteration aktualisiert werden, und die aktualisierten Merkmale werden dann bei der nächsten Iteration zur Berechnung der Aufmerksamkeit verwendet. Jedes Umgebungnelement kann durch verschiedene Arten von Interaktionen L-mal informiert werden.

Für die Vorhersage des Endpunkts bei Verwendung einer agentenorientierten Darstellung kann MLP verwendet werden, was aufgrund seiner Vorteile bei der Vorhersage durch einen einzelnen Agenten vorzuziehen ist. Bei der Verwendung einer umgebungnzentrierten Darstellung wird jedoch empfohlen, einen adaptiven Kopf mit dynamischen Gewichten zu verwenden, der bei der Vorhersage von Trajektorienendpunkten durch mehrere Agenten effektiver ist.

Nachdem er den Endpunkt für jeden Agenten erhalten hat, interpoliert der Algorithmus mithilfe von MLP die zukünftigen Koordinaten zwischen dem Start- und dem Endpunkt. Hier „entkoppeln“ wir die Endpunkte, um sicherzustellen, dass die Gewichtungsaktualisierungen für die Vorhersage der gesamten Trajektorie von der Endpunktvorhersage entkoppelt sind. In ähnlicher Weise sagen wir die Wahrscheinlichkeit für jede Trajektorie mit entkoppelten Endpunkten voraus.

Um Modelle zu trainieren, sagen wir K Trajektorien voraus und wenden den Sortenverlust an, um multimodale Zukunftsszenarien zu erfassen. Der Fehlergradient wird nur durch die genaueste Trajektorie zurückverfolgt. Da wir die vollständigen Trajektorien in Abhängigkeit von den Endpunkten vorhersagen, ist die Genauigkeit der Endpunktvorhersage für die Vorhersage der vollständigen Trajektorie entscheidend. Daher wenden die Autoren der Methode eine separate Verlustfunktion an, um die Endpunktvorhersage zu verbessern. Das letzte Element der ursprünglichen Verlustfunktion ist der Klassifizierungsverlust, der die den Trajektorien zugewiesenen Wahrscheinlichkeiten bestimmt.

Das Original der von den Verfassern des Papiers vorgestellten Methode ist unter visualization zu finden.

2. Implementierung mit MQL5

Die obige Beschreibung der ADAPT-Methode ist recht kurz gehalten, was auf den großen Arbeitsaufwand und die Beschränkungen des Artikelformats zurückzuführen ist. Auf einige Aspekte werden wir bei der Umsetzung der vorgeschlagenen Ansätze noch näher eingehen. Bitte beachten Sie, dass sich unsere Implementierung in vielerlei Hinsicht von der ursprünglichen Methode unterscheiden wird. Hier sind die Unterschiede.

Erstens werden wir keine separaten Tensoren für die Codierung von Agenten und Polylinien verwenden. Die Agenten sind in unserem Fall die analysierten Merkmale. Jedes Merkmal wird durch 2 Parameter charakterisiert: Wert und Zeit. Während des untersuchten Zeitraums bewegt sie sich auf einer bestimmten Bahn. Obwohl jeder Indikator seinen eigenen Wertebereich hat, haben wir eigentlich keine Karte der Umgebung. Wir haben jedoch einen Schnappschuss der Umgebung zu einem einzigen Zeitpunkt mit allen Agenten darin. Technisch gesehen, können wir eine Entität durch eine andere ersetzen. Es scheint nicht notwendig zu sein, einen separaten Tensor dafür zu erstellen, da es sich um eine Betrachtung der gleichen Daten in einer anderen Dimension handelt. Daher werden wir einen Tensor mit verschiedenen Akzenten verwenden.

2.1 Block der Kreuz-Beziehungen

Als ich über die Umsetzung der vorgeschlagenen Ansätze nachdachte, stellte ich fest, dass mir die Umsetzung des Blocks „Cross-Relationship“ (Kreuz-Beziehungen) noch fehlte. Zuvor waren unsere Aufgaben eher autoregressiver Natur. Für solche Aufgaben war die Verwendung eines Selbstaufmerksamkeitsblocks völlig ausreichend. Diesmal müssen wir die Beziehungen zwischen verschiedenen Einheiten analysieren. Wir werden also eine neue neuronale Schicht CNeuronMH2AttentionOCL implementieren. Die Algorithmen für die Klassenimplementierung sind größtenteils aus dem Block „Selbstaufmerksamkeit“ übernommen. Der Unterschied besteht darin, dass die Entitäten Abfrage (Query), Schlüssel (Key) und Wert (Value) aus verschiedenen Dimensionen des Quelldatentensensors gebildet werden. Dies erforderte erhebliche Änderungen. Daher habe ich beschlossen, eine neue Klasse zu erstellen, anstatt die bestehende zu modernisieren.

class CNeuronMH2AttentionOCL       :  public CNeuronBaseOCL
  {
protected:
   uint              iHeads;                                      ///< Number of heads
   uint              iWindow;                                     ///< Input window size
   uint              iUnits;                                      ///< Number of units
   uint              iWindowKey;                                  ///< Size of Key/Query window
   //---
   CNeuronConvOCL    Q_Embedding;
   CNeuronConvOCL    KV_Embedding;
   CNeuronTransposeOCL Transpose;
   int               ScoreIndex;
   CNeuronBaseOCL    MHAttentionOut;
   CNeuronConvOCL    W0;
   CNeuronBaseOCL    AttentionOut;
   CNeuronConvOCL    FF[2];
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      attentionOut(void);
   //---
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      AttentionInsideGradients(void);
public:
   /** Constructor */
                     CNeuronMH2AttentionOCL(void);
   /** Destructor */~CNeuronMH2AttentionOCL(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint heads, 
                          uint units_count, ENUM_OPTIMIZATION optimization_type, 
                          uint batch);
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   //---
   virtual int       Type(void)   const   {  return defNeuronMH2AttentionOCL;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   virtual CLayerDescription* GetLayerInfo(void);
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

Im Klassenkonstruktor werden nur Anfangswerte für lokale Variablen gesetzt.

CNeuronMH2AttentionOCL::CNeuronMH2AttentionOCL(void)  :  iHeads(0),
                                                         iWindow(0),
                                                         iUnits(0),
                                                         iWindowKey(0)
  {
   activation = None;
  }

Der Destruktor der Klasse bleibt leer.

Die Initialisierung der Objekte der Klasse CNeuronMH2AttentionOCL ist in der Methode Init implementiert. Zu Beginn der Methode rufen wir eine entsprechende Methode der Elternklasse auf, in der die vom externen Programm empfangenen Daten geprüft und geerbte Objekte initialisiert werden.

bool CNeuronMH2AttentionOCL::Init(uint numOutputs, uint myIndex, 
                                  COpenCLMy *open_cl, uint window,
                                  uint window_key, uint heads, 
                                  uint units_count, 
                                  ENUM_OPTIMIZATION optimization_type, 
                                  uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count,
                                                       optimization_type, batch))
      return false;

Wir speichern die Werte der wichtigsten Parameter.

   iWindow = fmax(window, 1);
   iWindowKey = fmax(window_key, 1);
   iUnits = fmax(units_count, 1);
   iHeads = fmax(heads, 1);
   activation = None;

Da wir die Quelldaten in verschiedenen Dimensionen analysieren werden, müssen wir den Tensor der Quelldaten transponieren.

   if(!Transpose.Init(0, 0, OpenCL, iUnits, iWindow, optimization_type, batch))
      return false;
   Transpose.SetActivationFunction(None);

Zur Erzeugung der Abfrage-, Schlüssel- und Werteinheiten werden Faltungsschichten verwendet. Die Anzahl der Filter ist gleich der Dimension des Vektors einer Entität. Die Abfrage wird aus einer Dimension des ursprünglichen Datentensors erzeugt, während Schlüssel und Wert aus einer anderen Dimension erzeugt werden. Daher werden wir 2 Ebenen erstellen (eine für jede Dimension).

   if(!Q_Embedding.Init(0, 0, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 
                                                                     optimization_type, batch))
      return false;
   Q_Embedding.SetActivationFunction(None);

   if(!KV_Embedding.Init(0, 0, OpenCL, iUnits, iUnits, 2 * iWindowKey * iHeads, iWindow, 
                                                                     optimization_type, batch))
      return false;
   KV_Embedding.SetActivationFunction(None);

Wir benötigen nur die Abhängigkeits-Koeffizientenmatrix auf der OpenCL-Kontextseite. Um Ressourcen zu sparen, wird nur im Kontext ein Puffer angelegt. Auf der Seite des Hauptprogramms wird nur ein Zeiger auf den Puffer gespeichert.

   ScoreIndex = OpenCL.AddBuffer(sizeof(float) * iUnits * iWindow * iHeads, CL_MEM_READ_WRITE);
   if(ScoreIndex == INVALID_HANDLE)
      return false;

Als Nächstes kommen Objekte, die dem Block der Selbstaufmerksamkeit ähneln. Hier erstellen wir eine mehrköpfige Aufmerksamkeitsausgabeschicht.

//---
   if(!MHAttentionOut.Init(0, 0, OpenCL, iWindowKey * iUnits * iHeads, optimization_type, batch))
      return false;
   MHAttentionOut.SetActivationFunction(None);

Schicht zur Reduzierung der Dimensionalität.

   if(!W0.Init(0, 0, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, 
                                                                      optimization_type, batch))
      return false;
   W0.SetActivationFunction(None);

Am Ausgang des Aufmerksamkeitsblocks fassen wir die mit den Originaldaten erzielten Ergebnisse in einer separaten Schicht zusammen.

   if(!AttentionOut.Init(0, 0, OpenCL, iWindow * iUnits, optimization_type, batch))
      return false;
   AttentionOut.SetActivationFunction(None);

Es folgt ein Block von linearen MLPs.

   if(!FF[0].Init(0, 0, OpenCL, iWindow, iWindow, 4 * iWindow, iUnits, optimization_type, batch))
      return false;
   if(!FF[1].Init(0, 0, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, optimization_type, 
                                                                                          batch))
      return false;
   for(int i = 0; i < 2; i++)
      FF[i].SetActivationFunction(None);

Um unnötiges Kopieren von Fehlergradienten aus dem Puffer der Elternklasse in den Puffer der internen Schicht während des Backpropagation-Durchgangs zu vermeiden, werden wir Zeiger durch Objekte ersetzen.

   Gradient.BufferFree();
   delete Gradient;
   Gradient = FF[1].getGradient();
//---
   return true;
  }

Bei der Beschreibung des Feedforward-Passes ist zu beachten, dass trotz der großen Anzahl interner Schichten, die bestimmte Funktionen implementieren, die Beziehungen direkt analysiert werden müssen. Obwohl diese Funktionalität mathematisch völlig identisch mit dem Selbstaufmerksamkeitsblock ist, werden wir mit der Tatsache konfrontiert, dass die Anzahl der Abfrage-Entitäten höchstwahrscheinlich von der Anzahl der Schlüssel- und Wert-Entitäten abweicht, was zu einer rechteckigen Score-Matrix führt und die Logik der zuvor erstellten Kernel verletzt. Deshalb werden wir neue Kernel erstellen.

Für den Vorwärtsdurchgang erstellen wir den Kernel MH2AttentionOut. Der Kernel erhält als Parameter 4 Zeiger auf Datenpuffer und die Vektordimension eines Entity-Elements. Alle unsere Einheiten haben die gleiche Größe der Elemente.

__kernel void MH2AttentionOut(__global float *q,      ///<[in] Matrix of Querys
                              __global float *kv,     ///<[in] Matrix of Keys
                              __global float *score,  ///<[out] Matrix of Scores
                              __global float *out,    ///<[out] Matrix of Scores
                              int dimension           ///< Dimension of Key
                             )
  {
//--- init
   const int q_id = get_global_id(0);
   const int k = get_global_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int kunits = get_global_size(1);
   const int heads = get_global_size(2);

Wir werden den Kernel in einem Aufgabenraum mit bis zu 3 Dimensionen für die Elemente Abfrage, Schlüssel und Aufmerksamkeitsköpfe (Attention headers) starten. Außerdem werden alle Threads innerhalb eines Abfrageelements und eines Aufmerksamkeitskopfes zu Gruppen zusammengefasst, da die Score-Matrix innerhalb der angegebenen Gruppen mit der SoftMax-Funktion normalisiert werden muss.

Im Kernelkörper identifizieren wir zunächst jeden Thread und bestimmen den Offset in den globalen Datenpuffern.

   const int shift_q = dimension * (q_id + qunits * h);
   const int shift_k = dimension * (k + kunits * h);
   const int shift_v = dimension * (k + kunits * (heads + h));
   const int shift_s = q_id * kunits * heads + h * kunits + k;

Wir definieren auch andere Konstanten und deklarieren ein lokales Array.

   const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE);
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;
   __local float temp[LOCAL_ARRAY_SIZE];

Danach berechnen wir die Matrix der Abhängigkeitskoeffizienten.

//--- sum of exp
   uint count = 0;
   if(k < ls)
      do
        {
         if((count * ls) < (kunits - k))
           {
            float sum = 0;
            for(int d = 0; d < dimension; d++)
               sum = q[shift_q + d] * kv[shift_k + d];
            sum = exp(sum / koef);
            if(isnan(sum))
               sum = 0;
            temp[k] = (count > 0 ? temp[k] : 0) + sum;
           }
         count++;
        }
      while((count * ls + k) < kunits);
   barrier(CLK_LOCAL_MEM_FENCE);

   count = min(ls, (uint)kunits);
//---
   do
     {
      count = (count + 1) / 2;
      if(k < ls)
         temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0);
      if(k + count < ls)
         temp[k + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

//--- score
   float sum = temp[0];
   float sc = 0;
   if(sum != 0)
     {
      for(int d = 0; d < dimension; d++)
         sc = q[shift_q + d] * kv[shift_k + d];
      sc = exp(sc / koef);
      if(isnan(sc))
         sc = 0;
     }
   score[shift_s] = sc;
   barrier(CLK_LOCAL_MEM_FENCE);

Wir berechnen auch neue Werte für die Abfrage-Entität, wobei wir die Abhängigkeitskoeffizienten für jedes Element des Vektors separat berücksichtigen.

//--- out
   for(int d = 0; d < dimension; d++)
     {
      uint count = 0;
      if(k < ls)
         do
           {
            if((count * ls) < (kunits - k))
              {
               float sum = q[shift_q + d] * kv[shift_v + d] * 
                                (count == 0 ? sc : score[shift_s + count * ls]);
               if(isnan(sum))
                  sum = 0;
               temp[k] = (count > 0 ? temp[k] : 0) + sum;
              }
            count++;
           }
         while((count * ls + k) < kunits);
      barrier(CLK_LOCAL_MEM_FENCE);
      //---
      count = min(ls, (uint)kunits);
      do
        {
         count = (count + 1) / 2;
         if(k < ls)
            temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0);
         if(k + count < ls)
            temp[k + count] = 0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      //---
      out[shift_q + d] = temp[0];
     }
  }

Als Nächstes erstellen wir einen neuen Kernel, um die Backpropagation-Funktionalität MH2AttentionInsideGradients zu implementieren. Wir werden diesen Kernel auch in einem 3-dimensionalen Aufgabenraum ausführen.

In den Kernel-Parametern übergeben wir 6 Zeiger auf Datenpuffer. Dazu gehören Fehlergradientenpuffer für alle Entitäten.

__kernel void MH2AttentionInsideGradients(__global float *q, __global float *q_g,
                                          __global float *kv, __global float *kv_g,
                                          __global float *scores,
                                          __global float *gradient,
                                          int kunits)
  {
//--- init
   const int q_id = get_global_id(0);
   const int d = get_global_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int dimension = get_global_size(1);
   const int heads = get_global_size(2);

Im Kernelkörper identifizieren wir, wie immer, den Thread und erstellen die notwendigen Konstanten.

   const int shift_q = dimension * (q_id + qunits * h) + d;
   const int shift_k = dimension * (q_id + kunits * h) + d;
   const int shift_v = dimension * (q_id + kunits * (heads + h)) + d;
   const int shift_s = q_id * kunits * heads + h * kunits;
   const int shift_g = h * qunits * dimension + d;
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;

Zunächst berechnen wir die Fehlergradienten für die Entität Wert. Dazu multiplizieren wir einfach den Vektor der Fehlergradienten am Ausgang des Aufmerksamkeitsblocks mit den entsprechenden Abhängigkeitskoeffizienten.

//--- Calculating Value's gradients
   int step_score = q_id * kunits * heads;
   for(int v = q_id; v < kunits; v += qunits)
     {
      int shift_score = h * kunits + v;
      float grad = 0;
      for(int g = 0; g < qunits; g++)
         grad += gradient[shift_g + g * dimension] * scores[shift_score + g * step_score];
      kv_g[shift_v + v * dimension]=grad;
     }

Anschließend berechnen wir die Fehlergradienten für die Entität Abfrage. Diesmal müssen wir zunächst den Fehlergradienten an den Elementen der Abhängigkeits-Koeffizientenmatrix berechnen, wobei die Ableitung der Funktion SoftMax berücksichtigt wird. Dann sollte es mit dem entsprechenden Element des Schlüssel-Tensors multipliziert werden.

//--- Calculating Query's gradients
   float grad = 0;
   float out_g = gradient[shift_g + q_id * dimension];
   int shift_val = (heads + h) * kunits * dimension + d;
   int shift_key = h * kunits * dimension + d;
   for(int k = 0; k < kunits; k++)
     {
      float sc_g = 0;
      float sc = scores[shift_s + k];
      for(int v = 0; v < kunits; v++)
         sc_g += scores[shift_s + v] * out_g * kv[shift_val + v * dimension] * 
                                                        ((float)(k == v) - sc);
      grad += sc_g * kv[shift_key + k * dimension];
     }
   q_g[shift_q] = grad / koef;

Auf ähnliche Weise berechnen wir den Fehlergradienten für die Entität Schlüssel. Diesmal berechnen wir jedoch die Fehlergradienten der Abhängigkeitskoeffizienten entlang der entsprechenden Tensorsäule.

//--- Calculating Key's gradients
   for(int k = q_id; k < kunits; k += qunits)
     {
      int shift_score = h * kunits + k;
      int shift_val = (heads + h) * kunits * dimension + d;
      grad = 0;
      float val = kv[shift_v];
      for(int scr = 0; scr < qunits; scr++)
        {
         float sc_g = 0;
         int shift_sc = scr * kunits * heads;
         float sc = scores[shift_sc + k];
         for(int v = 0; v < kunits; v++)
            sc_g += scores[shift_sc + v] * gradient[shift_g + scr * dimension] * val * 
                                                                ((float)(k == v) - sc);
         grad += sc_g * q[shift_q + scr * dimension];
        }
      kv_g[shift_k + k * dimension] = grad / koef;
     }
  }

Nachdem wir den Algorithmus auf der OpenCL-Kontextseite erstellt haben, kehren wir zu unserer Klasse zurück, um den Prozess auf der Hauptprogrammseite zu organisieren. Schauen wir uns zunächst die Methode feedForward (Vorwärtsdurchgang) an. Ähnlich wie bei den entsprechenden Methoden für andere neuronale Schichten erhalten wir in den Parametern einen Zeiger auf die vorherige neuronale Schicht, die die Quelldaten liefert.

bool CNeuronMH2AttentionOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//---
   if(!Q_Embedding.FeedForward(NeuronOCL))
      return false;

Wir überprüfen jedoch nicht die Relevanz des empfangenen Zeigers. Stattdessen rufen wir die Feed-Forward-Methode der inneren Schicht Q_Embedding auf, um einen Tensor von Query-Entitäten zu erstellen, und übergeben den resultierenden Zeiger an diese. Im Körper der angegebenen Methode sind alle erforderlichen Steuerelemente bereits implementiert und müssen nicht erneut implementiert werden.

Als Nächstes werden wir die Entitäten Schlüssel und Wert erzeugen. Wie bereits erwähnt, verwenden wir für diese eine andere Dimension des ursprünglichen Datentensors. Daher transponieren wir zunächst die Quelldatenmatrix und rufen dann die Vorwärtsdurchgangs-Methode der entsprechenden inneren Schicht auf.

   if(!Transpose.FeedForward(NeuronOCL) || !KV_Embedding.FeedForward(NeuronOCL))
      return false;

Die Kernelaufrufe MH2AttentionOut werden in einer separaten Methode attentionOut implementiert.

   if(!attentionOut())
      return false;

Wir komprimieren den Tensor der Mehrkopf-Aufmerksamkeitsergebnisse auf die Größe der Originaldaten.

   if(!W0.FeedForward(GetPointer(MHAttentionOut)))
      return false;

Dann addieren wir die erhaltenen Werte zu den Originaldaten und normalisieren sie. Die Methode SumAndNormilize wird von der übergeordneten Klasse geerbt.

//---
   if(!SumAndNormilize(W0.getOutput(), NeuronOCL.getOutput(), AttentionOut.getOutput(), iWindow))
      return false;

Am Ende des Aufmerksamkeitsblocks leiten wir die Daten durch MLP.

   if(!FF[0].FeedForward(GetPointer(AttentionOut)))
      return false;
   if(!FF[1].FeedForward(GetPointer(FF[0])))
      return false;

Zusammenfassung und Normalisierung.

   if(!SumAndNormilize(FF[1].getOutput(), AttentionOut.getOutput(), Output, iWindow))
      return false;
//---
   return true;
  }

Um das Bild des Feedforward-Algorithmus zu vervollständigen, betrachten wir die AttentionOut-Methode. Die Methode erhält keine Parameter und funktioniert nur mit klasseninternen Objekten. Daher prüfen wir im Hauptteil der Methode nur die Relevanz des Zeigers auf den Kontext OpenCL.

bool CNeuronMH2AttentionOCL::attentionOut(void)
  {
   if(!OpenCL)
      return false;

Als Nächstes erstellen wir die Arrays für Aufgabenraum und Abstand. Wie bei der Erstellung des Kerns besprochen, erstellen wir einen 3-dimensionalen Problemraum mit einer lokalen Gruppe entlang der zweiten Dimension.

   uint global_work_offset[3] = {0};
   uint global_work_size[3] = {iUnits, iWindow, iHeads};
   uint local_work_size[3] = {1, iWindow, 1};

Wir übergeben die notwendigen Parameter an den Kernel.

   ResetLastError();
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionOut, def_k_mh2ao_q, 
                                                       Q_Embedding.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                            GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionOut, def_k_mh2ao_kv, 
                                                       KV_Embedding.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                             GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionOut, def_k_mh2ao_score, ScoreIndex))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                             GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionOut, def_k_mh2ao_out, 
                                                       MHAttentionOut.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                              GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_MH2AttentionOut, def_k_mh2ao_dimension, (int)iWindowKey))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                              GetLastError(), __LINE__);
      return false;
     }

Dann stellen wir den Kernel in die Ausführungswarteschlange.

   if(!OpenCL.Execute(def_k_MH2AttentionOut, 3, global_work_offset, global_work_size, 
                                                                    local_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

Wir haben den Prozess des Vorwärtsdurchgangs sowohl auf der Seite des Hauptprogramms als auch auf der Seite des Kontexts OpenCL implementiert. Als Nächstes müssen wir das Verfahren des Rückwärtsdurchgangs einrichten. Um den Algorithmus auf der Kontextseite OpenCL zu implementieren, haben wir bereits den Kernel MH2AttentionInsideGradients erstellt. Nun müssen wir die Methode AttentionInsideGradients erstellen, um diesen Kernel aufzurufen. In den Parametern der Methode wird nichts übergeben, ähnlich wie bei der entsprechenden Vorwärtsdurchgangs-Methode.

bool CNeuronMH2AttentionOCL::AttentionInsideGradients(void)
  {
   if(!OpenCL)
      return false;

Im Hauptteil der Methode prüfen wir die Relevanz des Zeigers auf den Kontext OpenCL. Danach erstellen wir Arrays, die die Dimension des Aufgabenraums und der Abstände (offset) darin angeben.

   uint global_work_offset[3] = {0};
   uint global_work_size[3] = {iUnits, iWindowKey, iHeads};

Übergeben wir die erforderlichen Parameter an den Kernel.

   ResetLastError();
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionInsideGradients, def_k_mh2aig_q, 
                                                            Q_Embedding.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), 
                                                                                 __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionInsideGradients, def_k_mh2aig_qg, 
                                                            Q_Embedding.getGradientIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), 
                                                                                 __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionInsideGradients, def_k_mh2aig_kv, 
                                                            KV_Embedding.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), 
                                                                                  __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionInsideGradients, def_k_mh2aig_kvg, 
                                                           KV_Embedding.getGradientIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), 
                                                                                  __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionInsideGradients, def_k_mh2aig_score, 
                                                                                ScoreIndex))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), 
                                                                                  __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionInsideGradients, def_k_mh2aig_outg,
                                                         MHAttentionOut.getGradientIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), 
                                                                                  __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_MH2AttentionInsideGradients, def_k_mh2aig_kunits, (int)iWindow))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), 
                                                                                  __LINE__);
      return false;
     }

Den Kernel stellen wir in die Ausführungswarteschlange.

   if(!OpenCL.Execute(def_k_MH2AttentionInsideGradients, 3, global_work_offset, 
                                                             global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

Im Allgemeinen ist dies ein Standardalgorithmus für solche Aufgaben. Und der gesamte Algorithmus zur Verteilung des Fehlergradienten innerhalb unserer Schicht wird durch die Methode calcInputGradients beschrieben. In den Parametern erhält die Methode einen Zeiger auf das Objekt der vorherigen Schicht, an das der Fehlergradient übergeben werden muss.

bool CNeuronMH2AttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!FF[1].calcInputGradients(GetPointer(FF[0])))
      return false;

Im Hauptteil der Methode wird der Fehlergradient abwechselnd von der Blockausgabe zur vorherigen Schicht propagiert. Wie Sie sich erinnern, haben wir bei der Initialisierung der Klasse den Zeiger durch den Fehlergradientenpuffer ersetzt. Und die nachfolgende Schicht schrieb den Fehlergradienten direkt in die letzte Schicht des inneren MLP. Von dort aus wird der Fehlergradient auf die Ausgangsebene des Aufmerksamkeitsblocks übertragen.

   if(!FF[0].calcInputGradients(GetPointer(AttentionOut)))
      return false;

Auf dieser Ebene haben wir die Ergebnisse des Aufmerksamkeitsblocks zu den ursprünglichen Daten hinzugefügt. In ähnlicher Weise erfassen wir einen Gradienten aus 2 Richtungen.

   if(!SumAndNormilize(FF[1].getGradient(), AttentionOut.getGradient(), W0.getGradient(), 
                                                                           iWindow, false))
      return false;

Als Nächstes propagieren wir den Fehlergradienten über die Aufmerksamkeits-Köpfe.

   if(!W0.calcInputGradients(GetPointer(MHAttentionOut)))
      return false;

Übertragen wir den Fehlergradienten auf die Entitäten.

   if(!AttentionInsideGradients())
      return false;

Wir übertragen den Fehlergradienten von Schlüssel und Wert auf die Transpositionsschicht. Im Vorwärtsdurchgang wurde die Quelldatenmatrix transponiert. Mit dem Fehlergradienten müssen wir den umgekehrten Vorgang durchführen.

   if(!KV_Embedding.calcInputGradients(GetPointer(Transpose)))
      return false;

Als Nächstes müssen wir den Fehlergradienten von allen Entitäten auf die vorherige Schicht übertragen.

   if(!Q_Embedding.calcInputGradients(prevLayer))
      return false;

Bitte beachten Sie hier, dass der Fehlergradient zur vorherigen Ebene von 4 Threads geht:

• Abfrage
• Schlüssel
• Wert
• Umgehung der Aufmerksamkeitsblock.

Unsere Methoden der inneren Schicht löschen jedoch bei der Übergabe des Fehlergradienten die zuvor aufgezeichneten Daten. Nachdem wir also den Fehlergradienten von der Abfrage erhalten haben, fügen wir ihn dem Fehlergradienten am Ausgang des Aufmerksamkeitsblocks im Puffer der inneren Schicht hinzu.

   if(!SumAndNormilize(prevLayer.getGradient(), W0.getGradient(), AttentionOut.getGradient(), 
                                                                              iWindow, false))
      return false;

Und nachdem wir die Daten von Schlüssel und Wert erhalten haben, addieren wir alle Threads.

   if(!Transpose.calcInputGradients(prevLayer))
      return false;
   if(!SumAndNormilize(prevLayer.getGradient(), AttentionOut.getGradient(), 
                                                      prevLayer.getGradient(), iWindow, false))
      return false;
//---
   return true;
  }

Die Methode zur Aktualisierung der Gewichte ist recht einfach. Wir rufen einfach die entsprechenden Methoden in den inneren Schichten auf.

bool CNeuronMH2AttentionOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!Q_Embedding.UpdateInputWeights(NeuronOCL))
      return false;
   if(!KV_Embedding.UpdateInputWeights(GetPointer(Transpose)))
      return false;
   if(!W0.UpdateInputWeights(GetPointer(MHAttentionOut)))
      return false;
   if(!FF[0].UpdateInputWeights(GetPointer(AttentionOut)))
      return false;
   if(!FF[1].UpdateInputWeights(GetPointer(FF[0])))
      return false;
//---
   return true;
  }

Damit sind unsere Überlegungen zu den Methoden für die Organisation des Kreuz-Beziehungs-Prozesses abgeschlossen. Den vollständigen Code der Klasse und alle ihre Methoden finden Sie im Anhang. Wir gehen nun dazu über, Expert Advisors für das Training und Testen der Modelle zu erstellen.

2.2 Modellarchitektur

Wie aus der theoretischen Beschreibung der Methode ADAPT hervorgeht, hat der vorgeschlagene Ansatz eine recht komplexe hierarchische Struktur. Für uns bedeutet das eine große Anzahl von trainierten Modellen. Wir werden die Beschreibung ihrer Architektur in 2 Methoden unterteilen. Zunächst werden wir 3 Modelle erstellen, die mit der Endpunktvorhersage in Zusammenhang stehen.

bool CreateTrajNetDescriptions(CArrayObj *encoder, CArrayObj *endpoints, CArrayObj *probability)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
   if(!endpoints)
     {
      endpoints = new CArrayObj();
      if(!endpoints)
         return false;
     }
   if(!probability)
     {
      probability = new CArrayObj();
      if(!probability)
         return false;
     }

Der Umweltzustandscodierer empfängt rohe Eingangsdaten, die einen Zustand beschreiben.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

 Wie immer normalisieren wir die empfangenen Daten.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = MathMax(1000, GPTBars);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Wir erzeugen auch eine Einbettung, die wir dem Puffer für die historische Sequenzakkumulation hinzufügen.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronEmbeddingOCL;
     {
      int temp[] = {prev_count};
      ArrayCopy(descr.windows, temp);
     }
   prev_count = descr.count = GPTBars;
   int prev_wout = descr.window_out = EmbeddingSize;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Dann führen wir die Positionskodierung ein.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronPEOCL;
   descr.count = prev_count;
   descr.window = prev_wout;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Es folgen die Blöcke der umfassenden Aufmerksamkeit. Um die Verwaltung der Modellarchitektur zu erleichtern, wird eine Schleife auf der Grundlage der Anzahl der Blockiterationen erstellt.

   for(int l = 0; l < Lenc; l++)
     {
      //--- layer 4
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronTransposeOCL;
      descr.count = prev_count;
      descr.window = prev_wout;
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }

Nach dem von den Autoren der ADAPT-Methode vorgeschlagenen Algorithmus überprüfen wir zunächst die Beziehungen zwischen den Polylinien (in unserem Fall den Zuständen) und den Agenten. Bevor wir unseren Block mit den Querverbindungen in dieser Richtung verwenden, müssen wir die resultierende Informationsmenge umsetzen. Dann fügen wir unsere neue Ebene hinzu.

      //--- layer 5
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronMH2AttentionOCL;
      descr.count = prev_wout;
      descr.window = prev_count;
      descr.step = 8;
      descr.window_out = 16;
      descr.optimization = ADAM;
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }

Dann kommt der Block für die Selbstaufmerksamkeit der Trajektorie.

      //--- layer 6
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronMLMHAttentionOCL;
      descr.count = prev_wout;
      descr.window = prev_count;
      descr.step = 8;
      descr.window_out = 16;
      descr.layers = 1;
      descr.optimization = ADAM;
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }

Als Nächstes werden wir die Beziehung auf einer anderen Ebene analysieren. Dazu transponieren wir die Daten und wiederholen die Aufmerksamkeitsblöcke.

      //--- layer 7
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronTransposeOCL;
      descr.count = prev_wout;
      descr.window = prev_count;
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }

      //--- layer 8
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronMH2AttentionOCL;
      descr.count = prev_count;
      descr.window = prev_wout;
      descr.step = 8;
      descr.window_out = 16;
      descr.layers = 1;
      descr.optimization = ADAM;
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }

      //--- layer 9
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronMLMHAttentionOCL;
      descr.count = prev_count;
      descr.window = prev_wout;
      descr.step = 8;
      descr.window_out = 16;
      descr.layers = 1;
      descr.optimization = ADAM;
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }
     }

Wie bereits erwähnt, haben wir den Encoder-Block in eine Schleife eingeschlossen. Die Anzahl der Schleifenwiederholungen wird in Konstanten angegeben.

#define        Lenc                    3             //Number ADAPT Encoder blocks

Durch die Änderung einer Konstante können wir also die Anzahl der Aufmerksamkeitsblöcke im Encoder schnell ändern.

Die Ergebnisse des Encoders werden verwendet, um mehrere Sätze von Endpunkten vorherzusagen. Die Anzahl solcher Sätze wird durch die Konstante NForecast bestimmt.

#define        NForecast               5             //Number of forecast

Wir werden ein einfaches MLP-Modell für die Endpunktvorhersage verwenden. In diesem Modell durchlaufen die vom Encoder empfangenen Daten vollständig verbundene Schichten.

//--- Endpoints
   endpoints.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = (prev_count * prev_wout);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!endpoints.Add(descr))
     {
      delete descr;
      return false;
     }

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!endpoints.Add(descr))
     {
      delete descr;
      return false;
     }

Der latente Zustand wird durch die SoftMax-Funktion normalisiert.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = LatentCount;
   descr.step = 1;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!endpoints.Add(descr))
     {
      delete descr;
      return false;
     }

Als Nächstes erzeugen wir Endpunkte in der vollständig verbundenen Schicht.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 3 * NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!endpoints.Add(descr))
     {
      delete descr;
      return false;
     }

Das Modell zur Vorhersage der Wahrscheinlichkeiten für die Wahl der Trajektorien verwendet ebenfalls die Ergebnisse des Encoders als Eingabedaten.

//--- Probability
   probability.Clear();
//--- Input layer
   if(!probability.Add(endpoints.At(0)))
      return false;

Darin werden sie jedoch unter Berücksichtigung der prognostizierten Endpunkte analysiert.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = 3 * NForecast;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }

Operationen mit probabilistischen Größen ermöglichen es uns, die SoftMax-Schicht am Ausgang des Modells zu verwenden.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = NForecast;
   descr.step = 1;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Nun kommen wir zu dem Punkt, an dem wir grundlegende Änderungen am Algorithmus der Methode ADAPT vorgenommen haben. Unsere Änderungen sind aufgrund der Besonderheiten der Finanzmärkte erforderlich. Meiner Meinung nach stehen sie jedoch keineswegs im Widerspruch zu den von den Autoren der Methode vorgeschlagenen Ansätzen.

Die Autoren haben einen eigenen Algorithmus für die Lösung von Problemen im Zusammenhang mit der Navigation autonomer Fahrzeuge vorgeschlagen. Hier ist die Qualität der Trajektorievorhersage von großer Bedeutung. Denn ein Zusammenstoß von 2 oder mehr Fahrzeugen auf einem beliebigen Teil der Trajektorie kann zu kritischen Folgen führen.

Im Falle des Finanzmarkthandels wird den Kontrollpunkten mehr Aufmerksamkeit geschenkt. Wir interessieren uns nicht so sehr für den Verlauf der Kursbewegung und ihre kleinen Schwankungen im Rahmen des allgemeinen Trends. Was uns wichtiger ist, sind die Extreme der maximal möglichen Gewinne und Drawdowns im Rahmen dieser Bewegung.

Daher haben wir den Block zur Vorhersage der Trajektorie ausgeschlossen und ihn durch ein Akteursmodell ersetzt, das die Parameter der Transaktion generiert. Gleichzeitig haben wir den allgemeinen Ansatz für das Training der Modelle beibehalten. Wir werden etwas später darauf zurückkommen.

Unser Akteur nutzt 4 Datenquellen, um eine Entscheidung zu treffen:

• Zustands-Einbettung
• Beschreibungen des Kontostatus
• Vorausgesagte Endpunkteinstellungen
• Wahrscheinlichkeiten für jeden vorhergesagten Satz von Endpunkten

Zuvor haben wir einen Mechanismus entwickelt, der nur 2 Informationsströme kombiniert. Um 4 Ströme zu kombinieren, werden wir eine Kaskade von Modellen erstellen.

bool CreateDescriptions(CArrayObj *actor, CArrayObj *end_encoder, CArrayObj *state_encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!end_encoder)
     {
      end_encoder = new CArrayObj();
      if(!end_encoder)
         return false;
     }
   if(!state_encoder)
     {
      state_encoder = new CArrayObj();
      if(!state_encoder)
         return false;
     }

Wir kombinieren Sätze von vorhergesagten Endpunkten und deren Wahrscheinlichkeiten zu einer Endpunkteinbettung.

//--- Endpoints Encoder
   end_encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = 3 * NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!end_encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = NForecast;
   descr.optimization = ADAM;
   descr.activation = LReLU;
   if(!end_encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Wir kombinieren die Einbettung des Umweltzustands mit den Parametern Gleichgewicht und offene Positionen.

//--- State Encoder
   state_encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = GPTBars * EmbeddingSize;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!state_encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = AccountDescr;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!state_encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Wir übergeben die Ergebnisse der Arbeit der 2 spezifizierten Modelle an den Akteur zur Entscheidungsfindung.

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = LatentCount;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = LatentCount;
   descr.optimization = ADAM;
   descr.activation = LReLU;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Innerhalb des Akteurs verwenden wir vollständig verbundene Schichten.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Wir erzeugen sein stochastisches Verhalten.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 2 * NActions;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronVAEOCL;
   descr.count = NActions;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Wie Sie sehen können, planen wir, möglichst einfache Modellarchitekturen zu verwenden. Dies ist einer der Vorteile der Methode ADAPT.

In diesem Artikel verzichte ich auf eine detaillierte Beschreibung der Expert Advisors für die Interaktion mit der Umwelt. Die Struktur der gesammelten Daten und die Methoden der Interaktion mit der Umwelt haben sich nicht geändert. Natürlich hat sich die Reihenfolge des Aufrufs von Modellen zur Entscheidungsfindung geändert. Ich schlage vor, dass Sie den Code studieren, um die Reihenfolge zu erkennen. Der vollständige Code des EAs befindet sich im Anhang. Aber der EA für das Modelltraining hat mehrere einzigartige Aspekte.

2.3 Modelltraining

Im Gegensatz zu den letzten Artikeln werden wir dieses Mal alle Modelle in einem EA „...\Experts\ADAPT\Study.mq5“ trainieren. Das liegt daran, dass wir den Fehlergradienten von fast allen Modellen auf den Environmental Encoder übertragen müssen.

Die EA-Initialisierungsmethode ist nach einem Standardschema aufgebaut. Zuerst laden wir den Trainingsdatensatz.

int OnInit()
  {
//---
   ResetLastError();
   if(!LoadTotalBase())
     {
      PrintFormat("Error of load study data: %d", GetLastError());
      return INIT_FAILED;
     }

Anschließend werden in zwei Schritten die zuvor erstellten Modelle geladen und gegebenenfalls neue Modelle erstellt.

//--- load models
   float temp;
   if(!ADAPTEncoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) ||
      !ADAPTEndpoints.Load(FileName + "Endp.nnw", temp, temp, temp, dtStudied, true) ||
      !ADAPTProbability.Load(FileName + "Prob.nnw", temp, temp, temp, dtStudied, true)
     )
     {
      CArrayObj *encoder = new CArrayObj();
      CArrayObj *endpoint = new CArrayObj();
      CArrayObj *prob = new CArrayObj();
      if(!CreateTrajNetDescriptions(encoder, endpoint, prob))
        {
         delete endpoint;
         delete prob;
         delete encoder;
         return INIT_FAILED;
        }
      if(!ADAPTEncoder.Create(encoder) ||
         !ADAPTEndpoints.Create(endpoint) ||
         !ADAPTProbability.Create(prob))
        {
         delete endpoint;
         delete prob;
         delete encoder;
         return INIT_FAILED;
        }
      delete endpoint;
      delete prob;
      delete encoder;
     }

   if(!StateEncoder.Load(FileName + "StEnc.nnw", temp, temp, temp, dtStudied, true) ||
      !EndpointEncoder.Load(FileName + "EndEnc.nnw", temp, temp, temp, dtStudied, true) ||
      !Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true))
     {
      CArrayObj *actor = new CArrayObj();
      CArrayObj *endpoint = new CArrayObj();
      CArrayObj *encoder = new CArrayObj();
      if(!CreateDescriptions(actor, endpoint, encoder))
        {
         delete actor;
         delete endpoint;
         delete encoder;
         return INIT_FAILED;
        }
      if(!Actor.Create(actor) || 
         !StateEncoder.Create(encoder) || 
         !EndpointEncoder.Create(endpoint))
        {
         delete actor;
         delete endpoint;
         delete encoder;
         return INIT_FAILED;
        }
      delete actor;
      delete endpoint;
      delete encoder;
      //---
     }

Wir übertragen alle Modelle in einen einzigen OpenCL-Kontext.

   OpenCL = Actor.GetOpenCL();
   StateEncoder.SetOpenCL(OpenCL);
   EndpointEncoder.SetOpenCL(OpenCL);
   ADAPTEncoder.SetOpenCL(OpenCL);
   ADAPTEndpoints.SetOpenCL(OpenCL);
   ADAPTProbability.SetOpenCL(OpenCL);

Kontrolle der Modellarchitektur.

   Actor.getResults(Result);
   if(Result.Total() != NActions)
     {
      PrintFormat("The scope of the actor does not match the actions count (%d <> %d)", 
                                                                NActions, Result.Total());
      return INIT_FAILED;
     }
//---
   ADAPTEndpoints.getResults(Result);
   if(Result.Total() != 3 * NForecast)
     {
      PrintFormat("The scope of the Endpoints does not match forecast endpoints (%d <> %d)", 
                                                            3 * NForecast, Result.Total());
      return INIT_FAILED;
     }
//---
   ADAPTEncoder.GetLayerOutput(0, Result);
   if(Result.Total() != (HistoryBars * BarDescr))
     {
      PrintFormat("Input size of Encoder doesn't match state description (%d <> %d)", 
                                                Result.Total(), (HistoryBars * BarDescr));
      return INIT_FAILED;
     }

Wir erstellen einen Hilfspuffer

   if(!bGradient.BufferInit(MathMax(AccountDescr, NForecast), 0) ||
      !bGradient.BufferCreate(OpenCL))
     {
      PrintFormat("Error of create buffers: %d", GetLastError());
      return INIT_FAILED;
     }

und erzeugen ein nutzerdefiniertes Ereignis für den Start des Modelltrainings.

   if(!EventChartCustom(ChartID(), 1, 0, 0, "Init"))
     {
      PrintFormat("Error of create study event: %d", GetLastError());
      return INIT_FAILED;
     }
//---
   return(INIT_SUCCEEDED);
  }

Der Ausbildungsprozess selbst ist nach der Methode Train organisiert.

void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);

Im Hauptteil der Methode erstellen wir zunächst einen Vektor von Wahrscheinlichkeiten für die Auswahl von Trajektorien aus dem Erfahrungswiedergabepuffer. Dann erstellen wir die erforderlichen lokalen Variablen.

   vector<float> result, target;
   matrix<float> targets, temp_m;
   bool Stop = false;
//---
   uint ticks = GetTickCount();

Das Training wird, wie üblich, in einem System von verschachtelten Schleifen durchgeführt. Im Hauptteil der äußeren Schleife werden die Trajektorie und das Paket der Lernzustände auf ihr abgetastet.

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++)
     {
      int tr = SampleTrajectory(probability);
      int batch = GPTBars + 48;
      int state = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * 
                             (Buffer[tr].Total - 2 - PrecoderBars - batch));
      if(state <= 0)
        {
         iter--;
         continue;
        }
      ADAPTEncoder.Clear();
      int end = MathMin(state + batch, Buffer[tr].Total - PrecoderBars);

Der Prozess des Trainings von Modellen auf einer Sequenz von historischen Daten wird in der verschachtelten Schleife aufgebaut.

      for(int i = state; i < end; i++)
        {
         bState.AssignArray(Buffer[tr].States[i].state);

Wir nehmen einen Umweltzustand und geben ihn an den Encoder weiter.

         //--- Trajectory
         if(!ADAPTEncoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, 
                                                              (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Dann erstellen wir Sätze von vorhergesagten Endpunkten und deren Wahrscheinlichkeiten.

         if(!ADAPTEndpoints.feedForward((CNet*)GetPointer(ADAPTEncoder), -1, 
                                                             (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

         if(!ADAPTProbability.feedForward((CNet*)GetPointer(ADAPTEncoder), -1, 
                                               (CNet*)GetPointer(ADAPTEndpoints)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Um das Endpunkttraining zu organisieren, müssen wir als Nächstes Zielwerte generieren. Die nachfolgenden Zustände entnehmen wir dem Erfahrungswiedergabepuffer bis zu einer bestimmten Planungstiefe.

         targets = matrix<float>::Zeros(PrecoderBars, 3);
         for(int t = 0; t < PrecoderBars; t++)
           {
            target.Assign(Buffer[tr].States[i + 1 + t].state);
            if(target.Size() > BarDescr)
              {
               matrix<float> temp(1, target.Size());
               temp.Row(target, 0);
               temp.Reshape(target.Size() / BarDescr, BarDescr);
               temp.Resize(temp.Rows(), 3);
               target = temp.Row(temp.Rows() - 1);
              }
            targets.Row(target, t);
           }

Aber wir verwenden in ihnen nicht den letzten Zustand, wie man aufgrund der Definition der Endpunkte annehmen könnte. Stattdessen suchen wir nach den nächstgelegenen Extrema. Zunächst berechnen wir die kumulierte Summe der Abweichung des Schlusskurses jeder Kerze vom analysierten Zustand. Und zu den erhaltenen Werten addieren wir die Intervalle bis zum Hoch und Tief eines jeden Balkens. Wir speichern die Berechnungsergebnisse in einer Matrix.

         target = targets.Col(0).CumSum();
         targets.Col(target, 0);
         targets.Col(target + targets.Col(1), 1);
         targets.Col(target + targets.Col(2), 2);

In der sich ergebenden Matrix finden wir das nächstgelegene Extremum.

         int extr = 1;
         if(target[0] == 0)
            target[0] = target[1];
         int direct = (target[0] > 0 ? 1 : -1);
         for(int i = 1; i < PrecoderBars; i++)
           {
            if((target[i]*direct) < 0)
               break;
            extr++;
           }

Wir bilden einen Vektor aus den gefundenen nächstgelegenen Extrema.

         targets.Resize(extr, 3);
         if(direct >= 0)
           {
            target = targets.Max(AXIS_HORZ);
            target[2] = targets.Col(2).Min();
           }
         else
           {
            target = targets.Min(AXIS_HORZ);
            target[1] = targets.Col(1).Max();
           }

Aus der Menge der vorhergesagten Endpunkte ermitteln wir den Vektor mit der geringsten Abweichung und ersetzen ihn durch Zielwerte.

         ADAPTEndpoints.getResults(result);
         targets.Reshape(1, result.Size());
         targets.Row(result, 0);
         targets.Reshape(NForecast, 3);
         temp_m = targets;
         for(int i = 0; i < 3; i++)
            temp_m.Col(temp_m.Col(i) - target[i], i);
         temp_m = MathPow(temp_m, 2.0f);
         ulong pos = temp_m.Sum(AXIS_VERT).ArgMin();
         targets.Row(target, pos);

Wir verwenden die resultierende Matrix, um ein Modell zur Vorhersage von Zielpunkten zu trainieren.

         Result.AssignArray(targets);
         //---
         if(!ADAPTEndpoints.backProp(Result, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Wir übertragen den Fehlergradienten auf das Encoder-Modell und aktualisieren seine Parameter.

         if(!ADAPTEncoder.backPropGradient((CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Hier trainieren wir auch ein Modell für die Vorhersage von Trajektionswahrscheinlichkeiten. Die Fehlergradienten werden jedoch nicht auf andere Modelle übertragen.

         bProbs.AssignArray(vector<float>::Zeros(NForecast));
         bProbs.Update((int)pos, 1);
         bProbs.BufferWrite();
         if(!ADAPTProbability.backProp(GetPointer(bProbs), GetPointer(ADAPTEndpoints)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Nach der Aktualisierung der Parameter der Endpunktvorhersagemodelle gehen wir zum Training der Politik unseres Akteurs über. Um die Vorwärtsdurchgangs-Operationen unseres Akteurs auszuführen, benötigen wir in diesem Stadium nur einen Tensor, der den Zustand des Kontos und der offenen Positionen beschreibt. Bilden wir diesen Tensor.

         //--- Policy
         float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
         float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
         bAccount.Clear();
         bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance);
         bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance);
         bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity);
         bAccount.Add(Buffer[tr].States[i].account[2]);
         bAccount.Add(Buffer[tr].States[i].account[3]);
         bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance);
         bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance);
         bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance);
         double time = (double)Buffer[tr].States[i].account[7];
         double x = time / (double)(D'2024.01.01' - D'2023.01.01');
         bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_MN1);
         bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_W1);
         bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_D1);
         bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         if(bAccount.GetIndex() >= 0)
            bAccount.BufferWrite();

Als Nächstes rufen wir nacheinander die Vorwärtsdurchgangs-Methoden unserer Kaskade von Akteursmodellen auf.

         //--- State embedding
         if(!StateEncoder.feedForward((CNet *)GetPointer(ADAPTEncoder), -1, 
                                      (CBufferFloat*)GetPointer(bAccount)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

An dieser Stelle sei angemerkt, dass wir anstelle von Vorhersagewerten von Endpunktsätzen und deren Wahrscheinlichkeiten Tensoren von Zielwerten verwenden, die wir oben zum Trainieren der entsprechenden Modelle genutzt haben.

         //--- Endpoint embedding
         if(!EndpointEncoder.feedForward(Result, -1, false, (CBufferFloat*)GetPointer(bProbs)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

         //--- Actor
         if(!Actor.feedForward((CNet *)GetPointer(StateEncoder), -1, 
                                                          (CNet*)GetPointer(EndpointEncoder)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Nach dem Feed-Forward-Durchgang müssen wir die Modellparameter aktualisieren. Hierfür benötigen wir Zielwerte. Nach der Methode ADAPT sollte ein Modell zur Vorhersage von Trajektorien anhand von realen Daten aus dem Erfahrungswiedergabepuffer trainiert werden. Wir könnten, wie bisher, Agentenaktionen aus dem Erfahrungswiederholungspuffer übernehmen. Aber in diesem Fall haben wir keinen Mechanismus, um solche Maßnahmen zu bewerten und nach Prioritäten zu ordnen.

In dieser Situation habe ich beschlossen, einen anderen Ansatz zu wählen. Da wir bereits Zielendwerte haben, die auf realen Daten der nachfolgenden Kursbewegungen aus dem Trainingsdatensatz basieren, warum verwenden wir sie nicht, um den „optimalen“ Handel unter den analysierten Bedingungen zu generieren. Wir bestimmen die Richtung und die Handelsstufen des „optimalen“ Handels. Wir nehmen das Positionsvolumen unter Berücksichtigung des Risikos von 1% des Eigenkapitals pro Handel.

         result = vector<float>::Zeros(NActions);
         double value = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_VALUE_LOSS);
         double risk = AccountInfoDouble(ACCOUNT_EQUITY) * 0.01;
         if(direct > 0)
           {
            float tp = float(target[1] / _Point / MaxTP);
            result[1] = tp;
            int sl = int(MathMax(MathMax(target[1] / 3, -target[2]) / _Point, MaxSL/10));
            result[2] = float(sl) / MaxSL;
            result[0] = float(MathMax(risk / (value * sl), 0.01))+FLT_EPSILON;
           }
         else
           {
            float tp = float((-target[2]) / _Point / MaxTP);
            result[4] = tp;
            int sl = int(MathMax(MathMax((-target[2]) / 3, target[1]) / _Point, MaxSL/10));
            result[5] = float(sl) / MaxSL;
            result[3] = float(MathMax(risk / (value * sl), 0.01))+FLT_EPSILON;
           }

Bei der Berechnung des Positionsvolumens verwenden wir das Kapital, da das Konto zum Zeitpunkt des Handels bereits offene Positionen haben kann, deren Gewinn (Verlust) im Kontosaldo nicht berücksichtigt wird.

Die so erzeugte „optimale“ Position wird zum Trainieren von Akteurs-Modellen verwendet.

         Result.AssignArray(result);
         if(!Actor.backProp(Result, (CNet *)GetPointer(EndpointEncoder)) ||
            !StateEncoder.backPropGradient(GetPointer(bAccount), 
                                  (CBufferFloat *)GetPointer(bGradient)) ||
            !EndpointEncoder.backPropGradient(GetPointer(bProbs), 
                                  (CBufferFloat *)GetPointer(bGradient))
           )
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Wir verwenden den Fehlergradienten aus dem Training des Akteurs-Modells, um die Encoder-Parameter zu aktualisieren.

         if(!ADAPTEncoder.backPropGradient((CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Bitte beachten Sie, dass wir die Parameter des Endpunktvorhersagemodells in diesem Stadium nicht aktualisieren. Diese Einschränkung wurde von den Autoren der Methode ADAPT eingeführt, um die Stabilität des Modelltrainings zu erhöhen.

Nach der Aktualisierung der Parameter aller Modelle müssen wir den Nutzer nur noch über den Fortschritt des Trainingsprozesses informieren und mit der nächsten Iteration des Schleifensystems fortfahren.

         //---
         if(GetTickCount() - ticks > 500)
           {
            double percent = (double(i - state) / ((end - state)) + iter) * 100.0 / (Iterations);
            string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent, 
                                                                  Actor.getRecentAverageError());
            str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Endpoints", percent, 
                                                         ADAPTEndpoints.getRecentAverageError());
            str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Probability", percent, 
                                                       ADAPTProbability.getRecentAverageError());
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }

Am Ende der Methode wird das Kommentarfeld im Chart gelöscht. Die Ergebnisse des Modelltrainings werden in das Journal ausgedruckt. Dann leiten wir die Beendigung des EA ein.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, 
                                                       "Actor", Actor.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, 
                                          "Endpoints", ADAPTEndpoints.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, 
                                      "Probability", ADAPTProbability.getRecentAverageError());
   ExpertRemove();
//---
  }

Damit ist die Beschreibung der MQL5-Implementierung unserer Vision des Algorithmus abgeschlossen. Den vollständigen Code aller im Artikel verwendeten Programme finden Sie im Anhang.

3. Tests

Wir haben viel Arbeit in die Implementierung der Methode ADAPT mit MQL5 gesteckt. Unsere Implementierung ist weit von dem ursprünglichen Algorithmus entfernt. Dennoch ist es im Sinne der vorgeschlagenen Ansätze und nutzt die ursprüngliche Idee im Zusammenhang mit der umfassenden Analyse der Beziehungen zwischen den Objekten der analysierten Umgebung. Nun ist es an der Zeit, die Ergebnisse unserer Arbeit an echten historischen Daten im Strategietester zu testen.

Die Modelle wurden anhand historischer Daten von EURUSD, H1, für die ersten 7 Monate des Jahres 2023 trainiert. Alle Indikatoren werden mit Standardparametern verwendet.

Die trainierten Modelle wurden in voller Übereinstimmung mit den Trainingsparametern getestet. Wir haben nur das Zeitintervall der historischen Daten geändert. In diesem Stadium haben wir historische Daten vom August 2023 verwendet.

Da sich die Struktur der im Rahmen der Interaktion mit der Umwelt gesammelten Daten nicht geändert hat, habe ich in meinem Experiment keine neuen Trainingsdaten gesammelt. Um die Modelle zu trainieren, verwende ich die Pässe, die beim Training früherer Modelle gesammelt wurden. Darüber hinaus können wir mit dem vorgeschlagenen Ansatz zur Berechnung des „optimalen Handels“ die Berechnung zusätzlicher Durchgänge vermeiden, die den Trainingsdatenraum verfeinern und ergänzen.

Hier könnte man meinen, dass ein Durchgang ausreicht, um das Modell zu trainieren. Während des Trainingsprozesses müssen wir dem Modell jedoch so viele unterschiedliche Informationen wie möglich zur Verfügung stellen, einschließlich Informationen über den Zustand des Kontos und der offenen Positionen.

Auf der Grundlage der Testergebnisse können wir eine Schlussfolgerung über die Wirksamkeit der betrachteten Methode ziehen. Die Einfachheit der Modelle ermöglicht ein schnelleres Training der Modelle. Die Effektivität der vorgeschlagenen Ansätze wird durch die Ergebnisse des trainierten Modells bestätigt, das sowohl in den Trainings- als auch in den Testdatensätzen Gewinne erzielen konnte.

Schlussfolgerung

Die in diesem Artikel vorgestellte Methode ADAPT ist ein innovativer Ansatz zur Vorhersage von Agententrajektorien in verschiedenen komplexen Szenarien. Dieser Ansatz ist effizient, erfordert nur geringe Rechenressourcen und liefert qualitativ hochwertige Vorhersagen für jeden Agenten in der Umgebung.

Zu den Verbesserungen der Methode ADAPT gehören ein adaptiver Kopf, der die Kapazität des Modells erhöht, ohne seine Größe zu vergrößern, und die Verwendung des dynamischen Lernens von Gewichten, um sich besser an die individuellen Situationen der einzelnen Agenten anzupassen. Diese Innovationen tragen wesentlich zu einer effektiven Trajektorievorhersage bei.

Im praktischen Teil des Artikels haben wir unsere Vision der vorgeschlagenen Ansätze mit MQL5 umgesetzt. Wir haben die Modelle anhand echter historischer Daten trainiert und getestet. Auf der Grundlage der erzielten Ergebnisse können wir eine Schlussfolgerung über die Wirksamkeit der Methode ADAPT und die Möglichkeit der Verwendung ihrer Varianten zur Erstellung eines Modells und dessen Einsatz auf den Finanzmärkten ziehen.

Ich möchte Sie jedoch daran erinnern, dass die in diesem Artikel vorgestellten Programme nur zur Demonstration der Technologie dienen und nicht für den realen Finanzhandel geeignet sind.

Referenzen

ADAPT: Efficient Multi-Agent Trajectory Prediction with Adaptation

Andere Artikel dieser Serie

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	Expert Advisor	Beispielsammlung EA
2	ResearchRealORL.mq5	Expert Advisor	EA zum Sammeln von Beispielen mit der Real-ORL-Methode
3	Study.mq5	Expert Advisor	Modelltraining EA
4	Test.mq5	Expert Advisor	Modelltraining EA
5	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
6	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
7	NeuroNet.cl	Code Base	Die Bibliothek des Programmcodes von OpenCL