Elemente der Korrelationsanalyse in MQL5: Chi-Quadrat-Test nach Pearson auf Unabhängigkeit und Korrelationsverhältnis

Einführung

In diesem Artikel möchte ich einen so wichtigen Bereich der mathematischen Statistik wie die Korrelationsanalyse, einschließlich der Ermittlung und Bewertung von Abhängigkeiten zwischen Zufallsvariablen, behandeln. Das beliebteste Instrument im Arsenal der Korrelationsanalyse ist natürlich das Korrelationsverhältnis. Die Berechnung des Korrelationsverhältnisses allein ist jedoch völlig unzureichend, wenn es darum geht, Abhängigkeiten in Daten zu bewerten, insbesondere bei Aktienkurssteigerungen. Erstens bewertet das Verhältnis nur die lineare Abhängigkeit. Zweitens bedeuten Nullwerte des Korrelationsverhältnisses nicht, dass keine Abhängigkeit besteht, wenn die Datenstichprobe, aus der es berechnet wird, eine andere Verteilung als die Normalverteilung aufweist. Um die Frage zu beantworten, ob die Daten abhängig sind, sollten wir die Unabhängigkeitskriterien definieren. Wir werden über das berühmteste Kriterium sprechen – den Chi-Quadrat-Test von Pearson für die Unabhängigkeit. Wir werden auch über ein numerisches Merkmal wie das Korrelationsverhältnis sprechen, mit dessen Hilfe festgestellt werden kann, ob die untersuchte Abhängigkeit nichtlinear ist.

Unabhängigkeitshypothese

Es wird angenommen, dass die Daten Beobachtungen einer zweidimensionalen Zufallsvariablen (X, Y) mit einer unbekannten Verteilungsfunktion F(X, Y) darstellen, für die die Unabhängigkeitshypothese H0 getestet werden soll: F(X, Y) = F(X)*F(Y), wobei F(X) und F(Y) eindimensionale Verteilungsfunktionen sind.

Unter den Zufallsvariablen X und Y verstehe ich in diesem Artikel entweder Inkremente der logarithmierten Preise verschiedener Finanzinstrumente oder Inkremente der Preise eines Instruments mit der Verzögerung von eins.

Chi-Quadrat-Test nach Pearson auf Unabhängigkeit

Das Chi-Quadrat-Unabhängigkeitskriterium wird sowohl für diskrete Zufallsvariablen mit einer endlichen Anzahl von Ergebnissen als auch für kontinuierliche Zufallsvariablen verwendet, allerdings mit der obligatorischen Bedingung ihrer vorläufigen Gruppierung. In diesem Fall wird die Menge aller möglichen Werte der Zufallsvariablen X in i disjunkte Intervalle A1, A2, Ai und die Menge aller Werte von Y in eine Menge von j disjunkte Intervallen B1, B2, Bj unterteilt. So wird die Menge der Werte einer zweidimensionalen Größe (X, Y) in i*j Rechtecke (Zellen) unterteilt. Der Übersichtlichkeit halber werden diese Daten in Form einer sogenannten Merkmalskontingenztabelle (Korrelationstabelle, Wahrscheinlichkeitsverteilungstabelle einer zweidimensionalen Zufallsvariablen usw.) dargestellt.

                              

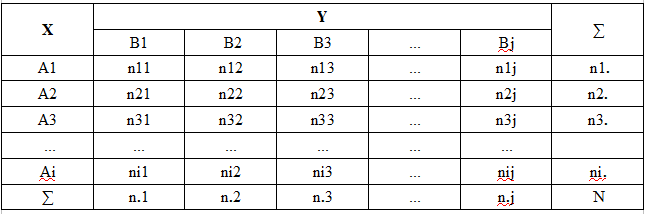
In der Tabelle:

• Ai = (Xi-1, Xi) – das i-te Intervall einer zufälligen Gruppierung von X-Werten

• Bj = (Yj-1,Yj) – das i-te Intervall einer zufälligen Gruppierung von Y-Werten

• nij – tatsächliche Häufigkeit der Zellengruppen (Anzahl der Beobachtungspaare (X, Y), deren Werte in das Intervall Ai und Bj fallen)

• ni. – Anzahl der Beobachtungen in der i-ten Zeile

• n.j – Anzahl der Beobachtungen in der j-ten Spalte

• N – Volumen der Probe

Die folgende Statistik wird als Chi-Quadrat-Test der Unabhängigkeit verwendet:

CHI2 = (Actual – Expected) ^2 / Expected,

wobei

• Actual – tatsächliche Gruppenhäufigkeit der Zelle nij,

• Expected – erwartete Gruppenhäufigkeit der Zelle nij.

Diese Statistiken sind Chi-Quadrat-verteilt mit v = (j-1)(i-1) Freiheitsgraden.

Die Nullhypothese der Unabhängigkeit wird abgelehnt, wenn die geschätzte CHI2-Statistik die kritischen Werte der Chi-Quadrat-Verteilung mit v Freiheitsgraden bei einem bestimmten Signifikanzniveau „alpha“ überschreitet.

Wir werden die tatsächlichen Häufigkeiten auf der Grundlage der Stichprobendaten berechnen. Das Prinzip für die Konstruktion der erwarteten Häufigkeiten lautet wie folgt: Wenn die Zufallsvariablen X und Y unabhängig sind, gilt die folgende Gleichung:

P {Ai, Bj} = P {Ai}*P{Bj},

Mit anderen Worten: Die Wahrscheinlichkeit des gleichzeitigen Auftretens der Ereignisse Ai und Bj ist gleich dem Produkt aus der Wahrscheinlichkeit des Auftretens des Ereignisses Ai und der Wahrscheinlichkeit des Auftretens des Ereignisses Bj.

Um die mathematischen Erwartungen der Ereignisse {Ai, Bj}, {Ai} und {Bj} zu ermitteln, multipliziert man beide Teile dieser Gleichung mit N*N, d. h. mit dem Quadrat der Anzahl der Beobachtungen.

N*N * P {Ai, Bj} = N *P{Ai} * N* P{Bj}

Dann bekommen wir:

• N *P{Ai} - die mathematische Erwartung der Anzahl der Beobachtungen in der i-ten Zeile

• N* P{Bj} – die mathematische Erwartung der Anzahl der Beobachtungen in der j-ten Spalte

• N * P {Ai, Bj} = (N *P{Ai} * N* P{Bj})/N – die mathematische Erwartung der Anzahl der Zellentreffer im Schnittpunkt der i-ten Zeile und j-ten Spalte

Wenn man dann die Schätzungen ni und n.j anstelle der mathematischen Erwartungen N *P{Ai} und N* P{Bj} (die tatsächlichen Häufigkeiten aus der Korrelationstabelle) einsetzt, erhält man die gewünschte Schätzung der erwarteten Häufigkeiten

Erwartet = (ni. * n.j)/N

Gemäß der Unabhängigkeitshypothese ist die erwartete Häufigkeit, eine Zelle im Schnittpunkt der i-ten Zeile und der j-ten Spalte zu treffen, gleich dem Produkt der Summen der Anzahl der Beobachtungen in der i-ten Zeile und der j-ten Spalte geteilt durch den Stichprobenumfang.

Bei der Berechnung des Kriteriums ist es daher naheliegend, dass die Wahrscheinlichkeit, dass die Daten nicht unabhängig sind, umso größer ist, je stärker die tatsächlichen Häufigkeiten von den erwarteten abweichen.

Chi2Test-Indikator

Die Berechnung des Chi-Quadrat-Unabhängigkeitstests nach Pearson ist im Indikator Chi2Test implementiert. Der Indikator testet die Unabhängigkeitshypothese auf jedem Balken zwischen benachbarten Kursinkrementen für ein einzelnes Finanzinstrument.

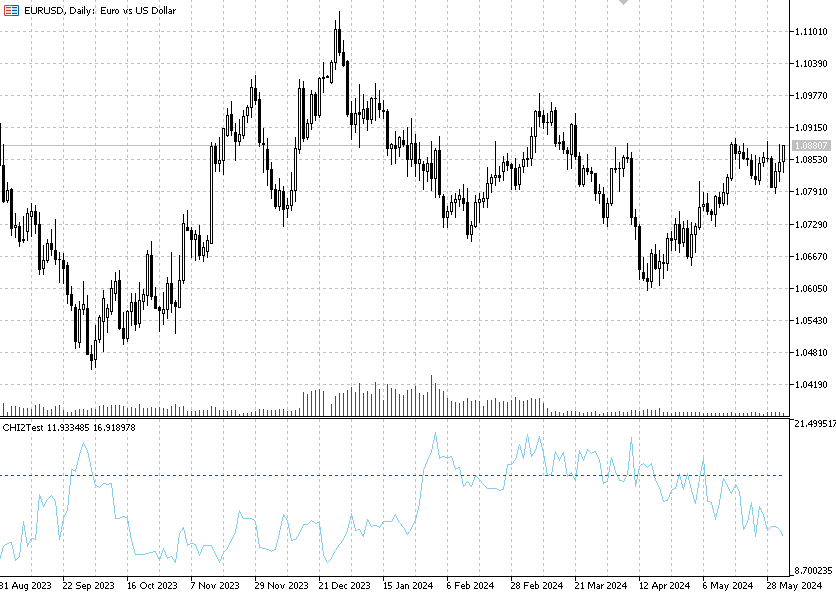
Der Indikator hat vier Eingänge:

• alpha – Signifikanzniveau

• Data – Datenfenster für die Berechnung

• Tails – Anzahl der Standardabweichungen

• Kontingenzkoeffizient

Um die Chi-Quadrat-Statistik zu berechnen, müssen wir zunächst die tatsächlichen Häufigkeiten in der Kontingenztabelle der Merkmale berechnen. Dies geschieht mit Hilfe der Kreuztabellenfunktion.

//+------------------------------------------------------------------+
//|  Calculate the table of contingency of two random values (X,Y)   |
//+------------------------------------------------------------------+
bool Crosstab(const double &dataX[],const double &dataY[],const double &bins[],matrix &freq)
  {

   int datasizeX=ArraySize(dataX);
   int datasizeY=ArraySize(dataY);
   int binssize=ArraySize(bins);
   if(datasizeX==0 || datasizeY==0 || binssize==0)
      return(false);
   if(datasizeX != datasizeY)
      return(false);

   for(int i=0; i<datasizeX; i++)
     {
      if(!MathIsValidNumber(dataX[i]) || !MathIsValidNumber(dataY[i]))
         return(false);
     }

   matrix m_freq=matrix::Zeros(binssize, binssize);
   
   for(int x=0; x<binssize; x++)
     {
      for(int i=0; i<datasizeX; i++)
        {
         for(int y=0; y<binssize; y++)
           {
            if(dataX[i]<=bins[x] && dataY[i]<=bins[y]) 
              {
               m_freq[x,y]=m_freq[x,y]+1;
               break;
              }
           }
        }
     }
     
   matrix Actual = m_freq;
   vector p1,p2,diffp;
   for (int j=1; j<binssize; j++)
   {
   p1 = m_freq.Row(j-1);
   p2 = m_freq.Row(j);
   diffp = p2-p1;
   Actual.Row(diffp,j);   
   }
   freq = Actual; 
   
   return(true);
  }

Da die Daten, mit denen wir arbeiten, kontinuierlich sind, müssen wir sie zunächst gruppieren. In diesem Fall können wir Empfehlungen finden, die besagen, dass es für eine korrekte Berechnung des Tests wünschenswert ist, dass der Mindestwert der erwarteten Häufigkeit in den Zellen nicht kleiner als eins ist, während die Anzahl der Zellen, in denen die erwartete Häufigkeit kleiner als fünf ist, nicht groß sein sollte (zum Beispiel sind zwei solcher Zellen erlaubt, wenn die Gesamtzahl der Zellen kleiner als 10 ist). Da die Verteilungen der Bestandsdaten starke „Tails“ bzw. seitliche Enden aufweisen, ergibt sich eine gewisse Schwierigkeit bei der Konstruktion von Gruppierungsintervallen, die die oben genannten Anforderungen erfüllen.

Ich schlage vor, die Daten nach der Standardisierung zu gruppieren. Danach werden die starken seitlichen Enden der Verteilung auf 2-3-4 Sigma gekürzt, je nach der Menge der zu analysierenden Daten. Im Indikator wird dies durch den Parameter „Tails“ erreicht. Wenn die Datenmenge beispielsweise klein ist (200-300 Werte), sollte der Wert von „Tails“ gleich 2 Sigma gewählt werden. Daraus ergeben sich folgende Gruppierungsintervalle: (-2,-1), (-1,0), (0,1), (1,2) und folglich eine Kontingenztabelle mit 4x4 Merkmalen. Daher werden wir benachbarte Gruppierungsintervalle mit kleinen erwarteten Häufigkeiten kombinieren, um die Chi-Quadrat-Statistik korrekt zu berechnen.

Cramerscher Kontingenzkoeffizient

Leider kann die CHI2-Statistik nicht als numerisches Maß für die Wahrscheinlichkeitsabhängigkeit herangezogen werden, sodass zu diesem Zweck der Kontingenzkoeffizient von Cramer verwendet wird. Seine Werte variieren zwischen null und eins. Null bedeutet keine Abhängigkeit zwischen Daten, eins bedeutet funktionale Abhängigkeit.

Der Kontingenzkoeffizient von Cramer basiert auf der Chi-Quadrat-Statistik:

Kontingenzkoeffizient = sqrt (CHI2 / N*(Bins_count-1)),

wobei Bins_count die Anzahl der Zeilen (oder Spalten) in der Kontingenztabelle des Merkmals ist.

Somit sind zwei Statistiken in einem einzigen Indikator enthalten: die Chi-Quadrat-Hauptstatistik und der auf ihrer Grundlage berechnete Kontingenzkoeffizient.

Wenn Sie die Unabhängigkeit von zwei verschiedenen Finanzinstrumenten testen möchten, verwenden Sie das Skript Crosstab. Dazu aktivieren Sie den Parameter „X vs Y“ (true). Andernfalls berechnet das Skript die Statistik auf der Grundlage der aktuellen Symboldaten. Die Stichprobendaten für die Berechnung werden ab dem vorletzten Balken im Chart gezählt.

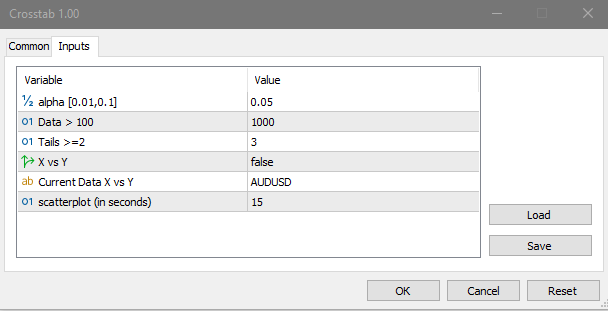
Das Skript von Crosstab berechnet und protokolliert die folgenden Informationen:

• Die Matrizen der tatsächlichen (Actual ) und der erwarteten (Expected) Häufigkeiten.

• Das Korrelationsverhältnis r, berechnet durch gruppierte Daten.

• Das Pearson-Korrelationsverhältnis, berechnet aus nicht gruppierten Daten (um die Genauigkeit der Berechnungen zu vergleichen, da die aus gruppierten Daten berechneten Statistiken weniger genau sind).

• Korrelationsverhältnis Nxy, Nyx (Correlation ratio)

• Ergebnisse der Prüfung der Hypothese der Abwesenheit einer Korrelationsabhängigkeit (f-statistische Korrelationsunabhängigkeit)

• Ergebnisse der Prüfung der Hypothese der Linearität der Korrelationsabhängigkeit (f-Statistik Linear/Nichtlinear),

• CHI2-Chi-Quadrat-Statistik

• Cramerscher Kontingenzkoeffizient

Zur visuellen Beurteilung der Paarabhängigkeit wird auf dem Bildschirm auch ein Streudiagramm (Korrelationsfeld) angezeigt.

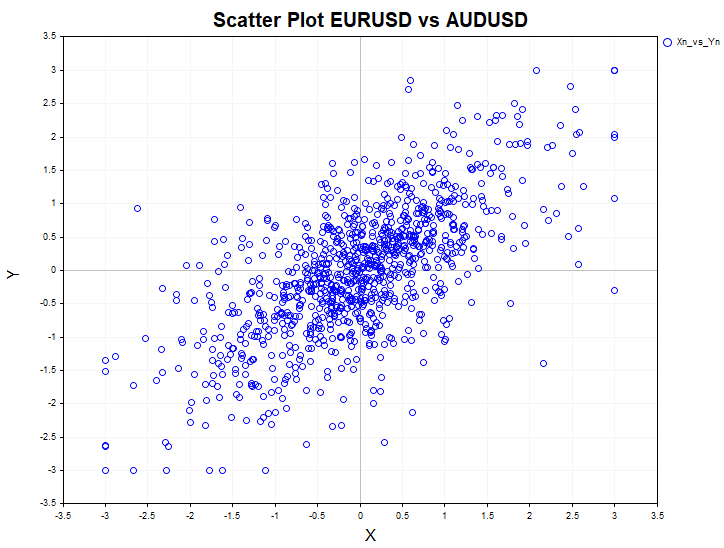
Verwenden Sie das Skript Crosstab_Models, um Modelldaten auf Unabhängigkeit zu testen. Die verwendeten Modelle sind Gleichverteilung, Autoregression erster Ordnung, ARCH-autoregressive bedingte Heteroskedastizität und logistisches Mapping.

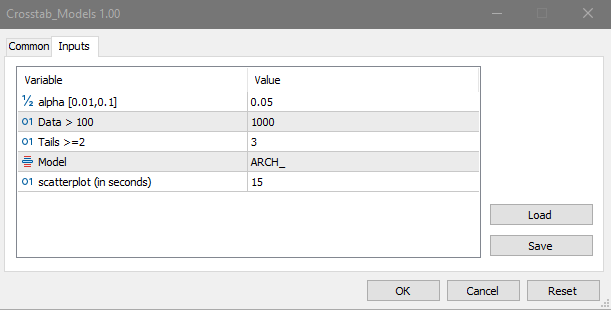
Modelldaten dienen als eine Art Schablone für den Vergleich von Ergebnissen, die aus realen Daten gewonnen wurden. So sieht zum Beispiel eine nichtlineare Abhängigkeit in einem eindimensionalen nichtlinearen dynamischen System aus – eine logistische Abbildung:

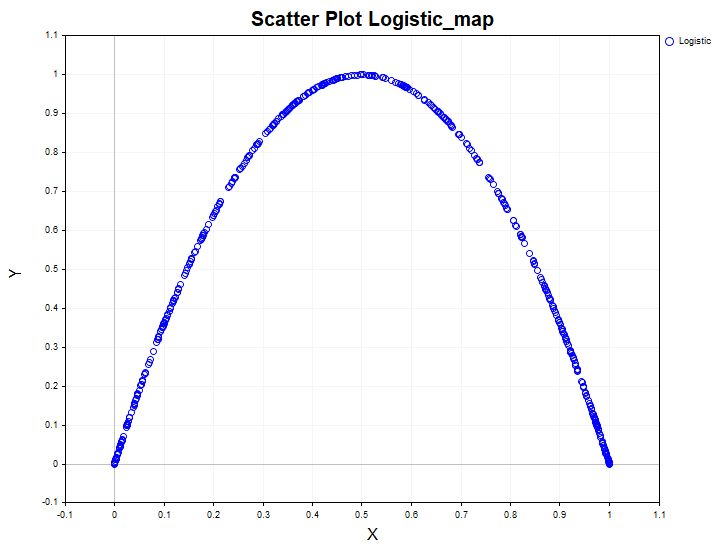
Analysiert man die Daten eines solchen Systems nur anhand des linearen Korrelationsverhältnisses, könnte man fälschlicherweise zu dem Schluss kommen, dass es sich bei diesem Prozess um weißes Rauschen handelt. Gleichzeitig zeigt der Chi-Quadrat-Unabhängigkeitstest leicht, dass die Daten abhängig sind, und das Korrelationsverhältnis bestätigt, dass die Abhängigkeit nicht linear ist.

Korrelationsverhältnis

Das Korrelationsverhältnis wird verwendet, um die Nichtlinearität der Korrelationsabhängigkeit zu bewerten:

Nyx = sqrt (D[E(Y|X)]/Sy)

Nxy = sqrt (D[E(X|Y)])/Sx)

wobei:

• E(Y|X) – die bedingte mathematische Erwartung des Zufallswertes Y

• E(X|Y) – die bedingte mathematische Erwartung des Zufallswertes X

• D[E(Y|X)] – der bedingte mathematische Erwartungswert der Varianz des Zufallswertes Y

• D[E(X|Y)] – die bedingte mathematische Erwartungsvarianz des Zufallswertes X

• Sy, Sx – die unbedingten Varianzen der Zufallswerte Y und X

Das sollten wir uns merken:

• E(Y|X), die bedingte mathematische Erwartung, ist ein Zufallswert.

• E[E(Y|X)] = E[Y] (der mathematische Erwartungswert des Zufallswertes Y, der unbedingte mathematische Erwartungswert ist gleich dem unbedingten mathematischen Erwartungswert Y).

• Die Streuung von Y ist D[Y] = E[(Y – E(Y) )^2)], der mathematische Erwartungswert des Quadrats der Abweichung des Zufallswertes Y vom mathematischen Erwartungswert E[Y].

• Dann ist D[E(Y|X)] = E{[ E(Y|X) – E[Y] ] ^ 2}. Mit anderen Worten: Die Varianz der unbedingten, mathematischen Erwartung E(Y|X) ist gleich der mathematischen Erwartung des Quadrats der Abweichung der unbedingten, mathematischen Erwartung E(Y|X) von der unbedingten, mathematischen Erwartung E[Y].

Anders gesagt: Das Korrelationsverhältnis ist die Quadratwurzel aus dem Verhältnis der beiden Varianzen – der bedingten und der unbedingten Varianz. Das Korrelationsverhältnis kann nur auf der Grundlage der Korrelationstabelle, d. h. auf der Grundlage von gruppierten Daten, berechnet werden. Listen wir die Eigenschaften auf, die es hat:

• Das Korrelationsverhältnis ist asymmetrisch in Bezug auf X und Y, d. h. Nxy != Nyx.

• 0 ≤ | r | ≤ Nxy ≤ 1, 0 ≤ | r | ≤ Nyx ≤ 1, liegen die Werte des Indikators im Bereich [0,1] und sind immer größer oder gleich dem linearen Korrelationskoeffizienten r modulo.

• Wenn die Daten unabhängig sind, dann gilt Nxy=Nyx=0. Der umgekehrte Fall trifft nicht zu, d. h. Unkorreliertheit bedeutet nicht Unabhängigkeit.

• Wenn | r | = Nyx =Nyx <1 ist, dann ist die Korrelation zwischen X und Y linear, d. h. es lässt sich keine bessere Kurve als eine Gerade für die Regressionsgleichung finden.

• wenn die Korrelation zwischen X und Y nicht linear ist, dann ist | r | < min (Nxy, Nyx). Je kleiner die Differenz zwischen dem Korrelationsverhältnis und der Korrelationsbeziehung ist, desto näher ist die Beziehung zwischen X und Y an der linearen Beziehung.

Durch die Berechnung des Stichprobenkorrelationsverhältnisses können wir die Hypothese des Fehlens einer Korrelation zwischen zwei Zufallsvariablen überprüfen (H0: Nyx = 0).

Zu diesem Zweck werden die folgenden Statistiken berechnet:

F = Nyx^2 * (N-Bins_count) / (1- Nyx^2) *(Bins_count-1)

Wenn die getestete Hypothese wahr ist, ist die F-Statistik nach dem Fisher'schen Gesetz mit v1 = Bins_count-1 und v2 = N-Bins_count Freiheitsgraden verteilt.

Die Nullhypothese wird auf dem Signifikanzniveau Alpha verworfen, wenn der berechnete Wert der F-Statistik den kritischen Wert dieser Statistik übersteigt (dann wird die Alternative H1 angenommen: Nyx >0)

Nehmen wir an, wir sind davon überzeugt, dass die Korrelationsabhängigkeit vorhanden ist. Es stellt sich die Frage: Ist diese Abhängigkeit linear oder nicht-linear? Die Hypothese über die Linearität der Korrelationsabhängigkeit zwischen zwei Zufallsvariablen beantwortet diese Frage.

Bei der Prüfung der Hypothese über die Linearität der Korrelationsabhängigkeit von Y von X (H0: Nyx^2 = r^2), wird die folgende Statistik verwendet:

F = (Nyx^2 - r^2) * (N-Bins_count) / (1- Nyx^2) *(Bins_count-2)

Wenn die getestete Hypothese wahr ist, ist die F-Statistik nach dem Fisher'schen Gesetz mit v1= Bins_count-2 und v2 = N-Bins_count Freiheitsgraden verteilt.

Die Nullhypothese der Korrelationslinearität wird auf dem Signifikanzniveau „alpha“ verworfen, wenn der berechnete Wert der F-Statistik den kritischen Wert dieser Statistik übersteigt (dann wird die Alternative H1 angenommen: Nyx^2 != r^2 )

Schlussfolgerung

In dem Artikel wurden so wichtige Instrumente der Korrelationsanalyse wie der Chi-Quadrat-Test von Pearson für die Unabhängigkeit und das Korrelationsverhältnis untersucht. Mit ihrer Hilfe ist es möglich, das Vorhandensein verborgener Beziehungen in den Daten viel genauer zu beurteilen. Der CHI2Test-Indikator testet die Unabhängigkeitshypothese und ermöglicht es, statistisch gültige Schlussfolgerungen über das Vorhandensein von Beziehungen in den Daten zu ziehen.

Zusätzlich zur Chi-Quadrat-Statistik berechnen die Skripte Crosstab und Crosstab_Models auch das Korrelationsverhältnis und testen die Hypothese über die Korrelationsabhängigkeit und die Linearität dieser Abhängigkeit, auch für Modelldaten. Zusätzlich wird ein Korrelationsfelddiagramm auf dem Bildschirm angezeigt, um die Paarabhängigkeit visuell zu beurteilen. Der Nutzer kann die Genauigkeit der statistischen Tests regulieren, indem er das gewünschte Alpha-Signifikanzniveau wählt. Je niedriger das Signifikanzniveau ist, desto geringer ist die Wahrscheinlichkeit einer falschen Antwort.