Wichtigste Änderungen des Algorithmus für die künstliche kooperative Suche (ACSm)
145
0
Inhalt
1. Einführung
Im vorigen Artikel haben wir einen interessanten und vielversprechenden Optimierungsalgorithmus kennengelernt, der als Artificial Cooperative Search (ACS) bekannt ist. Dieser Algorithmus ist inspiriert von Beobachtungen der Interaktion und Kooperation lebender Organismen in der Natur, wo sie sich zusammenschließen, um gemeinsame Ziele zu erreichen und gegenseitigen Nutzen zu erzielen. Die Grundidee von ACS besteht darin, solche wechselseitigen Beziehungen zwischen „Räubern“ und „Beute“ zu modellieren, um komplexe mehrdimensionale Probleme zu optimieren.
Nachdem wir uns nun mit der Grundversion von ACS vertraut gemacht haben, werden wir versuchen, seine Möglichkeiten mit modifizierten Versionen des Algorithmus zu erweitern. Diese verbesserten Versionen von ACS werden zusätzliche Mechanismen nutzen, die von Beobachtungen natürlicher Ökosysteme inspiriert sind, um die Effizienz der Suche nach optimalen Lösungen zu verbessern.
Die Untersuchung bekannter modifizierter Versionen von ACS wird es uns ermöglichen, ein tieferes Verständnis dafür zu erlangen, wie die Prinzipien der Kooperation und der für beide Seiten vorteilhaften Koexistenz lebender Organismen erfolgreich zur Lösung komplexer Optimierungsprobleme eingesetzt werden können, und wird dazu beitragen, neue Perspektiven im Bereich der künstlichen Intelligenz aufzuzeigen und weitere Entwicklungen in diesem spannenden Bereich anzuregen.
2. Implementierung des Algorithmus
Die erste und geringfügige Änderung des ACS (Modifizierter Künstlicher Kooperativer Suchalgorithmus) umfasst zwei wesentliche Änderungen:
1. Verwendung erweiterter Formen von A- und B-Matrizen (Populationen):
- Bei dieser Änderung haben die Matrizen A und B zusätzliche Spalten. Jede Zeile der Matrix enthält N Variablen und eine zusätzliche Spalte, die den auf der Grundlage der ersten N Variablen berechneten Funktionswert speichert. Dies erleichtert die Verfolgung der Funktionswerte und verbessert die Genauigkeit der Lösungen.
2. Änderung der Art und Weise, wie die binäre Matrix M erstellt wird:
- Beim ursprünglichen Algorithmus wird die M-Matrix mit „0“-Werten gefüllt, und dann werden einige Elemente ausgewählt und auf „1“ gesetzt. Diese Änderung führt zu einer kleinen Verbesserung der Genauigkeit der Lösungen, zumindest für die Testfunktionen, mit denen die Experimente durchgeführt wurden.
Diese Änderungen in der ersten und geringfügigen Modifikation des ACS-Algorithmus zielen also darauf ab, die Genauigkeit der Lösungen und die Effizienz des Algorithmus bei der Lösung von Optimierungsproblemen zu verbessern. Anstatt eine zusätzliche Spalte zur Speicherung der Fitnesswerte der Individuen hinzuzufügen, wie die Autoren vorschlagen, werden wir das bereits bekannte Feld „f“ in der Struktur der Agenten verwenden, das die Individuen der Population beschreibt.
Die zweite und wesentliche Änderung des ACS-Algorithmus umfasst die folgenden Änderungen, die sich von der ursprünglichen Version unterscheiden:
1. Wir ändern einen Ansatz zum Füllen der Raubtier- und Beute-Matrizen:
- Bei dieser Änderung wird jede Zeile in den erweiterten A- und B-Matrizen nach dem Wert der Fitnessfunktion sortiert. Die Zeilen der sortierten A- und B-Matrizen werden dann verglichen, und auf der Grundlage dieses Vergleichs wird bestimmt, welche Zeilen in die Matrizen für Raubtier (Predator) und Beute (Prey) aufgenommen werden. Dieser Ansatz ermöglicht die Auswahl von Kandidaten für die Aktualisierung auf der Grundlage ihrer Verdienste (Merkmalswert) anstelle einer zufälligen Auswahl.
2. Zufallsvergleiche zur Aktualisierung der Matrizen A und B:
- Am Ende jeder Iteration der Hauptschleife in dieser Modifikation werden die A- und B-Matrizen durch zufällige Vergleiche aktualisiert. Dies bedeutet, dass beide Matrizen die gleiche Wahrscheinlichkeit haben, aktualisiert zu werden. Dieser Ansatz ermöglicht es, beide Populationen gleichmäßig zu aktualisieren und verbessert die Vielfalt bei der Suche nach der optimalen Lösung.
Die zweite Änderung des ACS-Algorithmus verbessert also die Auswahl der Kandidaten und die Aktualisierung der A- und B-Populationen, wodurch sie effizienter und vielfältiger bei der Suche nach der optimalen Lösung werden. Er unterscheidet sich von der ursprünglichen Version des Algorithmus durch die Art und Weise, wie die Raubtier- und Beutepopulationen gebildet werden, und durch die Verwendung von Zufallsvergleichen zur Aktualisierung der Matrizen.
Die dritte und große Änderung des ACS-Algorithmus stellt einen völlig anderen Ansatz für die Bildung der Raubtier- und Beute-Matrizen dar. Detaillierte Beschreibung der in der dritten Änderung vorgenommenen Änderungen:
1. Die Population Pop:
- Durch diese Änderung entsteht eine neue Matrix Pop, die die erweiterten A- und B-Matrizen kombiniert. Pop enthält alle Zeilen der Matrizen A und B. Dann wird sie nach den Werten der Fitnessfunktion sortiert. Die ersten popSize-Zeilen in Pop werden zur Predator-Population, während die letzten popSize-Zeilen zur Prey-Population werden.
2. Aktualisierung von Raubtier und Beute:
- Nach der Bildung von Raubtier- und Beutepopulationen setzt der Algorithmus die Aktualisierung auf der Grundlage der Fitness der Individuen fort. Die besten Lösungen, die als Predator ausgewählt werden, erhalten den Vorzug, was die Genauigkeit und Konvergenzgeschwindigkeit des Algorithmus verbessert.
3. Verwendung von Zufallsvergleichen:
- Ähnlich wie bei der zweiten Änderung werden am Ende jeder Iteration der Hauptschleife die Matrizen A und B durch zufällige Vergleiche aktualisiert. Dieser Ansatz gewährleistet gleiche Chancen für die Erneuerung beider Populationen und fördert die Vielfalt bei der Suche nach der optimalen Lösung.
Die dritte Modifikation des ACS-Algorithmus konzentriert sich daher auf die Nutzung der Fitness zur Bildung der Raubtier- und Beutepopulationen. Sie stellt einen fortschrittlicheren und effizienteren Ansatz für die Auswahl von Kandidaten und die Aktualisierung von Populationen bei der Suche nach einer optimalen Lösung dar.
Nachdem wir die möglichen Änderungen an der Grundversion des Algorithmus (ACS) geprüft haben, können wir nun zur Implementierung der ersten verbesserten Version dieser vielversprechenden Optimierungsmethode übergehen. Unser Ziel ist es, die Effizienz bei der Suche nach optimalen Lösungen zu erhöhen. Schritt für Schritt werden wir neue Elemente in die Grundstruktur von ACS einführen und ihre Auswirkungen auf die Leistung und Konvergenz des Algorithmus sorgfältig analysieren.
Beginnen wir mit der Implementierung der ersten modifizierten Version des Algorithmus und erkunden wir sein Potenzial. In jeder nachfolgenden Version des Algorithmus sind die Teile des Codes, die sich von der vorherigen Version unterscheiden, grün gekennzeichnet.
Beschreibung des Klassencodes von C_AO_ACSm1:
1. C_AO_ACSm1 ist eine von der Basisklasse C_AO abgeleitete Klasse.
2. Die Klasse hat einen öffentlichen Konstruktor und Destruktor.
3. Die folgenden Datenelemente werden im Konstruktor initialisiert:
- ao_name, ao_desc, ao_link - beschreibende Zeilen zum Algorithmus
- popSize - Größe der Population
- bioProbab - Wahrscheinlichkeit einer biologischen Interaktion
- params - Array von Algorithmusparametern, in diesem Fall haben wir zwei Parameter: popSize und bioProbab
4. SetParams() - die Methode setzt die Werte popSize und bioProbab basierend auf den Parametern aus dem Array params.
5. Init() - die Methode nimmt als Eingabe die Bereiche und Suchschritte sowie die Anzahl der Epochen und gibt einen logischen Wert zurück, der den Erfolg der Initialisierung anzeigt.
6. Moving() und Revision() - die Methoden enthalten die grundlegende Logik des Algorithmus zum Verschieben und Überarbeiten der Agenten.
7. Zu den privaten Datenmitgliedern gehören Arrays von Strukturen der Typen S_AO_Agent und S_C sowie die im Algorithmus verwendeten Schlüssel- und Phasenvariablen.
8. ArrayShuffle() - die private Methode mischt Array-Elemente.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ACSm1 : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ACSm1 () { } C_AO_ACSm1 () { ao_name = "ACS"; ao_desc = "Artificial Cooperative Search m1"; ao_link = "https://www.mql5.com/ru/articles/15014"; popSize = 1; //population size bioProbab = 0.9; //biological interaction probability ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "bioProbab"; params [1].val = bioProbab; } void SetParams () { popSize = (int)params [0].val; bioProbab = params [1].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double bioProbab; //biological interaction probability private: //------------------------------------------------------------------- S_AO_Agent A []; S_AO_Agent B []; S_AO_Agent Predator []; S_AO_Agent Prey []; S_C M []; int Key; int phase; void ArrayShuffle (double &arr []); }; //——————————————————————————————————————————————————————————————————————————————
Die Methode Init der Klasse C_AO_ACSm1 führt die Objektinitialisierung durch:
1. Init() - die Deklaration der Methode. Sie benötigt vier Argumente: minimaler Suchbereich „rangeMinP“, maximaler Suchbereich „rangeMaxP“, Suchschritt „rangeStepP“ und die Anzahl der Epochen „epochsP“, die standardmäßig 0 ist.
2. if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; - der Aufruf der Funktion StandardInit, die die Standardinitialisierung der Basisklasse durchführt. Wenn StandardInit false zurückgibt, wird die Init-Methode sofort beendet und gibt false zurück.
3. In der Schleife for (int i = 0; i < popSize; i++) wird jedes Element der Arrays A, B, Predator, Prey und M mit der Methode Init initialisiert.
4. ArrayResize (A, popSize) und ähnliche Zeilen ändern die Größe der Arrays A, B, Predator, Prey und M auf popSize.
5. In der verschachtelten Schleife for (int j = 0; j < coords; j++) wird jedes c-Element (individuelle Koordinaten) jedes Objekts in den Arrays A und B mit einem Zufallswert im angegebenen Bereich initialisiert.
6. phase = 0 setzt die Phase auf 0.
7. Die Methode gibt true zurück, wenn die Initialisierung erfolgreich war.
Der Code ist für die anfängliche Einrichtung und Vorbereitung der für den weiteren Betrieb des Algorithmus erforderlichen Daten zuständig. Er erstellt Arrays von Objekten, initialisiert deren Werte und legt den Anfangszustand des Algorithmus fest.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ACSm1::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) //number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (A, popSize); ArrayResize (B, popSize); ArrayResize (Predator, popSize); ArrayResize (Prey, popSize); ArrayResize (M, popSize); for (int i = 0; i < popSize; i++) { A [i].Init (coords); B [i].Init (coords); Predator [i].Init (coords); Prey [i].Init (coords); M [i].Init (coords); } // Initialization for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { A [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab (); B [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab (); } } phase = 0; return true; } //——————————————————————————————————————————————————————————————————————————————
Die Methode Moving der Klasse C_AO_ACSm1 implementiert die grundlegende Logik des Verschiebens von Individuen im Algorithmus:
1. if (phase == 0) - hier werden Individuen aus der Population A in das Array a kopiert (das Array „а“ wird verwendet, um Individuen für die Berechnung der Fitnessfunktion zu übergeben).
- Für jedes Element in der Schleife for (int i = 0; i < popSize; i++) werden die einzelnen Koordinaten vom Array A in das Array a kopiert.
- Der Wert der Variablen phase wird um 1 erhöht und die Methode wird zurückgegeben.
2. if (phase == 1) - hier wird die Fitness den Individuen der Population A zugewiesen und die Individuen der Population B werden kopiert.
- Für jedes Element in der Schleife for (int i = 0; i < popSize; i++) wird der Fitnesswert a[i].f nach A[i].f kopiert.
- Anschließend werden für jedes Element in der Schleife for (int i = 0; i < popSize; i++) die Koordinaten der Individuen aus dem Array B in das Array a für die weitere Berechnung der Anpassungsfähigkeit der Individuen kopiert.
- Der Wert von phase wird um 1 erhöht und die Methode wird zurückgegeben.
3. if (phase == 2) - hier wird die Fitness an die Individuen der Population B zurückgegeben.
- Für jedes Element in der Schleife for (int i = 0; i < popSize; i++) wird der Fitnesswert von a[i].f nach B[i].f kopiert.
- Der Wert von phase wird um 1 erhöht und die weitere Algorithmuslogik wird ausgeführt.
4. Selection - hier wird die Auswahl durchgeführt.
- Wenn der Zufallswert u.RNDprobab() kleiner als 0,5 ist, wird für jedes Element in der Schleife for (int i = 0; i < popSize; i++) das Individuum A[i] in Predator[i] kopiert, während Key auf 1 gesetzt wird.
- Andernfalls wird für jedes Element in der Schleife for (int i = 0; i < popSize; i++) das Individuum B[i] nach Predator[i] kopiert, während Key auf 2 gesetzt wird.
- Die Auswahl für das Array Prey erfolgt auf ähnliche Weise.
5. Permutation der Prey - hier werden die Koordinaten in jedem Individuum der Population Prey zufällig permutiert.
- Für jedes Individuum in der Schleife for (int i = 0; i < popSize; i++) wird ArrayShuffle (Prey[i].c) ausgeführt, indem die individuellen Koordinaten gemischt werden (die Koordinaten jedes Individuums werden separat gemischt, während die Koordinaten zwischen den Individuen nicht gemischt werden).
6. Mutation und Crossover - hier werden Mutation und Crossover durchgeführt.
- Der Wert R wird in Abhängigkeit von einer Zufallszahl berechnet.
- Die binäre Matrix M wird mit Einsen gefüllt.
- Zusätzliche Operationen werden mit der Matrix M durchgeführt, indem einige ihrer Elemente auf 0 oder 1 geändert werden, je nach der Wahrscheinlichkeit bioProbab für eine biologischen Interaktion.
- Für jedes Individuum in der Schleife for (int i = 0; i < popSize; i++) werden Mutation und Crossover durchgeführt, wobei die Werte im Array Populations aktualisiert werden.
7. Kontrolle der Grenzen - Der Block führt eine Grenzkontrolle durch, bei der die Koordinaten der Individuen a in der Population, die außerhalb des angegebenen Bereichs der optimierten Parameter liegen, durch Zufallswerte innerhalb des Bereichs ersetzt werden.
Diese Methode implementiert die grundlegenden Operationen des Algorithmus, wie Selektion, Mutation, Crossover und Boundary Control, die auf eine Population von Individuen angewendet werden, um die optimale Lösung zu finden.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACSm1::Moving () { //---------------------------------------------------------------------------- if (phase == 0) { for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c); phase++; return; } //---------------------------------------------------------------------------- if (phase == 1) { for (int i = 0; i < popSize; i++) A [i].f = a [i].f; for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c); phase++; return; } //---------------------------------------------------------------------------- if (phase == 2) { for (int i = 0; i < popSize; i++) B [i].f = a [i].f; phase++; } //---------------------------------------------------------------------------- // Selection if (u.RNDprobab () < 0.5) { for (int i = 0; i < popSize; i++) { Predator [i] = A [i]; } Key = 1; } else { for (int i = 0; i < popSize; i++) { Predator [i] = B [i]; } Key = 2; } if (u.RNDprobab () < 0.5) { for (int i = 0; i < popSize; i++) { Prey [i] = A [i]; } } else { for (int i = 0; i < popSize; i++) { Prey [i] = B [i]; } } // Permutation of Prey for (int i = 0; i < popSize; i++) { ArrayShuffle (Prey [i].c); } double R; if (u.RNDprobab () < 0.5) { R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0); } else R = 1 / MathExp (4 * MathRand () / 32767.0); // Fill binary matrix M with 0s for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { M [i].c [j] = 0; } } // Additional operations with matrix M for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { if (u.RNDprobab () < bioProbab) { M [i].c [j] = 1; } } } for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { if (u.RNDprobab () < bioProbab) { M [i].c [j] = 1; } } } for (int i = 0; i < popSize; i++) { int sum = 0; for (int c = 0; c < coords; c++) sum += M [i].c [c]; if (sum == coords) { int j = MathRand () % coords; M [i].c [j] = 0; } } // Mutation for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]); // Crossover if (M [i].c [j] > 0) { a [i].c [j] = Predator [i].c [j]; } // Boundary control if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j]) { a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab (); } } } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } } //——————————————————————————————————————————————————————————————————————————————
Betrachten wir nun den Code der Methode Revision der Klasse C_AO_ACSm1. Sie führt die folgenden Operationen durch:
1. Prüfung, ob die Vorbereitungsphase der Population phase bereits abgeschlossen ist, phase >= 3. Wenn diese Bedingung nicht erfüllt ist, kehrt die Methode ohne weitere Maßnahmen zurück.
2. Aktualisieren der Auswahl der Personen durch Selection update:
- Wir prüfen für jedes Individuum in der Population a, ob sein Fitnesswert f den entsprechenden Wert im Array Predator übersteigt. Wenn ja, wird der Wert in Predator aktualisiert.
- Je nach dem Wert der Variablen Key werden die Individuen der Population Predator in die Population A oder B kopiert.
3. Wir bestimmen den besten Fitnesswert Ybest und seinen Index Ibest im Array Predator:
- Wir iterieren über das Predator-Array, finden den maximalen Fitnesswert und seinen Index.
4. Aktualisieren der besten, globalen Lösung fB:
- Wenn Ybest den aktuellen besten Wert fB übersteigt, wird fB aktualisiert, während die entsprechenden Array-Elemente a und cB aus dem Predator-Array kopiert werden.
Diese Methode aktualisiert die individuelle Auswahl, bestimmt die beste Lösung und aktualisiert die globale beste Lösung innerhalb des Optimierungsalgorithmus.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACSm1::Revision () { if (phase < 3) return; // Selection update for (int i = 0; i < popSize; i++) { double d = a [i].f; if (d > Predator [i].f) { Predator [i] = a [i]; } } if (Key == 1) { for (int i = 0; i < popSize; i++) { A [i] = Predator [i]; } } else { for (int i = 0; i < popSize; i++) { B [i] = Predator [i]; } } double Ybest = -DBL_MAX; int Ibest = -1; for (int i = 0; i < popSize; i++) { if (Predator [i].f > Ybest) { Ybest = Predator [i].f; Ibest = i; } } if (Ybest > fB) { fB = Ybest; ArrayCopy (a [Ibest].c, Predator [Ibest].c); ArrayCopy (cB, Predator [Ibest].c); } } //——————————————————————————————————————————————————————————————————————————————
Die Methode ArrayShuffle der Klasse C_AO_ACS wird in allen drei Modifikationen angewandt und führt ein zufälliges Mischen der Elemente im Array durch:
1. Definieren der Größe des Arrays „arr“ mit der Funktion ArraySize.
2. Iterieren über das Array arr in umgekehrter Reihenfolge, beginnend mit dem letzten Element.
3. Für jedes Element i wird ein Zufallsindex j von 0 bis i erzeugt.
4. Vertauscht die Elemente arr[i] und arr[j] unter Verwendung der temporären Variablen tmp.
Infolgedessen werden die Elemente des Arrays arr nach dem Zufallsprinzip gemischt.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACSm1::ArrayShuffle (double &arr []) { int n = ArraySize (arr); for (int i = n - 1; i > 0; i--) { int j = MathRand () % (i + 1); double tmp = arr [i]; arr [i] = arr [j]; arr [j] = tmp; } } //——————————————————————————————————————————————————————————————————————————————
Nun ist es an der Zeit, den Code der zweiten Änderung des ACS-Algorithmus zu analysieren. Der Code der Methode Moving der Klasse C_AO_ACSm2 wurde entsprechend den Änderungen angepasst:
1. Phase 0:
- Wenn die Phase gleich 0 ist, erhält jedes Individuum in der Population a die Werte aus der Population A.
- Der Phasenwert wird erhöht und aus der Methode wird zurückgekehrt.
2. Phase 1:
- Wenn die Phase 1 ist, erhält jedes Individuum in der Population a die Fitnesswerte f aus der Population A.
- Jedes Individuum in der Population a erhält die Werte aus der Population B.
- Der Phasenwert wird erhöht und aus der Methode wird zurückgekehrt.
3. Phase 2:
- Wenn die Phase 2 ist, erhält jedes Individuum in der Population B die Fitnesswerte „f“ aus der Population a.
- Der Phasenwert erhöht sich und die weitere Algorithmuslogik wird fortgesetzt.
4. Selection:
- Für jedes Individuum in den Populationen A und B werden f Fitnesswerte verglichen.
- Wenn der Wert f in A größer ist als in B, wird ein Individuum aus A in Predator kopiert, während ein Individuum aus B in Prey kopiert wird. Andernfalls ist es umgekehrt (die fittesten Individuen werden als „predators“ bezeichnet und die weniger fitten werden zur „prey“).
5. Permutation der Prey:
- Die Koordinaten jedes Individuums in der Population Prey werden mit der Funktion ArrayShuffle permutiert.
6. Mutation und Crossover:
- Der Wert von R wird in Abhängigkeit von einer Zufallszahl definiert.
- Die Binärmatrix M ist mit Nullen gefüllt.
- Weitere Operationen werden mit der Matrix M durchgeführt, wobei einige Elemente je nach der Wahrscheinlichkeit bioProbab auf 1 gesetzt werden.
Für jedes Individuum in einer Population:
- Es wird eine Mutation durchgeführt: Das Element a[i].c[j] wird berechnet als Summe von Predator[i].c[j] und dem Produkt aus R und der Differenz zwischen Prey[i].c[j] und Predator[i].c[j].
- Crossover wird durchgeführt: Wenn M[i].c[j] gleich 1 ist, wird a[i].c[j] durch Predator[i].c[j] ersetzt.
- Grenzprüfung: Liegt a[i].c[j] außerhalb von rangeMin[j] und rangeMax[j], wird es durch einen Zufallswert innerhalb dieses Bereichs ersetzt.
7. Überprüfung der Koordinaten:
- Für jedes Individuum in der Population a werden die Koordinaten mit der Funktion SeInDiSp überprüft.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACSm2::Moving () { //---------------------------------------------------------------------------- if (phase == 0) { for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c); phase++; return; } //---------------------------------------------------------------------------- if (phase == 1) { for (int i = 0; i < popSize; i++) A [i].f = a [i].f; for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c); phase++; return; } //---------------------------------------------------------------------------- if (phase == 2) { for (int i = 0; i < popSize; i++) B [i].f = a [i].f; phase++; } //---------------------------------------------------------------------------- // Selection for (int i = 0; i < popSize; i++) { if (A [i].f > B [i].f) { Predator [i] = A [i]; Prey [i] = B [i]; } else { Predator [i] = B [i]; Prey [i] = A [i]; } } // Permutation of Prey for (int i = 0; i < popSize; i++) { ArrayShuffle (Prey [i].c); } double R; if (u.RNDprobab () < 0.5) { R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0); } else R = 1 / MathExp (4 * MathRand () / 32767.0); // Fill binary matrix M with 0s for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { M [i].c [j] = 0; } } // Additional operations with matrix M for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { if (u.RNDprobab () < bioProbab) { M [i].c [j] = 1; } } } for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { if (u.RNDprobab () < bioProbab) { M [i].c [j] = 1; } } } for (int i = 0; i < popSize; i++) { int sum = 0; for (int c = 0; c < coords; c++) sum += M [i].c [c]; if (sum == coords) { int j = MathRand () % coords; M [i].c [j] = 0; } } // Mutation for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]); // Crossover if (M [i].c [j] > 0) { a [i].c [j] = Predator [i].c [j]; } // Boundary control if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j]) { a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab (); } } } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } } //——————————————————————————————————————————————————————————————————————————————
Auf die Methode Revision der zweiten Algorithmusänderung werde ich hier nicht eingehen, da sie unverändert geblieben ist.
Kommen wir nun zur dritten Änderung. In der Definition der dritten Modifikationsklasse C_AO_ACSm3, die von der Basisklasse C_AO abgeleitet ist, wurden die folgenden Änderungen vorgenommen:
Die Liste der Datenmitglieder hat sich geändert:
- bioProbab - die Wahrscheinlichkeit einer biologischen Interaktion.
- A[], B[], Predator[], Prey[], Pop[], pTemp[] - Arrays, die verschiedene Populationen von Individuen speichern.
- M[] - das Array, in dem zusätzliche Daten zu den Individuen gespeichert werden.
- phase - die aktuelle Phase im Algorithmus.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ACSm3 : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ACSm3 () { } C_AO_ACSm3 () { ao_name = "ACS"; ao_desc = "Artificial Cooperative Search m3"; ao_link = "https://www.mql5.com/ru/articles/15014"; popSize = 10; //population size bioProbab = 0.9; //biological interaction probability ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "bioProbab"; params [1].val = bioProbab; } void SetParams () { popSize = (int)params [0].val; bioProbab = params [1].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double bioProbab; //biological interaction probability private: //------------------------------------------------------------------- S_AO_Agent A []; S_AO_Agent B []; S_AO_Agent Predator []; S_AO_Agent Prey []; S_AO_Agent Pop []; S_AO_Agent pTemp []; S_C M []; int phase; void ArrayShuffle (double &arr []); }; //——————————————————————————————————————————————————————————————————————————————
An der Initialisierungsmethode Init der Klasse C_AO_ACSm3 wurden die folgenden Änderungen vorgenommen:
1. Es wird Speicher für die Arrays A, B, Predator, Prey, Pop, pTemp und M von popSize oder popSize * 2 reserviert.
2. Jedes Element der Arrays A, B, Predator, Prey, Pop und M wird mit der Methode Init initialisiert.
Die Autoren der ursprünglichen Version des Algorithmus haben keine Einteilung der Logik in Phasen vorgenommen. Ich habe eine Unterteilung in Phasen hinzugefügt, um den Algorithmus in dem Stil zu implementieren, den ich für alle Bevölkerungsalgorithmen übernommen habe. Dies war notwendig, weil das ACS eine Vorausberechnung der Agentenfitness für die Populationen А und B verwendet. Diese Vorgänge sollten nacheinander in Methoden durchgeführt werden.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ACSm3::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) //number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (A, popSize); ArrayResize (B, popSize); ArrayResize (Predator, popSize); ArrayResize (Prey, popSize); ArrayResize (Pop, popSize * 2); ArrayResize (pTemp, popSize * 2); ArrayResize (M, popSize); for (int i = 0; i < popSize; i++) { A [i].Init (coords); B [i].Init (coords); Predator [i].Init (coords); Prey [i].Init (coords); M [i].Init (coords); } for (int i = 0; i < popSize * 2; i++) Pop [i].Init (coords); // Initialization for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { A [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab (); B [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab (); } } phase = 0; return true; } //——————————————————————————————————————————————————————————————————————————————
Werfen wir nun einen Blick auf den Code der Methode Moving innerhalb der Klasse C_AO_ACSm3 der dritten Änderung. Die Änderungen betreffen die folgenden Codebereiche:
- Verschmelzung der Populationen A und B zu einer einzigen Population.
- Sortierung der Population nach den Fitnesswerten der Individuen.
- Ausfüllen der Populationen von Predator und Prey aus dem sortierten Array Pop, wobei die beste Hälfte der Population zu „predators“ (Raubtieren) und die andere Hälfte zu „prey“ (Beute) wird.
- Auffüllen der binären Matrix M mit Einsen.
- Zusätzliche Operationen mit der Matrix M, in der einige Elemente in Abhängigkeit von einer Zufallszahl und der Wahrscheinlichkeit bioProbab der biologischen Interaktion auf 0 oder 1 wechseln.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACSm3::Moving () { //---------------------------------------------------------------------------- if (phase == 0) { for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c); phase++; return; } //---------------------------------------------------------------------------- if (phase == 1) { for (int i = 0; i < popSize; i++) A [i].f = a [i].f; for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c); phase++; return; } //---------------------------------------------------------------------------- if (phase == 2) { for (int i = 0; i < popSize; i++) B [i].f = a [i].f; phase++; } //---------------------------------------------------------------------------- // Merge matrices A and B to create matrix Pop for (int i = 0; i < popSize; i++) { Pop [i] = A [i]; Pop [i + popSize] = B [i]; } // Sort matrix Pop using column N as sort key values u.Sorting (Pop, pTemp, popSize * 2); // Populate Predator and Prey matrices for (int i = 0; i < popSize; i++) { Predator [i] = Pop [i]; Prey [i] = Pop [i + popSize]; } // Permutation of Prey for (int i = 0; i < popSize; i++) { ArrayShuffle (Prey [i].c); } double R; if (u.RNDprobab () < 0.5) { R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0); } else R = 1 / MathExp (4 * MathRand () / 32767.0); // Fill binary matrix M with 1s for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { M [i].c [j] = 1; } } // Additional operations with matrix M for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { if (u.RNDprobab () < bioProbab) { M [i].c [j] = 0; } } } for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { if (u.RNDprobab () < bioProbab) { if (u.RNDprobab() < bioProbab) { M[i].c[j] = 1; } else { M[i].c[j] = 0; } } } } for (int i = 0; i < popSize; i++) { int sum = 0; for (int c = 0; c < coords; c++) sum += M [i].c [c]; if (sum == coords) { int j = MathRand () % coords; M [i].c [j] = 0; } } // Mutation for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]); // Crossover if (M [i].c [j] > 0) { a [i].c [j] = Predator [i].c [j]; } // Boundary control if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j]) { a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab (); } } } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } } //——————————————————————————————————————————————————————————————————————————————
3. Testergebnisse
Wir haben alle bekannten Versionen dieses Algorithmus sorgfältig geprüft und analysiert. Nun ist es an der Zeit, sich auf die praktischen Ergebnisse und die Schlussfolgerungen zu konzentrieren, die wir daraus ziehen können. Ich möchte im Detail darauf eingehen, wie sich die einzelnen Änderungen auf Produktivität, Genauigkeit und Effizienz auswirken. Auf diese Weise können wir besser verstehen, welche Änderungen am erfolgreichsten waren und wo wir als Nächstes ansetzen sollten.
Die erste Version der Modifikation zeigte annähernd vergleichbare Ergebnisse in der Gesamtbewertung, aber die Ergebnisse verbesserten sich signifikant bei der Hilly-Funktion mit 1000 Variablen und bei der Forest-Funktion mit 50 und 1000 Variablen.
ACS|Artificial Cooperative Search m1|1.0|0.7|
=============================
5 Hilly's; Func runs: 10000; result: 0.7130880902279995
25 Hilly's; Func runs: 10000; result: 0.7565145335137569
500 Hilly's; Func runs: 10000; result: 0.31899537529427235
=============================
5 Forest's; Func runs: 10000; result: 0.9999999999866176
25 Forest's; Func runs: 10000; result: 0.9555551824899264
500 Forest's; Func runs: 10000; result: 0.24186829565864398
=============================
5 Megacity's; Func runs: 10000; result: 0.6607692307692307
25 Megacity's; Func runs: 10000; result: 0.5038461538461539
500 Megacity's; Func runs: 10000; result: 0.13922307692307825
=============================
All score: 5.28986 (58.78%)
Die zweite Version des Algorithmus zeigte eine deutliche Verbesserung der Ergebnisse bei allen Testfunktionen mit 50 und 1000 Variablen, aber die Ergebnisse wurden bei Megacity mit 10 Variablen (extrem große Streuung der Ergebnisse) im Vergleich zur Basisversion deutlich schlechter. Dies deutet darauf hin, dass die Entwicklung in diese Richtung vielversprechend ist (auch wenn es strittige Punkte gibt), und es lohnt sich, an weiteren Änderungen zu arbeiten.
ACS|Artificial Cooperative Search m2|2.0|0.7|
=============================
5 Hilly's; Func runs: 10000; result: 0.7682797921658492
25 Hilly's; Func runs: 10000; result: 0.7664893907210706
500 Hilly's; Func runs: 10000; result: 0.31831672493319296
=============================
5 Forest's; Func runs: 10000; result: 0.9999997349437437
25 Forest's; Func runs: 10000; result: 0.9534110489423269
500 Forest's; Func runs: 10000; result: 0.24425762117784502
=============================
5 Megacity's; Func runs: 10000; result: 0.6176923076923077
25 Megacity's; Func runs: 10000; result: 0.5384615384615385
500 Megacity's; Func runs: 10000; result: 0.14057692307692446
=============================
All score: 5.34749 (59.42%)
Leider hat die dritte Modifikation, die am vielversprechendsten zu sein schien, die Erwartungen nicht erfüllt und ein etwas schlechteres Gesamtergebnis als die Grundversion des Algorithmus gezeigt. Es ist jedoch erwähnenswert, dass sich die Ergebnisse für die glatte Hilly-Funktion mit 10 Variablen deutlich verbessert haben. Der Algorithmus zeigt gerade bei glatten Funktionen mit einer geringen Anzahl von Variablen eine höhere Konvergenzgenauigkeit.
ACS|Artificial Cooperative Search m3|10.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.8836798635515516
25 Hilly's; Func runs: 10000; result: 0.715438105666966
500 Hilly's; Func runs: 10000; result: 0.3011611038405591
=============================
5 Forest's; Func runs: 10000; result: 0.9893902762645717
25 Forest's; Func runs: 10000; result: 0.7954795408759185
500 Forest's; Func runs: 10000; result: 0.21910399769909533
=============================
5 Megacity's; Func runs: 10000; result: 0.6315384615384615
25 Megacity's; Func runs: 10000; result: 0.49876923076923074
500 Megacity's; Func runs: 10000; result: 0.12683076923077044
=============================
All score: 5.16139 (57.35%)
Visualisierung der zweiten Modifikation des Algorithmus. Bei einer geringen Anzahl von Variablen ist die Streuung der Ergebnisse bei den Funktionen Hilly und Megacity recht groß, während der Algorithmus bei der stacheligen, glatten Funktion Forest hervorragend funktioniert.
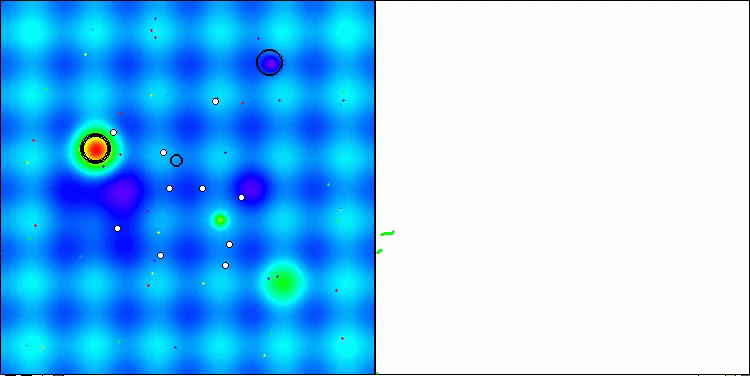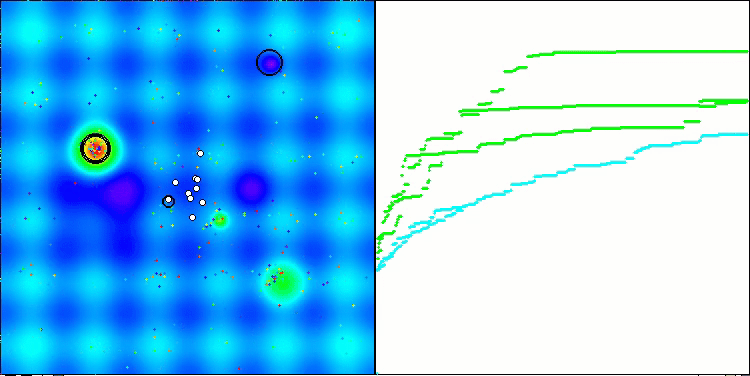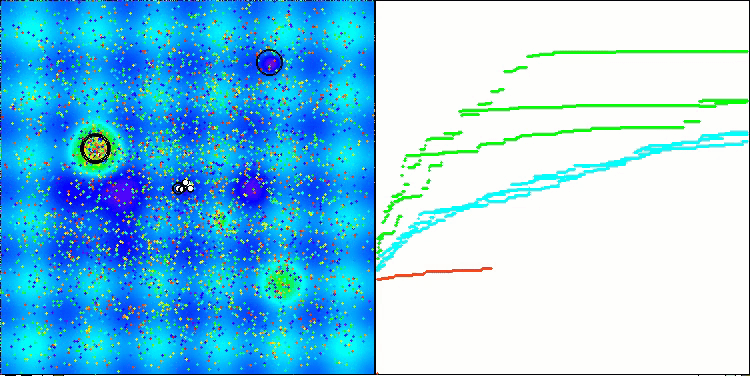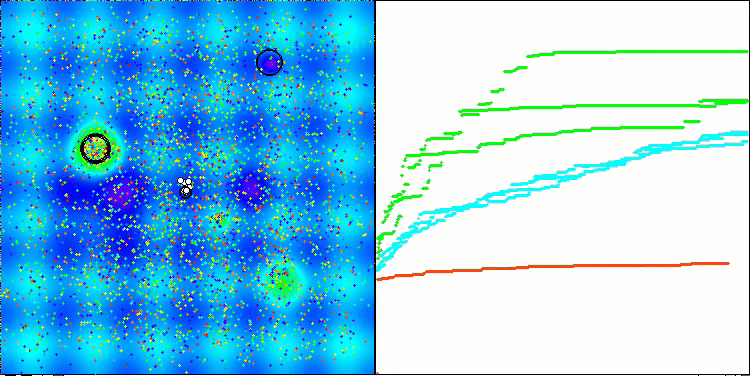
ACSm2 mit der Testfunktion Hilly
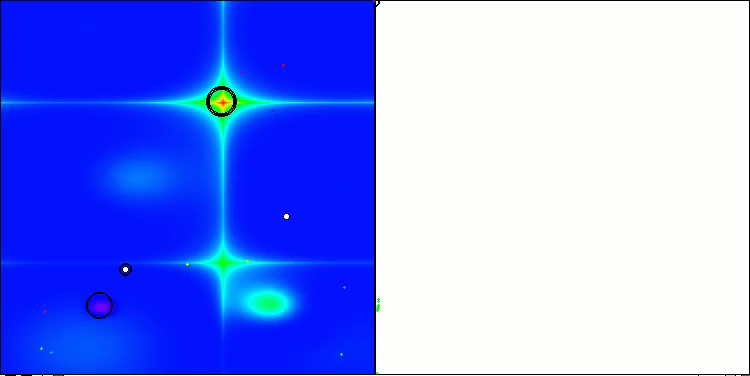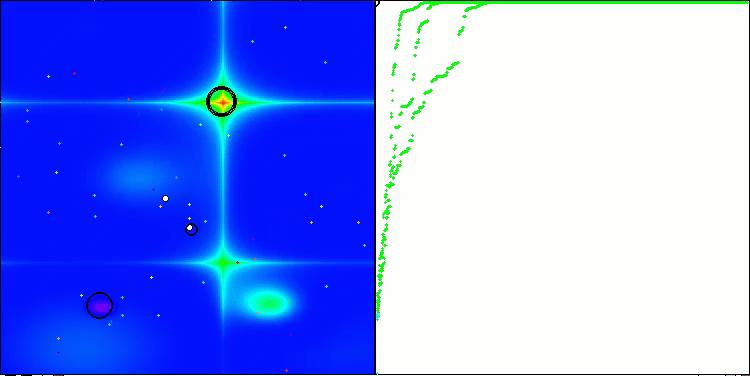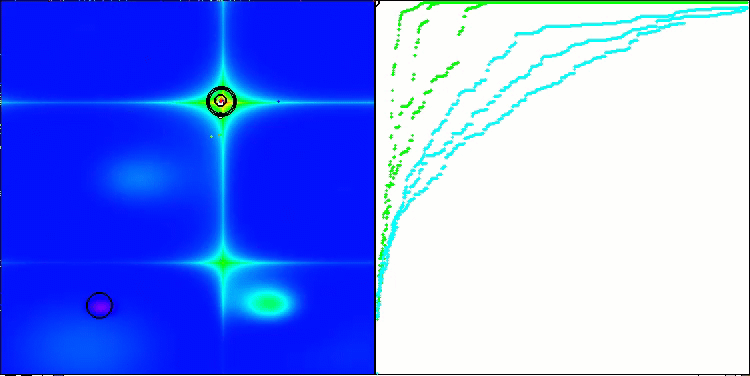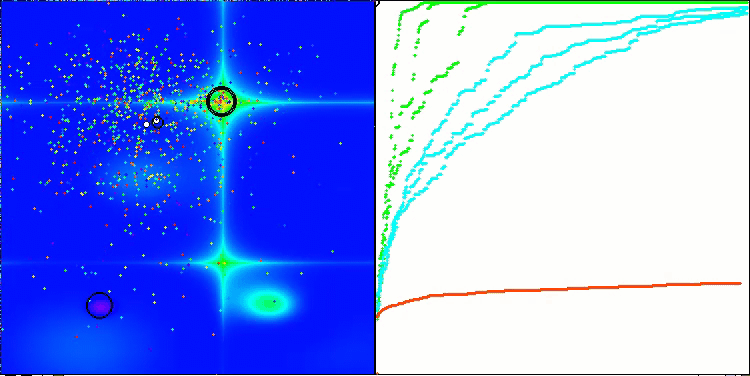
ACSm2 mit der Testfunktion Forest
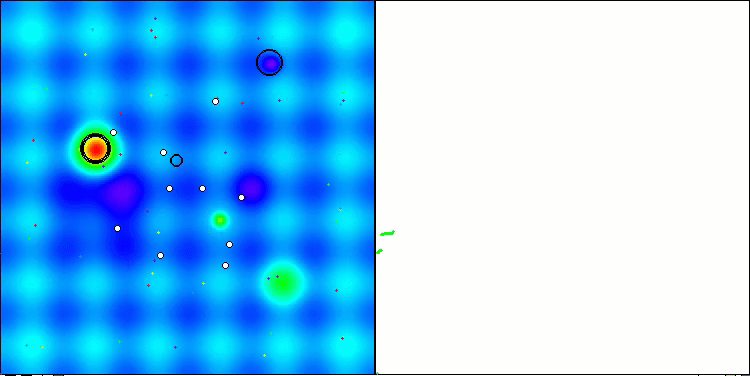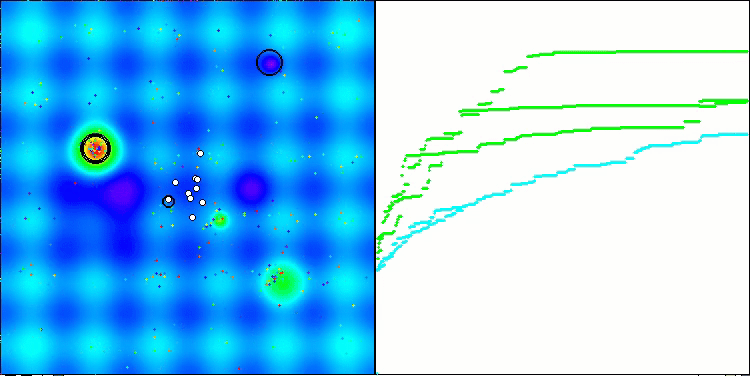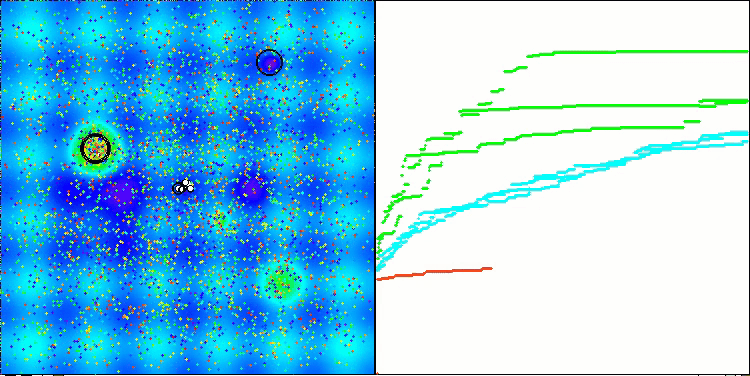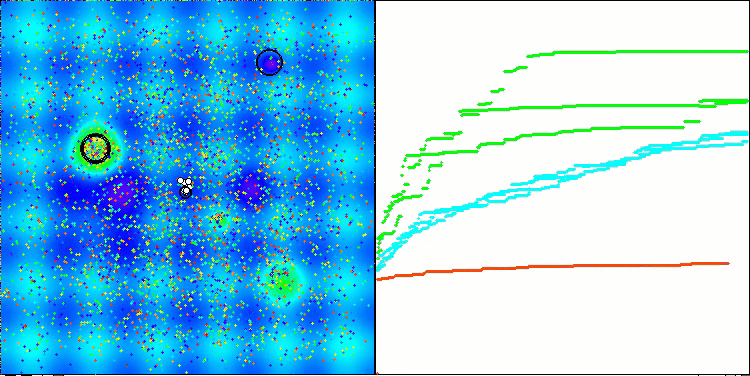
ACSm2 mit der Testfunktion Megacity
Zusammenfassung
Die allgemeinen Schlussfolgerungen lauten wie folgt:
1. Die erste Modifikation des ACS-Algorithmus mit der Hinzufügung von augmentierten Formen der A- und B-Matrizen verbesserte die Genauigkeit der Lösungen, insbesondere bei Hilly-Funktionen mit 1000 Variablen und Forest-Funktionen mit 50 und 1000 Variablen.
2. Die zweite Modifikation, die den Ansatz zum Füllen der Raubtier- und Beute-Matrizen ändert und zufällige Vergleiche zur Aktualisierung der Matrizen verwendet, zeigte eine deutliche Verbesserung der Ergebnisse bei allen Testfunktionen mit 50 und 1000 Variablen, führte aber zu einer größeren Streuung der Ergebnisse bei der Megacity-Funktion mit 10 Variablen.
3. Die dritte Modifikation, bei der der Schwerpunkt auf der Verwendung von Fitness zur Bildung der Raubtier- und Beutepopulationen lag, erfüllte die Erwartungen nicht und zeigte ein etwas schlechteres Gesamtergebnis als die Grundversion des Algorithmus, obwohl sie die Konvergenzgenauigkeit bei glatten Funktionen mit einer geringen Anzahl von Variablen verbesserte.
Jede Modifikation hat also ihre eigenen Stärken und Schwächen, und bei der weiteren Entwicklung des Algorithmus müssen diese Merkmale berücksichtigt werden, um eine effizientere und universellere Version des ACS-Algorithmus zu schaffen.
Mögliche Bereiche für Verbesserungen:
1. Modifizierung der Suchmechanismen:
- Analysieren Sie die derzeit im Algorithmus verwendeten Suchmechanismen und prüfen Sie die Möglichkeit ihrer weiteren Optimierung.
- Untersuchen Sie, ob zusätzliche Mechanismen wie adaptive Suchschritte eingeführt werden können, um die Sucheffizienz zu verbessern.
2. Erforschung hybrider Ansätze:
- Erwägen Sie die Kombination des aktuellen Algorithmus mit anderen Optimierungsmethoden, um die Stärken der verschiedenen Ansätze zu nutzen. Wir können beispielsweise versuchen, Elemente von evolutionären Algorithmen oder Methoden der Schwarmintelligenz zu integrieren, um die Vielfalt und Konvergenzgeschwindigkeit zu erhöhen.
3. Analyse und Verbesserung des Mechanismus der Interaktion zwischen den Populationen:
- Finden Sie heraus, wie das Zusammenspiel der Populationen A und B verbessert werden kann, damit sie sich bei der Suche besser ergänzen. Es könnte sich lohnen, über komplexere Strukturen des Informationsaustauschs oder des kooperativen Lernens zwischen Bevölkerungsgruppen nachzudenken.
Abbildung 1. Farbabstufung der Algorithmusänderungen gemäß den einschlägigen Tests zum Vergleich mit der Grundversion. Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben.
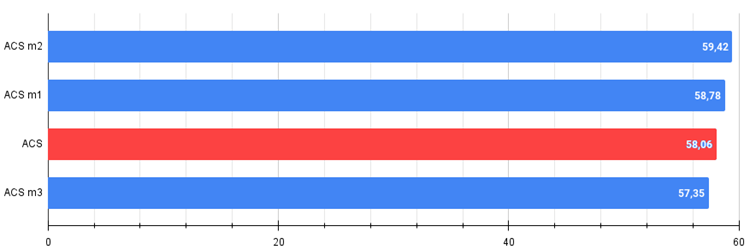
Abbildung 2. Das Histogramm der Ergebnisse der Algorithmusänderung (auf einer Skala von 0 bis 100, je mehr, desto besser,
wobei 100 das maximal mögliche theoretische Ergebnis ist; das Archiv enthält ein Skript zur Berechnung der Bewertungstabelle)
Allgemeine Vor- und Nachteile der modifizierten Versionen des ACS-Algorithmus:
Vorteile:
- Geringe Anzahl von externen Parametern (nur einer).
- Gute Konvergenz bei verschiedenen Arten von Funktionen.
Nachteile
- Streuung der Ergebnisse bei niedrigdimensionalen Funktionen.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Algorithmuscodes begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15014
Elemente der Korrelationsanalyse in MQL5: Chi-Quadrat-Test nach Pearson auf Unabhängigkeit und Korrelationsverhältnis
Neuronale Netze leicht gemacht (Teil 92): Adaptive Vorhersage im Frequenz- und Zeitbereich
Entwicklung eines Expertenberaters für mehrere Währungen (Teil 13): Automatisierung der zweiten Phase — Aufteilung in Gruppen
Entwicklung eines Replay Systems (Teil 51): Die Dinge werden kompliziert (III)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.