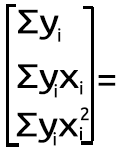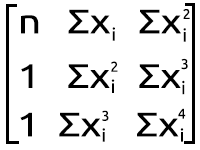
Datenwissenschaft und maschinelles Lernen (Teil 07): Polynome Regression

Inhaltsverzeichnis

• Einführung
• Auffrischung über Polynome
• Ordnung der Polynome
• Polynome Regression
• Wann sollten Sie es verwenden?
• Bayessches Informationskriterium
• Ermittlung der Koeffizienten des Modells
• Das beste Modell zu finden
• Das Merkmal der Skalierung
• Vor- und Nachteile der polynomen Regression
• Abschließende Überlegungen

Einführung

Wir sind noch nicht fertig mit den Regressionsmodellen, wir kehren für kurze Zeit zurück. Wie bereits im ersten Artikel dieser Reihe erwähnt, dient die lineare Regression als Grundlage für viele Modelle des maschinellen Lernens. Heute werden wir uns mit einer etwas anderen Form der linearen Regression beschäftigen, der polynomen Regression.

Das maschinelle Lernen hat unsere Welt in vielerlei Hinsicht verändert. Wir verfügen über verschiedene Methoden, um die Trainingsdaten für Klassifizierungs- und Regressionsprobleme zu lernen, z. B. lineare Regression, logistische Regression, Support Vector Machine, polynome Regression und viele andere Techniken.

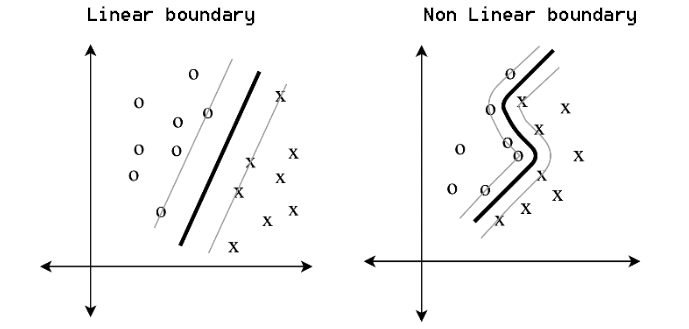
Sie schaffen einfache Grenzen für einfache Probleme und nichtlineare Grenzen für komplexe Probleme.

Erinnerung an Polynome

Ein Polynom ist ein beliebiger mathematischer Ausdruck, der wie folgt aussieht;

polynome Gleichung 01:

Wir haben unsere Daten x, dann werden sie mit immer höheren Potenzen multipliziert und wir haben einige Koeffizienten, die unsere Daten skalieren.

Hier ein weiteres Beispiel für polynome Regression;

polynome Gleichung 02

5 entspricht ao -7 entspricht a1, 4 entspricht a2, und 11,3 entspricht a3. 

Bei Polynomen muss nicht unbedingt jeder einzelne x-Term enthalten sein, siehe diese Gleichung;

polynome Gleichung 03

Sie können sich das so vorstellen, dass Sie schreiben

Ordnung der Polynome 

Es gibt ein weiteres Konzept für Polynome, die Ordnung. Die Ordnung des Polynoms wird mit n bezeichnet. Es ist der höchste Koeffizient in einem mathematischen Ausdruck :

1. Die obige Polynomgleichung 01 ist eine polynome Regression n-ter Ordnung
2. Bei der obigen Polynomgleichung 02 handelt es sich um eine polynome Regression dritter Ordnung/Grad
3. Die obige Polynomgleichung 03 ist ebenfalls eine polynome Regression dritten Grades

Manche Leute sind verwirrt, weil in der zweiten Gleichung 3 Variablen mit x multipliziert werden und ihre Koeffizienten in aufsteigender Reihenfolge 1,2,3 sind, während wir in der zweiten Gleichung nur zwei Variablen haben. Nun, die Ordnung des Polynoms wird in erster Linie durch den höchsten Koeffizienten des Ausdrucks bestimmt.

Polynome Regression

Die polynome Regression ist einer der Algorithmen des maschinellen Lernens, die zur Erstellung von Vorhersagen verwendet werden. Ich habe gehört, dass er häufig zur Vorhersage der Ausbreitungsrate von COVID-19 und anderen Infektionskrankheiten verwendet wurde;
Betrachtung eines einfachen linearen Regressionsmodells.

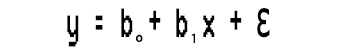
Haben Sie etwas bemerkt?

Diese einfache lineare Regression ist nichts anderes als eine polynome Regression erster Ordnung. Je nach der Reihenfolge der polynomen Regression können wir Variablen hinzufügen, eine polynome Regression zweiter Ordnung würde zum Beispiel so aussehen;

Wir können diesen Ausdruck in eine höhere Ordnung bringen,

Dies ist die polynome Regression k. Ordnung. Moment mal, ist das immer noch eine lineare Regression? Was ist mit dem linearen Modell passiert?
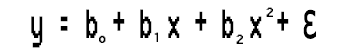
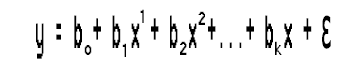
Was ist mit den Linearitäten passiert?

Habe ich in den vorangegangenen Artikeln nicht gesagt, dass sich bei der Regression alles um das lineare Modell dreht? Wie können wir diese polynome Regression an die Linearitäten anpassen, wenn wir diese quadrierten Koeffizienten des Terms haben?

Es kommt darauf an, was linear sein muss und was nichtlinear sein kann. Die Koeffizienten/Betas sind alle linear, es sind nur die Daten selbst, die auf höhere Potenzen gebracht werden.

Wann sollte man eine polynome Regression verwenden?

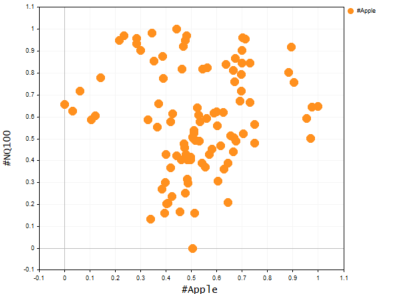
Wir alle wissen, dass das lineare Basismodell nicht geeignet ist, um leicht komplexe Daten (nichtlinear) zu erfassen oder komplexe Beziehungen im Datensatz zu erkennen, und dass die polynome Regression dieses Problem lösen kann. Stellen Sie sich vor, Sie versuchen, den NASDAQ-Kurs anhand des APPLE-Aktienkurses vorherzusagen. Da Apple einer der größten Einflussfaktoren für den NASDAQ-Kurs ist, ist die Beziehung trotzdem nicht linear, sodass das lineare Modell möglicherweise nicht in der Lage ist, unseren Daten so weit anzupassen, dass wir ihm bei zukünftigen Vorhersageentscheidungen vertrauen können. Schauen wir uns an, wie das Chart dieser beiden Symbole auf derselben Achse aussieht, indem wir ein Streudiagramm zur Darstellung der Preiswerte erstellen.

Nachfolgend die Funktion zur Erstellung eines Streudiagramms auf dem Terminal, dank CGraphics (ich wusste nicht, dass so etwas möglich ist, bis ich diesen Artikel schrieb).

bool ScatterPlot(
                 string obj_name,
                 vector &x,
                 vector &y,
                 string legend,
                 string x_axis_label = "x-axis",
                 string y_axis_label = "y-axis", 
                 color  clr = clrDodgerBlue,
                 bool   points_fill = true                 
                )
 { 
   if (!graph.Create(0,obj_name,0,30,70,440,320))
     {
       printf("Failed to Create graphical object on the Main chart Err = %d",GetLastError());
       return(false);
     }
   
   ChartSetInteger(0,CHART_SHOW,ChartShow);
   
   double x_arr[], y_arr[]; 
   
   pol_reg.vectortoArray(x,x_arr);
   pol_reg.vectortoArray(y,y_arr);
   
   CCurve *curve = graph.CurveAdd(x_arr,y_arr,clr,CURVE_POINTS);
   curve.PointsSize(10);
   curve.PointsFill(points_fill); 
   curve.Name(legend);
   graph.XAxis().Name(x_axis_label);
   graph.XAxis().NameSize(10);
   graph.YAxis().Name(y_axis_label);
   graph.YAxis().NameSize(10);
   graph.FontSet("Lucida Console",10);
   graph.CurvePlotAll();
   graph.Update();
 
   delete(curve);
   
   return(true);
 }

   string plot_name = "x vs y"; 
   
   ObjectDelete(0,plot_name);    
   ScatterPlot(plot_name,x_v,y_v,X_symbol,X_symbol,Y_symol,clrOrange); 

Ausgabe:

Grafik von Nasdaq vs. Apple

Es lässt sich nicht leugnen, dass das lineare Modell bei dieser Art von Problem nicht gut funktioniert, also versuchen wir es mit polynomer Regression. Dies wirft nun die Frage auf, welche Ordnung man verwenden sollte, um ein Polynommodell zu erstellen.

Blick auf den Modellausdruck;

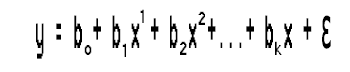
Da wir nur eine unabhängige Variable haben, können wir sie auf jede beliebige Potenz bringen. Woher wissen wir wiederum, welche Potenz wir diese eine unabhängige Variable erhöhen sollten, mit anderen Worten, woher wissen wir, welche Ordnung das Polynom haben sollte? Um dies zu verstehen, müssen wir zunächst etwas verstehen, das als Bayessches Informationskriterium BIC bezeichnet wird.

Bayessches Informationskriterium

Ihre Formel lautet wie folgt.

BIC = n log(SSE) + k log (n)

 n = Anzahl der Datenpunkte 

 k = Anzahl der Parameter

Bevor wir jedoch das beste Modell herausfinden, sollten wir eine einfache polynome Regression erstellen und sehen, was sie ausmacht, um dann die beste Reihenfolge zu finden.

Ermitteln der Koeffizienten des Modells.

Aus der Gleichung,

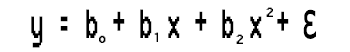
Lösen wir diese Aufgabe der polynomen Regression zweiten Grades, indem wir die Werte von b0, b1 und b2 ermitteln.

Wir verwenden das folgende Gleichungssystem,

n = Anzahl der Datenpunkte

Um die Werte zu berechnen, verwenden wir diesen einfachen Datensatz.

X	y
3	2.5
4	3.2
5	3.8
6	6.5
7	11.5.

Wir haben nun eine Reihe von Simultangleichungen für unser Problem und den einfachen Datensatz, auf dem wir aufbauen können. Sie können die Werte einfach einfügen und die Koeffizienten in einem wissenschaftlichen Taschenrechner, Microsoft Excel oder einem anderen Programm finden, das Sie bevorzugen, und Sie erhalten die Werte;

• b0 = 12.4285714
• b1= -5.5128571
• b2 = 0.7642857

Aber das ist nicht unsere Sache hier in MQL5, lassen Sie uns herausfinden, wie man dieses Ergebnis in Meta-Editor aus dem Satz der obigen Gleichung zu erreichen, Lassen Sie uns es in die Matrixform zu transformieren, Es wird jetzt dann

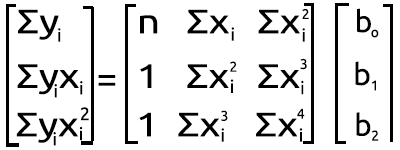polynome Matrixgestalt

Das Ergebnis dieser Multiplikation führt uns zurück zur simultanen Gleichung. Sie wissen also, dass wir mathematisch korrekt sind.

Lassen Sie uns etwas Code schreiben-

Klasse der Polynomen Regression:

class CPolynomialRegression
  {
   private:
                        ulong  m_degree; //depends on independent vars
                        int    n;   //number of samples in the dataset
                        vector x;
                        vector y;
                        matrix PolyNomialsXMatrix; //x matrix 
                        matrix PolynomialsYMatrix; //y matrix 
                        matrix Betas;
                        double Betas_A[];  //coefficients of the model stored in Array

                        void   Poly_model(vector &Predictions,ulong degree);
                        
   public:
                        CPolynomialRegression(vector& x_vector,vector &y_vector,int degree=2);
                       ~CPolynomialRegression(void);
                        
                        double RSS(vector &Pred);               //sum of squared residuals
                        void   BIC(ulong k, vector &bic,int &best_degree);      //Bayessian information Criterion
                        void   PolynomialRegressionfx(ulong degree, vector &Pred);
                        double r_squared(vector &y,vector &y_predicted); 
                        
                        void   matrixtoArray(matrix &mat, double &Array[]);
                        void   vectortoArray(vector &v, double &Arr[]);
                        void   MinMaxScaler(vector &v);
  };

Unsere Klasse ist in erster Linie einfach und hat keine komplizierten Code zu lesen, auf den ersten, wenn irgendwelche Änderungen vorgenommen werden, wird der Code auf die Dateien unten angehängt aktualisiert werden, weil ich diesen Code zu der Zeit schreibe ich auch diesen Beitrag schreiben.

Aus unserem Matrix-Ausdruck der Polynom-Matrix-Bild Abbildung oben, können wir sehen, dass wir eine Menge von Summierung für jedem Datenpunkt mit seinen eigenen Exponenten haben, da fast jedes Element in unserem ersten Array auf der rechten Seite des Gleichheitszeichens berechnet werden muss. Unten ist ein kurzes Beispiel-Code, wie es zu tun.

    vector c;
    vector x_pow;
    
    for (ulong i=0; i<PolynomialsYMatrix.Rows(); i++)
       for (ulong j=0; j<PolynomialsYMatrix.Cols(); j++) 
         {
            if (i+j == 0)  PolynomialsYMatrix[i][j] = y.Sum(); 
            else         
               {
                   x_pow = MathPow(x,i);       c = y*x_pow; //x vector elements are raised to the power i then the resulting vector is  
                                                                //Then multiplied to the vector of y values the output is stored in a vector c
                   PolynomialsYMatrix[i][j] =  c.Sum();     //Finally the sum of all the elements in a vector c is stored in the matrix of polynomials
               }
         }

Wenn Sie sich die Matrix auf der rechten Seite der Abbildung Abbildung der Polynom-Matrix oben ansehen, werden Sie auch feststellen, dass wir die Funktionen Σxy und Σxy^2 haben. Dies ist ein etwas anderer Ansatz, also lassen Sie uns auch den Code dafür sehen

  
   double pow = 0;
   ZeroMemory(x_pow);
   
    for (ulong i=0,index = 0; i<PolyNomialsXMatrix.Rows(); i++)
       for (ulong j=0; j<PolyNomialsXMatrix.Cols(); j++, index++)
          {
             pow = (double)i+j; //The power corresponds to the access index of rows and cols i+j
             if (pow == 0) PolyNomialsXMatrix[i][j] = n;
             else          
                 {
                   x_pow = MathPow(x,pow); //x_pow is a vector to store the x vector raised to a certain power
                   
                   PolyNomialsXMatrix[i][j] =  x_pow.Sum(); //find the sum of the power vector
                 }
          }
    

Nun, da wir diese Summationszeilen haben, die sich als sehr wichtig für die polynome Regression erweisen, lassen Sie uns fortfahren, indem wir die Matrix erstellen, die diese Werte beinhalten wird, genau wie die zweite Matrix mit folgender Gestalt der polynomen Matrix.

Beginnen Sie mit der Matrix auf der linken Seite des Gleichheitszeichens.

    ulong order_size = degree+1;
    PolyNomialsXMatrix.Resize(order_size,order_size);
    
    PolynomialsYMatrix.Resize(order_size,1);
    
    vector c;
    vector x_pow;
    
    for (ulong i=0; i<PolynomialsYMatrix.Rows(); i++)
       for (ulong j=0; j<PolynomialsYMatrix.Cols(); j++) 
         {
            if (i+j == 0)  PolynomialsYMatrix[i][j] = y.Sum(); 
            else         
               {
                   x_pow = MathPow(x,i);       c = y*x_pow;
                   PolynomialsYMatrix[i][j] =  c.Sum(); 
               }
         }
    
   if (debug) Print("Polynomials y vector \n",PolynomialsYMatrix);

Wenn man sich ansieht, wie die Elemente in der Matrix angeordnet sind, weiß man, dass nur das erste Element nicht mit den Werten von x multipliziert wird, alle anderen werden mit den Werten von x multipliziert, die um den Index ihrer Position in der Matrix erhöht sind.

Umarrangieren des Arrays um das Zentrum der Gleichung

Meine erste Beobachtung ist, dass diese Matrix-Array-Größe gleich der quadrierten Größe der Y-Matrix/Matrix auf der linken Seite ist, die wir gerade zuvor berechnet haben, und dass die Potenz, auf die die X-Elemente angehoben werden, darauf basiert, wo das Element in der Matrix positioniert ist, indem man die Zeilen und Spalten betrachtet. Da diese Matrix quadriert ist, müssen wir sie aufbauen, indem wir ihre Spalten zweimal in zwei entsprechenden Schleifen durchlaufen, siehe den folgenden Code.

    ulong order_size = degree+1;
    PolyNomialsXMatrix.Resize(order_size,order_size);
    
    PolynomialsYMatrix.Resize(order_size,1);
     
    vector x_pow;
    
//---
   
   PolyNomialsXMatrix.Resize(order_size, order_size);
   
   double pow = 0;
   ZeroMemory(x_pow);
   //x_pow.Copy(x);
   
    for (ulong i=0,index = 0; i<PolyNomialsXMatrix.Rows(); i++)
       for (ulong j=0; j<PolyNomialsXMatrix.Cols(); j++, index++)
          {
             pow = (double)i+j;
             if (pow == 0) PolyNomialsXMatrix[i][j] = n;
             else          
                 {
                   x_pow = MathPow(x,pow);
                   
                   PolyNomialsXMatrix[i][j] =  x_pow.Sum();
                 }
          }
  //---

   if (debug) Print("Polynomial x matrix\n",PolyNomialsXMatrix);
   

Nachfolgend sehen Sie die Ausgabe der obigen Codeschnipsel.

CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  Polynomials y vector 
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  [[27.5]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [158.8]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [966.2]]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  Polynomial x matrix
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  [[5,25,135]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [25,135,775]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [135,775,4659]]

Um die Werte der unbekannten Matrix der Beta-Werte zu finden, müssen wir uns mit der Mathematik der Matrizen befassen.

Ermitteln der unbekannten Werte der multiplizierten Matrix:

Wir folgen dem gleichen Verfahren für unsere Matrizen, deren Werte wir gerade oben erhalten haben.

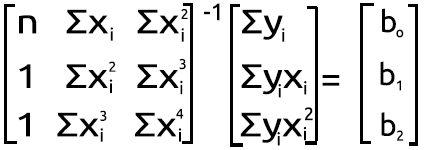
Der Prozess der Suche nach der Inversen einer Matrix ist relativ einfach und erfordert zwei, wenn nicht sogar nur eine Zeile Code unter Verwendung der Standardbibliothek für Matrix.

    PolyNomialsXMatrix = PolyNomialsXMatrix.Inv(); //find the inverse of the matrix then assign it to the original matrix 

Um schließlich die Koeffizienten des Modells zu ermitteln, müssen wir die inverse Matrix mit der Matrix multiplizieren, in der die y-Werte summiert sind.

    Betas = PolyNomialsXMatrix.MatMul(PolynomialsYMatrix);

Jetzt ist es an der Zeit, die Betamatrix auszudrucken, um zu sehen, was wir aus diesem Prozess gewonnen haben;

CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  Betas 
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  [[12.42857142857065]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [-5.512857142857115]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [0.7642857142856911]]

Großartig, genau das, wonach wir gesucht haben. Jetzt, da wir die Koeffizienten der polynomen Regression 2.

void CPolynomialRegression::Poly_model(vector &Predictions, ulong degree)
 {
   ulong order_size = degree+1;
   Predictions.Resize(n);
   
   matrixtoArray(Betas,Betas_A); 
   
    for (ulong i=0; i<(ulong)n; i++)
     {
      double sum = 0;
       for (ulong j=0; j<order_size; j++) 
         {
           if (j == 0) sum += Betas_A[j];
           else        sum += Betas_A[j] * MathPow(x[i],j);
         }
       Predictions[i] = sum;
     }
 }

So einfach der Code des Modells auch aussehen mag, er kann so viele Grade verarbeiten, wie Sie wollen, zumindest im Moment. Stellen wir die Modellvorhersagen auf der gleichen Achse der x- und y-Werte dar

   ObjectDelete(0,plot_name);
   plot_name = "x vs y";   
   ScatterCurvePlots(plot_name,x_v,y_v,Predictions,"Predictions","x","y",clrDeepPink);

bool ScatterCurvePlots(
                       string obj_name,
                       vector &x,
                       vector &y,
                       vector &curveVector, 
                       string legend,
                       string x_axis_label = "x-axis",
                       string y_axis_label = "y-axis", 
                       color  clr = clrDodgerBlue,
                       bool   points_fill = true                 
                      )
 {
 
   if (!graph.Create(0,obj_name,0,30,70,440,320))
     {
       printf("Failed to Create graphical object on the Main chart Err = %d",GetLastError());
       return(false);
     }
   
   ChartSetInteger(0,CHART_SHOW,ChartShow);
   
   
//--- additional curves

   double x_arr[], y_arr[]; 
   
   pol_reg.vectortoArray(x,x_arr);
   pol_reg.vectortoArray(y,y_arr);

   double curveArray[]; //curve matrix array
   
   pol_reg.vectortoArray(curveVector,curveArray);
   
   graph.CurveAdd(x_arr,y_arr,clrBlack,CURVE_POINTS,y_axis_label);
   graph.CurveAdd(x_arr,curveArray,clr,CURVE_POINTS_AND_LINES,legend);
    
//---

   graph.XAxis().Name(x_axis_label);
   graph.XAxis().NameSize(10);
   graph.YAxis().Name(y_axis_label);
   graph.YAxis().NameSize(10);
   graph.FontSet("Lucida Console",10);
   graph.CurvePlotAll();
   graph.Update();
   
   return(true);
 } 

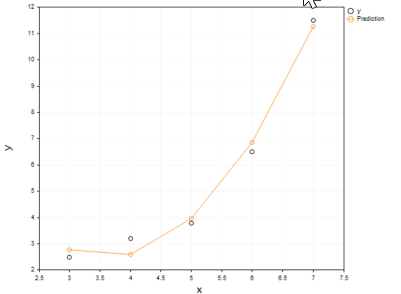
Ausgabe:

Es ist unbestreitbar, dass sich das polynome Modell unseren Daten gut anpasst und in diesem Fall ein lineares Modell übertreffen könnte.

Suche nach dem besten Polynomgrad

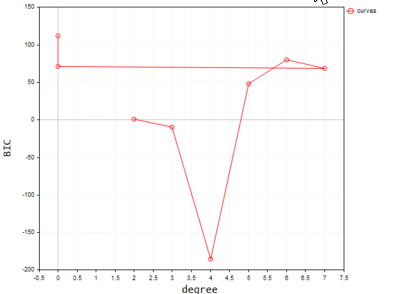
Wie bereits erwähnt, ist das Bayessche Informationskriterium der Algorithmus, den wir verwenden, um das beste Modell zu finden. Nach BIC ist das Modell mit dem niedrigsten BIC-Wert das beste Modell, weil es die geringste Summe von Residuen/Fehlern aufweist.

void  CPolynomialRegression::BIC(ulong k, vector &bic,int &best_degree)
 {
   vector Pred;
   
   bic.Resize(k-2); 
   best_degree = 0;
   
    for (ulong i=2, counter = 0; i<k; i++)
      {         
         PolynomialRegressionfx(i,Pred);         
         bic[counter] = ( n * log(RSS(Pred)) ) + (i * log(n));  
         
         counter++;
      }
      
//--- 

   bool positive = false;
   for (ulong i=0; i<bic.Size(); i++)
      if (bic[i] > 0) { positive = true; break; }
   
  
   double low_bic = DBL_MAX;
   
   if (positive == true) 
    for (ulong i=0; i<bic.Size(); i++) 
     {
      if (bic[i] < low_bic && bic[i] > 0) low_bic = bic[i];
     }
   else  low_bic = bic.Min(); //bic[ best_degree = ArrayMinimum(bic) ];
      
   printf("Best Polynomial Degree(s) is = %d with BIC = %.5f",best_degree = best_degree+2,low_bic);

 }

Aus dem Code ist die Funktion RSS Residuenquadratsumme. Diese Funktion ermittelt die Summe der quadrierten Residuen.

double CPolynomialRegression::RSS(vector &Pred)
 {
  if (Pred.Size() != y.Size()) Print(__FUNCTION__," Predictions Array and Y matrix doesn't have the same size");
 
   double sum =0;
    for (int i=0; i<(int)y.Size(); i++)
      sum += MathPow(y[i] - Pred[i],2);
      
    return(sum);
 }

Lassen Sie mich nun diese Funktion ausführen, um das beste Polynom unter den 10 Graden zu finden.

   vector bic_; //A vector to store the model BIC values for visualization purposes only
   
   int best_order; //A variable to store the best model order 
   
   pol_reg.BIC(polynomia_degrees,bic_,best_order);

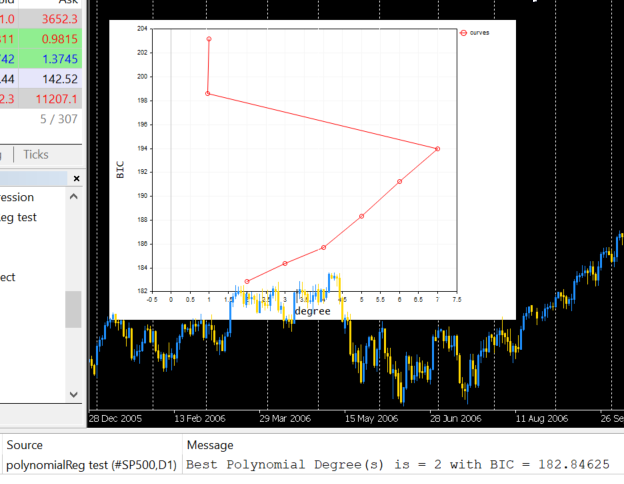
Unten sehen Sie die Ausgabe, wenn sie auf dem Terminal dargestellt wird;

Nach unserem Code hat das beste Modell einen Polynomgrad von 2. Es ist unbestreitbar, dass das Modell mit dem Grad 2 das beste für diesen einfachen Datensatz ist.

2022.09.22 20:58:21.540 polynomialReg test (#NQ100,D1)  Best Polynomial Degree(s) is = 2 with BIC = 0.93358

Nachfolgend finden Sie die Ergebnisse der Vorhersagen der einzelnen Modelle.

7 der Degree-Ergebnisse werden auf derselben Achse aufgetragen.

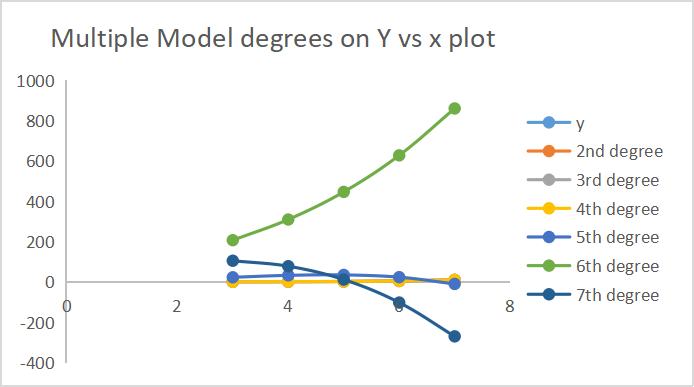
Funktionsskalierung ist unerlässlich

Da wir bei der polynomen Regression nur eine unabhängige Variable haben, die wir auf eine beliebige Potenz erhöhen können, wird die Skalierung des Merkmals an erster Stelle sehr wichtig, denn wenn Ihre unabhängige Variable Merkmale im Bereich von 100-1000 hat, werden diese Merkmale im zweiten Grad zwischen 10000 und 1000.000 liegen und im dritten Grad zwischen 10^6 und 10^9. OMG, das ist eine ganze Menge.

Es gibt viele Möglichkeiten und Algorithmen, um den Datensatz zu skalieren, aber wir werden die Min-Max-Skalierungsfunktion verwenden, um die Vektoren zu skalieren. Beachten Sie, dass dieser Prozess vor jeder Manipulation des Datensatzes durchgeführt werden sollte. Nachfolgend finden Sie den Code für die Funktion, die zur Skalierung der Vektoren aus dem Datensatz verwendet wird.

void MinMaxScaler(vector &v)
 {
   //Normalizing vector using Min-max scaler
   
   double min, max, mean;
   min = v.Min();
   max = v.Max();
   mean = v.Mean();
   
   for (int i=0; i<(int)v.Size(); i++)
     v[i] = (v[i] - min) / (max - min);  
   
 } 

Jetzt haben wir alles, was wir brauchen. Es ist an der Zeit, das Modell anhand der Live-Marktdaten zu erstellen, siehe die Grafik Nasdaq vs. Apple von oben. Um die Ergebnisse zu erzielen, müssen wir einige wenige Schritte unternehmen.

Extraktion von Marktpreisdaten und Skalierung.

   if (!SymbolSelect(X_symbol,true))   printf("%s not found on Market watch Err = %d",X_symbol,GetLastError());  
   if (!SymbolSelect(Y_symol,true))    printf("%s not found on Market watch Err = %d",Y_symol,GetLastError());  
  
   matrix rates(bars, 2);
   vector price_close;

//---

   vector x_v, y_v;

   price_close.CopyRates(X_symbol,PERIOD_H1,COPY_RATES_CLOSE,1,bars); //extracting prices
   
   rates.Col(price_close,0);
   
   x_v.Copy(price_close);

//---
   
   price_close.CopyRates(Y_symol,PERIOD_H1,COPY_RATES_CLOSE,1,bars);
   
   y_v.Copy(price_close);
    
   rates.Col(price_close,1);
   
//---

   MinMaxScaler(x_v); //scalling all the close prices
   MinMaxScaler(y_v); //scalling all the close prices

//---

Im Folgenden wird das Ergebnis in einem Streudiagramm dargestellt:

02: Suche nach dem besten Modell mit der Bic-Funktion

//--- FINDING BEST MODEL USING BIC
   
   vector bic_; //A vector to store the model BIC values for visualization purposes only
   
   int best_order; //A variable to store the best model order 
   
   pol_reg.BIC(polynomia_degrees,bic_,best_order);
   
   ulong bic_cols = polynomia_degrees-2; //2 is the first in the polynomial order 
   
//--- Plot BIc vs model degrees

   vector x_bic;
   x_bic.Resize(bic_cols);  
   for (ulong i=2,counter =0; i<bic_cols; i++)  {   x_bic[counter] = (double)i;   counter++;   }     
    
   ObjectDelete(0,plot_name);
   plot_name = "curves";
   ScatterCurvePlots(plot_name,x_bic,y_v,bic_,"curves","degree","BIC",clrBlue);
   Sleep(10000);

Hier ist die Ausgabe,

Schließlich 

Wir wissen jetzt, dass die beste Modellreihenfolge 2 ist. Wir erstellen ein Modell mit 2 Graden und verwenden es, um die Werte vorherzusagen, und zeichnen die Werte schließlich in das Diagramm ein.

   vector Predictions;
   pol_reg.PolynomialRegressionfx(best_order,Predictions); //Create model with the best order then use it to predict
   
   ObjectDelete(0,plot_name);
   plot_name = "Actual vs predictions";   
   ScatterCurvePlots(plot_name,x_v,y_v,Predictions,string(best_order)+"degree Predictons",X_symbol,Y_symol,clrDeepPink);

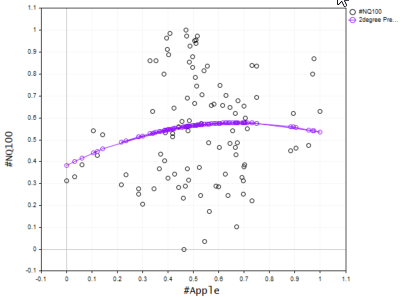
Das resultierende Diagramm ist unten abgebildet:

Überprüfung der Modellgenauigkeit

Obwohl wir den besten Grad für das Modell gefunden haben, müssen wir immer noch wissen, wie dieses Modell die Beziehung in unserem Datensatz verstehen kann, indem wir seine Vorhersagegenauigkeit überprüfen.

   Print("Model Accuracy = ",DoubleToString(pol_reg.r_squared(y,Predictions)*100,2),"%");

Ausgabe:

2022.09.30 16:19:31.735 polynomialReg test (#SP500,D1)  Model Accuracy = 2.36%

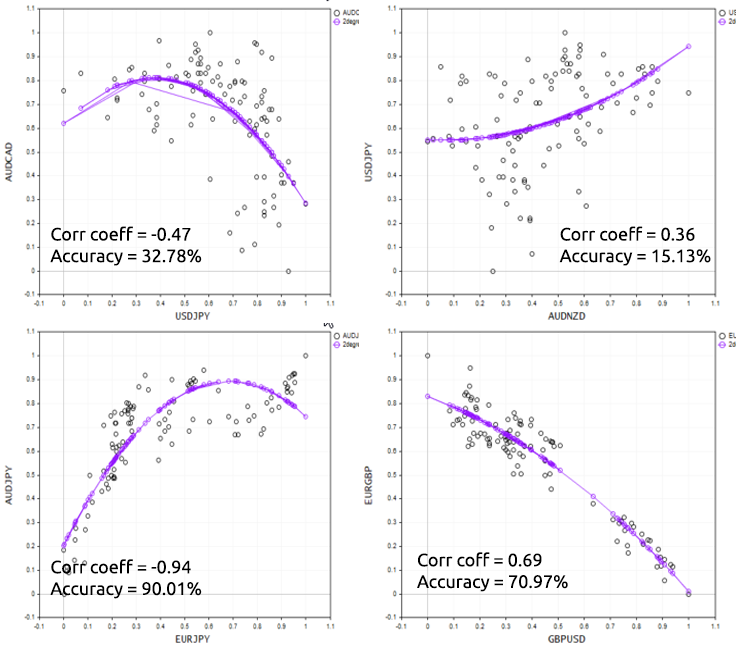
Die schlechte Nachricht für uns: Wir haben uns das schlechteste Modell unter den schlechtesten Modellen ausgesucht. Bevor Sie sich nun entscheiden, eine polynome Regression zur Lösung einer bestimmten Aufgabe zu verwenden, denken Sie daran, dass die polynome Regression ein lineares Modell als Grundlage hat, sodass Sie immer Daten haben, die korrelieren. Sie müssen nicht linear korreliert sein, aber eine Korrelation von etwa 50 % könnte ideal sein; wenn ich mir unseren NASDAQ- vs. APPLE-Datensatz anschaue und seine Korrelation prüfe, habe ich einen Korrelationskoeffizienten von weniger als 1 %. Dies ist wahrscheinlich der Grund dafür, dass wir aus diesem Datensatz kein gutes Modell erstellen konnten. 

   Print("correlation coefficient ",x_v.CorrCoef(y_v));

Um diesen Punkt gut zu demonstrieren, probieren wir das Skript mit verschiedenen Forex-Instrumenten aus.

Vor- und Nachteile der polynomen Regression

Vorteile

• Sie können eine nichtlineare Beziehung zwischen den Variablen modellieren
• Es gibt eine breite Palette von Funktionen, die Sie für die Anpassung verwenden können
• Gut für explorative Zwecke; Sie können verschiedene Polynomordnungen/Grade testen, um herauszufinden, welche für Ihren Datensatz am besten geeignet sind.
• Es ist einfach zu kodieren und die Ergebnisse zu interpretieren und dennoch leistungsstark

Nachteile:

• Ausreißer können die Ergebnisse erheblich verfälschen 
• Polynome Regressionsmodelle sind anfällig für Überanpassung (zweifeln Sie daran)
• Als Folge der Überanpassung funktioniert das Modell möglicherweise nicht mit den externen Daten.

Abschließende Überlegungen

Die polynome Regression ist in vielen Fällen eine nützliche Technik des maschinellen Lernens, da die Beziehung zwischen einer unabhängigen und einer abhängigen Variable nicht linear sein sollte. Sie gibt Ihnen mehr Freiheit bei der Arbeit mit verschiedenen Datensätzen und hilft, die Lücke zu füllen, die das lineare Modell nicht füllen kann, diese Technik ist eine bessere Wahl, wenn das lineare Modell die Daten nicht ausreichend anpasst. Da dieses parametrische Modell sehr flexibel ist, kann es bei untrainierten Daten/Testdaten sehr schlecht abschneiden. Ich würde sagen, wählen Sie die niedrigsten Modellordnungen und geben Sie dem Modell Raum für Fehler. 

Danke fürs Lesen.

Weitere Informationen über Matrizen in Array-Form finden Sie unter >> Matrizen und Vektoren

Weiterführende Literatur | Bücher | Referenzen

• Neural Networks for Pattern Recognition (Advanced Texts in Econometrics)
• Neural Networks: Tricks of the Trade (Lecture Notes in Computer Science, 7700)
• Deep Learning (Adaptive Computation and Machine Learning series)

Artikel Referenzen:

• Datenwissenschaft und maschinelles Lernen (Teil 01): Lineare Regression
• Datenwissenschaft und maschinelles Lernen (Teil 02): Logistische Regression 
• Datenwissenschaft und maschinelles Lernen (Teil 03): Matrix-Regressionen
• Datenwissenschaft und maschinelles Lernen (Teil 06): Gradientenverfahren