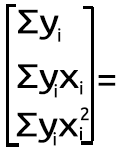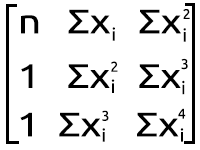
数据科学与机器学习（第 07 部分）：多项式回归
1 016
0
内容目录:
概述
我们还没有贯穿回归模型，我们再回退一会儿。 正如我在本系列的第一篇文章中所说，基本线性回归是许多机器学习模型的基础，今天我们将讨论的一些东西，与称为多项式回归的线性回归略有不同。 机器学习在很多方面改变了我们的世界，我们有不同的方法来学习分类和回归问题的训练数据，例如线性回归、逻辑回归、支持向量机、多项式回归、和许多其它技术。一些参数方法如多项式回归和支持向量机脱颖而出，在于它们的多用途。
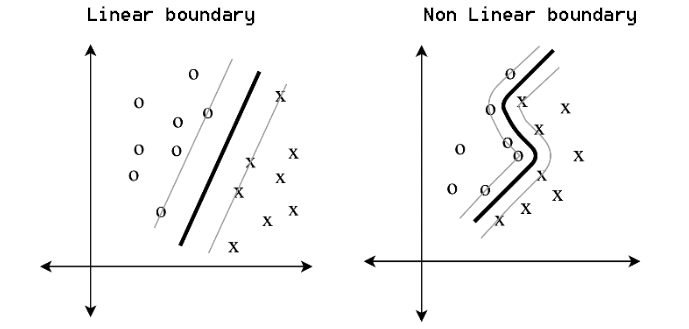
它们为简单问题创建简单边界，亦可为复杂问题创建非线性边界
多项式提醒
多项式是任何看起来像这样的数学表达式；
多项式方程 01：
我们已有数据 x，然后取它来升幂，然后我们也有一些系数能缩放我们的数据。
此处是多项式回归的另一个示例
多项式方程 02：
5 对应于 ao -7 对应于 a1，4 对应于 a2，且 11.3 对应于 a3。
在多项式中，您不一定需要在此处包含每个 x 项，我们来看看这个等式；
多项式方程 03：
您可以想象它如书写
多项式的阶
多项式中还有另一个概念叫阶，多项式的阶用 n 表示。 它是数学表达式中的最高系数，例如：- 上面的多项式方程 01，是一个 n 阶多项式回归
- 上面的多项式方程 02，是一个三阶/次多项式回归
- 上面的多项式方程 03，也是三阶/次多项式回归
一些人感到困惑，因为在第二个方程中，我们有 3 个变量乘以 x，它们的系数按升序排列 1、2、3，同时在第二个方程中我们只有两个变量。 好吧，多项式的阶数主要由表达式中的最高系数决定。
多项式回归
多项式回归是进行预测的机器学习算法之一，我听说它已被广泛用于预测 COVID-19 和其它传染病的传播率，我们来看看这个算法是由什么组成的。来看一个简单的线性回归模型。
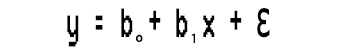
注意到什么了吗？
这个简单的线性回归并无特别之处，只不过是一阶多项式回归，根据多项式回归我们可以向其添加变量的阶，例如，二阶多项式回归如下所示：
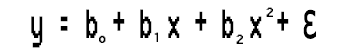
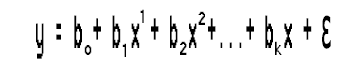
这是 k 阶多项式回归，等一下，这还是线性回归吗？线性模型发生了什么。
线性度发生了什么？
我在前面的文章中不是说过，回归全部是关于线性模型的吗？ 当我们已有这些平方项系数时，我们如何将这种多项式回归拟合到线性度。 这一切都归结到哪些需要线性，哪些可以是非线性的。 系数/Beta 都是线性的，它只是数据本身升到更高的幂。
什么时候应该使用多项式回归？
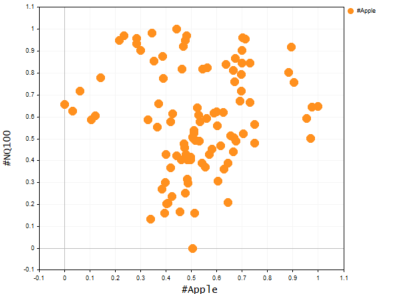
我们都知道，基本线性模型不擅长拟合稍微复杂的数据（非线性）或计算数据集中的复杂关系，而多项式回归就是为了解决这个问题。 想象一下，尝试取苹果股价预测纳斯达克的价格，苹果是纳斯达克价格背后最大的影响者之一，它的关系仍然不是线性的，那么线性模型也许无法将我们的数据集拟合到我们可以信任它，并据其制定未来预测决策的程度。 我们创建散点图来显示价格值，看看这两个交易品种的图形在同一数轴上的样子。
下面是在终端上创建散点图的函数，这要归功于 CGraphics（直到我撰写这篇文章的那一刻，我才知道这样的事情是可能的）
bool ScatterPlot( string obj_name, vector &x, vector &y, string legend, string x_axis_label = "x-axis", string y_axis_label = "y-axis", color clr = clrDodgerBlue, bool points_fill = true ) { if (!graph.Create(0,obj_name,0,30,70,440,320)) { printf("Failed to Create graphical object on the Main chart Err = %d",GetLastError()); return(false); } ChartSetInteger(0,CHART_SHOW,ChartShow); double x_arr[], y_arr[]; pol_reg.vectortoArray(x,x_arr); pol_reg.vectortoArray(y,y_arr); CCurve *curve = graph.CurveAdd(x_arr,y_arr,clr,CURVE_POINTS); curve.PointsSize(10); curve.PointsFill(points_fill); curve.Name(legend); graph.XAxis().Name(x_axis_label); graph.XAxis().NameSize(10); graph.YAxis().Name(y_axis_label); graph.YAxis().NameSize(10); graph.FontSet("Lucida Console",10); graph.CurvePlotAll(); graph.Update(); delete(curve); return(true); }
string plot_name = "x vs y"; ObjectDelete(0,plot_name); ScatterPlot(plot_name,x_v,y_v,X_symbol,X_symbol,Y_symol,clrOrange);
输出:
您不能否认线性模型在这类问题中表现不佳的事实，所以我们来尝试多项式回归。 那么现在，这就提出了一个问题，即制作多项式模型应该使用几阶？
Nasdaq vs Apple 图形
查看模型表达式；
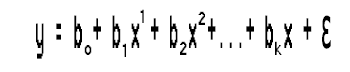
鉴于我们只有一个自变量，我们可以将其带到我们想要的任何幂，再次我们如何知道我们应该提高这个自变量的幂，换言之，我们如何知道多项式应该是几阶？若要理解这一点，我们首先了解一种称为贝叶斯（Bayesian）信息准则的东西，表示为 BIC。
贝叶斯（Bayesian）信息准则
其公式给出如下；
BIC = n log(SSE) + k log (n)
n = 数据点数量
k = 参数数量
但在我们找到最佳模型之前，我们创建一个基本的多项式回归，看看是什么让它跳升，从那里我们就可以继续寻找最佳阶数。
查找模型的系数。
从方程；
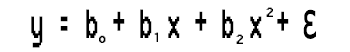
我们通过查找 b0、b1 和 b2 的值来求解这个二阶多项式回归任务。
我们使用以下方程组，
n = 数据点数量
为了计算这些值，我们使用这个简单的数据集。
| X | y |
|---|---|
| 3 | 2.5 |
| 4 | 3.2 |
| 5 | 3.8 |
| 6 | 6.5 |
| 7 | 11.5 |
我们现在拥有一组针对我们问题的联立方程，和简单的数据集，可据其构建事物，您可以轻松地插入值，并在科学计算器、Microsoft excel、或您喜欢的工具中找到系数。您将获得值;
- b0 = 12.4285714
- b1= -5.5128571
- b2 = 0.7642857
但这不是我们要在在 MQL5 中做的事情，我们从上面的联立方程组中找出如何在 MetaEditor 中实现此结果。我们将其转换为矩阵形式，现在它变成了
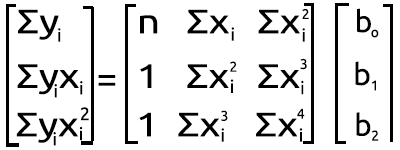多项式矩阵图
这种乘法的结果将我们带回到联立方程。 所以您知道我们在数学上是正确的，
现在我们编写一些代码；
多项式回归类：
class CPolynomialRegression { private: ulong m_degree; //depends on independent vars int n; //number of samples in the dataset vector x; vector y; matrix PolyNomialsXMatrix; //x matrix matrix PolynomialsYMatrix; //y matrix matrix Betas; double Betas_A[]; //coefficients of the model stored in Array void Poly_model(vector &Predictions,ulong degree); public: CPolynomialRegression(vector& x_vector,vector &y_vector,int degree=2); ~CPolynomialRegression(void); double RSS(vector &Pred); //sum of squared residuals void BIC(ulong k, vector &bic,int &best_degree); //Bayessian information Criterion void PolynomialRegressionfx(ulong degree, vector &Pred); double r_squared(vector &y,vector &y_predicted); void matrixtoArray(matrix &mat, double &Array[]); void vectortoArray(vector &v, double &Arr[]); void MinMaxScaler(vector &v); };
我们的类主要部分很简单，没有复杂的代码要读，若是进行任何修改，代码将在下面附加的文件中更新，因为我在撰写这篇文章的同时，正在编写这段代码。
我们从上面的多项式矩阵图像示意图里的矩阵表达式中，我们可以看到每个数据点在随其自己的指数上升有很多求和，因为这个计算几乎需要我们等号右侧第一个数组内的每个元素，下面是如何做到这一点的简短示例代码。
vector c; vector x_pow; for (ulong i=0; i<PolynomialsYMatrix.Rows(); i++) for (ulong j=0; j<PolynomialsYMatrix.Cols(); j++) { if (i+j == 0) PolynomialsYMatrix[i][j] = y.Sum(); else { x_pow = MathPow(x,i); c = y*x_pow; //x vector elements are raised to the power i then the resulting vector is //Then multiplied to the vector of y values the output is stored in a vector c PolynomialsYMatrix[i][j] = c.Sum(); //Finally the sum of all the elements in a vector c is stored in the matrix of polynomials } }
查看上面多项式矩阵图像示意图右侧的矩阵，您还会注意到我们有函数 Σxy 和 Σxy^2，现在这是一种略有不同的方式，如此我们也看看代码如何做到这一点
double pow = 0; ZeroMemory(x_pow); for (ulong i=0,index = 0; i<PolyNomialsXMatrix.Rows(); i++) for (ulong j=0; j<PolyNomialsXMatrix.Cols(); j++, index++) { pow = (double)i+j; //The power corresponds to the access index of rows and cols i+j if (pow == 0) PolyNomialsXMatrix[i][j] = n; else { x_pow = MathPow(x,pow); //x_pow is a vector to store the x vector raised to a certain power PolyNomialsXMatrix[i][j] = x_pow.Sum(); //find the sum of the power vector } }
现在我们有了这些代码行的总和，其可证明对多项式回归非常重要，我们继续创建矩阵携带这些值，就像多项式矩阵示意图上的第二个矩阵一样。
从等号左侧的矩阵开始。
ulong order_size = degree+1; PolyNomialsXMatrix.Resize(order_size,order_size); PolynomialsYMatrix.Resize(order_size,1); vector c; vector x_pow; for (ulong i=0; i<PolynomialsYMatrix.Rows(); i++) for (ulong j=0; j<PolynomialsYMatrix.Cols(); j++) { if (i+j == 0) PolynomialsYMatrix[i][j] = y.Sum(); else { x_pow = MathPow(x,i); c = y*x_pow; PolynomialsYMatrix[i][j] = c.Sum(); } } if (debug) Print("Polynomials y vector \n",PolynomialsYMatrix);
只要看看矩阵中的元素是如何排列的，我们就知道只有第一个元素没有乘以 x 的值，其余的元素都乘以 x 的幂值，升幂按它们在矩阵中所在位置的索引提高。
在等式的焦点处切换阵列
我的第一个观察结果是，这个矩阵数组大小等于我们之前计算的左侧 Y 矩阵/矩阵的平方大小，而且 x 项的幂要基于元素在矩阵中的行和列位置。 由于这个矩阵是一个平方矩阵，我们必须按其列数循环两次来构建两个相应的循环，请参阅下面的代码。
ulong order_size = degree+1; PolyNomialsXMatrix.Resize(order_size,order_size); PolynomialsYMatrix.Resize(order_size,1); vector x_pow; //--- PolyNomialsXMatrix.Resize(order_size, order_size); double pow = 0; ZeroMemory(x_pow); //x_pow.Copy(x); for (ulong i=0,index = 0; i<PolyNomialsXMatrix.Rows(); i++) for (ulong j=0; j<PolyNomialsXMatrix.Cols(); j++, index++) { pow = (double)i+j; if (pow == 0) PolyNomialsXMatrix[i][j] = n; else { x_pow = MathPow(x,pow); PolyNomialsXMatrix[i][j] = x_pow.Sum(); } } //--- if (debug) Print("Polynomial x matrix\n",PolyNomialsXMatrix);
下面是上述代码片段的输出。
CS 0 02:10:15.429 polynomialReg test (#SP500,D1) Polynomials y vector CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [[27.5] CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [158.8] CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [966.2]] CS 0 02:10:15.429 polynomialReg test (#SP500,D1) Polynomial x matrix CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [[5,25,135] CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [25,135,775] CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [135,775,4659]]
太赞了！ 现在，这就是事情变得棘手的地方。 为了找到未知的 Beta 值矩阵的值，我们必须查看矩阵上的一些数学。
查找乘法矩阵的未知值：
我们针对刚刚在上面获得其值的矩阵遵循相同的过程。
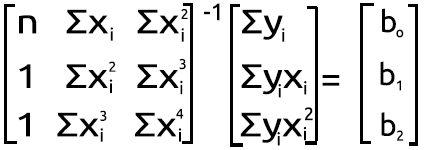
查找矩阵逆的过程相对简单，只需两行甚至一行代码调用标准库的矩阵。
PolyNomialsXMatrix = PolyNomialsXMatrix.Inv(); //find the inverse of the matrix then assign it to the original matrix 最后，为了找到模型的系数，我们必须将逆矩阵乘以矩阵，并将 y 值相加。
Betas = PolyNomialsXMatrix.MatMul(PolynomialsYMatrix);
现在，是时候打印 Betas 矩阵，以便查看我们从该过程中获得的结果；
CS 0 02:10:15.429 polynomialReg test (#SP500,D1) Betas CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [[12.42857142857065] CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [-5.512857142857115] CS 0 02:10:15.429 polynomialReg test (#SP500,D1) [0.7642857142856911]]
太棒了，正是我们一直在寻找的，现在，我们有了二阶多项式回归的系数，我们来继续在这些系数上构建模型。
void CPolynomialRegression::Poly_model(vector &Predictions, ulong degree) { ulong order_size = degree+1; Predictions.Resize(n); matrixtoArray(Betas,Betas_A); for (ulong i=0; i<(ulong)n; i++) { double sum = 0; for (ulong j=0; j<order_size; j++) { if (j == 0) sum += Betas_A[j]; else sum += Betas_A[j] * MathPow(x[i],j); } Predictions[i] = sum; } }
尽管模型的代码看起来很简单，但它可以处理您需要的任意多项式次项数，至少目前可以。我们在 x 和 y 值的同一轴上绘制模型预测
ObjectDelete(0,plot_name); plot_name = "x vs y"; ScatterCurvePlots(plot_name,x_v,y_v,Predictions,"Predictions","x","y",clrDeepPink);
bool ScatterCurvePlots( string obj_name, vector &x, vector &y, vector &curveVector, string legend, string x_axis_label = "x-axis", string y_axis_label = "y-axis", color clr = clrDodgerBlue, bool points_fill = true ) { if (!graph.Create(0,obj_name,0,30,70,440,320)) { printf("Failed to Create graphical object on the Main chart Err = %d",GetLastError()); return(false); } ChartSetInteger(0,CHART_SHOW,ChartShow); //--- additional curves double x_arr[], y_arr[]; pol_reg.vectortoArray(x,x_arr); pol_reg.vectortoArray(y,y_arr); double curveArray[]; //curve matrix array pol_reg.vectortoArray(curveVector,curveArray); graph.CurveAdd(x_arr,y_arr,clrBlack,CURVE_POINTS,y_axis_label); graph.CurveAdd(x_arr,curveArray,clr,CURVE_POINTS_AND_LINES,legend); //--- graph.XAxis().Name(x_axis_label); graph.XAxis().NameSize(10); graph.YAxis().Name(y_axis_label); graph.YAxis().NameSize(10); graph.FontSet("Lucida Console",10); graph.CurvePlotAll(); graph.Update(); return(true); }
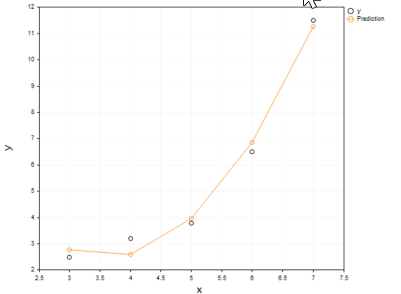
输出:
不可否认，多项式模型能够很好地拟合我们的数据，且在这种情况下，其在拟合数据方面可能优于线性模型。
寻找最佳多项式次项数
如前所述，贝叶斯信息准则是我们寻找最佳模型的算法，我们将公式转换为代码。 根据 BIC，BIC 值最低的模型是最佳模型，因为该模型是残差/误差总和最小的模型。
void CPolynomialRegression::BIC(ulong k, vector &bic,int &best_degree) { vector Pred; bic.Resize(k-2); best_degree = 0; for (ulong i=2, counter = 0; i<k; i++) { PolynomialRegressionfx(i,Pred); bic[counter] = ( n * log(RSS(Pred)) ) + (i * log(n)); counter++; } //--- bool positive = false; for (ulong i=0; i<bic.Size(); i++) if (bic[i] > 0) { positive = true; break; } double low_bic = DBL_MAX; if (positive == true) for (ulong i=0; i<bic.Size(); i++) { if (bic[i] < low_bic && bic[i] > 0) low_bic = bic[i]; } else low_bic = bic.Min(); //bic[ best_degree = ArrayMinimum(bic) ]; printf("Best Polynomial Degree(s) is = %d with BIC = %.5f",best_degree = best_degree+2,low_bic); }
从代码来看，函数 RSS 是残差平方和。 该函数查找残差平方和。
double CPolynomialRegression::RSS(vector &Pred) { if (Pred.Size() != y.Size()) Print(__FUNCTION__," Predictions Array and Y matrix doesn't have the same size"); double sum =0; for (int i=0; i<(int)y.Size(); i++) sum += MathPow(y[i] - Pred[i],2); return(sum); }
现在我运行这个函数来找到 10 次项数中最好的多项式。
vector bic_; //A vector to store the model BIC values for visualization purposes only int best_order; //A variable to store the best model order pol_reg.BIC(polynomia_degrees,bic_,best_order);
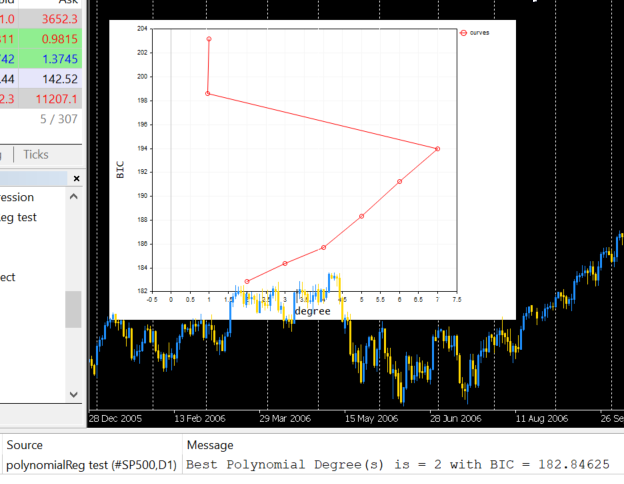
下面是在终端上绘制时的输出;
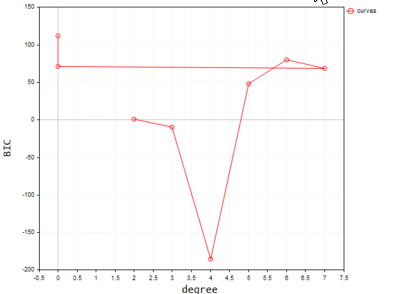
根据我们的代码，最佳模型的多项式次项数为 2。 不可否认，次项数为 2 的模型是这个简单数据集的最佳模型。
2022.09.22 20:58:21.540 polynomialReg test (#NQ100,D1) Best Polynomial Degree(s) is = 2 with BIC = 0.93358
下面是每个模型如何进行预测的输出。
7 次项输出绘制在同一轴上。
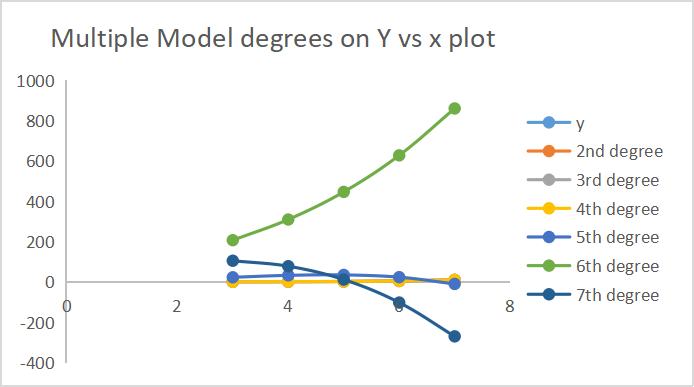
功能缩放至关重要
由于在多项式回归中，我们只有一个自变量，我们可以将其提高到我们想要的任何幂，那么第一次项缩放特征变得十分重要，因为如果您的自变量的特征范围在 100-1000，那第二次项上的特征范围将在 10000 - 1000,000 之间，第三次项的特征范围将在 10^6 - 10^9 之间。 天啊，这太多了。
有很多方式和算法可以缩放数据集，但我们将使用 Min-max 缩放器函数来缩放向量。请记住，此过程应针对数据集进行任何操作之前完成。 下面的代码是缩放数据集中向量的函数。
void MinMaxScaler(vector &v) { //Normalizing vector using Min-max scaler double min, max, mean; min = v.Min(); max = v.Max(); mean = v.Mean(); for (int i=0; i<(int)v.Size(); i++) v[i] = (v[i] - min) / (max - min); }
我们现在拥有了所需的一切，是时候在实时市场数据上构建模型了，请参阅上面的纳斯达克 vs 苹果图表。 为了能够获得结果，我们需要采取若干步。
提取市场价格数据并进行缩放。
if (!SymbolSelect(X_symbol,true)) printf("%s not found on Market watch Err = %d",X_symbol,GetLastError()); if (!SymbolSelect(Y_symol,true)) printf("%s not found on Market watch Err = %d",Y_symol,GetLastError()); matrix rates(bars, 2); vector price_close; //--- vector x_v, y_v; price_close.CopyRates(X_symbol,PERIOD_H1,COPY_RATES_CLOSE,1,bars); //extracting prices rates.Col(price_close,0); x_v.Copy(price_close); //--- price_close.CopyRates(Y_symol,PERIOD_H1,COPY_RATES_CLOSE,1,bars); y_v.Copy(price_close); rates.Col(price_close,1); //--- MinMaxScaler(x_v); //scalling all the close prices MinMaxScaler(y_v); //scalling all the close prices //---
下面是散点图上显示的输出；
02: 使用 Bic 函数查找最佳模型
//--- FINDING BEST MODEL USING BIC vector bic_; //A vector to store the model BIC values for visualization purposes only int best_order; //A variable to store the best model order pol_reg.BIC(polynomia_degrees,bic_,best_order); ulong bic_cols = polynomia_degrees-2; //2 is the first in the polynomial order //--- Plot BIc vs model degrees vector x_bic; x_bic.Resize(bic_cols); for (ulong i=2,counter =0; i<bic_cols; i++) { x_bic[counter] = (double)i; counter++; } ObjectDelete(0,plot_name); plot_name = "curves"; ScatterCurvePlots(plot_name,x_bic,y_v,bic_,"curves","degree","BIC",clrBlue); Sleep(10000);
下面是输出
后记
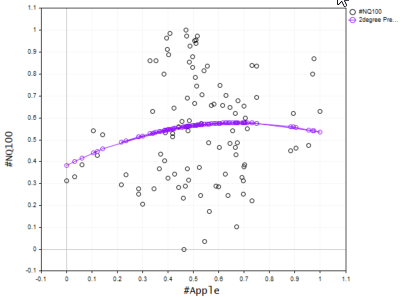
我们现在知道最佳模型阶数是 2。 我们制作一个 2 次项的模型，然后使用它来预测值，最后我们把数值绘制在图形上。
vector Predictions; pol_reg.PolynomialRegressionfx(best_order,Predictions); //Create model with the best order then use it to predict ObjectDelete(0,plot_name); plot_name = "Actual vs predictions"; ScatterCurvePlots(plot_name,x_v,y_v,Predictions,string(best_order)+"degree Predictons",X_symbol,Y_symol,clrDeepPink);
结果制图显示如下
检查模型精度
尽管找到了模型的最佳次项数，但我们仍然需要明白该模型如何通过检查其预测准确性来理解数据集中的关系。
Print("Model Accuracy = ",DoubleToString(pol_reg.r_squared(y,Predictions)*100,2),"%");
输出，
2022.09.30 16:19:31.735 polynomialReg test (#SP500,D1) Model Accuracy = 2.36%
对我们来说是个坏消息，我们让自己成为最糟糕的模型之一。 现在，在决定使用多项式回归来解决特定任务之前，请记住多项式回归依然以线性模型为基础，因此始终具有相关的数据，它不必是线性相关的，但可能的理想情况是拥有大约 50% 的相关性 ，回顾我们的纳斯达克 vs 苹果数据集，并检查其相关性，我得到的相关系数小于 1%。 这可能就是我们无法从这个数据集中获得优良模型的原因。
Print("correlation coefficient ",x_v.CorrCoef(y_v));
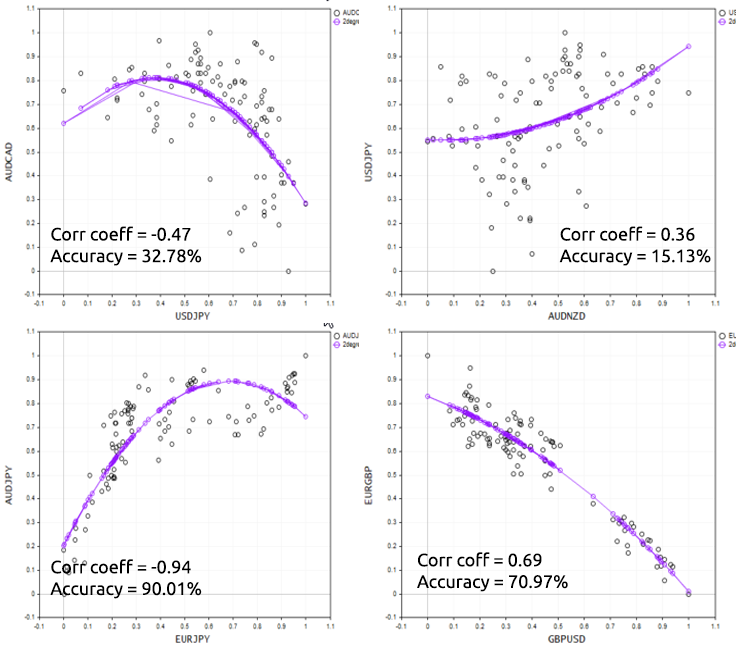
为了很好地证明这一点，我们针对不同的外汇工具上尝试脚本。
多项式回归的优缺点
优点：
- 您可以针对变量之间的非线性关系进行建模
- 有范围广泛的函数可供您用来拟合
- 适合探索目的。 您可以测试不同的多项式阶数/次项数，以便查看哪种最适合您拥有的数据集
- 编码很简单，但解释结果更强大
缺点：
- 异常值会严重扰乱结果
- 多项式回归模型容易过度拟合（对此表示怀疑）
- 作为过度拟合的后果，模型可能无法处理外围数据
最后的思考
在许多情况下，多项式回归是一种实用的机器学习技术，因为自变量和因变量之间的关系不是推测中的线性，它在处理不同的数据集时为您提供了更多的自由，并且有助于填补线性模型无法顾及的空白，当线性模型拟合数据低下时，这种技术就是更好的选择。 虽然话说，您能意识到过度拟合至关重要，因为由于这个参数模型非常灵活，它也许在未经训练的数据/测试数据上表现非常糟糕，我只好说选择最低的模型阶数，并给模型留出错的空间。
感谢您的阅读。
有关数组形式矩阵的更多信息，请阅读 >> 矩阵和向量
延伸阅读 | 书籍 | 参考
文章参考：
本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/11477
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
利用智能系统进行风险和资本管理
您应该知道的 MQL5 向导技术（第 03 部分）：香农（Shannon）熵
