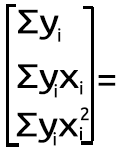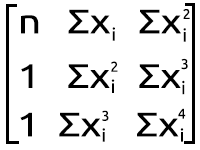
Aprendizaje automático y Data Science (Parte 07): Regresión polinomial

Contenido:

• Introducción
• Recordando los polinomios
• Orden de los polinomios
• Regresión polinomial
• ¿Cuándo usar los polinomios?
• Criterio de información bayesiano
• Hallando los coeficientes del modelo
• Hallando el mejor modelo
• Escalado de características
• Ventajas y desventajas de la regresión polinomial
• Reflexiones finales

Introducción

Aún no hemos terminado con los modelos de regresión, así que volveremos a ellos por un segundo. Como comentamos en el primer artículo de esta serie, la regresión lineal básica es la base de muchos modelos de aprendizaje automático. Hoy iremos un poco más allá de la regresión lineal y nos familiarizaremos con la regresión polinomial.

El aprendizaje automático ha cambiado mucho nuestro mundo en diversas formas: existen varios métodos de entrenamiento disponibles para problemas de clasificación y regresión, como la regresión lineal y logística, la máquina de vectores de soporte, la regresión polinomial y muchos otros métodos. Por separado, los métodos paramétricos, como la regresión polinomial y los métodos de vectores de soporte, se pueden destacar por su versatilidad.

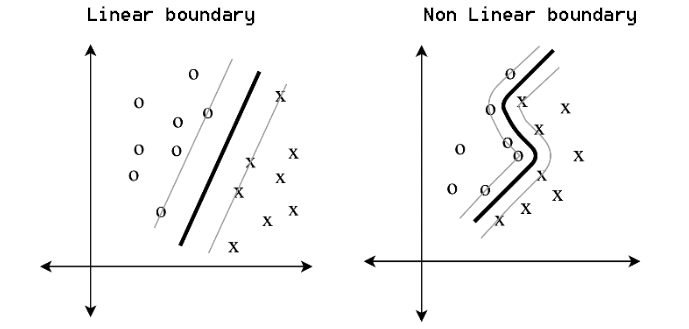
Además, crean límites simples para tareas sencillas y límites no lineales para tareas complejas.

Recordando los polinomios

Un polinomio es cualquier expresión matemática semejante a esto:

 - ecuación polinomial 1

Tenemos x datos que están elevados a una potencia, así como coeficientes que se usan para escalar los datos.

Aquí tenemos otro ejemplo de regresión polinomial:

- ecuación polinomial 2

5 se corresponde con ao, -7 se corresponde con a1, 4 se corresponde con a2, y 11.3 se corresponde con a3. 

Un polinomio no tiene que contener todos los términos x, veamos la siguiente ecuación:

- ecuación polinomial 3

También podemos imaginarlo como:

Orden polinomial 

Los polinomios tienen un concepto llamado orden. El orden de un polinomio se indica con la letra n. Este es el coeficiente más alto en términos matemáticos. Por ejemplo:

1. La ecuación polinomial 1 anterior es una regresión polinomial de orden n
2. Ecuación polinomial 2 es una regresión polinomial de tercer orden/grado.
3. La ecuación polinomial 03, mostrada anteriormente, también es una regresión polinomial de tercer orden/grado.

Esto puede resultar confuso porque en la segunda ecuación, tenemos 3 variables multiplicadas por x y sus coeficientes están en orden ascendente 1,2,3, mientras que en la segunda ecuación solo tenemos dos variables. El orden polinomial está determinado principalmente por el coeficiente principal de la expresión.

Regresión polinomial

La regresión polinomial es un algoritmo de aprendizaje automático que se usa para hacer predicciones. Tengo entendido que se ha utilizado ampliamente para predecir la tasa de propagación del COVID-19 y otras enfermedades infecciosas. Veamos en qué consiste este algoritmo.
Tenemos un modelo lineal simple.

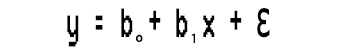
¿Ha notado algo?

Esta regresión lineal simple no es más que una regresión polinomial de primer orden. Dependiendo de la regresión polinomial, podemos añadir variables a esta, por ejemplo, una regresión polinomial de segundo orden se verá así:

Esta expresión podría ser de mayor orden:

Esta es una regresión polinomial de k-ésimo orden. Espere un segundo, ¿sigue siendo una regresión lineal? ¿Qué ha pasado con el modelo lineal?
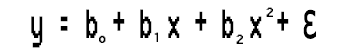
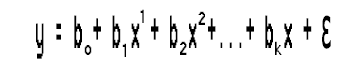
¿Qué ha ocurrido con la linealidad?

¿No dijimos en artículos anteriores que cualquier regresión está asociada a un modelo lineal? Entonces, ¿cómo podemos ajustar esta regresión polinomial a la linealidad cuando tenemos estos coeficientes al cuadrado?

Todo se reduce a lo que debe ser lineal y lo que puede ser no lineal. Todos los coeficientes/betas son lineales, solo que los datos en sí mismos se elevan a potencias más altas.

¿Cuándo se usa la regresión polinomial?

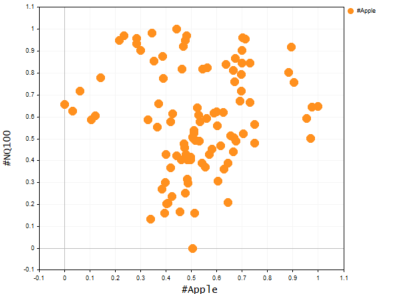
Como sabemos, el modelo lineal básico no resulta adecuado para datos complejos (no lineales) o para buscar relaciones complejas en un conjunto de datos. Para resolver estos problemas, se utiliza la regresión polinomial. Imagine que intentamos predecir el precio del NASDAQ utilizando el precio de las acciones de APPLE. Apple supone uno de los factores más fuertes que influyen en el precio del NASDAQ y, sin embargo, la relación no es lineal. Por consiguiente, para un conjunto de datos de este tipo, el modelo lineal no resultará lo suficientemente adecuado como para confiar en él a la hora de tomar decisiones sobre futuros pronósticos. Veamos el aspecto de la gráfica de estos dos símbolos en el mismo eje. Para hacer esto, usaremos un diagrama de dispersión en el que presentaremos los valores de los precios.

A continuación, mostramos una función que crea un diagrama de dispersión en el terminal usando CGraphics (probablemente no hubiera sabido sobre esta posibilidad de no comenzar a escribir este artículo).

bool ScatterPlot(
                 string obj_name,
                 vector &x,
                 vector &y,
                 string legend,
                 string x_axis_label = "x-axis",
                 string y_axis_label = "y-axis", 
                 color  clr = clrDodgerBlue,
                 bool   points_fill = true                 
                )
 { 
   if (!graph.Create(0,obj_name,0,30,70,440,320))
     {
       printf("Failed to Create graphical object on the Main chart Err = %d",GetLastError());
       return(false);
     }
   
   ChartSetInteger(0,CHART_SHOW,ChartShow);
   
   double x_arr[], y_arr[]; 
   
   pol_reg.vectortoArray(x,x_arr);
   pol_reg.vectortoArray(y,y_arr);
   
   CCurve *curve = graph.CurveAdd(x_arr,y_arr,clr,CURVE_POINTS);
   curve.PointsSize(10);
   curve.PointsFill(points_fill); 
   curve.Name(legend);
   graph.XAxis().Name(x_axis_label);
   graph.XAxis().NameSize(10);
   graph.YAxis().Name(y_axis_label);
   graph.YAxis().NameSize(10);
   graph.FontSet("Lucida Console",10);
   graph.CurvePlotAll();
   graph.Update();
 
   delete(curve);
   
   return(true);
 }

   string plot_name = "x vs y"; 
   
   ObjectDelete(0,plot_name);    
   ScatterPlot(plot_name,x_v,y_v,X_symbol,X_symbol,Y_symol,clrOrange); 

Información mostrada:

Gráfico de Nasdaq y Apple

Obviamente, el modelo lineal no funciona bien con este tipo de tareas, así que intentaremos resolverlo usando la regresión polinomial. Aquí surge la siguiente pregunta: ¿qué orden debemos usar para crear un modelo polinomial?

Echemos un vistazo a la expresión del modelo:

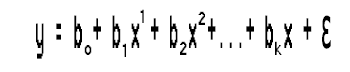
Como solo tenemos una variable independiente, podemos elevarla a cualquier potencia que deseemos. Pero, ¿cómo sabemos a qué potencia necesitaremos elevar esta única variable independiente, en otras palabras, cómo sabemos en qué orden debe estar el polinomio? Para entender esto, primero deberemos entender el llamado Criterio de Información Bayesiano (BIC).

Criterio de información bayesiano

Su fórmula es como sigue:

BIC =  n log(SSE) + k log (n)

 n = número de puntos de datos 

 k = número de parámetros

Pero antes de averiguar qué modelo se ajusta mejor, crearemos una regresión polinomial básica y veremos qué hace que funcione. Comenzaremos por esto y seguiremos con la búsqueda de un orden adecuado.

Hallando los coeficientes del modelo

Tenemos la ecuación

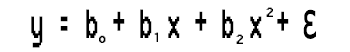
Resolveremos este problema de regresión polinomial de segundo grado hallando los valores b0, b1 y b2.

Para ello, usaremos el siguiente sistema de ecuaciones:

n = número de puntos de datos

Para calcular los valores, usaremos un conjunto de datos simple.

X	y
3	2.5
4	3.2
5	3.8
6	6.5
7	11.5

Entonces, ahora tenemos un conjunto de ecuaciones simultáneas para el problema y un conjunto de datos simple sobre el cual construiremos los cálculos. Podemos sustituir fácilmente los valores y encontrar los coeficientes en una calculadora científica, Microsoft Excel u otra herramienta, según nuestras preferencias. Obtendremos los siguientes valores:

• b0 = 12.4285714
• b1= -5.5128571
• b2 = 0.7642857

Sin embargo, en general, este no es el caso al trabajar con MQL5. Entonces, vamos a ver cómo podemos lograr el mismo resultado en el MetaEditor a partir del conjunto de ecuaciones simultáneas anterior. Lo convertiremos en la forma matricial. Ahora tenemos lo siguiente:

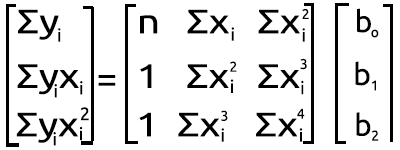Figura matricial polinomial

El resultado de la multiplicación nos devuelve a la ecuación. Entonces, desde un punto de vista matemático, todo es correcto.

Vamos a escribir el código.

Clase de regresión polinomial:

class CPolynomialRegression
  {
   private:
                        ulong  m_degree; //depends on independent vars
                        int    n;   //number of samples in the dataset
                        vector x;
                        vector y;
                        matrix PolyNomialsXMatrix; //x matrix 
                        matrix PolynomialsYMatrix; //y matrix 
                        matrix Betas;
                        double Betas_A[];  //coefficients of the model stored in Array

                        void   Poly_model(vector &Predictions,ulong degree);
                        
   public:
                        CPolynomialRegression(vector& x_vector,vector &y_vector,int degree=2);
                       ~CPolynomialRegression(void);
                        
                        double RSS(vector &Pred);               //sum of squared residuals
                        void   BIC(ulong k, vector &bic,int &best_degree);      //Bayessian information Criterion
                        void   PolynomialRegressionfx(ulong degree, vector &Pred);
                        double r_squared(vector &y,vector &y_predicted); 
                        
                        void   matrixtoArray(matrix &mat, double &Array[]);
                        void   vectortoArray(vector &v, double &Arr[]);
                        void   MinMaxScaler(vector &v);
  };

Nuestra clase es bastante simple, así que su código debería resultar claro. Si hay algún cambio, actualizaremos el código en los archivos adjuntos más abajo, porque el código se está escribiendo al mismo tiempo que el artículo.

Como podemos ver a partir de nuestra expresión matricial en la figura de la matriz polinomial anterior, en cada punto hay muchas sumas, y luego una exponenciación. Este cálculo resulta necesario para casi todos los elementos de la primera matriz a la derecha del signo igual. A continuación, mostramos un ejemplo de código breve que indica cómo hacer esto.

    vector c;
    vector x_pow;
    
    for (ulong i=0; i<PolynomialsYMatrix.Rows(); i++)
       for (ulong j=0; j<PolynomialsYMatrix.Cols(); j++) 
         {
            if (i+j == 0)  PolynomialsYMatrix[i][j] = y.Sum(); 
            else         
               {
                   x_pow = MathPow(x,i);       c = y*x_pow; //x vector elements are raised to the power i then the resulting vector is  
                                                                //Then multiplied to the vector of y values the output is stored in a vector c
                   PolynomialsYMatrix[i][j] =  c.Sum();     //Finally the sum of all the elements in a vector c is stored in the matrix of polynomials
               }
         }

Mire la matriz a la derecha en la figura de la matriz polinomial de más arriba. Como podemos ver, también tenemos las funciones Σxy y Σxy^2. Este es un enfoque ligeramente distinto, veamos también el código que lo implementa.

  
   double pow = 0;
   ZeroMemory(x_pow);
   
    for (ulong i=0,index = 0; i<PolyNomialsXMatrix.Rows(); i++)
       for (ulong j=0; j<PolyNomialsXMatrix.Cols(); j++, index++)
          {
             pow = (double)i+j; //The power corresponds to the access index of rows and cols i+j
             if (pow == 0) PolyNomialsXMatrix[i][j] = n;
             else          
                 {
                   x_pow = MathPow(x,pow); //x_pow is a vector to store the x vector raised to a certain power
                   
                   PolyNomialsXMatrix[i][j] =  x_pow.Sum(); //find the sum of the power vector
                 }
          }
    

Entonces tenemos estas filas para encontrar las sumas que resultan tan importantes para la regresión polinomial. Ahora comenzaremos a crear una matriz que represente estos valores, como la segunda matriz en la imagen de la figura de la matriz polinomial.

Comenzaremos con la matriz a la izquierda del signo igual.

    ulong order_size = degree+1;
    PolyNomialsXMatrix.Resize(order_size,order_size);
    
    PolynomialsYMatrix.Resize(order_size,1);
    
    vector c;
    vector x_pow;
    
    for (ulong i=0; i<PolynomialsYMatrix.Rows(); i++)
       for (ulong j=0; j<PolynomialsYMatrix.Cols(); j++) 
         {
            if (i+j == 0)  PolynomialsYMatrix[i][j] = y.Sum(); 
            else         
               {
                   x_pow = MathPow(x,i);       c = y*x_pow;
                   PolynomialsYMatrix[i][j] =  c.Sum(); 
               }
         }
    
   if (debug) Print("Polynomials y vector \n",PolynomialsYMatrix);

Con solo mirar cómo se ordenan los elementos dentro de la matriz, podremos entender que el primer elemento es el único que no se multiplica por valores de x, mientras que todos los demás se multiplican por valores de x aumentados por el índice de su ubicación en la matriz.

Cambiando el array al punto focal de la ecuación

Mi primera observación es que este tamaño del array Matrix es igual al tamaño del cuadrado de la matriz Y/matriz en el lado izquierdo calculado anteriormente, y la potencia a la que se elevan los elementos x dependerá de dónde se encuentre el elemento en la matriz, y eso dependerá de las filas y columnas. Como esta matriz está al cuadrado, deberemos construirla haciendo bucles dos veces por sus columnas en dos ciclos correspondientes. El código se muestra a continuación.

    ulong order_size = degree+1;
    PolyNomialsXMatrix.Resize(order_size,order_size);
    
    PolynomialsYMatrix.Resize(order_size,1);
     
    vector x_pow;
    
//---
   
   PolyNomialsXMatrix.Resize(order_size, order_size);
   
   double pow = 0;
   ZeroMemory(x_pow);
   //x_pow.Copy(x);
   
    for (ulong i=0,index = 0; i<PolyNomialsXMatrix.Rows(); i++)
       for (ulong j=0; j<PolyNomialsXMatrix.Cols(); j++, index++)
          {
             pow = (double)i+j;
             if (pow == 0) PolyNomialsXMatrix[i][j] = n;
             else          
                 {
                   x_pow = MathPow(x,pow);
                   
                   PolyNomialsXMatrix[i][j] =  x_pow.Sum();
                 }
          }
  //---

   if (debug) Print("Polynomial x matrix\n",PolyNomialsXMatrix);
   

Más abajo, le mostramos el resultado de los fragmentos de código anteriores.

CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  Polynomials y vector 
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  [[27.5]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [158.8]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [966.2]]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  Polynomial x matrix
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  [[5,25,135]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [25,135,775]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [135,775,4659]]

Aquí es donde surgen ya las dificultades. Para encontrar los valores de una matriz desconocida de valores beta, deberemos recurrir a ciertas operaciones matemáticas con matrices.

Encontrando los valores desconocidos de una matriz multiplicada:

Vamos a repetir el mismo procedimiento para nuestras matrices, cuyos valores acabamos de obtener.

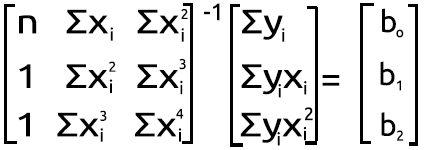
El proceso de encontrar la inversa de una matriz es relativamente simple y requiere dos, si no una sola línea de código usando la biblioteca estándar de matrices.

    PolyNomialsXMatrix = PolyNomialsXMatrix.Inv(); //find the inverse of the matrix then assign it to the original matrix 

Finalmente, para encontrar los coeficientes del modelo, deberemos multiplicar la matriz inversa por la matriz con las sumas de los valores de y.

    Betas = PolyNomialsXMatrix.MatMul(PolynomialsYMatrix);

Ahora es el momento de imprimir la matriz beta para ver qué hemos obtenido como resultado de todas nuestras acciones:

CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  Betas 
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)  [[12.42857142857065]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [-5.512857142857115]
CS      0       02:10:15.429    polynomialReg test (#SP500,D1)   [0.7642857142856911]]

Genial, esto es exactamente lo que buscábamos. Ahora tenemos los coeficientes de regresión polinómica de segundo grado y podemos construir un modelo basado en ellos.

void CPolynomialRegression::Poly_model(vector &Predictions, ulong degree)
 {
   ulong order_size = degree+1;
   Predictions.Resize(n);
   
   matrixtoArray(Betas,Betas_A); 
   
    for (ulong i=0; i<(ulong)n; i++)
     {
      double sum = 0;
       for (ulong j=0; j<order_size; j++) 
         {
           if (j == 0) sum += Betas_A[j];
           else        sum += Betas_A[j] * MathPow(x[i],j);
         }
       Predictions[i] = sum;
     }
 }

Aunque el código del modelo parezca simple, puede procesar tantas potencias como sea necesario, al menos por ahora. A continuación, construiremos las predicciones del modelo en el mismo eje de los valores de x e y.

   ObjectDelete(0,plot_name);
   plot_name = "x vs y";   
   ScatterCurvePlots(plot_name,x_v,y_v,Predictions,"Predictions","x","y",clrDeepPink);
bool ScatterCurvePlots(
                       string obj_name,
                       vector &x,
                       vector &y,
                       vector &curveVector, 
                       string legend,
                       string x_axis_label = "x-axis",
                       string y_axis_label = "y-axis", 
                       color  clr = clrDodgerBlue,
                       bool   points_fill = true                 
                      )
 {
 
   if (!graph.Create(0,obj_name,0,30,70,440,320))
     {
       printf("Failed to Create graphical object on the Main chart Err = %d",GetLastError());
       return(false);
     }
   
   ChartSetInteger(0,CHART_SHOW,ChartShow);
   
   
//--- additional curves

   double x_arr[], y_arr[]; 
   
   pol_reg.vectortoArray(x,x_arr);
   pol_reg.vectortoArray(y,y_arr);

   double curveArray[]; //curve matrix array
   
   pol_reg.vectortoArray(curveVector,curveArray);
   
   graph.CurveAdd(x_arr,y_arr,clrBlack,CURVE_POINTS,y_axis_label);
   graph.CurveAdd(x_arr,curveArray,clr,CURVE_POINTS_AND_LINES,legend);
    
//---

   graph.XAxis().Name(x_axis_label);
   graph.XAxis().NameSize(10);
   graph.YAxis().Name(y_axis_label);
   graph.YAxis().NameSize(10);
   graph.FontSet("Lucida Console",10);
   graph.CurvePlotAll();
   graph.Update();
   
   return(true);
 } 

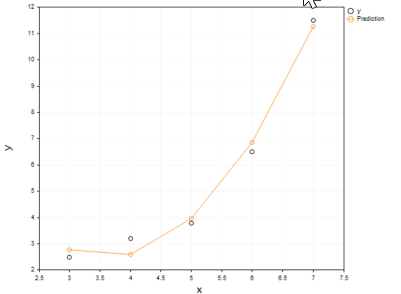
Información mostrada:

Estará de acuerdo con que el modelo polinomial se adecuaba mejor a nuestros datos y que en esto puede superar al modelo lineal al seleccionar los datos.

Hallando la mejor potencia de un polinomio

Como ya hemos explicado antes, el criterio de información bayesiano es un algoritmo que se utiliza para encontrar el mejor modelo. Vamos a convertir la fórmula en código. Según el BIC, el modelo con el valor BIC más bajo será el mejor modelo porque tendrá la suma más pequeña de restos/errores.

void  CPolynomialRegression::BIC(ulong k, vector &bic,int &best_degree)
 {
   vector Pred;
   
   bic.Resize(k-2); 
   best_degree = 0;
   
    for (ulong i=2, counter = 0; i<k; i++)
      {         
         PolynomialRegressionfx(i,Pred);         
         bic[counter] = ( n * log(RSS(Pred)) ) + (i * log(n));  
         
         counter++;
      }
      
//--- 

   bool positive = false;
   for (ulong i=0; i<bic.Size(); i++)
      if (bic[i] > 0) { positive = true; break; }
   
  
   double low_bic = DBL_MAX;
   
   if (positive == true) 
    for (ulong i=0; i<bic.Size(); i++) 
     {
      if (bic[i] < low_bic && bic[i] > 0) low_bic = bic[i];
     }
   else  low_bic = bic.Min(); //bic[ best_degree = ArrayMinimum(bic) ];
      
   printf("Best Polynomial Degree(s) is = %d with BIC = %.5f",best_degree = best_degree+2,low_bic);

 }

La función RSS en el código es la Suma Residual de Cuadrados. Esta función encuentra la suma residual de cuadrados.

double CPolynomialRegression::RSS(vector &Pred)
 {
  if (Pred.Size() != y.Size()) Print(__FUNCTION__," Predictions Array and Y matrix doesn't have the same size");
 
   double sum =0;
    for (int i=0; i<(int)y.Size(); i++)
      sum += MathPow(y[i] - Pred[i],2);
      
    return(sum);
 }

Ahora ejecutaremos esta función para encontrar el mejor polinomio entre los 10 grados.

   vector bic_; //A vector to store the model BIC values for visualization purposes only
   
   int best_order; //A variable to store the best model order 
   
   pol_reg.BIC(polynomia_degrees,bic_,best_order);

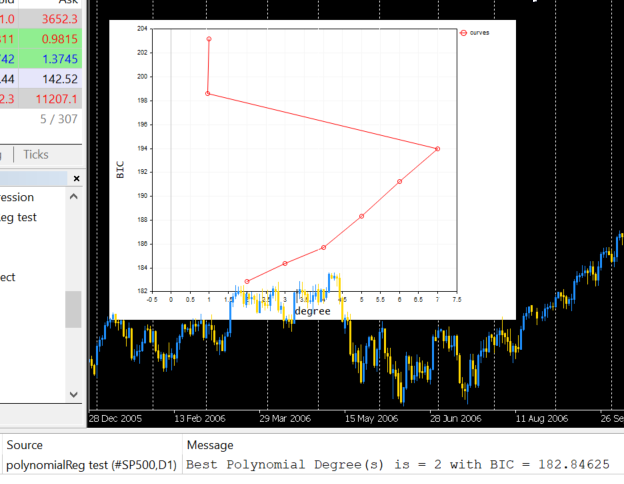
El resultado del funcionamiento tendrá el aspecto que sigue:

Según este código, el mejor modelo lo tiene el polinomio de grado 2. Entonces, para nuestra muestra simple, el modelo con el grado 2 será el mejor.

2022.09.22 20:58:21.540 polynomialReg test (#NQ100,D1)  Best Polynomial Degree(s) is = 2 with BIC = 0.93358

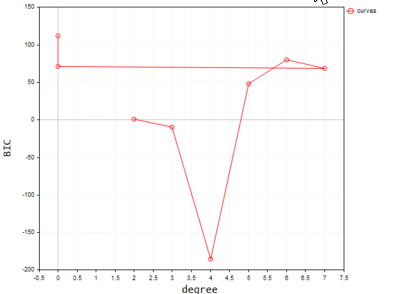
A continuación, le mostramos los resultados de las predicciones que ha hecho cada uno de los modelos.

En el eje, hemos trazado 7 resultados en grados.

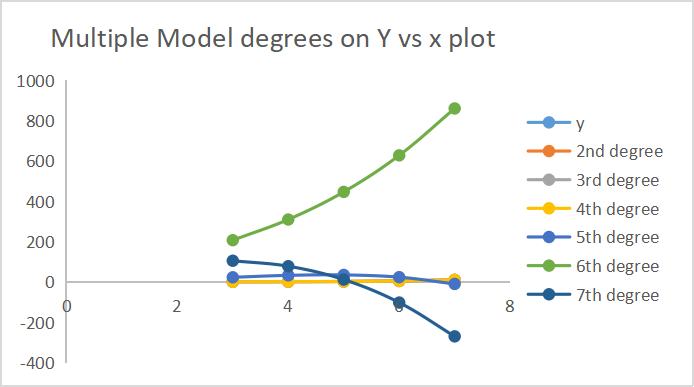
El escalado de características tiene gran importancia

Como solo hay una variable independiente en la regresión polinomial que se pueda elevar a cualquier potencia, la capacidad de escalar las características se vuelve muy importante, porque si una variable independiente tiene características en el rango de 100-1000, en la segunda potencia estas características fluctuarán entre los valores 10000 - 1000000, y en la tercera, entre 10^6 - 10^9, y esto es mucho.

Hay muchas formas y algoritmos para escalar un conjunto de datos, pero usaremos la función de escalado Min-Max para escalar los vectores. Tenga en cuenta que este proceso deberá realizarse antes de cualquier manipulación del conjunto de datos. A continuación, le mostramos el código de la función que se utilizará para escalar los vectores del conjunto de datos.

void MinMaxScaler(vector &v)
 {
   //Normalizing vector using Min-max scaler
   
   double min, max, mean;
   min = v.Min();
   max = v.Max();
   mean = v.Mean();
   
   for (int i=0; i<(int)v.Size(); i++)
     v[i] = (v[i] - min) / (max - min);  
   
 } 

Todo lo que necesitamos ya está listo. Es hora de construir un modelo con datos reales del mercado: consulte el gráfico anterior de Nasdaq vs Apple. Para obtener los resultados, deberemos seguir varios pasos.

Extraer y escalar los datos de precio del mercado.

   if (!SymbolSelect(X_symbol,true))   printf("%s not found on Market watch Err = %d",X_symbol,GetLastError());  
   if (!SymbolSelect(Y_symol,true))    printf("%s not found on Market watch Err = %d",Y_symol,GetLastError());  
  
   matrix rates(bars, 2);
   vector price_close;

//---

   vector x_v, y_v;

   price_close.CopyRates(X_symbol,PERIOD_H1,COPY_RATES_CLOSE,1,bars); //extracting prices
   
   rates.Col(price_close,0);
   
   x_v.Copy(price_close);

//---
   
   price_close.CopyRates(Y_symol,PERIOD_H1,COPY_RATES_CLOSE,1,bars);
   
   y_v.Copy(price_close);
    
   rates.Col(price_close,1);
   
//---

   MinMaxScaler(x_v); //scalling all the close prices
   MinMaxScaler(y_v); //scalling all the close prices

//---

A continuación, le mostraremos el resultado presentado en un diagrama de dispersión:

2. Encontramos el mejor modelo

//--- FINDING BEST MODEL USING BIC
   
   vector bic_; //A vector to store the model BIC values for visualization purposes only
   
   int best_order; //A variable to store the best model order 
   
   pol_reg.BIC(polynomia_degrees,bic_,best_order);
   
   ulong bic_cols = polynomia_degrees-2; //2 is the first in the polynomial order 
   
//--- Plot BIc vs model degrees

   vector x_bic;
   x_bic.Resize(bic_cols);  
   for (ulong i=2,counter =0; i<bic_cols; i++)  {   x_bic[counter] = (double)i;   counter++;   }     
    
   ObjectDelete(0,plot_name);
   plot_name = "curves";
   ScatterCurvePlots(plot_name,x_bic,y_v,bic_,"curves","degree","BIC",clrBlue);
   Sleep(10000);

El resultado será el siguiente:

Y en último lugar. 

Ahora sabemos que el mejor orden de los modelos es 2. Vamos a crear un modelo de 2 potencias, que luego usaremos para predecir los valores y finalmente mostrar estos en el gráfico.

   vector Predictions;
   pol_reg.PolynomialRegressionfx(best_order,Predictions); //Create model with the best order then use it to predict
   
   ObjectDelete(0,plot_name);
   plot_name = "Actual vs predictions";   
   ScatterCurvePlots(plot_name,x_v,y_v,Predictions,string(best_order)+"degree Predictons",X_symbol,Y_symol,clrDeepPink);

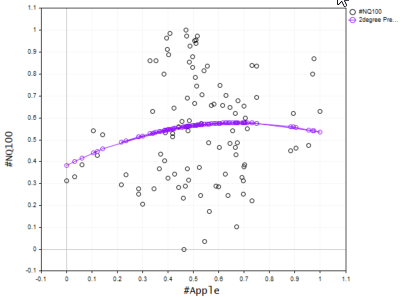
Podrá ver el gráfico resultante a continuación:

Comprobamos la precisión del modelo

Aunque hemos encontrado el mejor grado para el modelo, aún no sabemos cómo este modelo puede comprender la interrelación en nuestro conjunto de datos. Vamos a comprobar la precisión de sus predicciones.

   Print("Model Accuracy = ",DoubleToString(pol_reg.r_squared(y,Predictions)*100,2),"%");

Output,

2022.09.30 16:19:31.735 polynomialReg test (#SP500,D1)  Model Accuracy = 2.36%

La mala noticia es que hemos obtenido un mal modelo de entre los peores modelos. Antes de decidir usar la regresión polinomial para un problema en particular, recuerde que esta se basa en un modelo lineal, por lo que los datos siempre deberán estar correlacionados. No tienen que estar correlacionados linealmente, pero una correlación de alrededor del 50% resultaría ideal. Volviendo al conjunto de datos de NASDAQ y APPLE, verificaremos la correlación: hemos obtenido un coeficiente de correlación de menos del 1%. Este es probablemente el motivo por el que no hemos podido obtener un buen modelo de este conjunto de datos. 

   Print("correlation coefficient ",x_v.CorrCoef(y_v));

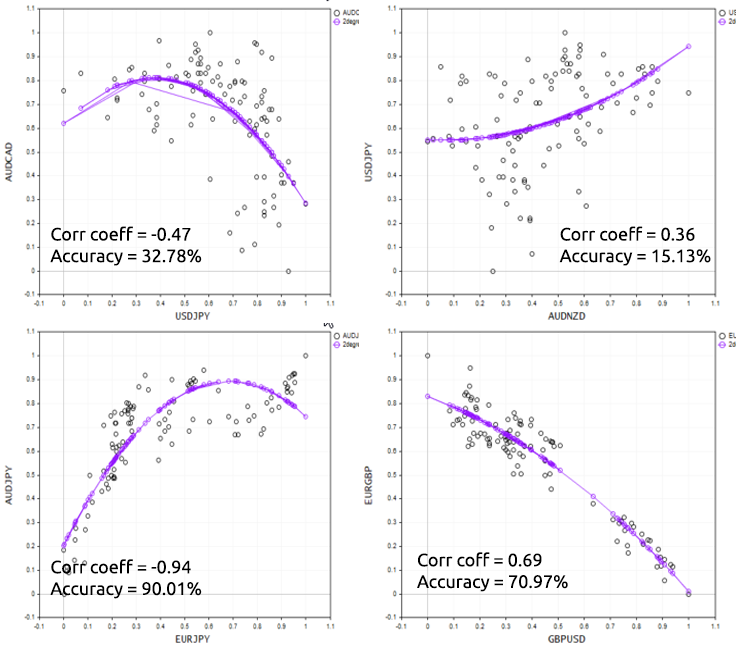
Para demostrar bien este punto, vamos a probar el script en diferentes instrumentos fórex.

Ventajas y desventajas de la regresión polinomial

Ventajas:

• Permite modelar una relación no lineal entre variables
• Existe un amplio espectro de funciones que están de moda utilizar para la configuración
• Resulta adecuado para realizar investigaciones; puede probar diferentes órdenes/grados de polinomios para ver cuál funciona mejor para un conjunto de datos en particular.
• Resulta sencillo programar e interpretar los resultados, y además, es una herramienta poderosa

Desventajas:

• Los valores atípicos pueden distorsionar seriamente los resultados 
• Los modelos de regresión polinómica son propensos al sobreajuste
• Debido al sobreajuste, puede suceder que el modelo no funcione con los datos fuera de la muestra

Reflexiones finales

La regresión polinomial es una técnica útil de aprendizaje automático en multitud de casos en los que se espera que la relación entre la variable independiente y las variables dependientes no sea lineal. Por ello, ofrece una mayor libertad al trabajar con diferentes conjuntos de datos. Asimismo, permite rellenar los huecos del modelo lineal. También podemos utilizarla para trabajar con los datos para los que un modelo lineal no resulta adecuado. Al hacer esto, resultará vital ser conscientes del riesgo de sobreajuste, porque, siendo este modelo paramétrico tan flexible, podría funcionar muy mal con datos no entrenados o de prueba. Posiblemente sea mejor elegir órdenes más bajos y dejar espacio para errores en el modelo. 

¡Gracias por su atención!

Más información sobre matrices: Matrices y vectores

Bibliografía adicional

• Neural Networks for Pattern Recognition (Advanced Texts in Econometrics)
• Neural Networks: Tricks of the Trade (Lecture Notes in Computer Science, 7700)
• Deep Learning (Adaptive Computation and Machine Learning series)

Artículos:

• Aprendizaje automático y data science (Parte 01): Regresión lineal
• Aprendizaje automático y data science (Parte 02): Regresión logística 
• Aprendizaje automático y data science (Parte 03): Regresión matricial
• Aprendizaje automático y data science (Parte 06): Descenso de gradiente