群体优化算法：抵抗陷入局部极值（第二部分）

目录

1.算法
2.改进 BGA 的代理
3.结论

作为研究的一部分，我们深入研究了群体优化算法的鲁棒性，以及它们克服局部陷阱并在各种测试函数上达到全局最大值的能力。在上一篇文章中，我们介绍了一些在排名方面效果一般的算法。现在是时候关注表现最出色的算法们了。

我们努力对每种算法进行深入分析，同时找出它们的优势和独特之处。我们的目标是了解是哪些策略和方法使这些算法成功克服了复杂性并实现了全局优化目标。

在这一研究阶段，我们不仅能更好地了解群体算法在陷入局部陷阱后的恢复能力，还能找出在面对多样而复杂的测试函数时，有助于这些算法取得成功的关键因素。我的工作旨在加深人们对如何优化和改进这些算法的理解，并寻找共同使用和混合使用这些算法的机会，以便在未来有效解决各种优化问题。

1.算法

让我们继续研究在对比表中排名靠前的算法。它们绝对值得更详细的探讨和关注。让我们对它们的功能进行详细分析，揭示它们在解决复杂优化问题时之所以如此有价值和有效的各个方面。

以下是有关算法运行的报告，请阅读如下内容：

• C_AO_FSS:50;0.01;0.8 - 算法名称和外部参数
  
• 5 Hilly's - 测试函数名称及其在测试中的编号
  
•  Func runs:10000 - 运行次数
  
• result:0.32457068874346456 - 得出的结果，其中 0.0 为测试函数的最小值，1.0 为最大值。数值越大越好
  
• All score:1.33084 - 得分的总值，数值越大越好

进化策略，(P+O)ES

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
5 Hilly's; Func runs:10000; result：0.45574011563217454
25 Hilly's；Func runs：10000; result：0.5979154724556998
500 Hilly's；Func runs：10000; result：0.3415203622112476
=============================
5 Forest's; Func runs：10000; result：0.18929181937830403
25 Forest's; Func runs：10000; result：0.1837517532554242
500 Forest's; Func runs：10000; result：0.15411134176683486
=============================
5 Megacity's; Func runs:10000; result：0.10153846153846155
25 Megacity's; Func runs:10000; result：0.12030769230769231
500 Megacity's；Func runs：10000; result：0.08793846153846216
=============================
All score:2.23212

与它的小兄弟 (PO)ES 不同，(P+O)ES 在搜索空间中非常活跃，尤其是在平滑的 Hilly 函数上，群体被分为几个组，每个组探索不同的区域。然而，由于某种原因，它在平滑 Forest 函数上的效率降低了，而在离散函数上的表现却很差（只能到达最近的山丘）。一般来说，该算法对光滑可微分函数非常有趣，但有明显的卡壳倾向。此外，它还缺乏完善结果的功能。

灰狼优化器（GWO）

C_AO_GWO:50;10
=============================
5 Hilly's; Func runs:10000; result：0.5385541648909985
25 Hilly's；Func runs：10000; result：0.33060651191769963
500 Hilly's；Func runs：10000; result：0.25796885816873344
=============================
5 Forest's; Func runs：10000; result：0.33256641908450685
25 Forest's; Func runs：10000; result：0.2040563379483599
500 Forest's; Func runs：10000; result：0.15278428644972566
=============================
5 Megacity's; Func runs:10000; result：0.2784615384615384
25 Megacity's; Func runs:10000; result：0.1587692307692308
500 Megacity's；Func runs：10000; result：0.133153846153847
=============================
All score:2.38692

一群 GWO 算法的狼群在广袤的虚拟世界中奔腾，在各种测试函数上迅速向四面八方扩散。这一特性可以在初始迭代中得到有效利用，尤其是当算法与另一种方法配对使用时，可以对找到的解进行改进和补充。它们出色的研究能力说明了它们的潜力，但遗憾的是，识别区域的准确性仍然是它们的弱项。有趣的是，该算法显示出的结果甚至优于在代理均匀分布情况下进行的传统测试。

洗牌蛙跳算法（SFL）

C_AO_SFL:50;25;15;5;0.7
=============================
5 Hilly's; Func runs:10000; result：0.5009251084703008
25 Hilly's；Func runs：10000; result：0.3175649450809088
500 Hilly's；Func runs：10000; result：0.25514153268631673
=============================
5 Forest's; Func runs：10000; result：0.4165336325557746
25 Forest's; Func runs：10000; result：0.21617658684174407
500 Forest's; Func runs：10000; result：0.15782134182434096
=============================
5 Megacity's; Func runs:10000; result：0.2892307692307692
25 Megacity's; Func runs:10000; result：0.14892307692307696
500 Megacity's；Func runs：10000; result：0.10636923076923148
=============================
All score:2.40869

与列表中的前一种算法相比，SFL 算法在搜索空间的不同方向上展示了更广泛的传播能力，甚至在离散 Megacity 函数上也是如此。SFL 甚至能在给定的迭代次数内达到全局最大区域。然而，改进所找到的解决方案的准确性并不是 SFL 的强项。与 GWO 相似，该算法显示出优于传统测试的结果。

随机搜索算法(RND)

C_AO_RND:50
=============================
5 Hilly's; Func runs:10000; result：0.5024853724464499
25 Hilly's；Func runs：10000; result：0.3284469438564529
500 Hilly's；Func runs：10000; result：0.2600678718550755
=============================
5 Forest's; Func runs：10000; result：0.3989291459162246
25 Forest's; Func runs：10000; result：0.22913381881119183
500 Forest's; Func runs：10000; result：0.16727444696703453
=============================
5 Megacity's; Func runs:10000; result：0.2753846153846154
25 Megacity's; Func runs:10000; result：0.14861538461538465
500 Megacity's；Func runs：10000; result：0.09890769230769311
=============================
All score:2.40925

在这场别开生面的比赛中，这种最简单的优化方法击败了许多受人尊敬的知名参赛者。大家可能还记得，RND 算法的策略是 50%概率：要么从群体中随机选择一个个体的坐标，要么生成一个均匀分布的随机坐标。不过，这也使得该算法上升到了参与者名单的中间位置。尽管在这种情况下没有必要谈论精确度，但由于其广泛的空间探索能力，这一点成为可能。

社会群体演变（ESG）

C_AO_ESG:200:100:0.1:2.0:10.0
=============================
5 Hilly's; Func runs:10000; result：0.3695915822772909
25 Hilly's；Func runs：10000; result：0.3396716009249312
500 Hilly's；Func runs：10000; result：0.2727013729189837
=============================
5 Forest's; Func runs：10000; result：0.2956316169252261
25 Forest's; Func runs：10000; result：0.2875217303660672
500 Forest's; Func runs：10000; result：0.16124201361354124
=============================
5 Megacity's; Func runs:10000; result：0.30769230769230765
25 Megacity's; Func runs:10000; result：0.306153846153846
500 Megacity's；Func runs：10000; result：0.13183076923077003
=============================
All score:2.47204

ESG 算法在探索搜索空间、划分特征组方面表现出良好的能力。然而，它忽略了遥远的空间区域，这可能会在探索问题的全部范围时造成问题。还有迹象表明，局部地区正陷入严重的极端状态，这可能导致难以实现全局最优。尽管如此，该算法在处理离散 Megacity 函数时仍取得了巨大成功，凸显了其在某些条件和任务中的潜力。

智能水滴算法（IWDm）

C_AO_IWDm:50;10;3.0
=============================
5 Hilly's; Func runs:10000; result：0.4883273901756646
25 Hilly's；Func runs：10000; result：0.34290016593207995
500 Hilly's；Func runs：10000; result：0.2581256124908963
=============================
5 Forest's; Func runs：10000; result：0.5119191969436073
25 Forest's; Func runs：10000; result：0.2564038040639046
500 Forest's; Func runs：10000; result：0.1675925588605327
=============================
5 Megacity's; Func runs:10000; result：0.34153846153846157
25 Megacity's; Func runs:10000; result：0.15784615384615389
500 Megacity's；Func runs：10000; result：0.09889230769230851
=============================
All score:2.62355

IWDm 算法就像汹涌的河水，在搜索空间中快速滑行，很快就到达了全局最大值区域，显示出卓越的搜索能力。但值得注意的是，这种算法的清晰度不够，因此很难准确确定最优解。

在传统的排名中，这种算法并不名列前茅，但在这次测试中，与其他算法相比，它的表现令人印象深刻。建议在优化的初始阶段使用 IWDm，然后再使用更精确的算法，丰富和改进整个优化过程。

粒子群（PSO）

C_AO_PSO:50;0.8;0.4;0.4
=============================
5 Hilly's; Func runs:10000; result：0.5548169875802522
25 Hilly's；Func runs：10000; result：0.3407594364160912
500 Hilly's；Func runs：10000; result：0.2525297014321252
=============================
5 Forest's; Func runs：10000; result：0.4573903259815636
25 Forest's; Func runs：10000; result：0.27561812346057046
500 Forest's; Func runs：10000; result：0.19079124396445962
=============================
5 Megacity's; Func runs:10000; result：0.3092307692307693
25 Megacity's; Func runs:10000; result：0.14923076923076928
500 Megacity's；Func runs：10000; result：0.09553846153846236
=============================
All score:2.62591

PSO 算法在本次实验中取得了出人意料的优异成绩，与之前的 IWDm 算法相比，PSO 算法在未知领域的移动速度更快。这种突如其来的成功可以解释为，PSO 中的粒子在第一次迭代中随机选择了一个初始速度，这使得它们能够迅速离开原来的位置。算法的初始步骤就像粒子在空间中跳舞，直到它们找到自己的特殊和弦。遗憾的是，这种和弦并不总能带来全局最优。缺乏清晰的特质会延缓理想解决方案的实现。

与 IWDm 一样，PSO 也可推荐用于优化的初始阶段，其快速探索搜索空间的能力是发现有前途解决方案的关键。

蝙蝠算法（BA）

C_AO_BA:50;0.0;1.0;0.0;1.5;0.0;1.0;0.3;0.3
=============================
5 Hilly's; Func runs:10000; result：0.5127608047854995
25 Hilly's；Func runs：10000; result：0.4239882910506281
500 Hilly's；Func runs：10000; result：0.3127353914885268
=============================
5 Forest's; Func runs：10000; result：0.4355521825589907
25 Forest's; Func runs：10000; result：0.29303187383086005
500 Forest's; Func runs：10000; result：0.19433130092541523
=============================
5 Megacity's; Func runs:10000; result：0.28769230769230764
25 Megacity's; Func runs:10000; result：0.16030769230769232
500 Megacity's；Func runs：10000; result：0.10907692307692407
=============================
All score:2.72948

BA 算法中的蝙蝠有一个惊人的特性，那就是能快速找到全局极值区域，在第一次迭代中就能立即移动。但这种搜索方法中的声脉冲等式会导致蝙蝠的动作很快消失，尽管它们显然需要继续搜索。BA 在常规排名中靠后，但在本次挑战赛中却名列前茅。

 入侵杂草优化（IWO）

C_AO_IWO:50;12;5;2;0.2;0.01
=============================
5 Hilly's; Func runs:10000; result：0.4570149872637351
25 Hilly's；Func runs：10000; result：0.4252105325836707
500 Hilly's；Func runs：10000; result：0.28299287471456525
=============================
5 Forest's; Func runs：10000; result：0.43322917175445896
25 Forest's; Func runs：10000; result：0.33438950288190694
500 Forest's; Func runs：10000; result：0.18632383795879612
=============================
5 Megacity's; Func runs:10000; result：0.3061538461538461
25 Megacity's; Func runs:10000; result：0.24369230769230765
500 Megacity's；Func runs：10000; result：0.12887692307692397
=============================
All score:2.79788

入侵杂草算法与蝙蝠算法（BA）一样，也将传播速度作为当前迭代的函数。不过，与 BA 相比，在这种情况下，代理能够更有效、更全面地探索空间，从而能够快速、准确地找到最优解，同时考虑到函数的关键特征和全局最大值区域。但是，如果从起点到目标的距离很大，那么杂草就无法达到全局最大面积。这一点在 Megacity 函数中尤为明显 - 代理会陷入最近的重要极值。

人工蜂群（ABC）

C_AO_ABC:50;45;10;0.1;0.4
=============================
5 Hilly's; Func runs:10000; result：0.5969246550857782
25 Hilly's；Func runs：10000; result：0.3899058056869557
500 Hilly's；Func runs：10000; result：0.26574506946962373
=============================
5 Forest's; Func runs：10000; result：0.536535405336652
25 Forest's; Func runs：10000; result：0.29048311417293887
500 Forest's; Func runs：10000; result：0.17322987568991322
=============================
5 Megacity's; Func runs:10000; result：0.3307692307692308
25 Megacity's; Func runs:10000; result：0.18492307692307694
500 Megacity's；Func runs：10000; result：0.11512307692307773
=============================
All score:2.88364

ABC 算法的有趣之处在于，它能将一个群体分割成不同的蜂群，这些蜂群会积极探索局部极值。不过，该算法可能还不够清晰，这一点从其在标准评级表中的位置就能看出来。不过，在混合算法中改进和使用其搜索能力还是有潜力的。通过与其他优化方法相结合，该算法找到全局最优点的能力及其在各种优化问题中的整体效率都能得到显著提高。

思维进化计算（MEC）

C_AO_MEC:50;10;0.4
=============================
5 Hilly's; Func runs:10000; result：0.5566946043237988
25 Hilly's；Func runs：10000; result：0.430203412538813
500 Hilly's；Func runs：10000; result：0.2724348221662864
=============================
5 Forest's; Func runs：10000; result：0.4548936450507163
25 Forest's; Func runs：10000; result：0.3156014530351309
500 Forest's; Func runs：10000; result：0.17625852850331755
=============================
5 Megacity's; Func runs:10000; result：0.3415384615384615
25 Megacity's; Func runs:10000; result：0.23107692307692304
500 Megacity's；Func runs：10000; result：0.1186615384615393
=============================
All score:2.89736

MEC 算法的速度惊人，它能立即检测到几乎所有重要的局部极值，并成功识别全局最大值区域。尽管 MEC 稍微落后于传统测试，但它在寻找最佳解决方案方面仍然表现出很高的稳定性和效率。

布谷鸟优化算法（COAm）

C_AO_COAm:100;40;0.6;0.6;0.63
=============================
5 Hilly's; Func runs:10000; result：0.600998666320958
25 Hilly's；Func runs：10000; result：0.42709404776275245
500 Hilly's；Func runs：10000; result：0.26571090745735276
=============================
5 Forest's; Func runs：10000; result：0.5533129896276743
25 Forest's; Func runs：10000; result：0.30413063297063025
500 Forest's; Func runs：10000; result：0.1703031415266755
=============================
5 Megacity's; Func runs:10000; result：0.3261538461538461
25 Megacity's; Func runs:10000; result：0.2046153846153847
500 Megacity's；Func runs：10000; result：0.1112615384615393
=============================
All score:2.96358

在传统的 COAm 评分表中，我们的平均成绩在搜索空间中显示出惊人的移动速度，轻松摆脱了全局最小值。然而，它也有一定的困难，会在局部出现明显的极值，从而无法达到全局最大值。

微人工免疫系统（Micro-AIS）

C_AO_Micro_AIS:50:1:2:0.3
=============================
5 Hilly's; Func runs:10000; result：0.6193671060348247
25 Hilly's；Func runs：10000; result：0.4656896752001433
500 Hilly's；Func runs：10000; result：0.24995620778886124
=============================
5 Forest's; Func runs：10000; result：0.7121901446084455
25 Forest's; Func runs：10000; result：0.4254191301238518
500 Forest's; Func runs：10000; result：0.211517515004865
=============================
5 Megacity's; Func runs:10000; result：0.2676923076923077
25 Megacity's; Func runs:10000; result：0.16461538461538466
500 Megacity's；Func runs：10000; result：0.10927692307692398
=============================
All score:3.22572

Micro-AIS 算法可以识别抗原形成的非常均匀的云，这使得整个过程具有一定的秩序，让人联想到和谐而非混乱。尽管算法具有良好的搜索能力，但其澄清特性仍需改进。不过，它也容易陷入局部的陷阱。

和弦搜索（HS）

C_AO_HS:50;0.9;0.1;0.2
=============================
5 Hilly's; Func runs:10000; result：0.602082991833691
25 Hilly's；Func runs：10000; result：0.5533985889779909
500 Hilly's；Func runs：10000; result：0.2820448101527182
=============================
5 Forest's; Func runs：10000; result：0.6503798132320532
25 Forest's; Func runs：10000; result：0.5104503170911219
500 Forest's; Func runs：10000; result：0.19337757947865844
=============================
5 Megacity's; Func runs:10000; result：0.30769230769230765
25 Megacity's; Func runs:10000; result：0.29538461538461525
500 Megacity's；Func runs：10000; result：0.12826153846153937
=============================
All score:3.52307

在这一特定问题中，HS 表现出了惊人的搜索能力和在空间中寻找全局最大值的高速运动能力。然而，当遇到第一个显著的局部极值时，由于其依赖于当前的纪元数，速度会减慢。不过，这一缺点只出现在离散的 Megacity 函数上，而在流畅的 Hilly 和 Forest 函数上，其搜索能力仍然令人印象深刻。在评级表中，和弦搜索占据了榜首位置，这也证明了它在当前测试中的效率。

螺旋动态优化（SDOm）

C_AO_SDOm:100;0.5;4.0;10000.0
=============================
5 Hilly's; Func runs:10000; result：0.7132463872323508
25 Hilly's；Func runs：10000; result：0.43264564401427485
500 Hilly's；Func runs：10000; result：0.25506574720969816
=============================
5 Forest's; Func runs：10000; result：0.804287574819851
25 Forest's; Func runs：10000; result：0.4249161540200845
500 Forest's; Func runs：10000; result：0.2193817986301354
=============================
5 Megacity's; Func runs:10000; result：0.4938461538461539
25 Megacity's; Func runs:10000; result：0.22030769230769232
500 Megacity's；Func runs：10000; result：0.11410769230769328
=============================
All score:3.67780

SDOm 算法突然出现在排名前列。这种算法以谐波振荡为基础，在实验框架内以一种非常不寻常的独特方式表现出来，留下了一个难以揭开的谜团。悬挂在绳索上的摆球会突然脱离绳索，进入自由飞行状态。算法行为有许多特殊之处，几乎不可能预测导致这种意外行为的条件。正因为如此，很难建议将其用于当前形式的各种任务。不过，与其他算法相结合（例如，将一些代理从普通群体转为 SDOm 控制），可以帮助识别任务中的周期性模式。

细菌觅食优化 - 遗传算法（BFO-GA）

C_AO_BFO_GA:50;0.01;0.8;50;10.0
=============================
5 Hilly's; Func runs:10000; result：0.8233662999080027
25 Hilly's；Func runs：10000; result：0.5031148772790799
500 Hilly's；Func runs：10000; result：0.27434497581097494
=============================
5 Forest's; Func runs：10000; result：0.8611314745481611
25 Forest's; Func runs：10000; result：0.45038118646429437
500 Forest's; Func runs：10000; result：0.1806538222176609
=============================
5 Megacity's; Func runs:10000; result：0.3907692307692308
25 Megacity's; Func runs:10000; result：0.272
500 Megacity's；Func runs：10000; result：0.11061538461538559
=============================
All score:3.86638

BFO_GA 算法在快速检测全局最大值区域方面表现出惊人的能力 - 在最初的迭代过程中，已有多个代理接近目标坐标。然而，它在离散函数方面的结果却不尽如人意。显然，测试中有限的迭代次数不足以完全找到全局最优。不过，需要注意的是，我们的测试是在一个严格的框架内进行的，在这个框架内，我们对算法实现预期目标的能力进行评估。

随机扩散搜索（SDSm）

C_AO_SDSm:100;100;0.05
=============================
5 Hilly's; Func runs:10000; result：0.6838494804548411
25 Hilly's；Func runs：10000; result：0.6796828568841194
500 Hilly's；Func runs：10000; result：0.32584905164208583
=============================
5 Forest's; Func runs：10000; result：0.6703019775594297
25 Forest's; Func runs：10000; result：0.6398441335988195
500 Forest's; Func runs：10000; result：0.24899123954861618
=============================
5 Megacity's; Func runs:10000; result：0.5307692307692308
25 Megacity's; Func runs:10000; result：0.49446153846153845
500 Megacity's；Func runs：10000; result：0.14973846153846293
=============================
All score:4.42349

在讨论 SDSm 算法时，关注代理在整个搜索空间的传播速度并不完全合适，因为代理的坐标是在环境中随机选择的区域内指定的。从本质上讲，这些代理在第一次迭代后就会立即分布到整个搜索领域。这种独特的方法取得了显著的成果，证明了算法策略的高效性。

SDSm 的与众不同之处在于，它能够利用随机性的力量，增加搜索空间中任何一个角落都不被遗漏的可能性。考虑到这种随机性，该算法可以有效地覆盖广阔的区域，并揭示函数面的宝贵信息，使其成为解决问题的真正强大工具。

二进制遗传算法（BGA）

C_AO_BGA:50:50:1.0:3:0.001:0.7:3
=============================
5 Hilly's; Func runs:10000; result：1.0
25 Hilly's；Func runs：10000; result：1.0
500 Hilly's；Func runs：10000; result：0.8703352617259978
=============================
5 Forest's; Func runs：10000; result：0.8872607468925364
25 Forest's; Func runs：10000; result：0.8177419261242314
500 Forest's; Func runs：10000; result：0.2603521654104144
=============================
5 Megacity's; Func runs:10000; result：0.7492307692307694
25 Megacity's; Func runs:10000; result：0.5833846153846155
500 Megacity's；Func runs：10000; result：0.24415384615384667
=============================
All score:6.41246

二进制遗传算法（BGAs）的优势在于基因突变，无需额外的迭代，就能立即到达搜索空间的任何区域。不过，在这个特定的测试场景中，尽管 BGA 有时会陷入局部最优状态，但最终还是胜出了。在这方面，SDSm 似乎更可取，因为它能更好地避免出现这种情况。

不过，即使考虑到其不足之处，也必须将取得最佳总体成果的功劳归于 BGA。这一成就凸显了该算法的潜力，以及在搜索过程中兼顾研究与开发的重要性。如果我们深入比较，就会发现每种算法都有自己独特的优缺点。

总之，我们可以说，BGA 在这项测试中取得了骄人的成绩，稳居榜首。

2.改进 BGA 的代理

为开展这项研究，有必要针对这一特定测试任务修改 BGA 算法代码。如果需要从用户定义的集合开始优化，将代理放置在搜索空间任意位置的功能会非常有用。

在 BGA 中，问题的解决方案是以二进制代码的形式呈现的，因此，为了将群体代理放置在给定的坐标上，有必要将坐标值从实数表示转换为二进制表示，在这种情况下就是转换为二进制格雷代码。

让我们在代理描述中添加 "DoubleToGene" 方法，将 "double" 类型的值转换为 "genes" 数组中的基因表示。这种方法的主要步骤是：

• 如果输入的数值小于最小有效值，函数会创建一个零数组（用格雷码符号表示为实数 "0.0"），以确保数值保持在有效范围内。

• 如果输入的数字超过了允许的最大值，函数会创建一个数组，从包含格雷编码允许的最大值的原始数组中复制数值（这个数值是为这种情况而保存的，当出现超出范围的增加时，我们需要返回到范围内）。
  

• 如果数字在可接受的范围内，则按比例将其转换为格雷代码。然后将该值存储到一个数组中，用于基因表示。

因此，"DoubleToGene" 方法将实数值转换为基因表示，并将其写入相应的 "基因" 数组。该函数通过初始化或复制特定数组并提前终止执行，来处理输入值超出范围的情况。否则，函数会对数值进行缩放，将整数和小数部分转换为格雷码，并将它们合并为最终的遗传表示。

调整后的 BGA 代理代码：

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (const int coords, const double &min [], const double &max [], int doubleDigitsInChromo)
  {
    ArrayResize(c, coords);
    f = -DBL_MAX;

    ArrayResize(genes, coords);
    ArrayResize(chromosome, 0, 1000);

    for(int i = 0; i < coords; i++)
    {
      genes [i].Init(min [i], max [i], doubleDigitsInChromo);
      ArrayCopy(chromosome, genes [i].gene, ArraySize(chromosome), 0, WHOLE_ARRAY);
    }
  }

  void ExtractGenes ()
  {
    uint pos = 0;

    for (int i = 0; i < ArraySize (genes); i++)
    {
      c [i] = genes [i].ToDouble (chromosome, pos);
      pos  += genes [i].length;

    }
  }

  void DoubleToGene (const double val, const int genePos)
  {
    double value = val;

    //--------------------------------------------------------------------------
    if (value < genes [genePos].rangeMin)
    {
      ArrayInitialize(genes [genePos].gene, 0);
      ArrayCopy (chromosome, genes [genePos].gene, genePos * genes [genePos].length, 0, WHOLE_ARRAY);
      return;
    }

    //--------------------------------------------------------------------------
    else
    {
      if (value > genes [genePos].rangeMax)
      {
        ArrayCopy (chromosome, genes [genePos].geneMax, genePos * genes [genePos].length, 0, WHOLE_ARRAY);
        return;
      }
    }

    //--------------------------------------------------------------------------
    value = Scale(value, genes [genePos].rangeMin, genes [genePos].rangeMax, 0.0, genes [genePos].maxCodedDistance);

    DecimalToGray ((ulong)value, genes [genePos].integPart);

    value = value - (int)value;

    value *= genes [genePos].digitsPowered;

    DecimalToGray ((ulong)value, genes [genePos].fractPart);

    ArrayInitialize(genes [genePos].gene, 0);

    uint   integGrayDigits = genes [genePos].integGrayDigits;
    uint   fractGrayDigits = genes [genePos].fractGrayDigits;
    uint   digits = ArraySize (genes [genePos].integPart);

    if (digits > 0) ArrayCopy (genes [genePos].gene, genes [genePos].integPart, integGrayDigits - digits, 0, WHOLE_ARRAY);

    digits = ArraySize (genes [genePos].fractPart);

    if (digits > 0) ArrayCopy (genes [genePos].gene, genes [genePos].fractPart, genes [genePos].length - digits, 0, WHOLE_ARRAY);

    ArrayCopy (chromosome, genes [genePos].gene, genePos * genes [genePos].length, 0, WHOLE_ARRAY);
  }

  void InjectGeneToChromosome ()
  {

  }

  //----------------------------------------------------------------------------
  double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX)
  {
    if (OutMIN == OutMAX) return (OutMIN);
    if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0));
    else
    {
      if (In < InMIN) return OutMIN;
      if (In > InMAX) return OutMAX;

      return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
    }
  }

  double c [];           //coordinates
  double f;              //fitness

  S_BinaryGene genes []; //there are as many genes as there are coordinates
  char chromosome    [];
};
//——————————————————————————————————————————————————————————————————————————————

3.总结

让我们来总结一下大规模群体算法比较研究的结果，这意味着退出全局最小值，克服一切障碍，实现全局最大值。
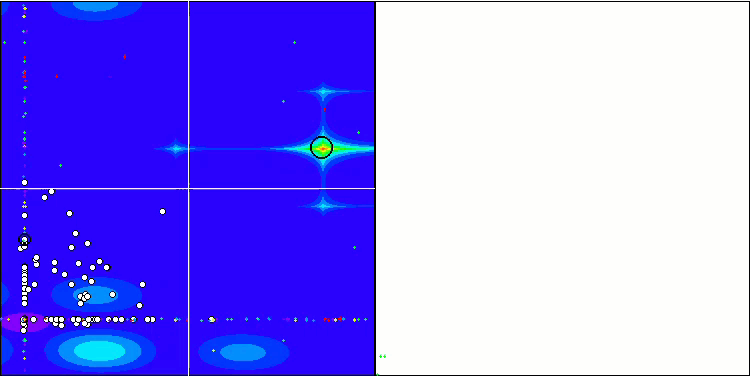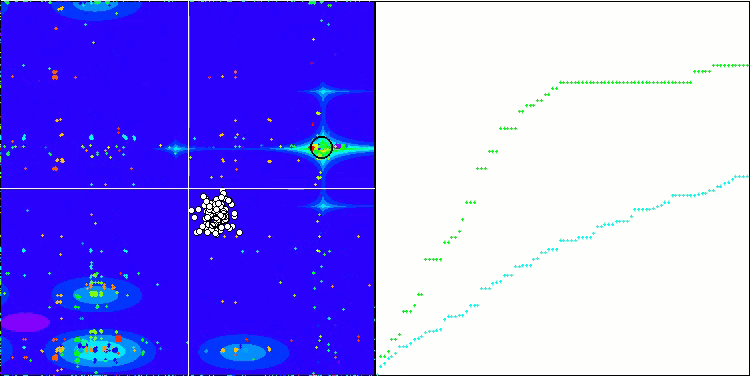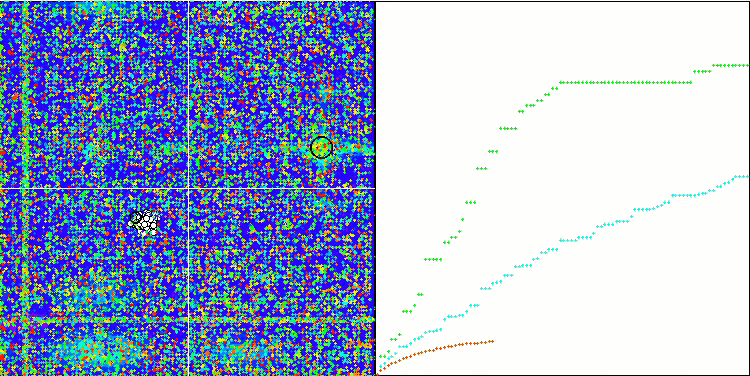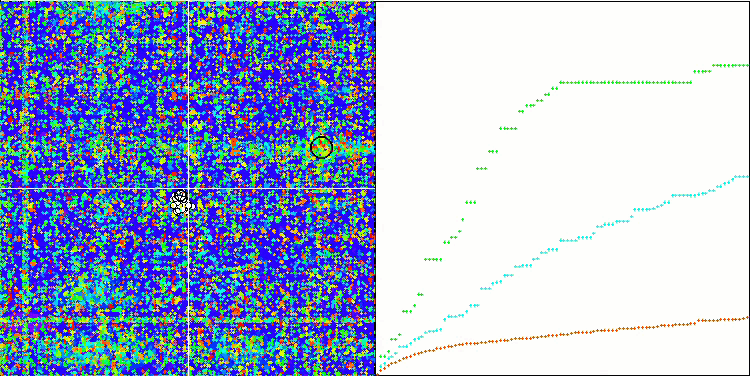
首先，我们将对测试过程中最有趣的算法行为进行可视化。

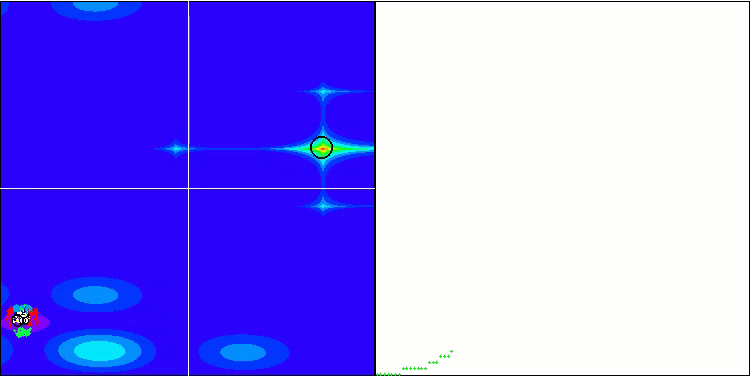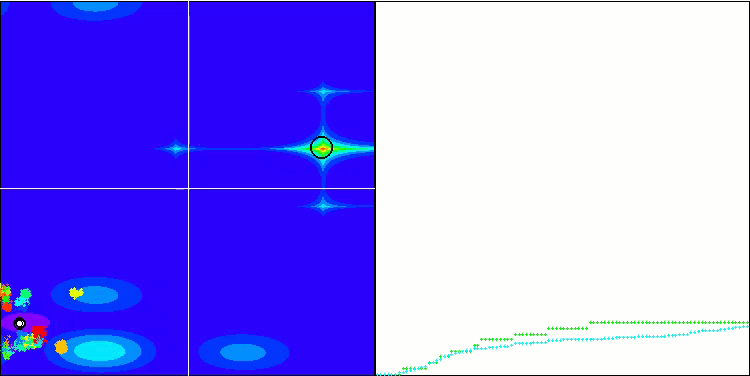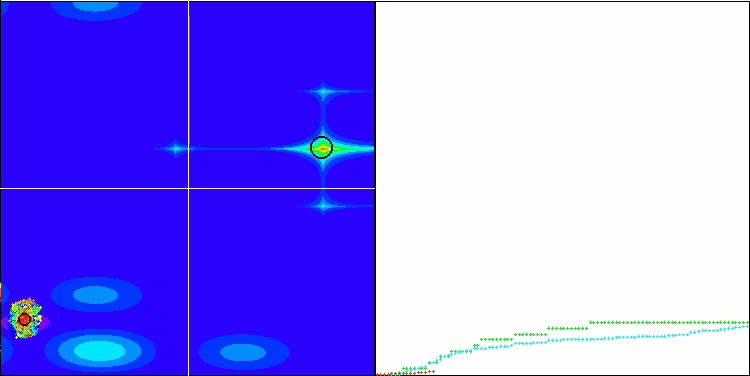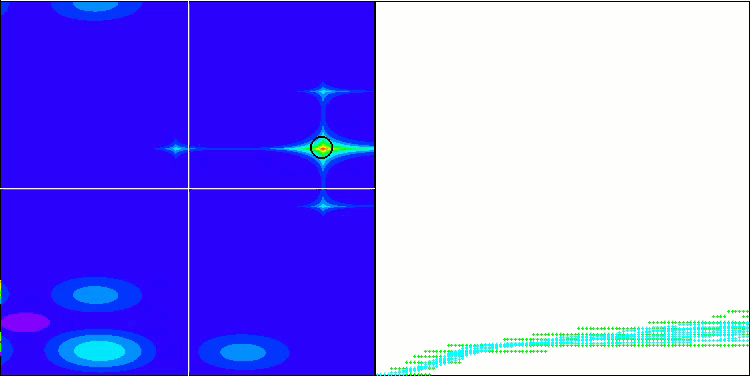
Megacity 上的 (PO)ES

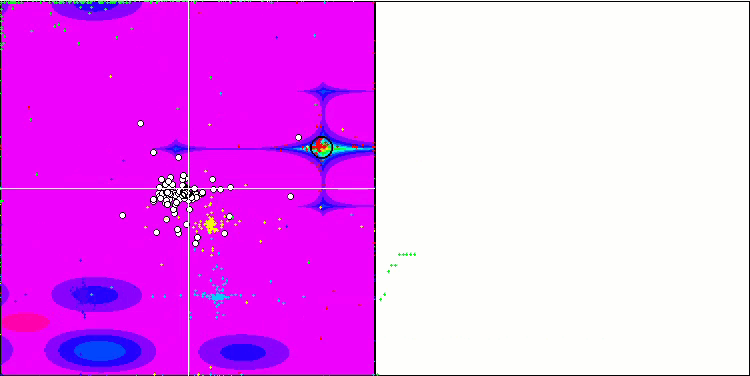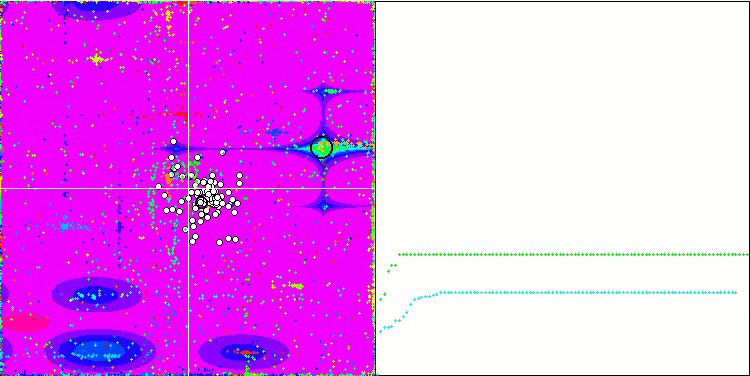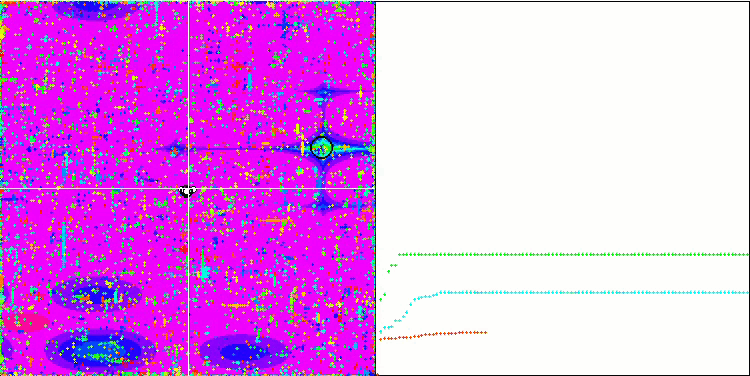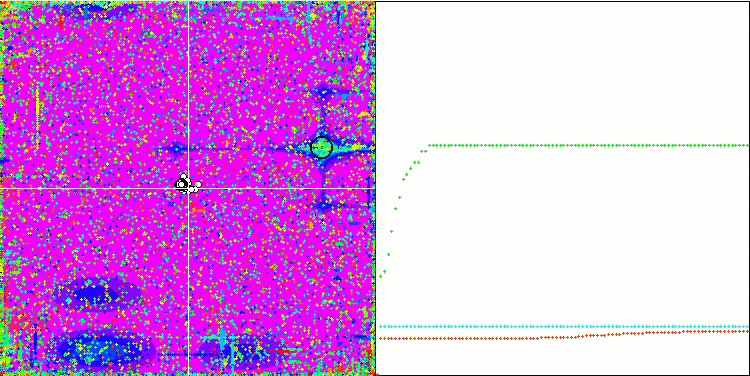
Megacity 上的 SDOm

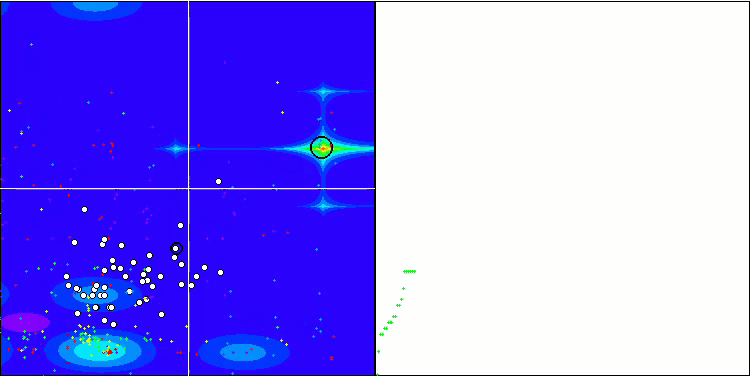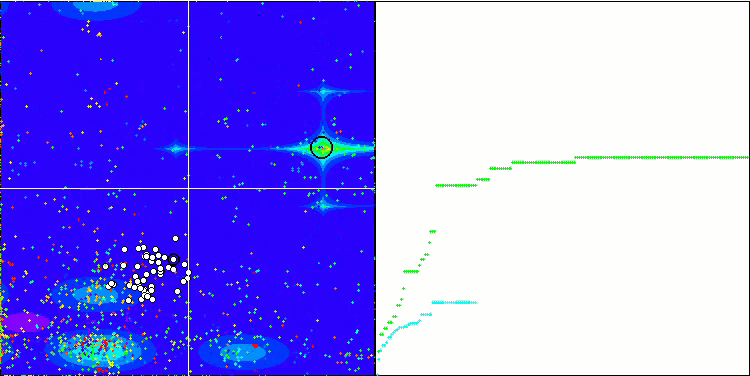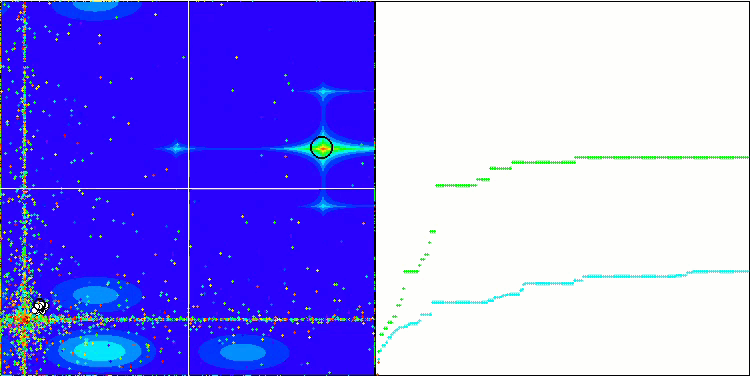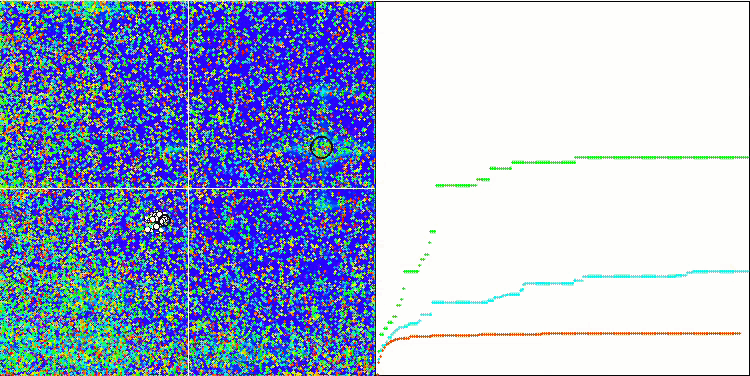
Megacity 上的 BFO_GA

Megacity 上的 SDSm

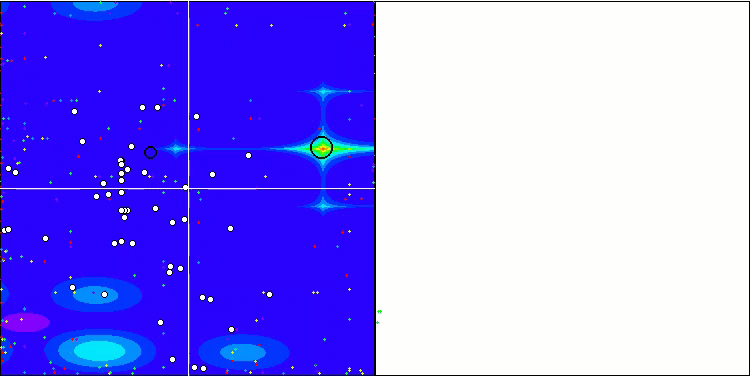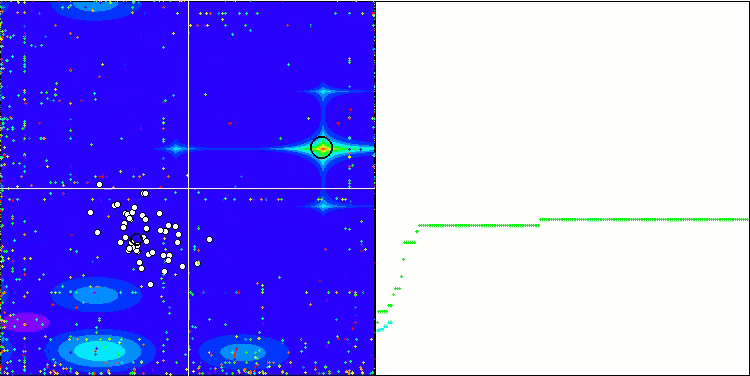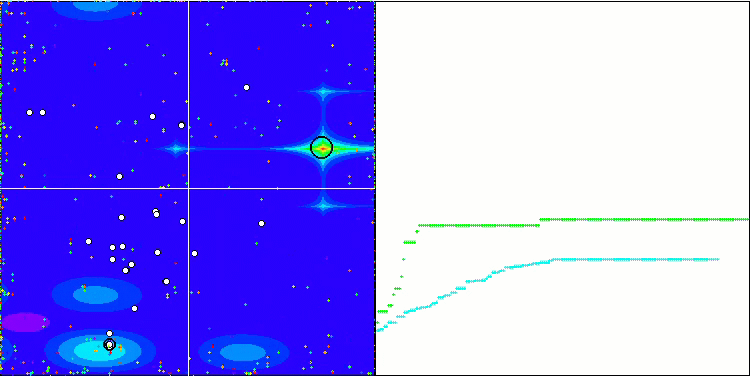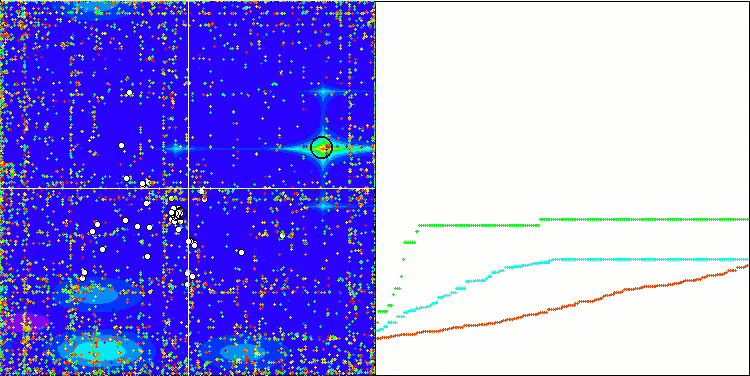
Megacity 上的 BGA

下面是最终比较表，详细显示了每种算法在测试函数上的工作情况。

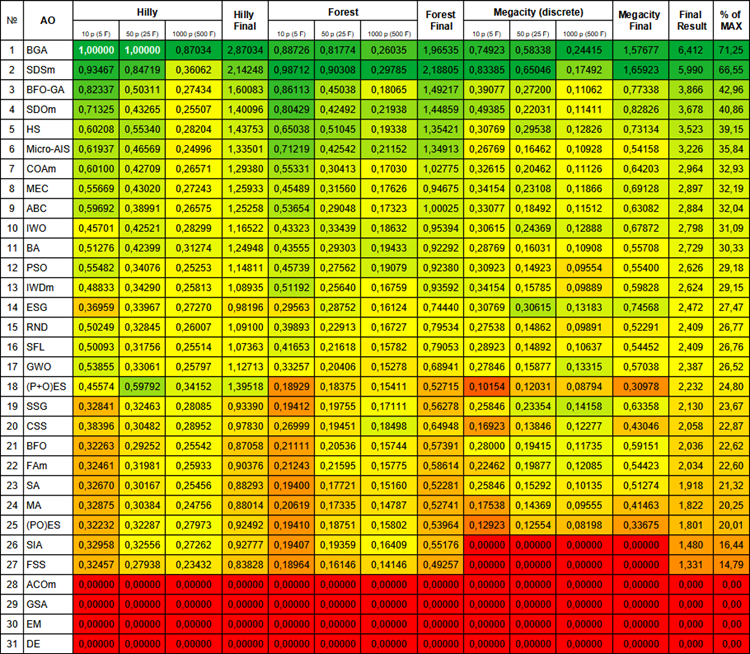
图 1.根据相关测试对算法进行颜色渐变，大于或等于 0.99 的结果用白色标出

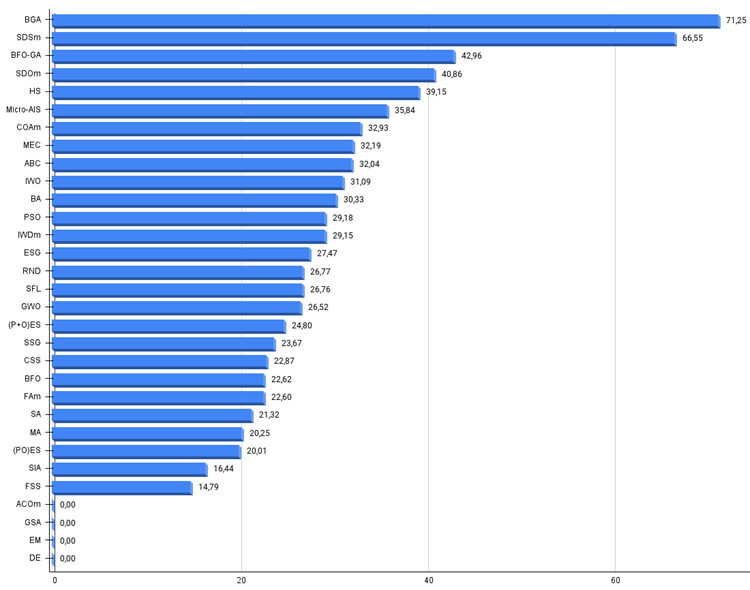
图 2.算法测试结果柱状图（从 0 到 100，越多越好、

其中 100 是最大可能的理论结果，归档中有一个计算评级表的脚本）。

最后，我要特别强调，对每种算法的所有结论和判断都是在实验框架内做出的。

对群体优化算法行为的整个讨论和分析表明，算法的成功与否在很大程度上取决于其应用的初始条件。对于某些方法，如 DE、EM、GSA、ACOm，从测试函数最小点退出的测试可能非常复杂，以至于一开始就会遇到困难。与此同时，其他算法，如 (P+O)ES、ESG（最初在排名中占据前列，但后来成为局外者），效率则急剧下降。相反，对于 PSO、GWO、SFL、BA 和 ABC 等算法来说，特意选择的初始坐标可以显著改善结果。一些算法（BFO-GA 和 SDOm）采用这种方法后甚至表现出了卓越的性能，超过了随机均匀代理初始化。

其他算法，如 IWO、HS、SDSm 和 BGA，无论代理的起始位置如何，都显示出普遍的稳定性。这项特别实验突出表明，虽然有些算法在测试过程中表现不佳，但它们在实验的某些阶段仍然表现出了令人印象深刻的能力。它们中的一些在早期阶段成功地开拓了空间，而另一些则在后期阶段显著改善了成果。每种算法的这些独特功能都可以成功地结合和杂交，增强其积极方面，减少其不利因素，从而最终产生更高效的优化方法。