Deep Neural Networks (Part V). Bayesian optimization of DNN hyperparameters
28 617
5
Contents
- Introduction
- 1. Determining the optimal hyperparameters of the DNN (darch)
- Generating the source data sets
- Removing statistically insignificant predictors
- Determining the DNN hyperparameters to be optimized and their value ranges
- Defining the pretraining and fine-tuning functions for the DNN
- Defining the fitness function for optimization
- Calculating the optimal parameters of the DNN
- 2. Training and testing the DNN with the optimal parameters
- 3. Analyzing the results of testing the DNN with the optimal parameters
- 4. Forward testing the models with optimal parameters
- Conclusion
- Application
Introduction
The previous article considered a basic model and the DNN model with default parameters. The classification quality of that model turned out to be unsatisfactory. What can be done to improve the quality of the classification?
- Optimize the DNN hyperparameters
- Improve the DNN regularization
- Increase the number of training samples
- Change the structure of the neural network
All the listed opportunities for improving the existing DNN will be considered in this and upcoming articles. Let us start with optimization of the network's hyperparameters.
1. Determining the optimal hyperparameters of the DNN
In the general case, hyperparameters of the neural network can be divided into two groups: global and local (nodal). Global hyperparameters include the number of hidden layers, the number of neurons in each layer, level of learning, momentum, initialization of neuron weights. Local hyperparameters — layer type, activation function, dropout/dropconnect and other regularization parameters.
The structure of hyperparameters optimization is shown in the figure:
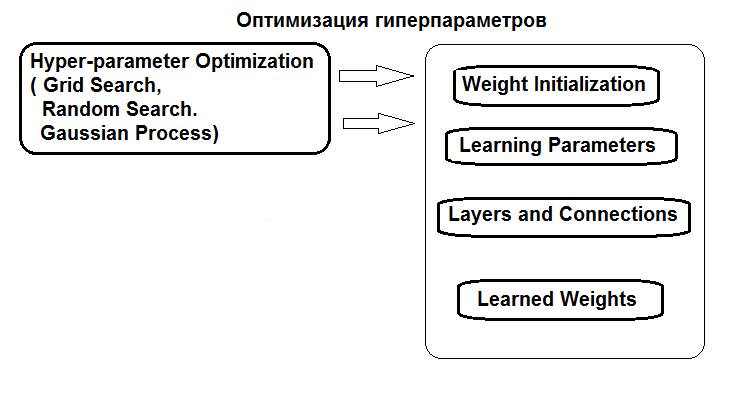
Fig.1. Structure of the neural network hyperparameters and optimization methods
Hyperparameters can be optimized in three ways:
- Grid search: for each hyperparameter, a vector with several fixed values is defined. Then, using the caret::train() function or a custom script, the model is trained on all combinations of hyperparameter values. After that, the model with the best values of classification quality is selected. Its parameters will be taken as optimal. The disadvantage of this method is that defining a grid of values is more likely to miss the optimum.
- Genetic optimization: stochastic search for the best parameters using genetic algorithms. Several algorithms of genetic optimization have been discussed in details earlier. Therefore, they will not be repeated.
- And, finally, Bayesian optimization. It will be used in this article.
The Bayesian approach includes Gaussian processes and MCMC. The rBayesianOptimization (version 1.1.0) package will be used. The theory of applied methods is widely available in literature and given in this article, for instance.
To perform a Bayesian optimization, it is necessary to:
- determine the fitness function;
- determine the list and boundaries of changes in the hyperparameters.
The fitness function (FF) should return a quality score (optimization criterion, scalar) which should be maximized during the optimization, and the predicted values of the objective function. FF will return the value of mean(F1) — the average value of F1 for two classes. The DNN model will be trained with pretraining.
Generating the source data sets
For the experiments, the new version of MRO 3.4.2 will be used. It features several new packages which were not used before.
Run RStudio, go to GitHub/Part_I to download the Cotir.RData file with quotes obtained from the terminal, and fetch the FunPrepareData.R file with data preparation functions from GitHub/Part_IV.
Previously, it was determined that a set of data with imputed outliers and normalized data makes it possible to obtain better results in training with pretraining. You can also test the other preprocessing options considered earlier.
When dividing into pretrain/train/val/test subsets, we use the first opportunity to improve the classification quality — increase the number of samples for training. The number of samples in the pretrain subset will be increased to 4000.
#----Prepare------------- library(anytime) library(rowr) library(darch) library(rBayesianOptimization) library(foreach) library(magrittr) #source(file = "FunPrepareData.R") #source(file = "FUN_Optim.R") #---prepare---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt, 4000, 1000, 500, 100, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) preproc <- PreNorm(DTcap, meth = meth) DTcap.n <- NormData(DTcap, preproc = preproc) }, env)
By changing the start parameter in the SplitData() function, it is possible to obtain sets shifted right by the amount of start. This allows checking the quality in different parts of the price range in the future and determining how it changes in history.
Removing statistically insignificant predictors
Remove two statistically insignificant variables c(v.rstl, v.pcci). They have been determined in the previous article in this series.
##---Data DT-------------- require(foreach) evalq({ foreach(i = 1:4) %do% { DTcap.n[[i]] %>% dplyr::select(-c(v.rstl, v.pcci)) } -> DT list(pretrain = DT[[1]], train = DT[[2]], val = DT[[3]], test = DT[[4]]) -> DT }, env)
Create data sets (pretrain/train/test/test1) for pretraining, fine-tuning and testing, gathered in the X list.
#-----Data X------------------
evalq({
list(
pretrain = list(
x = DT$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$pretrain$Class %>% as.data.frame()
),
train = list(
x = DT$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$train$Class %>% as.data.frame()
),
test = list(
x = DT$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$val$Class %>% as.data.frame()
),
test1 = list(
x = DT$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$test$Class %>% as.vector()
)
) -> X
}, env)
Sets for the experiments are ready.
A function is needed to calculate the metrics from the test results. The value of mean(F1) will be used as the optimization (maximization) criterion. Load this function into the env environment.
evalq( #input actual & predicted vectors or actual vs predicted confusion matrix # https://github.com/saidbleik/Evaluation/blob/master/eval.R Evaluate <- function(actual=NULL, predicted=NULL, cm=NULL){ if (is.null(cm)) { actual = actual[!is.na(actual)] predicted = predicted[!is.na(predicted)] f = factor(union(unique(actual), unique(predicted))) actual = factor(actual, levels = levels(f)) predicted = factor(predicted, levels = levels(f)) cm = as.matrix(table(Actual = actual, Predicted = predicted)) } n = sum(cm) # number of instances nc = nrow(cm) # number of classes diag = diag(cm) # number of correctly classified instances per class rowsums = apply(cm, 1, sum) # number of instances per class colsums = apply(cm, 2, sum) # number of predictions per class p = rowsums / n # distribution of instances over the classes q = colsums / n # distribution of instances over the predicted classes #accuracy accuracy = sum(diag) / n #per class recall = diag / rowsums precision = diag / colsums f1 = 2 * precision * recall / (precision + recall) #macro macroPrecision = mean(precision) macroRecall = mean(recall) macroF1 = mean(f1) #1-vs-all matrix oneVsAll = lapply(1:nc, function(i){ v = c(cm[i,i], rowsums[i] - cm[i,i], colsums[i] - cm[i,i], n - rowsums[i] - colsums[i] + cm[i,i]); return(matrix(v, nrow = 2, byrow = T))}) s = matrix(0, nrow = 2, ncol = 2) for (i in 1:nc) {s = s + oneVsAll[[i]]} #avg accuracy avgAccuracy = sum(diag(s))/sum(s) #micro microPrf = (diag(s) / apply(s,1, sum))[1]; #majority class mcIndex = which(rowsums == max(rowsums))[1] # majority-class index mcAccuracy = as.numeric(p[mcIndex]) mcRecall = 0*p; mcRecall[mcIndex] = 1 mcPrecision = 0*p; mcPrecision[mcIndex] = p[mcIndex] mcF1 = 0*p; mcF1[mcIndex] = 2 * mcPrecision[mcIndex] / (mcPrecision[mcIndex] + 1) #random accuracy expAccuracy = sum(p*q) #kappa kappa = (accuracy - expAccuracy) / (1 - expAccuracy) #random guess rgAccuracy = 1 / nc rgPrecision = p rgRecall = 0*p + 1 / nc rgF1 = 2 * p / (nc * p + 1) #rnd weighted rwgAccurcy = sum(p^2) rwgPrecision = p rwgRecall = p rwgF1 = p classNames = names(diag) if (is.null(classNames)) classNames = paste("C",(1:nc),sep = "") return(list( ConfusionMatrix = cm, Metrics = data.frame( Class = classNames, Accuracy = accuracy, Precision = precision, Recall = recall, F1 = f1, MacroAvgPrecision = macroPrecision, MacroAvgRecall = macroRecall, MacroAvgF1 = macroF1, AvgAccuracy = avgAccuracy, MicroAvgPrecision = microPrf, MicroAvgRecall = microPrf, MicroAvgF1 = microPrf, MajorityClassAccuracy = mcAccuracy, MajorityClassPrecision = mcPrecision, MajorityClassRecall = mcRecall, MajorityClassF1 = mcF1, Kappa = kappa, RandomGuessAccuracy = rgAccuracy, RandomGuessPrecision = rgPrecision, RandomGuessRecall = rgRecall, RandomGuessF1 = rgF1, RandomWeightedGuessAccurcy = rwgAccurcy, RandomWeightedGuessPrecision = rwgPrecision, RandomWeightedGuessRecall = rwgRecall, RandomWeightedGuessWeightedF1 = rwgF1))) }, env) #-------------------------
The function returns a wide range of metrics, of which only F1 is necessary at the moment.
A neural network with two hidden layers will be used, as in the previous part of the article. DNN will be trained in two stages, with pretraining. The possible options are:
- Pretraining:
- train only SRBM;
- train SRBM + the top layer of the neural network.
- Fine-tuning:
- use the backpropagation training method;
- use the rpropagation training method.
Each of the four training options has a different set of hyperparameters for optimization.
Defining the hyperparameters for optimization
Let us define the list of hyperparameters with values to be optimized, as well as their value ranges:
- n1, n2 — the number of neurons in each hidden layer. Values range from 1 to 25. Before feeding to the model, the parameter is multiplied by 2, since it requires a multiple of 2 (poolSize). This is necessary for the maxout activation function.
- fact1, fact2 — indexes of the activation function for each hidden layer, selected from the list of activation functions defined by the vector Fact <- c("tanhUnit", "maxoutUnit", "softplusUnit", "sigmoidUnit"). You can also add other functions.
- dr1, dr2 — the dropout value in each layer, range from 0 to 0.5.
- Lr.rbm — level of StackedRBM training, range from 0.01 to 1.0 at the pretraining stage.
- Lr.top — level of training of the neural network's top layer at the pretraining stage, range from 0.01 to 1.0. This parameter is not necessary for pretraining without training the top layer of the neural network.
- Lr.fine — neural network training level at the fine-tuning stage when using backpropagation, range from 0.01 to 1.0. This parameter is not necessary when using rpropagation.
A detailed description of all parameters is provided in the previous article and in the description of the package. All parameters of the darch() function have default values. They can be divided into several groups.
- Global parameters. Used both for pretraining and for fine-tuning.
- Data preprocessing parameters. The features of caret::preProcess() are used.
- Parameters for SRBM. Used only for pretraining.
- Parameters of NN. Used both for pretraining and for fine-tuning but may have different values for each stage.
The default parameter values can be changed by specifying a list of their new values or by explicitly writing them in the darch() function. Here is a brief description of the hyperparameters to be optimized.
First, set the global parameters of DNN, common for the pretrain/train stages.
Ln <- c(0, 2*n1, 2*n2, 0) — vector indicating that a 4-layer neural network with two hidden layers is to be created. The number of neurons in the input and output layers is determined from the input data, they cannot be specified explicitly. The number of neurons in hidden layers is 2*n1 and 2*n2, respectively.
Then define the training levels for RBM (Lr.rbm), for the top layer of DNN during pretraining (Lr.top), and for all layers during fine-tuning (Lr.fine).
fact1/fact2 — indexes of the activation function for each hidden layer from a list defined by the Fact vector. The softmax function is used in the output layer.
dr1/dr2 — dropout level in each hidden layer.
darch.trainLayers — indicates the layers to be trained using pretraining and layers to be trained during fine-tuning.
Let us write the hyperparameters and their value ranges for each of the 4 training/optimization options. In addition, the parameters Bs.rbm = 100 (rbm.batchSize) and Bs.nn = 50 (darch.batchSize) are made external for convenience in finding the best training options. When they are decreased, the classification quality improves, but the optimization time increases considerably.
#-2---------------------- evalq({ #--InitParams--------------------- Fact <- c("tanhUnit","maxoutUnit","softplusUnit", "sigmoidUnit") wUpd <- c("weightDecayWeightUpdate", "maxoutWeightUpdate", "weightDecayWeightUpdate", "weightDecayWeightUpdate") #---SRBM + RP---------------- bonds1 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0)#, ) #---SRBM + BP---------------- bonds2 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0), Lr.fine = c(0.01, 1.0) ) #---SRBM + upperLayer + BP---- bonds3 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0), Lr.top = c(0.01, 1.0), Lr.fine = c(0.01, 1.0) ) #---SRBM + upperLayer + RP----- bonds4 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0), Lr.top = c(0.01, 1.0) ) Bs.rbm <- 100L Bs.nn <- 50L },envir = env)
Defining the pretraining and fine-tuning function
DNN will be trained using all four options. All the functions necessary for this are available in the FUN_Optim.R script, which should be downloaded before starting calculations with Git/PartV.
The pretraining and fine-tuning functions for each option:
- pretrainSRBM(Ln, fact1, fact2, dr1, dr2, Lr.rbm ) — pretraining only SRBM
- pretrainSRBM_topLayer(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) — pretraining SRBM + upper Layer (backpropagation)
- fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) — fine-tuning DNN using rpropagation
- fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) — fine-tuning DNN using backpropagation
In order not to clutter the article with the listing of similar functions, only the option with pretraining (SRBM + topLayer) + RP(fine-tuning rpropagation) will be considered. In many experimentations, this option showed the best result in most cases. Functions for other options are similar.
# SRBM + upper Layer (backpropagation) pretrainSRBM_topLayer <- function(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) # SRBM + upper Layer (backpropagation) { darch( x = X$pretrain$x, y = X$pretrain$y, xValid = X$train$x, yValid = X$train$y, #=====constant====================================== layers = Ln, paramsList = list(), darch = NULL, shuffleTrainData = T, seed = 54321, logLevel = "WARN", #FATAL, ERROR, WARN, DEBUG, and TRACE. #--optimization parameters---------------------------------- darch.unitFunction = c(Fact[fact1], Fact[fact2], "softmaxUnit"), darch.weightUpdateFunction = c(wUpd[fact1], wUpd[fact2], "weightDecayWeightUpdate"), rbm.learnRate = Lr.rbm, bp.learnRate = Lr.top, darch.dropout = c(0, dr1, dr2), #=== params RBM ============== rbm.numEpochs = 30L, rbm.allData = T, rbm.batchSize = Bs.rbm, rbm.consecutive = F, rbm.errorFunction = mseError, #rmseError rbm.finalMomentum = 0.9, rbm.initialMomentum = 0.5, rbm.momentumRampLength = 1, rbm.lastLayer = -1, rbm.learnRateScale = 1, rbm.numCD = 1L, rbm.unitFunction = tanhUnitRbm, rbm.updateFunction = rbmUpdate, rbm.weightDecay = 2e-04, #=== parameters NN ======================== darch.numEpochs = 30L, darch.batchSize = Bs.nn, darch.trainLayers = c(FALSE, FALSE,TRUE ), darch.fineTuneFunction = "backpropagation", #rpropagation bp.learnRateScale = 1, #0.99 #--weight----------------- generateWeightsFunction = generateWeightsGlorotUniform, # generateWeightsUniform (default), # generateWeightsGlorotUniform, # generateWeightsHeUniform. # generateWeightsNormal, # generateWeightsGlorotNormal, # generateWeightsHeNormal, darch.weightDecay = 2e-04, normalizeWeights = T, normalizeWeightsBound = 15, #--parameters regularization----------- darch.dither = F, darch.dropout.dropConnect = F, darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2L, darch.maxout.unitFunction = "exponentialLinearUnit", darch.elu.alpha = 2, darch.returnBestModel = T #darch.returnBestModel.validationErrorFactor = 0, ) }
In this function, the values of the X$train set are used as the validation set.
Function for fine-tuning using rpropagation. Apart from the parameters, a pretrained structure Dnn is passed to this function.
fineTuneRP <- function(Ln, fact1, fact2, dr1, dr2, Dnn) # rpropagation { darch( x = X$train$x, y = X$train$y, #xValid = X$test$x, yValid = X$test$y, xValid = X$test$x %>% head(250), yValid = X$test$y %>% head(250), #=====constant====================================== layers = Ln, paramsList = list(), darch = Dnn, shuffleTrainData = T, seed = 54321, logLevel = "WARN", #FATAL, ERROR, WARN, DEBUG, and TRACE. rbm.numEpochs = 0L, #--optimization parameters---------------------------------- darch.unitFunction = c(Fact[fact1], Fact[fact2], "softmaxUnit"), darch.weightUpdateFunction = c(wUpd[fact1], wUpd[fact2], "weightDecayWeightUpdate"), darch.dropout = c(0, dr1, dr2), #=== parameters NN ======================== darch.numEpochs = 50L, darch.batchSize = Bs.nn, darch.trainLayers = c(TRUE,TRUE, TRUE), darch.fineTuneFunction = "rpropagation", #"rpropagation" "backpropagation" #=== params RPROP ====== rprop.decFact = 0.5, rprop.incFact = 1.2, rprop.initDelta = 1/80, rprop.maxDelta = 50, rprop.method = "iRprop+", rprop.minDelta = 1e-06, #--weight----------------- darch.weightDecay = 2e-04, normalizeWeights = T, normalizeWeightsBound = 15, #--parameters regularization----------- darch.dither = F, darch.dropout.dropConnect = F, darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2L, darch.maxout.unitFunction = "exponentialLinearUnit", darch.elu.alpha = 2, darch.returnBestModel = T #darch.returnBestModel.validationErrorFactor = 0, ) }
Here, the first 250 values of the X$test set are used as the validation set. All functions for all training options should be loaded into the env environment.
Defining the fitness function
Use these two functions to write a fitness function required for optimization of hyperparameters. It returns the value of the optimization criterion Score = mean(F1), which should be optimized, and the predicted values of the objective function Ypred.
#---SRBM + upperLayer + RP---- fitnes4.DNN <- function(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) { Ln <- c(0, 2*n1, 2*n2, 0) #-- pretrainSRBM_topLayer(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) -> Dnn fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) -> Dnn predict(Dnn, newdata = X$test$x %>% tail(250) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(250) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics$F1 %>% mean() return(list(Score = Score, Pred = Ypred) }
Determining the optimal parameters for DNN
The optimization function BayesianOptimization() is started using 10 initial points in the space of hyperparameters obtained randomly. Despite the fact that the calculation is parallelized on all processor cores (Intel MKL), it still takes considerable time and depends on the number of iterations and the size of 'batchsize'. To save time, start with 10 iterations. In the future, if the results are unsatisfactory, optimization can be continued by using the optimal values of the previous optimization run as the initial values.
Variant of training SRBM + RP
#---SRBM + RP---------------- evalq( OPT_Res1 <- BayesianOptimization(fitnes1.DNN, bounds = bonds1, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env) Best Parameters Found: Round = 7 n1 = 22.0000 n2 = 2.0000 fact1 = 3.0000 fact2 = 2.0000 dr1 = 0.4114 dr2 = 0.4818 Lr.rbm = 0.7889 Value = 0.7531
Let us see the obtained variants of the optimal parameters and F1. The BayesianOptimization() function returns multiple values: the best parameter values — Best_Par, the best value of the optimization criterion for these optimal parameters — Best_Value, optimization history — History, and the obtained predictions after all iterations — Pred. Let us see the history of optimization, preliminarily sorting it in descending order by 'Value'.
evalq({
OPT_Res1 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init1
best.init1
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Value
1 22 2 3 2 0.41136623 0.48175897 0.78886312 0.7531204
2 23 8 4 2 0.16814464 0.16221565 0.08381839 0.7485614
3 19 17 3 3 0.17274258 0.46809117 0.72698789 0.7485614
4 25 25 4 2 0.30039573 0.26894463 0.11226139 0.7473266
5 11 24 3 2 0.31564303 0.11091751 0.40387209 0.7462520
6 1 6 3 4 0.36876218 0.17403265 0.90387675 0.7450260
7 25 25 3 1 0.06872059 0.42459582 0.40072731 0.7447972
8 1 25 4 1 0.24871843 0.18593687 0.31920691 0.7445628
9 18 1 4 3 0.49846810 0.38517469 0.51115471 0.7423566
10 13 25 4 1 0.37052548 0.07603925 0.87100360 0.7402597
This is a good result. Let us do one more optimization run but using the values of the previous run best_init1 to initialize 10 points in the space of hyperparameters.
evalq( OPT_Res1.1 <- BayesianOptimization(fitnes1.DNN, bounds = bonds1, init_grid_dt = best.init1, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env) Best Parameters Found: Round = 1 n1 = 4.0000 n2 = 1.0000 fact1 = 1.0000 fact2 = 4.0000 dr1 = 0.1870 dr2 = 0.0000 Lr.rbm = 0.9728 Value = 0.7608
Let us see the 10 best results of this run.
evalq({
OPT_Res1.1 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init1
best.init1
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Value
1 4 1 1 4 0.18701522 2.220446e-16 0.9728164 0.7607811
2 3 24 1 4 0.12698982 1.024231e-01 0.5540933 0.7549180
3 5 5 1 3 0.07366640 2.630144e-01 0.2156837 0.7542661
4 1 18 1 4 0.41907554 4.641130e-02 0.6092082 0.7509800
5 1 23 1 4 0.25279461 1.365197e-01 0.2957633 0.7504026
6 4 25 4 1 0.09500347 3.083338e-01 0.2522729 0.7488496
7 17 3 3 3 0.36117416 3.162195e-01 0.4214501 0.7458489
8 13 4 3 3 0.22496776 1.481455e-01 0.4448280 0.7437376
9 21 24 1 3 0.36154287 1.335931e-01 0.6749752 0.7435897
10 5 11 3 3 0.29627244 3.425604e-01 0.1251956 0.7423566
Not only the best result has improved, but also the quality composition of the top 10, the 'Value' statistics increased. Optimization can be repeated several times, selecting different initial points (for example, try to optimize for the worst 10 values, etc.).
For this training variant, take the following best hyperparameters:
> env$OPT_Res1.1$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm 4.0000 1.0000 1.0000 4.0000 0.1870 0.0000 0.9728
Let us interpret them. The following optimal parameters were obtained:
- the number of neurons of the first hidden layer - 2*n1 = 8
- the number of neurons of the second hidden layer - 2*n2 = 2
- activation function of the first hidden layer Fact[fact1] ="tanhdUnit"
- activation function of the second hidden layer Fact[fact2] = "sigmoidUnit"
- dropout level of the first hidden layer dr1 = 0.187
- dropout level of the second hidden layer dr2 = 0.0
- training level of SRBM at pretraining Lr.rbm = 0.9729
In addition to obtaining a generally good result, an interesting structure DNN (10-8-2-2) was formed.
Variant of training SRBM + BP
#---SRBM + BP---------------- evalq( OPT_Res2 <- BayesianOptimization(fitnes2.DNN, bounds = bonds2, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env)
Let us see the 10 best results:
> evalq({
+ OPT_Res2 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
+ dplyr::select(-Round) -> best.init2
+ best.init2
+ }, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.fine Value
1 23 24 2 1 0.45133494 0.14589979 0.89897498 0.2325569 0.7612619
2 3 24 4 3 0.07673542 0.42267387 0.59938522 0.4376796 0.7551184
3 15 13 4 1 0.32812018 0.45708556 0.09472489 0.8220925 0.7516732
4 7 18 3 1 0.15980725 0.12045896 0.82638047 0.2752569 0.7473167
5 7 23 3 3 0.37716019 0.23287775 0.61652190 0.9749432 0.7440724
6 21 23 3 1 0.22184400 0.08634275 0.08049532 0.3349808 0.7440647
7 23 8 3 4 0.26182910 0.11339229 0.31787446 0.9639373 0.7429621
8 5 2 1 1 0.25633998 0.27587931 0.17733507 0.4987357 0.7429471
9 1 24 1 2 0.12937722 0.22952235 0.19549144 0.6538553 0.7426660
10 18 8 4 1 0.44986721 0.28928018 0.12523905 0.2441150 0.7384895
The result is good, additional optimization is not required.
The best hyperparameters for this variant:
> env$OPT_Res2$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.fine 23.0000 24.0000 2.0000 1.0000 0.4513 0.1459 0.8990 0.2326
Variant of training SRBM + upperLayer + BP
#---SRBM + upperLayer + BP---- evalq( OPT_Res3 <- BayesianOptimization(fitnes3.DNN, bounds = bonds3, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env)Best Parameters Found: Round = 20 n1 = 24.0000 n2 = 5.0000 fact1 = 1.0000 fact2 = 2.0000 dr1 = 0.4060 dr2 = 0.2790 Lr.rbm = 0.9586 Lr.top = 0.8047 Lr.fine = 0.8687 Value = 0.7697
Let us see the 10 best results:
evalq({
OPT_Res3 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init3
best.init3
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top Lr.fine Value
1 24 5 1 2 0.40597650 0.27897269 0.9585567 0.8046758 0.86871454 0.7696970
2 24 13 1 1 0.02456308 0.08652276 0.9807432 0.8033236 0.87293155 0.7603146
3 7 8 3 3 0.24115850 0.42538540 0.5970306 0.2897183 0.64518524 0.7543239
4 9 15 3 3 0.14951302 0.04013773 0.3734516 0.2499858 0.14993060 0.7521897
5 4 20 3 3 0.45660260 0.12858958 0.8280872 0.1998107 0.08997839 0.7505357
6 21 6 3 1 0.38742051 0.12644262 0.5145560 0.3599426 0.24159111 0.7403176
7 22 3 1 1 0.13356602 0.12940396 0.1188595 0.8979277 0.84890568 0.7369316
8 7 18 3 4 0.44786101 0.33788727 0.4302948 0.2660965 0.75709349 0.7357294
9 25 13 2 1 0.02456308 0.08652276 0.9908265 0.8065841 0.87293155 0.7353894
10 24 17 1 1 0.23273972 0.01572794 0.9193522 0.6654211 0.26861297 0.7346243
The result is good, additional optimization is not required.
The best hyperparameters for this training variant:
> env$OPT_Res3$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top Lr.fine 24.0000 5.0000 1.0000 2.0000 0.4060 0.2790 0.9586 0.8047 0.8687
Variant of training SRBM + upperLayer + RP
#---SRBM + upperLayer + RP---- evalq( OPT_Res4 <- BayesianOptimization(fitnes4.DNN, bounds = bonds4, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env)Best Parameters Found: Round = 15 n1 = 23.0000 n2 = 7.0000 fact1 = 3.0000 fact2 = 1.0000 dr1 = 0.3482 dr2 = 0.4726 Lr.rbm = 0.0213 Lr.top = 0.5748 Value = 0.7625
Top 10 variants of hyperparameters:
evalq({
OPT_Res4 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init4
best.init4
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top Value
1 23 7 3 1 0.34823851 0.4726219 0.02129964 0.57482890 0.7625131
2 24 13 3 1 0.38677878 0.1006743 0.72237324 0.42955366 0.7560023
3 1 1 4 3 0.17036760 0.1465872 0.40598393 0.06420964 0.7554773
4 23 7 3 1 0.34471936 0.4726219 0.02129964 0.57405944 0.7536946
5 19 16 3 3 0.25563914 0.1349885 0.83913339 0.77474220 0.7516732
6 8 12 3 1 0.23000115 0.2758919 0.54359416 0.46533472 0.7475112
7 10 8 3 1 0.23661048 0.4030048 0.15234740 0.27667214 0.7458489
8 6 19 1 2 0.18992796 0.4779443 0.98278107 0.84591090 0.7391758
9 11 10 1 2 0.47157135 0.2730922 0.86300945 0.80325083 0.7369316
10 18 21 2 1 0.05182149 0.3503253 0.55296502 0.86458533 0.7359324
The result is good, additional optimization is not required.
Take the best hyperparameters for this training variant:
> env$OPT_Res4$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top 23.0000 7.0000 3.0000 1.0000 0.3482 0.4726 0.0213 0.5748
Training and testing the DNN with the optimal parameters
Let us consider metrics obtained by testing the variants.
Variant SRBM + RP
To test the DNN with the optimal parameters, let us create a special function. It will be shown here, only for this training variant. It is similar for other variants.
#---SRBM + RP---------------- test1.DNN <- function(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm) { Ln <- c(0, 2*n1, 2*n2, 0) #-- pretrainSRBM(Ln, fact1, fact2, dr1, dr2, Lr.rbm) -> Dnn fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) -> Dnn.opt predict(Dnn.opt, newdata = X$test$x %>% tail(250) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(250) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3) return(list(Score = Score, Pred = Ypred, Dnn = Dnn, Dnn.opt = Dnn.opt)) }
Parameters of the test1.DNN() function are the optimal hyperparameters obtained earlier. Next, perform a pretraining using the pretrainSRBM() function, obtain a pretrained DNN, which is later fed to the fine-tuning function fineTuneRP(), resulting in a trained Dnn.opt. Using this Dnn.opt and the last 250 values of the X$test set, obtain the predicted values of the objective function Ypred. Using the predicted Ypred and the actual values of the objective function yTest, calculate a number of metrics with the Evaluate() function. Multiple options for selecting metrics are available here. As a result, the function generates a list of the following objects: Score — testing metrics, Pred — predicted values of the objective function, Dnn — pretrained DNN, Dnn.opt — fully trained DNN.
Test and view the result with hyperparameters obtained after additional optimization:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res1.1$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Ln <- c(0, 2*n1, 2*n2, 0)
#---train/test--------
Res1 <- test1.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm)
}, env)
env$Res1$Score
Accuracy Precision Recall F1
-1 0.74 0.718 0.724 0.721
1 0.74 0.759 0.754 0.757
The result is worse than after the first optimization, overfitting is evident. Testing with the initial values of hyperparameters:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res1$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Ln <- c(0, 2*n1, 2*n2, 0)
#---train/test--------
Res1 <- test1.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm)
}, env)
env$Res1$Score
Accuracy Precision Recall F1
-1 0.756 0.757 0.698 0.726
1 0.756 0.755 0.806 0.780
The result is good. Let us plot a graph of training history:
plot(env$Res1$Dnn.opt, type = "class")
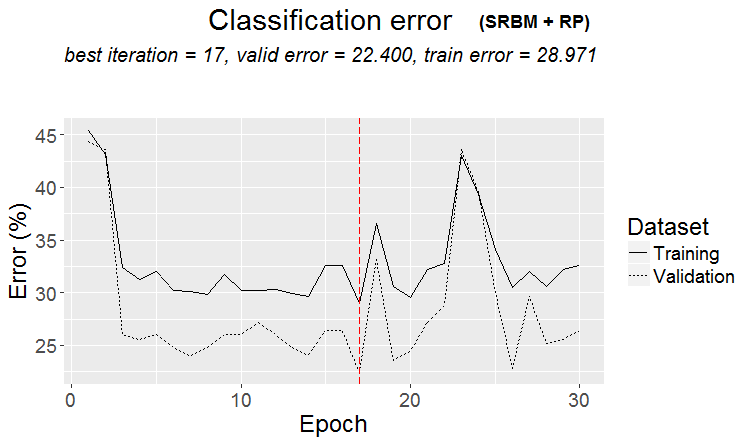
Fig.2. History of DNN training by variant SRBM + RP
As it can be seen from the figure, the error on the validation set is less than error on the training set. This means that the model is not overfitted and has a good generalizing ability. The red vertical line indicates the results of the model that is deemed the best and returned as a result after training.
For other three training variants, only the results of calculations and history graphs without further details will be provided. Everything is calculated similarly.
Variant SRBM + BP
Testing:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res2$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]; Lr.fine = best.par[8]
Ln <- c(0, 2*n1, 2*n2, 0)
#----train/test-------
Res2 <- test2.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine)
}, env)
env$Res2$Score
Accuracy Precision Recall F1
-1 0.768 0.815 0.647 0.721
1 0.768 0.741 0.873 0.801
It can be said that the result is excellent. Let us see the training history:
plot(env$Res2$Dnn.opt, type = "class")
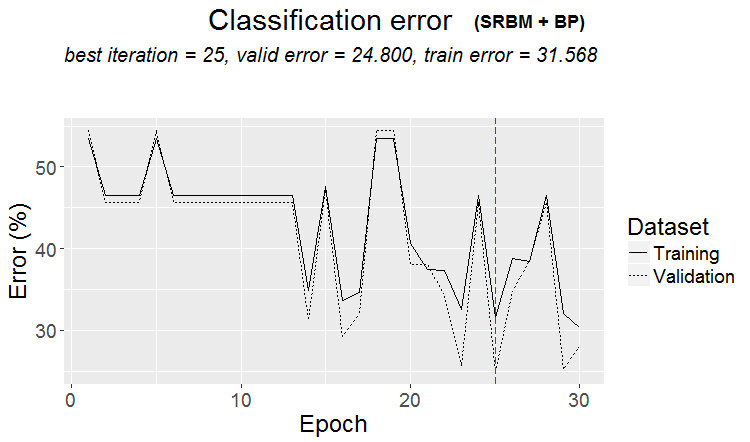
Fig.3. History of DNN training by variant SRBM + ВP
Variant SRBM + upperLayer + BP
Testing:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res3$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Lr.top = best.par[8]
Lr.fine = best.par[9]
Ln <- c(0, 2*n1, 2*n2, 0)
#----train/test-------
Res3 <- test3.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top, Lr.fine)
}, env)
env$Res3$Score
Accuracy Precision Recall F1
-1 0.772 0.771 0.724 0.747
1 0.772 0.773 0.813 0.793
Excellent result. Note that using the average value of F1 as the optimization criterion yields the same quality for both classes, despite the imbalance between them.
Graphs of training history:
plot(env$Res3$Dnn.opt, type = "class")
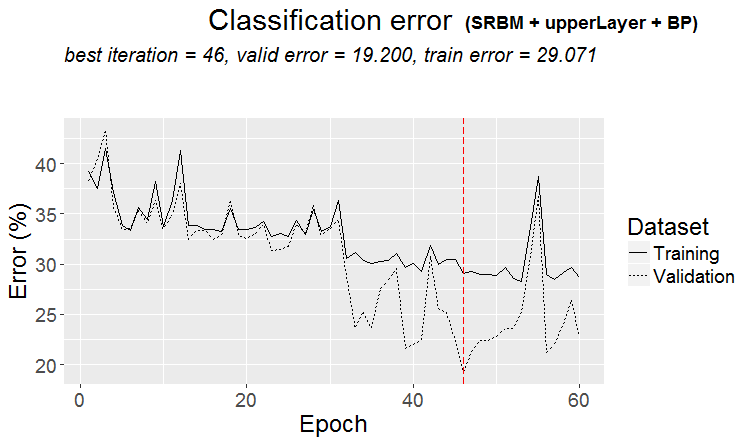
Fig. 4. History of DNN training by variant SRBM + upperLayer + BP
Variant SRBM + upperLayer + RP
Testing:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res4$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Lr.top = best.par[8]
Ln <- c(0, 2*n1, 2*n2, 0)
#----train/test-------
Res4 <- test4.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top)
}, env)
env$Res4$Score
Accuracy Precision Recall F1
-1 0.768 0.802 0.664 0.726
1 0.768 0.747 0.858 0.799
Very good result. Let us see the graph of training history:
plot(env$Res4$Dnn.opt, type = "class")
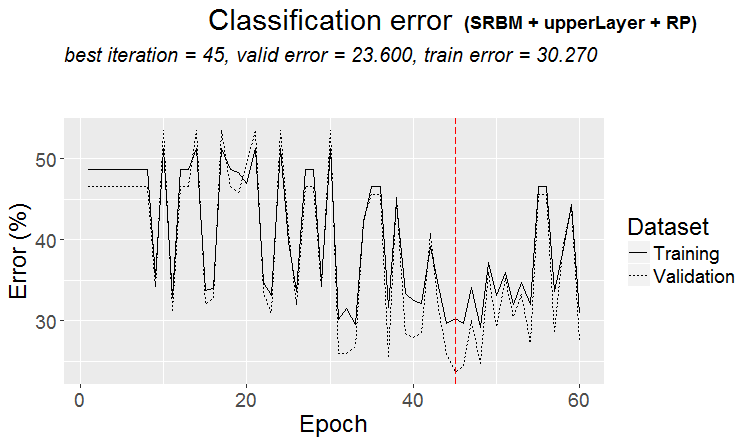
Fig. 5. History of DNN training by variant SRBM + upperLayer + RP
Analyzing the results of testing the DNN with the optimal parameters
The results of training and testing the DNN models trained by different variants with optimized values of hyperparameters yield good results with an accuracy of 75 (+/-5)%. The classification error of 25% is stable, does not depend on the training method, and suggests that the structure of data does not match the structure of the objective function in a quarter of cases. The same result was observed when studying the presence of noise samples in the source data set. There, their number was about 25% as well and did not depend on the methods of transforming the predictors. This is normal. Question: how to improve the prediction without overfitting the model? There are several options:
- using an ensemble of neural networks composed of the best models trained by 4 variants;
- using ensembles of neural networks composed of 10 best models, obtained during optimization by each variant of training;
- relabel the noise samples in the training set to an additional class "0" and use this objective function (with three classes с("-1", "0", "1")) to train the DNN model;
- relabel the misclassified samples with the additional class "0" and use this objective function (with three classes с("-1", "0", "1")) to train the DNN model.
Creation, training and use of ensembles will be considered in detail in the next article of this series.
The experiment with relabeling the noise samples deserves a separate study and exceeds the scope of this article. The idea is simple. Using the ORBoostFilter::NoiseFiltersR function considered in the previous part, determine the noise samples in the training and validation sets simultaneously. In the objective function, the values of classes ("-1"/"1") corresponding to these samples are replaced by the class "0". That is, the objective function will have three classes. This way we try to teach the model not to classify noise samples, which usually cause the classification error. At the same time, we will rely on the assumption that the lost profit is not a loss.
Forward testing the models with optimal parameters
Let us check how long the optimal parameters of DNN will produce results with acceptable quality for the tests of "future" quotes values. The test will be performed in the environment remaining after the previous optimizations and testing as follows.
Use a moving window of 1350 bars, train = 1000, test = 350 (for validation — the first 250 samples, for testing — the last 100 samples) with step 100 to go through the data after the first (4000 + 100) bars used for pretraining. Make 10 steps "forward". At each step, two models will be trained and tested:
- one — using the pretrained DNN, i.e., perform a fine-tuning on a new range at each step;
- second — additionally training the DNN.opt, obtained after optimization at the fine-tuning stage, on a new range.
#---prepare----
evalq({
step <- 1:10
dt <- PrepareData(Data, Open, High, Low, Close, Volume)
DTforv <- foreach(i = step, .packages = "dplyr" ) %do% {
SplitData(dt, 4000, 1000, 350, 10, start = i*100) %>%
CappingData(., impute = T, fill = T, dither = F, pre.outl = pre.outl)%>%
NormData(., preproc = preproc) -> DTn
foreach(i = 1:4) %do% {
DTn[[i]] %>% dplyr::select(-c(v.rstl, v.pcci))
} -> DTn
list(pretrain = DTn[[1]],
train = DTn[[2]],
val = DTn[[3]],
test = DTn[[4]]) -> DTn
list(
pretrain = list(
x = DTn$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$pretrain$Class %>% as.data.frame()
),
train = list(
x = DTn$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$train$Class %>% as.data.frame()
),
test = list(
x = DTn$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$val$Class %>% as.data.frame()
),
test1 = list(
x = DTn$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$test$Class %>% as.vector()
)
)
}
}, env)
Perform the first part of the forward test using the pretrained DNN and optimal hyperparameters, obtained from the training variant SRBM + upperLayer + BP.
#----#---SRBM + upperLayer + BP---- evalq({ #--BestParams-------------------------- best.par <- OPT_Res3$Best_Par %>% unname # n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine n1 = best.par[1]; n2 = best.par[2] fact1 = best.par[3]; fact2 = best.par[4] dr1 = best.par[5]; dr2 = best.par[6] Lr.rbm = best.par[7] Lr.top = best.par[8] Lr.fine = best.par[9] Ln <- c(0, 2*n1, 2*n2, 0) foreach(i = step, .packages = "darch" ) %do% { DTforv[[i]] -> X if(i==1) Res3$Dnn -> Dnn #----train/test------- fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(100) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3) } -> Score3_dnn }, env)
The second stage of the forward test using Dnn.opt obtained during optimization:
evalq({
foreach(i = step, .packages = "darch" ) %do% {
DTforv[[i]] -> X
if(i==1) {Res3$Dnn.opt -> Dnn}
#----train/test-------
fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt
predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred
yTest <- X$test$y[ ,1] %>% tail(100)
#numIncorrect <- sum(Ypred != yTest)
#Score <- 1 - round(numIncorrect/nrow(xTest), 2)
Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>%
round(3)
} -> Score3_dnnOpt
}, env)
Compare the testing results, placing them in a table:
env$Score3_dnn env$Score3_dnnOpt
| iter | Score3_dnn | Score3_dnnOpt |
|---|---|---|
| Accuracy Precision Recall F1 | Accuracy Precision Recall F1 | |
| 1 | -1 0.76 0.737 0.667 0.7 1 0.76 0.774 0.828 0.8 |
-1 0.77 0.732 0.714 0.723 1 0.77 0.797 0.810 0.803 |
| 2 | -1 0.79 0.88 0.746 0.807 1 0.79 0.70 0.854 0.769 |
-1 0.78 0.836 0.78 0.807 1 0.78 0.711 0.78 0.744 |
| 3 | -1 0.69 0.807 0.697 0.748 1 0.69 0.535 0.676 0.597 |
-1 0.67 0.824 0.636 0.718 1 0.67 0.510 0.735 0.602 |
| 4 | -1 0.71 0.738 0.633 0.681 1 0.71 0.690 0.784 0.734 |
-1 0.68 0.681 0.653 0.667 1 0.68 0.679 0.706 0.692 |
| 5 | -1 0.56 0.595 0.481 0.532 1 0.56 0.534 0.646 0.585 |
-1 0.55 0.578 0.500 0.536 1 0.55 0.527 0.604 0.563 |
| 6 | -1 0.61 0.515 0.829 0.636 1 0.61 0.794 0.458 0.581 |
-1 0.66 0.564 0.756 0.646 1 0.66 0.778 0.593 0.673 |
| 7 | -1 0.67 0.55 0.595 0.571 1 0.67 0.75 0.714 0.732 |
-1 0.73 0.679 0.514 0.585 1 0.73 0.750 0.857 0.800 |
| 8 | -1 0.65 0.889 0.623 0.733 1 0.65 0.370 0.739 0.493 |
-1 0.68 0.869 0.688 0.768 1 0.68 0.385 0.652 0.484 |
| 9 | -1 0.55 0.818 0.562 0.667 1 0.55 0.222 0.500 0.308 |
-1 0.54 0.815 0.55 0.657 1 0.54 0.217 0.50 0.303 |
| 10 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 |
-1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 |
The table shows that the first two steps produce good results. The quality is actually the same at the first two steps of both variants, and then it falls. Therefore, it can be assumed that after optimization and testing, DNN will maintain the quality of classification at the level of the test set on at least 200-250 following bars.
There are many other combinations for additional training of models on forward tests mentioned in the previous article and numerous adjustable hyperparameters.
Conclusion
- The darch v.0.12 package provides access to a huge list of DNN hyperparameters, providing great opportunities for deep and fine-tuning.
- The use of the Bayesian approach to optimize the DNN hyperparameters gives a wide choice of models with good quality, which can be used to create ensembles.
- Optimization of DNN hyperparameters using Bayesian method gives a 7-10% improvement in the quality of classification.
- To obtain the best result, it is necessary to perform multiple optimizations (10 - 20), followed by the selection of the best result.
- The optimization process can be continued step by step, feeding the parameters obtained in the preliminary runs as the initial values.
- The use of hyperparameters obtained during optimization in the DNN ensures that the quality of classification of a forward test is maintained at the test level in the section with the length equal to the test set.
For further improvement, it makes sense to supplement the list of optimized parameters with the rpropagation training function in 4 variants, normalization of neuron weights in the hidden layers normalizeWeights(TRUE, FALSE) and the upper bound of this normalization normalizeWeightsBound. You can experiment with other parameters, which, in your opinion, can influence the classification quality of the model. One of the main advantages of the darch package is that it provides access to all parameters of the neural network. It is possible to experimentally determine how each parameter affects the classification quality.
Despite considerable time costs, the use of Bayesian optimization is advisable.
The use of an ensemble of neural network appears to be another possibility to improve the quality of classification. This option of reinforcement in different variants will be discussed in the next part of the article.
Application
GitHub/PartV contains:
1. FUN_Optim.R — functions required for performing all calculations described in this article.
2. RUN_Optim.R — calculations performed in this article.
3. SessionInfo. txt — packages used in calculations.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/4225
Multi-symbol balance graph in MetaTrader 5
Comparing speeds of self-caching indicators
Synchronizing several same-symbol charts on different timeframes
How to create a graphical panel of any complexity level
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
How to Installation and launching ？
DEEP NEURAL NETWORK WITH STACKED RBM. SELF-TRAINING, SELF-CONTROL
).
Forward testing the models with optimal parameters
Let us check how long the optimal parameters of DNN will produce results with acceptable quality for the tests of "future" quotes values. The test will be performed in the environment remaining after the previous optimizations and testing as follows.
Use a moving window of 1350 bars, train = 1000, test = 350 (for validation — the first 250 samples, for testing — the last 100 samples) with step 100 to go through the data after the first (4000 + 100) bars used for pretraining. Make 10 steps "forward". At each step, two models will be trained and tested:
- one — using the pretrained DNN, i.e., perform a fine-tuning on a new range at each step;
- second — additionally training the DNN.opt, obtained after optimization at the fine-tuning stage, on a new range.
First, create the test data for testing:#---prepare---- evalq({ step <- 1:10 dt <- PrepareData(Data, Open, High, Low, Close, Volume) DTforv <- foreach(i = step, .packages = "dplyr" ) %do% { SplitData(dt, 4000, 1000, 350, 10, start = i*100) %>% CappingData(., impute = T, fill = T, dither = F, pre.outl = pre.outl)%>% NormData(., preproc = preproc) -> DTn foreach(i = 1:4) %do% { DTn[[i]] %>% dplyr::select(-c(v.rstl, v.pcci)) } -> DTn list(pretrain = DTn[[1]], train = DTn[[2]], val = DTn[[3]], test = DTn[[4]]) -> DTn list( pretrain = list( x = DTn$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTn$pretrain$Class %>% as.data.frame() ), train = list( x = DTn$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTn$train$Class %>% as.data.frame() ), test = list( x = DTn$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTn$val$Class %>% as.data.frame() ), test1 = list( x = DTn$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTn$test$Class %>% as.vector() ) ) } }, env)Perform the first part of the forward test using the pretrained DNN and optimal hyperparameters, obtained from the training variant SRBM + upperLayer + BP.
The second stage of the forward test using Dnn.opt obtained during optimization:
evalq({ foreach(i = step, .packages = "darch" ) %do% { DTforv[[i]] -> X if(i==1) {Res3$Dnn.opt -> Dnn} #----train/test------- fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(100) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3) } -> Score3_dnnOpt }, env)Compare the testing results, placing them in a table:
1 0.76 0.774 0.828 0.8
1 0.77 0.797 0.810 0.803
1 0.79 0.70 0.854 0.769
1 0.78 0.711 0.78 0.744
1 0.69 0.535 0.676 0.597
1 0.67 0.510 0.735 0.602
1 0.71 0.690 0.784 0.734
1 0.68 0.679 0.706 0.692
1 0.56 0.534 0.646 0.585
1 0.55 0.527 0.604 0.563
1 0.61 0.794 0.458 0.581
1 0.66 0.778 0.593 0.673
1 0.67 0.75 0.714 0.732
1 0.73 0.750 0.857 0.800
1 0.65 0.370 0.739 0.493
1 0.68 0.385 0.652 0.484
1 0.55 0.222 0.500 0.308
1 0.54 0.217 0.50 0.303
1 0.71 0.533 0.516 0.525
1 0.71 0.533 0.516 0.525
The table shows that the first two steps produce good results. The quality is actually the same at the first two steps of both variants, and then it falls. Therefore, it can be assumed that after optimization and testing, DNN will maintain the quality of classification at the level of the test set on at least 200-250 following bars.
There are many other combinations for additional training of models on forward tests mentioned in the previous articleand numerous adjustable hyperparameters.
Hi, What's the question?
New article Deep Neural Networks (Part V). Bayesian optimization of DNN hyperparameters has been published:
Author: Vladimir Perervenko