Оценка и выбор переменных для моделей машинного обучения
17 632
24
Введение
В статье будут рассмотрены особенности выбора, предподготовки и оценки входных переменных для использования в моделях машинного обучения. Будут рассмотрены множественные методы нормализации и их особенности. Будут указаны важные моменты этого процесса, сильно влияющие на конечный результат обучения моделей. Рассмотрим и оценим новые и малоизвестные методы определения информативности входных данных и визуализации их.
С помощью пакета "RandomUniformForests" вычислим и рассмотрим понятие важности переменной на различных уровнях и в различных сочетаниях, соответствие предикторов и целевой, а также взаимодействие между предикторами, выбор оптимального набора предикторов с учетом всех аспектов важности.
С помощью пакета "RoughSets" рассмотрим эту же проблему выбора предикторов под другим углом и на основании другой концепции. Покажем, что не только набор предикторов может быть оптимальным, но и набор примеров для обучения тоже может быть оптимизирован.
Все расчеты и эксперименты будут проводиться на языке R, конкретнее на Revolution R Open 3.2.1 .
1. Входные переменные (признаки, предикторы)
Все переменные, и входные (независимые, предикторы), и выходные (целевые) , могут быть следующих типов:
Бинарные, принимают два значения: {0,1}, {-1,1}, {«да», «нет»}, {«мужской», «женский}.
Номинальные (факторы), имеют конечное количество уровней. Например фактор «день_недели» имеет семь уровней, каждый из которых может быть поименован (понедельник, вторник и т. д.). Факторы могут быть упорядоченными и неупорядоченными. Например фактор «час_суток» имеет 24 уровня и он упорядочен. Фактор «район_города» с 32 уровнями не упорядочен, так как все уровни имеют равную значимость. При объявлении упорядоченного фактора нужно явно об этом указывать.
Количественные (числовые) непрерывные. Диапазон непрерывных переменных от — Inf (бесконечности) до +Inf.
В качестве числовых входных переменных не используют «сырые» данные котировок (OHLC). Применяют логарифм разности или логарифм отношения котировок. Но чаще применяются разнообразные индикаторы, объединенные в наборы. Как правило, набор входных данных формируют в виде матрицы, если все переменные однородны, или, что чаще, в виде датафрейма, в котором каждый столбец — переменная, строка — состояние переменных в конкретный момент. В последней (или первой) колонке располагают целевую переменную.
1.1. Очистка
Под очисткой понимают:
а) Удаление или преобразование пропущенных (неопределенных) данных "NA".
Многие модели не допускают во входных данных пропуски. Поэтому или удаляем строки с пропущенными данными, или заполняем пропуски интерполированными данными. Во многих пакетах для этого предусмотрены соответствующие функции. Удаление неопределенных данных NA, как правило, заложено в моделях по умолчанию, но лучше это сделать самому через na.omit(dt) до начала обучения.
б) Удаление «нуль-вариантных» переменных (числовых и номинальных).
В некоторых ситуациях (особенно при трансформации или преобразовании переменных) могут появится предикторы с единственным уникальным значением или несколькими такими значениями, происходящими с очень низкой частотой. Для многих моделей это может привести к краху или к нестабильной работе. Эти «почти-нулевой-дисперсии» ("near-zero-variance") предикторы должны быть выявлены и устранены до моделирования. Для выявления и удаления таких предикторов в пакете "caret" существует специальная функция caret::nearZeroVar(). Обязательность этого пункта не бесспорна.
в) Выявление и удаление коррелированых предикторов (числовых).
В то время как некоторые модели отлично справляются с коррелированными предикторами (например PLS, LARS и подобные, использующие регуляризацию L1), другие модели могут получить преимущества от снижения уровня корреляции между предикторами. Для выявления и удаления сильно коррелированных предикторов (задается порог коэффициента корреляции, например > 0.9) используем функцию caret::findCorrelation() из того же пакета "caret". Очень мощный пакет, рекомендую для изучения.
г) Выявление и удаление линейных зависимостей (факторы).
Функция caret::findLinearCombos() используя QR-разложение матрицы перечислений устанавливает линейные комбинации из них (если они есть). Например рассмотрим следующую матрицу:
ltfrDesign <- matrix(0, nrow = 6, ncol = 6) ltfrDesign[, 1] <- c(1, 1, 1, 1, 1, 1) ltfrDesign[, 2] <- c(1, 1, 1, 0, 0, 0) ltfrDesign[, 3] <- c(0, 0, 0, 1, 1, 1) ltfrDesign[, 4] <- c(1, 0, 0, 1, 0, 0) ltfrDesign[, 5] <- c(0, 1, 0, 0, 1, 0) ltfrDesign[, 6] <- c(0, 0, 1, 0, 0, 1)
Обратите внимание, что столбцы 2 и 3 являются дополнениями первого. Аналогично, 4, 5 и 6 столбец складываются в первый. Функция caret::findLinearCombos() вернет список, который перечислит эти зависимости, а также вектор позиций столбцов, которые могут быть удалены для устранения линейной зависимости.
comboInfo <- findLinearCombos(ltfrDesign) comboInfo $linearCombos $linearCombos[[1]] [1] 3 1 2 $linearCombos[[2]] [1] 6 1 4 5 $remove [1] 3 6 ltfrDesign[, -comboInfo$remove] [,1] [,2] [,3] [,4] [1,] 1 1 1 0 [2,] 1 1 0 1 [3,] 1 1 0 0 [4,] 1 0 1 0 [5,] 1 0 0 1 [6,] 1 0 0 0
Этот тип зависимостей может возникнуть, когда используется большое число бинарных предикторов, или когда факторные предикторы преобразовываются в "dummy".
1.2. Трансформация, препроцессинг данных
Многие модели требуют, чтобы числовые входные данные находились в определенном диапазоне (нормализация, стандартизация) или были преобразованы определенным образом (факторы). Например нейросети и машины опорных векторов (SVM) воспринимают входные данные в диапазоне [-1:1] или [0:1]. Многие пакеты в языке R предлагают специальные функции для такого преобразования либо самостоятельно преобразовывают их. Необходимо помнить, что определение параметров препроцессинга выполняется только на тренировочном наборе входных данных. Тестовый и валидационный наборы и новые данные, поступающие модели для предсказания, преобразовываются с параметрами, полученными на тренировочном наборе.
Нормализация (масштабирование)
Общая формула приведения переменной в диапазон {+h, -l}. В зависимости от необходимого диапазона h = +1; l = (-1 или 0). В некоторых источниках рекомендуют сужать диапазон до {-0.9; 0.9} или {0.1; 0.9} с тем, чтобы не использовать участки насыщения функций активации (tanh/sig). Это относится к нейросетям, SVM и другим моделям с названными функциями активации.
Xn = (x - min(x)) / (max(x) - min(x)) * (h - l) + l;
Обратное преобразование (денормализация) производится по формуле
x = (x - l) / (h - l) * (max(x) - min(x)) + min(x);
Стандартизация
Если известно, что распределение переменной близко к нормальному, можно нормализовать по формуле
x = (x - mean(x)) / sd(x)
В некоторых пакетах для препроцессинга предусмотрены специальные функции. Так, в пакете "caret" функция preProcess() предоставляет следующие методы препроцессинга: "BoxCox", "YeoJohnson", "expoTrans", "center", "scale", "range", "knnImpute", "bagImpute", "medianImpute", "pca", "ica" и "spatialSign".
"BoxCox", "YeoJohnson", "expoTrans"
Yeо-Johnson преобразование немного схоже с моделью Бокс-Кокс, но может принять предикторы с нулевыми или отрицательными значениями (в то время как значения предикторов для Бокс-Кокс преобразования должны быть строго положительными). Экспоненциальное преобразование Мэнли (1976) может также использоваться для положительных или отрицательных данных.
"range" преобразование масштабирует данные в пределах [0, 1]. Важно! Если новые образцы будут иметь значения больше или меньше, чем те, что были в обучающем наборе, значения будут за пределами этого диапазона, и результат прогноза будет некорректным.
"center" — вычитается среднее, "scale" — делим на стандартное отклонение (шкалирование). Как правило, применяются вместе, и это называется "стандартизация".
"knnImpute", "bagImpute", "medianImpute" — вычисление пропущенных или неопределенных данных различными алгоритмами.
"spatialSign" — трансформация, проецирует данные предикторов на единичную окружность в р измерениях, где р — число предикторов. По сути, вектор данных делится на его норму. Данные перед трансформацией должны быть центрированы и шкалированы.
"pca" — в некоторых случаях существует необходимость в использовании анализа главных компонент (principal component analysis) для преобразования данных в меньшее подпространство, где новые переменные не коррелируют друг с другом. При использовании этого метода автоматически проводится центрирование и шкалирование, и изменяются имена столбцов на РС1, РС2 и т.д.
"isa" — точно так же, анализ независимых компонент (independent component analysis) может быть использован, чтобы найти новые переменные, которые являются линейными комбинациями исходного набора, такими, что компоненты являются независимыми (в отличии от некоррелированных в PCA). Новые переменные будут помечены как IC1, IC2 и т.д.
В отличном пакете "clusterSim", предназначенном для поиска оптимальных процедур кластеризации данных, имеется функция dataNormalization() , которая нормализует данные 18 способами, причем не только по столбцам, но и по строкам. Просто перечислю:
n1 — (standardization) стандартизация ((x – mean) / sd);
n2 — (positional standardization) позиционная стандартизация ((x – median) / mad);
n3 — unitization ((x – mean) / range);
n3а — positional unitization ((x – median) / range);
n4 — unitization with zero minimum ((x – min) / range);
n5 — (normalization in range) нормализация в диапазон <-1, 1> ((x – mean) / max(abs(x – mean)));
n5a — positional normalization in range <-1,1> ((x – median) / max(abs(x-median)));
n6 — (quotient transformation) долевая трансформация (x/sd);
n6a — (positional quotient transformation) позиционная долевая трансформация (x/mad);
n7 — quotient transformation (x/range);
n8 — quotient transformation (x/max);
n9 — quotient transformation (x/mean);
n9a — positional quotient transformation (x/median);
n10 — quotient transformation (x/sum);
n11 — quotient transformation (x/sqrt(SSQ));
n12 — normalization ((x-mean)/sqrt(sum((x-mean)^2)));
n12a — positional normalization ((x-median)/sqrt(sum((x-median)^2)));
n13 — (normalization with zero being the central point) нормализация, когда ноль является центральной точкой ((x-midrange)/(range/2)).
"Dummy Variables" — многие модели требуют преобразовывать факторные предикторы в «фиктивные переменные». Для этого может быть использована функция dummyVar() из пакета "caret". Функция принимает формулу и набор данных и выводит объект, который можно использовать для создания фиктивных переменных.
2. Выходные данные (целевая переменная)
Поскольку мы решаем задачу классификации, целевая переменная является фактором с некоторым количеством уровней (классов). Большинство моделей дают лучшие результаты при обучении на целевой с двумя классами. При наличии большего количества классов принимаются специальные дополнительные меры для решения таких задач. Целевая переменная при подготовке данных для обучения кодируется, а после предсказания декодируется.
Кодируются классы несколькими способами. В пакете RSNNS «Симулятор нейросетей Штутгартского университета» предусмотрены две функции — decodeClassLabels() кодирует вектор с классами в матрицу, содержащую столбцы, соответствующие классам, и encodeClassLabels(), которая делает обратное преобразование после предсказания модели. Просто для примера:
> data(iris) > labels <- decodeClassLabels(iris[,5]) > class <- encodeClassLabels(labels) > head(labels) setosa versicolor virginica [1,] 1 0 0 [2,] 1 0 0 [3,] 1 0 0 [4,] 1 0 0 [5,] 1 0 0 [6,] 1 0 0 > head(class) [1] 1 1 1 1 1 1
Таким образом, количество выходов модели равно количеству классов целевой. Это не единственный способ кодирования (один-к-одному), применяемый для целевой. Если целевая имеет два класса, можно обойтись одним выходом. Кодирование целевой переменной в матрицу имеет ряд преимуществ.
3. Оценка и выбор предикторов
Как показывает практика, увеличение количества входных данных (предикторов) не всегда ведет к улучшению модели, а скорее наоборот. Как правило, на результат реально влияют 3-5 предикторов. Во многих агрегирующих пакетах, таких как "rminer", "caret", "SuperLearner" и "mlr", существуют встроенные функции по вычислению «важности» переменных (importance of variable) и их отбору. Большинство подходов по сокращению количества предикторов могут быть разнесены в две категории (используя терминологию John, Kohavi и Pfleger, 1994):
- Фильтрация. Методы фильтрации оценивают актуальность предикторов вне моделей предсказания, и впоследствии модель использует только те предикторы, которые соответствуют каким-либо критериям. Например, для задач классификации каждый предиктор может быть индивидуально оценен, чтобы проверить, есть ли правдоподобное отношение между ним и наблюдаемыми классами. Только предикторы с важными прогностическими зависимостями будут затем включены в классификационную модель.
Обертка. Оберточные методы оценивают различные модели, используя процедуры, которые добавляют и/или удаляют предикторы для поиска оптимальной комбинации, оптимизирующей эффективность модели. В сущности, оберточные методы — это поисковые алгоритмы, которые рассматривают предикторы как входы и используют эффективность модели как выходы, которые должны быть оптимизированы. Существует множество способов перебора предикторов (рекурсивное удаление/добавление, генетические алгоритмы, имитация отжига и многие другие).
В настоящей статье мы не будем рассматривать оберточные методы, а рассмотрим новые методы и подходы методов фильтрации, которые, по моему мнению, устраняют указанные выше недостатки.
3.1. Фильтрация
С помощью различных сторонних методов и критериев определяют важность (информативность) предикторов. Под важностью здесь понимается вклад каждой переменной в повышение качества предсказания модели.
После этого, как правило, возможны три варианта:
Берется конкретное количество предикторов с наибольшей важностью.
Берется процент от общего количества предикторов с наибольшей важностью.
- Берутся предикторы, важность которых превышает установленный порог.
Во всех случаях возможна оптимизация количества, процента или порога.
Для рассмотрения конкретных методов и проведения экспериментов давайте сформируем набор входных и выходных данных.
Входные данные
Во входной набор включим 11 индикаторов (осцилляторов) без предварительных предпочтений. Из некоторых индикаторов возьмем по нескольку переменных. Напишем функцию, формирующую входной набор из 17 переменных.
Берем котировки из последних 4000 баров на ТФ = М30 /EURUSD.
In <- function(p = 16){ require(TTR) require(dplyr) require(magrittr) adx <- ADX(price, n = p) %>% as.data.frame %>% mutate(.,oscDX = DIp -DIn) %>% transmute(.,DX, ADX, oscDX) %>% as.matrix() ar <- aroon(price[ ,c('High', 'Low')], n = p)%>% extract(,3) atr <- ATR(price, n = p, maType = "EMA") %>% extract(,1:2) cci <- CCI(price[ ,2:4], n = p) chv <- chaikinVolatility(price[ ,2:4], n = p) cmo <- CMO(price[ ,'Med'], n = p) macd <- MACD(price[ ,'Med'], 12, 26, 9) %>% as.data.frame() %>% mutate(., vsig = signal %>% diff %>% c(NA,.) %>% multiply_by(10)) %>% transmute(., sign = signal, vsig) %>% as.matrix() rsi <- RSI(price[ ,'Med'], n = p) stoh <- stoch(price[ ,2:4], nFastK = p, nFastD =3, nSlowD = 3, maType = "EMA")%>% as.data.frame() %>% mutate(., oscK = fastK - fastD)%>% transmute(.,slowD, oscK)%>% as.matrix() smi <- SMI(price[ ,2:4],n = p, nFast = 2, nSlow = 25, nSig = 9) vol <- volatility(price[ ,1:4], n = p, calc = "yang.zhang", N = 144) In <- cbind(adx, ar, atr, cci, chv, cmo, macd, rsi, stoh, smi, vol) return(In) }
Эти индикаторы общеизвестны и широко применяемы. Не будем разбирать их снова. Прокомментирую только применяемый при вычислении метод "pipe"(%>%) из пакета "magrittr" на примере индикатора MACD. В порядке записи:
Вычисляем индикатор, который возвращает две переменных (macd, signal).
Преобразовываем полученную матрицу в датафрейм.
Добавляем в датафрейм новую переменную vsig ( в порядке записи):
- берем переменную signal;
- вычисляем первую разность;
- добавляем в начало вектора NA, так как при вычислении первой разности вектор короче исходного на единицу;
- умножим его на 10.
Выберем из датафрейма только нужные нам переменные (столбцы) vsig, signal.
Превратим датафрейм в матрицу.
Этот способ вычислений очень удобен в случае, когда промежуточные результаты вычислений нам не нужны. Кроме того, формулы намного легче читаются и понимаются.
Получим матрицу входных данных и посмотрим на содержание.
x <- In(p = 16) > summary(x) DX ADX oscDX Min. : 0.02685 Min. : 5.291 Min. :-93.889 1st Qu.: 8.11788 1st Qu.:14.268 1st Qu.: -9.486 Median :16.63550 Median :18.586 Median : 5.889 Mean :20.70162 Mean :20.716 Mean : 4.227 3rd Qu.:29.90428 3rd Qu.:24.885 3rd Qu.: 19.693 Max. :79.80812 Max. :59.488 Max. : 64.764 NA's :16 NA's :31 NA's :16 ar tr atr Min. :-100.0000 Min. :0.0000000 Min. :0.000224 1st Qu.: -50.0000 1st Qu.:0.0002500 1st Qu.:0.000553 Median : -6.2500 Median :0.0005600 Median :0.000724 Mean : -0.8064 Mean :0.0008031 Mean :0.000800 3rd Qu.: 50.0000 3rd Qu.:0.0010400 3rd Qu.:0.000970 Max. : 100.0000 Max. :0.0150300 Max. :0.003104 NA's :16 NA's :1 NA's :16 cci chv cmo Min. :-515.375 Min. :-0.67428 Min. :-88.5697 1st Qu.: -84.417 1st Qu.:-0.33704 1st Qu.:-29.9447 Median : -5.674 Median : 0.03057 Median : -2.4055 Mean : -1.831 Mean : 0.11572 Mean : -0.6737 3rd Qu.: 83.517 3rd Qu.: 0.44393 3rd Qu.: 28.0323 Max. : 387.814 Max. : 3.25326 Max. : 94.0649 NA's :15 NA's :31 NA's :16 sign vsig rsi Min. :-0.38844 Min. :-0.43815 Min. :12.59 1st Qu.:-0.07124 1st Qu.:-0.05054 1st Qu.:39.89 Median :-0.00770 Median : 0.00009 Median :49.40 Mean :-0.00383 Mean :-0.00013 Mean :49.56 3rd Qu.: 0.05075 3rd Qu.: 0.05203 3rd Qu.:58.87 Max. : 0.38630 Max. : 0.34871 Max. :89.42 NA's :33 NA's :34 NA's :16 slowD oscK SMI Min. :0.0499 Min. :-0.415723 Min. :-74.122 1st Qu.:0.2523 1st Qu.:-0.043000 1st Qu.:-33.002 Median :0.4720 Median : 0.000294 Median : -5.238 Mean :0.4859 Mean :-0.000017 Mean : -4.089 3rd Qu.:0.7124 3rd Qu.: 0.045448 3rd Qu.: 22.156 Max. :0.9448 Max. : 0.448486 Max. : 75.079 NA's :19 NA's :17 NA's :25 signal vol Min. :-71.539 Min. :0.003516 1st Qu.:-31.749 1st Qu.:0.008204 Median : -5.319 Median :0.011274 Mean : -4.071 Mean :0.012337 3rd Qu.: 19.128 3rd Qu.:0.015312 Max. : 71.695 Max. :0.048948 NA's :33 NA's :16
Выходные данные (целевая)
В качестве целевой переменной возьмем сигналы, полученные с ZZ. Формула вычисления зигзага и сигнала:
ZZ <- function(pr = price, ch = ch , mode="m") { require(TTR) if(ch > 1) ch <- ch/(10 ^ (Dig - 1)) if(mode == "m"){pr <- pr[ ,'Med']} if(mode == "hl") {pr <- pr[ ,c("High", "Low")]} if(mode == "cl") {pr <- pr[ ,c("Close")]} zz <- ZigZag(pr, change = ch, percent = F, retrace = F, lastExtreme = T) n <- 1:length(zz) for(i in n) { if(is.na(zz[i])) zz[i] = zz[i-1]} dz <- zz %>% diff %>% c(0,.) sig <- sign(dz) return(cbind(zz, sig)) }
В параметрах функции:
- pr = price — матрица котировок OHLCMed;
- ch — минимальная длина колена зигзага в пунктах (4 знака);
- mode — применяемая цена (m — средняя, hl — High и Low, cl — Close). По умолчанию применяем среднюю.
Функция возвращает матрицу с двумя переменными — собственно зигзаг и сигнал, полученный на базе наклона зигзага в диапазоне [-1;1].
Вычисляем сигналы для двух ZZ с разной длиной колен:
out1 <- ZZ(ch = 25) out2 <- ZZ(ch = 50)
На графике они будут выглядеть так:
> matplot(tail(cbind(out1[ ,1], out2[ ,1]), 500), t="l")
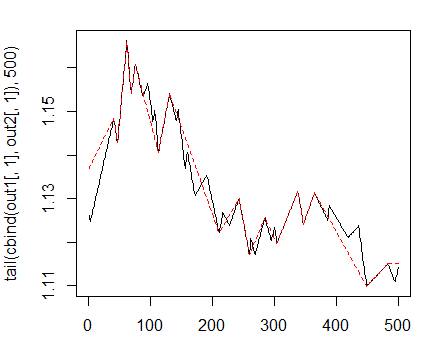
Рис. 1. Зигзаги с минимальной длиной колен 25/75 п
Дальше будем использовать первый ZZ с меньшим коленом. Объединим входные переменные и целевую в общий датафрейм, уберем неопределенные данные, данные, где состояние = "0" и уберем из целевой класс "0".
> data <- cbind(as.data.frame(x) , Class = factor(out1[ ,2])) %>% + na.omit > data <- data[data$Class != 0, ] > data$Class <- rminer::delevels(data$Class, c("0", "1"), "1")
Посмотрим на распределение классов в целевой:
> table(data$Class) -1 1 1980 1985
Как видим, классы хорошо сбалансированы. Сейчас у нас готов набор входных и выходных данных, и мы можем приступить к оценке важности предикторов.
Сначала проверим, насколько коррелированы входные данные:
> descCor <- cor(data[ ,-ncol(data)]) > summary(descCor[upper.tri(descCor)]) Min. 1st Qu. Median Mean 3rd Qu. Max. -0.20170 0.03803 0.26310 0.31750 0.57240 0.95730
У каких входных переменных корреляция более 90%?
> highCor <- caret::findCorrelation(descCor, cutoff = .90) > highCor [1] 12 15
Это rsi и SMI. Сформируем набор данных без этих двух и посмотрим корреляцию оставшихся.
> data.f <- data[ ,-highCor] > descCor <- cor(data.f[ ,-ncol(data.f)]) > summary(descCor[upper.tri(descCor)]) Min. 1st Qu. Median Mean 3rd Qu. Max. -0.20170 0.03219 0.21610 0.27060 0.47820 0.89880
Для оценки «важности переменных» (Variable Importance, VI) используем новый пакет «Random Uniform Forests», в котором есть широкий набор инструментов для ее глубокого анализа и визуализации. По замыслу разработчиков пакета: основная цель определения важности переменных — это оценка того, какие переменные, когда, где и как влияют на решаемую проблему.
Пакет предоставляет различные меры важности переменной по глубине. Рассмотрим их, прежде чем пойдем к более глубоким оценкам.
Глобальная важность переменной (Global Variable Importance) — определяет переменные, которые сильнее уменьшают ошибку предсказания, но она ничего не говорит нам о том, как важная переменная влияет на отклики.
Мы хотели бы знать, например, какие переменные сильнее влияют на отдельный класс или мы хотели бы знать взаимодействие между переменными.
Важность переменной измеряется по всем узлам и всем деревьям, что позволяет всем переменным иметь значение, так как точки нарезки случайны. Следовательно, каждая переменная имеет равные шансы быть выбранной, но она будет получать важность, только если будет сильнее остальных уменьшать энтропию в каждом узле.
Локальная важность переменной (Local Variable Importance)
Определение: Предиктор локально важен в первом порядке, если для того же наблюдения и всех деревьев это тот, который имеет самую высокую частоту возникновения в терминальном узле.
Частичная важность (Partial importance)
Определение: Предиктор частично важен, если для того же наблюдения, одного класса и на всех порядках это тот, который имеет самую высокую частоту возникновения на терминальном узле.
Взаимодействия (Interactions)
Мы хотим знать, как предикторы влияют на проблему, когда мы рассматриваем их все. Например, некоторые переменные могут иметь низкое относительное влияние на проблему, но сильное влияние на более релевантные переменные, или переменная может иметь множество взаимодействий с другими, что делает переменную влиятельной. Дадим определение взаимодействию.
Определение: Предиктор взаимодействует с другим, если по тому же наблюдению и для всех деревьев оба имеют соответственно первую и вторую высшую частоту встречаемости в терминальном узле.
Частичные зависимости (Partial dependencies)
Это инструменты, которые позволяют определить, насколько переменная (или пара переменных) влияет на значение отклика, зная значения всех других переменных. Более наглядно, частичная зависимость — это участок, где проявляется максимальный эффект влияния переменной на значение отклика. Идея частичной зависимости пришла от Фридмана (Friedman, 2002), который использовал ее в Gradient Boosting Machines (GBM), но в Random Uniform Forests она реализована различно.
В соответствии с идеями пакета Random Uniform Forests мы можем определить важность переменной по следующей схеме: Важность = вклад + взаимодействия, где вклад является влиянием переменной (по отношению к воздействию всех) на ошибки предсказания, а взаимодействие — влияние на другие переменные.
Перейдем к экспериментам
Разобьем наш набор данных data.f[] на тренировочный и тестовый c соотношением 2/3, нормализуем в диапазон -1;1 и протестируем пробно модель. Для разбиения используем функцию rminer::holdout() , которая стратифицированно разделяет набор на два. Для нормализации используем функцию caret::preProcess() и метод method = c("spatialSign"). При обучении модели пакет автоматически распараллеливает вычисления между наличными ядрами процессора минус один, используя пакет "doParallel". Можно указать конкретное число ядер, которое нужно использовать при вычислениях с помощью опции "threads".> idx <- rminer::holdout(y = data.f$Class)
> prep <- caret::preProcess(x = data.f[idx$tr, -ncol(data.f)],
+ method = c("spatialSign"))
> x.train <- predict(prep, data.f[idx$tr, -ncol(data.f)])
> x.test <- predict(prep, data.f[idx$ts, -ncol(data.f)])
> y.train <- data.f[idx$tr, ncol(data.f)]
> y.test <- data.f[idx$ts, ncol(data.f)]
> ruf <- randomUniformForest( X = x.train,
+ Y = y.train,
+ xtest = x.test,
+ ytest = y.test,
+ mtry = 1, ntree = 300,
+ threads = 2,
+ nodesize = 2
+ )
Labels -1 1 have been converted to 1 2 for ease of computation and will be used internally as a replacement.
> print(ruf)
Call:
randomUniformForest.default(X = x.train, Y = y.train, xtest = x.test,
ytest = y.test, ntree = 300, mtry = 1, nodesize = 2, threads = 2)
Type of random uniform forest: Classification
paramsObject
ntree 300
mtry 1
nodesize 2
maxnodes Inf
replace TRUE
bagging FALSE
depth Inf
depthcontrol FALSE
OOB TRUE
importance TRUE
subsamplerate 1
classwt FALSE
classcutoff FALSE
oversampling FALSE
outputperturbationsampling FALSE
targetclass -1
rebalancedsampling FALSE
randomcombination FALSE
randomfeature FALSE
categorical variables FALSE
featureselectionrule entropy
Out-of-bag (OOB) evaluation
OOB estimate of error rate: 20.2%
OOB error rate bound (with 1% deviation): 21.26%
OOB confusion matrix:
Reference
Prediction -1 1 class.error
-1 1066 280 0.2080
1 254 1043 0.1958
OOB estimate of AUC: 0.798
OOB estimate of AUPR: 0.7191
OOB estimate of F1-score: 0.7962
OOB (adjusted) estimate of geometric mean: 0.7979
Breiman's bounds
Expected prediction error (under approximatively balanced classes): 18.42%
Upper bound: 27.76%
Average correlation between trees: 0.0472
Strength (margin): 0.4516
Standard deviation of strength: 0.2379
Test set
Error rate: 19.97%
Confusion matrix:
Reference
Prediction -1 1 class.error
-1 541 145 0.2114
1 119 517 0.1871
Area Under ROC Curve: 0.8003
Area Under Precision-Recall Curve: 0.7994
F1 score: 0.7966
Geometric mean: 0.8001
Расшифруем немного:
- Ошибка при обучении (внутренняя ошибка) с учетом 1% отклонения = 21.26%.
- Breiman's bounds — теоретические свойства, предложенные Breiman (2001), так как Random Uniform Forests наследуют свойства Random Forests, то они применимы здесь. Для классификации это дает две границы ошибки предсказания, среднюю коррелляцию между деревьями, прочность (strength) и стандартное отклонение прочности.
- Ожидаемая ошибка предсказания = 18.42%. Верхняя граница ошибки = 27.76%.
- Ошибка при тестировании = 19.97% (внешняя ошибка). (Если внешняя оценка меньше или равна внутренней оценке и меньше верхней границы Breiman's bounds, переобучение скорее всего не произойдет.)
Посмотрим график ошибки обучения:
> plot(ruf)
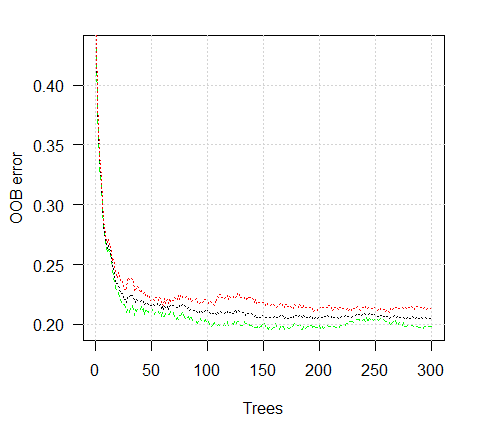
Рис. 2. Ошибка обучения в зависимости от количества деревьев
> summary(ruf) Global Variable importance: Note: most predictive features are ordered by 'score' and plotted. Most discriminant ones should also be taken into account by looking 'class' and 'class.frequency'. variables score class class.frequency percent 1 cci 2568 1 0.50 100.00 2 signal 2438 1 0.51 94.92 3 slowD 2437 1 0.51 94.90 4 oscK 2410 1 0.50 93.85 5 ADX 2400 -1 0.51 93.44 6 vol 2395 1 0.51 93.24 7 atr 2392 -1 0.51 93.15 8 sign 2388 1 0.50 92.97 9 vsig 2383 1 0.50 92.81 10 ar 2363 -1 0.51 92.01 11 chv 2327 -1 0.50 90.62 12 cmo 2318 -1 0.51 90.28 13 DX 2314 1 0.50 90.10 14 oscDX 2302 -1 0.51 89.64 15 tr 2217 1 0.52 86.31 percent.importance 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7 11 7 12 7 13 6 14 6 15 6 Average tree size (number of nodes) summary: Min. 1st Qu. Median Mean 3rd Qu. Max. 3 1044 1313 1213 1524 1861 Average Leaf nodes (number of terminal nodes) summary: Min. 1st Qu. Median Mean 3rd Qu. Max. 2 522 657 607 762 931 Leaf nodes size (number of observations per leaf node) summary: Min. 1st Qu. Median Mean 3rd Qu. Max. 1.000 1.000 2.000 4.355 3.000 2632.000 Average tree depth : 10 Theoretical (balanced) tree depth : 11
Мы видим, что все наши входные переменные значимы и важны. Указано, в каких классах переменные появляются чаще.
И еще немного статистики:
> pr.ruf <- predict(ruf, x.test, type = "response"); > ms.ruf <- model.stats(pr.ruf, y.test) Test set Error rate: 19.97% Confusion matrix: Reference Prediction -1 1 class.error -1 540 144 0.2105 1 120 518 0.1881 Area Under ROC Curve: 0.8003 Area Under Precision-Recall Curve: 0.7991 F1-score: 0.7969 Geometric mean: 0.8001
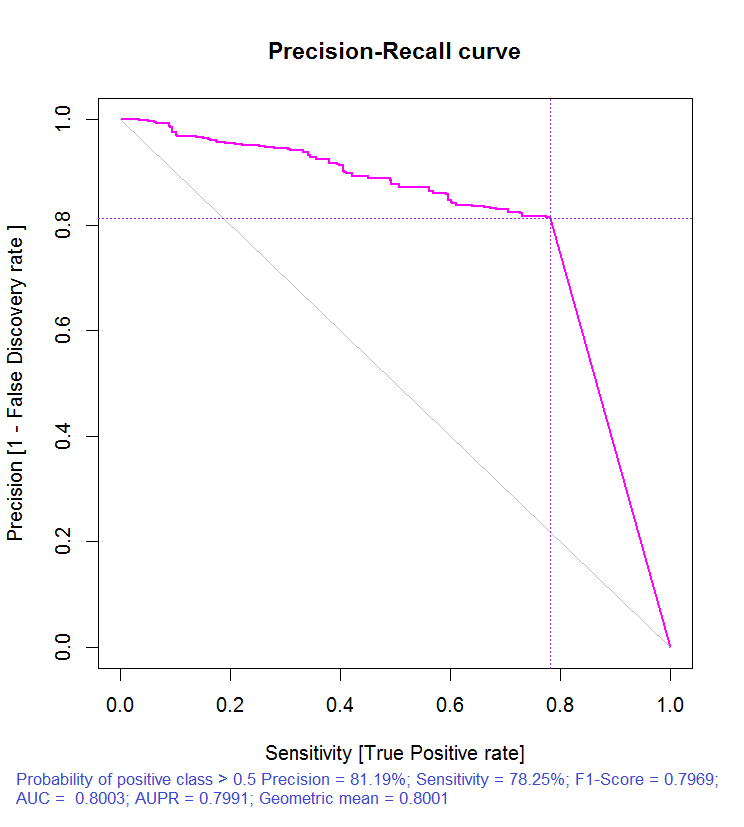
Рис. 3. Кривая точности-отзыва
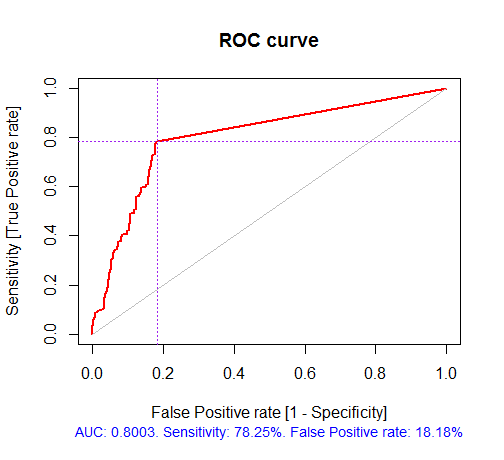
Рис. 4. ROC-кривая или кривая ошибок
Если остановиться на этом, а это, как правило, и предлагают многие пакеты фильтров, то нам нужно было бы выбрать несколько предикторов с наилучшими показателями глобальной важности. Такой выбор не дает хороших результатов, так как он не учитывает взаимное влияние предикторов.
> imp.ruf <- importance(ruf, Xtest = x.test, maxInteractions = 3) 1 - Global Variable Importance (15 most important based on information gain) : Note: most predictive features are ordered by 'score' and plotted. Most discriminant ones should also be taken into account by looking 'class' and 'class.frequency'. variables score class class.frequency percent 1 cci 2568 1 0.50 100.00 2 signal 2438 1 0.51 94.92 3 slowD 2437 1 0.51 94.90 4 oscK 2410 1 0.50 93.85 5 ADX 2400 -1 0.51 93.44 6 vol 2395 1 0.51 93.24 7 atr 2392 -1 0.51 93.15 8 sign 2388 1 0.50 92.97 9 vsig 2383 1 0.50 92.81 10 ar 2363 -1 0.51 92.01 11 chv 2327 -1 0.50 90.62 12 cmo 2318 -1 0.51 90.28 13 DX 2314 1 0.50 90.10 14 oscDX 2302 -1 0.51 89.64 15 tr 2217 1 0.52 86.31 percent.importance 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7 11 7 12 7 13 6 14 6 15 6 2 - Local Variable importance Variables interactions (10 most important variables at first (columns) and second (rows) order) : For each variable (at each order), its interaction with others is computed. cci cmo slowD oscK signal atr chv cmo 0.1933 0.1893 0.1345 0.1261 0.1146 0.1088 0.1062 cci 0.1770 0.1730 0.1182 0.1098 0.0983 0.0925 0.0899 slowD 0.1615 0.1575 0.1027 0.0943 0.0828 0.0770 0.0744 signal 0.1570 0.1530 0.0981 0.0897 0.0782 0.0725 0.0698 atr 0.1490 0.1450 0.0902 0.0818 0.0703 0.0646 0.0619 ADX 0.1468 0.1428 0.0879 0.0795 0.0680 0.0623 0.0596 ar 0.1452 0.1413 0.0864 0.0780 0.0665 0.0608 0.0581 oscK 0.1441 0.1401 0.0853 0.0769 0.0654 0.0596 0.0570 DX 0.1407 0.1367 0.0819 0.0735 0.0620 0.0562 0.0536 oscDX 0.1396 0.1356 0.0807 0.0723 0.0608 0.0551 0.0524 avg1rstOrder 0.1483 0.1443 0.0895 0.0811 0.0696 0.0638 0.0612 ADX tr ar vsig DX oscDX sign cmo 0.1026 0.1022 0.1013 0.1000 0.0977 0.0973 0.0964 cci 0.0864 0.0859 0.0850 0.0837 0.0815 0.0810 0.0802 slowD 0.0708 0.0704 0.0695 0.0682 0.0660 0.0655 0.0647 signal 0.0663 0.0659 0.0650 0.0637 0.0614 0.0610 0.0601 atr 0.0584 0.0579 0.0570 0.0557 0.0535 0.0531 0.0522 ADX 0.0561 0.0557 0.0548 0.0534 0.0512 0.0508 0.0499 ar 0.0546 0.0541 0.0533 0.0519 0.0497 0.0493 0.0484 oscK 0.0534 0.0530 0.0521 0.0508 0.0486 0.0481 0.0473 DX 0.0500 0.0496 0.0487 0.0474 0.0452 0.0447 0.0439 oscDX 0.0489 0.0485 0.0476 0.0463 0.0440 0.0436 0.0427 avg1rstOrder 0.0577 0.0572 0.0563 0.0550 0.0528 0.0524 0.0515 vol avg2ndOrder cmo 0.0889 0.1173 cci 0.0726 0.1010 slowD 0.0571 0.0855 signal 0.0526 0.0810 atr 0.0447 0.0730 ADX 0.0424 0.0707 ar 0.0409 0.0692 oscK 0.0397 0.0681 DX 0.0363 0.0647 oscDX 0.0352 0.0636 avg1rstOrder 0.0439 0.0000 Variable Importance based on interactions (10 most important) : cmo cci slowD signal oscK atr ADX ar 0.1447 0.1419 0.0877 0.0716 0.0674 0.0621 0.0563 0.0533 chv DX 0.0520 0.0485 Variable importance over labels (10 most important variables conditionally to each label) : Class -1 Class 1 cci 0.16 0.23 cmo 0.20 0.18 slowD 0.09 0.10 oscK 0.09 0.07 signal 0.05 0.07 tr 0.02 0.07 ADX 0.06 0.03 chv 0.06 0.04 atr 0.05 0.06 ar 0.05 0.03
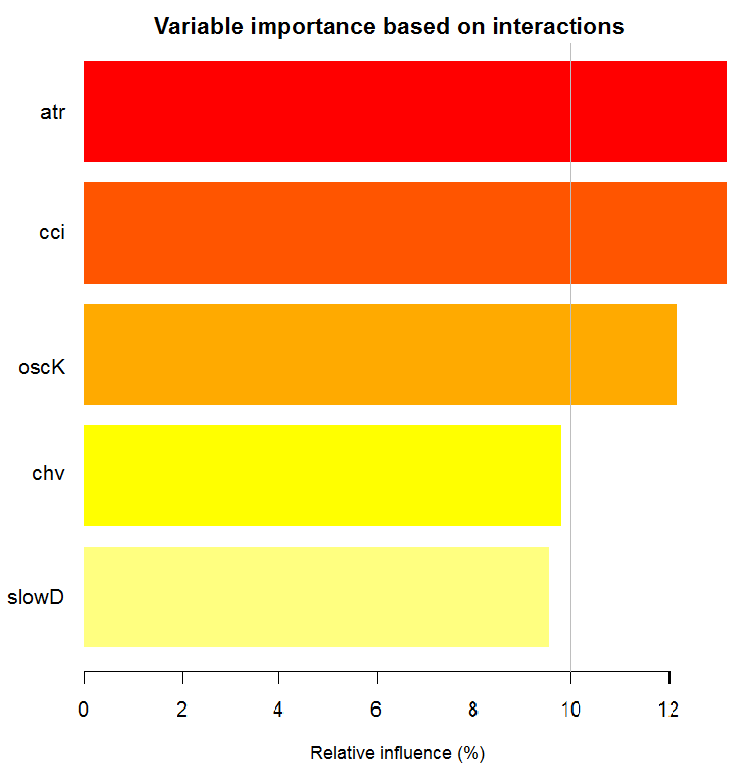
Как видим, важность переменных на базе взаимодействия с другими выделяет десять лучших, которые не совпадают с порядком по глобальной важности. И наконец, важность переменных по классам с учетом их вклада и взаимодействия. Обратите внимание, что переменная tr, которая на базе глобальной важности была на последнем месте и по идее должна была быть отброшена, на базе сильного взаимодействия поднялась на шестое место.
Таким образом, 10 лучших переменных:
> best <- Cs(cci, cmo, slowD, oscK, signal, tr, ADX. chv, atr, ar)Проверим, как улучшилось качество модели с набором наиболее важных предикторов.
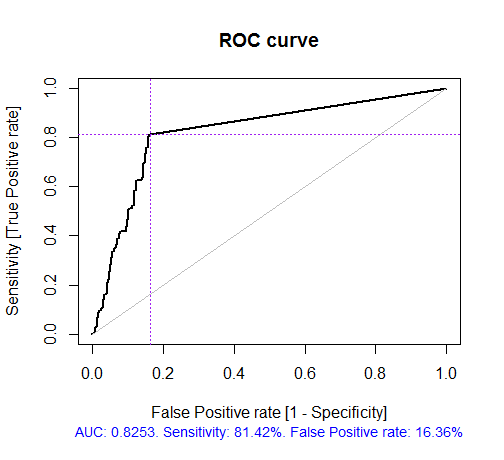
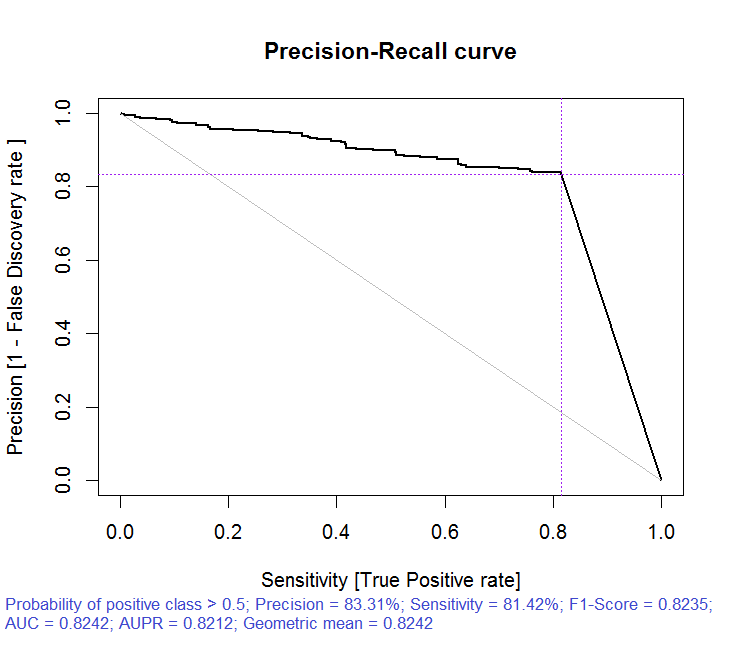
> x.tr <- x.train[ ,best] > x.tst <- x.test[ ,best] > ruf.opt <- randomUniformForest(X = x.tr, + Y = y.train, + xtest = x.tst, + ytest = y.test, + ntree = 300, + mtry = "random", + nodesize = 1, + threads = 2) Labels -1 1 have been converted to 1 2 for ease of computation and will be used internally as a replacement. > ruf.opt Call: randomUniformForest.default(X = x.tr, Y = y.train, xtest = x.tst, ytest = y.test, ntree = 300, mtry = "random", nodesize = 1, threads = 2) Type of random uniform forest: Classification paramsObject ntree 300 mtry random nodesize 1 maxnodes Inf replace TRUE bagging FALSE depth Inf depthcontrol FALSE OOB TRUE importance TRUE subsamplerate 1 classwt FALSE classcutoff FALSE oversampling FALSE outputperturbationsampling FALSE targetclass -1 rebalancedsampling FALSE randomcombination FALSE randomfeature FALSE categorical variables FALSE featureselectionrule entropy Out-of-bag (OOB) evaluation OOB estimate of error rate: 18.69% OOB error rate bound (with 1% deviation): 19.67% OOB confusion matrix: Reference Prediction -1 1 class.error -1 1079 253 0.1899 1 241 1070 0.1838 OOB estimate of AUC: 0.8131 OOB estimate of AUPR: 0.7381 OOB estimate of F1-score: 0.8125 OOB (adjusted) estimate of geometric mean: 0.8131 Breiman's bounds Expected prediction error (under approximatively balanced classes): 14.98% Upper bound: 28.18% Average correlation between trees: 0.0666 Strength (margin): 0.5548 Standard deviation of strength: 0.2945 > pr.ruf.opt <- predict(ruf.opt, x.tst, type = "response") > ms.ruf.opt <- model.stats(pr.ruf.opt, y.test) Test set Error rate: 17.55% Confusion matrix: Reference Prediction -1 1 class.error -1 552 124 0.1834 1 108 538 0.1672 Area Under ROC Curve: 0.8245 Area Under Precision-Recall Curve: 0.8212 F1-score: 0.8226 Geometric mean: 0.8244
Рис. 5. ROC-кривая или кривая ошибок
Рис. 6. Кривая точности-отклика
Как видим, качество улучшилось. Ошибка предсказания на тестовом наборе 17.55% меньше верхней границы 28.18%, значит, переобучение маловероятно. Модель имеет множество других гиперпараметров, тюнинг которых может позволить еще более повысить качество модели, но это не есть задача настоящей статьи.
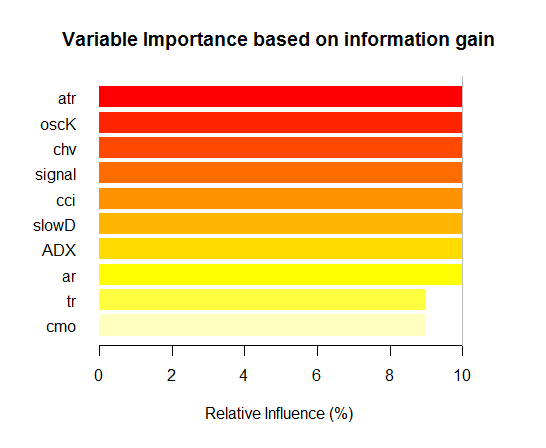
> imp.ruf.opt <- importance(ruf.opt, Xtest = x.tst) Relevant variables have been extracted. 1 - Global Variable Importance (10 most important based on information gain) : Note: most predictive features are ordered by 'score' and plotted. Most discriminant ones should also be taken into account by looking 'class' and 'class.frequency'. variables score class class.frequency percent 1 atr 3556 -1 0.50 100.00 2 oscK 3487 -1 0.51 98.07 3 chv 3465 1 0.51 97.45 4 signal 3432 1 0.51 96.51 5 cci 3424 1 0.50 96.30 6 slowD 3415 1 0.51 96.04 7 ADX 3397 -1 0.50 95.52 8 ar 3369 -1 0.50 94.76 9 tr 3221 1 0.53 90.59 10 cmo 3177 -1 0.50 89.36 percent.importance 1 10 2 10 3 10 4 10 5 10 6 10 7 10 8 10 9 9 10 9 2 - Local Variable importance Variables interactions (10 most important variables at first (columns) and second (rows) order) : For each variable (at each order), its interaction with others is computed. atr cci oscK slowD ADX tr chv cci 0.1748 0.1625 0.1620 0.1439 0.1411 0.1373 0.1349 atr 0.1650 0.1526 0.1522 0.1341 0.1312 0.1274 0.1251 oscK 0.1586 0.1462 0.1457 0.1277 0.1248 0.1210 0.1186 chv 0.1499 0.1375 0.1370 0.1190 0.1161 0.1123 0.1099 ar 0.1450 0.1326 0.1321 0.1140 0.1112 0.1074 0.1050 signal 0.1423 0.1300 0.1295 0.1114 0.1085 0.1047 0.1024 ADX 0.1397 0.1273 0.1268 0.1088 0.1059 0.1021 0.0997 slowD 0.1385 0.1262 0.1257 0.1076 0.1048 0.1010 0.0986 cmo 0.1276 0.1152 0.1147 0.0967 0.0938 0.0900 0.0876 tr 0.1242 0.1118 0.1113 0.0932 0.0904 0.0866 0.0842 avg1rstOrder 0.1466 0.1342 0.1337 0.1156 0.1128 0.1090 0.1066 signal ar cmo avg2ndOrder cci 0.1282 0.1182 0.1087 0.1412 atr 0.1184 0.1084 0.0989 0.1313 oscK 0.1120 0.1020 0.0925 0.1249 chv 0.1033 0.0933 0.0838 0.1162 ar 0.0984 0.0884 0.0789 0.1113 signal 0.0957 0.0857 0.0762 0.1086 ADX 0.0931 0.0831 0.0736 0.1060 slowD 0.0919 0.0819 0.0724 0.1049 cmo 0.0810 0.0710 0.0615 0.0939 tr 0.0776 0.0676 0.0581 0.0905 avg1rstOrder 0.0999 0.0900 0.0804 0.0000 Variable Importance based on interactions (10 most important) : atr cci oscK chv slowD ADX signal ar 0.1341 0.1335 0.1218 0.0978 0.0955 0.0952 0.0898 0.0849 tr cmo 0.0802 0.0672 Variable importance over labels (10 most important variables conditionally to each label) : Class -1 Class 1 atr 0.17 0.14 oscK 0.16 0.11 tr 0.03 0.16 cci 0.14 0.13 slowD 0.12 0.09 ADX 0.10 0.10 chv 0.08 0.10 signal 0.09 0.07 cmo 0.07 0.03 ar 0.06 0.06
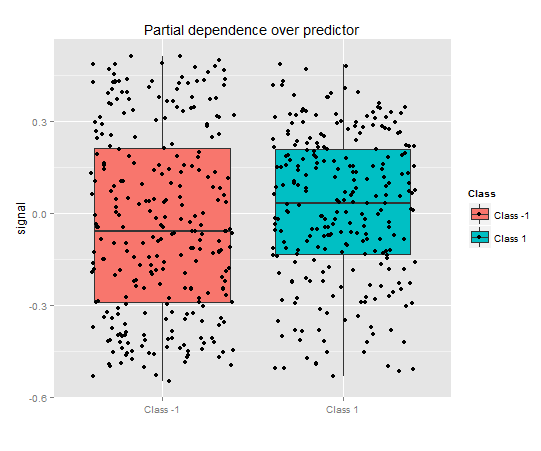
Рис. 7. Важность переменных на базе информационной ценности
Как видим, глобальная важность переменных практически выровнялась, но важность переменных по классам ранжирована совсем по-другому. Переменная tr — на третьем месте.
Частичная зависимость над предиктором
Рассмотрим частичную зависимость наиболее важных переменных.
> plot(imp.ruf.opt, Xtest = x.tst)
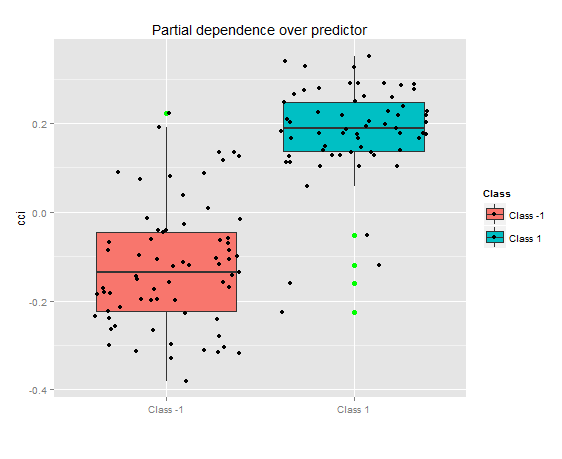
Рис. 8. Частичная зависимость переменной cci
> pd.signal <- partialDependenceOverResponses(x.tst, + imp.ruf.opt, + whichFeature = "signal", + whichOrder = "all" + )
Рис. 9. Частичная зависимость переменной signal
Совсем другая картина частичной зависимости для предиктора signal на рисунке выше. Практически полное перекрытие данных для обоих классов.
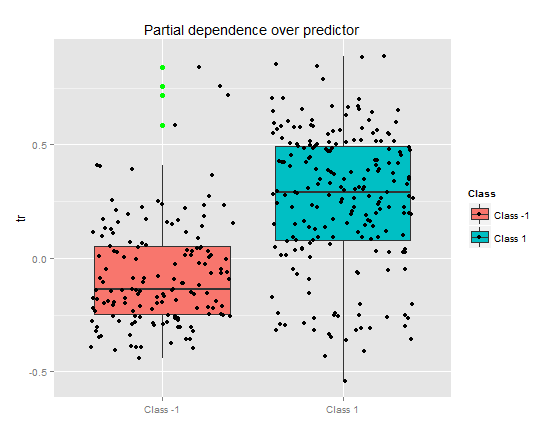
> pd.tr <- partialDependenceOverResponses(x.tst,
imp.ruf.opt,
whichFeature = "tr",
whichOrder = "all"
)
Частичная зависимость предиктора tr показывает неплохое разделение по классам, но и здесь есть значительное перекрытие.
Рис. 10. Частичная зависимость переменной tr
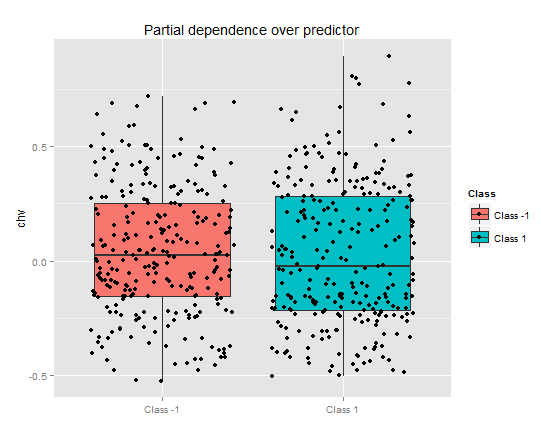
> pd.chv <- partialDependenceOverResponses(x.tst,
imp.ruf.opt,
whichFeature = "chv",
whichOrder = "all")
Частичная зависимость предиктора chv совсем плачевна. Полное перекрытие данных по классам.
Рис. 11. Частичная зависимость переменной chv
Таким образом можно визуально определить, как связаны данные предикторов с классами, насколько они разделяемы.
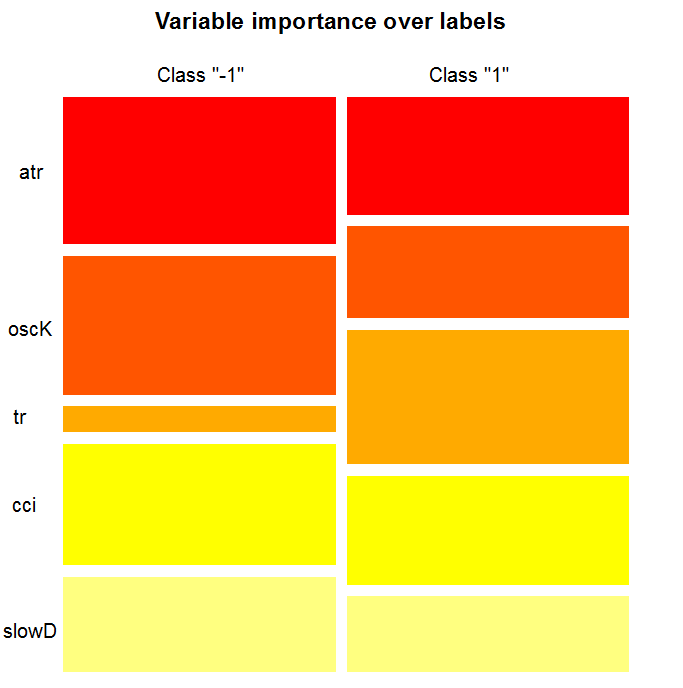
Важность переменной на классах
«Важность переменной» по классам обеспечивает локальную точку зрения: класс фиксируется, это означает, что сначала принимается решение фиксировать класс, рассматривая переменные, которые важны и действуют как константы, после чего рассматриваются важные переменные для каждого класса. Следовательно, каждая переменная имеет важность, как если бы другие классы не существовали.
Здесь мы не интересуемся переменными, которые привели к выбору класса, но переменными, которые будут важны в классе, когда этот последний будет выбран. Порядок переменных дает их сводное ранжирование относительно их ранга в каждом классе, без учета важности класса.
Что показывает нам график? Предиктор tr гораздо важнее для класса "1", чем для класса "-1". И наоборот, предиктор oscK для класса "-1" намного более важен, чем для класса "1". Предикторы имеют различную важность в разных классах.
Рис. 12. Важность переменных по классам
Важность переменной на базе взаимодействия
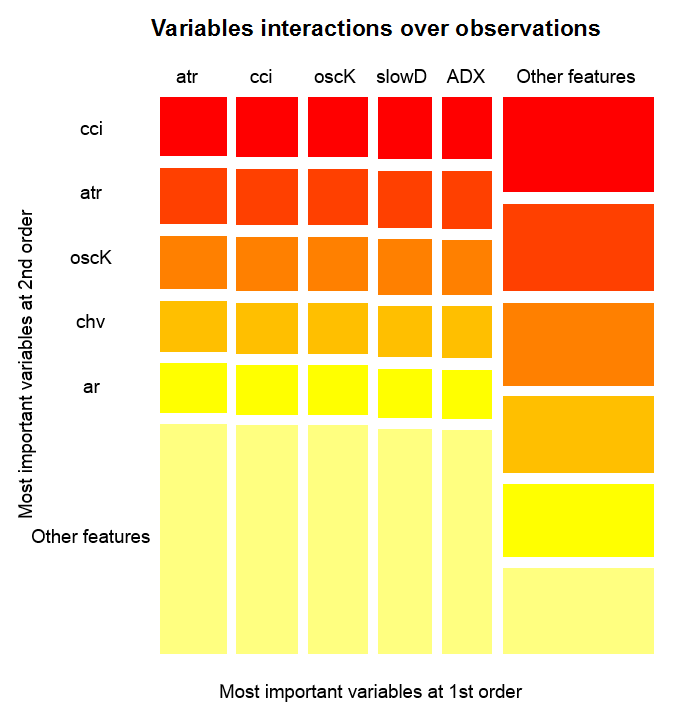
Диаграмма ниже показывает, как каждая переменная представлена при объединенном взаимодействии с любой другой переменной. Одно важное замечание: самой важной является не обязательно первая переменная, но та, которая имеет наибольшее взаимное влияние с другими.
Взаимодействие переменных на наблюдениях
Рис. 14. Важность переменных на наблюдениях
Рисунок выше показывает взаимодействия первого и второго порядка для всех предикторов в соответствии с определением, которое мы дали для взаимодействия. Его площадь равна единице. Первый порядок указывает, что переменные (упорядоченные по убыванию влияния) являются самыми важными, если решение должно быть принято, принимая во внимание одну и только одну переменную. Второй порядок указывает, что если неизвестная переменная уже выбрана в первом порядке, тогда вторая по важности переменная будет одной из тех во втором порядке.
Чтобы было яснее, взаимодействия предоставляют таблицу упорядоченных возможностей. Первый порядок дает упорядоченные возможности наиболее важных переменных. Второй порядок дает упорядоченные возможности вторых по важности переменных. Пересечение пары переменных дает их относительное взаимное влияние из всех возможных взаимных влияний. Можно отметить, что эти измерения зависят как от модели, так и от данных. Следовательно, уверенность в измерениях напрямую зависит от уверенности в предсказаниях. Можно также отметить, что появляется мета-переменная, называемая «другие признаки» , означающая, что мы позволяем алгоритму показать вид по умолчанию для визуализации сгруппированных переменных, которые являются менее актуальными.
Частичная важность
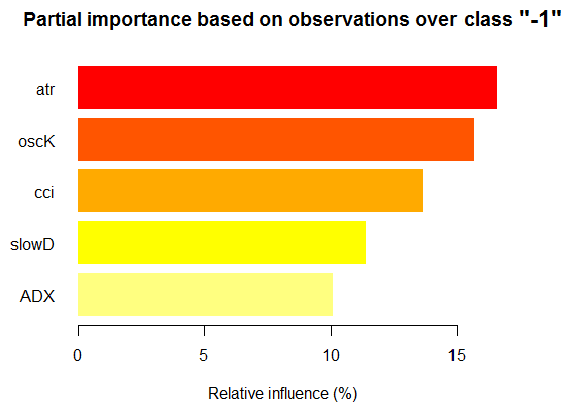
Можно посмотреть частичную важность на базе наблюдений x.tst над классом "-1".
> par.imp.ruf <- partialImportance(X = x.tst, + imp.ruf.opt, + whichClass = "-1") Relative influence: 67.41% На базе x.tst и класса «-1»
Рис. 15. Частичная важность переменных на базе наблюдений на классе "-1"
Как видим, для класса "-1" наиболее важны пять предикторов, показанных на рисунке выше.
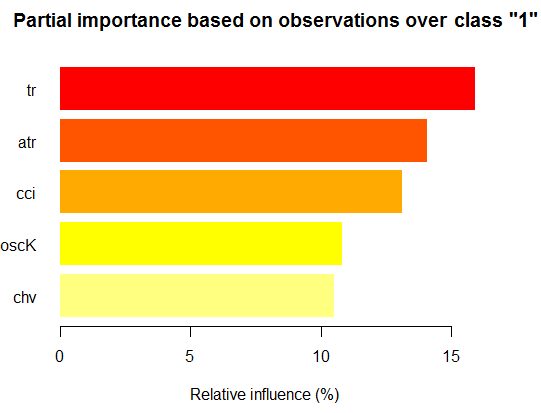
Теперь то же, но для класса "+1"
> par.imp.ruf <- partialImportance(X = x.tst, + imp.ruf.opt, + whichClass = "1") Relative influence: 64.45%
Рис. 16. Частичная важность переменных на базе наблюдений на классе "+1"
Видим, что предикторы отличаются как по составу, так и по ранжированию.
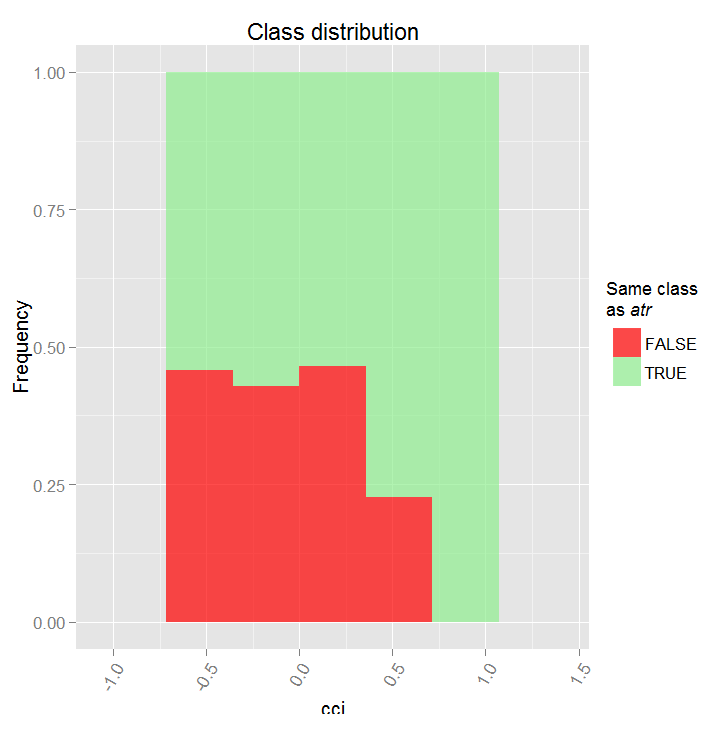
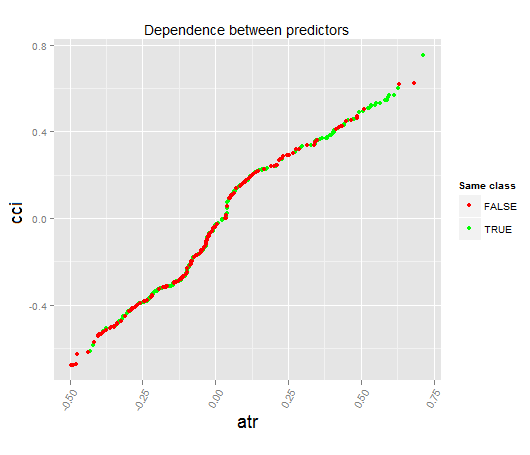
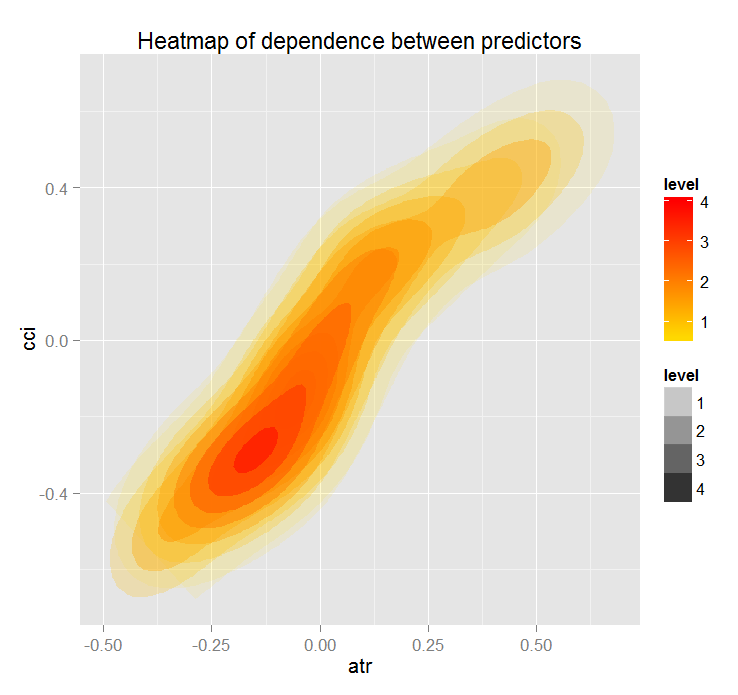
Посмотрим частичную зависимость между предикторами cci и atr, которые наиболее важны в первом и втором порядке взаимодействия предикторов.
> par.dep.1 <- partialDependenceBetweenPredictors(Xtest = x.tst, + imp.ruf.opt, + features = Cs(atr, cci), + whichOrder = "all", + perspective = T) Level of interactions between atr and cci at first order: 0.1748 (99.97% of the feature(s) with maximum level) Level of interactions between atr and cci at second order: 0.1526 (87.28% of the feature(s) with maximum level) Class distribution : for a variable of the pair, displays the estimated probability that the considered variable has the same class than the other. If same class tends to be TRUE then the variable has possibly an influence on the other (for the considered category or values)when predicting a label. Распределение класса: Для переменной из пары, отображается приблизительная вероятность того, что рассматриваемая переменная имеет тот же класс что и другая. Если предсказанный класс TRUE то переменная, возможно, имеет влияние на другую(для рассматриваемой категории или значения)при прогнозиро- вании класса. Dependence : for the pair of variables, displays the shape of their dependence and the estimated agreement in predicting the same class, for the values that define dependence. In case of categorical variables, cross-tabulation is used. Зависимость: для пары переменных отображается форма их зависимости и предполагаемая согласованность в предсказании того же класса, для значений, которые определяют зависимость. Heatmap : for the pair of variables, displays the area where the dependence is the most effective. The darker the colour, the stronger is the dependence. Тепловая карта: для пары переменных отображается область, где зависимость является наиболее эффективной. Чем темнее цвет, тем сильнее зависимость. From the pair of variables, the one that dominates is, possibly, the one that is the most discriminant one (looking 'Global variable Importance') and/or the one that has the higher level of interactions(looking 'Variable Importance based on interactions'). Из пары переменных та, что доминирует, возможно является самой отличающейся (смотрим «глобальная важность переменной») и/или той, которая имеет более высокий уровень взаимодействия.
Рис. 17. Частичная зависимость между предикторами cci и atr
Рис. 18. Зависимость между предикторами atr и cci
Рис. 19. Теплокарта зависимости предикторов atr и cci
Глобальная важность переменной была определена, чтобы описать, какие переменные в глобальном масштабе имеют наибольшее влияние на снижение ошибки предсказания.
Локальная важность переменной описывает то, что делает переменную влиятельной, используя ее взаимодействие с другими.
Это приводит к частичной важности, которая показывает, когда переменная является более важной. Последний шаг в анализе важности переменной — это частичная зависимость, определяющая, где и/или как каждая переменная связана с ответом.
Подводя итог: важность переменной в Random Uniform Forests идет от высшего уровня к нижнему с детализацией. Во-первых, мы узнаем, какие переменные важны, нюансы по весу в каждом классе. Затем мы находим, что делает их влиятельными, рассматривая их взаимодействия, и делаем выбор переменной, сперва рассматривая все классы как один. Следующий шаг — узнаем, где они получают свое влияние, рассматривая внутри каждого класса, когда он фиксирован. Наконец, мы получаем, когда и как переменная бывает важной, глядя на «частичную зависимость». Все измерения, кроме «глобальной важности переменной», работают на любом тренировочном или тестовом наборе.
Представленная многоуровневая оценка предикторов позволяет отобрать наиболее важные предикторы и сформировать оптимальные наборы, значительно понизив размерность данных и улучшив качество предсказания.
Можно оценить и выбрать не только предикторы, но и наиболее информативные экземпляры наблюдений.
Рассмотрим другой интересный пакет — "RoughSet".
Краткое описание: Есть две основные части, рассматриваемые в этом пакете — это Теория приближенных множеств (Rough Set Theory (RST)) и Теория нечетких приближенных множеств (Fuzzy Rough Set Theory (FRST)). RST была предложена Z. Pawlak (1982, 1991), она предоставляет сложные математические инструменты для моделирования и анализа информационных систем, которые включают неоднородности и неточности. Используя отношения неразличимости между объектами, RST не требует дополнительных параметров для извлечения информации.
Теория FRST, расширение RST, была предложена D. Dubois и H. Prade (1990), она сочетает понятия неопределенности и неразличимости, которые выражены в нечетких множествах, предложенных L.A. Zadeh (1965), и RST. Эта концепция позволяет анализировать непрерывные атрибуты (переменные) без предварительной дискретизации данных. На основании вышеописаных концепций многие методы были предложены и применены в нескольких различных областях. Для того чтобы решать проблемы, методы используют отношение неразличимости и концепцию нижней и верхней апроксимации.
Небольшое отступление
Способ представления знаний в информационной системе играет, как правило, большую роль. Наиболее известными способами представления знаний в системах индуктивного формирования понятий являются: продукционные правила, решающие деревья, исчисление предикатов и семантические сети.
При извлечении и обобщении знаний, хранящихся в реальных информационных массивах, возникают следующие основные проблемы:
- Данные являются разнородными (количественными, качественными, структурными).
- Реальные базы данных, как правило, велики, а потому алгоритмы экспоненциальной сложности для извлечения знаний из баз данных могут оказаться неприемлемыми.
- Информация, содержащаяся в реальных массивах данных, может быть неполна, избыточна, искажена, противоречива, а также некоторые значения ряда атрибутов могут вовсе отсутствовать. Поэтому для построения классификационных правил следует использовать только существенные атрибуты.
В настоящее время для извлечения знаний из баз данных (Data Mining) теория приближенных множеств (rough sets theory) все чаще используется как теоретическая база и набор практических методов.
Приближенные множества — это множества с неопределенными границами, т.е. множества, которые не могут быть точно описаны доступным набором признаков.
Теория приближенных множеств была предложена Здиславом Павлаком в 1982 году и явилась новым математическим инструментом работы с неполной информацией. Важнейшими понятиями данной теории являются так называемые верхняя и нижняя аппроксимации (lower and upper approximation) приближенного множества, позволяющие оценить возможность или необходимость принадлежности элемента множеству с «размытыми» границами .
Нижнюю аппроксимацию (приближение) составляют элементы, которые точно принадлежат X, верхнюю аппроксимацию (приближение) составляют элементы, которые возможно принадлежат X . Граничной областью (boundary region) множества X называется разность между верхней и нижней аппроксимацией, т.е. в граничную область входят элементы множества Х, принадлежащие верхней аппроксимации и не принадлежащие нижней аппроксимации.
Простая, но мощная концепция приближенных множеств стала базовой как в теоретических исследованиях — логике, алгебре, топологии, так и в прикладных — задачах искусственного интеллекта, приближенных рассуждениях, интеллектуальном анализе данных, теории принятия решений, обработке изображений и распознавании образов.
Концепция «приближенного множества» имеет дело с «несовершенством данных» (imperfection), относящимся к «гранулярности» информации (granularity). Эта концепция по своей природе является топологической и дополняет другие известные подходы, используемые для работы с неполной информацией, такие как нечеткие множества (fuzzy sets), методы Байеса (Bayesian reasoning), нейронные сети (neural networks), эволюционные алгоритмы (evolutionary algorithms), статистические методы анализа данных.
Продолжим. Все методы, представленные в этом пакете, можно сгруппировать следующим образом:
Базовые понятия RST и FRST. В этой части мы можем видеть четыре различные задачи — отношение неразличимости (indiscernibility relation), нижнее и верхнее приближение (lower and upper approximation), положительный регион (positive region) и матрица отличий (discernibility matrix).
Дискретизация. Он используется для преобразования вещественных данных в номинальные. С точки зрения RST эта задача пытается поддержать различимость (discernibility) между объектами.
Выбор предикторов (Feature selection). Это процесс нахождения подмножества предикторов, которые пытаются получить то же качество, что и полный набор предикторов. Иными словами, цель заключается в выборе существенных особенностей и ликвидации их зависимости. Это полезно и необходимо, когда мы сталкиваемся с наборами данных, содержащих большое количество признаков. С точки зрения RST и FRST выбор предикторов относится к поиску superreducts и reducts.
Выбор экземпляров (Instance selection). Этот процесс направлен на удаление шумных, лишних или противоречивых экземпляров из учебных наборов данных, но сохранение согласованных. Таким образом, хорошая точность классификации достигается путем удаления экземпляров, которые не дают позитивного вклада.
Индукция правил (Rule induction). Как мы уже говорили, задача индукции правил используется для генерации правил, представляющих знания таблицы решений. Как правило, этот процесс называется фазой обучения в машинном обучении.
Прогноз/классификация (Prediction/classification). Эта задача используется для предсказания значения переменной от нового набора данных (тестового набора).
Из этого перечня мы будем исследовать два — выбор предикторов и выбор экземпляров.
Сформируем наборы входных и выходных данных. Будем использовать те же данные, которые мы получили выше, но преобразуем их в класс "DecisionTable", с которым оперирует пакет.> library(RoughSets) Loading required package: Rcpp > require(magrittr) > data.tr <- SF.asDecisionTable(data.f[idx$tr, ], + decision.attr = 16, + indx.nominal = 16) > data.tst <- SF.asDecisionTable(data.f[idx$ts, ], + decision.attr = 16, + indx.nominal = 16 + ) > true.class <- data.tst[ ,ncol(data.tst)]Как мы сказали выше, RST использует номинальные данные. Поскольку у нас данные числовые непрерывные, мы преобразуем их в номинальные с помощью одной из специализированных функций дискретизации, имеющихся в пакете.
> cut.values <- D.global.discernibility.heuristic.RST(data.tr) > data.tr.d <- SF.applyDecTable(data.tr, cut.values)
Посмотрим, что у нас в результате
> summary(data.tr.d) DX ADX (12.5,20.7]: 588 (17.6,19.4]: 300 (20.7, Inf]:1106 (19.4,25.4]: 601 [-Inf,12.5]: 948 (25.4,31.9]: 294 (31.9, Inf]: 343 [-Inf,17.6]:1104 oscDX ar (1.81, Inf]:1502 (-40.6,40.6]:999 [-Inf,1.81]:1140 (40.6,71.9] :453 (71.9, Inf] :377 [-Inf,-40.6]:813 tr atr (0.000205,0.000365]:395 (0.00072,0.00123]:1077 (0.000365,0.0005] :292 (0.00123, Inf] : 277 (0.0005,0.00102] :733 [-Inf,0.00072] :1288 (0.00102,0.00196] :489 (0.00196, Inf] :203 [-Inf,0.000205] :530 cci chv (-6.61, Inf]:1356 (-0.398,0.185]:1080 [-Inf,-6.61]:1286 (0.185,0.588] : 544 (0.588, Inf] : 511 [-Inf,-0.398] : 507 cmo sign (5.81,54.1]: 930 [-Inf, Inf]:2642 (54.1, Inf]: 232 [-Inf,5.81]:1480 vsig slowD (0.0252, Inf]:1005 [-Inf, Inf]:2642 [-Inf,0.0252]:1637 oscK signal (-0.0403,0.000545]:633 (-11.4, Inf]:1499 (0.000545,0.033] :493 [-Inf,-11.4]:1143 (0.033, Inf] :824 [-Inf,-0.0403] :692 vol Class (0.0055,0.00779]:394 -1:1319 (0.00779,0.0112]:756 1 :1323 (0.0112,0.0154] :671 (0.0154, Inf] :670 [-Inf,0.0055] :151
Мы видим, что предикторы дискретизированы различно. Такие переменные, как slowD, sign, вообще не разделены. Переменные signal, vsig, cci, oscDX просто разделены на два участка. Остальные переменные разбиты от 3 до 6 классов.
Выберем важные переменные:
> reduct1 <- FS.quickreduct.RST(data.tr.d, control = list()) > best1 <- reduct1$reduct > best1 DX ADX oscDX ar tr atr cci 1 2 3 4 5 6 7 chv cmo vsig oscK signal vol 8 9 11 13 14 15
Те данные, которые не были разделены (slowD, sign), выброшены из набора. Проведем дискретизацию тестового набора и преобразуем их в соответствии с проведенной редукцией.
> data.tst.d <- SF.applyDecTable(data.tst, cut.values) > new.data.tr <- SF.applyDecTable(data.tr.d, reduct1) > new.data.tst <- SF.applyDecTable(data.tst.d, reduct1)
А теперь, используя одну замечательную возможность пакета, которая называется «индукция правил», извлечем набор правил, которые связывают предикторы и целевую. Используем одну из функций:
> rules <- RI.AQRules.RST(new.data.tr, confidence = 0.9, timesCovered = 3)
Проверим на тестовом наборе, как работают эти правила при предсказании:
> pred.vals <- predict(rules, new.data.tst) > table(pred.vals) pred.vals -1 1 655 667
Метрики:
> caret::confusionMatrix(true.class, pred.vals[ ,1]) Confusion Matrix and Statistics Reference Prediction -1 1 -1 497 163 1 158 504 Accuracy : 0.7572 95% CI : (0.7331, 0.7801) No Information Rate : 0.5045 P-Value [Acc > NIR] : <2e-16 Kappa : 0.5144 Mcnemar's Test P-Value : 0.8233 Sensitivity : 0.7588 Specificity : 0.7556 Pos Pred Value : 0.7530 Neg Pred Value : 0.7613 Prevalence : 0.4955 Detection Rate : 0.3759 Detection Prevalence : 0.4992 Balanced Accuracy : 0.7572 'Positive' Class : -1
Ну а теперь — выбор значимых примеров:
> ##-----Instance Selection----------- > res.1 <- IS.FRIS.FRST(decision.table = data.tr, control = list(threshold.tau = 0.5, alpha = 1, type.aggregation = c("t.tnorm", "lukasiewicz"), t.implicator = "lukasiewicz")) > new.data.tr <- SF.applyDecTable(data.tr, res.1) > nrow(new.data.tr) [1] 2353Около 300 примеров были оценены как незначительные и отброшены. Извлечем набор правил из этого набора и сравним качество предсказания с предыдущим набором.
> rules <- RI.AQRules.RST(new.data.tr, confidence = 0.9,
timesCovered = 3)
> pred.vals <- predict(rules, new.data.tst)
> table(pred.vals)
pred.vals
-1 1
638 684
> caret::confusionMatrix(true.class, pred.vals[ ,1])
Confusion Matrix and Statistics
Reference
Prediction -1 1
-1 506 154
1 132 530
Accuracy : 0.7837
95% CI : (0.7605, 0.8056)
No Information Rate : 0.5174
P-Value [Acc > NIR] : <2e-16
Kappa : 0.5673
Mcnemar's Test P-Value : 0.2143
Sensitivity : 0.7931
Specificity : 0.7749
Pos Pred Value : 0.7667
Neg Pred Value : 0.8006
Prevalence : 0.4826
Detection Rate : 0.3828
Detection Prevalence : 0.4992
Balanced Accuracy : 0.7840
'Positive' Class : -1
Качество выше, чем в предыдущем случае. Нужно заметить, что как и в случае с RandomUniformForests, получить воспроизводимые результаты при повторных экспериментах невозможно. Каждый новый запуск дает немного различный результат.
Как выглядят правила? Посмотрим:> head(rules) [[1]] [[1]]$idx [1] 6 4 11 [[1]]$values [1] "(85.1, Inf]" "(0.00137, Inf]" "(0.0374, Inf]" [[1]]$consequent [1] "1" [[1]]$support [1] 1335 1349 1363 1368 1372 1390 1407 1424 1449 1454 [11] 1461 1472 1533 1546 1588 1590 1600 1625 1630 1661 [21] 1667 1704 1720 1742 1771 1777 1816 1835 1851 1877 [31] 1883 1903 1907 1912 1913 1920 1933 1946 1955 1981 [41] 1982 1998 2002 2039 2040 2099 2107 2126 2128 2191 [51] 2195 2254 2272 2298 2301 2326 2355 2356 2369 2396 [61] 2472 2489 2497 2531 2564 2583 2602 2643 [[1]]$laplace 1 0.9857143
Это лист, содержащий следующие данные:
- $idx — индексы предикторов, участвующие в этом правиле. В примере выше это 6("atr") , 4("ar") и 11("vsig").
- $values — диапазон значений индикаторов, в котором работает это правило.
- $consequent — решение (следствие): class = "1". На «человеческом» это звучит так: если "atr" в диапазоне "(85.1, Inf]" И "ar" в диапазоне "(0.00137, Inf]" И "vsig" в диапазоне "(0.0374, Inf]" ТО Class = "1".
- $support — индексы примеров, поддерживающих это решение.
- $laplace — оценка уровня доверия для этого правила.
Вычисление правил занимает значительное время.
Заключение
Мы рассмотрели новые возможности по оценке предикторов, их визуализации, выбору наиболее значимых. Рассмотрели различные уровни важности, зависимости предикторов и их влияние на отклики. Результаты экспериментов будут применены в следующей статье, где мы рассмотрим глубокие сети с RBM.
Обработка ошибок и логирование в MQL5
Применение нечеткой логики в трейдинге средствами MQL4
MQL5 для начинающих: Антивандальная защита графических объектов
Работаем с ZIP-архивами средствами MQL5 без использования сторонних библиотек
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Я отвечал Vladimir
Сначала дается определение Классификации на уровне детского сада. Потом рассказывается о том, что порождается неопределенность(!?) А заканчивается как всегда : "Где ключ от квартиры где деньги лежат?"
Вам нужно повысить теоретическую подготовку. Учиться, учиться и еще раз ... Ну вы знаете.
И будьте скромнее.
ПС. Свое предложение разместите во Фриланс. Получите реальный продукт.
О ключе от квартиры слышал не в первый раз. Перечитайте мое предложение: "Детали модели, нормализации данных, и их выбора меня не интересуют. Меня интересуют результаты предсказаний ..." Причём предсказаний на прошлом участке истории от 2000 года по сегодня. Так что читать видимо мы тут все не умеем. Короче, теория продолжается. Перечитали другие книги и статьи и написали свою. Вы хоть попробуйте сначала поторговать на реальном рынке ипользуя свои методы, а потом пишите статьи. Ну ладно, теоретики-академики. Дал я вам тут рекламы немного, а то ветка начала тонуть в навале новых статей.
Вот ещё пара статей на данную тему:
http://robotwealth.com/machine-learning-financial-prediction-david-aronson/
http://robotwealth.com/machine-learning-for-financial-prediction-experimentation-with-david-aronsons-latest-work-part-2/
Возможно, кому-то покажется полезным.
Статья объёмная, спасибо за труд.
Однако, вызывает сомнение:
1. Использование стратификации с выбранной целевой, которая размечается на каждом баре. Перемешивание двух нерепрезентативных выборок обычно улучшают результат, что его искажает.
2. Отбор признаков на базе построенных моделей, особенно учитывая рандом первого сплита и метод жадности, - это скорей способ уменьшения признаков для метода построения моделей. Не всегда жадный метод оказывается правильным и устойчивым. Тут, возможно нужно использовать разные подвыборки, как минимум.
Второй метод не понял до конца - там так же случайный первый предиктор, а потом пытаемся построить лист или строится дерево и оставляется лучший лист, по которому и происходит оценка?