Сингулярный спектральный анализ на MQL5

Что такое SSA?

В последних версиях MetaTrader 5 впервые реализована начальная интеграция методов OpenBLAS в основные векторные и матричные типы данных. Особый интерес представляет набор методов, связанных с сингулярным спектральным анализом (SSA). В настоящей статье мы рассмотрим новые связанные с SSA инструменты, доступные на MQL5, расскажем, как их можно использовать для анализа и прогнозирования. Целью настоящего руководства является предоставление ресурса трейдерам, стремящимся раскрыть весь потенциал SSA. Мы углубимся в основную методологию SSA, демистифицируем ее двухэтапный процесс декомпозиции и реконструкции. Что еще важнее, обсудим, что делает каждый из новых векторных методов SSA, и покажем, как интерпретировать и оптимально объединять их результаты для получения практических идей.

Сингулярный спектральный анализ — это непараметрический метод, предназначенный для анализа и прогнозирования данных временных рядов. Его цель — разложить временной ряд на несколько аддитивных компонентов, которые обычно включают медленно меняющийся тренд, различные циклы и остаточный шум. Отличительной особенностью SSA является его минимальная зависимость от заранее определенных предположений относительно базового процесса генерации данных. Концептуальная основа SSA объединяет элементы статистики и обработки сигналов. По сути, SSA основан на спектральном разложении, что позволяет ему выявлять частотные характеристики временного ряда путем анализа его главных компонентов в реконструированном пространстве вложений. Его можно эффективно концептуализировать как форму анализа главных компонентов (PCA), специально адаптированного для данных временных рядов, использующего принципы снижения размерности для выявления скрытых структур и паттернов, которые могут быть замаскированы шумом или сложными взаимодействиями.

SSA на MQL5

В MQL5 вычисления SSA реализованы изначально как методы векторного типа данных, а также в математической библиотеке Alglib. Преимущество реализации SSA в Alglib заключается прежде всего в обработке в реальном времени, в то время как новая функциональность SSA, доступная напрямую из векторов, больше подходит для исследовательского анализа. Обратите внимание, что хотя этот текст в первую очередь посвящен операциям с использованием действительных чисел, для комплексных чисел также доступны и работают аналогичным образом эквивалентные методы, причем их интерпретация адаптирована для комплексной области.

В каждом из новых векторных методов SSA первым обязательным параметром является указание длины окна. Этот параметр определяет, как временной ряд преобразуется в многомерную структуру, известную как матрица траекторий. Кто-то может спросить: «Зачем нужна эта многомерная структура?» Подсказка кроется в отношении SSA к PCA. Помните, PCA — это метод снижения размерности, применяемый к многомерным наборам данных. SSA реконструирует одномерный временной ряд в структуру, напоминающую многомерный набор данных. Это делается путем расположения разделов серии в рядах одинакового размера. Здесь размер ряда определяется параметром длины окна.

Рассмотрим временной ряд Y=[y1 ,y2 ,y3 ,y4 ,y5 ,y6 ] с длиной N=6. Если выбрана длина окна L=3, то получится матрица траектории, эквивалентная приведенной ниже.

Количество рядов R в матрице рассчитывается как R=N−L+1. В данном примере: R=6−3+1=4. Эта матрица размером R×L (в нашем примере 4×3) является матрицей траекторий. Паттерны, наблюдаемые на антидиагоналях этой матрицы, характерны для матрицы Ханкеля. Построение матрицы траекторий является первым шагом метода SSA. Поэтому неудивительно, что длина окна является определяющим параметром метода SSA, поскольку она напрямую определяет размеры матрицы траекторий, что, в свою очередь, существенно влияет на разрешение и разделимость спектрального разложения.

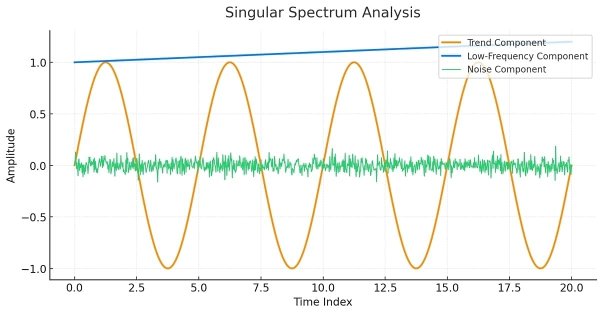
Чтобы пояснить концепции методологии SSA, мы продемонстрируем ее применение к изображенному ниже детерминированному ряду.

Этот ряд был построен из заранее определенных аддитивных компонентов, состоящих из тренда, пары периодических компонентов и случайного шума. При сложении этих компонентов получается несколько нетипичный ряд. Целью SSA является выявление этих базовых компонентов. Это делается путем разложения либо матрицы траекторий, либо ковариационной матрицы матрицы траектории, в результате чего собственные моды, как и в PCA, раскрывают главные компоненты ряда.

Относительные и кумулятивные вклады компонентов

Векторный метод MQL5, SingularSpectrumAnalysisSpectrum(), выводит вектор, представляющий относительные вклады компонентов ряда. Этот вектор содержит действительные числа, сумма которых равна единице, что указывает на дробное доминирование каждого компонента, расположенного в порядке убывания. Эти вклады соответствуют относительным величинам собственных значений, рассчитанных путем разложения матрицы.

//---
   vector relative_contributions;
   if(!full_process.SingularSpectrumAnalysisSpectrum(WindowLen,relative_contributions))
     {
      Print(" error ", GetLastError());
      return;
     }
//---
   relative_contributions*=100.0;
   vector cumulative_contributions = relative_contributions.CumSum();

При подсчете совокупной суммы относительных вкладов получаем кумулятивные вклады. Эти значения позволяют нам быстро определить наименьшее количество компонентов, необходимое для достижения относительно близкого приближения к исходному ряду. График относительных вкладов часто демонстрирует четкие приблизительные плато, что позволяет предположить, что вклады некоторых компонентов имеют схожую величину. Это сходство обычно указывает на то, что эти компоненты могут представлять собой один периодический элемент.

Ниже приведены графики относительного и кумулятивного вклада для нашего примера.

Они показывают, что первые два компонента обеспечивают около 68% и 12% общей дисперсии в ряду.

Только первые пять компонентов составляют более 98%. График относительных вкладов образует уникальную форму, демонстрирующую доминирование первых 5 компонентов. Точка, которая отделяет доминирующие компоненты от остальных, обычно называется «точкой изгиба», а компоненты ниже этого уровня называются «уровнем шума». Она дает грубую оценку разделения сигнала и шума. Еще одним примечательным аспектом графика относительных вкладов является то, как компоненты номер два и три сгруппированы вместе вдали от четвертого и пятого компонентов. Это указывает на то, что данные парные группы связаны между собой и могут представлять собой уникальные особенности ряда.

Извлечение компонентов рядов

Проанализировав нашу серию примеров, мы имеем представление об основных компонентах, определяющих большую часть ее поведения. Для оценки их регулярности может быть полезно визуализировать эти компоненты. Здесь оказывается нужным векторный метод SingularSpectrumAnalysisReconstructComponents(). Особый интерес представляет собой матрица рядов компонентов. Однако следует помнить, что, хотя в документации MQL5 предполагается, что столбцы представляют собой оценочные ряды компонентов, метод на самом деле сохраняет каждый ряд компонентов как ряд в матрице. Кроме того, векторный вывод метода содержит необработанные собственные значения разложения репрезентативной матрицы ряда.

//---
   matrix components;
   vector eigvalues;
   if(!full_process.SingularSpectrumAnalysisReconstructComponents(WindowLen,components,eigvalues))
     {
      Print(" error ", GetLastError());
      return;
     }
//---

Строки матрицы рядов компонентов расположены в порядке убывания относительной величины вклада. Следовательно, первая строка содержит компонент, соответствующий наибольшему собственному значению, который также представляет собой компонент с наибольшим относительным вкладом. Ниже представлен график, на котором показаны все компоненты нашего примера серии.

Если сравнить его с графиком исходных компонентов, можно заметить некоторые несоответствия. Это подчеркивает тот факт, что декомпозиция SSA не является точной. Этот метод никогда не сможет точно расшифровать периодические компоненты ряда. Все, что он может сделать - найти оптимальные приближения или оценки этих компонентов. Тем не менее, суммирование рядов отдельных компонентов приведет к получению исходного ряда.

Фильтрация

Имея в своем распоряжении набор рядов компонентов, можно использовать полученную в результате анализа SSA информацию, чтобы определить, какие компоненты описывают основной сигнал, а какие представляют собой недетерминированный шум. Если нашей основной задачей являются доминирующие циклы, можно отбросить компоненты с меньшим относительным вкладом, чтобы получить отфильтрованный ряд. Поступая таким образом, мы предполагаем, что эти меньшие компоненты представляют собой шум, затемняющий основной сигнал.

Пользователи могут выполнять эту фильтрацию непосредственно по ряду с помощью метода SingularSpectrumAnalysisReconstructSeries(). Пользователь указывает количество доминирующих компонентов, которые будут включены в отфильтрованный ряд.

//---
   vector filtered;
   if(!full_process.SingularSpectrumAnalysisReconstructSeries(WindowLen,FilterComponents,filtered))
     {
      Print(" error ", GetLastError());
      return;
     }

Метод SSA, как правило, позволяет эффективно изолировать шум, но его эффективность зависит от характера шума, присутствующего в процессе. Простого удаления компонентов с меньшим относительным вкладом может оказаться недостаточно для окончательного устранения шума. Следовательно, это также оказывает влияние на извлечение сигналов, тенденций или конкретных периодических компонентов. Интерпретация этих компонентов часто нуждается в проверке с помощью статистических тестов на значимость. Другой аспект, который может повлиять на изоляцию конкретных компонентов, связан с наличием сильных трендов, доминирование которых может маскировать другие низкочастотные колебания в данных.

Прогнозирование

Одним из наиболее интересных аспектов методологии SSA является ее применение для прогнозирования. Эта функциональность обеспечивается методом SingularSpectrumAnalysisForecast(). После декомпозиции и реконструкции временного ряда на этапе прогнозирования обычно используется алгоритм рекуррентного прогнозирования. Этот алгоритм использует присущее ему линейное рекуррентное соотношение (Linear Recurrent Relation, LRR), которому часто удовлетворяют реконструированные компоненты. Предполагается, что эти реконструированные компоненты следуют предсказуемому паттерну. На основе сингулярных векторов и реконструированного ряда определяется набор коэффициентов. Эти коэффициенты представляют собой линейную зависимость между прошлыми и будущими значениями в восстановленном сигнале. Для прогнозирования новой точки данных алгоритм применяет линейную комбинацию предыдущих значений «длины окна» реконструированного ряда, взвешенных по определенным коэффициентам. Затем этот процесс повторяется итеративно для создания множества прогнозов.

//---
   vector forecast;
   if(!full_process.SingularSpectrumAnalysisForecast(WindowLen,FilterComponents,ForecastLen,forecast))
     {
      Print(" error ", GetLastError());
      return;
     }
//---

Должно быть очевидно, что такие прогнозы предполагают, что предыдущие паттерны проявятся в будущем точно так же, как они проявлялись в прошлом. Конечно, это вряд ли справедливо для реальных временных рядов. Несмотря на это, SSA может быть полезен для повышения предсказуемости сложных процессов за счет концентрации внимания на определенных компонентах с обычными формами сигналов.

Выбор и предварительная обработка параметров

Уже установлено, что разложение ряда с помощью SSA никогда не сможет извлечь точные периодические компоненты временного ряда. Все, что он может сделать — извлечь оценки компонентов. Это очевидное ограничение метода, которое еще больше усугубляется чувствительностью метода к выбранной длине окна. Выбор правильной длины окна может определяться целями декомпозиции. Если интерес в первую очередь заключается в выделении тренда, то чем больше длина окна, тем лучше. Однако если колебательные компоненты имеют большее значение, специалистам следует учитывать периоды колебаний; например, если ищется периодический компонент, который колеблется с периодом 20, то установите длину окна равной 20.

По-видимому, представленные в научной литературе эмпирические данные указывают на то, что длина окна соответствует разрешению колебаний с периодами в диапазоне от L/5 до L, где L — длина окна. Проблема в том, что период интересующего компонента может быть заранее неизвестен, поэтому необходимо множество проб и ошибок. Общее практическое правило заключается в том, чтобы установить длину окна в диапазоне от двух до половины длины изучаемого ряда. Большая длина окна усиливает медленно меняющиеся компоненты, тогда как меньшая длина окна улавливает более мелкие детали.

Помимо чувствительности SSA к длине окна, специалисты также должны знать, как сильные тенденции, присутствующие во временных рядах, могут повлиять на результаты разложения. Сильные тренды могут маскировать другие низкочастотные компоненты в ряду. Эту проблему можно решить, в первую очередь, путем исключения тренда из исходного ряда перед применением SSA. Типы предварительной обработки, которые можно применять, включают центрирование или удаление линейного тренда, как показано во фрагменте кода ниже.

//---
   if(m_detrend)
     {
      vector reg = m_buffer.LinearRegression();
      m_buffer -= reg;
     }
//---

Когда дело доходит до принятия решения о том, сколько компонентов следует выбрать при фильтрации или прогнозировании, большую помощь могут оказать графики относительных и кумулятивных вкладов. На графике относительных вкладов следует выделить точку «изгиба», которая отличает сигнал от шума. Точки на графике, соответствующие сигналу, будут отображаться выше четкого разрыва точек, значения которых медленно уменьшаются до нуля. То же самое должно быть заметно при исследовании распада исходных собственных значений процесса разложения. Другой приемлемый вариант — указать целевой показатель общего процента охватываемой дисперсии (обычно от 85% до 95%), а затем получить количество компонентов, которым соответствует это значение, в ряду кумулятивных вкладов.

Группировка компонентов

Мы знаем, что разложение SSA не сможет волшебным образом воспроизвести точные базовые компоненты ряда; мы видели это на простом примере. В результате мы получаем набор компонентов, которые аппроксимируют фактический составной ряд. Нам нужно только выяснить, как объединить наши оценки, чтобы получить более полную картину фактических элементов, определяющих процесс. Этого можно достичь путем построения взвешенной корреляционной матрицы ряда компонентов. Взвешенная корреляционная матрица измеряет, насколько пара компонентных рядов отличается от идеальной перпендикулярности. Если пара компонентов рядов идеально прямоугольна, то они, скорее всего, являются различными компонентами.

Более высокие значения корреляции указывают на то, что пару следует объединить. Фрагмент кода ниже иллюстрирует процедуру, которая вычисляет взвешенную корреляционную матрицу с учетом матрицы ряда компонентов и параметра длины окна разложения SSA. Функция объявлена в файле ssa.mqh, приложенном к статье. 

//+------------------------------------------------------------------+
//| component correlations                                           |
//+------------------------------------------------------------------+
matrix component_corr(ulong windowlen,matrix &components)
  {
   double w[];
   ulong fsize = components.Cols();
   ulong r = fsize - windowlen + 1;
  
   for(ulong i = 0; i<fsize; i++)
     {
      if(i>=0 && i<=windowlen-1)
         w.Push(i+1);
      else
         if(i>=windowlen && i<=r-1)
            w.Push(windowlen);
         else
            if(i>=r && i<=fsize-1)
               w.Push(fsize-i);
     }

   vector weights;
   weights.Assign(w);
   ulong d = windowlen;

   vector norms(d);
   matrix out = matrix::Identity(d,d);

   for(ulong i = 0; i<d; i++)
     {
      norms[i] = weights.Dot(pow(components.Row(i),2.0));
      norms[i] = pow(norms[i],-0.5);
     }

   for(ulong i = 0; i<d; i++)
     {
      for(ulong j = i+1; j<d; j++)
        {
         out[i][j] = MathAbs(weights.Dot(components.Row(i)*components.Row(j))*norms[i]*norms[j]);
         out[j][i] = out[i][j];
        }
     }

   return out;
  }

Ниже показан фрагмент корреляций компонентов, составляющих шесть верхних компонентов ряда, служащего нашим примером.

На графике показана высокая корреляция между компонентами с индексом (1:2), что соответствует взаимосвязи компонентов 2 и 3, в то время как компоненты, указанные с индексом (3:4), относятся к взаимосвязи между компонентами 4 и 5. По-видимому, этот анализ согласуется с визуальным обзором рассмотренного ранее графика относительных вкладов. Исходя из этого, мы могли бы выдвинуть гипотезу, что две группы компонентов могут указывать на периодические компоненты рядов из нашего примера. Единственный самый верхний компонент является отчетливым и, вероятно, является трендом. Как мы уже видели из кумулятивных взносов, на эти 5 компонентов приходится 98% взносов; следовательно, остальное, скорее всего, является шумом.

Обзор разложения ценовых рядов

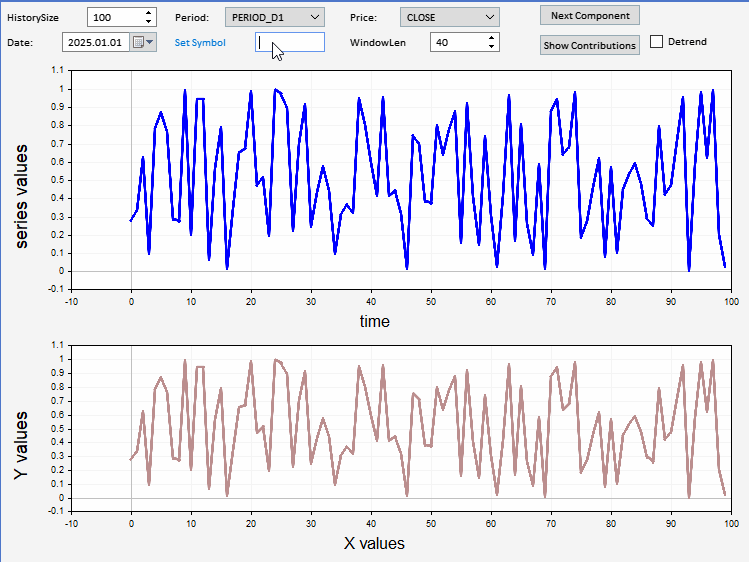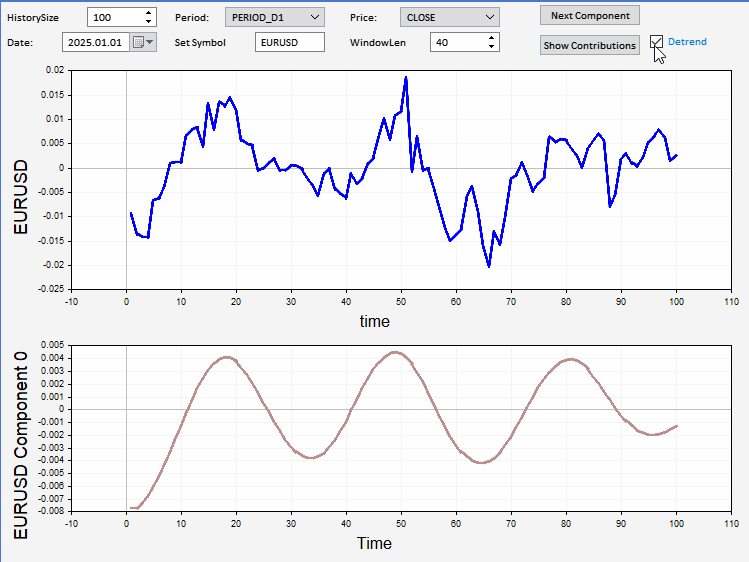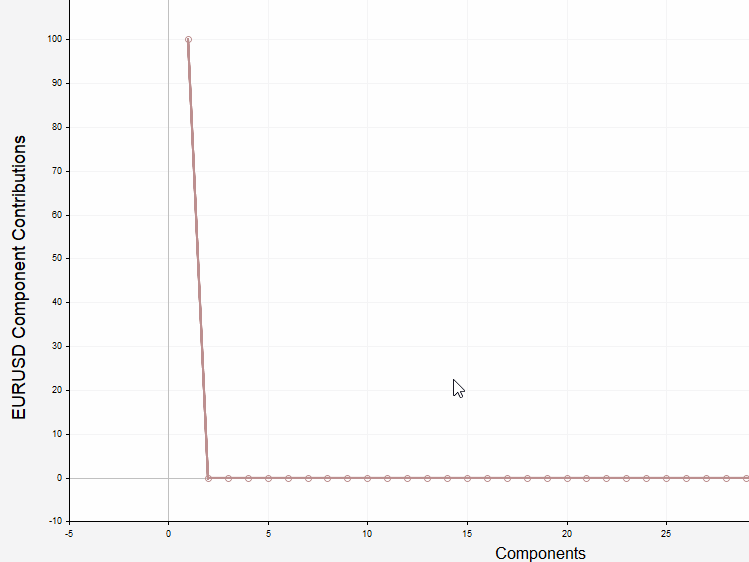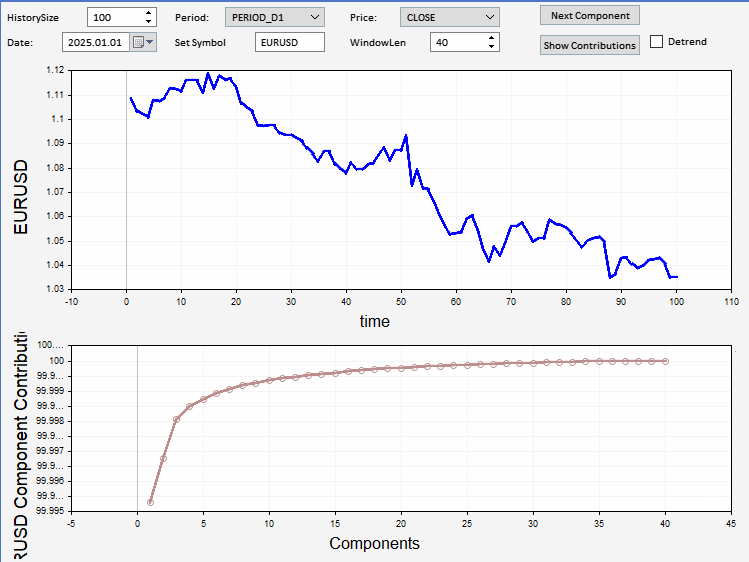
В данном разделе представляем реализованное в виде советника приложение, которое можно использовать для просмотра компонентов произвольной выборки цен. Приложение имеет графический пользовательский интерфейс, позволяющий пользователям устанавливать символ, дату и длину ценового ряда для отображения и разложения. Перед разложением ряда имеется возможность исключить его из тренда. При желании можно также просмотреть графики относительного и кумулятивного вклада. Ниже представлен скриншот приложения, отображающего выборку цен закрытия EURUSD, с разложенным компонентом, показанным на графике внизу.

Заключение

В настоящей статье рассматриваются новые инструменты на MQL5 для сингулярного спектрального анализа (SSA). Особое внимание уделяется дополнениям OpenBLAS к векторному типу данных. Мы представили краткий обзор метода SSA, намеренно избегая подробных математических объяснений. Подводя итог, SSA является ценным инструментом для любого практикующего специалиста, но для его полной эффективности требуется тщательный выбор параметров и понимание нюансов его работы. Весь код, на который даны ссылки, включен и прикреплен ниже. 

Название файла	Описание файла
MQL5/include/ssa.mqh	Этот заголовочный файл содержит определение функции, реализующей корреляции компонентов расчета, описанные в разделе "Группировка компонентов".
MQL5/scripts/SSA_Filtered_Demo.mq5	Это скрипт, используемый для демонстрации фильтрации с помощью SSA.
MQL5/scripts/SSA_Decomposition_Demo.mq5	Это скрипт, используемый для демонстрации разложения ряда с помощью SSA.
MQL5/scripts/SSA_ComponentContributions_Demo.mq5	Это скрипт, используемый для демонстрации отображения относительных вкладов компонентов.
MQL5/scripts/SeriesPlot.mq5	Этот скрипт использован для графического представления различных упомянутых в статье компонентов рядов, послуживших примерами.
MQL5/experts/SSA_PriceDecomposition.ex5	Данный советник представляет собой программу, которую можно использовать для отображения разложения произвольного ценового ряда.
MQL5/experts/SSA_PriceDecomposition.mq5	Это исходный код для указанного выше советника.