Разложение по динамическим модам в применении к одномерным временным рядам в языке MQL5

MetaTrader 5 — Статистика и анализ | 25 ноября 2025, 12:58

393

Francis Dube

Введение

Разложение по динамическим модам (DMD) — метод, который используется для анализа сложных динамических систем. Инженеры используют его при анализе потока жидкости для извлечения пространственно-временных структур из сложных наборов данных. DMD действует посредством разбиения данных системы на более простые представления, которые называют модами. Каждая мода представляет собой отдельную пространственную модель со своей собственной частотой колебаний и скоростью роста или затухания. Это позволяет инженерам анализировать динамику, находящуюся в основе жидкостной системы, без необходимости решать зачастую сложные основные уравнения.

Пространственно-временные структуры — это модели, которые сохраняют свою форму и идентичность во времени и пространстве. Представьте себе кольцо дыма, плывущее по воздуху. Кольцо дыма представляет собой структуру, сохраняющую свою форму, которая движется как единое целое, даже если воздух вокруг него приходит в турбулентное движение.

Инженеры используют такие методы, как DMD, для определения и анализа таких структур внутри сложных потоков жидкости. В этой статье мы рассмотрим реализацию метода DMD в MetaTrader 5. С помощью практической демонстрации кодов читатели научатся использовать новый матричный метод DynamicModeDecomposition(). Обсудим его входные данные, а также представим основные утилиты кода, необходимые для обработки его выходных данных.

Алгоритм DMD

Алгоритм разложения по динамическим модам был разработан для расчетов динамики жидкостей Петером Шмидом и Йорном Сестерхенном. По своей сути DMD представляет собой метод снижения размерности, который также позволяет выявлять колебания, присутствующие в данных. Это похоже на метод анализа главных компонент в сочетании с преобразованием Фурье для обнаружения сигналов. Одним из главных преимуществ метода является тот факт, что он не делает никаких предположений относительно изучаемого набора данных. Он работает с нестационарными временными рядами, а современные вариации могут даже обрабатывать данные, собранные в неравномерные моменты времени. Основное требование к DMD — сама структура данных: рекомендуется обеспечить достаточную многомерность набора данных.

Метод опирается на серию «моментальных снимков» динамической системы, которые собираются с течением времени. Эти моментальные снимки, которые могут содержать любые относящиеся к системе данные, организованы в матрицу, где каждый столбец соответствует определенному моменту времени.

Матрица X моментальных снимков

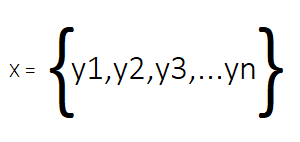
Столбцы этой матрицы, которую мы будем называть X, представляют собой моментальные снимки системы. При практическом применении наборы данных DMD часто являются многомерными, то есть в каждый момент времени происходит сбор сотен и даже тысяч измеренных переменных. В результате получается матрица, в которой строк (переменных или признаков) больше, чем столбцов (моментальных снимков).

Матрица X1 исходных снимков

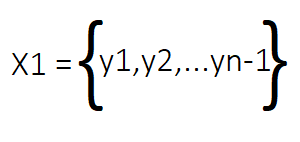
Из имеющейся матрицы X мы выводим две новые матрицы: X1 и X2. Вместе две эти матрицы представляют собой прогрессию динамической системы во времени. Матрица X1 содержит все столбцы матрицы X, за исключением последнего, который представляет состояние системы на начальных временных интервалах. Напротив, матрица X2 содержит все столбцы матрицы X со второго до последнего, представляя состояние системы на последующих временных шагах.

Матрица X2 последующих снимков

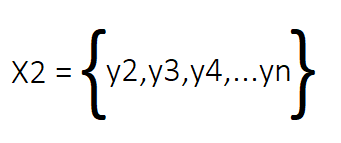
Математической основой DMD является предполагаемая связь между матрицами X1 и X2, а именно: что существует такая матрица A, чтобы AX1 могла в достаточной степени аппроксимировать матрицу X2. Целью DMD является определение собственной структуры матрицы A без необходимости вычислять в явном виде саму эту матрицу.

Для достижения этой цели DMD использует процедуру, подобную процедуре Рейли-Ритца. Это стандартный метод линейной алгебры для аппроксимации собственных значений и собственных векторов большой матрицы. Метод работает посредством проецирования задачи на подпространство меньшего размера, которое тщательно отбирается на основе данных. В DMD это подпространство представляет собой часть пространства столбцов матрицы данных X1. Обычно он строится с помощью ведущих левых сингулярных векторов матрицы X1, которые обнаруживаются посредством разложения по сингулярным значениям (Singular Value Decomposition, SVD).

Алгоритм образуем приближение A, используя матрицу данных X2 и результаты SVD матрицы X1. Усечение ранга представлено ниже как k.

Это приближение операторной матрицы A представляет собой матрицу DMD или отношение Рейли. Собственные значения этой меньшей матрицы называются значениями Ритца или собственными значениями DMD, а их соответствующие собственные векторы используются для вычисления векторов Ритца или проектируемых мод DMD.

Значения и векторы Ритца образуют пары Ритца, представляющие собой разложение набора данных по динамическим модам. Моды обеспечивают низкоранговую аппроксимацию динамики системы на основе данных.

Качество этого приближения непосредственно соединяется с выбором подпространства, которое в DMD неразрывно связано с данными моментального снимка. Моды DMD описывают закономерности, которые развиваются во времени в соответствии с собственными значениями DMD, то есть моды представляют собой структуры, а собственные значения определяются, как эти структуры развиваются в определенный момент времени.

Временную эволюцию моды можно визуализировать, вычислив её динамику. А это, в свою очередь, требует вычисления амплитуды моды. Амплитуды служат начальными весами или коэффициентами, которые показывают, какой вклад каждая мода вносит в начальное состояние системы и её общую эволюцию. Мода с большой амплитудой является доминирующей характеристикой динамики системы, тогда как мода с малой амплитудой оказывает меньшее влияние на характеристики. Объединяя моды, собственные значения и амплитуды, DMD может построить приближение системы. Кроме того, эту реконструированную модель можно экстраполировать вперёд во времени, чтобы обеспечить прогнозы будущего системы.

Встраивание с задержкой во времени

Наряду с классическим алгоритмом DMD существуют другие вариации, каждая из которых разработана для обеспечения деятельности определенных типов наборов данных и вариантов использования. Большинство из них отличаются от классического DMD посредством включения процедур предварительной или последующей обработки для повышения качества основного метода. Например, встраивание с задержкой во времени — это метод, который используется для расширения пространства состояний системы, что делает ее более подходящей для анализа с помощью DMD.

Стандартный метод DMD предполагает, что динамику системы можно линейно аппроксимировать от одного моментального снимка к другому. Такое предположение можно разбить для систем с сильной нелинейностью или для данных с небольшим количеством пространственных переменных (строк). Встраивая прошлые наблюдения в вектор текущего состояния, координаты задержки могут раскрывать сложную динамику. Это позволяет применять линейное приближение, подобное используемому в DMD, чтобы отразить основные особенности нелинейной или хаотической системы. Это подразумевает, что сферу применения DMD можно расширить, включив в него наборы данных, которые могут быть недостаточно многомерными.

Идея заключается в создании дополненной матрицы данных. Вместо использования на каждом временном этапе одного моментального снимка мы создаем новый вектор «состояния», который включает в себя текущий снимок и ряд прошлых снимков, каждый из которых задержан на определенный временной интервал или промежуток. Это похоже на построение матрицы траектории при анализе сингулярных спектров (Singular Spectrum Analysis). Приведенный ниже код определяет функцию time_delay_embedding(), которую можно использовать для применения к матрице встраиваний с задержкой во времени.

//+------------------------------------------------------------------+
//|  pseudo hankelization                                            |
//+------------------------------------------------------------------+
matrix time_delay_embedding(matrix &data, ulong delay=2)
  {

   if(delay>=data.Cols() || delay<1)
     {
      Print(__FUNCTION__, " invalid input parameters ");
      return matrix::Zeros(0,0);
     }

   ulong rows = data.Rows();
   matrix matrices;

   matrix out(rows*delay,data.Cols()-(delay-1));

   for(ulong i = 0; i<delay; i++)
     {
      matrices = np::sliceMatrixCols(data,long(i),long(i+data.Cols()-(delay-1)));
      if(!np::matrixCopyRows(out,matrices,long(i*rows),long((i*rows)+matrices.Rows())))
        {
         Print(__FUNCTION__, " failed copy operation ");
         return matrix::Zeros(0,0);
        }
     }

   return out;

Функцию time_delay_reconstruction() можно использовать на результатах реконструкции методом DMD или прогнозов для набора данных, предварительно обработанного с применением встраиваний с задержкой по времени, что позволяет вернуться к исходной форме набора данных.

//+------------------------------------------------------------------+
//| rebuild original shape of data after augmentation                |
//+------------------------------------------------------------------+
matrix time_delay_reconstruction(matrix &data, ulong delay)
  {

   ulong rows = data.Rows();
   ulong cols = data.Cols();

   if(rows<delay)
     {
      Print(__FUNCTION__," invalid inputs");
      return data;
     }

   matrix out(rows/delay,cols + delay - 1);

   matrix splitted[];

   ulong splits = data.Hsplit(delay,splitted);

   for(ulong i = 0; i<splits; i++)
      if(!np::matrixCopyCols(out,splitted[i],long(i),long(i+cols)))
        {
         Print(__FUNCTION__, " failed copy operation ");
         return data;
        }

   return out;
  }

Независимо от используемой вариации DMD, все они в конечном итоге производят схожие выходные данные: собственные значения DMD, моды DMD и амплитуды DMD. Суть DMD-анализа состоит в том, чтобы интерпретировать эти выходные данные, в частности — собственных значений DMD. Лучшим способом продемонстрировать способы интерпретации результатов работы DMD является использование примера, а для этого нужно углубиться в код.

DMD на языке MQL5

Расширение поддержки процедур OpenBIAS в MetaTrader привело к появлению двух методов, которые реализуют подход DMD. Первый из них, DynamicModeDecomposition(), реализует стандартный алгоритм DMD, основанный на SVD, а второй, DynamicModeDecompositionQR(), использует реализацию на основе разложения QR-матрицы. В этом тексте основное внимание будет уделено версии на основе SVD. Обсудим этот метод, разложив вымышленный ряд, который описан в следующем фрагменте кода.

//+------------------------------------------------------------------+
//| univariate process                                               |
//+------------------------------------------------------------------+
vector f(vector &in)
  {
   return cos(in)*sin(cos(in))*cos(in*0.2);
  }

Код описывает ряд, который является произведением трех отдельных колебательных компонентов, что приводит к сложной волне с переменной амплитудой и частотой.

Пример ряда

Сочетание этих трех компонентов создает сложный рисунок, который является периодическим, а не простым гармоническим. Быстрые колебания от cos(x)*sin(cos(x)) «растягиваются» и «сжимаются» более медленным элементом cos(0.2*x), что приводит к сложной осциллограмме, показанной на графике. Разложение этого ряда выполняется в скрипте DMD_Demo.mq5. Для этого начинается подготовка ряда к разложению посредством помещения его в подходящий контейнер.

//+------------------------------------------------------------------+
//|                                                     DMD_Demo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
//---
#include<np.mqh>
#include<cmath.mqh>
//---
input ENUM_DMD_SCALE jobs = DMDSCALE_N;
input ENUM_DMD_EIGV jobz = DMDEIGV_V;
input ENUM_DMD_RESIDUALS jobr = DMDRESIDUALS_R;
input ENUM_DMD_REFINE jobf = DMDREFINE_R;
input ENUM_SVD_ALG whtsvd = SVDALG_1;
input long nrnk = -1;
input double tol_ = 1.e-9;//tol
input ulong Delay = 50;//apply time delay embedding
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   ulong series_len = 100;
   double dt = 0.1010101;
   double first_time_point = 0.0;
   vector t = np::arange(series_len,first_time_point,dt);
   vector F = f(t);
   matrix X(1,series_len);
   X.Row(F,0);

Функция DynamicModeDecomposition() в языке MQL5 — это матричный метод, который возвращает логическое значение, указывающее на успех или неудачу при выполнении разложения. Если судить по документации, у метода есть несколько обязательных входных данных, некоторые из которых следует тщательно отбирать, поскольку они оказывают значительное влияние на конечные результаты. Далее следует обсуждение параметров метода DynamicModeDecomposition().

//---
   if(Delay)
      X = time_delay_embedding(X,Delay);
//---
   Print("X shape is ", X.Rows(),":",X.Cols());
//---
   matrix X1 = np::sliceMatrixCols(X,0,X.Cols()-1);
   matrix X2 = np::sliceMatrixCols(X,1);
//---
   vectorc eigen_values;
   matrix W;
   matrix B;
   vector residuals;
   matrix left_vectors;
   matrix res_vectors;
   matrix Z,S;

   if(!X1.DynamicModeDecomposition(X2,jobs,jobz,jobr,jobf,whtsvd,nrnk,tol_,eigen_values,left_vectors,Z,residuals,res_vectors,B,W,S))
     {
      Print(" DMD error ",GetLastError());
      return;

Начиная с самих матриц, метод DynamicModeDecomposition() требует в качестве входных параметров две матрицы. Первой будет матрица начальных снимков, на которой будет вызываться метод. Матрица последующих снимков передается методу в качестве первого параметра. Единственное требование к матрицам — они должны быть в достаточной степени многомерными. Метод предполагает «высокие» или «тонкие» матрицы. Если в какой-то из матриц количество столбцов превышает количество строк, во время выполнения возникнет ошибка. Когда дело дойдет до применения внедрения с временной задержкой, это должно привести к получению расширенной матрицы, имеющей подходящую форму. Размерность внедрения определяет количество строк для расширенной матрицы.

Рассмотрим наш пример, который при преобразовании в матрицу имеет одну строку и 100 столбцов или мгновенных снимков. Применение внедрения с задержкой по времени с размерностью 50 создает расширенную матрицу с 50 строками (исходное количество столбцов × размерность внедрения) и 51 столбцами (исходное количество столбцов - размерность внедрения + 1). Выбор подходящего внедрения с задержкой по времени представляет собой компромисс между увеличением пространства состояний и обеспечением количества оставшихся моментальных снимков, достаточного для эффективного анализа.

input ENUM_DMD_SCALE jobs = DMDSCALE_N

Вторым параметром DynamicModeDecomposition() является перечисление, которое определяет встроенный шаг предварительной обработки. Оно позволяет выбирать процедуру масштабирования, которую нужно применять к данным. Существует четыре опции, включая вариант без масштабирования. Приведя все столбцы к одному и тому же масштабу, алгоритм снижает вероятность, что над ним будут доминировать несколько столбцов с очень большими нормами, в результате чего вычисления могут стать более сбалансированными и численно устойчивыми. Это гарантирует, что каждый моментальный снимок вносит равный вклад в общую динамику, предотвращая смещение результатов в сторону нескольких событий высокой значимости. Таким образом, алгоритм может идентифицировать моды, которые актуальны для всего временного ряда, даже те, которые связаны с явлениями меньшего масштаба.

input ENUM_SVD_ALG whtsvd = SVDALG_1;

Параметр whtsvd — это перечисление ENUM_SVD_ALG, представляющие четыре реализации SVD, которые пользователь может указать для процедуры DMD. Реализации SVD различаются с точки зрения точности и могут оказывать влияние на конечные результаты.

input long nrnk = -1;

Параметр nrnk можно использовать для явного определения подпространства столбцов, которое ляжет в основу редуцированной модели. Его можно указать в виде положительного значения, которое должно быть меньше или равно количеству столбцов в наборе данных. Другой вариант предусматривает возможность установить этот параметр на -1 или -2, что применяет основанный на данных подход к усечению ранга с помощью параметра tol.

input double tol_ = 1.e-9;//tol

Допуск — это пороговое значение, которое накладывается на сингулярные значения из операции SVD для определения оптимального ранга набора данных. Остальные входные параметры метода относятся к результатам операции. Обсудим их, когда будем рассматривать результаты разложения. После того как будут определены все параметры, мы сможем запустить программу и наблюдать результаты, начиная с собственных значений DMD.

Анализ собственных значений

Собственные значения DMD, или значения Рица, возвращаются в векторном параметре eigen_values. Собственные значения определяют временные характеристики системы. Это комплексные числа, которые кодируют общую тенденцию соответствующей моды. Количество собственных значений эквивалентно рангу модели сниженного порядка, которую рассчитывает DMD. Мнимая часть собственного значения отображает частоту колебаний, тогда как действительная его часть определяет устойчивость моды.

Выводы относительно устойчивости моды можно сделать, оценив величину ее собственного значения:

Величина > 1: мода нестабильна и возрастает с течением времени.
Величина < 1: мода считается устойчивой, даже если имеются признаки распада.
Величина = 1: мода устойчива, а ее колебания происходят без возрастания или затухания. Это характерно для чисто колебательного или стационарного поведения.

Другой способ оценки устойчивости мод — использовать построение графика значений Рица на плоскости комплексной переменной. Суть этой визуализации — определить, где находятся собственные значения относительно единичной окружности. Нам нужны действительно устойчивые моды, поскольку это указывает на согласующиеся структуры или закономерности. У стабильных мод есть собственные значения, которые более или менее лежат на единичной окружности. Вот график собственных значений для нашего примера.

График собственных значений

Что касается частот, действительные колебания фиксируются как пары комплексно сопряжённых собственных значений. Одна комплексная экспонента не может описывать действительные данные, которые представляют собой комбинацию синусов и косинусов. В соответствии с формулой Эйлера для действительной функции требуется пара комплексных экспонент, поэтому DMD и производит сопряженные пары. Если взглянуть на наш набор синтетических данных, можно увидеть, что у функции есть несколько периодических компонентов. Поэтому ожидается, что DMD выведет несколько пар комплексно-сопряженных собственных значений, соответствующих этим колебаниям. Кроме того, мнимую часть собственных значений можно использовать для того, чтобы охарактеризовать компоненты, которые представляют соответствующие моды. Мнимые значения, близкие к нулю, отображают тенденции или медленно изменяющиеся компоненты.

IN      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      DMD eigenvalues or Ritz values
NF      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.5094085277495803,0.8361736631055409)
MR      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.5094085277495803,-0.8361736631055409)
LH      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9997963823571733,0.02020000684364618)
IG      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9997963823571733,-0.02020000684364618)
CQ      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9835155147230954,0.1808172385894571)
DN      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9835155147230954,-0.1808172385894571)
RG      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9754097172453285,0.2203989043734001)
QS      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9754097172453285,-0.2203989043734001)
LL      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9272204223699192,0.3744766566706951)
CE      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9272204223699192,-0.3744766566706951)
MR      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9113505757240357,0.4116425317268657)
FO      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9113505757240357,-0.4116425317268657)
LH      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.8329207590629218,0.5528761024511968)
KP      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.8329207590629218,-0.5528761024511968)
KN      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.810278335748567,0.5863411580059696)
NI      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.810278335748567,-0.5863411580059696)
CP      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.6775746857433339,0.740515480806191)
JL      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.6775746857433339,-0.740515480806191)
JH      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.6991117585413807,0.7090540641602167)
QQ      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.6991117585413807,-0.7090540641602167)
CM      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      Eigenvalues shape - (20,)

Частоту генерирующей моды можно определить только в том случае, если известен интервал между моментами сбора данных снимков. Это то, что в методе DynamicModeDecomposition() не подчеркивается. Важен объем времени между последовательными снимками, потому что DMD вычисляет оператор дискретного времени, а время между снимками данных выполняет функцию моста, соединяющего дискретные результаты с базовой динамикой непрерывного времени системы. Без этого мы не сможем точно перевести собственные значения дискретного времени в значимые непрерывные по времени частоты и скорости роста или спада. Частоты и темпы рости или спада рассчитываются с использованием времени между моментальными снимками по следующим формулам.

Формула частоты

Формула темпа роста (спада)

Левые сингулярные векторы

Матрица, возвращаемая в параметре left_vectors, держит все левые сингулярные векторы из SVD исходных снимков в матрице X1. Столбцы матрицы left_vectors известны как моды собственного ортогонального разложения (Proper Orthogonal Decomposition, POD) набора данных. Это термин используется в технических областях и концептуально аналогичен понятию «главные компоненты» в статистике.

Left singular vectors -> left_vectors 
[[-0.2186571002130553,0.2532378192042484,-0.03145683319876429,-0.08784983133100939,0.3705873208513075,0.2206528031484838,0.1522505585095688,0.2508786634158028,0.4005453375455179,-0.2070914249820868,-0.256938973254042,0.1083123043478309,0.3743749436717269,-0.08325285604985129,0.2153162921311084,0.03514527602276374,0.2660964556173894,-0.02288502160553232,0.08420865568250724,-0.1244960454833032,-0.05915206418948179,0.1412740898453582,-0.06378450251683798,0.05225051446648973,0.04596520897629693,0.05533900119077329,-0.03035343487604242,0.01632904421933207,0.02488201223142909,0.009443994581533457,0.003233076671905151,-0.007000002498680975,-0.0003763343596269273,-0.002249960643275939,0.006083378336102527,0.002738028494735405,-0.003071412428518359,0.007630930463007241,0.0006780866248171729,-0.001537236018891231,0.001097628276266037,0.002549189417918068,-0.00121555935468654,0.0002914617225681344,-0.001329425380550676,-0.0008417462519557183,-0.0001925572219431676,0.0006672631970817051,1.658425254616608e-07,-0.003517246244801298]
,[-0.2120650337138182,0.2460711108749398,0.02614922665855949,-0.06095346519256405,0.316287819867838,0.1367332022924505,0.1608350411867044,0.08971817028514953,0.1591329520755127,0.016649392674401,-0.02435104895770137,-0.1166535735451681,-0.1350117043919009,0.1534878122543588,-0.2129032230923289,0.07705593536128043,-0.375021818402949,-0.07706813579203413,-0.1050339399444373,0.2860161516006371,0.08475158498594149,-0.3855235413551042,0.1862630616541108,-0.1991183017470892,-0.1509536720131326,-0.2375913171609213,0.1371371152602869,-0.0898699217072978,-0.1292195766965235,-0.06648667026234195,-0.01812981549697532,0.0417051043959161,0.009525456359058087,0.01011521692378288,-0.03803922672356531,-0.02106190474509607,0.01766810797476536,-0.04822406797849837,-0.003057210631146539,0.006231539022859201,-0.006288330102253714,-0.0156751476701437,0.009093777375705452,-0.003891906142160671,0.01113869460673238,0.005700478320541056,0.001323281173233992,-0.004963029289243439,0.002210166681645755,0.01885563684292829]
,[-0.2050754583292416,0.2276848333084614,0.08120826878905353,-0.0401725018668373,0.255713699260657,0.06031724967005543,0.1260872837922681,-0.05233055144856189,-0.02895470981613132,0.1414817752150981,0.1496548155010341,-0.1633919339675757,-0.2909072792943354,0.1170695606024898,-0.2104477264601786,-0.05761666740975601,-0.1642196356337907,0.09376106622320569,-0.09917019230808037,-0.0512314209072473,0.07533085329520638,0.2045397680225845,-0.1172476831676734,0.2373535055615748,0.1327391899523122,0.363322598165184,-0.2353759964165236,0.2001199525018012,0.2797917856739792,0.2087875622138012,0.03391328469051902,-0.1093628961879368,-0.04980659874835306,-0.009841138497083401,0.1071536601377198,0.07721338502591252,-0.04348696114962958,0.1359693579381065,0.005776723545380768,-0.00329638274325811,0.01197007184135679,0.04141926298403621,-0.03188888672341144,0.02029703016126579,-0.0411903406233533,-0.02103491458905859,-0.004064246582866178,0.01736432751085308,-0.01540381295312496,-0.04519633129179929]
,[-0.197864304332741,0.198939547987894,0.1313736616978487,-0.02558290784786304,0.1925995771445337,-0.006134276320507245,0.05852103373207649,-0.1566416078904816,-0.1489006796224137,0.1767605998850408,0.2187235587134117,-0.08102546015612813,-0.2025179789413045,-0.02467023236462294,0.007177707826474537,-0.1394599646494139,0.1774528338997285,0.1254318761473469,0.06991185536803274,-0.2322392434345509,-0.1022804195006251,0.2595084087385101,-0.1385151209344889,0.02231602330043558,0.08496345787013258,-0.1181672772615679,0.1251167503291135,-0.1942278207520568,-0.2798025229501522,-0.3656598349104803,0.01139657187065844,0.1552588902748942,0.1253960619854343,-0.03868294575932402,-0.1774709498310883,-0.172412195179344,0.05203395600508887,-0.2094389089818375,-0.004270301693629558,-0.03143829332941872,0.006497267040059443,-0.05389031613821053,0.06861563190685697,-0.0601060573479536,0.08699077151177441,0.05297098886227182,0.005414702197319015,-0.03549882813964893,0.05199258221374336,0.05778558739229585…]
Left singular vectors shape - (50,50)

Моды DMD

Спроецированные моды DMD, или векторы Ритца, возвращаются в выходной матрице Z. Параметр jobz — это перечисление ENUM_DMD_EIGV, которое используется для управления выходными данными, предоставляемыми в матрице Z. С его помощью пользователи могут решить не вычислять моды, если они не требуются. Рассмотрим моды, полученные в результате разложения нашего синтетического набора данных. Внимательные читатели заметят, что параметр Z представляет собой матрицу с вещественными элементами, хотя соответствующие собственные значения являются комплексными. Как это возможно? Оказывается, моды на самом деле являются комплексными. Метод DynamicModeDecomposition() возвращает комплексные значения в компактной форме.

KN      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      Z
MJ      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      [[-0.2115833899347683,0.04066707935807452,0.1309479910169292,-0.05340607539953211,-0.1311407627226479,-0.05294578413949149,0.1307327748372062,-0.05393554251234634,0.1300831102003118,0.05561343290756637,0.05476143012438625,0.1303708466035617,-0.0602971275669671,0.1290171409159042,0.1325833779653352,-0.0474567460410165,0.03953679964167294,0.1224969410523646,-0.08648845700023616,0.1302991571594397]
KL      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [-0.1410082298469801,-0.1561422002553993,0.1320001302525303,-0.05075005112167052,-0.1194054633670081,-0.07578550974758559,0.1394053542006602,-0.02379589291884476,0.09978976936668775,0.1002790127266047,-0.003759313795174276,0.1413556653516757,-0.1215537937113269,0.07412474322962503,0.1352548790995219,0.03928642939266112,-0.06394467904383667,0.1123039293425674,-0.1528368724559976,0.02980086078332629]
KE      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.0571288895384227,-0.1979205129165305,0.1329984050115342,-0.0480733131719782,-0.1037338006863208,-0.09612679258491226,0.1412219243613748,0.007514043825130007,0.05497499123596727,0.1303496653103515,-0.06161407873237246,0.1272770978516157,-0.1422252875452086,-0.00546499036287681,0.08655973711477287,0.1111375957285514,-0.1264360522083525,0.02869970692204134,-0.1280036213687715,-0.0876039346033588]
QM      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.1946438003924811,-0.0523269950779746,0.1339424057467836,-0.04537695566367969,-0.08464242182804624,-0.1132990516514234,0.1360931500665304,0.03845442944292374,0.002161029940774177,0.1414497110787759,-0.1085446923168975,0.09063109173113748,-0.1154409995132384,-0.08318535501859128,0.004972784147358847,0.1408055296621761,-0.1069381563322531,-0.07420079524911123,-0.02739821515064329,-0.1519997996523627]
MD      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.1442714745004026,0.1362363903857534,0.1348317466067521,-0.04266207939022894,-0.06276071186776834,-0.1267361823950489,0.1242712682729774,0.06750360361706979,-0.05096588923209126,0.1319643397659119,-0.1362298611687498,0.03791506074287562,-0.0501630100812688,-0.133110472474709,-0.07853144874233632,0.1170082970122646,-0.01755245167388933,-0.1294221063050899,0.08865106243357559,-0.1256351416263412]
FO      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [-0.03992077677928203,0.1893519332890936,0.1356660661019982,-0.03992979099864888,-0.03881004602829696,-0.1359952192100831,0.10633768314148,0.09323292091368418,-0.09667419061156554,0.1032745163734511,-0.139760607057441,-0.02152411345851591,0.0318114520997212,-0.1386035419997053,-0.1322392470005959,0.04876382240238289,0.08394555153666447,-0.1006538267573124,0.1510967437027885,-0.02495855075802432]
IE      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [-0.1796559181414814,0.06272269832359235,0.1364450246963949,-0.03718120464898366,-0.01358000327434823,-0.1407709344456745,0.08317437492830956,0.1143770068564059,-0.1283121621102718,0.05955600024366348,-0.1185106827077816,-0.07714740932760773,0.103127741913013,-0.09785844890997622,-0.1357422735154563,-0.03802553162801222,0.1314496877308521,-0.006061975670165805,0.123318478664932,0.08964429318551075]
ON      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [-0.145052625469143,-0.1177739752477081,0.1371683036826087,-0.03441744261256562,0.01209766591051641,-0.140905898452734,0.05592052522418876,0.1298959869971385,-0.1412759661384557,0.007171600964583176,-0.07624763897835488,-0.1190923437906344,0.1400016038285632,-0.02449262903763641,-0.08769262768666558,-0.1104036026020508,0.09357636250498216,0.09318079023848276,0.02260518070773477,0.1500697490161283]
OD      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.02477722278466908,-0.1806550663349361,0.1378356065274133,-0.03163963382212003,0.03737645720044752,-0.1363956708335061,0.02591649044609354,0.1390266308270787,-0.1336795590605116,-0.04625490379734653,-0.02046485321417844,-0.1399216409042799,0.1301514645240822,0.05700280745582626,-0.006321464342295452,-0.1408756808015346,-0.00561461203492375,0.1324202843066922,-0.09062222999370595,0.1209556314953582]
FO      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.1648424157584578,-0.07139540484283648,0.1384466607105591,-0.02884891198589165,0.06142301561190965,-0.1273889490658437,-0.005362119258359672,0.141319891110143,-0.1066290580133119,-0.09294834217094237,0.03894705870314489,-0.1359418964516609,0.0768895241650633,0.1194373735899043,0.0774784937512529,-0.1178541799925052,-0.1018942505428861,0.08561003773138477,-0.149086741625562,0.0203522730386399…]
ID      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      Z shape - (50,20)

Для каждой моды (столбца в матрице Z), если соответствующее собственное значение имеет ненулевую мнимую часть, мнимые значения находятся в следующем столбце матрицы Z. Кроме того, это предполагает существование другого собственного вектора, который представляет собой комплексно сопряженным элементом результирующего комплексного собственного вектора. В противном случае, если собственное значение не имеет мнимой части, соседний столбец связывает с другим собственным значением. Приведенный ниже код определяет вспомогательную функцию, которая называется compact_to_complex() и принимает в качестве входных данных контейнеры с действительными числами (комплексными числами в компактной форме), и вектор комплексных чисел, который действует как ключ для декодирования истинной формы комплексных чисел. Эта функция возвращает контейнер фактических комплексных чисел.

//+------------------------------------------------------------------+
//|process vector representing complex numbers in compact form       |
//+------------------------------------------------------------------+
vectorc compact_to_complex(vector& v,vectorc& bp)
  {
   vectorc v_out = vectorc::Zeros(v.Size());

   for(ulong i = 0; i<v.Size() && i<bp.Size();)
     {
      if(bp[i].imag)
        {
         v_out[i].real = v[i];
         if(i+1 < v.Size())
           {
            v_out[i].imag = v[i+1];
            v_out[i+1].real = v_out[i].real;
            v_out[i+1].imag = -1.0*v_out[i].imag;
            i+=2;
           }
        }
      else
        {
         v_out[i].real = v[i];
         i+=1;
        }
     }

   return v_out;
  }
//+------------------------------------------------------------------+
//| process matrix representing complex numbers in compact form      |
//+------------------------------------------------------------------+
matrixc compact_to_complex(matrix& m, vectorc& bp)
  {
   matrixc m_out = matrixc::Zeros(m.Rows(), m.Cols());

   for(ulong i = 0; i<m.Rows(); i++)
     {
      vector row = m.Row(i);
      vectorc row_c = compact_to_complex(row,bp);
      m_out.Row(row_c,i);
     }
   return m_out;
  }

Ниже мы можем увидеть разницу между модами в компактной форме и модами в их истинной комплексной форме.

CF      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      DMD modes or Ritz Vectors -> Z
PS      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      [[(-0.2115833899347683,0.04066707935807452),(-0.2115833899347683,-0.04066707935807452),(0.1309479910169292,-0.05340607539953211),(0.1309479910169292,0.05340607539953211),(-0.1311407627226479,-0.05294578413949149),(-0.1311407627226479,0.05294578413949149),(0.1307327748372062,-0.05393554251234634),(0.1307327748372062,0.05393554251234634),(0.1300831102003118,0.05561343290756637),(0.1300831102003118,-0.05561343290756637),(0.05476143012438625,0.1303708466035617),(0.05476143012438625,-0.1303708466035617),(-0.0602971275669671,0.1290171409159042),(-0.0602971275669671,-0.1290171409159042),(0.1325833779653352,-0.0474567460410165),(0.1325833779653352,0.0474567460410165),(0.03953679964167294,0.1224969410523646),(0.03953679964167294,-0.1224969410523646),(-0.08648845700023616,0.1302991571594397),(-0.08648845700023616,-0.1302991571594397)]
OO      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [(-0.1410082298469801,-0.1561422002553993),(-0.1410082298469801,0.1561422002553993),(0.1320001302525303,-0.05075005112167052),(0.1320001302525303,0.05075005112167052),(-0.1194054633670081,-0.07578550974758559),(-0.1194054633670081,0.07578550974758559),(0.1394053542006602,-0.02379589291884476),(0.1394053542006602,0.02379589291884476),(0.09978976936668775,0.1002790127266047),(0.09978976936668775,-0.1002790127266047),(-0.003759313795174276,0.1413556653516757),(-0.003759313795174276,-0.1413556653516757),(-0.1215537937113269,0.07412474322962503),(-0.1215537937113269,-0.07412474322962503),(0.1352548790995219,0.03928642939266112),(0.1352548790995219,-0.03928642939266112),(-0.06394467904383667,0.1123039293425674),(-0.06394467904383667,-0.1123039293425674),(-0.1528368724559976,0.02980086078332629),(-0.1528368724559976,-0.02980086078332629)]
MN      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [(0.0571288895384227,-0.1979205129165305),(0.0571288895384227,0.1979205129165305),(0.1329984050115342,-0.0480733131719782),(0.1329984050115342,0.0480733131719782),(-0.1037338006863208,-0.09612679258491226),(-0.1037338006863208,0.09612679258491226),(0.1412219243613748,0.007514043825130007),(0.1412219243613748,-0.007514043825130007),(0.05497499123596727,0.1303496653103515),(0.05497499123596727,-0.1303496653103515),(-0.06161407873237246,0.1272770978516157),(-0.06161407873237246,-0.1272770978516157),(-0.1422252875452086,-0.00546499036287681),(-0.1422252875452086,0.00546499036287681),(0.08655973711477287,0.1111375957285514),(0.08655973711477287,-0.1111375957285514),(-0.1264360522083525,0.02869970692204134),(-0.1264360522083525,-0.02869970692204134),(-0.1280036213687715,-0.0876039346033588),(-0.1280036213687715,0.0876039346033588)]
OI      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [(0.1946438003924811,-0.0523269950779746),(0.1946438003924811,0.0523269950779746),(0.1339424057467836,-0.04537695566367969),(0.1339424057467836,0.04537695566367969),(-0.08464242182804624,-0.1132990516514234),(-0.08464242182804624,0.1132990516514234),(0.1360931500665304,0.03845442944292374),(0.1360931500665304,-0.03845442944292374),(0.002161029940774177,0.1414497110787759),(0.002161029940774177,-0.1414497110787759),(-0.1085446923168975,0.09063109173113748),(-0.1085446923168975,-0.09063109173113748),(-0.1154409995132384,-0.08318535501859128),(-0.1154409995132384,0.08318535501859128),(0.004972784147358847,0.1408055296621761),(0.004972784147358847,-0.1408055296621761),(-0.1069381563322531,-0.07420079524911123),(-0.1069381563322531,0.07420079524911123),(-0.02739821515064329,-0.1519997996523627),(-0.02739821515064329,0.1519997996523627)]
CH      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [(0.1442714745004026,0.1362363903857534),(0.1442714745004026,-0.1362363903857534),(0.1348317466067521,-0.04266207939022894),(0.1348317466067521,0.04266207939022894),(-0.06276071186776834,-0.1267361823950489),(-0.06276071186776834,0.1267361823950489),(0.1242712682729774,0.06750360361706979),(0.1242712682729774,-0.06750360361706979),(-0.05096588923209126,0.1319643397659119),(-0.05096588923209126,-0.1319643397659119),(-0.1362298611687498,0.03791506074287562),(-0.1362298611687498,-0.03791506074287562),(-0.0501630100812688,-0.133110472474709),(-0.0501630100812688,0.133110472474709),(-0.07853144874233632,0.1170082970122646),(-0.07853144874233632,-0.1170082970122646),…]
KG      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      DMD modes or Ritz Vectors shape (50,20)

Остатки

Следующие два выходных параметра, residuals и res_vectors, связаны между собой. Каждое значение в векторе остатков является евклидовой нормой для соответствующего вектора (столбца) в матрице res_vectors. Остаточный вектор для каждого снимка данных представляет собой разницу между фактическим снимком и снимком, предсказанным моделью DMD. Это вектор ошибки для заданного шага времени. Нормы остаточных векторов, как правило, используют в качестве количественной меры погрешности. Говоря в общих чертах, чем они ближе к нулю, тем лучше модель.

CD      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      Residual norms -> residuals
FO      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      [0.008836676346169272,0.008836676346169272,9.235187494765224e-09,9.235187494765224e-09,1.742579533919419e-08,1.742579533919419e-08,1.653443663139743e-08,1.653443663139743e-08,2.597847624528849e-07,2.597847624528849e-07,2.320987987120818e-07,2.320987987120818e-07,9.788834713137558e-06,9.788834713137558e-06,8.123609086522145e-06,8.123609086522145e-06,0.0004010758671648529,0.0004010758671648529,0.0004371025994576595,0.0004371025994576595]
EN      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      Residuals shape - (20,)

Выходной параметр residuals представляет собой вектор действительных чисел, тогда как res_vectors — матрица комплексных чисел в компактной форме.

CD      0       20:54:02.690    DMD_univariate (AUDUSD,D1)      Residual vectors -> res_vectors
OR      0       20:54:02.690    DMD_univariate (AUDUSD,D1)      [[(0.0007788944957199118,6.210241253423732E-05),(0.0007788944957199118,-6.210241253423732E-05),(-5.316966866786288E-10,-4.560266955722092E-10),(-5.316966866786288E-10,4.560266955722092E-10),(9.00277352666734E-10,9.748073598325746E-10),(9.00277352666734E-10,-9.748073598325746E-10),(7.854966954656817E-10,-9.872156113421848E-10),(7.854966954656817E-10,9.872156113421848E-10),(-1.459522849800443E-08,1.377941803715199E-08),(-1.459522849800443E-08,-1.377941803715199E-08),(1.069276902784799E-08,-1.449544934084557E-08),(1.069276902784799E-08,1.449544934084557E-08),(-5.704307382975449E-07,5.291619083608312E-07),(-5.704307382975449E-07,-5.291619083608312E-07),(-4.031761563494385E-07,5.112246791380559E-07),(-4.031761563494385E-07,-5.112246791380559E-07),(-2.293253034875431E-05,2.549073482446818E-05),(-2.293253034875431E-05,-2.549073482446818E-05),(1.737165621398806E-05,3.217988337436348E-05),(1.737165621398806E-05,-3.217988337436348E-05)]
PH      0       20:54:02.690    DMD_univariate (AUDUSD,D1)       [(-0.001602312423460747,-0.0004729759518786458),(-0.001602312423460747,0.0004729759518786458),(9.344054696658333E-10,8.094462253249723E-10),(9.344054696658333E-10,-8.094462253249723E-10),(-1.519821102302643E-09,-1.798446391809705E-09),(-1.519821102302643E-09,1.798446391809705E-09),(-1.489875889326697E-09,1.679088970293896E-09),(-1.489875889326697E-09,-1.679088970293896E-09),(2.855568843884715E-08,-2.24272293236627E-08),(2.855568843884715E-08,2.24272293236627E-08),(-2.198151384524838E-08,2.429971562856181E-08),(-2.198151384524838E-08,-2.429971562856181E-08),(1.189711697907603E-06,-8.400539607544832E-07),(1.189711697907603E-06,8.400539607544832E-07),(8.892800195531292E-07,-8.493346006915869E-07),(8.892800195531292E-07,8.493346006915869E-07),(5.40418365579387E-05,-4.256796091403961E-05),(5.40418365579387E-05,4.256796091403961E-05),(-2.314522858359869E-05,-6.846121833149754E-05),(-2.314522858359869E-05,6.846121833149754E-05)]
FG      0       20:54:02.690    DMD_univariate (AUDUSD,D1)       [(4.593660886884066E-05,0.0007257275432220045),(4.593660886884066E-05,-0.0007257275432220045),(3.019065830667245E-10,2.421602848801108E-10),(3.019065830667245E-10,-2.421602848801108E-10),(-6.415215442201472E-10,-3.751031429910512E-10),(-6.415215442201472E-10,3.751031429910512E-10),(-2.171667012884626E-10,6.773338626087089E-10),(-2.171667012884626E-10,-6.773338626087089E-10),(2.210737475895341E-09,-1.156460674445192E-08),(2.210737475895341E-09,1.156460674445192E-08),(5.990476170669723E-10,1.068699011230745E-08),(5.990476170669723E-10,-1.068699011230745E-08),(-6.762525454895307E-08,-4.884491409673508E-07),(-6.762525454895307E-08,4.884491409673508E-07),(-1.490076587543424E-07,-3.929403302738166E-07),(-1.490076587543424E-07,3.929403302738166E-07),(-1.571073502396048E-05,-1.913611580105223E-05),(-1.571073502396048E-05,1.913611580105223E-05),(-2.530414087616173E-05,6.629116600515017E-06),(-2.530414087616173E-05,-6.629116600515017E-06)]
DS      0       20:54:02.690    DMD_univariate (AUDUSD,D1)       [(0.001363806542495044,0.0001361882900650091),(0.001363806542495044,-0.0001361882900650091),(-9.180490534443919E-10,-7.880395988535405E-10),(-9.180490534443919E-10,7.880395988535405E-10),(1.549437189662939E-09,1.690010908994566E-09),(1.549437189662939E-09,-1.690010908994566E-09),(1.36508163106619E-09,-1.700071097787692E-09),(1.36508163106619E-09,1.700071097787692E-09),(-2.543471129545782E-08,2.364815934741138E-08),(-2.543471129545782E-08,-2.364815934741138E-08),(1.871941607278771E-08,-2.493395216685013E-08),(1.871941607278771E-08,2.493395216685013E-08),(-1.000003475026823E-06,9.064440836814569E-07),(-1.000003475026823E-06,-9.064440836814569E-07),(-7.106895980740768E-07,8.787577454316686E-07),(-7.106895980740768E-07,-8.787577454316686E-07),(-4.07015728396895E-05,4.38344900164922E-05),(-4.07015728396895E-05,-4.38344900164922E-05),(2.940113570619463E-05,5.652142258574799E-05),(2.940113570619463E-05,-5.652142258574799E-05)]
OK      0       20:54:02.690    DMD_univariate (AUDUSD,D1)       [(0.0005033857628483629,-0.0006840539757191899),(0.0005033857628483629,0.0006840539757191899),(-6.779790617805759E-10,-5.646610123921647E-10),(-6.779790617805759E-10,5.646610123921647E-10),(1.278677420890606E-09,1.06406300437456E-09),(1.278677420890606E-09,-1.06406300437456E-09),…]
PG      0       20:54:02.690    DMD_univariate (AUDUSD,D1)      
OJ      0       20:54:02.690    DMD_univariate (AUDUSD,D1)      Residual vectors shape - (50,20)

Параметр перечисления ENUM_DMD_RESIDUALS, jobr, предлагает пользователям возможность не вычислять остатки, если они не нужны.

Параметр jobf — перечисление ENUM_DMD_REFINE, которое определяет выходные данные матрицы B.

Если jobf является DMDREFINE_N, матрица B будет пустой.
Если параметр jobf установлен на DMDREFINE_E, матрица B будет содержать точные моды DMD как комплексные числа в сжатой форме. Различие между точными модами DMD и проектируемыми модами DMD заключается в том, как они соотносятся с базовым линейным оператором, который аппроксимирует динамику системы. Хотя они создают одни и те же собственные значения, их пространственные структуры (сами моды) различаются. Спроектированные моды DMD являются результатом проекции на набор базисных векторов, что подчеркивает: они являются приближениями, а не истинными собственными векторами наиболее подходящего линейного оператора. Способ расчёта точных мод DMD представляет собой альтернативный подход к решению той же задачи. Такой подход обходит этап проецирования и непосредственно находит собственные векторы линейного оператора. Полученные моды считаются точными, потому что они являются истинными собственными векторами оптимального линейного приближения системы. Это связано с тем, что они не ограничены пределами диапазона снимков исходных данных.
Если параметр jobf равен DMDREFINE_R, то матрица B вернет значения, которые можно использовать в процедуре постобработки. Эта процедура называется уточнением Ритца. Напомним, что пары Ритца рассчитываются на основе приближения линейного оператора A. Уточнение Ритца — способ дальнейшего улучшения векторов Ритца. Матрица B будет содержать значения, необходимые для минимизации начальных остатков. Уточнение Ритца выходит за рамки этой статьи, но это этап, который обычно бывает полезен для улучшения прогнозов.

Коэффициент Рэлея

Выходной параметр W — ещё одна матрица с комплексными значениями в компактной форме.

DQ      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      DMD matrix eigenvectors - W 
CQ      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      [[(0.03397841954159109,0.03317980055719008),(0.03397841954159109,-0.03317980055719008),(-0.9002396504998079,0),(-0.9002396504998079,-0),(0.01119040053117125,0.1182840538877034),(0.01119040053117125,-0.1182840538877034),(-0.08933258155433688,-0.07445561873978643),(-0.08933258155433688,0.07445561873978643),(0.002252288602000291,-0.07268070968789277),(0.002252288602000291,0.07268070968789277),(0.06363962546273101,-0.06242908185135146),(0.06363962546273101,0.06242908185135146),(0.05937239512593095,0.01490455626039135),(0.05937239512593095,-0.01490455626039135),(-0.02589857176991502,-0.03197379959572326),(-0.02589857176991502,0.03197379959572326),(0.03403147435273887,-0.02518975096744712),(0.03403147435273887,0.02518975096744712),(0.04814500369424651,0.0006646006481806285),(0.04814500369424651,-0.0006646006481806285)]
LK      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [(-0.03856865140041035,-0.04728745684412225),(-0.03856865140041035,0.04728745684412225),(-0.07418687400224905,-0.02671782636983063),(-0.07418687400224905,0.02671782636983063),(-0.6278925369875541,0),(-0.6278925369875541,-0),(0.6611296439031247,0),(0.6611296439031247,-0),(-0.01948319607116129,0.1638582051901045),(-0.01948319607116129,-0.1638582051901045),(-0.1160509917189585,0.04684553196764583),(-0.1160509917189585,-0.04684553196764583),(-0.06080699466607752,-0.007252509160005485),(-0.06080699466607752,0.007252509160005485),(0.04824148800646633,0.0544753020238296),(0.04824148800646633,-0.0544753020238296),(-0.02631424783289801,0.02396317634823539),(-0.02631424783289801,-0.02396317634823539),(-0.05371125803952446,-0.01772350219292688),(-0.05371125803952446,0.01772350219292688)]
JS      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [(0.01927996329670138,-0.003323809768950481),(0.01927996329670138,0.003323809768950481),(-0.001092132447284393,-0.08813408560005521),(-0.001092132447284393,0.08813408560005521),(-0.01686362521399225,-0.6191005830078983),(-0.01686362521399225,0.6191005830078983),(0.02637345886634726,0.5944648032143058),(0.02637345886634726,-0.5944648032143058),(-0.1052128591626567,-0.008385210070686162),(-0.1052128591626567,0.008385210070686162),(-0.004565995041448841,-0.09830093201273357),(-0.004565995041448841,0.09830093201273357),(0.02484135400580122,-0.004386892506558514),(0.02484135400580122,0.004386892506558514),(-0.01604018998961423,0.01817361621091497),(-0.01604018998961423,-0.01817361621091497),(0.01513765754343997,-0.01442045062996068),(0.01513765754343997,0.01442045062996068),(0.02301961366729926,-0.02281949313848668),(0.02301961366729926,0.02281949313848668)]
DQ      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [(0.01349178032453495,0.04031036542801018),(0.01349178032453495,-0.04031036542801018),(0.2800915230663114,0.2610589921860959),(0.2800915230663114,-0.2610589921860959),(0.07750855775646105,-0.2950535943034701),(0.07750855775646105,0.2950535943034701),(-0.2337105682364486,0.0040858569402831),(-0.2337105682364486,-0.0040858569402831),(0.06293226732327413,-0.1508577239678987),(0.06293226732327413,0.1508577239678987),(-0.03484731631897012,0.1006710384526284),(-0.03484731631897012,-0.1006710384526284),(-0.01073717194453397,-0.1026561241299194),(-0.01073717194453397,0.1026561241299194),(-0.08143509356008606,-0.07823035735671989),(-0.08143509356008606,0.07823035735671989),(-0.06786249180652332,-0.01131117739979555),(-0.06786249180652332,0.01131117739979555),(-0.01459517002905221,0.04968638335424509),(-0.01459517002905221,-0.04968638335424509)]
DS      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [(-0.06312195367435448,-0.05788238216619907),(-0.06312195367435448,0.05788238216619907),(-0.106179393196619,-0.1067792237431208),(-0.106179393196619,0.1067792237431208),(0.2228105336536818,-0.09464986022387956),(0.2228105336536818,0.09464986022387956),(-0.1223565828897724,-0.2665717534473687),(-0.1223565828897724,0.2665717534473687),(0.0407625323894802,0.0608679763109657),(0.0407625323894802,-0.0608679763109657),(-0.0236347933639726,0.2167362736925585),(-0.0236347933639726,-0.2167362736925585),(-0.1397842805702028,0.002686549243340094),(-0.1397842805702028,-0.002686549243340094),(0.0494448535458599,0.07175076524193082),(0.0494448535458599,-0.07175076524193082),(-0.05089933082548433,0.06350343732496355),…]
LP      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      
FK      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      W shape - (20,20)

Он содержит собственные векторы матрицы, полученные в результате вычисления коэффициента Рэлея. Выходная матрица S используется для хранения соответствующего результата коэффициента Рэлея. Коэффициент Рэлея — это выражение, которое в данном контексте имеет следующий вид.

Результатом является квадратная матрица, которая используется в качестве аппроксимации линейного оператора A.

RF      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      DMD matrix or Rayleigh Quotient -> S
HR      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      [[0.5094085277495803,-0.8604610082897919,0.0002006138033779966,0.04760027059805147,-0.002803306343440372,-0.0391415882078795,-0.0003134843372287616,0.07893996206869613,0.001757225544053047,0.05891514022091245,0.1021418500890567,0.0154878531271508,0.08161025402145326,-0.01322727684398736,0.05289807915719862,0.1366031199179701,0.09067443894366256,0.02387635894976379,-0.1337617534319445,0.3158438887995204]
GG      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.8125718517577054,0.5094085277495803,0.03212818037482736,0.07731373949333104,-0.004523461571676836,-0.06365727084560829,0.07166331416570983,0.1149560436517001,0.0417897026770658,0.0807703163043338,0.1168290328074077,-0.07784523729378179,0.08134266010864513,0.0457586690177342,-0.05281322289935021,0.1041166865025129,0.06016908821880863,-0.02262883866060445,0.01864963663274376,0.1592958144288718]
QM      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0,0,0.9997963823571733,-0.06841114291664024,0.003677630227929817,0.05134906476950822,0.001010343646915456,-0.1036712695688504,-0.001982116115745312,-0.07741467176450138,-0.1344061700387433,-0.02117211346836873,-0.1074879052755059,0.01790950142871103,-0.07054528189524574,-0.180179648794732,-0.1196714016226133,-0.0318305136919558,0.177441519638216,-0.4172515456746314]
PO      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0,0,0.005964529447791189,0.9997963823571733,-6.130430193796907e-05,0.0001608255296355939,-0.1417177910594132,0.02603215499459065,-0.07645245784783392,0.02929171223870932,0.09632863544056425,0.2022679146534209,0.1005224694321643,-0.1320544694433864,0.2724705351116244,0.2311524902397419,0.1709822160686499,0.1206265129749707,-0.4633910086326531,0.6944803173283216]
RG      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0.9835155147230954,-0.1807872789366,-0.01287650437961382,0.002273054758487322,-0.006948726541217937,0.002592615695004415,0.008633127046368962,0.01836065518926932,0.009038166070419178,-0.01198352209799287,0.02469606203936868,0.02084314801005234,0.01542969758433841,0.01093290292806937,-0.04194970752430172,0.06273377057840418]
OE      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0.1808472032071591,0.9835155147230954,0.1161226589750725,-0.02159149420945333,0.06263828964805583,-0.02419610245484403,-0.07926824162748283,-0.1657867613281642,-0.08263670791881386,0.1082473436056935,-0.2234334894897005,-0.1898550808858993,-0.1404004467922538,-0.09891860736477874,0.3801384435040523,-0.5700922000360884]
QE      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0.9754097172453285,-0.3671559385031988,-0.005735330959573934,-0.1752131166062669,-0.3034665524406584,-0.0447757385532624,-0.2423096107440454,0.03850758043656835,-0.1556886673590776,-0.4051646386927485,-0.2688190825258632,-0.07028522559611267,0.3951927856107862,-0.935685263814825]
ES      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0.1323025776105538,0.9754097172453285,-0.1277498034867074,0.01635682016747238,0.1038905065841927,0.3269719154788018,0.122074385755231,-0.211766280182049,0.4229381295746578,0.3086378423896532,0.2339698855185775,0.1869911903713443,-0.6953365989256011,0.9790102802912404]
EJ      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0.9272204223699192,-0.4253756556605945,-0.1675761806365016,-0.0322689202475039,-0.1347517961361585,0.0260709867621285,-0.09491983678538948,-0.2278476057705441,-0.1518792160120434,-0.04275596295515771,0.2317849265989918,-0.532635511016381]
FM      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0.3296680581625781,0.9272204223699192,0.05633171550556969,0.2408424337338481,0.07416894629162182,-0.1553200191742876,0.3047043287502109,0.2020029040523848,0.1558084075499993,0.1346159453957157,-0.4912332208887085,0.6651615829764952]
HG      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0,0,0.9113505757240357,-0.2568972073981867,0.05055669367035209,-0.2566052078814798,0.4776439687989247,0.2195895146754944,0.1834173442058648,0.2105372198999828,-0.7236933009079901,0.8511605081274156]
JD      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0,0,0.6596006848134373,0.9113505757240357,0.3140920520023247,-0.01324336135550369,0.1361348333013918,0.5052672912884386,0.3296699228616658,0.06220880832355302,-0.4176612853765882,1.116102030438296]
JE      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0,0,0,0,0.8329207590629218,0.4624722437908844,0.355960803548531,0.1072881843791952,0.1013740688581597,0.1566216030021757,-0.5124168716630659,0.5231145883642944]
LP      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0,0,0,0,-0.6609520652656545,0.8329207590629218,-0.07009147383110947,-0.3140620624168415,-0.2035214647743208,-0.03229751959115882…]
NH      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      S shape - (20,20)

На этом обсуждение параметров DynamicModeDecomposition() завершается. Далее покажем, как объединить эти результаты для реконструкции, фильтрации и прогнозирования. Но перед этим необходимо решить проблему ограниченности поддержки комплексных чисел в языке MQL5. Некоторые встроенные функции не работают с комплексными аргументами, поэтому нам приходится реализовывать собственные утилиты. Для достижения этой цели представляем библиотеку cmath, определённую в cmath.mqh.

Работа с комплексными числами в языке MQL5

Файл cmath.mqh содержит определения различных утилит для работы с комплексными числами. У нас есть функции для извлечения мнимых и действительных частей из комплексных массивов, векторов и матриц.

//+------------------------------------------------------------------+
//| get real part from container of complex numbers                  |
//+------------------------------------------------------------------+
void real(complex& data[],double& out[])
  {
   ArrayResize(out,data.Size());
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = data[i].real;
  }
//+-------------------------------------------------------------------+
//| get imaginary part from container of complex numbers              |
//+-------------------------------------------------------------------+
void imaginary(complex& data[],double& out[])
  {
   ArrayResize(out,data.Size());
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = data[i].imag;
  }

//+------------------------------------------------------------------+
//| get real part from container of complex numbers                  |
//+------------------------------------------------------------------+
vector real(vectorc& data)
  {
   vector out=vector::Zeros(data.Size());
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = data[i].real;
   return out;
  }
//+-------------------------------------------------------------------+
//| get imaginary part from container of complex numbers              |
//+-------------------------------------------------------------------+
vector imaginary(vectorc& data)
  {
   vector out=vector::Zeros(data.Size());
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = data[i].imag;
   return out;
  }
//+------------------------------------------------------------------+
//| get real part from container of complex numbers                  |
//+------------------------------------------------------------------+
matrix real(matrixc& data)
  {
   matrix out=matrix::Zeros(data.Rows(),data.Cols());
   for(ulong i = 0; i<out.Rows(); i++)
      for(ulong j = 0; j<out.Cols(); j++)
         out[i,j] = data[i,j].real;
   return out;
  }
//+-------------------------------------------------------------------+
//| get imaginary part from container of complex numbers              |
//+-------------------------------------------------------------------+
matrix imaginary(matrixc& data)
  {
   matrix out=matrix::Zeros(data.Rows(),data.Cols());
   for(ulong i = 0; i<out.Rows(); i++)
      for(ulong j = 0; j<out.Cols(); j++)
         out[i,j] = data[i,j].imag;
   return out;
  }

Кроме того, существуют процедуры для преобразования контейнеров действительных чисел в комплексные числа и наоборот.

//+------------------------------------------------------------------+
//| create complex containers from real numbers                      |
//+------------------------------------------------------------------+
vectorc as_complex(vector& re,vector& im)
  {
   vectorc out = vectorc::Zeros(MathMax(re.Size(),im.Size()));
   for(ulong i = 0; i<out.Size(); i++)
     {
      out[i].real = i<re.Size()?re[i]:0.0;
      out[i].imag = i<im.Size()?im[i]:0.0;
     }
   return out;
  }
//+------------------------------------------------------------------+
//| create complex containers from real numbers                      |
//+------------------------------------------------------------------+
matrixc as_complex(matrix& re,matrix& im)
  {
   matrixc out = matrixc::Zeros((ulong)MathMax(re.Rows(),im.Rows()),(ulong)MathMax(re.Cols(),im.Cols()));
   for(ulong i = 0; i<out.Rows(); i++)
     {
      for(ulong j = 0; j<out.Cols(); j++)
        {
         out[i,j].real = (i<re.Rows() && j<re.Cols())?re[i,j]:0.0;
         out[i,j].imag = (i<im.Rows() && j<im.Cols())?im[i,j]:0.0;
        }
     }
   return out;
  }
//+------------------------------------------------------------------+
//| create complex containers from real numbers                      |
//+------------------------------------------------------------------+
vectorc as_complex(vector& re)
  {
   vectorc out = vectorc::Zeros(re.Size());
   for(ulong i = 0; i<out.Size(); i++)
     {
      out[i].real = re[i];
      out[i].imag = 0.0;
     }
   return out;
  }
//+------------------------------------------------------------------+
//| create complex containers from real numbers                      |
//+------------------------------------------------------------------+
matrixc as_complex(matrix& re)
  {
   matrixc out = matrixc::Zeros(re.Rows(),re.Cols());
   for(ulong i = 0; i<out.Rows(); i++)
     {
      for(ulong j = 0; j<out.Cols(); j++)
        {
         out[i,j].real = re[i,j];
         out[i,j].imag = 0.0;
        }
     }
   return out;

Наконец, библиотека включает в себя реализации для экспоненты, степени, абсолютного значения и натурального логарифма комплексных чисел и их контейнеров.

//+------------------------------------------------------------------+
//|        power of complex number                                   |
//+------------------------------------------------------------------+
complex c_pow(complex base, complex exponent)
  {
   return c_exp(exponent*c_log(base));
  }
//+------------------------------------------------------------------+
//| simple power of complex number                                   |
//+------------------------------------------------------------------+
vectorc c_pow(vectorc &vect, complex exponent)
  {
   vectorc out(vect.Size());
   for(ulong i = 0; i<vect.Size(); i++)
      out[i] = c_pow(vect[i],exponent);
   return out;
  }
//+------------------------------------------------------------------+
//| simple power of complex number                                   |
//+------------------------------------------------------------------+
matrixc c_pow(matrixc &matrx, complex exponent)
  {
   matrixc out(matrx.Rows(),matrx.Cols());
   for(ulong i = 0; i<out.Cols(); i++)
      out.Col(c_pow(matrx.Col(i),exponent),i);
   return out;
  }


//+------------------------------------------------------------------+
//|        power of complex number                                   |
//+------------------------------------------------------------------+
complex c_pow(complex value, double alpha)
  {
   complex out = value;
   double r = c_abs(value);
   double theta = atan2(value.imag,value.real);
   double n_r = pow(r,alpha);
   double n_theta = alpha*theta;

   out.real = n_r*cos(n_theta);
   out.imag = n_r*sin(n_theta);
   return out;
  }
//+------------------------------------------------------------------+
//| simple power of complex number                                   |
//+------------------------------------------------------------------+
vectorc c_pow(vectorc &vect, double alpha)
  {
   vectorc out(vect.Size());
   for(ulong i = 0; i<vect.Size(); i++)
      out[i] = c_pow(vect[i],alpha);
   return out;
  }
//+------------------------------------------------------------------+
//| simple power of complex number                                   |
//+------------------------------------------------------------------+
matrixc c_pow(matrixc &matrx, double alpha)
  {
   matrixc out(matrx.Rows(),matrx.Cols());
   for(ulong i = 0; i<out.Cols(); i++)
      out.Col(c_pow(matrx.Col(i),alpha),i);
   return out;
  }

//+------------------------------------------------------------------+
//|  Complex Signum Function                                         |
//+------------------------------------------------------------------+
complex signum(complex z)
  {
   double magnitude = sqrt((z.real*z.real) + (z.imag*z.imag));
   if(!magnitude)
      return 0+0i;
   complex magz;
   magz.real = magnitude;
   magz.imag = 0.0;

   return z/magz;
  }

//+------------------------------------------------------------------+
//| absolute value of a complex number (magnitude)                   |
//+------------------------------------------------------------------+
double c_abs(complex z)
  {
   return sqrt((z.real*z.real) + (z.imag*z.imag));
  }
//+------------------------------------------------------------------+
//| absolute value of a complex number (magnitude)                   |
//+------------------------------------------------------------------+
vector c_abs(vectorc &z)
  {
   CComplexVector v(z);
   return sqrt((v.re*v.re) + (v.im*v.im));
  }
//+------------------------------------------------------------------+
//| absolute value of a complex number (magnitude)                   |
//+------------------------------------------------------------------+
matrix abs(matrixc &z)
  {
   CComplexMatrix v(z);
   return sqrt((v.re*v.re) + (v.im*v.im));
  }
//+------------------------------------------------------------------+
//| sqrt of complex number                                           |
//+------------------------------------------------------------------+
complex c_sqrt(complex z)
  {
   double mag_z = c_abs(z);
   mag_z=sqrt(mag_z);
   double theta = atan2(z.imag,z.real);
   complex out;
   out.real = mag_z*cos(theta/2.0);
   out.imag = mag_z*sin(theta/2.0);
   return out;
  }
//+------------------------------------------------------------------+
//| sqrt of complex vector                                           |
//+------------------------------------------------------------------+
vectorc c_sqrt(vectorc &z)
  {
   vectorc out = z;
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = c_sqrt(z[i]);
   return out;
  }
//+------------------------------------------------------------------+
//| sqrt of complex vector                                           |
//+------------------------------------------------------------------+
matrixc c_sqrt(matrixc &z)
  {
   matrixc out = z;
   for(ulong i = 0; i<out.Cols(); i++)
      out.Col(c_sqrt(z.Col(i)),i);
   return out;
  }
//+------------------------------------------------------------------+
//|  log of complex number                                           |
//+------------------------------------------------------------------+
complex c_log(complex z)
  {
   complex out;
   out.real = c_abs(z);
   out.imag = atan2(z.imag,z.real);
   return out;
  }
//+------------------------------------------------------------------+
//|  log of complex number                                           |
//+------------------------------------------------------------------+
vectorc c_log(vectorc &z)
  {
   vectorc out = z;
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = c_log(z[i]);
   return out;
  }
//+------------------------------------------------------------------+
//|  log of complex number                                           |
//+------------------------------------------------------------------+
matrixc c_log(matrixc &z)
  {
   matrixc out = z;
   for(ulong i = 0; i<out.Cols(); i++)
      out.Col(c_log(z.Col(i)),i);
   return out;
  }
//+------------------------------------------------------------------+
//|  exp function of complex number                                  |
//+------------------------------------------------------------------+
complex c_exp(complex z)
  {
   complex out;
   out.real = exp(z.real)*cos(z.imag);
   out.imag = exp(z.real)*sin(z.imag);
   return out;
  }
//+------------------------------------------------------------------+
//|  exp function of complex number                                  |
//+------------------------------------------------------------------+
vectorc c_exp(vectorc &z)
  {
   vectorc out = z;
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = c_exp(z[i]);
   return out;
  }
//+------------------------------------------------------------------+
//|  exp function of complex number                                  |
//+------------------------------------------------------------------+
matrixc c_exp(matrixc &z)
  {
   matrixc out = z;
   for(ulong i = 0; i<out.Cols(); i++)
      out.Col(c_exp(z.Col(i)),i);
   return out;
  }

Амплитуда и динамика мод

Реконструкция в DMD — это воспроизведение входных данных с использованием только тех мод, которые выведены с помощью разложения. Фильтрация с помощью DMD — это реконструкция входных данных с использованием только выбранных мод. Прогнозирование просто экстраполирует реконструкцию вперед во времени. Чтобы выполнить одно из этих действий, нам нужно рассчитать соответствующие амплитуды и динамику мод. Амплитуты не представляют собой непосредственный результат использования метода DynamicModeDecomposition(); их необходимо вычислять на отдельном этапе посредством подгонки мод к моментальному снимку. Обычно это делается с помощью метода наименьших квадратов или путем вычисления псевдообратных мод.

Для нахождения решения задачи наименьших квадратов для сложной несимметричной матрицы можно использовать LU-разложение нормальных уравнений. Нормальные уравнения преобразуют переопределенную систему в решаемую систему квадратных уравнений. Это можно выполнить с помощью утилит из библиотеки Alglib, как показано во фрагменте кода ниже.

//+------------------------------------------------------------------+
//|  compute the DMD amplitudes                                      |
//+------------------------------------------------------------------+
vectorc              compute_amplitudes(matrix& snapshots, matrixc& modes)
  {
   vectorc amplitudes(0);

   vectorc x0 = as_complex(snapshots.Col(0));
   matrixc A_h = modes.TransposeConjugate();
   matrixc B = np::matmul(A_h,modes);
   vectorc c = np::matmul(A_h,x0);
   complex right_side[], solution[];
   int pivots[];
   CMatrixComplex lua = B;

   if(!np::vecAsArray(c,right_side))
     {
      Print(__FUNCTION__, " vector as array failure ");
      return amplitudes;
     }

   vector check_pivots;
   ResetLastError();
   CAlglib::CMatrixLU(lua,lua.Rows(),lua.Cols(),pivots);
   int info;
   check_pivots.Assign(pivots);
   if(check_pivots.Max() == check_pivots.Min())
     {
      Print(__FUNCTION__," CAlglib::CMatrixLU()  failure ", GetLastError());
      return amplitudes;
     }

   CDenseSolverReportShell shell;

   CAlglib::CMatrixLUSolve(lua,pivots,int(pivots.Size()),right_side,info,shell,solution);

   if(info < 1)
     {
      Print(__FUNCTION__, " modes matrix is singular, or VERY close to singular. ", GetLastError());
      return amplitudes;
     }

   amplitudes.Assign(solution);

   return amplitudes;

Код определяет функцию, которая вычисляет амплитуды по заданной матрице снимков и мод. Обратите внимание, что в этом примере используется первый снимок, но можно применить моментальный снимок с из любой точки времени. Решением для подгонки методом наименьших квадратов являются амплитуды, которые являются комплексными. Кроме того, амплитуды позволяют рассчитывать наиболее доминирующие моды, как показывает процедура DMD. Делаем этот расчет путем вычисления величины амплитуд. Эту информацию можно использовать во время фильтрации.

//---
   vector abs_dmd_amplitudes = c_abs(dmd_amplitudes);
//---
   long amp_indices[];
   if(!np::arange(amp_indices,int(abs_dmd_amplitudes.Size())) ||
      !np::quickSortIndices(abs_dmd_amplitudes,false,amp_indices,amp_indices[0],amp_indices[amp_indices.Size()-1]))
     {
      Print(" error ");
      return;
     }
//---

Располагая амплитудами, мы можем вычислить динамику мод. Матрица динамики DMD представляет собой матрицу Вандермонда, в которой каждая строка показывает эволюцию моды во времени. Для вычисления требуются дискретные временные точки снимков и собственные значения DMD. Собственные значения организованы в векторы-столбцы и возводятся в степень дискретной точки во времени внутри набора данных. Наконец, каждый вектор-столбец умножается на амплитуды. Функция compute_dynamics() вычисляет матрицу динамики DMD, учитывая амплитуды, значения Ритца и вектор временных точек моментальных снимков.

//+------------------------------------------------------------------+
//|   calculate the mode dynamics                                    |
//+------------------------------------------------------------------+
matrixc           compute_dynamics(vectorc& amplitudes,vectorc& eigs, vector& timesteps)
  {
   matrixc mat_eigs = np::repeat_vector_as_rows_cols(eigs,timesteps.Size(),false);
   vector tpow = (timesteps - timesteps[0])/(timesteps[1] - timesteps[0]);
   matrixc dyn = mat_eigs;

   for(ulong i = 0; i<mat_eigs.Cols(); i++)
     {
      vectorc column = mat_eigs.Col(i);
      column = c_pow(column,tpow[i]);
      column*=amplitudes;
      dyn.Col(column,i);
     }

   return dyn;
  }

Ниже представлен график эволюции во времени наиболее доминирующей моды для нашего примера. Графика создана с помощью скрипта DMD_Mode_Dynamics.ex5.

Динамика доминирующей моды

Реконструкция и прогнозирование

Моды DMD, амплитуды и собственные значения можно объединять для построения аппроксимации входных данных. Реконструированный набор данных будет представлять собой низкоранговое представление, которое фиксирует доминирующую динамику исходных данных. Это достигается посредством умножения мод с учетом динамики.

//+------------------------------------------------------------------+
//|  reconstruct the input data based on the dominant dmd dynamics   |
//+------------------------------------------------------------------+
matrixc            reconstructed_data(matrixc& dynamics, matrixc& modes)
  {
   return np::matmul(modes,dynamics);
  }

Ниже представлен реконструированный ряд, определенный с помощью модели DMD.

Реконструированный ряд

Если нам нужно отфильтровать данные, придется «отключить» моды, которые хотим отбросить. Это можно сделать, установив отброшенные моды (столбцы) на ноль, а затем умножив на показатели динамики.

//---
   vector time_steps = np::arange(X1.Cols()+1,t[0],dt);
   matrixc dmd_dynamics = compute_dynamics(dmd_amplitudes,eigen_values,time_steps);
   matrixc masked_modes;
//---
   if(NumTop)
     {
      double min_amp = abs_dmd_amplitudes[amp_indices[NumTop]];
      masked_modes = matrixc::Zeros(dmd_modes.Rows(),dmd_modes.Cols());
      for(ulong i = 0; i<dmd_modes.Cols(); i++)
        {
         bool select = c_abs(dmd_amplitudes[i])>min_amp;
         if(select)
            masked_modes.Col(dmd_modes.Col(i),i);
        }
     }
   else
      masked_modes = dmd_modes;
//---
   matrixc reconstructed = reconstructed_data(dmd_dynamics,masked_modes);
//---
   matrix real_rec = real(reconstructed);
//---
   real_rec = time_delay_reconstruction(real_rec,Delay);
//--

На графике ниже показана отфильтрованная реконструкция с использованием только наиболее доминирующих мод.

Демонстрация отфильтрованной реконструкции

Прогнозирование осуществляется путем расширения дискретных временных точек за пределы окончания входных данных при расчете динамики. Затем модель DMD экстраполирует моды вперед во времени для генерации прогнозов. Точность прогноза зависит от того, насколько эффективно полученная с помощью DMD линейная модель отражает динамику системы.

//---
   vector time_steps = np::arange((X1.Cols())+Num_future_points+1,first_time_point,dt);
//---
   matrixc dmd_dynamics = compute_dynamics(dmd_amplitudes,eigen_values,time_steps);
//---
   matrixc reconstruction = reconstructed_data(dmd_dynamics,dmd_modes);
//--

Здесь мы можем видеть результат прогнозирования на 10 шагов вперед.

Прогноз для серии Demo

Следует отметить, что в нашей демонстрации используется серия с четким сигналом, свободным от какого-либо шума. В следующем разделе мы увидим, насколько оправдываются прогнозы DMD, когда данные зашумлены.

Применение DMD к ценовым данным

Скрипт DMD_Price_Decomposition.ex5 демонстрирует применение DMD на реальных данных. Он загружает пример ценовых котировок и разбивает серию на части. Затем полученная модель DMD используется для составления определенного пользователем количества прогнозов. После этого прогнозируемый ряд визуализируется относительно фактических ценовых котировок для сравнения.

//+------------------------------------------------------------------+
//|                                       DMD_Price_Decompostion.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<dmd_utils.mqh>
//--- input parameters
input string   Symbol_="AUDUSD";
input ENUM_TIMEFRAMES   TimeFrame=PERIOD_D1;
input datetime StartDate=D'2025.06.02';
input ENUM_DMD_SCALE jobs = DMDSCALE_N;
input ENUM_DMD_EIGV jobz = DMDEIGV_V;
input ENUM_DMD_RESIDUALS jobr = DMDRESIDUALS_R;
input ENUM_DMD_REFINE jobf = DMDREFINE_R;
input ENUM_SVD_ALG whtsvd = SVDALG_1;
input long nrnk = 20;
input double tol_ = 1.e-9;//tol
input ulong Delay = 50;//apply time delay embedding
input ulong Num_Future_steps = 10;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   vector prices;
   if(!prices.CopyRates(Symbol_,TimeFrame,COPY_RATES_CLOSE,StartDate,100+Num_Future_steps))
    {
     Print(" failed to get close prices for ", Symbol_,". Error ", GetLastError());
     return;
    }
//---
   matrix X = matrix::Zeros(1,100);
   vector input_series = np::sliceVector(prices,0,100);
   X.Row(input_series,0);
   np::matrix2csv("AUDUSD.csv",X.Transpose());
//---
   CDmd dmd;
   if(!dmd.fit(X,1,tol_,nrnk,Delay,jobs,whtsvd,jobz,jobr,jobf))
      return;
   else
      Print(" It worked! ");
   
   vectorc egs = dmd.dmd_eigs();  
   Print("DMD eigenvalues or Ritz values\n",egs);
   
   matrix forecast = dmd.reconstructed_data(Num_Future_steps);
   vector time = np::arange(prices.Size(),0.0,dmd.dmd_time_delta());
   plot_forecast(prices,forecast.Row(0),time,Num_Future_steps," Price forecast",0,0,0,0,500,400,true,30);
  }

Программа использует класс CDmd, определенный в файле dmd_utils.mqh. Этот класс объединяет функциональность, предоставляемую встроенным методом DynamicModeDecomposition(), с возможностями, описанными в этом тексте. Его интерфейс состоит из метода fit() для проведения разложений. Для этого требуется ряд входных переменных, которые определяют параметры процедуры DMD, включая возможность применения внедренной задержки во времени.

virtual bool              fit(matrix &X,double time_delta, double tolerance, long svd_rank = -1,ulong embedding_dimension = 0,ENUM_DMD_SCALE scale = DMDSCALE_N,ENUM_SVD_ALG svd_method = SVDALG_1, ENUM_DMD_EIGV eigv = DMDEIGV_V,ENUM_DMD_RESIDUALS resid = DMDRESIDUALS_R,ENUM_DMD_REFINE refine = DMDREFINE_R)
     {
      reset();

      matrix z,res_vectors,b,w,s;
      vector residuals;
      m_delay = embedding_dimension;
      matrix snapshots = m_delay>1?time_delay_embedding(X,m_delay):X;
      if(!snapshots.Cols())
         return false;
      m_snapshots_x = np::sliceMatrixCols(snapshots,0,snapshots.Cols()-1);
      m_snapshots_y = np::sliceMatrixCols(snapshots,1);
      if(!m_snapshots_x.DynamicModeDecomposition(m_snapshots_y,scale,eigv,resid,refine,svd_method,svd_rank,tolerance,m_eigs,m_left_vectors,z,m_residuals,res_vectors,b,w,s))
        {
         Print(__FUNCTION__, " DMD error ", GetLastError());
         return false;
        }

      if(eigv != DMDEIGV_N)
         m_modes = compact_to_complex(z,m_eigs);

      m_eigenvectors = compact_to_complex(w,m_eigs);

      if(refine == DMDREFINE_E)
        {
         m_modes = compact_to_complex(b,m_eigs);
         m_exact_modes = true;
        }
      else
         if(refine == DMDREFINE_R)
            m_residual_vectors = compact_to_complex(res_vectors,m_eigs);

      m_og_first = m_dmd_first = 0.0;
      m_og_dt = m_dmd_dt = time_delta;
      m_og_timesteps = m_dmd_timesteps = np::arange(m_snapshots_x.Cols()+1,m_dmd_first,m_dmd_dt);
      m_og_last = m_dmd_last = m_dmd_timesteps.Size()-1;

      m_fitted = compute_amplitudes() ;

      return m_fitted;
     }

После настройки модели ее различные характеристики можно получить, вызвав один из показанных ниже методов получения данных.

matrixc           dmd_modes(void)
     {
      return m_modes;
     }
   double            dmd_time_delta(void)
     {
      return m_dmd_dt;
     }
   double            dmd_first_time(void)
     {
      return m_dmd_first;
     }
   ulong             dmd_last_time(void)
     {
      return m_dmd_last;
     }
   double            og_first_time(void)
     {
      return m_og_first;
     }
   ulong             og_last_time(void)
     {
      return m_og_last;
     }
   vector            dmd_time_steps(void)
     {
      return m_dmd_timesteps;
     }
   vector            og_time_steps(void)
     {
      return m_og_timesteps;
     }
   vectorc           dmd_eigs(void)
     {
      return m_eigs;
     }
   vectorc           dmd_amplitudes(void)
     {
      return m_amplitudes;
     }
   matrixc           exact_dmd_modes(void)
     {
      if(m_exact_modes)
         return m_modes;
      else
         return matrixc::Zeros(0,0);
     }
   matrixc           eigenvectors(void)
     {
      return m_eigenvectors;
     }
   vector            growth_rate(void)
     {
      return real(m_eigs)/m_dmd_dt;
     }

   vector            frequency(void)
     {
      vectorc f = c_log(m_eigs);
      return imaginary(f)/(2.0*M_PI*m_dmd_dt);
     }
   matrixc           residual_vectors(void)
     {
      return m_residual_vectors;
     }
   vector            residuals(void)
     {
      return m_residuals;
     }

Реконструкции, прогнозы и операции фильтрования обрабатываются перегруженными методами reconstructed_data(). Оба выводят контейнеры с действительными значениями в исходной форме входных данных. Версия метода reconstructed_data() с одним необязательным параметром в основном используется для прогнозов и реконструкций без какой-либо фильтрации. Если единственный необязательный параметр установлен на ненулевое значение, этот метод выдаст запрошенное количество прогнозов. В противном случае он будет выводить реконструкцию входных данных.

matrix            reconstructed_data(ulong num_future_steps = 0)
     {
      if(num_future_steps)
        {
         m_dmd_last+=num_future_steps;
         m_dmd_timesteps = np::arange(m_dmd_last+1,m_dmd_first,m_dmd_dt);
        }

      matrixc d = dynamics();
      matrixc data = np::matmul(m_modes,d);
      if(!num_future_steps)
         data = np::sliceMatrixCols(data,0,long(m_og_last+1));
      matrix rdata = real(data);
      if(m_delay>1)
         rdata = time_delay_reconstruction(rdata,m_delay);
      return rdata;
     }

Вторая версия метода reconstructed_data() принимает дополнительный векторный параметр. Этот метод предполагает, что пользователь предоставит вектор из единиц и нулей, размер которого соответствует количеству мод. Ноль в векторе указывает на то, что соответствующая мода будет отброшена. Это никоим образом не изменяет исходные моды, но позволяет вычислять отфильтрованные прогнозы или реконструкции.

matrix            reconstructed_data(vector& modes_mask, ulong num_future_steps = 0)
     {
      if(num_future_steps)
        {
         m_dmd_last+=num_future_steps;
         m_dmd_timesteps = np::arange(m_dmd_last+1,m_dmd_first,m_dmd_dt);
        }

      matrixc d = dynamics();
      matrixc masked_modes = matrixc::Zeros(m_modes.Rows(),m_modes.Cols());
      if(modes_mask.Size() == m_modes.Cols())
        {
         for(ulong i = 0; i<masked_modes.Cols(); i++)
            if(modes_mask[i])
               masked_modes.Col(m_modes.Col(i),i);
        }
      matrixc data = np::matmul(masked_modes,d);
      if(!num_future_steps)
         data = np::sliceMatrixCols(data,0,long(m_og_last+1));
      matrix rdata = real(data);
      if(m_delay>1)
         rdata = time_delay_reconstruction(rdata,m_delay);
      return rdata;
     }

Запустив программу, получаем следующие выходные данные.

Реконструкция DMD и прогноз ценовых котировок

Мы можем видеть, что DMD испытывает затруднения при выводе динамики, вероятно, из-за присутствующего в серии шума. Прогнозы, которые выходят за рамки нескольких шагов от входных данных, безнадежны. Это подтверждает, что метод DMD по-настоящему полезен только для краткосрочных прогнозов. Стоит продвинуться более, чем на пару шагов в будущее, и модель начинает распадаться.

Заключение

Статья продемонстрировала, как применять разложение по динамическим модам к одномерным временным рядам в MQL5, используя новый матричный метод DynamicModeDecompostion(). Мы обсудили входные данные этого метода, а также способы интерпретации и обработки его выходных данных для анализа. При этом были представлены основные инструменты, необходимые для работы с комплексными числами. Метод DMD может стать желательным дополнением к возможностям MQL5, но для извлечения из него максимальной пользы пользователям необходимо обладать значительными познаниями в данной области. Не только о самом методе DMD, но и об анализируемом наборе данных. Весь упомянутый в этой статье код перечисляется и прилагается ниже.

Имя файла	Описание
MQL5/include/np.mqh	Это заголовочный файл векторных и матричных функций утилит
MQL5/include/cmath.mqh	Заголовочный файл функций утилиты для работы с комплексными числами
MQL5/include/dmd_utils.mqh	Заголовочный файл, содержащий определение класса CDmd и различные полезные для анализа DMD функции
MQL5/scripts/DMD_Demo.mq5	Скрипт, которые используется для построения графика собственных значений.
MQL5/scripts/DMD_Mode_Dynamics.mq5	Скрипт, демонстрирующий расчет и отображение динамики моды
MQL5/scripts/DMD_Reconstruction.mq5	Этот скрипт демонстрирует реконструкцию модели DMD, а также использование DMD для фильтрации
MQL5/scripts/DMD_Forecast_Demo.m5	Скрипт показывает, как делать прогнозы с помощью модели DMD
MQL5/scripts/DMD_Price_Decomposition.mq5	Этот скрипт демонстрирует использование класса CDmd и применение DMD к реальным ценовым котировкам

Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/19188

Прикрепленные файлы |

Загрузить ZIP

Mql5.zip (37.62 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Python + API LLM + MetaTrader 5: реальный опыт построения автономного торгового бота

Статья описывает создание MVP-прототипа автономного торгового бота для MetaTrader 5, использующего большие языковые модели (LLM) через API OpenRouter для анализа рынка и принятия торговых решений. Скрипт на Python получает исторические данные OHLCV, отправляет их в LLM для технического анализа на основе уровней поддержки/сопротивления и паттернов Price Action, после чего автоматически размещает ордера с заданными стоп-лоссом и тейк-профитом.

Разработка инструментария для анализа движения цен (Часть 15): Введение в теорию четвертей (I) — Скрипт Quarters Drawer

Точки поддержки и сопротивления являются критическими уровнями, которые сигнализируют о возможном развороте и продолжении тренда. Хотя определение этих уровней может оказаться непростой задачей, ее решение позволит вам хорошо ориентироваться на рынке. В статье представлен инструмент Quarters Drawer. Он поможет вам определить как основные, так и второстепенные уровни поддержки и сопротивления.

Нейросети в трейдинге: Пространственно-временная модель состояния для анализа финансовых данных (E-STMFlow)

Предлагаем познакомиться с фреймворком E-STMFlow, который эффективно обрабатывает потоки событий, извлекая информативные эмбеддинги, фильтруя шум и выявляя ключевые движения. Его архитектура позволяет выявлять сложные взаимосвязи между признаками и обеспечивает масштабируемость, точность и высокую вычислительную эффективность для интеллектуального анализа и прогнозирования.

Обучаем нейросети на осцилляторах без подглядывания в будущее

В статье описывается подход к разметке сделок с помощью осцилляторов для моделей машинного обучения. Это позволяет избавиться от look ahead bias. Показано, что такая разметка не приводит к переобучению моделей, а стратегии продолжают работать продолжительное время.