MQL5における特異スペクトル解析

SSAとは何か

MetaTrader 5の最近のバージョンでは、コアとなるベクトルおよび行列データ型にOpenBLASメソッドが初めて統合されました。なかでも注目すべきは、特異スペクトル解析(SSA)に関連する一連のメソッドです。本記事では、MQL5で新たに利用可能となったSSA関連ツールを取り上げ、その活用方法を分析および予測の観点から解説していきます。このガイドは、SSAの可能性を最大限に活用したいトレーダーにリソースを提供することを目的としています。SSAの基本的な手法を理解し、2段階の「分解」と「再構成」プロセスをわかりやすく説明します。さらに、MQL5における各SSAベクトルメソッドの機能を詳細に解説し、それらの出力結果をどのように読み取り、最適に組み合わせて実用的なインサイトを得るかについても紹介します。

SSAは、非パラメトリック手法として設計された時系列データの分析および予測手法です。その目的は、時系列をいくつかの加法的成分に分解することにあります。これらの成分には、ゆるやかに変動するトレンド、さまざまな周期的要素、そして残差ノイズなどが含まれます。SSAの際立った特徴は、基礎となるデータ生成過程に関する事前の仮定にほとんど依存しない点にあります。その概念的基盤は、統計学および信号処理の要素を融合したものです。SSAは本質的にスペクトル分解に基づいており、再構成された埋め込み空間内で主成分を解析することによって、時系列の周波数特性を明らかにします。SSAは、時系列データに特化した主成分分析(PCA: Principal Component Analysis)の一形態と考えることができ、次元削減の原理を活用して、ノイズや複雑な相互作用に隠れた構造やパターンを抽出する手法です。

MQL5におけるSSA

MQL5では、SSAの計算はベクトルデータ型のメソッドとしてネイティブに実装されており、またAlglib数学ライブラリにも同様の機能が提供されています。AlglibによるSSAの強みは主にリアルタイム処理にあり、一方でベクトルから直接利用可能な新しいSSA機能は、探索的分析に適しています。ここで述べる内容は主に実数を用いた操作に焦点を当てていますが、複素数に対応した同等のメソッドも用意されており、基本的な操作は同様です。複素数の場合は、その解釈が複素領域向けに調整されます。

新しいベクトルSSAメソッドでは、最初の必須パラメータとしてウィンドウ長の指定が求められます。このパラメータは、時系列データを「軌跡行列」と呼ばれる高次元構造に変換する際に用いられます。なぜこの高次元構造が必要なのかと疑問に思う人もいるかもしれません。そのヒントはSSAとPCAの関係にあります。PCAは多変量データに対して適用される次元削減手法です。一方、SSAは単一の時系列を再構成し、多変量データに似た構造を作り出します。これは、時系列の区間を等しいサイズの行に並べることでおこなわれます。この際の「行のサイズ」を決めるのがウィンドウ長パラメータです。

長さN=6の時系列、Y=[y1​,y2​,y3​,y4​,y5​,y6​]を考えます。ここでウィンドウ長L=3選択すると、次のような軌跡行列が得られます。

軌跡行列の行数Rは、R=N−L+1として計算されます。この例では、R=6−3+1=4です。この行列は、R×L（この例では4×3）であり、軌跡行列です。軌跡行列の反対角線上に見られるパターンは、ハンケル行列の特徴です。軌跡行列の構築はSSAの最初のステップであり、ウィンドウ長がSSAにおける決定的なパラメータである理由もここにあります。ウィンドウ長は軌跡行列の次元を直接決定し、スペクトル分解の解像度や成分の分離性に大きく影響するためです。

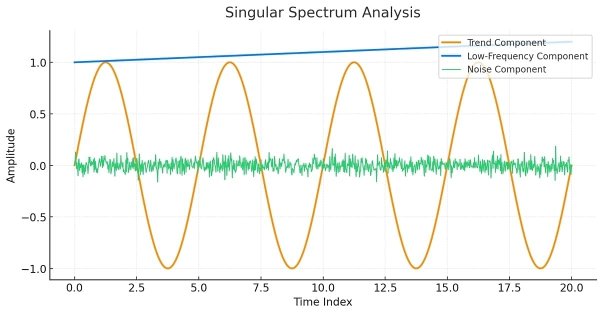
SSAの概念を明確にするため、決定論的な時系列に適用した例を示します。

この時系列は、あらかじめ決められた加法的成分（トレンド、周期成分数個、ランダムノイズ）から構成されています。これらの成分を合成すると、やや不規則な時系列が得られます。SSAの目的は、これらの基礎成分を明らかにすることです。SSAでは、軌跡行列またはその共分散行列を分解し、固有モードを抽出します。PCAと同様に、これらの固有モードから時系列の主成分を見つけ出すことができます。

相対寄与率と累積寄与率

MQL5のベクトルメソッドSingularSpectrumAnalysisSpectrum()は、時系列の相対寄与率を表すベクトルを出力します。このベクトルには実数が格納されており、合計は1になります。各値は各成分の寄与の割合を示しており、降順に並べられています。これらの寄与率は、軌跡行列や共分散行列の分解によって求められた固有値の相対的な大きさに対応しています。

//---
   vector relative_contributions;
   if(!full_process.SingularSpectrumAnalysisSpectrum(WindowLen,relative_contributions))
     {
      Print(" error ", GetLastError());
      return;
     }
//---
   relative_contributions*=100.0;
   vector cumulative_contributions = relative_contributions.CumSum();

相対寄与率を累積和として計算することで、累積寄与率を得ることができます。累積寄与率を用いると、元の時系列を比較的近似するために必要な成分の最小数を迅速に把握することが可能です。相対寄与率のプロットを見ると、いくつかの成分でほぼ同じ値の概ね水平なプラトーが現れることがあります。この傾向は、これらの成分が同一の周期成分を表している可能性を示唆します。

例として用いた時系列における相対寄与率と累積寄与率のプロットは以下の通りです。

最初の2成分がそれぞれ全体分散の約68%と12%を占めていることがわかります。

最初の5成分だけで、全体の98%以上を占めています。相対寄与率のプロットは、最初の5成分が他を圧倒的に上回る形を示しており、支配的な成分と残りの成分を分ける「エルボーポイント」が確認できます。このポイントより下の成分は一般に「ノイズフロア」と呼ばれ、信号とノイズの分離の概算に利用できます。さらに、相対寄与率のプロットでは、成分番号2と3が4と5から離れてまとまっている様子が見て取れます。このことから、これらの成分がペアとして関連しており、時系列の固有の特徴を表している可能性があることが示唆されます。

時系列成分の抽出

例として用いた時系列を分析したことで、時系列の振る舞いの大部分を支配する主要な成分が把握できました。これらの成分の規則性を確認するためには、成分を可視化することが有効です。ここで役立つのが、ベクトルメソッドSingularSpectrumAnalysisReconstructComponents()です。特に注目すべき出力は、成分時系列の行列です。ただし、MQL5の公式ドキュメントでは「列が推定された成分時系列を表す」と記載されていますが、実際には各成分時系列が行として格納されています。さらに、このメソッドのベクトル出力には、級数の代表的な行列の分解の生の固有値が含まれます。

//---
   matrix components;
   vector eigvalues;
   if(!full_process.SingularSpectrumAnalysisReconstructComponents(WindowLen,components,eigvalues))
     {
      Print(" error ", GetLastError());
      return;
     }
//---

成分時系列の行列は、相対寄与率の大きい順に行が並べられています。したがって、最初の行には最も大きな固有値に対応する成分、すなわち最も相対寄与率の高い成分が含まれます。以下の図は、例として用いた時系列のすべての成分をプロットしたものです。

元の成分のプロットと比較すると、若干の差異が見られるかもしれません。これは、SSAによる分解が完全に正確ではないことを示しています。SSAは時系列の正確な周期成分を解読することはできません。SSAがおこなうことができるのは、各成分の最適な近似や推定を見つけることです。それでも、分解された成分時系列をすべて合計すれば、元の時系列を再現することが可能です。

フィルタリング

SSAで得られた成分時系列を利用することで、どの成分が基礎となる信号を表し、どの成分が非決定的なノイズを表すかを推定できます。主に支配的な周期成分に注目したい場合、相対寄与率の低い成分を除外してフィルタリング済みの時系列を作成することが可能です。この操作では、低寄与成分を主要な信号を隠すノイズとみなして除外することを前提としています。

このフィルタリングはSingularSpectrumAnalysisReconstructSeries()メソッドを用いて直接おこなうことができます。ここでは、フィルタ後の時系列に含める支配的な成分の数を指定します。

//---
   vector filtered;
   if(!full_process.SingularSpectrumAnalysisReconstructSeries(WindowLen,FilterComponents,filtered))
     {
      Print(" error ", GetLastError());
      return;
     }

SSAは一般にノイズの分離に優れていますが、その効果は対象となるプロセス内のノイズの性質に依存します。単純に相対寄与率の低い成分を除外するだけでは、ノイズを完全に分離できない場合もあります。そのため、信号やトレンド、特定の周期成分の抽出にも影響が出ることがあります。これらの成分の解釈は、統計的有意性の検定によって検証することが望ましいです。また、強いトレンドが存在する場合、その支配力によって低周波の振動がマスクされ、特定の成分の分離が困難になる場合もあります。

予測

SSAの手法で特に興味深い応用のひとつが、時系列予測です。この機能はSingularSpectrumAnalysisForecast()メソッドによって提供されます。時系列をSSAで分解・再構成した後、予測ステップでは通常、再帰型予測アルゴリズムが使用されます。このアルゴリズムは、再構成された成分がしばしば満たす線形再帰関係(LRR: Linear Recurrent Relation)を利用します。再構成された成分は、ある程度予測可能なパターンに従うと仮定されます。具体的には、特異ベクトルと再構成時系列を基に、過去の値と未来の値の線形関係を表す一連の係数が算出されます。新しいデータ点を予測する際には、再構成時系列の直近「ウィンドウ長」の値を、算出された係数で重み付けした線形結合を適用します。このプロセスを繰り返すことで、複数の予測値を生成することが可能です。

//---
   vector forecast;
   if(!full_process.SingularSpectrumAnalysisForecast(WindowLen,FilterComponents,ForecastLen,forecast))
     {
      Print(" error ", GetLastError());
      return;
     }
//---

この予測手法は、過去のパターンが未来でも同様に現れることを前提としています。もちろん、現実の時系列データではこの仮定が正確に成り立つことは稀です。それでも、SSAを用いることで、一定の規則性を持つ成分に注目して複雑なプロセスをより予測可能にすることができます。

パラメータの選択と前処理

SSAによる時系列の分解では、元の時系列の正確な周期成分を抽出することはできず、あくまで成分の推定を得るに留まることがすでに示されています。これはSSAの明白な制約であり、さらにウィンドウ長の選択に非常に敏感である点が、この制約をより顕著にします。ウィンドウ長の適切な選択は、分解の目的によって決まります。トレンドの抽出が主目的の場合、ウィンドウ長は大きいほど望ましいです。ただし、振動成分の抽出が主目的の場合は、振動の周期を考慮してウィンドウ長を設定します。たとえば、周期20の成分を抽出したい場合、ウィンドウ長を20に設定します。

学術文献に基づく経験則では、ウィンドウ長Lに対して、周期L/5からLの振動を分解する解像度が得られるとされています。しかし、対象とする成分の周期は事前にわからないことが多いため、試行錯誤が必要です。一般的な目安として、ウィンドウ長は解析対象時系列の長さの半分から全長の半分程度に設定することが推奨されます。ウィンドウ長が長いほど、ゆっくり変動する成分が強調され、短いほど、細かい変動を捉えやすくなります。

SSAはウィンドウ長の選択に敏感であることに加えて、実務者は時系列内に存在する強いトレンドが分解結果にどのような影響を及ぼすかも理解しておく必要があります。強いトレンドは、時系列中の他の低周波成分を覆い隠してしまうことがあります。この問題は、SSAを適用する前に元の時系列をデトレンド（トレンド除去）することで主に対処できます。適用可能な前処理としては、平均値の除去や線形トレンドの除去などがあり、以下のコードスニペットにその例を示します。

//---
   if(m_detrend)
     {
      vector reg = m_buffer.LinearRegression();
      m_buffer -= reg;
     }
//---

フィルタリングや予測の際に選択する成分数を決定する場合、相対寄与率および累積寄与率のプロットが非常に有用です。相対寄与率のプロットで注目すべき特徴は「エルボー」ポイントであり、これによって信号とノイズを区別できます。信号に対応するプロット上の点は、値がゆるやかにゼロへ近づく点の手前で明確な区切りを持つ領域の上に現れます。同様の傾向は、分解過程で得られる生の固有値の減衰を観察する際にも確認できます。もう一つの有効な方法として、総分散のうちどの程度を説明したいか（通常85%～95%）という目標値を設定し、累積寄与率の系列の中からその値に対応する成分数を取得するという手段もあります。

コンポーネントのグループ化

SSAによる分解は、時系列の基礎となる成分を完全に再現する魔法のような手法ではないことはすでに確認しています。先ほどの単純な例でも見たように、SSAによって得られるのは、実際の構成成分を近似した一連の成分です。ここで重要なのは、それらの推定成分をどのように組み合わせれば、プロセスを定義する実際の要素をより正確に把握できるかを見極めることです。これを実現する方法のひとつが、成分時系列の加重相関行列を構築することです。加重相関行列は、成分時系列のペアが完全な直交性からどの程度ずれているかを測定します。もし成分のペアが完全に直交している場合、それらはおそらく異なる成分を表していると考えられます。

一方で、相関が高い成分同士は、同一の特徴や周期を表している可能性が高く、組み合わせて再構成することが望ましいと判断されます。以下のコードスニペットは、SSA分解で得られた成分時系列の行列およびウィンドウ長パラメータをもとに、加重相関行列を計算するルーチンの一例です。この関数は記事に添付されたssa.mqh内で定義されています。 

//+------------------------------------------------------------------+
//| component correlations                                           |
//+------------------------------------------------------------------+
matrix component_corr(ulong windowlen,matrix &components)
  {
   double w[];
   ulong fsize = components.Cols();
   ulong r = fsize - windowlen + 1;
  
   for(ulong i = 0; i<fsize; i++)
     {
      if(i>=0 && i<=windowlen-1)
         w.Push(i+1);
      else
         if(i>=windowlen && i<=r-1)
            w.Push(windowlen);
         else
            if(i>=r && i<=fsize-1)
               w.Push(fsize-i);
     }

   vector weights;
   weights.Assign(w);
   ulong d = windowlen;

   vector norms(d);
   matrix out = matrix::Identity(d,d);

   for(ulong i = 0; i<d; i++)
     {
      norms[i] = weights.Dot(pow(components.Row(i),2.0));
      norms[i] = pow(norms[i],-0.5);
     }

   for(ulong i = 0; i<d; i++)
     {
      for(ulong j = i+1; j<d; j++)
        {
         out[i][j] = MathAbs(weights.Dot(components.Row(i)*components.Row(j))*norms[i]*norms[j]);
         out[j][i] = out[i][j];
        }
     }

   return out;
  }

以下は、例として用いた時系列における上位6つの成分間の相関関係の一部を示したものです。

このグラフィックでは、インデックス(1:2)の成分間に高い相関が見られ、これは成分2と成分3が互いに関連していることを示しています。同様に、インデックス(3:4)で参照されるのは、成分4と成分5の関係です。この分析結果は、先に示した相対寄与率プロットの視覚的観察と一致しているように見えます。ここから、これら2つの成分グループが、例として用いた時系列の周期成分を表している可能性があると仮定できます。一方で、最上位の単一成分は他の成分とは明確に区別されており、トレンド成分である可能性が高いと考えられます。先に確認した累積寄与率の結果からも、この5つの成分だけで全体の約98%を説明しており、残りの成分はノイズ成分であると推定されます。

価格系列の分解の表示

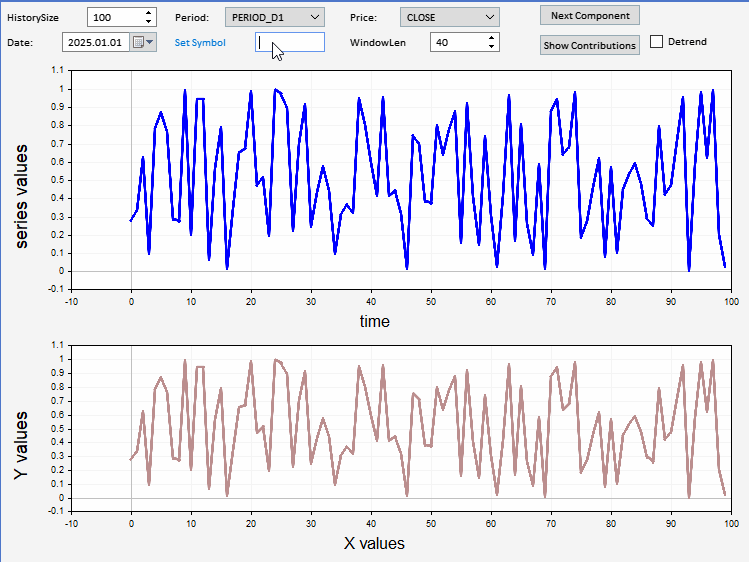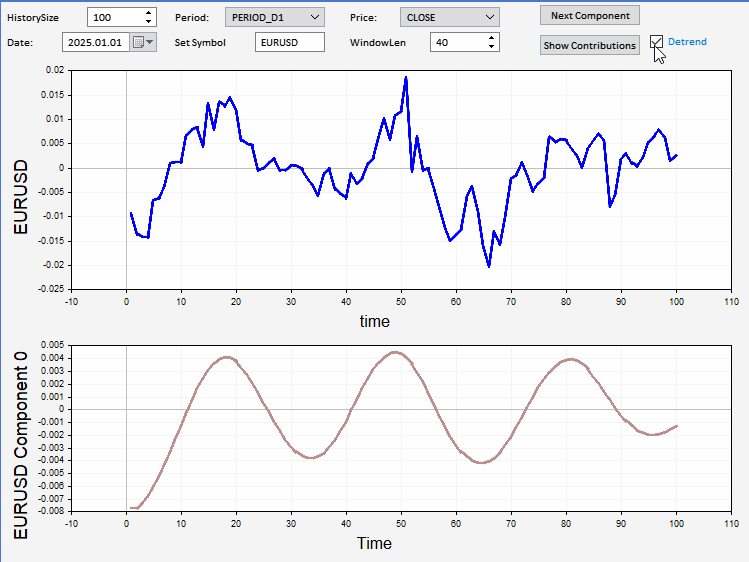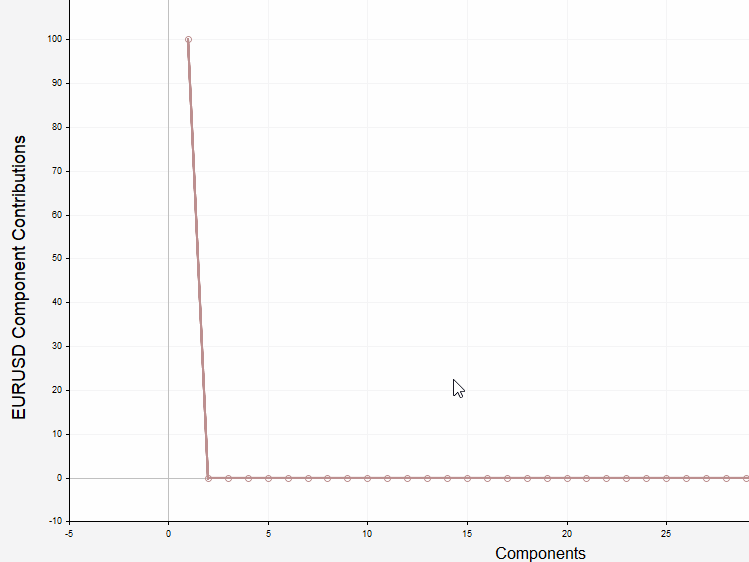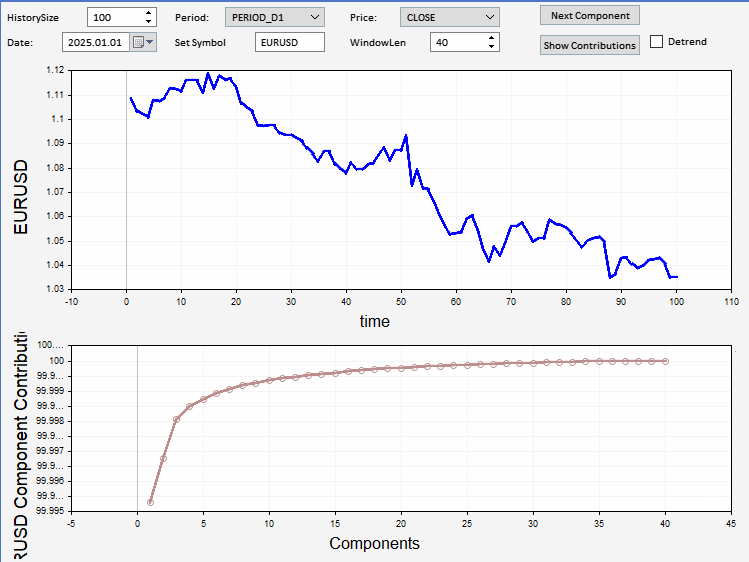
このセクションでは、任意の価格サンプルの成分を可視化できるように実装されたエキスパートアドバイザー(EA)の応用例を紹介します。このアプリケーションにはグラフィカルユーザーインターフェース(GUI)が備わっており、ユーザーは表示および分解をおこなう銘柄、日付、および価格時系列の長さを設定することができます。また、分解をおこなう前にデトレンド処理をおこなうオプションも用意されています。さらに、相対寄与率プロットおよび累積寄与率プロットを表示するオプションも選択可能です。以下のスクリーンショットは、アプリケーションがEURUSDの終値サンプルを表示し、その分解成分の一部を下部のプロットに描画している様子を示しています。

結論

本記事では、MQL5における新しい特異スペクトル解析(SSA: Singular Spectrum Analysis)ツールについて取り上げ、ベクトルデータ型へのOpenBLASの追加機能に焦点を当てて解説しました。SSA手法の概要を、数理的な詳細説明を避けながらも簡潔に紹介し、その仕組みと実用上のポイントを整理しました。まとめると、SSAは非常に有用な分析ツールではあるものの、パラメータ選択の慎重さと手法の動作特性に対する理解が不可欠であり、これらを踏まえることで初めて高い効果を発揮します。参照されるすべてのコードは以下に含まれており、添付されています。 

ファイル名	ファイルの説明
MQL5/include/ssa.mqh	「成分のグループ化」セクションで説明した、成分相関の計算を実装する関数の定義を含むヘッダファイル
MQL5/scripts/SSA_Filtered_Demo.mq5	SSAを用いたフィルタリング処理を実演するためのスクリプト
MQL5/scripts/SSA_Decomposition_Demo.mq5	SSAによる時系列分解を実演するためのスクリプト
MQL5/scripts/SSA_ComponentContributions_Demo.mq5	成分の相対寄与率を表示するデモ用スクリプト
MQL5/scripts/SeriesPlot.mq5	本記事で参照した例示時系列の各成分をプロットするために使用されたスクリプト
MQL5/experts/SSA_PriceDecomposition.ex5	任意の価格時系列を分解して表示するためのEAプログラム
MQL5/experts/SSA_PriceDecomposition.mq5	上記のEAのソースコード