Singuläre Spektralanalyse in MQL5

Was ist die SSA?

In den letzten Iterationen von MetaTrader 5 wurden die ersten OpenBLAS-Methoden in die zentralen Vektor- und Matrix-Datentypen integriert. Von besonderem Interesse sind eine Reihe von Methoden im Zusammenhang mit der Singular Spectrum Analysis (SSA). In diesem Artikel untersuchen wir die neuen Werkzeuge, die in MQL5 im Zusammenhang mit SSA zur Verfügung stehen, und erläutern, wie sie bei Analysen und Prognosen eingesetzt werden können. Dieser Leitfaden soll ein Hilfsmittel für Händler sein, die das volle Potenzial der SSA ausschöpfen wollen. Wir werden uns mit der SSA-Methode befassen und ihren zweistufigen Zerlegungs- und Rekonstruktionsprozess entmystifizieren. Vor allem aber werden wir erörtern, was die einzelnen neuen SSA-Vektormethoden bewirken, und zeigen, wie man ihre Ergebnisse interpretiert und optimal kombiniert, um verwertbare Erkenntnisse zu gewinnen.

Die Singularspektralanalyse ist ein nichtparametrisches Verfahren, das für die Analyse und Vorhersage von Zeitreihendaten entwickelt wurde. Ihr Ziel ist es, eine Zeitreihe in einige wenige additive Komponenten zu zerlegen, zu denen in der Regel ein sich langsam verändernder Trend, verschiedene Zyklen und Restrauschen gehören. Die SSA zeichnet sich dadurch aus, dass sie sich nur in geringem Maße auf vorher festgelegte Annahmen über den zugrunde liegenden Datenerzeugungsprozess stützt. Die konzeptionelle Grundlage von SSA integriert Elemente aus Statistik und Signalverarbeitung. SSA basiert im Wesentlichen auf der spektralen Zerlegung, die es ermöglicht, die Frequenzmerkmale einer Zeitreihe durch die Analyse ihrer Hauptkomponenten in einem rekonstruierten Einbettungsraum aufzudecken. Sie kann effektiv als eine Form der Hauptkomponentenanalyse (PCA) betrachtet werden, die speziell für Zeitreihendaten angepasst wurde und die Prinzipien der Dimensionenreduktion nutzt, um verborgene Strukturen und Muster aufzudecken, die durch Rauschen oder komplexe Interaktionen verdeckt werden könnten.

SSA in MQL5

In MQL5 sind SSA-Berechnungen nativ als Methoden des Vektordatentyps und auch in der mathematischen Bibliothek Alglib implementiert. Die Stärke der Alglib-Implementierung von SSA liegt vor allem in der Echtzeitverarbeitung, während die neue SSA-Funktionalität, die direkt von Vektoren aus zugänglich ist, eher für explorative Analysen geeignet ist. Beachten Sie, dass sich dieser Text zwar in erster Linie mit Operationen mit reellen Zahlen befasst, es aber auch äquivalente Methoden für komplexe Zahlen gibt, die in ähnlicher Weise funktionieren und deren Interpretation auf den komplexen Bereich zugeschnitten ist.

Bei jeder der neuen Vektor-SSA-Methoden ist der erste erforderliche Parameter die Angabe einer Fensterlänge. Dieser Parameter bestimmt, wie die Zeitreihe in eine höherdimensionale Struktur, die so genannte Trajektorienmatrix, umgewandelt wird. Man mag sich fragen: „Warum ist diese höherdimensionale Struktur notwendig?“ Der Schlüssel dazu liegt in der Beziehung zwischen SSA und PCA. Zur Erinnerung: PCA ist ein Verfahren zur Dimensionenreduktion, das bei multivariaten Datensätzen eingesetzt wird. SSA rekonstruiert eine univariate Zeitreihe in eine Struktur, die einem multivariaten Datensatz ähnelt. Dies geschieht durch die Anordnung von Abschnitten der Serie in gleich großen Reihen. Hier wird die Größe einer Zeile durch den Parameter Fensterlänge definiert.

Betrachten Sie eine Zeitreihe Y=[y1,y2​,y3​,y4​,y5​,y6​] der Länge N=6. Wählt man eine Fensterlänge von L=3, so ergibt sich eine Trajektorienmatrix, die der folgenden entspricht.

Die Anzahl der Zeilen, R, in der Matrix wird berechnet als R=N-L+1. In diesem Beispiel ist R=6-3+1=4. Diese Matrix mit der Dimension R×L (in unserem Beispiel 4×3) ist die Trajektorienmatrix. Die auf den Antidiagonalen dieser Matrix beobachteten Muster sind charakteristisch für eine Hankel-Matrix. Die Konstruktion der Trajektorienmatrix ist der erste Schritt der SSA-Methode. Es überrascht daher nicht, dass die Fensterlänge ein entscheidender Parameter der SSA-Methode ist, da sie direkt die Dimensionen der Trajektorienmatrix bestimmt, die wiederum die Auflösung und Trennbarkeit der spektralen Zerlegung erheblich beeinflusst.

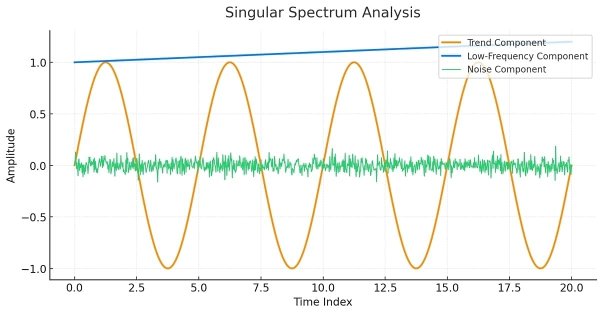
Um die Konzepte der SSA-Methode zu verdeutlichen, werden wir ihre Anwendung auf eine deterministische Reihe demonstrieren, die im Folgenden dargestellt wird.

Diese Reihe wurde aus vorgegebenen additiven Komponenten konstruiert, die aus einem Trend, einigen periodischen Komponenten und zufälligem Rauschen bestehen. Wenn diese Komponenten addiert werden, ergibt sich eine etwas unregelmäßige Reihe. Das Ziel von SSA ist es, diese zugrunde liegenden Komponenten aufzudecken. Dazu wird entweder die Trajektorienmatrix oder die Kovarianzmatrix der Trajektorienmatrix zerlegt, was die Eigenmoden ergibt, die, wie bei der PCA, die Hauptkomponenten der Reihe aufzeigen.

Relative und kumulative Beiträge der Komponenten

Die MQL5-Vektormethode, SingularSpectrumAnalysisSpectrum(), gibt einen Vektor aus, der die relativen Komponentenbeiträge einer Reihe darstellt. Dieser Vektor enthält reelle Zahlen, deren Summe eins ergibt und die die fraktionale Dominanz jeder Komponente in absteigender Reihenfolge angeben. Diese Beiträge entsprechen den relativen Größenordnungen der Eigenwerte, die durch die Zerlegung einer Matrix berechnet werden.

//---
   vector relative_contributions;
   if(!full_process.SingularSpectrumAnalysisSpectrum(WindowLen,relative_contributions))
     {
      Print(" error ", GetLastError());
      return;
     }
//---
   relative_contributions*=100.0;
   vector cumulative_contributions = relative_contributions.CumSum();

Wenn die kumulierte Summe der relativen Beiträge berechnet wird, erhält man die kumulierten Beiträge. Anhand dieser Werte lässt sich schnell die geringste Anzahl von Komponenten ermitteln, die erforderlich ist, um eine relativ gute Annäherung an die ursprüngliche Reihe zu erreichen. Ein Diagramm der relativen Beiträge zeigt oft deutliche, ungefähre Plateaus, was darauf hindeutet, dass einige Komponentenbeiträge einen ähnlichen Wert haben. Diese Ähnlichkeit deutet in der Regel darauf hin, dass diese Komponenten ein einziges periodisches Element darstellen können.

Nachfolgend sind die relativen und kumulativen Beiträge für unsere Beispielreihen dargestellt.

Diese zeigen, dass die ersten beiden Komponenten etwa 68 % und 12 % der Gesamtvarianz der Reihe ausmachen.

Allein auf die ersten fünf Komponenten entfallen über 98 %. Die Darstellung der relativen Beiträge zeigt eine einzigartige Form, die die Dominanz der ersten 5 Komponenten deutlich macht. Der Punkt, der die dominanten Komponenten vom Rest trennt, wird in der Regel als „Ellbogenpunkt“ bezeichnet, und die Komponenten unterhalb dieses Pegels werden als „Grundrauschen“ bezeichnet. Sie liefert eine grobe Schätzung der Trennung des Signals vom Rauschen. Ein weiterer bemerkenswerter Aspekt der Darstellung der relativen Beiträge ist die Tatsache, dass die Komponenten Nummer zwei und drei von der vierten und fünften Komponente getrennt sind. Dies ist ein Hinweis darauf, dass diese gepaarten Gruppen miteinander verwandt sind und möglicherweise einzigartige Merkmale der Serie darstellen.

Extraktion von Serienkomponenten

Nachdem wir unsere Beispielreihe analysiert haben, kennen wir nun die wichtigsten Komponenten, die den Großteil ihres Verhaltens bestimmen. Um ihre Regelmäßigkeit zu beurteilen, kann es von Vorteil sein, diese Komponenten zu visualisieren. An dieser Stelle erweist sich die Vektormethode SingularSpectrumAnalysisReconstructComponents() als nützlich. Die Ausgabe von besonderem Interesse ist die Matrix der Komponentenreihen. Beachten Sie jedoch, dass die MQL5-Dokumentation zwar nahelegt, dass die Spalten die geschätzten Komponentenreihen darstellen, die Methode aber tatsächlich jede Komponentenreihe als eine Zeile in der Matrix speichert. Außerdem enthält die Vektorausgabe der Methode die rohen Eigenwerte der Zerlegung der repräsentativen Matrix der Reihe.

//---
   matrix components;
   vector eigvalues;
   if(!full_process.SingularSpectrumAnalysisReconstructComponents(WindowLen,components,eigvalues))
     {
      Print(" error ", GetLastError());
      return;
     }
//---

Die Zeilen der Matrix der Komponentenreihen sind in abnehmender Reihenfolge der relativen Höhe der Beiträge angeordnet. Folglich enthält die erste Zeile die Komponente mit dem größten Eigenwert, die auch die Komponente mit dem größten relativen Beitrag darstellt. Nachfolgend sehen Sie eine Darstellung aller Komponenten unserer Beispielreihe.

Wenn Sie dies mit einem Diagramm der Originalkomponenten vergleichen, werden Sie einige Diskrepanzen feststellen. Dies unterstreicht die Tatsache, dass die SSA-Zerlegung nicht exakt ist. Die Methode wird niemals in der Lage sein, die genauen periodischen Komponenten einer Reihe zu entschlüsseln. Alles, was es tun kann, ist, optimale Annäherungen oder Schätzungen für diese Komponenten zu finden. Dennoch ergibt die Summierung der einzelnen Teilreihen die ursprüngliche Reihe.

Filtern

Mit dem Satz von Komponentenreihen in der Hand können wir die Informationen aus der SSA-Analyse nutzen, um abzuleiten, welche Komponenten das zugrunde liegende Signal beschreiben und welche nicht-deterministisches Rauschen darstellen. Wenn unser Hauptaugenmerk auf den dominanten Zyklen liegt, können wir Komponenten mit geringeren relativen Beiträgen verwerfen, um eine gefilterte Reihe zu erhalten. Dabei gehen wir davon aus, dass diese geringeren Komponenten Rauschen darstellen, das das Hauptsignal verdeckt.

Nutzer können diese Filterung direkt für eine Reihe mit der Methode SingularSpectrumAnalysisReconstructSeries() durchführen. Der Nutzer gibt die Anzahl der dominanten Komponenten an, die in die gefilterte Reihe aufgenommen werden sollen.

//---
   vector filtered;
   if(!full_process.SingularSpectrumAnalysisReconstructSeries(WindowLen,FilterComponents,filtered))
     {
      Print(" error ", GetLastError());
      return;
     }

Die SSA-Methode ist im Allgemeinen gut geeignet, um Rauschen zu isolieren, aber ihre Wirksamkeit hängt von der Art des im Prozess vorhandenen Rauschens ab. Das einfache Ausschließen von Komponenten mit geringeren relativen Beiträgen reicht möglicherweise nicht aus, um das Rauschen endgültig zu isolieren. Dies hat folglich auch Auswirkungen auf die Extraktion von Signalen, Trends oder spezifischen periodischen Komponenten. Die Interpretation dieser Komponenten muss häufig durch statistische Signifikanztests validiert werden. Ein weiterer Aspekt, der die Isolierung bestimmter Komponenten beeinträchtigen kann, ist das Vorhandensein starker Trends, deren Dominanz andere niederfrequente Schwingungen in den Daten überdecken kann.

Vorhersagen

Einer der interessantesten Aspekte der SSA-Methodik ist ihre Anwendung auf die Vorhersage. Diese Funktion wird von der Methode SingularSpectrumAnalysisForecast() bereitgestellt. Sobald die Zeitreihe zerlegt und rekonstruiert ist, wird für die Vorhersage in der Regel ein rekurrenter Vorhersagealgorithmus verwendet. Dieser Algorithmus nutzt die inhärente Linear Recurrent Relation (LRR), die die rekonstruierten Komponenten häufig erfüllen. Es wird davon ausgegangen, dass diese rekonstruierten Komponenten einem vorhersehbaren Muster folgen. Auf der Grundlage der singulären Vektoren und der rekonstruierten Reihe wird ein Satz von Koeffizienten bestimmt. Diese Koeffizienten stellen die lineare Beziehung zwischen vergangenen und zukünftigen Werten innerhalb des rekonstruierten Signals dar. Zur Vorhersage eines neuen Datenpunktes wendet der Algorithmus eine lineare Kombination der vorherigen Werte der rekonstruierten Reihe mit „Fensterlänge“ an, gewichtet mit den ermittelten Koeffizienten. Dieser Prozess wird dann iterativ wiederholt, um mehrere Prognosen zu erstellen.

//---
   vector forecast;
   if(!full_process.SingularSpectrumAnalysisForecast(WindowLen,FilterComponents,ForecastLen,forecast))
     {
      Print(" error ", GetLastError());
      return;
     }
//---

Es sollte klar sein, dass solche Prognosen davon ausgehen, dass sich frühere Muster in der Zukunft genauso manifestieren werden wie in der Vergangenheit. Natürlich ist es unwahrscheinlich, dass dies auf reale Zeitreihen zutrifft. Trotzdem kann SSA nützlich sein, um komplexe Prozesse berechenbarer zu machen, indem man sich auf bestimmte Komponenten mit regelmäßigen Wellenformen konzentriert.

Parameterauswahl und Vorverarbeitung

Es wurde bereits festgestellt, dass die Zerlegung von Reihen mit SSA niemals in der Lage sein wird, die genauen periodischen Komponenten einer Zeitreihe zu extrahieren. Es kann lediglich Schätzungen der Komponenten extrahieren. Dies ist eine offensichtliche Einschränkung der Methode, die durch die Empfindlichkeit der Methode gegenüber der gewählten Fensterlänge noch verschärft wird. Die Wahl der richtigen Fensterlänge kann sich an den Zielen der Zerlegung orientieren. Wenn das Interesse in erster Linie darin besteht, den Trend zu isolieren, dann ist es umso besser, je größer die Fensterlänge ist. Wenn jedoch oszillierende Komponenten von größerer Bedeutung sind, sollten Praktiker die Schwingungsperioden berücksichtigen; wenn man beispielsweise nach einer periodischen Komponente sucht, die mit einer Periode von 20 schwingt, sollte man die Fensterlänge auf 20 einstellen.

Die in der Fachliteratur vorgestellten empirischen Belege legen nahe, dass die Fensterlänge der Auflösung von Schwingungen mit Perioden im Bereich von L/5 bis L entspricht, wobei L die Fensterlänge ist. Das Problem besteht darin, dass die Periode der interessierenden Komponente möglicherweise nicht im Voraus bekannt ist, sodass eine Menge Versuch und Irrtum erforderlich ist. Als allgemeine Faustregel gilt, dass die Länge des Fensters zwischen zweieinhalb Mal der Länge der untersuchten Reihe liegen sollte. Eine größere Fensterlänge verstärkt die langsamer schwankenden Komponenten, während kleinere Fensterlängen feinere Details erfassen.

Neben der Empfindlichkeit von SSA gegenüber der Fensterlänge sollten Praktiker auch wissen, wie starke Trends in Zeitreihen die Ergebnisse der Zerlegung beeinflussen können. Starke Trends können andere niederfrequente Komponenten in den Reihen verdecken. Dieses Problem kann in erster Linie durch Detrending der Rohreihen vor der Anwendung von SSA gelöst werden. Zu den Arten der Vorverarbeitung, die angewandt werden können, gehören das Zentrieren oder das Entfernen des linearen Trends, wie im nachstehenden Codeschnipsel gezeigt.

//---
   if(m_detrend)
     {
      vector reg = m_buffer.LinearRegression();
      m_buffer -= reg;
     }
//---

Wenn es darum geht zu entscheiden, wie viele Komponenten bei der Filterung oder Vorhersage ausgewählt werden sollen, können Darstellungen der relativen und kumulativen Beiträge eine große Hilfe sein. Das Merkmal, das auf einer Grafik der relativen Beiträge zu erkennen ist, ist der „Ellbogenpunkt“, der das Signal vom Rauschen unterscheidet. Die Punkte auf dem Diagramm, die mit einem Signal verbunden sind, erscheinen oberhalb einer deutlichen Unterbrechung von Punkten, deren Werte langsam gegen Null sinken. Das Gleiche sollte bei der Untersuchung des Abklingens der rohen Eigenwerte des Zerlegungsprozesses zu sehen sein. Eine andere Möglichkeit besteht darin, einen Zielwert für den Gesamtprozentsatz der zu erfassenden Varianz festzulegen, in der Regel 85 % bis 95 %, und dann die Anzahl der Komponenten zu ermitteln, denen dieser Wert in der Reihe der kumulativen Beiträge entspricht.

Gruppierung der Komponenten

Wir wissen, dass die SSA-Zerlegung nicht auf magische Weise die genauen zugrundeliegenden Komponenten einer Reihe wiedergibt; wir haben dies an einem einfachen Beispiel gesehen. Wir erhalten eine Reihe von Komponenten, die der tatsächlichen Reihe der Bestandteile nahe kommen. Wir müssen nur herausfinden, wie wir unsere Schätzungen kombinieren können, um ein besseres Bild von den tatsächlichen Elementen zu erhalten, die den Prozess bestimmen. Dies kann durch die Konstruktion der gewichteten Korrelationsmatrix der Komponentenreihen erreicht werden. Die gewichtete Korrelationsmatrix misst, inwieweit ein Paar von Komponentenreihen von der perfekten Orthogonalität abweicht. Wenn ein Paar von Serienkomponenten vollkommen orthogonal ist, handelt es sich wahrscheinlich um unterschiedliche Komponenten.

Höhere Korrelationen zeigen an, dass ein Paar kombiniert werden sollte. Der nachstehende Codeausschnitt zeigt eine Routine, die die gewichtete Korrelationsmatrix aus einer Matrix von Komponentenreihen und dem Parameter für die Fensterlänge der SSA-Zerlegung berechnet. Die Funktion wird in ssa.mqh deklariert, die dem Artikel beigefügt ist. 

//+------------------------------------------------------------------+
//| component correlations                                           |
//+------------------------------------------------------------------+
matrix component_corr(ulong windowlen,matrix &components)
  {
   double w[];
   ulong fsize = components.Cols();
   ulong r = fsize - windowlen + 1;
  
   for(ulong i = 0; i<fsize; i++)
     {
      if(i>=0 && i<=windowlen-1)
         w.Push(i+1);
      else
         if(i>=windowlen && i<=r-1)
            w.Push(windowlen);
         else
            if(i>=r && i<=fsize-1)
               w.Push(fsize-i);
     }

   vector weights;
   weights.Assign(w);
   ulong d = windowlen;

   vector norms(d);
   matrix out = matrix::Identity(d,d);

   for(ulong i = 0; i<d; i++)
     {
      norms[i] = weights.Dot(pow(components.Row(i),2.0));
      norms[i] = pow(norms[i],-0.5);
     }

   for(ulong i = 0; i<d; i++)
     {
      for(ulong j = i+1; j<d; j++)
        {
         out[i][j] = MathAbs(weights.Dot(components.Row(i)*components.Row(j))*norms[i]*norms[j]);
         out[j][i] = out[i][j];
        }
     }

   return out;
  }

Nachfolgend ist ein Ausschnitt der Komponenten-Korrelationen dargestellt, aus denen sich die sechs wichtigsten Komponenten unserer Beispielreihe zusammensetzen.

Die Grafik zeigt die hohe Korrelation zwischen den Komponenten bei Index (1:2), was der Beziehung zwischen den Komponenten 2 und 3 entspricht, während die Komponenten bei Index (3:4) auf die Beziehung zwischen den Komponenten 4 und 5 verweisen. Diese Analyse scheint mit der visuellen Inspektion der relativen Beiträge übereinzustimmen, die wir zuvor gesehen haben. Von hier aus könnte man die Hypothese aufstellen, dass die beiden Gruppen von Komponenten auf die periodischen Komponenten unserer Beispielreihe hinweisen könnten. Die einzelne oberste Komponente ist deutlich und wahrscheinlich der Trend. Wie wir bereits bei den kumulierten Beiträgen gesehen haben, tragen diese 5 Komponenten zu 98 % bei; der Rest ist also wahrscheinlich Rauschen.

Anzeige von Preisreihenzerlegungen

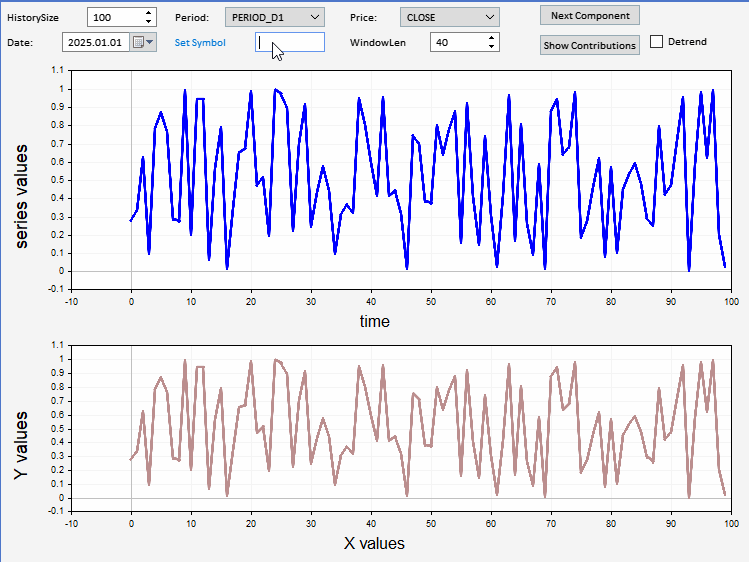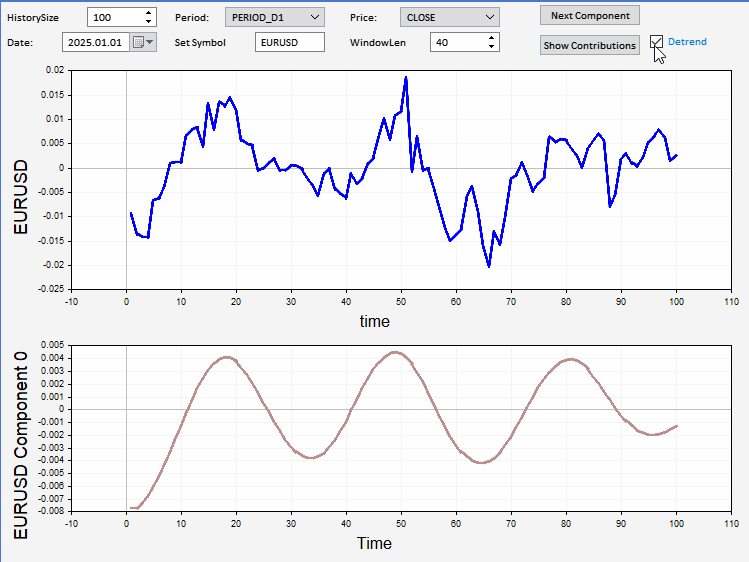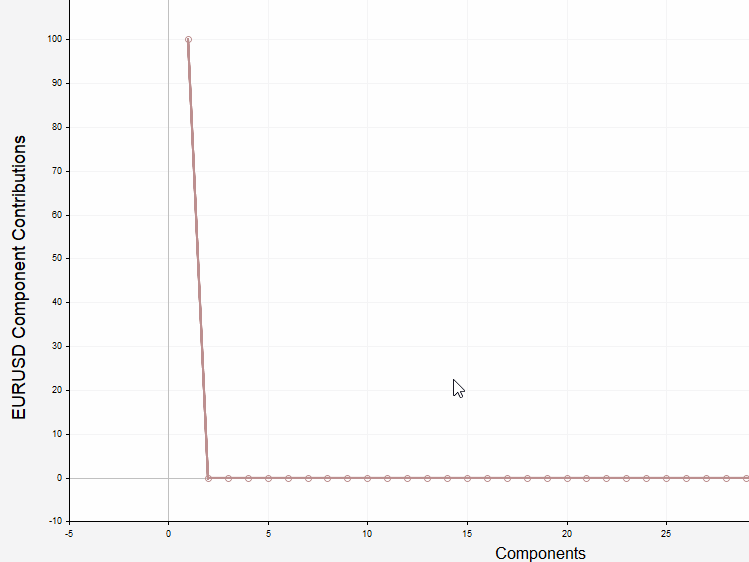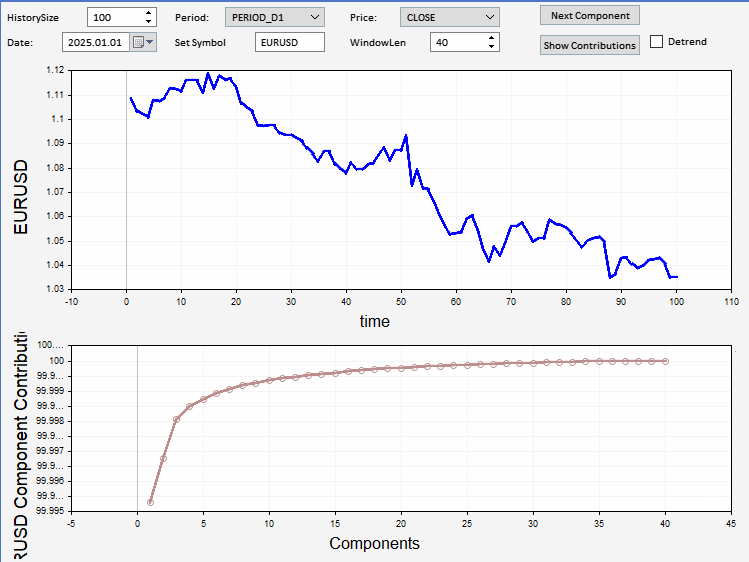
In diesem Abschnitt stellen wir eine als Expert Advisor implementierte Anwendung vor, mit der die Komponenten einer beliebigen Preisstichprobe angezeigt werden können. Die Anwendung verfügt über eine grafische Nutzeroberfläche, die es dem Nutzer ermöglicht, das Symbol, das Datum und die Länge der anzuzeigenden und aufzuschlüsselnden Preisreihen einzustellen. Es besteht die Möglichkeit, die Reihen vor der Zerlegung zu detrendieren. Die relativen und kumulativen Beiträge können optional ebenfalls angezeigt werden. Unten sehen Sie einen Screenshot der Anwendung, der ein Beispiel für EURUSD-Schlusskurse anzeigt, mit einer zerlegten Komponente, die im unteren Diagramm angezeigt wird.

Schlussfolgerung

In diesem Artikel wurden die neuen MQL5-Werkzeuge für die Singular Spectrum Analysis (SSA) untersucht, wobei die OpenBLAS-Ergänzungen zum Vektordatentyp hervorgehoben wurden. Wir haben einen knappen Überblick über die SSA-Methode gegeben und dabei bewusst auf tiefgreifende mathematische Erklärungen verzichtet. Zusammenfassend lässt sich sagen, dass SSA ein wertvolles Instrument für jeden Praktiker ist, das jedoch eine sorgfältige Auswahl der Parameter und ein Verständnis der operativen Nuancen erfordert, um seine volle Wirkung zu entfalten. Der gesamte referenzierte Code ist enthalten und unten angefügt. 

Dateiname	Beschreibung der Datei
MQL5/include/ssa.mqh	Diese Header-Datei enthält die Definition der Funktion, die die im Abschnitt Komponentengruppierung beschriebenen Berechnungskomponenten-Korrelationen implementiert.
MQL5/scripts/SSA_Filtered_Demo.mq5	Dies ist das Skript, das zur Demonstration der Filterung mit SSA verwendet wird.
MQL5/scripts/SSA_Decomposition_Demo.mq5	Dies ist das Skript, das zur Demonstration der Zerlegung einer Reihe mit SSA verwendet wird.
MQL5/scripts/SSA_ComponentContributions_Demo.mq5	Dies ist das Skript, mit dem die Anzeige der relativen Komponentenbeiträge demonstriert wird.
MQL5/scripts/SeriesPlot.mq5	Dieses Skript wurde verwendet, um die verschiedenen Komponenten der im Artikel erwähnten Beispielreihe darzustellen.
MQL5/experts/SSA_PriceDecomposition.ex5	Dieser EA ist ein Programm, mit dem man die Zerlegung einer beliebigen Preisreihe darstellen kann.
MQL5/experts/SSA_PriceDecomposition.mq5	Dies ist der Quellcode für den oben genannten EA.