Применение ансамблевых методов для задач классификации на языке MQL5

MetaTrader 5 — Статистика и анализ | 11 августа 2025, 08:06

345

Francis Dube

Введение

В предыдущей статье мы исследовали методы комбинирования моделей для численных прогнозов. Данная статья дополняет это исследование, делая акцент на ансамблевых методах, предназначенных специально для задач классификации. Одновременно с этим мы также рассмотрим стратегии по использованию компонентных классификаторов, которые генерируют классовые ранги на порядковой шкале. Несмотря на то, что применение численных методик комбинирования допустимо для решения задач классификации в некоторых ситуациях, в которых модели полагаются на числовые выводы, многие классификаторы придерживаются менее гибкого подхода, производя только дискретные классовые решения. Кроме того, классификаторы на основе численных методов зачастую демонстрируют нестабильные прогнозы, что подчеркивает необходимость в разработке специализированных методов комбинирования.

Ансамбли-классификаторы, обсуждаемые в данной статье, работают на основе определенных предположений об их моделях-компонентах. Во-первых, предполагается, что эти модели обучаются на данных со взаимоисключающими и исчерпывающими целевыми классами, обеспечивая, чтобы каждый экземпляр принадлежал только к одному классу. Когда требуется опция "ничего из вышеперечисленного", ее следует либо рассматривать как отдельный класс, либо управлять ею с помощью численных методов комбинирования с определенным порогом принадлежности. Также, когда предоставляется входной вектор из предикторов, ожидается, что модели-компоненты будут производить N выводов, где N представляет количество классов. Этими выводами могут быть значения вероятности или рейтинги достоверности, которые обозначают вероятность принадлежности для каждого из классов. Ими также могут быть бинарные решения, когда один вывод равен 1.0 (true), а остальные – 0.0 (false), либо выводы модели могут быть целыми числами от 1 до N, отражающими относительную вероятность принадлежности к классу.

Некоторые из ансамблевых методов, которые мы рассмотрим, получают значительные преимущества за счет классификаторов-компонентов, которые производят ранжированные выводы. Модели, способные точно оценивать вероятности принадлежности к классам, обычно высоко ценятся, но существует значительный риск рассмотрения выводов как вероятностей, в то время как они не являются таковыми. Когда имеются сомнения касательно того, что представляют собой выводы модели, может быть полезно конвертировать их в ранги. Полезность информации о рангах растет с увеличением числа классов. Для бинарной классификации ранги не предоставляют какой-либо дополнительной информации, и их ценность для решения задач трех классов остается скромной. Тем не менее, в сценариях с большим количеством классов способность интерпретировать второстепенные варианты выбора модели становится крайне полезной, в частности когда отдельные прогнозы сопряжены с высокой неопределенностью. К примеру, машины опорных векторов (SVM) могут быть усовершенствованы таким образом, чтобы выдавать не только бинарную классификацию, но также и расстояния между границами решений для каждого класса, тем самым предлагая более детальную информацию о достоверности в прогнозах.

Ранги также помогают справится с ключевой задачей при работе с ансамблевыми методами, а именно с нормализацией выводов от различных моделей классификации. Рассмотрим две модели Рассмотрим две модели, анализирующие рыночные движения: одна из них специализируется на краткосрочных колебаниях цены на высоколиквидных рынках, в то время как другая работает с долгосрочными трендами, длящимися недели или месяцы. Более широкий фокус второй модели может привнести шум в краткосрочные прогнозы. Конвертация достоверности классовых решений в ранги минимизирует данную проблему, гарантируя, что ценная краткосрочная информация не будет оставлена в тени более долгосрочных трендовых сигналов. Данный подход обеспечивает более сбалансированное и эффективное ансамблевое прогнозирование.

Альтернативные цели комбинирования классификаторов

Основной целью применения ансамблевых классификаторов обычно является улучшение точности классификации. Но это не обязательно так всегда, поскольку в некоторых задачах классификации может быть полезно посмотреть дальше этой конкретной цели. Помимо базовой точности классификации можно принять более замысловатые критерии успеха на случай сценариев, в которых первоначальное решение может быть неверным. Учитывая это, подходы к классификации могут преследовать две различные, но взаимодополняющие цели, каждая из которых может выступать в качестве метрики эффективности для стратегий комбинирования классов:

Сокращение множества классов: Данный подход ставит целью выявление наименьшего подмножества среди первоначальных классов, которое сохраняет высокую вероятность содержания истинного класса. Здесь внутреннее ранжирование в рамках подмножества является вторичным по сравнению с обеспечением того, чтобы подмножество как было компактным, так и с высокой вероятностью содержало корректную классификацию.
Упорядочение классов: Данный метод фокусируется на ранжировании вероятностей принадлежности к классу таким образом, чтобы расположить истинный класс как можно выше по рангу. Вместо использования фиксированных порогов рангов, эффективность оценивается путем измерения среднего расстояния между истинным классом и позицией с наивысшим рангом.

В определенных сценариях применения придание одной из этих схем большего приоритета по отношению к другой может предоставить значительные преимущества. Даже когда такой приоритет не требуется явно. Выбор наиболее релевантной цели и реализация соответствующих ей критериев ошибки зачастую дает более надежные метрики эффективности чем полагание исключительно на точность классификации. Кроме того, эти две цели не обязательно должны быть взаимоисключающими. Гибридный подход может быть чрезвычайно эффективным: сперва примените метод комбинирования, ориентированный на сокращение множества классов, для выявления небольшого подмножества классов с высокой вероятностью включения истинного класса. Затем используйте вторичный метод для ранжирования классов в рамках этого уточненного подмножества. Класс с наивысшим рангом, полученный в результате такого двухэтапного процесса, становится конечным решением, на которое положительно влияют как эффективность сокращения множества, так и точность, обеспечиваемая упорядоченным ранжированием. Такая двухцелевая стратегия может предложить более надежную технику классификацию чем традиционные одноклассовые методы прогнозирования, особенно в сложных сценариях, в которых определенность при классификации имеет большой разброс. Учитывая вышесказанное, мы приступим к нашему исследованию ансамблевых классификаторов.

Ансамбли, основанные на правиле большинства

Правило большинства представляет собой простой интуитивно-понятный подход к ансамблевой классификации, происходящий от знакомого всем принципа голосования. Данный метод предполагает выбор класса, который получает большинство голосов от моделей-компонентов. Данный прямолинейный метод имеет определенную ценность в сценариях, в которых модели могут выдавать только дискретный выбор классов, что делает его идеальным выбором для систем с ограниченной изощренностью моделей. Формальное математическое представление правила большинства иллюстрируется уравнением ниже.

Уравнение правила большинства

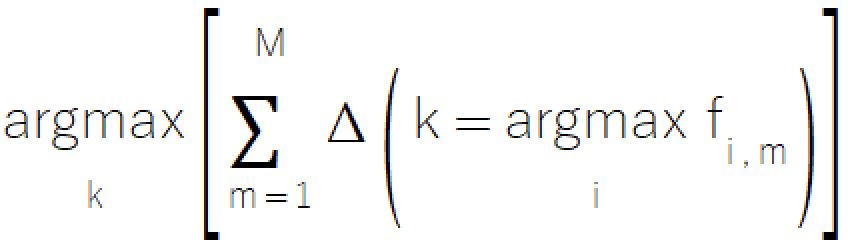
Правило большинства реализовано в файле ensemble.mqh, в котором класс CMajority управляет его основным функционалом с помощью метода classify().

//+------------------------------------------------------------------+
//| Compute the winner via simple majority                           |
//+------------------------------------------------------------------+
class CMajority
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
   matrix            m_out;
public:
                     CMajority(void);
                    ~CMajority(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
  };

Данный метод принимает на вход вектор из предикторов и массив моделей-компонентов, представленный в виде указателей IClassify. Интерфейс IClassify стандартизирует манипуляции с моделями по существу тем же способом, что и интерфейс IModel, описанный в предыдущей статье.

//+------------------------------------------------------------------+
//| IClassify interface defining methods for manipulation of         |
//|classification  algorithms                                        |
//+------------------------------------------------------------------+
interface IClassify
  {
//train a model
   bool train(matrix &predictors,matrix&targets);
//make a prediction with a trained model
   vector classify(vector &predictors);
//get number of inputs for a model
   ulong getNumInputs(void);
//get number of class outputs for a model
   ulong getNumOutputs(void);
  };

Функция classify() возвращает целое число, представляющее выбранный класс и принимающее значения от нуля до общего количества возможных классов минус один. Возвращаемый класс соответствует тому, который получает наибольшее количество "голосов" от моделей-компонентов. Реализация правила большинства может сперва показаться достаточно простой, но существует значимая проблема с ее применением на практике. Что происходит, когда два класса или более получают одинаковое количество голосов? При демократии такая ситуация приводит к следующему туру голосования, но в нашем контексте это не сработает. Для разрешения проблемы "ничьих" метод привносит небольшие отклонения в подсчет голосов для каждого из классов во время сравнения. Данная методика гарантирует, что классы, набравшие одинаковое количество голосов, будут иметь равную вероятность выбора, что поддерживает целостность метода и исключает систематическое отклонение.

//+------------------------------------------------------------------+
//|   ensemble classification                                        |
//+------------------------------------------------------------------+
ulong CMajority::classify(vector &inputs,IClassify *&models[])
  {
   double best, sum, temp;
   ulong ibest;
   best =0;
   ibest = 0;
   
   CHighQualityRandStateShell state;
   CHighQualityRand::HQRndRandomize(state.GetInnerObj());
   
   m_output = vector::Zeros(models[0].getNumOutputs());

   for(uint i  = 0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      m_output[classification.ArgMax()] += 1.0;
     }

   sum = 0.0;
   for(ulong i=0 ; i<m_output.Size() ; i++)
     {
      temp = m_output[i] + 0.999 * CAlglib::HQRndUniformR(state);
      if((i == 0)  || (temp > best))
        {
         best = temp ;
         ibest = i ;
        }
      sum += m_output[i] ;
     }

   if(sum>0.0)
      m_output/=sum;

   return ibest;
  }

Несмотря на свою полезность, правило большинства сопряжено с некоторыми ограничениями, которые следует учитывать:

Данный метод учитывает только наивысший выбор каждой из моделей, поэтому может отбрасывать ценную информацию, содержащуюся на более низких рангах. Хотя применение простого арифметического усреднения выводов по классам может показаться решением, данный подход влечет дополнительные сложности, связанные с шумом и масштабированием.
В сценариях со множеством классов механизм простого голосования может не учитывать тонкие взаимосвязи между различными вариантами классов.
Данный подход рассматривает все модели-компоненты как равные, независимо от характеристик эффективности или надежности каждой из них в различных контекстах.

Следующий метод, который мы обсудим, это еще одна система, основанная на "голосах", которая ставит целью нивелировать некоторые из недостатков правила большинства благодаря некоторым дополнительным нюансам.

Метод счета Борда

Метод счета Борда рассчитывает рейтинг для каждого класса путем агрегирования (по всем моделям) числа классов, имеющих ранг ниже рассматриваемого при каждой оценке, проводимой моделью. Данный метод достигает оптимального баланса между модерированием низкоранговых выборов и обращением их на пользу, предлагая тем самым более совершенную альтернативу по сравнению с механизмами простого голосования. В системе с 'm' моделями и 'k' классами, диапазон возможных рейтингов строго определен: класс, который стабильно ранжируется как последний во всех моделях, получает ноль баллов по Борда, в то время как класс, получающий наивысший ранг у всех моделей достигает максимального балла по Борда, равного m(k-1).

Ранги

Данный метод представляет собой значительное продвижение по сравнению с методами простого голосования, предлагая улучшенные возможности по определению и использованию полного спектра прогнозов моделей, при этом сохраняя вычислительную эффективность. Хотя метод эффективно справляется с проблемой "ничьих" между рангами отдельных моделей, следует уделить особое внимание "ничьим" в финальных подсчетах по Борда у разных моделей. Для задач бинарной классификации метод счета Борда функционально эквивалентен правилу большинства. Поэтому его явные преимущества проявляются, главным образом, в сценариях с участием трех или более классов. Эффективность метода является результатом используемого им подхода на основе сортировки, который обеспечивает оптимизированную обработку выводимых классов, при этом сохраняя точные индексные ассоциации.

Реализация счета Борда имеет структурные сходства с методологией для правила большинства, но предлагает дополнительную вычислительную эффективность. Процесс управляется классом CBorda в файле ensemble.mqh и работает без необходимости в фазе предварительного обучения.

//+------------------------------------------------------------------+
//|  Compute the winner via Borda count                              |
//+------------------------------------------------------------------+
class CBorda
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
   matrix            m_out;
   long              m_indices[];
public:
                     CBorda(void);
                    ~CBorda(void);
   ulong             classify(vector& inputs, IClassify* &models[]);
  };

Процедура классификации начинается с инициализации вектора выводов, предназначенного для хранения накопленных подсчетов по Борда. После этого все модели-компоненты проводят оценку предоставленного входного вектора. Создается массив индексов для отслеживания взаимосвязей между классами. Выводы классификации от каждой из моделей сортируются по возрастанию. И наконец, подсчеты Борда систематически накапливаются на основе отсортированных рангов.

//+------------------------------------------------------------------+
//| ensemble classification                                          |
//+------------------------------------------------------------------+
ulong CBorda::classify(vector &inputs,IClassify *&models[])
  {
   double best=0, sum, temp;
   ulong ibest=0;
   
   CHighQualityRandStateShell state;
   CHighQualityRand::HQRndRandomize(state.GetInnerObj());
   
   if(m_indices.Size())
      ArrayFree(m_indices);

   m_output = vector::Zeros(models[0].getNumOutputs());

   if(ArrayResize(m_indices, int(m_output.Size()))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return ULONG_MAX;
     }

   for(uint i = 0; i<models.Size(); i++)
     {
      vector classification  = models[i].classify(inputs);
      for(long j = 0; j<long(classification.Size()); j++)
         m_indices[j] = j;
      if(!classification.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortdsi(0,classification.Size()-1,classification,m_indices);
      for(ulong k =0; k<classification.Size(); k++)
         m_output[m_indices[k]] += double(k);
     }

   sum = 0.0;
   for(ulong i=0 ; i<m_output.Size() ; i++)
     {
      temp = m_output[i] + 0.999 * CAlglib::HQRndUniformR(state);
      if((i == 0)  || (temp > best))
        {
         best = temp ;
         ibest = i ;
        }
      sum += m_output[i] ;
     }

   if(sum>0.0)
      m_output/=sum;

   return ibest;

  }

В дальнейших разделах мы рассмотрим ансамбли, которые включают в себя большую часть (если не всю) информации, генерируемой моделями-компонентами при принятии финального решения по классам.

Усреднение выводов моделей-компонентов

Когда модели-компоненты генерируют выводы со значимыми и сопоставимыми (между моделями) относительными значениями, внедрение таких численных мер значительно повышает эффективность ансамбля. В то время как методы правила большинства и счета Борда пренебрегают существенной частью доступной информации, усреднение выводов моделей компонентов предоставляет собой более исчерпывающий подход к использованию данных. Метод рассчитывает средний вывод для каждого класса среди показаний от всех моделей-компонентов. При условии, что количество моделей остается постоянным, данный подход математически эквивалентен суммированию выводов. Данная техника по существу рассматривает каждую модель классификации как численный предиктор, объединяя их через методы простого усреднения. Конечное решение классификации определяется путем выявления класса с наибольшим агрегированным выводом.

Формула среднего

Усреднение в задачах численного прогнозирования имеет значительное отличие усреднения в задачах классификации. При численном прогнозировании модели-компоненты обычно имеют общую цель обучения, что обеспечивает единообразие выводов. Однако в задачах классификации, когда для отдельных моделей имеют значение только выходные ранги, могут непреднамеренно производится несравнимые выводы. Иногда результатом такого отсутствия связности может стать комбинация, фактически представляющая собой скорее неявное среднее взвешенное чем истинное среднее арифметическое. Также как вариант, отдельные модели могут оказывать непропорциональное влияние на конечную сумму, что ставит под угрозу эффективность ансамбля. Таким образом, чтобы сохранить целостность метамодели, крайне важна проверка связности выводов между всеми моделями-компонентами.

Предположение о том, что выводы моделей-компонентов являются по сути вероятностями, привело к разработке альтернативных методов комбинирования, концептуально схожих с усреднением. Одним из них является правило умножения. Оно заменяет сложение выводов моделей на их умножение. Проблема заключается в том, что данный подход демонстрирует чрезвычайную чувствительность даже к малейшим нарушениям вероятностных предположений. Значительная недооценка одной из моделей вероятности для класса может необратимо исключить такой класс из результатов, так как умножение на значения, близкие к нулю, дает результаты, которыми можно пренебречь, независимо от других факторов. Такая повышенная чувствительность делает правило умножения непрактичными для большинства сценариев, несмотря на ее элегантность в теории. Здесь мы используем этот пример как предупреждение о том, что даже безупречные с математической точки зрения подходы могут вызывать проблемы при реализации на практике.

Реализация правила усреднения представлена в классе CAvgClass, структура которого схожа со структурой класса CMajority.

//+------------------------------------------------------------------+
//| full resolution' version of majority rule.                       |
//+------------------------------------------------------------------+
class  CAvgClass
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
public:
                     CAvgClass(void);
                    ~CAvgClass(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
  };

В процессе классификации метод classify() собирает прогнозы от всех моделей-компонентов и накапливает их соответствующие выводы. Конечный класс выдается на основе максимального накопленного рейтинга.

//+------------------------------------------------------------------+
//| make classification with consensus model                         |
//+------------------------------------------------------------------+
ulong CAvgClass::classify(vector &inputs, IClassify* &models[])
  {
   m_output=vector::Zeros(models[0].getNumOutputs());
   vector model_classification;
   for(uint i =0 ; i<models.Size(); i++)
     {
      model_classification = models[i].classify(inputs);
      m_output+=model_classification;
     }

   double sum = m_output.Sum();
   ulong min = m_output.ArgMax();
   m_output/=sum;

   return min;
  }

Медиана

Агрегирование средних имеет преимущество в виде исчерпывающего использования данных, но ценой является чувствительность к выбросам, что может подвергнуть риску эффективность ансамбля. Медана представляет собой полезную альтернативу, которая, несмотря на незначительное сокращение использования информации, предоставляет надежные меры центра распределения, при этом сохраняя устойчивость к экстремальным значениям. Ансамблевый метод медианы, реализованный посредством класса CMedian в файле ensemble.mqh, предлагает прямолинейный, но в то же время эффективный подход к ансамблевой классификации решение. Такая реализация справляется с проблемами управления прогнозами-выбросами и сохранения значимого относительного упорядочивания классов. Проблема выбросов разрешается посредством реализации преобразования на основе рангов. Выводы от каждой модели-компонента ранжируются независимо друг от друга, а затем рассчитывается среднее значение этих рангов для каждого из классов. Такой подход эффективно уменьшает влияние экстремальных прогнозных значений, при этом сохраняя важнейшие иерархические взаимосвязи между классовыми прогнозами.

Медианный подход повышает стабильность при возможном наличии экстремальных прогнозов. Он сохраняет эффективность даже при работе с асимметрическими или скошенными распределениями прогнозов и достигает сбалансированного компромисса между использованием всей доступной информации и надежным управлением выбросами. При применении правила медианы рекомендуется оценивать специфические требования сценария использования. В сценариях, когда высока вероятность возникновения экстремальных прогнозов, либо когда крайне важна стабильность прогнозирования, метод медианы предлагает оптимальный баланс между надежностью и эффективностью.

//+------------------------------------------------------------------+
//|  median of predications                                          |
//+------------------------------------------------------------------+
class CMedian
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
   matrix            m_out;
public:
                     CMedian(void);
                    ~CMedian(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
  };
//+------------------------------------------------------------------+
//| constructor                                                      |
//+------------------------------------------------------------------+
CMedian::CMedian(void)
  {

  }
//+------------------------------------------------------------------+
//| destructor                                                       |
//+------------------------------------------------------------------+
CMedian::~CMedian(void)
  {

  }
//+------------------------------------------------------------------+
//| consensus classification                                         |
//+------------------------------------------------------------------+
ulong CMedian::classify(vector &inputs,IClassify *&models[])
  {
   m_out = matrix::Zeros(models[0].getNumOutputs(),models.Size());
   vector model_classification;
   for(uint i = 0; i<models.Size(); i++)
     {
      model_classification = models[i].classify(inputs);
      if(!m_out.Col(model_classification,i))
        {
         Print(__FUNCTION__, "   ", __LINE__, " failed row insertion ", GetLastError());
         return ULONG_MAX;
        }
     }

   m_output = vector::Zeros(models[0].getNumOutputs());
   for(ulong i = 0; i<m_output.Size(); i++)
     {
      vector row = m_out.Row(i);
      if(!row.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortd(0,row.Size()-1,row);
      m_output[i] = row.Median();
     }

   double sum = m_output.Sum();
   ulong mx = m_output.ArgMax(); 
   
   if(sum>0.0)
      m_output/=sum;

   return mx;
  }

Ансамблевые классификаторы MaxMax и MaxMin

Иногда в некоторых ансамблях моделей-компонентов, у отдельных моделей может быть заложена экспертность в определенных подмножествах множества классов. При работе в своих областях специализации такие модели генерируют выводы с высокой степенью достоверности, при этом выдавая менее значимые умеренные значения для классов вне области их экспертизы. Правило MaxMax предоставляет решение для такого сценария, путем оценки каждого класса на основе его максимального показателя среди всех моделей. Такой подход делает приоритетом высокую достоверность прогнозов, пренебрегая при этом потенциально менее информативными умеренными выходными значениями. Тем не менее, рекомендуется помнить о том, что данный метод не подходят для сценариев, в которых вторичные выводы имеют значительную аналитическую ценность.

Формула MaxMax

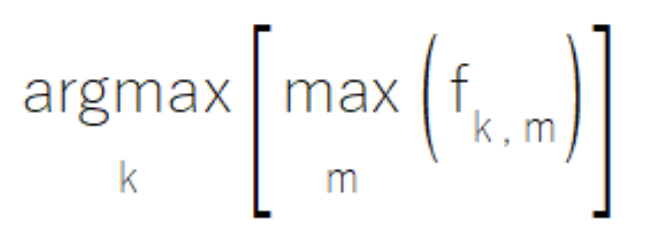
Правило MaxMax реализовано в классе CMaxmax в файле ensemble.mqh и предоставляет полноценную структуру для обращения к паттернам специализации моделей.

//+------------------------------------------------------------------+
//|Compute the maximum of the predictions                            |
//+------------------------------------------------------------------+
class CMaxMax
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
   matrix            m_out;
public:
                     CMaxMax(void);
                    ~CMaxMax(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
  };
//+------------------------------------------------------------------+
//|    constructor                                                   |
//+------------------------------------------------------------------+
CMaxMax::CMaxMax(void)
  {
  }
//+------------------------------------------------------------------+
//|    destructor                                                    |
//+------------------------------------------------------------------+
CMaxMax::~CMaxMax(void)
  {
  }
//+------------------------------------------------------------------+
//|   ensemble classification                                        |
//+------------------------------------------------------------------+
ulong CMaxMax::classify(vector &inputs,IClassify *&models[])
  {
   double sum;
   ulong ibest;
   m_output = vector::Zeros(models[0].getNumOutputs());
   for(uint i  = 0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      for(ulong j = 0; j<classification.Size(); j++)
         {
            if(classification[j] > m_output[j])
               m_output[j] = classification[j];
         }
     }

   ibest  = m_output.ArgMax();
   sum  = m_output.Sum();

   if(sum>0.0)
      m_output/=sum;

   return ibest;
  }

И наоборот, некоторые ансамблевые системы задействуют модели, которые отлично исключают определенные классы вместо того, чтобы их выявлять. В этих случаях, когда экземпляр принадлежит к определенному классу, по крайней мере одна модель в ансамбле сгенерирует выразительно низкий вывод для каждого некорректного класса, тем самым фактически исключая их из рассмотрения.

Формула MaxMin

Правило MaxMin использует эту методику, оценивая принадлежность к классу на основе минимального вывода среди всех моделей для каждого класса.
Данный подход, реализованный в классе CMaxmin в файле ensemble.mqh, предоставляет механизм, задействующий способности определенных моделей к исключениям.

//+------------------------------------------------------------------+
//| Compute the minimum of the predictions                           |
//+------------------------------------------------------------------+
class CMaxMin
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
   matrix            m_out;
public:
                     CMaxMin(void);
                    ~CMaxMin(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
  };
//+------------------------------------------------------------------+
//|  constructor                                                     |
//+------------------------------------------------------------------+
CMaxMin::CMaxMin(void)
  {

  }
//+------------------------------------------------------------------+
//|   destructor                                                     |
//+------------------------------------------------------------------+
CMaxMin::~CMaxMin(void)
  {
  }
//+------------------------------------------------------------------+
//|   ensemble classification                                        |
//+------------------------------------------------------------------+
ulong CMaxMin::classify(vector &inputs,IClassify *&models[])
  {
   double  sum;
   ulong ibest;

   for(uint i  = 0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      if(i == 0)
         m_output = classification;
      else
        {
         for(ulong j = 0; j<classification.Size(); j++)
            if(classification[j] < m_output[j])
               m_output[j] = classification[j];
        }
     }

   ibest  = m_output.ArgMax();
   sum  = m_output.Sum();

   if(sum>0.0)
      m_output/=sum;

   return ibest;
  }

При реализации одного из подходов, MaxMax или MaxMin, реализующему следует внимательно оценивать характеристики своего ансамбля моделей. Для подхода MaxMax крайне важно убедиться? что модели демонстрируют явные паттерны специализации. Особенно важно убедиться, что умеренные выходные значения представляют собой скорее шум чем ценную вторичную информацию, а также, наконец, обеспечить, чтобы ансамбль обеспечивал исчерпывающее покрытие всех соответствующих классов. Используя подход MaxMin, следует убедиться, что ансамбль в сборе успешно справляется со всеми потенциальными сценариями неверной классификации, а также найти все пробелы в покрытии исключениями.

Метод пересечений

Метод пересечений представляет собой специализированный подход к комбинированию классификаторов, предназначенный в основном скорее для сокращения множества классов чем для общих задач классификации. По всеобщему признанию, его прямое применение может быть ограничено, и он описан в данном тексте в качестве фундаментального прекурсора для более надежных методов, в частности для метода объединения. Данный подход требует, чтобы модели-компоненты генерировали ранжирования по классам для каждого вводимого образца, от наиболее к наименее вероятным. Многие классификаторы могут удовлетворять это требование, и процесс ранжирования выходных данных вещественного типа зачастую улучшает производительность за счет эффективной фильтрации шума и, в то же время, сохранения ценной информации. На этапе обучения в данном методе выявляется минимальное количество выводов с максимальным рангом, которые может сохранить каждая из моделей-компонентов, чтобы обеспечить устойчивое включение истинного класса на всем наборе обучающих данных. Для новых образцов комбинированное решение представляет собой минимальное подмножество, содержащее истинный класс и определяемое путем пересечения минимальных подмножеств от всех моделей-компонентов.

Диаграмма пересечений Венна

Рассмотрим практический пример с множеством классов и четырьмя моделями. Изучение пяти выборок в наборе обучающих данных показывает разнящиеся между моделями паттерны ранжирования для истинного класса.

Выборка	Модель 1	Модель 2	Модель 3	Модель 4
1	3	21	4	5
2	8	4	8	9
3	1	17	12	3
4	7	16	2	8
5	7	8	6	1
Максимум	8	21	12	9

Таблица показывает, что истинный класс во второй выборке получил восьмой ранг от первой модели, четвертый от второй и девятый от четвертой модели. Последняя строчка в таблице показывает максимальные ранги в каждом из столбцов, а именно 8, 21, 12 и 9, соответственно. При оценке неизвестных образцов ансамбль выбирает классов с наивысшими рангами от каждой из моделей в соответствии с этими порогами и выполняет пересечение этих классов, генерируя конечное подмножество классов, обычных для всех наборов обучающих данных.

Класс CIntersection реализует метод пересечений и имеет выделенную процедуру обучения в виде функции fit(). Данная функция анализирует обучающие данные для определения наихудших рангов для каждой из моделей, отслеживая минимальное количество классов с наивысшим рангом, требуемое для устойчивого включения верных классификаций.

//+------------------------------------------------------------------+
//| Use intersection rule to compute minimal class set               |
//+------------------------------------------------------------------+
class CIntersection
  {
private:
   ulong             m_nout;
   long              m_indices[];
   vector            m_ranks;
   vector            m_output;
public:
                     CIntersection(void);
                    ~CIntersection(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
   bool              fit(matrix &inputs, matrix &targets, IClassify* &models[]);
   vector            proba(void) { return m_output;}
  };

Вызов метода classify() из класса CIntersection производит последовательную оценку всех моделей-компонентов по входным данным. Для каждой модели ее выходной вектор сортируется, а индексы отсортированного вектора используются для расчета пересечения классов, которые принадлежат к подмножеству с наивысшим рангом для каждой из моделей.

//+------------------------------------------------------------------+
//|   fit an ensemble model                                          |
//+------------------------------------------------------------------+
bool CIntersection::fit(matrix &inputs,matrix &targets,IClassify *&models[])
  {
   m_nout = targets.Cols();

   m_output = vector::Ones(m_nout);
   m_ranks = vector::Zeros(models.Size());
   double best = 0.0;
   ulong nbad;
   if(ArrayResize(m_indices,int(m_nout))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return false;
     }

   ulong k;
   for(ulong i = 0; i<inputs.Rows(); i++)
     {
      vector trow = targets.Row(i);
      vector inrow = inputs.Row(i);
      k = trow.ArgMax();
      best = trow[k];

      for(uint j = 0; j<models.Size(); j++)
        {
         vector classification = models[j].classify(inrow);
         best = classification[k];
         nbad = 1;
         for(ulong ii = 0; ii<m_nout; ii++)
           {
            if(ii == k)
               continue;
            if(classification[ii] >= best)
               ++nbad;
           }
         if(nbad > ulong(m_ranks[j]))
            m_ranks[j] = double(nbad);
        }
     }

   return true;

  }
//+------------------------------------------------------------------+
//|  ensemble classification                                         |
//+------------------------------------------------------------------+
ulong CIntersection::classify(vector &inputs,IClassify *&models[])
  {
   
   for(long j =0; j<long(m_nout); j++)
         m_indices[j] = j;
         
   for(uint i =0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      ArraySort(m_indices);
      qsortdsi(0,classification.Size()-1,classification,m_indices);
      for(ulong j = 0; j<m_nout-ulong(m_ranks[i]); j++)
        {
         m_output[m_indices[j]] = 0.0;
        }
     }

   ulong n=0;
   double cut = 0.5;
   for(ulong i = 0; i<m_nout; i++)
     {
      if(m_output[i] > cut)
         ++n;
     }

   return n;
  }

Несмотря на теоретическую элегантность, метод пересечений имеет несколько значительных ограничений. Хотя он гарантирует включение истинных классов из обучающего набора, это преимущество сдерживается неотъемлемыми ограничениями данного метода. Метод также может производить пустые подмножества классов для образцов за пределами обучающего набора, в частности, когда у подмножеств с наивысшим рангом от различных моделей не имеется общих элементов. Что наиболее критично, тот факт, что метод полагается на анализ наиболее неблагоприятных показателей, зачастую приводит к излишне большим подмножествам классов, что негативно сказывается как на эффективности, так и на результативности метода.

Метод пересечений может представлять ценность в определенных контекстах, в которых все модели-компоненты демонстрируют стабильные показатели на всем наборе классов. Тем не менее, его чувствительность к низкой эффективности моделей в областях за пределами их специализации зачастую ограничивает его полезность на практике, особенно в приложениях, которые полагаются на специализированные модели для различных подмножеств классов. В конечном итоге, основная ценность данного метода заключается скорее в его концептуальном вкладе в более надежные подходы, такие как метод объединения, чем в непосредственном применении в большинстве задач классификации.

Правило объединения

Правило объединения представляет собой стратегическое усовершенствование метода пересечений, справляющееся с основным его ограничением, связанным с излишним полаганием на анализ наиболее неблагоприятных показателей. Данная модификация, в частности, подтверждает свою ценность при комбинировании специализированных моделей с различными сферами экспертизы, что смещает акцент с анализа неблагоприятных сценариев на анализ благоприятных. Первоначальный процесс отражает подход метода пересечений: анализ образцов из обучающего набора для получения ранжирований истинного класса от моделей-компонентов. Тем не менее, правило объединения отличается тем, что выявляет и отслеживает модели с наилучшими показателями для каждого из образцов вместо мониторинга вариантов с наихудшей эффективностью. Затем метод оценивает наименее предпочтительные из этих наилучших показателей в рамках набора обучающих данных. Для классификации неизвестных образцов система создает комбинированное подмножество классов путем объединения оптимальных подмножеств от каждой из моделей-компонентов. Рассмотрим набор данных из нашего предыдущего примера, теперь дополненный столбцами для отслеживания эффективности с префиксом "Perf".

Выборка	Модель 1	Модель 2	Модель 3	Модель 4	Perf_Model 1	Perf_Model 2	Perf_Model 3	Perf_Model 4
1	3	21	4	5	3	0	0	0
2	8	4	8	9	0	4	0	0
3	1	17	12	3	1	0	0	0
4	7	16	2	8	0	0	2	0
5	7	8	6	1	0	0	0	1
Максимум					3	4	2	1

В дополнительных столбцах отслеживаются случаи, когда каждая модель демонстрирует превосходящую эффективность, а в нижней строке указываются максимальные значения в таких наилучших сценариях.

Правило объединения предлагает несколько явных преимуществ по сравнению с методом пересечений. Оно устраняет вероятность пустых подмножеств, поскольку по крайней мере одна модель будет устойчиво демонстрировать оптимальные показатели на любом заданном образце. Метод также эффективно управляет специализированными моделями, исключая из рассмотрения низкие показатели эффективности за пределами сфер их экспертизы во время обучения, что позволяет моделям-специалистам получать контроль. И наконец, он предоставляет натуральный механизм для выявления и потенциального исключения моделей с устойчиво низкой эффективностью, которые обозначаются столбцами из нулей в матрице отслеживания.

Реализация метода объединения структурно очень похожа на метод пересечений, используя контейнер m_ranks для мониторинга максимальных значений из столбцов по отслеживанию эффективности.

//+------------------------------------------------------------------+
//| Use union rule to compute minimal class set                      |
//+------------------------------------------------------------------+
class CUnion
  {
private:
   ulong             m_nout;
   long              m_indices[];
   vector            m_ranks;
   vector            m_output;
public:
                     CUnion(void);
                    ~CUnion(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
   bool              fit(matrix &inputs, matrix &targets, IClassify* &models[]);
   vector            proba(void) { return m_output;}
  };

Тем не менее, ключевые отличия относятся к обработке классовых рангов и инициализации флагов. Во время обучения система отслеживает минимальные ранги по всем моделям для каждого образца, обновляя максимальные значения m_ranks, когда это необходимо.

//+------------------------------------------------------------------+
//|  fit an ensemble model                                           |
//+------------------------------------------------------------------+
bool CUnion::fit(matrix &inputs,matrix &targets,IClassify *&models[])
  {
   m_nout = targets.Cols();

   m_output = vector::Zeros(m_nout);
   m_ranks = vector::Zeros(models.Size());
   double best = 0.0;
   ulong nbad;
   if(ArrayResize(m_indices,int(m_nout))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return false;
     }

   ulong k, ibestrank=0, bestrank=0;
   for(ulong i = 0; i<inputs.Rows(); i++)
     {
      vector trow = targets.Row(i);
      vector inrow = inputs.Row(i);
      k = trow.ArgMax();

      for(uint j = 0; j<models.Size(); j++)
        {
         vector classification = models[j].classify(inrow);
         best = classification[k];
         nbad = 1;
         for(ulong ii = 0; ii<m_nout; ii++)
           {
            if(ii == k)
               continue;
            if(classification[ii] >= best)
               ++nbad;
           }
         if(j == 0 || nbad < bestrank)
           {
            bestrank = nbad;
            ibestrank = j;
           }
        }
      if(bestrank > ulong(m_ranks[ibestrank]))
         m_ranks[ibestrank] =  double(bestrank);
     }

   return true;
  }

Этап классификации прогрессивным способом включает классы, которые соответствуют определенным критериям эффективности.

//+------------------------------------------------------------------+
//| ensemble classification                                          |
//+------------------------------------------------------------------+
ulong CUnion::classify(vector &inputs,IClassify *&models[])
  {
   for(long j =0; j<long(m_nout); j++)
         m_indices[j] = j;
         
   for(uint i =0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      ArraySort(m_indices);
      qsortdsi(0,classification.Size()-1,classification,m_indices);
      for(ulong j =(m_nout-ulong(m_ranks[i])); j<m_nout; j++)
        {
         m_output[m_indices[j]] = 1.0;
        }
     }

   ulong n=0;
   double cut = 0.5;
   for(ulong i = 0; i<m_nout; i++)
     {
      if(m_output[i] > cut)
         ++n;
     }

   return n;
  }

Несмотря на способность правила объединения эффективно нивелировать многие из ограничений метода пересечений, он сохраняет уязвимость к возникновению выбросов, когда все модели-компоненты генерируют низкие ранги. Данный сценарий, хотя и является вызовом, обычно редко встречается в хорошо спроектированных приложениях и зачастую его риск может быть минимизирован через надлежащую систему проектирования и выбора моделей. Эффективность метода особенно заметна в средах со специализированными моделями, когда каждая модель-компонент хорошо работает в определенных областях, но может работать хуже в остальных. Данная характеристика делает его особенно ценным для комплексных задач классификации, требующих разносторонней экспертизы.

Комбинации классификаторов, основанные на логистической регрессии

Из всех ансамблевых классификаторов, которые мы успели обсудить, метод счета Борда выступает в качестве решения с универсальной эффективностью для комбинирования классификаторов, имеющих схожую эффективность, т.е. предполагает наличие равной способности к прогнозированию у всех моделей. Когда модели значительно отличаются по эффективности, может быть желательным реализовать дифференциальные веса на основе показателей эффективности отдельных моделей. Логистическая регрессия станет продвинутым дополнением к нашему методу взвешенного комбинирования.

Реализация логистической регрессии для комбинирования классификаторов строится на принципах обыкновенной линейной регрессии, но предназначено для решения определенных проблем классификации. Вместо прямого прогнозирования значений в непрерывном режиме логистическая регрессия рассчитывает класс вероятностей принадлежности, предлагая более тонкий подход к задачам классификации. Процесс начинается с преобразования исходных данных обучения в формат, совместимый с регрессией. Рассмотрим систему с тремя классами и четырьмя моделями, генерирующую представленные ниже выводы.

	Модель 1	Модель 2	Модель 3	Модель 4
1	0.7	0.1	0.8	0.4
2	0.8	0.3	0.9	0.3
3	0.2	0.2	0.7	0.2

Эти данные генерируют по три новых образца регрессионного обучения для каждого исходного образца, при этом для верного класса значение целевой переменной будет 1.0, а для неверных классов – 0.0. Предикторы используют пропорциональное ранжирование вместо сырых выходных данных, что улучшает устойчивость численных решений.

Класс CLogitReg в файле ensemble.mqh управляет реализацией метода взвешенного комбинирования для ансамблей классификаторов.

//+------------------------------------------------------------------+
//|  Use logistic regression to find best class                      |
//|           This uses one common weight vector for all classes.    |
//+------------------------------------------------------------------+
class ClogitReg
  {
private:
   ulong             m_nout;
   long              m_indices[];
   matrix            m_ranks;
   vector            m_output;
   vector            m_targs;
   matrix            m_input;
   logistic::Clogit  *m_logit;
public:
                     ClogitReg(void);
                    ~ClogitReg(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
   bool              fit(matrix &inputs, matrix &targets, IClassify* &models[]);
   vector            proba(void) { return m_output;}
  };

Метод fit() создает набор данных регрессионного обучения путем систематической обработки отдельных образцов. Сперва определяется принадлежность истинного класса для каждой из обучающих выборок. Затем результаты оценок от каждой из моделей-компонентов собираются в матрицу m_ranks. Данная матрица обрабатывается для генерации зависимых и независимых переменных для задачи регрессии, которая впоследствии решается с помощью объекта m_logit.

//+------------------------------------------------------------------+
//| fit an ensemble model                                            |
//+------------------------------------------------------------------+
bool ClogitReg::fit(matrix &inputs,matrix &targets,IClassify *&models[])
  {
   m_nout = targets.Cols();
   m_input = matrix::Zeros(inputs.Rows(),models.Size());
   m_targs = vector::Zeros(inputs.Rows());
   m_output = vector::Zeros(m_nout);
   m_ranks = matrix::Zeros(models.Size(),m_nout);

   double best = 0.0;
   ulong nbelow;
   if(ArrayResize(m_indices,int(m_nout))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return false;
     }

   ulong k;
   if(CheckPointer(m_logit) == POINTER_DYNAMIC)
      delete m_logit;

   m_logit = new logistic::Clogit();

   for(ulong i = 0; i<inputs.Rows(); i++)
     {
      vector trow = targets.Row(i);
      vector inrow = inputs.Row(i);
      k = trow.ArgMax();
      best = trow[k];

      for(uint j = 0; j<models.Size(); j++)
        {
         vector classification = models[j].classify(inrow);
         if(!m_ranks.Row(classification,j))
           {
            Print(__FUNCTION__, "   ", __LINE__, " failed row insertion ", GetLastError());
            return false;
           }
        }
      for(ulong j = 0; j<m_nout; j++)
        {
         for(uint jj =0; jj<models.Size(); jj++)
           {
            nbelow = 0;
            best = m_ranks[jj][j];
            for(ulong ii =0; ii<m_nout; ii++)
              {
               if(m_ranks[jj][ii]<best)
                  ++nbelow;
              }
            m_input[i][jj] = double(nbelow)/double(m_nout);
           }
         m_targs[i] = (j == k)? 1.0:0.0;
        }
     }

   return m_logit.fit(m_input,m_targs);
  }

Данная реализация демонстрирует усложненный подход к комбинированию классификаторов, имеющий определенную ценность для сценариев, в которых модели-компоненты демонстрируют разнящиеся уровни эффективности для различных задач классификации.

Процесс взвешенной классификации строится на основе метода счета Борда с использованием специальных весовых значений для моделей. Алгоритм начинается с инициализации векторов накопления и обработки неизвестных образцов каждой моделью-компонентом. Оптимальные веса, рассчитываемые объектом m_logit, применяются для корректировки вкладов компонентов-классификаторов. Конечный класс определяется как индекс, соответствующий наибольшему значению m_output.

//+------------------------------------------------------------------+
//| classify with ensemble model                                     |
//+------------------------------------------------------------------+
ulong ClogitReg::classify(vector &inputs,IClassify *&models[])
  {

   double temp;
   for(uint i =0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      for(long j =0; j<long(classification.Size()); j++)
         m_indices[j] = j;
      if(!classification.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortdsi(0,classification.Size()-1,classification,m_indices);
      temp = m_logit.coeffAt(i);
      for(ulong j = 0 ; j<m_nout; j++)
        {
         m_output[m_indices[j]] += j * temp;
        }
     }
   double sum = m_output.Sum();
   ulong ibest = m_output.ArgMax();
   double best = m_output[ibest];

   if(sum>0.0)
      m_output/=sum;

   return ibest;
  }

В данной реализации делается акцент на универсальных весах ввиду их высокой стабильности и низкого риска переобучения. Тем не менее, специфичные для классов веса остаются допустимым вариантом для сценариев с большим количеством обучающих данных. Метод, использующий специфичные для классов веса, рассматривается в следующем разделе. А пока мы уделим внимание тому, как определяются оптимальные веса, в частности, в модели логистической регрессии.

Центральным понятием логистической регрессии является логистическое или логит-преобразование, показанное ниже.

Логит-преобразование

Данная функция отображает неограниченную область в интервал [0, 1]. Когда x в уравнении выше крайне отрицательно, результат стремится к нулю. И наоборот, по мере увеличения x значение функции приближается к единице. Если x=0, функция возвращает значение, находящееся точно посередине между двумя экстремумами. Позволить x представлять прогнозируемую переменную в регрессионной модели означает, что при x меньше нуля существует шанс 50%, что выборка принадлежит к определенному классу. По мере увеличения значения x от нуля процентная вероятность такого шанса увеличивается соответствующим образом. С другой стороны, по мере уменьшения значения x от нуля процентная вероятность упомянутого шанса снижается.

Альтернативным способом описания вероятности являются коэффициенты шансов. Формально их называют отношением шансов, которое представляет собой вероятность наступления события, разделенную на вероятность его ненаступления. Если выразить e^x в логит-преобразовании через f(x), получим следующее уравнение.

Измененное логит-преобразование

Если удалить экспоненты из данного уравнения, применив логарифмы к обеим его сторонам, и допуская, что x является прогнозируемой переменной в задаче регрессии, мы получим уравнение, показанное ниже.

Логистическая регрессия

Данное выражение, упомянутое в контексте ансамблей классификаторов, гласит, что для каждой выборки в наборе обучающих данных линейная комбинация предикторов от классификаторов-компонентов представляет собой логарифм отношения шансов для соответствующей метки класса. Оптимальные веса, w, можно получить, использовав оценку максимального правдоподобия либо минимизировав целевую функцию. Подробности того, как это делается, не рассматриваются в настоящей статье.

Поначалу найти исчерпывающую реализацию логистической регрессии на языке MQL5 оказалось непросто. Портированная на MQL5 библиотека Alglib содержит специальные инструменты для логистической регрессии, но автор не смог добиться их успешной компиляции. Также отсутствуют какие-либо примеры их использования в демо-программах, показывающих работу инструментов Alglib. Тем не менее, библиотека Alglib пригодилась при реализации класса Clogit, определенного в файле logistic.mqh. Файл содержит определение класса CFg, который реализует интерфейс CNDimensional_Grad.

//+------------------------------------------------------------------+
//|  function and gradient calculation object                        |
//+------------------------------------------------------------------+
class CFg:public CNDimensional_Grad
  {
private:
   matrix            m_preds;
   vector            m_targs;
   ulong             m_nclasses,m_samples,m_features;
   double            loss_gradient(matrix &coef,double &gradients[]);
   void              weight_intercept_raw(matrix &coef,matrix &x, matrix &wghts,vector &intcept,matrix &rpreds);
   void              weight_intercept(matrix &coef,matrix &wghts,vector &intcept);
   double            l2_penalty(matrix &wghts,double strenth);
   void              sum_exp_minus_max(ulong index,matrix &rp,vector &pr);
   void              closs_grad_halfbinmial(double y_true,double raw, double &inout_1,double &intout_2);
public:
   //--- constructor, destructor
                     CFg(matrix &predictors,vector &targets, ulong num_classes)
     {
      m_preds = predictors;
      vector classes = np::unique(targets);
      np::sort(classes);
      vector checkclasses = np::arange(classes.Size());
      if(checkclasses.Compare(classes,1.e-1))
        {
         double classv[];
         np::vecAsArray(classes,classv);
         m_targs = targets;
         for(ulong i = 0; i<targets.Size(); i++)
            m_targs[i] = double(ArrayBsearch(classv,m_targs[i]));
        }
      else
         m_targs = targets;

      m_nclasses = num_classes;
      m_features = m_preds.Cols();
      m_samples = m_preds.Rows();
     }
                    ~CFg(void) {}

   virtual void      Grad(double &x[],double &func,double &grad[],CObject &obj);
   virtual void      Grad(CRowDouble &x,double &func,CRowDouble &grad,CObject &obj);
  };
//+------------------------------------------------------------------+
//| this function is not used                                        |
//+------------------------------------------------------------------+
void CFg::Grad(double &x[],double &func,double &grad[],CObject &obj)
  {
   matrix coefficients;
   arrayToMatrix(x,coefficients,m_nclasses>2?m_nclasses:m_nclasses-1,m_features+1);
   func=loss_gradient(coefficients,grad);
   return;
  }
//+------------------------------------------------------------------+
//| get function value and gradients                                 |
//+------------------------------------------------------------------+
void CFg::Grad(CRowDouble &x,double &func,CRowDouble &grad,CObject &obj)
  {
   double xarray[],garray[];
   x.ToArray(xarray);
   Grad(xarray,func,garray,obj);
   grad = garray;
   return;
  }
//+------------------------------------------------------------------+
//| loss gradient                                                    |
//+------------------------------------------------------------------+
double CFg::loss_gradient(matrix &coef,double &gradients[])
  {
   matrix weights;
   vector intercept;
   vector losses;
   matrix gradpointwise;
   matrix rawpredictions;
   matrix gradient;
   double loss;
   double l2reg;

//calculate weights intercept and raw predictions
   weight_intercept_raw(coef,m_preds,weights,intercept,rawpredictions);
   gradpointwise = matrix::Zeros(m_samples,rawpredictions.Cols());
   losses = vector::Zeros(m_samples);
   double sw_sum = double(m_samples);
//loss gradient calculations
   if(m_nclasses>2)
     {
      double max_value, sum_exps;
      vector p(rawpredictions.Cols()+2);
      //---
      for(ulong i = 0; i< m_samples; i++)
        {
         sum_exp_minus_max(i,rawpredictions,p);
         max_value = p[rawpredictions.Cols()];
         sum_exps = p[rawpredictions.Cols()+1];
         losses[i] = log(sum_exps) + max_value;
         //---
         for(ulong k  = 0; k<rawpredictions.Cols(); k++)
           {
            if(ulong(m_targs[i]) == k)
               losses[i] -= rawpredictions[i][k];
            p[k]/=sum_exps;
            gradpointwise[i][k] = p[k] - double(int(ulong(m_targs[i])==k));
           }
        }
     }
   else
     {
      for(ulong i = 0; i<m_samples; i++)
        {
         closs_grad_halfbinmial(m_targs[i],rawpredictions[i][0],losses[i],gradpointwise[i][0]);
        }
     }
//---
   loss = losses.Sum()/sw_sum;
   l2reg = 1.0 / (1.0 * sw_sum);
   loss += l2_penalty(weights,l2reg);
   gradpointwise/=sw_sum;
//---
   if(m_nclasses>2)
     {
      gradient = gradpointwise.Transpose().MatMul(m_preds) + l2reg*weights;
      gradient.Resize(gradient.Rows(),gradient.Cols()+1);
      vector gpsum = gradpointwise.Sum(0);
      gradient.Col(gpsum,m_features);
     }
   else
     {
      gradient = m_preds.Transpose().MatMul(gradpointwise) + l2reg*weights.Transpose();
      gradient.Resize(gradient.Rows()+1,gradient.Cols());
      vector gpsum = gradpointwise.Sum(0);
      gradient.Row(gpsum,m_features);
     }
//---
   matrixToArray(gradient,gradients);
//---
   return loss;
  }
//+------------------------------------------------------------------+
//|  weight intercept raw preds                                      |
//+------------------------------------------------------------------+
void CFg::weight_intercept_raw(matrix &coef,matrix &x,matrix &wghts,vector &intcept,matrix &rpreds)
  {
   weight_intercept(coef,wghts,intcept);
   matrix intceptmat = np::vectorAsRowMatrix(intcept,x.Rows());
   rpreds = (x.MatMul(wghts.Transpose()))+intceptmat;
  }
//+------------------------------------------------------------------+
//| weight intercept                                                 |
//+------------------------------------------------------------------+
void CFg::weight_intercept(matrix &coef,matrix &wghts,vector &intcept)
  {
   intcept = coef.Col(m_features);
   wghts = np::sliceMatrixCols(coef,0,m_features);
  }
//+------------------------------------------------------------------+
//|  sum exp minus max                                               |
//+------------------------------------------------------------------+
void CFg::sum_exp_minus_max(ulong index,matrix &rp,vector &pr)
  {
   double mv = rp[index][0];
   double s_exps = 0.0;

   for(ulong k = 1; k<rp.Cols(); k++)
     {
      if(mv<rp[index][k])
         mv=rp[index][k];
     }

   for(ulong k = 0; k<rp.Cols(); k++)
     {
      pr[k] = exp(rp[index][k] - mv);
      s_exps += pr[k];
     }

   pr[rp.Cols()] = mv;
   pr[rp.Cols()+1] = s_exps;
  }
//+------------------------------------------------------------------+
//|  l2 penalty                                                      |
//+------------------------------------------------------------------+
double CFg::l2_penalty(matrix &wghts,double strenth)
  {
   double norm2_v;
   if(wghts.Rows()==1)
     {
      matrix nmat = (wghts).MatMul(wghts.Transpose());
      norm2_v = nmat[0][0];
     }
   else
      norm2_v = wghts.Norm(MATRIX_NORM_FROBENIUS);

   return 0.5*strenth*norm2_v;
  }
//+------------------------------------------------------------------+
//|   closs_grad_half_binomial                                       |
//+------------------------------------------------------------------+
void CFg::closs_grad_halfbinmial(double y_true,double raw, double &inout_1,double &inout_2)
  {
   if(raw <= -37.0)
     {
      inout_2 = exp(raw);
      inout_1 = inout_2 - y_true * raw;
      inout_2 -= y_true;
     }
   else
      if(raw <= -2.0)
        {
         inout_2 = exp(raw);
         inout_1 = log1p(inout_2) - y_true * raw;
         inout_2 = ((1.0 - y_true) * inout_2 - y_true) / (1.0 + inout_2);
        }
      else
         if(raw <= 18.0)
           {
            inout_2 = exp(-raw);
            // log1p(exp(x)) = log(1 + exp(x)) = x + log1p(exp(-x))
            inout_1 = log1p(inout_2) + (1.0 - y_true) * raw;
            inout_2 = ((1.0 - y_true) - y_true * inout_2) / (1.0 + inout_2);
           }
         else
           {
            inout_2 = exp(-raw);
            inout_1 = inout_2 + (1.0 - y_true) * raw;
            inout_2 = ((1.0 - y_true) - y_true * inout_2) / (1.0 + inout_2);
           }
  }

Это необходимо для процедуры минимизации функции LBFGS. Clogit содержит знакомые нам методы для обучения и получения выводов.

//+------------------------------------------------------------------+
//| logistic regression implementation                               |
//+------------------------------------------------------------------+
class Clogit
  {
public:
                     Clogit(void);
                    ~Clogit(void);
   bool              fit(matrix &predictors, vector &targets);
   double            predict(vector &preds);
   vector            proba(vector &preds);
   matrix            probas(matrix &preds);
   double            coeffAt(ulong index);
private:
   ulong             m_nsamples;
   ulong             m_nfeatures;
   bool              m_trained;
   matrix            m_train_preds;
   vector            m_train_targs;
   matrix            m_coefs;
   vector            m_bias;
   vector            m_classes;
   double            m_xin[];
   CFg               *m_gradfunc;
   CObject           m_dummy;
   vector            predictProba(double &in);
  };
//+------------------------------------------------------------------+
//| constructor                                                      |
//+------------------------------------------------------------------+
Clogit::Clogit(void)
  {
  }
//+------------------------------------------------------------------+
//| destructor                                                       |
//+------------------------------------------------------------------+
Clogit::~Clogit(void)
  {
   if(CheckPointer(m_gradfunc) == POINTER_DYNAMIC)
      delete m_gradfunc;
  }
//+------------------------------------------------------------------+
//| fit a model to a dataset                                         |
//+------------------------------------------------------------------+
bool Clogit::fit(matrix &predictors, vector &targets)
  {
   m_trained = false;
   m_classes = np::unique(targets);
   np::sort(m_classes);

   if(predictors.Rows()!=targets.Size() || m_classes.Size()<2)
     {
      Print(__FUNCTION__," ",__LINE__," invalid inputs ");
      return m_trained;
     }

   m_train_preds = predictors;
   m_train_targs = targets;

   m_nfeatures = m_train_preds.Cols();
   m_nsamples = m_train_preds.Rows();

   m_coefs = matrix::Zeros(m_classes.Size()>2?m_classes.Size():m_classes.Size()-1,m_nfeatures+1);

   matrixToArray(m_coefs,m_xin);

   m_gradfunc = new CFg(m_train_preds,m_train_targs,m_classes.Size());
//---
   CMinLBFGSStateShell state;
   CMinLBFGSReportShell rep;
   CNDimensional_Rep   frep;
//---
   CAlglib::MinLBFGSCreate(m_xin.Size(),m_xin.Size()>=5?5:m_xin.Size(),m_xin,state);
//---
   CAlglib::MinLBFGSOptimize(state,m_gradfunc,frep,true,m_dummy);
//---
   CAlglib::MinLBFGSResults(state,m_xin,rep);
//---
   if(rep.GetTerminationType()>0)
     {
      m_trained = true;
      arrayToMatrix(m_xin,m_coefs,m_classes.Size()>2?m_classes.Size():m_classes.Size()-1,m_nfeatures+1);
      m_bias = m_coefs.Col(m_nfeatures);
      m_coefs = np::sliceMatrixCols(m_coefs,0,m_nfeatures);
     }
   else
      Print(__FUNCTION__," ", __LINE__, " failed to train the model ", rep.GetTerminationType());

   delete m_gradfunc;


   return m_trained;
  }

//+------------------------------------------------------------------+
//| get probability for single sample                                |
//+------------------------------------------------------------------+
vector Clogit::proba(vector &preds)
  {
   vector predicted;

   if(!m_trained)
     {
      Print(__FUNCTION__," ", __LINE__," no trained model available ");
      predicted.Fill(EMPTY_VALUE);
      return predicted;
     }

   predicted = ((preds.MatMul(m_coefs.Transpose())));
   predicted += m_bias;

   if(predicted.Size()>1)
     {
      if(!predicted.Activation(predicted,AF_SOFTMAX))
        {
         Print(__FUNCTION__," ", __LINE__," errror ", GetLastError());
         predicted.Fill(EMPTY_VALUE);
         return predicted;
        }
     }
   else
     {
      predicted = predictProba(predicted[0]);
     }

   return predicted;
  }
//+------------------------------------------------------------------+
//|  get probability for binary classification                       |
//+------------------------------------------------------------------+
vector Clogit::predictProba(double &in)
  {
   vector out(2);

   double n = 1.0/(1.0+exp(-1.0*in));

   out[0] = 1.0 - n;
   out[1] = n;

   return out;
  }
//+------------------------------------------------------------------+
//| get probabilities for multiple samples                           |
//+------------------------------------------------------------------+
matrix Clogit::probas(matrix &preds)
  {
   matrix output(preds.Rows(),m_classes.Size());
   vector rowin,rowout;
   for(ulong i = 0; i<preds.Rows(); i++)
     {
      rowin = preds.Row(i);
      rowout = proba(rowin);
      if(rowout.Max() == EMPTY_VALUE || !output.Row(rowout,i))
        {
         Print(__LINE__," probas error ", GetLastError());
         output.Fill(EMPTY_VALUE);
         break;
        }
     }

   return output;
  }
//+------------------------------------------------------------------+
//| get probability for single sample                                |
//+------------------------------------------------------------------+
double Clogit::predict(vector &preds)
  {
   vector prob = proba(preds);
   if(prob.Max() == EMPTY_VALUE)
     {
      Print(__LINE__," predict error ");
      return EMPTY_VALUE;
     }

   return m_classes[prob.ArgMax()];
  }
//+------------------------------------------------------------------+
//|  get model coefficient at specific index                         |
//+------------------------------------------------------------------+
double Clogit::coeffAt(ulong index)
  {
   if(index<(m_coefs.Rows()))
     {
      return (m_coefs.Row(index)).Sum();
     }
   else
     {
      return 0.0;
     }
  }
}
//+------------------------------------------------------------------+

Ансамблевые комбинации, основанные на логистической регрессии со специфичными для классов весами

Описанный в предыдущем разделе подход с единственным набором весов предлагает стабильность и эффективность, но ограничен в том плане, что не позволяет в полной мере воспользоваться специализацией модели. Если отдельные модели демонстрируют лучшие показатели эффективности для определенных классов, будь то по замыслу разработчика или в результате естественного развития, реализация отдельных наборов весов для каждого класса поможет более эффективно использовать эти возможности. Переход к наборам весов, специфичным для классов, значительно усложняет процесс оптимизации. Вместо оптимизации единственного набора весов ансамбль должен управлять K наборами (по одному на каждый класс), каждый из которых содержит M параметров, что дает суммарно K*M параметров. Такое увеличение числа параметров требует пристального внимания к требованиям в отношении данных и рискам реализации.

Надежное применение отдельных наборов весов требует существенного количества обучающих данных для подержания статистической достоверности. В качестве общего указания следует помнить, что каждый класс должен иметь обучающих образцов по крайней мере в десять раз больше, чем имеется моделей. Даже при достаточном количестве данных такой подход следует реализовывать с осторожностью и только в случаях, когда есть явные признаки наличия значимой специализации у моделей по определенным классам.

Класс CLogitRegSep управляет реализацией отдельных наборов весов, отличаясь от CLogitReg своим распределением отдельных объектов Clogit для каждого класса. Процесс обучения распределяет образцы регрессии по специфичным для классов наборам обучающих данных вместо объединения их в единый набор.

//+------------------------------------------------------------------+
//| Use logistic regression to find best class.                      |
//|              This uses separate weight vectors for each class.   |
//+------------------------------------------------------------------+
class ClogitRegSep
  {
private:
   ulong             m_nout;
   long              m_indices[];
   matrix            m_ranks;
   vector            m_output;
   vector            m_targs[];
   matrix            m_input[];
   logistic::Clogit  *m_logit[];
public:
                     ClogitRegSep(void);
                    ~ClogitRegSep(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
   bool              fit(matrix &inputs, matrix &targets, IClassify* &models[]);
   vector            proba(void) { return m_output;}
  };

Классификация неизвестных случаев происходит по тому же алгоритму, что и подход с одним набором весов, но есть одно существенное отличие: специфичные для классов веса применяются при вычислениях счета Борда. Данная специализация позволяет системе более эффективно использовать экспертизу моделей по определенным классам.

//+------------------------------------------------------------------+
//| classify with ensemble model                                     |
//+------------------------------------------------------------------+
ulong ClogitRegSep::classify(vector &inputs,IClassify *&models[])
  {

   double temp;
   for(uint i =0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      for(long j =0; j<long(classification.Size()); j++)
         m_indices[j] = j;
      if(!classification.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortdsi(0,classification.Size()-1,classification,m_indices);

      for(ulong j = 0 ; j<m_nout; j++)
        {
         temp = m_logit[j].coeffAt(i);
         m_output[m_indices[j]] += j * temp;
        }
     }
   double sum = m_output.Sum();
   ulong ibest = m_output.ArgMax();
   double best = m_output[ibest];

   if(sum>0.0)
      m_output/=sum;

   return ibest;
  }

При реализации отдельных наборов весов необходимы тщательные процедуры проверок. Специалисту следует отслеживать распределения весов на предмет не имеющих объяснения экстремальных значений, чтобы убедиться, что несоразмерность весов согласуется с известными характеристиками модели. Следует реализовать защитные меры для предотвращения нестабильности процесса регрессии. Все их можно эффективно реализовать, соблюдая исчерпывающие протоколы тестирования.

Успешность реализации наборов весов, специфичных для классов, зависит от тщательного внимания к нескольким критическим факторам: обеспечение достаточности обучающих данных для каждого класса, проверка того, что паттерны специализации оправдывают отдельные веса, мониторинг стабильности весов и подтверждение повышения точности классификации по сравнению с подходами с одним набором весов. Хотя как данная продвинутая реализация логистической регрессии предлагает расширенные возможности в части классификации, она требует внимательного управления для решения проблем повышенной сложности и минимизации потенциальных рисков.

Ансамбли, использующие локальную точность

Чтобы еще более эффективно пользоваться преимуществами отдельных моделей, мы можем учитывать их локальную точность в пространстве предикторов. Иногда классификаторы-компоненты демонстрируют более высокую эффективность в определенных областях пространства предикторов. Такая специализация проявляется, когда модели демонстрируют лучшие результаты при определенных условиях предикторных переменных: например, одна модель может оптимально работать при малых значениях переменной, а другая проявляет большую эффективность при более высоких значениях. Такие паттерны специализации, независимо от того, предусмотрены они намеренно или воспроизвелись естественным образом, могут значительно повысить точность классификации при надлежащем применении.

При реализации используется прямолинейный, но эффективный подход. При оценке неизвестного образца система собирает классификации от всех моделей-компонентов и выбирает модель, которая считается наиболее надежной для данного конкретного образца. Ансамбль оценивает надежность модели, используя метод, предлагаемый в работе под названием "Комбинирование нескольких классификаторов с помощью оценок локальной точности", авторы Вудс, Кегельмейер и Боуйер. Данный подход состоит из нескольких четко определенных этапов:

Расчет эвклидовых расстояний между неизвестным образцом и всеми обучающими образцами.
Выявление заранее определенного количества ближайших обучающих образцов для сравнительного анализа.
Оценка эффективности каждой из моделей конкретно на примере этих ближайших образцов, с особым акцентом на случаях, в которых модель присваивает тот же класс, что и для тестируемого образца.
Вычисление критерия эффективности на основе доли корректных классификаций среди образцов, когда модель предсказала один и тот же класс для тестируемого образца и соседних с ним образцов.

Рассмотрение сценария с анализом десяти ближайших соседних образцов. После нахождения таких соседних образцов через расчет эвклидовых расстояний ансамбль передает модели тестируемый образец, и она относит его к классу 3. Затем система оценивает эффективность модели по десяти ближайшим обучающим образцам. Если модель классифицирует шесть из этих образцов как класс 3, при этом четыре из этих шести классификаций являются корректными, модели присваивается критерий производительности 0,67 (4/6). Такой процесс оценки производится по всем моделям-компонентам, и модель, набравшая наибольшую оценку, в итоге определяет финальную классификацию. Данный подход гарантирует, что в решениях классификации будет использоваться наиболее надежная модель для контекста каждого конкретного образца.

Для решения проблемы "ничьих", мы выберем модель с наибольшей определенностью, которая рассчитывается как отношение ее максимального вывода к сумме всех выводов. Определение размера этого локального подмножества необходимо, поскольку чем меньше подмножество, тем оно чувствительнее к локальным вариациям, и чем подмножество больше, тем оно более устойчиво, но при этом характер оценки может становится менее "локальным". Перекрестная проверка может помочь определить оптимальный размер подмножества, при этом обычно приоритет отдается меньшим размерам для лучшей результативности в случае "ничьих". Применяя данный подход, ансамбль эффективно использует экспертизу моделей в определенных областях, при этом сохраняя вычислительную эффективность. Метод позволяет ансамблю динамически адаптироваться к различным областям пространства предикторов, и можно также реализовать критерий надежности, чтобы обеспечить прозрачную метрику для выбора моделей.

Класс ClocalAcc в файле ensemble.mqh разработан для определения наиболее вероятного класса на основе локальной точности с помощью ансамбля классификаторов.

//+------------------------------------------------------------------+
//|  Use local accuracy to choose the best model                     |
//+------------------------------------------------------------------+
class ClocalAcc
  {
private:
   ulong             m_knn;
   ulong             m_nout;
   long              m_indices[];
   matrix            m_ranks;
   vector            m_output;
   vector            m_targs;
   matrix            m_input;
   vector            m_dist;
   matrix            m_trnx;
   matrix            m_trncls;
   vector            m_trntrue;
   ulong             m_classprep;
   bool              m_crossvalidate;
public:
                     ClocalAcc(void);
                    ~ClocalAcc(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
   bool              fit(matrix &inputs, matrix &targets, IClassify* &models[], bool crossvalidate = false);
   vector            proba(void) { return m_output;}
  };

Метод fit() обучает объект ClocalAcc. Он принимает входные данные (inputs), целевые значения (targets), массив моделей-классификаторов (models) и опциональный флаг для перекрестной проверки (crossvalidate). В процессе обучения fit() рассчитывает расстояние между каждой точкой входных данных и всеми остальными точками данных. Затем он определяет k ближайших соседних образцов для каждой точки, где k определяется посредством перекрестной проверки, если crossvalidate присвоено значение true. Для каждого соседнего образца метод оценивает эффективность каждого из классификаторов в ансамбле.

//+------------------------------------------------------------------+
//|  fit an ensemble model                                           |
//+------------------------------------------------------------------+
bool ClocalAcc::fit(matrix &inputs,matrix &targets,IClassify *&models[], bool crossvalidate = false)
  {
   m_crossvalidate = crossvalidate;
   m_nout = targets.Cols();
   m_input = matrix::Zeros(inputs.Rows(),models.Size());
   m_targs = vector::Zeros(inputs.Rows());
   m_output = vector::Zeros(m_nout);
   m_ranks = matrix::Zeros(models.Size(),m_nout);
   m_dist = vector::Zeros(inputs.Rows());
   m_trnx = matrix::Zeros(inputs.Rows(),inputs.Cols());
   m_trncls = matrix::Zeros(inputs.Rows(),models.Size());
   m_trntrue = vector::Zeros(inputs.Rows());

   double best = 0.0;
   if(ArrayResize(m_indices,int(inputs.Rows()))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return false;
     }

   ulong k, knn_min,knn_max,knn_best=0,true_class, ibest=0;

   for(ulong i = 0; i<inputs.Rows(); i++)
     {
      np::matrixCopyRows(m_trnx,inputs,i,i+1,1);
      vector trow = targets.Row(i);
      vector inrow = inputs.Row(i);
      k = trow.ArgMax();
      best = trow[k];
      m_trntrue[i] = double(k);
      for(uint j=0; j<models.Size(); j++)
        {
         vector classification = models[j].classify(inrow);
         ibest = classification.ArgMax();
         best = classification[ibest];
         m_trncls[i][j] = double(ibest);
        }
     }
   m_classprep = 1;
   if(!m_crossvalidate)
     {
      m_knn=3;
      return true;
     }
   else
     {
      ulong ncases = inputs.Rows();
      if(inputs.Rows()<20)
        {
         m_knn=3;
         return true;
        }
      knn_min = 3;
      knn_max = 10;

      vector testcase(inputs.Cols()) ;
      vector clswork(m_nout) ;
      vector knn_counts(knn_max - knn_min + 1) ;

      for(ulong i = knn_min; i<=knn_max; i++)
         knn_counts[i-knn_min] = 0;
      --ncases;
      for(ulong i = 0; i<=ncases; i++)
        {
         testcase = m_trnx.Row(i);
         true_class = ulong(m_trntrue[i]);
         if(i<ncases)
           {
            if(!m_trnx.SwapRows(ncases,i))
              {
               Print(__FUNCTION__, "   ", __LINE__, " failed row swap ", GetLastError());
               return false;
              }
            m_trntrue[i] = m_trntrue[ncases];
            double temp;
            for(uint j = 0; j<models.Size(); j++)
              {
               temp = m_trncls[i][j];
               m_trncls[i][j] = m_trncls[ncases][j];
               m_trncls[ncases][j] = temp;
              }
           }

         m_classprep = 1;
         for(ulong knn = knn_min; knn<knn_max; knn++)
           {
            ulong iclass = classify(testcase,models);
            if(iclass == true_class)
              {
               ++knn_counts[knn-knn_min];
              }
            m_classprep=0;
           }
         if(i<ncases)
           {
            if(!m_trnx.SwapRows(i,ncases) || !m_trnx.Row(testcase,i))
              {
               Print(__FUNCTION__, "   ", __LINE__, " error ", GetLastError());
               return false;
              }
            m_trntrue[ncases] = m_trntrue[i];
            m_trntrue[i] = double(true_class);
            double temp;
            for(uint j = 0; j<models.Size(); j++)
              {
               temp = m_trncls[i][j];
               m_trncls[i][j] = m_trncls[ncases][j];
               m_trncls[ncases][j] = temp;
              }
           }
        }
      ++ncases;
      for(ulong knn = knn_min; knn<=knn_max; knn++)
        {
         if((knn==knn_min) || (ulong(knn_counts[knn-knn_min])>ibest))
           {
            ibest = ulong(knn_counts[knn-knn_min]);
            knn_best = knn;
           }
        }
      m_knn = knn_best;
      m_classprep = 1;
     }

   return true;
  }

Метод classify() предсказывает метку класса для заданного входного вектора. Он рассчитывает расстояния между входным вектором и всеми точками обучающих данных и определяет k ближайших соседних образцов. Метод определяет точность каждого классификатора в ансамбле по этим соседним образцам. Выбирается классификатор с наибольшей точностью по ближайшим соседним образцам, и возвращается предсказанная им метка класса.

//+------------------------------------------------------------------+
//|  classify with an ensemble model                                 |
//+------------------------------------------------------------------+
ulong ClocalAcc::classify(vector &inputs,IClassify *&models[])
  {
   double dist=0, diff=0, best=0, crit=0, bestcrit=0, conf=0, bestconf=0, sum ;
   ulong k, ibest, numer, denom, bestmodel=0, bestchoice=0 ;

   if(m_classprep)
     {
      for(ulong i = 0; i<m_input.Rows(); i++)
        {
         m_indices[i] = long(i);
         dist = 0.0;
         for(ulong j = 0; j<m_trnx.Cols(); j++)
           {
            diff = inputs[j] - m_trnx[i][j];
            dist+= diff*diff;
           }
         m_dist[i] = dist;
        }
      if(!m_dist.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortdsi(0, m_dist.Size()-1, m_dist,m_indices);
     }

   for(uint i = 0; i<models.Size(); i++)
     {
      vector vec = models[i].classify(inputs);
      sum = vec.Sum();
      ibest = vec.ArgMax();
      best = vec[ibest];
      conf = best/sum;
      denom = numer = 0;
      for(ulong ii = 0; ii<m_knn; ii++)
        {
         k = m_indices[ii];
         if(ulong(m_trncls[k][i]) == ibest)
           {
            ++denom;
            if(ibest == ulong(m_trntrue[k]))
               ++numer;
           }
        }
      if(denom > 0)
         crit = double(numer)/double(denom);
      else
         crit = 0.0;
      if((i == 0) || (crit > bestcrit))
        {
         bestcrit = crit;
         bestmodel = ulong(i);
         bestchoice = ibest;
         bestconf = conf;
         m_output = vec;
        }
      else
         if(fabs(crit-bestcrit)<1.e-10)
           {
            if(conf > bestconf)
              {
               bestcrit= crit;
               bestmodel = ulong(i);
               bestchoice = ibest;
               bestconf = conf;
               m_output = vec;
              }
           }
     }

   sum = m_output.Sum();
   if(sum>0)
      m_output/=sum;

   return bestchoice;
  }

Ансамбли, комбинируемые с помощью нечеткого интеграла

Нечеткая логика – это область математики, которая имеет дело со степенями истины вместо абсолютных значений "истина" и "ложь". В контексте комбинирования классификаторов, нечеткую логику можно использовать для интегрирования выводов нескольких моделей, учитывая при этом надежность каждой из них. Нечеткий интеграл, изначально предложенный Сугено (1977), задействует нечеткую меру, которая присваивает значения подмножествам универсума. Данная мера соответствует определенным характеристикам, включая граничные условия, монотонности и непрерывность. Сугено дополнил данное понятие нечеткой мерой λ, которая включает в себя дополнительный коэффициент для объединения мер непересекающихся множеств.

Сам нечеткий интеграл рассчитывается по определенной формуле, в которой используется функция принадлежности и нечеткая мера. Хотя возможно вычисление методом "грубой силы", существует и более эффективный метод для конечных множеств, в котором используется рекурсивный расчет. Значение λ определяется за счет обеспечения того, чтобы конечная мера равнялась единице. В контексте комбинирования классификаторов нечеткий интеграл можно применять, рассматривая каждый классификатор как элемент универсума с присущими ему значениями надежности и принадлежности. Затем нечеткий интеграл рассчитывается для каждого класса, и выбирается класс с наибольшим значением интеграла. Данный метод эффективно комбинирует выводы нескольких классификаторов, принимая во внимание надежность каждого из них в отдельности.

В классе CFuzzyInt реализован метод нечеткого интеграла для комбинирования классификаторов.

//+------------------------------------------------------------------+
//|  Use fuzzy integral to combine decisions                         |
//+------------------------------------------------------------------+
class CFuzzyInt
  {
private:
   ulong             m_nout;
   vector            m_output;
   long              m_indices[];
   matrix            m_sort;
   vector            m_g;
   double            m_lambda;
   double            recurse(double x);
public:
                     CFuzzyInt(void);
                    ~CFuzzyInt(void);
   bool              fit(matrix &predictors, matrix &targets, IClassify* &models[]);
   ulong             classify(vector &inputs, IClassify* &models[]);
   vector            proba(void) { return m_output;}
  };

Основой данного метода является функция recurse(), которая итеративно рассчитывает нечеткую меру. Ключевой параметр λ определяется путем нахождения значения, которое гарантирует, что нечеткая мера всех моделей сходится к единице. Мы начнем с некоторого первичного значения и постепенно будем корректировать его до момента, пока нечетка мера для всех моделей не сойдется к единице. Обычно для этого корректное значение λ берется в скобки, а затем делается более глубокий поиск методом деления пополам.

//+------------------------------------------------------------------+
//|  recurse                                                         |
//+------------------------------------------------------------------+
double CFuzzyInt::recurse(double x)
  {
   double val ;

   val = m_g[0] ;
   for(ulong i=1 ; i<m_g.Size() ; i++)
      val += m_g[i] + x * m_g[i] * val ;

   return val - 1.0 ;
  }

Для оценки надежности каждой модели мы оцениваем ее точность на наборе обучающих данных. Затем мы корректируем ее точность, вычитая ожидаемую точность от случайного угадывания и масштабируя результат к значению от нуля до единицы. Существуют и более изощренные методы оценки надежности моделей, и данный подход используется по причине его простоты.

//+------------------------------------------------------------------+
//|  fit ensemble model                                              |
//+------------------------------------------------------------------+
bool CFuzzyInt::fit(matrix &predictors,matrix &targets,IClassify *&models[])
  {
   m_nout = targets.Cols();
   m_output = vector::Zeros(m_nout);
   m_sort = matrix::Zeros(models.Size(), m_nout);
   m_g = vector::Zeros(models.Size());

   if(ArrayResize(m_indices,int(models.Size()))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return false;
     }

   ulong  k=0, iclass =0 ;
   double  best=0, xlo=0, xhi=0, y=0, ylo=0, yhi=0, step=0 ;

   for(ulong i = 0; i<predictors.Rows(); i++)
     {
      vector trow = targets.Row(i);
      vector inrow = predictors.Row(i);
      k = trow.ArgMax();
      best = trow[k];
      for(uint ii = 0; ii< models.Size(); ii++)
        {
         vector vec = models[ii].classify(inrow);
         iclass = vec.ArgMax();
         best = vec[iclass];
         if(iclass == k)
            m_g[ii] += 1.0;
        }
     }

   for(uint i = 0; i<models.Size(); i++)
     {
      m_g[i] /= double(predictors.Rows()) ;
      m_g[i] = (m_g[i] - 1.0 / m_nout) / (1.0 - 1.0 / m_nout) ;
      if(m_g[i] > 1.0)
         m_g[i] = 1.0 ;
      if(m_g[i] < 0.0)
         m_g[i] = 0.0 ;
     }

   xlo = m_lambda = -1.0 ;
   ylo = recurse(xlo) ;
   if(ylo >= 0.0)    // Theoretically should never exceed zero
      return true;       // But allow for pathological numerical problems

   step = 1.0 ;

   for(;;)
     {
      xhi = xlo + step ;
      yhi = recurse(xhi) ;
      if(yhi >= 0.0)    // If we have just bracketed the root
         break ;        // We can quit the search
      if(xhi > 1.e5)    // In the unlikely case of extremely poor models
        {
         m_lambda = xhi ; // Fudge a value
         return true ;       // And quit
        }
      step *= 2.0 ;     // Keep increasing the step size to avoid many tries
      xlo = xhi ;       // Move onward
      ylo = yhi ;
     }

   for(;;)
     {
      m_lambda = 0.5 * (xlo + xhi) ;
      y = recurse(m_lambda) ;                     // Evaluate the function here
      if(fabs(y) < 1.e-8)                       // Primary convergence criterion
         break ;
      if(xhi - xlo < 1.e-10 * (m_lambda + 1.1))   // Backup criterion
         break ;
      if(y > 0.0)
        {
         xhi = m_lambda ;
         yhi = y ;
        }
      else
        {
         xlo = m_lambda ;
         ylo = y ;
        }
     }

   return true;

  }

В процессе классификации выбирается класс с наибольшим нечетким интегралом. Нечеткий интеграл для каждого класса вычисляется итеративно путем сравнения вывода модели с рекурсивно вычисляемой нечеткой мерой и выбора минимального значения на каждом шаге. Конечный нечеткий интеграл для класса представляет собой комбинированную достоверность моделей для такого класса.

//+------------------------------------------------------------------+
//|   classify with ensemble                                         |
//+------------------------------------------------------------------+
ulong CFuzzyInt::classify(vector &inputs,IClassify *&models[])
  {
   ulong k, iclass;
   double sum, gsum, minval, maxmin, best ;

   for(uint i = 0; i<models.Size(); i++)
     {
      vector vec = models[i].classify(inputs);
      sum = vec.Sum();
      vec/=sum;
      if(!m_sort.Row(vec,i))
        {
         Print(__FUNCTION__, "   ", __LINE__, " row insertion error ", GetLastError());
         return false;
        }
     }

   for(ulong i = 0; i<m_nout; i++)
     {
      for(uint ii =0; ii<models.Size(); ii++)
         m_indices[ii] = long(ii);
      vector vec = m_sort.Col(i);
      if(!vec.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortdsi(0,long(vec.Size()-1), vec, m_indices);
      maxmin = gsum = 0.0;
      for(int j = int(models.Size()-1); j>=0; j--)
        {
         k = m_indices[j];
         if(k>=vec.Size())
           {
            Print(__FUNCTION__," ",__LINE__, " out of range ", k);
           }
         gsum += m_g[k] + m_lambda * m_g[k] * gsum;
         if(gsum<vec[k])
            minval = gsum;
         else
            minval = vec[k];
         if(minval > maxmin)
            maxmin = minval;
        }

      m_output[i] = maxmin;
     }

   iclass = m_output.ArgMax();
   best = m_output[iclass];

   return iclass;
  }

Попарное соединение

Попарное соединение – это уникальный подход к многоклассовой классификации, который эффективно использует возможности специализированных бинарных классификаторов. Он комбинирует набор из K(K−1)/2 бинарных классификаторов (где K – это количество классов), каждый из которых разработан для различения классов из определенной пары. Представьте, что у нас есть датасет, состоящий из целей с тремя классами. Чтобы сравнить их, мы создадим набор из 3*(3-1)/2 = 3 моделей. Каждая модель разработана для принятия решения только между двумя классами. Классы обозначены A, B и C. Три модели будут иметь следующую конфигурацию:

Модель 1: Принимает решение между классом A и классом B.
Модель 2: Принимает решение между классом A и классом C.
Модель 3: Принимает решение между классом B и классом C.

Обучающие данные должны быть разделены так, чтобы включать выборки, соответствующие задачам классификации каждой из моделей. Оценка, проводимая этими моделями, выдаст набор вероятностей, которые можно записать в виде матрицы размера K на K. Ниже представлен гипотетический пример такой матрицы.

	A	B	C
A	----	0.2	0.7
B	0.8	----	0.4
C	0.3	0.6	----

В этой матрице модель, которая проводит различия между классами A и B, присваивает вероятность 0.2 тому, что выборка принадлежит к классу A. Элементы диагонали, начинающейся с правого верхнего элемента матрицы, отражают полный набор вероятностей, рассчитанный для принятия решения между парами классов, так как матрица симметрична. После получения выводов моделей цель состоит в расчете вероятности того, что вневыборочный образец принадлежит к определенному классу. Это означает, что нам нужно найти множество вероятностей, чье распределение совпадает с распределением наблюдаемых попарных вероятностей или по крайней мере соответствует ему как можно ближе. Для обработки этих начальных оценок вероятностей используется итеративный подход, при этом нет необходимости использовать процедуру минимизации функции.

Такой итеративный процесс постепенно уточняет первоначальные вероятности принадлежности к классу таким образом, чтобы они лучше соответствовали попарным прогнозам от отдельных классификаторов. По сути, это похоже на постепенное дополнение карты до момента, пока она не будет соответствовать реальному миру. Мы начинаем с грубого наброска и затем вносим небольшие корректировки на основе новой информации до тех пор, пока не получим карту высокой точности. Такой итеративный подход эффективен и как правило быстро выдает решение.

Алгоритм попарного соединения реализован в классе CPairWise.

//+------------------------------------------------------------------+
//|  Use pairwise coupling to combine decisions                      |
//+------------------------------------------------------------------+
class CPairWise
  {
private:
   ulong             m_nout;
   ulong             m_npairs;
   vector            m_output;
   vector            m_rij;
   vector            m_uij;
public:
                     CPairWise(void);
                    ~CPairWise(void);
   ulong             classify(ulong numclasses,vector &inputs,IClassify *&models[],ulong &samplesPerModel[]);
   vector            proba(void) { return m_output;}
  };

Основные вычисления производятся в методе classify(), который использует структурированный процесс для вычисления классовых вероятностей на основе выводов попарных классификаторов. Метод начинает с оценки всех попарных моделей для заданного тестового образца. Каждая модель соответствует определенной паре классов и генерирует вывод, который представляет собой вероятность того, что тестовый образец принадлежит к одному из двух классов предложенной пары.

//+------------------------------------------------------------------+
//|  classify using ensemble model                                   |
//+------------------------------------------------------------------+
ulong CPairWise::classify(ulong numclasses,vector &inputs,IClassify *&models[],ulong &samplesPerModel[])
  {
   m_nout=numclasses;
   m_npairs = m_nout*(m_nout-1)/2;
   m_output = vector::Zeros(m_nout);
   m_rij = vector::Zeros(m_npairs);
   m_uij = vector::Zeros(m_npairs);

   long  k;
   ulong iclass=0 ;
   double rr, best=0, numer, denom, sum, delta, oldval ;

   for(ulong i = 0; i<m_npairs; i++)
     {
      vector vec = models[i].classify(inputs);
      rr = vec[0];
      if(vec[0]> 0.999999)
         vec[0] = 0.999999 ;
      if(vec[0] < 0.000001)
         vec[0] = 0.000001 ;
      m_rij[i] = vec[0] ;
     }

   k = 0 ;
   for(ulong i=0 ; i<m_nout-1 ; i++)
     {
      for(ulong j=i+1 ; j<m_nout ; j++)
        {
         rr = m_rij[k++] ;
         m_output[i] += rr ;
         m_output[j] += 1.0 - rr ;
        }
     }

   for(ulong i=0 ; i<m_nout ; i++)
      m_output[i] /= double(m_npairs) ;

   k = 0 ;
   for(ulong i=0 ; i<m_nout-1 ; i++)
     {
      for(ulong j=i+1 ; j<m_nout ; j++)
         m_uij[k++] = m_output[i] / (m_output[i] + m_output[j]) ;
     }

   for(int iter=0 ; iter<10000 ; iter++)
     {

      delta = 0.0 ;
      for(ulong i=0 ; i<m_nout ; i++)
        {

         numer = denom = 0.0 ;
         for(ulong j=0 ; j<m_nout ; j++)
           {
            if(i < j)
              {
               k = (long(i) * (2 * long(m_nout) - long(i) - 3) - 2) / 2 + long(j) ;
               numer += samplesPerModel[k] * m_rij[k] ;
               denom += samplesPerModel[k] * m_uij[k] ;
              }
            else
               if(i > j)
                 {
                  k = (long(j) * (2 * long(m_nout) - long(j) - 3) - 2) / 2 + long(i) ;
                  //Print(__FUNCTION__," ",__LINE__," k ", k);
                  numer += samplesPerModel[k] * (1.0 - m_rij[k]) ;
                  denom += samplesPerModel[k] * (1.0 - m_uij[k]) ;
                 }
           }

         oldval = m_output[i] ;
         m_output[i] *= numer / denom ;
         sum = 0.0 ;
         for(ulong j=0 ; j<m_nout ; j++)
            sum += m_output[j] ;
         for(ulong j=0 ; j<m_nout ; j++)
            m_output[j] /= sum ;

         if(fabs(m_output[i]-oldval) > delta)
            delta = fabs(m_output[i]-oldval) ;


         k = 0 ;
         for(ulong i=0 ; i<m_nout-1 ; i++)
           {
            for(ulong j=i+1 ; j<m_nout ; j++)
               m_uij[k++] = m_output[i] / (m_output[i] + m_output[j]) ;
           }

        }

      if(delta < 1.e-6)
         break ;

     }

   return m_output.ArgMax() ;

  }

Как только будут получены первичные выводы (вероятности), они используются в качестве стартовых оценок вероятностей принадлежности к классу. Затем метод итеративно уточняет эти оценки, чтобы повысить точность. Финальным этапом после уточнения вероятностей принадлежности к классу является определение класса, обладающего большей вероятностью. Класс с наибольшей вероятностью считается наиболее правдоподобным классом для заданного тестового образца, и метод classify() возвращает его индекс.

Заключение: Сравнение методов комбинирования

Скрипт ClassificationEnsemble_Demo.mq5 разработан для сравнения эффективности ансамблевых алгоритмов, которые обсуждались в этой статье, на различных сценариях. Запуская несколько репликаций Monte Carlo, скрипт проводит оценку эффективности каждого из ансамблевых методов при различных условиях. Скрипт позволяет пользователям указать количество обучающих выборок, которые будут использоваться в каждом запуске, позволяя проводить тестирование на различных датасетах различного размера, от небольших до крупных. Количество классов можно скорректировать для тестирования масштабируемости ансамблевых методов по мере того, как увеличивается сложность задачи. Можно изменять количество базовых классификаторов (моделей), используемых в ансамбле, для оценки того, насколько эффективно работают алгоритмы при различных уровнях сложности.

Пользователи могут указать количество репликаций Monte Carlo для каждого сценария, чтобы оценить стабильность и корректность ансамблевых алгоритмов. В качестве метрики эффективности используется вероятность вневыборочной неверной классификации, которая обеспечивает, что модели оцениваются по неизвестным данным для симуляции реальных задач классификации. Если используется четыре модели или более, одна модели умышленно делается бесполезной (например, делает случайные предсказания или выдает константы). Это позволяет протестировать надежность ансамблевых алгоритмов и оценить, как они справляются с включением нерелевантных или неинформативных моделей.

Если используется пять или более моделей, пятая модель настраивается так, чтобы изредка выдавать экстремальные или хаотичные прогнозы, симулируя реальные сценарии, в которых модель может быть нестабильной или зашумленной. Данный функционал позволяет оценить, как ансамблевые методы обрабатывают ненадежные модели, и могут ли они поддерживать надлежащее качество классификации, корректно взвешивая или уменьшая вес проблемных моделей. Коэффициент сложности классификации определяет спред между классами, который контролирует сложность задачи для моделей-компонентов. Чем больше данный спред, тем легче различать классы, чем он меньше, тем выше сложность. Данный функционал позволяет тестировать, насколько хорошо ансамблевые методы работают при разных уровнях сложности, оценивая их способность сохранять точность при сложных сценариях.

//+------------------------------------------------------------------+
//|                                  ClassificationEnsemble_Demo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<ensemble.mqh>
#include<multilayerperceptron.mqh>
//--- input parameters
input int      NumSamples=10;
input int      NumClasses=3;
input int      NumModels=3;
input int      NumReplications=1000;
input double   ClassificationDifficultyFactor=0.0;

//+------------------------------------------------------------------+
//|  normal(rngstate)                                                |
//+------------------------------------------------------------------+
double normal(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndNormal(state);
  }
//+------------------------------------------------------------------+
//|   unifrand(rngstate)                                             |
//+------------------------------------------------------------------+
double unifrand(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndUniformR(state);
  }
//+------------------------------------------------------------------+
//|Multilayer perceptron                                             |
//+------------------------------------------------------------------+
class CMLPC:public ensemble::IClassify
  {
private:
   CMlp              *m_mlfn;
   double             m_learningrate;
   double             m_tolerance;
   double             m_alfa;
   double             m_beyta;
   uint               m_epochs;
   ulong              m_in,m_out;
   ulong              m_hl1,m_hl2;

public:
                     CMLPC(ulong ins, ulong outs,ulong numhl1,ulong numhl2);
                    ~CMLPC(void);
   void              setParams(double alpha_, double beta_,double learning_rate, double tolerance, uint num_epochs);
   bool              train(matrix &predictors,matrix&targets);
   vector            classify(vector &predictors);
   ulong             getNumInputs(void) { return m_in;}
   ulong             getNumOutputs(void) { return m_out;}
  };
//+------------------------------------------------------------------+
//| constructor                                                      |
//+------------------------------------------------------------------+
CMLPC::CMLPC(ulong ins, ulong outs,ulong numhl1,ulong numhl2)
  {
   m_in = ins;
   m_out = outs;
   m_alfa = 0.3;
   m_beyta = 0.01;
   m_learningrate=0.001;
   m_tolerance=1.e-8;
   m_epochs= 1000;
   m_hl1 = numhl1;
   m_hl2 = numhl2;
   m_mlfn = new CMlp();
  }
//+------------------------------------------------------------------+
//| destructor                                                       |
//+------------------------------------------------------------------+
CMLPC::~CMLPC(void)
  {
   if(CheckPointer(m_mlfn) == POINTER_DYNAMIC)
      delete m_mlfn;
  }
//+------------------------------------------------------------------+
//| set other hyperparameters of the i_model                           |
//+------------------------------------------------------------------+
void CMLPC::setParams(double alpha_, double beta_,double learning_rate, double tolerance, uint num_epochs)
  {
   m_alfa = alpha_;
   m_beyta = beta_;
   m_learningrate=learning_rate;
   m_tolerance=tolerance;
   m_epochs= num_epochs;
  }
//+------------------------------------------------------------------+
//| fit a i_model to the data                                          |
//+------------------------------------------------------------------+
bool CMLPC::train(matrix &predictors,matrix &targets)
  {
   if(m_in != predictors.Cols() || m_out != targets.Cols())
     {
      Print(__FUNCTION__, " failed training due to invalid training data");
      return false;
     }

   return m_mlfn.fit(predictors,targets,m_alfa,m_beyta,m_hl1,m_hl2,m_epochs,m_learningrate,m_tolerance);
  }
//+------------------------------------------------------------------+
//| make a prediction with the trained i_model                         |
//+------------------------------------------------------------------+
vector CMLPC::classify(vector &predictors)
  {
   return m_mlfn.predict(predictors);
  }
//+------------------------------------------------------------------+
//| clean up dynamic array pointers                                  |
//+------------------------------------------------------------------+
void cleanup(ensemble::IClassify* &array[])
  {
   for(uint i = 0; i<array.Size(); i++)
      if(CheckPointer(array[i])==POINTER_DYNAMIC)
         delete array[i];
  }
//+------------------------------------------------------------------+
//| global variables                                                 |
//+------------------------------------------------------------------+
int nreplications, nsamps,nmodels, divisor, nreps_done ;
int n_classes, nnn, n_pairs, nh_g ;
ulong ntrain_pair[];
matrix xdata, xbad_data, xtainted_data, test[],x_targ,xbad_targ,xwild_targ;
vector inputdata;
double cd_factor, err_score, err_score_1, err_score_2, err_score_3 ;
vector classification_err_raw, output_vector;
double classification_err_average ;
double classification_err_median ;
double classification_err_maxmax ;
double classification_err_maxmin ;
double classification_err_intersection_1 ;
double classification_err_intersection_2 ;
double classification_err_intersection_3 ;
double classification_err_union_1 ;
double classification_err_union_2 ;
double classification_err_union_3 ;
double classification_err_majority ;
double classification_err_borda ;
double classification_err_logit ;
double classification_err_logitsep ;
double classification_err_localacc ;
double classification_err_fuzzyint ;
double classification_err_pairwise ;
//+------------------------------------------------------------------+
//| ensemble i_model objects                                         |
//+------------------------------------------------------------------+
ensemble::CAvgClass average_ensemble ;
ensemble::CMedian median_ensemble ;
ensemble::CMaxMax maxmax_ensemble ;
ensemble::CMaxMin maxmin_ensemble ;
ensemble::CIntersection intersection_ensemble ;
ensemble::CUnion union_rule ;
ensemble::CMajority majority_ensemble ;
ensemble::CBorda borda_ensemble ;
ensemble::ClogitReg logit_ensemble ;
ensemble::ClogitRegSep logitsep_ensemble ;
ensemble::ClocalAcc localacc_ensemble ;
ensemble::CFuzzyInt fuzzyint_ensemble ;
ensemble::CPairWise pairwise_ensemble ;

int n_hid = 4 ;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CHighQualityRandStateShell rngstate;
   CHighQualityRand::HQRndRandomize(rngstate.GetInnerObj());
//---
   nsamps = NumSamples ;
   n_classes = NumClasses ;
   nmodels = NumModels ;
   nreplications = NumReplications ;
   cd_factor = ClassificationDifficultyFactor ;

   if((nsamps <= 3)  || (n_classes <= 1)  || (nmodels <= 0)  || (nreplications <= 0) || (cd_factor < 0.0))
     {
      Alert(" Invalid inputs ");
      return;
     }

   divisor = 1 ;
   ensemble::IClassify* models[];
   ensemble::IClassify* model_pairs[];
   /*
      Allocate memory and initialize
   */
   n_pairs = n_classes * (n_classes-1) / 2 ;
   if(ArrayResize(models,nmodels)<0 || ArrayResize(model_pairs,n_pairs)<0 || ArrayResize(test,10)<0 ||
      ArrayResize(ntrain_pair,n_pairs)<0)
     {
      Print(" Array resize errors ", GetLastError());
      cleanup(models);
      cleanup(model_pairs);
      return;
     }

   ArrayInitialize(ntrain_pair,0);

   for(int i=0 ; i<nmodels ; i++)
      models[i] = new CMLPC(2,ulong(n_classes),4,0) ;

   xdata = matrix::Zeros(nsamps,(2+n_classes));
   xbad_data = matrix::Zeros(nsamps,(2+n_classes));
   xtainted_data = matrix::Zeros(nsamps,(2+n_classes));
   inputdata = vector::Zeros(3);

   for(uint i = 0; i<test.Size(); i++)
      test[i] = matrix::Zeros(nsamps,(2+n_classes));

   classification_err_raw = vector::Zeros(nmodels);
   classification_err_average = 0.0 ;
   classification_err_median = 0.0 ;
   classification_err_maxmax = 0.0 ;
   classification_err_maxmin = 0.0 ;
   classification_err_intersection_1 = 0.0 ;
   classification_err_intersection_2 = 0.0 ;
   classification_err_intersection_3 = 0.0 ;
   classification_err_union_1 = 0.0 ;
   classification_err_union_2 = 0.0 ;
   classification_err_union_3 = 0.0 ;
   classification_err_majority = 0.0 ;
   classification_err_borda = 0.0 ;
   classification_err_logit = 0.0 ;
   classification_err_logitsep = 0.0 ;
   classification_err_localacc = 0.0 ;
   classification_err_fuzzyint = 0.0 ;
   classification_err_pairwise = 0.0 ;

   for(int i_rep=0 ; i_rep<nreplications ; i_rep++)
     {
      nreps_done = i_rep + 1 ;

      if(i_rep>0)
         xdata.Fill(0.0);
      //---
      for(int i=0, z=0; i<nsamps ; i++)
        {
         xdata[i][0] = normal(rngstate) ;
         xdata[i][1] = normal(rngstate) ;
         if(i < n_classes)
            z = i ;
         else
            z = (int)(unifrand(rngstate) * n_classes) ;
         if(z >= n_classes)
            z = n_classes - 1 ;
         xdata[i][2+z] = 1.0 ;
         xdata[i][0] += double(z) * cd_factor ;
         xdata[i][1] -= double(z) * cd_factor ;
        }

      if(nmodels >= 4)
        {
         xbad_data = xdata;
         matrix arm = np::sliceMatrixCols(xbad_data,2);
         for(int i = 0; i<nsamps; i++)
            for(int z = 0; z<n_classes; z++)
               arm[i][z] = (unifrand(rngstate)<(1.0/double(n_classes)))?1.0:0.0;

         np::matrixCopy(xbad_data,arm,0,xbad_data.Rows(),1,2);
        }

      if(nmodels >= 5)
        {
         xtainted_data = xdata;
         matrix arm = np::sliceMatrixCols(xtainted_data,2);
         for(int i = 0; i<nsamps; i++)
            for(int z = 0; z<n_classes; z++)
               if(unifrand(rngstate)<0.1)
                  arm[i][z] = xdata[i][2+z] * 1000.0 - 500.0 ;

         np::matrixCopy(xtainted_data,arm,0,xtainted_data.Rows(),1,2);
        }

      for(int i=0 ; i<10 ; i++)         // Build a test dataset
        {
         if(i_rep>0)
            test[i].Fill(0.0);
         for(int j=0,z=0; j<nsamps; j++)
           {
            test[i][j][0] = normal(rngstate) ;
            test[i][j][1] = normal(rngstate) ;
            z = (int)(unifrand(rngstate) * n_classes) ;
            if(z >= n_classes)
               z = n_classes - 1 ;
            test[i][j][2+z] = 1.0 ;
            test[i][j][0] += double(z) * cd_factor ;
            test[i][j][1] -= double(z) * cd_factor ;
           }
        }

      for(int i_model=0 ; i_model<nmodels ; i_model++)
        {
         matrix preds,targs;
         if(i_model == 3)
           {
            targs = np::sliceMatrixCols(xbad_data,2);
            preds = np::sliceMatrixCols(xbad_data,0,2);
           }
         else
            if(i_model == 4)
              {
               targs = np::sliceMatrixCols(xtainted_data,2);
               preds = np::sliceMatrixCols(xtainted_data,0,2);
              }
            else
              {
               targs = np::sliceMatrixCols(xdata,2);
               preds = np::sliceMatrixCols(xdata,0,2);
              }

         if(!models[i_model].train(preds,targs))
           {
            Print(" failed to train i_model at shift ", i_model);
            cleanup(model_pairs);
            cleanup(models);
            return;
           }

         err_score = 0.0 ;
         for(int i=0 ; i<10 ; i++)
           {
            vector testvec,testin,testtarg;
            for(int j=0; j<nsamps; j++)
              {
               testvec = test[i].Row(j);
               testtarg = np::sliceVector(testvec,2);
               testin = np::sliceVector(testvec,0,2);
               output_vector = models[i_model].classify(testin) ;
               if(output_vector.ArgMax() != testtarg.ArgMax())
                  err_score += 1.0 ;
              }
           }
         classification_err_raw[i_model] += err_score / (10 * nsamps) ;
        }

      int i_model = 0;
      for(int i=0 ; i<n_classes-1 ; i++)
        {
         for(int j=i+1 ; j<n_classes ; j++)
           {

            ntrain_pair[i_model] = 0 ;
            for(int z=0 ; z<nsamps ; z++)
              {
               if((xdata[z][2+i]> 0.5)
                  || (xdata[z][2+j] > 0.5))
                  ++ntrain_pair[i_model] ;
              }
            nh_g = (n_hid < int(ntrain_pair[i_model]) - 1) ? n_hid : int(ntrain_pair[i_model]) - 1;
            model_pairs[i_model] = new CMLPC(2, 1, ulong(nh_g+1),0) ;
            matrix training;
            matrix preds,targs;
            ulong msize=0;
            for(int z=0 ; z<nsamps ; z++)
              {
               inputdata[0] = xdata[z][0] ;
               inputdata[1] = xdata[z][1] ;
               if(xdata[z][2+i]> 0.5)
                  inputdata[2] = 1.0 ;
               else
                  if(xdata[z][2+j] > 0.5)
                     inputdata[2] = 0.0 ;
                  else
                     continue ;
               training.Resize(msize+1,inputdata.Size());
               training.Row(inputdata,msize++);
              }
            preds = np::sliceMatrixCols(training,0,2);
            targs = np::sliceMatrixCols(training,2);
            model_pairs[i_model].train(preds,targs);
            ++i_model ;
           }
        }

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(average_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_average += err_score / (10 * nsamps) ;

      /*
      median_ensemble
      */

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(median_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_median += err_score / (10 * nsamps) ;

      /*
      maxmax_ensemble
      */

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(maxmax_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_maxmax += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(maxmin_ensemble.classify(rowtest,models) != rowtarg.ArgMax())   // If predicted class not true class
               err_score += 1.0 ;      // Count this misclassification
           }
        }
      classification_err_maxmin += err_score / (10 * nsamps) ;

      matrix preds,targs;
      err_score_1 = err_score_2 = err_score_3 = 0.0 ;
      preds = np::sliceMatrixCols(xdata,0,2);
      targs = np::sliceMatrixCols(xdata,2);

      intersection_ensemble.fit(preds,targs,models);
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            ulong class_ = intersection_ensemble.classify(rowtest,models) ;
            output_vector = intersection_ensemble.proba();

            if(output_vector[rowtarg.ArgMax()] < 0.5)
              {
               err_score_1 += 1.0 ;
               err_score_2 += 1.0 ;
               err_score_3 += 1.0 ;
              }
            else
              {
               if(class_ > 3)
                  err_score_3 += 1.0 ;
               if(class_ > 2)
                  err_score_2 += 1.0 ;
               if(class_ > 1)
                  err_score_1 += 1.0 ;
              }
           }
        }
      classification_err_intersection_1 += err_score_1 / (10 * nsamps) ;
      classification_err_intersection_2 += err_score_2 / (10 * nsamps) ;
      classification_err_intersection_3 += err_score_3 / (10 * nsamps) ;

      union_rule.fit(preds,targs,models);
      err_score_1 = err_score_2 = err_score_3 = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            ulong clss = union_rule.classify(rowtest,models) ;
            output_vector = union_rule.proba();

            if(output_vector[rowtarg.ArgMax()] < 0.5)
              {
               err_score_1 += 1.0 ;
               err_score_2 += 1.0 ;
               err_score_3 += 1.0 ;
              }
            else
              {
               if(clss > 3)
                  err_score_3 += 1.0 ;
               if(clss > 2)
                  err_score_2 += 1.0 ;
               if(clss > 1)
                  err_score_1 += 1.0 ;
              }
           }
        }

      classification_err_union_1 += err_score_1 / (10 * nsamps) ;
      classification_err_union_2 += err_score_2 / (10 * nsamps) ;
      classification_err_union_3 += err_score_3 / (10 * nsamps) ;

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(majority_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_majority += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(borda_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_borda += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      logit_ensemble.fit(preds,targs,models);
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(logit_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_logit += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      logitsep_ensemble.fit(preds,targs,models);
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(logitsep_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_logitsep += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      localacc_ensemble.fit(preds,targs,models);
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(localacc_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_localacc += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      fuzzyint_ensemble.fit(preds,targs,models);
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(fuzzyint_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_fuzzyint += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(pairwise_ensemble.classify(ulong(n_classes),rowtest,model_pairs,ntrain_pair)  != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_pairwise += err_score / (10 * nsamps) ;
      cleanup(model_pairs);
     }
   err_score = 0.0 ;
   PrintFormat("Test Config: Classification Difficulty - %8.8lf\nNumber of classes - %5d\nNumber of component models - %5d\n Sample Size - %5d", ClassificationDifficultyFactor,NumClasses,NumModels,NumSamples);
   PrintFormat("%5d    Replications:", nreps_done) ;
   for(int i_model=0 ; i_model<nmodels ; i_model++)
     {
      PrintFormat("  %.8lf", classification_err_raw[i_model] / nreps_done) ;
      err_score += classification_err_raw[i_model] / nreps_done ;
     }
   PrintFormat("       Mean raw error = %8.8lf", err_score / nmodels) ;
   PrintFormat("        average_ensemble error = %8.8lf", classification_err_average / nreps_done) ;
   PrintFormat("         median_ensemble error = %8.8lf", classification_err_median / nreps_done) ;
   PrintFormat("         maxmax_ensemble error = %8.8lf", classification_err_maxmax / nreps_done) ;
   PrintFormat("         maxmin_ensemble error = %8.8lf", classification_err_maxmin / nreps_done) ;
   PrintFormat("       majority_ensemble error = %8.8lf", classification_err_majority / nreps_done) ;
   PrintFormat("          borda_ensemble error = %8.8lf", classification_err_borda / nreps_done) ;
   PrintFormat("          logit_ensemble error = %8.8lf", classification_err_logit / nreps_done) ;
   PrintFormat("       logitsep_ensemble error = %8.8lf", classification_err_logitsep / nreps_done) ;
   PrintFormat("       localacc_ensemble error = %8.8lf", classification_err_localacc / nreps_done) ;
   PrintFormat("       fuzzyint_ensemble error = %8.8lf", classification_err_fuzzyint / nreps_done) ;
   PrintFormat("       pairwise_ensemble error = %8.8lf", classification_err_pairwise / nreps_done) ;
   PrintFormat(" intersection_ensemble error 1 = %8.8lf", classification_err_intersection_1 / nreps_done) ;
   PrintFormat(" intersection_ensemble error 2 = %8.8lf", classification_err_intersection_2 / nreps_done) ;
   PrintFormat(" intersection_ensemble error 3 = %8.8lf", classification_err_intersection_3 / nreps_done) ;
   PrintFormat("        Union error 1 = %8.8lf", classification_err_union_1 / nreps_done) ;
   PrintFormat("        Union error 2 = %8.8lf", classification_err_union_2 / nreps_done) ;
   PrintFormat("        Union error 3 = %8.8lf", classification_err_union_3 / nreps_done) ;
   cleanup(models);
  }

//+------------------------------------------------------------------+

Ниже представлены примеры результатов, получаемых после запуска скрипта. Эти результаты получены для задачи классификации с заданной максимальной сложностью.

ClassificationDifficultyFactor=0.0

DM      0       05:40:06.441    ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 0.00000000
RP      0       05:40:06.441    ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes -     3
QI      0       05:40:06.441    ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models -     3
EK      0       05:40:06.441    ClassificationEnsemble_Demo (BTCUSD,D1)  Sample Size -    10
MN      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)  1000    Replications:
CF      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)   0.66554000
HI      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)   0.66706000
DP      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)   0.66849000
II      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        Mean raw error = 0.66703000
JS      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)         average_ensemble error = 0.66612000
HR      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)          median_ensemble error = 0.66837000
QF      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmax_ensemble error = 0.66704000
MD      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmin_ensemble error = 0.66586000
GI      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        majority_ensemble error = 0.66772000
HR      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)           borda_ensemble error = 0.66747000
MO      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)           logit_ensemble error = 0.66556000
MP      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        logitsep_ensemble error = 0.66570000
JD      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        localacc_ensemble error = 0.66578000
OJ      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        fuzzyint_ensemble error = 0.66503000
KO      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        pairwise_ensemble error = 0.66799000
GS      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 1 = 0.96686000
DP      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 2 = 0.95847000
QE      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 3 = 0.95447000
OI      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 1 = 0.99852000
DM      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 2 = 0.97931000
JR      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 3 = 0.01186000

Далее представлены результаты теста, в котором сложность классификации была средней.

LF      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 1.00000000
IG      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes -     3
JP      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models -     3
FQ      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)  Sample Size -    10
KH      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)  1000    Replications:
NO      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)   0.46236000
QF      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)   0.45818000
II      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)   0.45779000
FR      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        Mean raw error = 0.45944333
DI      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)         average_ensemble error = 0.44881000
PH      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)          median_ensemble error = 0.45564000
JO      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmax_ensemble error = 0.46763000
GS      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmin_ensemble error = 0.44935000
GP      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        majority_ensemble error = 0.45573000
PI      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)           borda_ensemble error = 0.45593000
DF      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)           logit_ensemble error = 0.46353000
FO      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        logitsep_ensemble error = 0.46726000
ER      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        localacc_ensemble error = 0.46096000
KP      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        fuzzyint_ensemble error = 0.45098000
OD      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        pairwise_ensemble error = 0.66485000
IJ      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 1 = 0.93533000
RO      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 2 = 0.92527000
OL      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 3 = 0.92527000
OR      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 1 = 0.99674000
KG      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 2 = 0.97231000
NK      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 3 = 0.00877000

Последний набор демонстрирует результаты теста, проведенного при относительно низкой сложности классификации.

PL      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 10.00000000
CN      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes -     3
PK      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models -     3
LH      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)  Sample Size -    10
EQ      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)  1000    Replications:
MD      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)   0.02905000
LO      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)   0.02861000
CF      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)   0.02879000
IK      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        Mean raw error = 0.02881667
RN      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)         average_ensemble error = 0.02263000
PQ      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)          median_ensemble error = 0.02956000
QD      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmax_ensemble error = 0.03426000
KJ      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmin_ensemble error = 0.02263000
IO      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        majority_ensemble error = 0.02956000
HP      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)           borda_ensemble error = 0.02956000
KM      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)           logit_ensemble error = 0.03171000
OE      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        logitsep_ensemble error = 0.04840000
GK      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        localacc_ensemble error = 0.03398000
FO      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        fuzzyint_ensemble error = 0.02263000
QM      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        pairwise_ensemble error = 0.65277000
CQ      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 1 = 0.96303000
DF      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 2 = 0.96167000
IK      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 3 = 0.96167000
IK      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 1 = 0.98620000
CP      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 2 = 0.95624000
LD      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 3 = 0.00000000

Весь код, используемый в тексте статьи, прикреплен к ней. А в таблице ниже представлены описания всех исходных файлов.

Имя файла	Описание файла
MQL5/include/np.mqh	Набор служебных функций для выполнения операций с векторами и матрицами
MQL5/include/nom2ord.mqh	Данный файл содержит классы для кодирования категориальных данных
MQL5/include/multilayerperceptron.mqh	Содержит определение класса CMlp, представляющего собой нейронную сеть с прямой связью
MQL5/include/logistic.mqh	Содержит определение класса Clogit, который реализует логистическую регрессию
MQL5/include/ensemble.mqh	Содержит определения различных реализаций метамоделей
MQL5/scripts/ClassificationEnsemble_Demo.mq5	Данный скрипт сравнивает эффективность ансамблевых классификаторов, определенных в файле ensemble.mqh
MQL5/scripts/PairWise_Ensemble_Demo.mq5	Демонстрационный скрипт, показывающий, как применять класс CPairWise для попарного соединения

Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/16838

Прикрепленные файлы |

Загрузить ZIP

ensemble.mqh (146.05 KB)

logistic.mqh (15.51 KB)

multilayerperceptron.mqh (6.64 KB)

nom2ord.mqh (21.89 KB)

np.mqh (80.58 KB)

ClassificationEnsemble_Demo.mq5 (24.11 KB)

PairWise_Ensemble_Demo.mq5 (9.3 KB)

Mql5.zip (39.67 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Моделирование рынка (Часть 03): Вопрос производительности

Часто нам приходится делать шаг назад, а затем двигаться вперед. В этой статье мы покажем все изменения, необходимые для того, чтобы не нарушить работу индикаторов Mouse и Chart Trade. В качестве бонуса расскажем о других изменениях, произошедших в других заголовочных файлах, которые будут широко использоваться в будущем.

Риск-менеджер для торговых роботов (Часть I): Включаемый файл контроля рисков для советников

Трейдинг характеризуется высокими требованиями к дисциплине риск-менеджмента. Настоящая работа представляет анализ основных причин неудач трейдеров и предлагает техническое решение в виде класса CEnhancedRiskManager для платформы MQL5. Включает практическое тестирование на агрессивном сеточном советнике.

Нейросети в трейдинге: Декомпозиция вместо масштабирования (Окончание)

Предлагаем познакомиться с алгоритмом разложения временного ряда на смысловые слои и построения из них экономной модели. Мы последовательно показываем архитектуру, практическую реализацию на MQL5/OpenCL и реальные тесты на исторических рыночных данных.

Добавляем пользовательскую LLM в торгового робота (Часть 5): Разработка и тестирование торговой стратегии с помощью LLM (III) – Настройка адаптера

Языковые модели (LLM) являются важной частью быстро развивающегося искусственного интеллекта, поэтому нам следует подумать о том, как интегрировать мощные LLM в нашу алгоритмическую торговлю. Большинству людей сложно настроить эти модели в соответствии со своими потребностями, развернуть их локально, а затем применить к алгоритмической торговле. В этой серии статей будет рассмотрен пошаговый подход к достижению этой цели.