Методы повторной выборки для оценки прогнозирования и классификации в MQL5

Введение

Эффективность моделей машинного обучения обычно оценивают в рамках двух отдельных этапов: обучение на одном наборе данных и тестирование на другом. Однако в ситуациях, когда комплектование нескольких наборов данных может оказаться нецелесообразным из-за ограниченных ресурсов или ограничений материально-технического характера, необходимо применять альтернативные подходы.

Один из таких методов предполагает использование различных способов повторной выборки для оценки эффективности моделей прогнозирования или классификации. Было показано, что такой подход дает надежные результаты, несмотря на его потенциальные недостатки. В этой статье рассмотрим новую методологию оценки качества модели, которая использует один и тот же набор данных и для обучения, и для проверки. Основной причиной применения таких методов является ограниченная доступность данных для целей тестирования.

В связи с этим практическим специалистам приходится применять усложненные алгоритмы повторной выборки для получения показателей эффективности, сопоставимых с показателями, которые генерируются с помощью более простых подходов. Эти методы требуют значительных вычислительных ресурсов и могут усложнить процессы разработки моделей. Несмотря на этот компромисс, использование стратегий оценки на основе повторной выборки может быть ценным в определенных условиях, где выгоды перевешивают затраты.

Разбор ошибок

Для облегчения изложения алгоритмических концепций, представленных в этом тексте, введена система обозначений. Такая структура обозначений в первую очередь решает задачу разложения ошибки модели на составные элементы. Рассмотрим набор данных, обозначенный как T и полученная из совокупности, которая характеризуется неизвестным распределением F. Этот набор данных содержит n наблюдений, каждое из них состоит из переменной-предиктора x, которая может быть как скалярной, так и векторной, а также прогнозируемой переменной y, которая является скалярной. Чтобы подчеркнуть внутреннюю взаимозависимость предиктора и прогнозируемых переменных, для представления пары (x, y) используется составной термин t (от слова training — обучение). Таким образом, i-е наблюдение в наборе данных представлено в виде t_i = (x_i, y_i). Хотя эта нотация предполагает числовую структуру прогнозирования. Задачи классификации можно решать, интерпретируя элемент y_i как относящийся к классу i-го наблюдения.

Полный набор данных обозначается как T. Когда модель обучается с помощью T в качестве обучающего набора, полученная обученная модель будет обозначена как M_T. Применение этой обученной модели M_T к конкретному значению переменной-предиктору x для получения оценки соответствующей прогнозируемой переменной дает прогноз модели, обозначаемой как M_T(x). Для краткости обобщенный прогноз модели можно сократить как M. При оценке эффективности прогностической модели часто необходимо количественно оценить расхождение между прогнозом модели (M) и наблюдаемым значением (y) прогнозируемой переменной. Формально это расхождение определяется как мера ошибки, которая обозначается как Ef[y, M]. Распространенной мерой ошибки, которую используют в контексте регрессии, является среднеквадратическая ошибка, применяющая квадрат разности, как показано в уравнении ниже. В задачах классификации можно определять Ef[y, M] как бинарную функцию, присваивающую значение ноль, если y равно M, и единицу в ином случае.

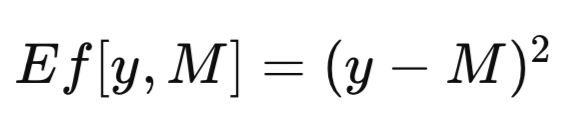
Когда обученная модель применяется к тому же набору данных, который использовался для ее обучения, средняя ошибка по всем случаям обучения обозначается как мнимая ошибка. В то время как традиционный подход предполагает обучение модели путем сведения такой мнимой ошибки к минимуму, представленная в этой статье методология такого ограничения не накладывает. Допустима оптимизация любой произвольной меры с последующей оценкой качества обученной модели на основе определенного критерия. Мнимая ошибка, описанная ниже, является исключительно функцией от производительности модели на обучающих данных и применения функции Ef[] к каждому прогнозу; при этом методология обучения значения не имеет.

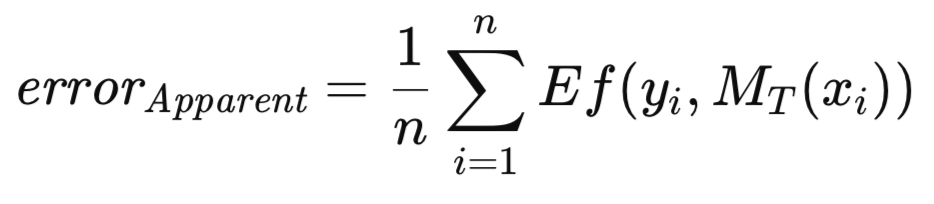
Хорошо известно, что мнимая ошибка демонстрирует оптимистический уклон — явление, которое иногда называют уклоном обучения, так как оценка модели выполняется на тех же данных, которые использовались для ее обучения. Для смягчения этого уклона при наличии достаточного количества данных обученная модель оценивается на независимом наборе данных. Такой алгоритм упрощает оценку ожидаемой ошибки обученной модели, если применить его к генеральной совокупности. Эта ожидаемая ошибка, обусловленная тем фактом, что модель обучалась на соответствующем наборе, называется ошибкой прогнозирования. Основное внимание здесь уделяется оценке ожидаемой будущей производительности конкретной обученной модели. Формально ошибка прогнозирования выражается следующим уравнением.

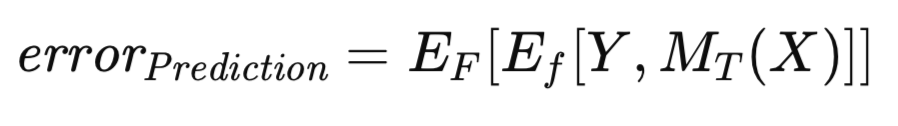
Рассмотрения заслуживает также связанная с этим, но концептуально иная мера ошибки. Ошибка прогнозирования, как было определено ранее, обусловлена конкретной реализованной моделью, обученной на определенном наборе данных. Однако можно расширить математическое ожидание таким образом, чтобы в него входила совокупность всех возможных обучающих наборов. В частности, учитывая, что в обучающий набор входят n наблюдений, выборка которых сделана из неизвестного распределения, можно оценить ошибку прогнозирования, связанную с обученной на этом конкретном обучающем наборе данных моделью, потенциально аппроксимируя ее с помощью независимого валидационного множества. Теперь рассмотрим сценарий, в котором формируется новый обучающий набор и повторяется алгоритм обучения. Неизбежно будет получена несколько иная ошибка прогнозирования. Следовательно, возникает необходимость сформулировать меру, которая фиксирует ожидаемую оценку прогнозирования по всему спектру потенциальных обучающих наборов. Эта мера, обозначенная как ошибка генеральной совокупности, описана ниже.

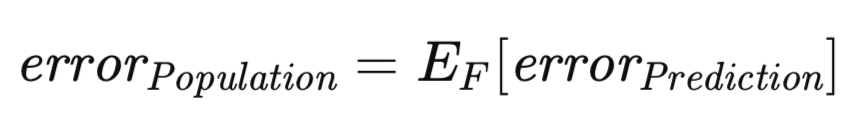
Общепризнанный принцип заключается в том, что для любого обучающего набора мнимая ошибка будет с высокой вероятностью недооценивать ошибку прогноза. Это несоответствие возникает из-за склонности модели переучивать определенные характеристики обучающих данных, ставя тем самым под угрозу возможность его обобщения для более широкой совокупности. Величина разницы между ошибкой прогноза и мнимой ошибкой определяется как ошибка превышения.

Особое значение в этом контексте имеет ожидаемая ошибка превышения. Признавая, что ошибка прогнозирования, как и мнимая ошибка, зависят от конкретного обучающего набора. Необходимо рассмотреть ожидаемое значение ошибки превышения по всей совокупности всех возможных обучающих наборов по аналогии с выводом ошибки совокупности. Формально оно представлено в уравнении ниже.

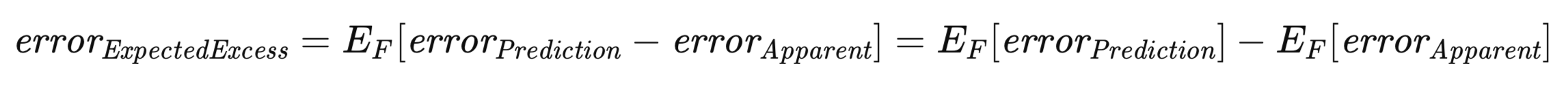
Приведенное выше уравнение подчеркивает двойственность при концептуализации ожидаемой ошибки превышения. Его можно рассматривать как ожидание (по всем возможным обучающим наборам) разницы между ошибкой прогнозирования и мнимой ошибкой для каждого конкретного обучающего набора. Такая интерпретация соответствует интуитивному пониманию концепции. Иначе его можно выразить как разницу между ошибкой совокупности и ожидаемой мнимой ошибкой.

Перекрестная проверка: методология и ограничения

Перекрестная проверка — это метод, который хорошо зарекомендовал себя в научном сообществе. Среди обсуждаемых в этом тексте алгоритмов перекрестная проверка отличается концептуальной простотой и легкостью реализации, нередко демонстрируя эффективность вычислений. У нее есть преимущество, которое заключается в том, что она дает практически непредвзятую оценку ожидаемой будущей эффективности модели.

Более того, ее широкая применимость распространяется на широкий спектр алгоритмов обучения моделей, что не всегда свойственно другим методам. Однако у перекрестной проверки есть существенное ограничение: присущая ей дисперсия часто значительна, иногда до неприемлемого уровня. Это подразумевает повышенную чувствительность к стохастическим изменениям, возникающим при случайной выборке исходного набора данных.

В частности, экспериментатор, который делает выборку, обучает модель и затем применяет перекрестную проверку для оценки ожидаемой будущей эффективности, может при повторении процедуры с независимой выборкой наблюдать совершенно другой результат. Хотя практически беспристрастный характер такой оценки представляет собой желательное свойство, его часто затмевает величина дисперсии. Важно отметить, что специалисты-практики часто недооценивают эту изменчивость.

Несмотря на существование более совершенных методологических подходов к решению аналогичных задач, перекрестная проверка по-прежнему широко применяется, зачастую благодаря ее простоте и применимости в таких сценариях, где альтернативные подходы невозможны. Тем не менее, учитывая ее распространенность и периодически возникающую потребность в ней, необходимо подробное изложение того, как выполняется процедура перекрестной проверки.

Основной принцип, лежащий в основе перекрестной проверки, концептуально прост. Он подразумевает разделение набора данных на два отдельных подмножества: обучающий набор, используемый для оценки параметров модели, и проверочный набор, применяемый для независимого количественного оценивания модели, что соответствует процедуре, применяемой в том случае, когда обилие данных не является ограничением.

Однако, в отличие от выделения значительной части данный в проверочный набор для надежной оценки производительности, перекрестная проверка использует минимальный проверочный набор, выделяя большую часть наблюдений в обучающий набор. В частности, общепринятая практика предполагает использование одного наблюдения в качестве проверочного набора.

После обучения и оценки модели с этим разделом проверочный набор повторно интегрируется в набор данных, а в качестве проверочного набора обозначается другое наблюдение. Итерация этого процесса совершается до тех пор, пока каждое наблюдение по одному разу не послужит точкой валидации. Средняя ошибка тестирования по всем итерациям представляет собой оценку ошибки перекрестной проверки.

Наиболее распространенный вариант перекрестной проверки предполагает последовательное исключение отдельных наблюдений. Адаптация этих алгоритмов для исключения множественных наблюдений должна быть достаточно простой. Учитывая, что M_T представляет собой модель, обученную на полном наборе данных T, пусть M_T(i) обозначает модель, обученную на наборе данных T, исключая i-е наблюдение. Оценка перекрестной проверки ожидаемой будущей ошибки модели формально выражается следующим образом.

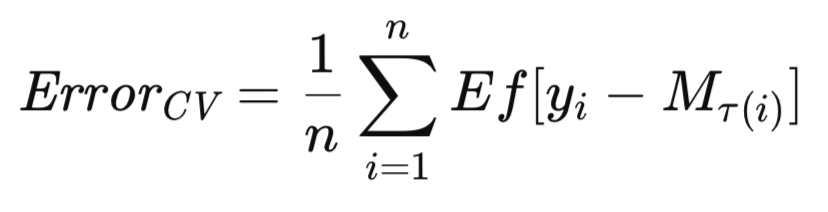
В этом разделе представлен алгоритм перекрестной проверки с пояснительными примечаниями. Сравнительные количественные оценки производительности приведены в конце статьи. Все алгоритмы, использованные для оценки ожидаемых ошибок, представлены в заголовочном файле error_variance_estimation.mqh. Алгоритм перекрестной проверки реализуется в виде метода cross_validation(). Эта процедура и те процедуры, которые используются для реализации других алгоритмов оценки ошибок имеют сходную структуру и параметры функций. Вот эти параметры:

• Первые два обязательных аргумента для этого метода — матрицы обучающего набора данных. Первая матрица содержит предикторы, а вторая — соответствующие им целевые значения.
  
• Третий аргумент процедуры — экземпляр модели, реализующий интерфейс IModel. Он представляет собой оцениваемую модель прогнозирования.
• Последний аргумент, переданный в cross_validation(), содержит окончательную меру погрешности, полученную в результате вычислений. При возникновении ошибки метод вернет логическое значение false.

//+------------------------------------------------------------------+
//| estimate error variance using cross validation testing           |
//+------------------------------------------------------------------+
bool CErrorVar::cross_validation(matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   out_err = 0.0;
   vector test;
   double test_target;
   matrix preds,targs;

   for(ulong i = 0; i<predictors.Rows(); i++)
     {
      test = predictors.Row(i);
      test_target = targets[i][0];
      
      predictors.SwapRows(i,(predictors.Rows()-1));
      targets.SwapRows(i,(targets.Rows()-1));
      
      preds = np::sliceMatrixRows(predictors,0,long(predictors.Rows()-1));
      targs = np::sliceMatrixRows(targets,0,long(targets.Rows()-1));

      if(!model.train(preds,targs))
        {
         Print(__FUNCTION__," failed to train model ");
         return false;
        }

      out_err += error_fun(test_target,model.forecast(test));
      
      predictors.SwapRows(i,(predictors.Rows()-1));
      targets.SwapRows(i,(targets.Rows()-1));
     }

   out_err/=double(predictors.Rows());

   return true;
  }

Вызов функции cross_validation() запускает начало цикла, который проходит по обучающему набору данных. Последняя позиция в обучающем наборе данных всегда используется в качестве тестовой точки. Цикл поочередно подставляет в эту позицию другие выборки в эту позицию в матрицах предикторов и матрицах целей. После разделения данных осуществляется обучение модели, которая затем тестируется на единственной выборке, исключенной из обучения. Ее ошибка накапливается и в конечном итоге возвращается в виде результата прохождения всего цикла.

Бутстрап-оценка ошибки генеральной совокупности

В этом разделе дается краткое описание базового бутстрап-алгоритма для оценки ошибки генеральной совокупности. Признанным фактом является то, что этот алгоритм, как правило, не рекомендуется для практического применения, поскольку алгоритмы E0 и E632, подробно описанные в последующих разделах, обычно обеспечивают превосходную производительность. Тем не менее, прямой бутстрап-метод служит основополагающим принципом, на котором строятся более сложные алгоритмы. Таким образом, всестороннее осмысление механизмов его работы необходимо для понимания последующих элементов.

В текущем сценарии мы установим совокупность F, из которой случайным образом отбираются наблюдения, составляющие наш обучающий набор. Модель обучается и оценивается на T, давая мнимую ошибку. Эта ошибка по своей сути оптимистична, и ожидается, что ошибка совокупности превысит мнимую ошибку на величину ошибки превышения. Однако в отсутствие независимого валидационного набора ни ошибка превышения, ни ошибка генеральной совокупности, то есть представляющие основной интерес величины, не поддаются непосредственному наблюдению. Мы ограничены оптимистичной мнимой ошибкой. Тем не менее, методологию бутстрапа можно использовать для оценки ошибки превышения, которую затем можно прибавить к мнимой ошибке, чтобы получить грубую оценку ошибки генеральной совокупности.

Использование бутстрапа для оценки ошибки превышения отражает процедуру оценки смещения параметров. Эмпирическая функция распределения замещает неизвестное распределение совокупности, и множество выборок составляется методом бутстрапа. Модель обучается для каждой выборки бутстрапа. Ошибка модели на выборке бутстрапа представляет собой очевидную ошибку для этой выборки. Ошибка модели на полном наборе данных представляет собой ошибку прогнозирования, поскольку эмпирическое распределение, по сути, функционирует как вся генеральная совокупность. Разница между этими двумя ошибками формирует ошибку превышения для данной бутстрап-выборки. Среднее значение этой ошибки превышения по множеству повторений бутстрапа составляет оценку ожидаемой ошибки превышения.

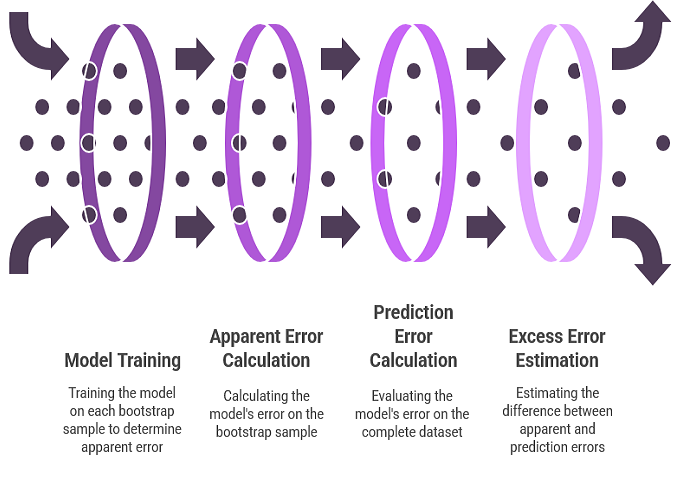
Для повышения устойчивости вышеупомянутого алгоритма вводится ряд определений и уравнений. Пусть B обозначает обучающий набор, сгенерированный с помощью бутстрап-выборки из исходного набора данных. В частности, B строится посредством случайного отбора n наблюдений из T с заменой. Впоследствии модель обучается с помощью B. Ошибка прогнозирования этой модели определяется путем усреднения ее ошибки по всем наблюдениям в генеральной совокупности, из которой была составлена бутстрап-выборка, являющаяся в данном контексте исходным набором данных. Формально оно представлено в уравнении ниже.

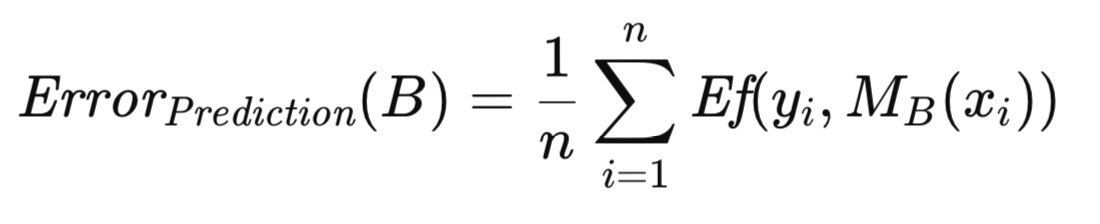
Пусть k_i представляет частоту, с которой i-е наблюдение из T появляется в B. Мнимая ошибка, связанная с B, вычисляется путем усреднения ошибки модели по наблюдениям, составляющим B, как показано в уравнении ниже.

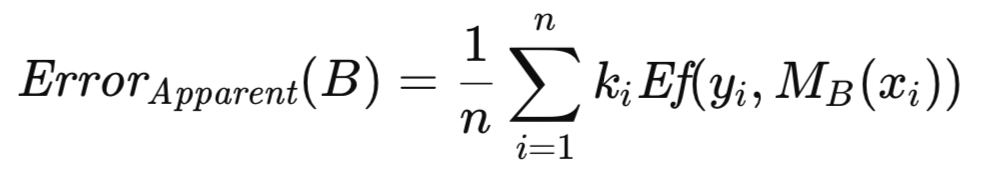
Ошибка превышения, связанная с B, определяется как разница между его ошибкой прогнозирования и его мнимой ошибкой. Вместо вычисления их по отдельности с последующим вычитанием, что было бы с вычислительной точки зрения избыточным из-за наличия общих компонентов ошибки, с помощью вынесения общей величины за скобки получена более эффективная формула. В результате получается выражение, которое необходимо оценить для каждого из значительного количества (порядка сотен или тысяч) повторений бутстрапа. Средняя ошибка превышения по этим повторениям обеспечивает оценку ожидаемой ошибки превышения, которая затем прибавляется к мнимой ошибке полной выборки для получения приближенного значения ошибки генеральной совокупности.

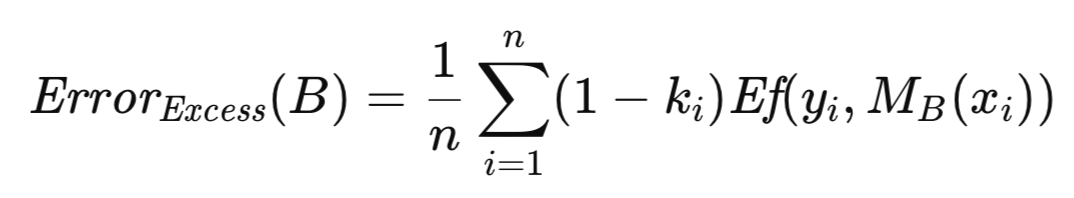
Способ бутстрапа для оценки погрешности реализуется как метод boot_strap(). Помимо параметров, перечисленных для реализации перекрестной проверки, этот метод включает в себя дополнительный параметр, указывая количество повторений бутстрапа. Процедура начинается с инициализации экземпляра генератора случайных чисел, предоставленного MQL5-реализацией библиотеки Alglib. Генератор случайных чисел используется для выбора случайного индекса строки в качестве бутстрап-выборки, которая помещается в матричные переменные preds и targs из исходного обучающего набора. Набор бутстрап-выборок используется для обучения модели с последующим ее тестированием в целях накопления ошибки превышения.

//+------------------------------------------------------------------+
//| estimate error variance using ordinary bootstrap                 |
//+------------------------------------------------------------------+
bool CErrorVar::boot_strap(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   double err,apparent,excess;
   excess = 0.0;
   ulong nsize = predictors.Rows();
   ulong count[];
   ulong k;

   ArrayResize(count,int(nsize));

   vector predicted(nsize);

   CHighQualityRandStateShell rstate;
   CHighQualityRand::HQRndRandomize(rstate.GetInnerObj());

   matrix preds = predictors;
   matrix targs = targets;

   for(ulong boot = 0; boot<nboot; boot++)
     {
      ArrayInitialize(count,0);
      //---
      for(ulong i=0; i<nsize; i++)
        {
         k=(int)(CAlglib::HQRndUniformR(rstate)*nsize);
         //---
         if(k>=nsize)
            k=nsize-1;
         //---
         preds.Row(predictors.Row(k),i);
         targs.Row(targets.Row(k),i);
         ++count[k];
        }

      if(!model.train(preds,targs))
        {
         Print(__FUNCTION__," failed to train model ", boot);
         return false;
        }

      for(ulong i=0; i<nsize; i++)
        {
         predicted[i] = model.forecast(predictors.Row(i));
         err = error_fun(targets[i][0],predicted[i]);
         excess+=(1.0 - double(count[i]))*err;
        }
     }

   excess/=double(nsize*nboot);

После завершения бутстрап-операции. Исходный набор обучающих данных используется для вычисления мнимой ошибки. Окончательная оценка ошибки представляет собой суммарное значение ошибки превышения и мнимой ошибки.

if(!model.train(predictors,targets))
     {
      Print(__FUNCTION__," failed to train model ");
      return false;
     }
   apparent = 0.0;
   for(ulong i=0; i<nsize; i++)
     {
      predicted[i] = model.forecast(predictors.Row(i));
      err = error_fun(targets[i][0],predicted[i]);
      apparent+=err;
     }
   apparent/=double(nsize);
   out_err = apparent+excess;
   return true;
  }

Блок оценки Эфрона E0 для ошибки генеральной совокупности

Значительной проблемой, возникающей при дублировании обучающих кейсов в бутстрап-выборках, является потенциальная возможность сделать некоторые классы моделей неработоспособными. В частности, особенно уязвимы вероятностные нейросети и нейросети обобщенной регрессии. Пока величина константы сглаживания не станет достаточно большой, тестовый кейс, идентичный обучающему, даст почти идеальный прогноз, усугубляя проблему оптимистичного смещения. Чтобы сделать эту проблему более решаемой, Брэдли Эфрон предложил простой способ: предотвращение появления артефактов дублирования. Это подразумевает генерацию обучающих наборов, полученных методом бутстрапа, с использованием стандартных процедур повторной выборки. Однако для каждого бутстрап-повторения модель оценивается исключительно на основе тех исходных наблюдений, которые отсутствуют в обучающем наборе. Средняя ошибка по этим исключенным наблюдениям используется затем в качестве оценки ошибки генеральной совокупности. Эта методология обозначена как блок оценки E0 ошибки генеральной совокупности.

В научной литературе представлены два разных подхода к вычислению E0. Первоначальный метод предполагает суммирование всех ошибок и деление на общее количество оцененных случаев. В этой статье принят именно такой подход. Последующие теоретические исследования свойств E0 предлагают альтернативный алгоритм, который разбивает процесс усреднения на два этапа. Во-первых, для каждого исходного наблюдения ошибки из всех бутстрап-повторений, в которых отсутствует это наблюдение, суммируются и делятся на количество таких повторений, что дает среднюю ошибку по этому наблюдению. Затем эти средние ошибки суммируются по всем наблюдениям и делятся на общее количество наблюдений для получения общего среднего арифметического. Хотя последний метод отличается повышенной вычислительной сложностью, асимптотически он эквивалентен первому, а эмпирические оценки демонстрируют незначительные различия в производительности. Поэтому ввиду его простоты был выбран исходный метод.

Чтобы обеспечить более качественное описание алгоритма, вводятся дополнительные обозначения. Как и прежде, T обозначает исходный набор данных, а B представляет собой бутстрап-выборку. Пусть C обозначает множество наблюдений в T, которые не включены в B. Пусть count(C) представляет собой мощность (количество наблюдений) множества C. Тогда исходная оценка E0 Эфрона для ошибки генеральной совокупности формально выражена ниже.

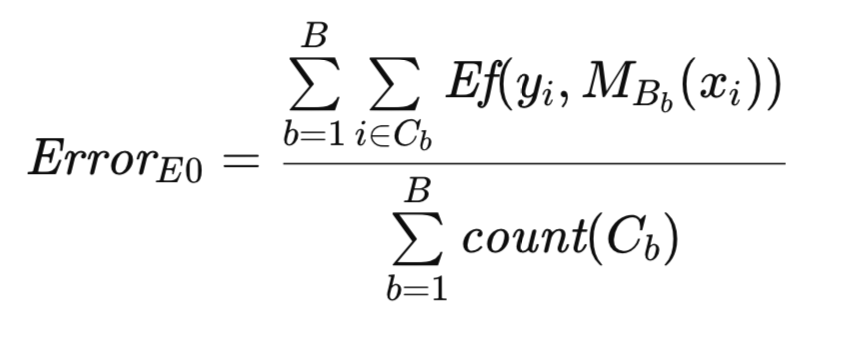
Алгоритмическая реализация блока оценки E0 имеет сходство с ранее описанной процедуры бутстрапа. Генерация и использование бутстрап-выборок для обучения модели согласуются друг с другом в обоих методах. Однако в этом контексте массив count служит двоичным индикатором, отображая наличие или отсутствие наблюдения, а не счетчиком частот, как предшествующая процедура. Этот алгоритм реализуется как метод efrons_0(). 

//+------------------------------------------------------------------+
//| estimate error variance using efron's E0 bootstrap               |
//+------------------------------------------------------------------+
bool CErrorVar::efrons_0(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   out_err = 0.0;
   ulong tot = 0;
   ulong nsize = predictors.Rows();
   ulong count[];
   ulong k;

   ArrayResize(count,int(nsize));

   vector predicted(nsize);

   CHighQualityRandStateShell rstate;
   CHighQualityRand::HQRndRandomize(rstate.GetInnerObj());

   matrix preds = predictors;
   matrix targs = targets;

   for(ulong boot = 0; boot<nboot; boot++)
     {
      ArrayInitialize(count,0);
      //---
      for(ulong i=0; i<nsize; i++)
        {
         k=(int)(CAlglib::HQRndUniformR(rstate)*nsize);
         //---
         if(k>=nsize)
            k=nsize-1;
         //---
         preds.Row(predictors.Row(k),i);
         targs.Row(targets.Row(k),i);
         ++count[k];
        }

      if(!model.train(preds,targs))
        {
         Print(__FUNCTION__," failed to train model ", boot);
         continue;//return false;
        }

      for(ulong i=0; i<nsize; i++)
        {
         if(count[i])
            continue;
         predicted[i] = model.forecast(predictors.Row(i));
         out_err+= error_fun(targets[i][0],predicted[i]);
         ++tot;
        }
     }

   if(tot)
      out_err/=double(tot);
   else
     {
      Print(__FUNCTION__, " zero denominator ");
      return false;
     }
   return true;
  }

Блок оценки Эфрона E632 для ошибки генеральной совокупности

Блок оценки E0, как было описано ранее, обладает нужными свойствами и обычно рекомендуется для практического применения. Избегание им оценки наблюдений, присутствующих в обучающем множестве, обеспечивает его совместимость с моделями различных классов. Более того, его дисперсия обоснованно ограничена, что отражает текущее состояние методологического развития.

Однако блок оценки E0 характеризуется умеренным ориентировочным смещением, имеющим тенденцию переоценивать истинную ошибку генеральной совокупности. Важно отметить, что если это смещение не чрезмерно, то оно обычно считается меньшей проблемой, чем недооценка. Недооценка, как это наблюдается в случае обычного бутстрапа, более пагубна из-за своей склонности способствовать возникновению необоснованного оптимизма. Использование метода E0 обычно обеспечивает уверенность в том, что фактическая ошибка генеральной совокупности, скорее всего, будет ниже вычисленного значения. Эта типичная осторожность в оценках, хотя и полезна в целом, может привести к ошибочному отказу от модели из-за неоправданного пессимизма. Блок оценки E632 предназначен для решения этой проблемы посредством уменьшения слишком осторожного смещения, характерного для E0.

Примите во внимание неотъемлемые ограничения при использовании мнимой ошибки (ошибки, полученной из количественной оценки обучающего набора) для оценки ошибки генеральной совокупности. Процедура оценки изначально предвзята, поскольку только наблюдения, используемые в обучении, подлежат оценке. Это подмножество не является репрезентативным для всей генеральной совокупности и демонстрирует чрезмерное сходство с обучающим набором, что приводит к смещению в сторону оптимистичных ожиданий.

И напротив, блок оценки E0 демонстрирует смещение в противоположную сторону. При преднамеренном исключении обучающих наблюдений из оценки тестовый набор становится нерепрезентативным для генеральной совокупности, демонстрируя избыточное несходство с обучающим набором. В реальных сценариях неизбежно будут возникать наблюдения, идентичные или практически идентичные учебным наблюдениям. Исключение E0 из этих наблюдений приводит к смещению в сторону пессимистических ожиданий.

Алгоритм E632 стремится установить компромисс между этими двумя крайностями. Более сбалансированный подход мог бы подразумевать количественную оценку модели путем выборки как внутри обучающего набора, так и вне его, с вероятностями, отражающими их возникновение в реальном мире. Как вариант, для учета расхождений в выборке можно внести корректировки. По мере увеличения размера выборки вероятность появления любого наблюдения в выборке, полученной методом бутстрапа, стремится к 1 − 1/e ≈ 0.632. Эвристика Эфрона предлагает оценивать ошибку генеральной совокупности как взвешенную сумму E0 и мнимой ошибки, при этом веса определяются этими вероятностями выборки. Его блок оценки, обозначенный как E632, формально представлен в уравнении ниже.

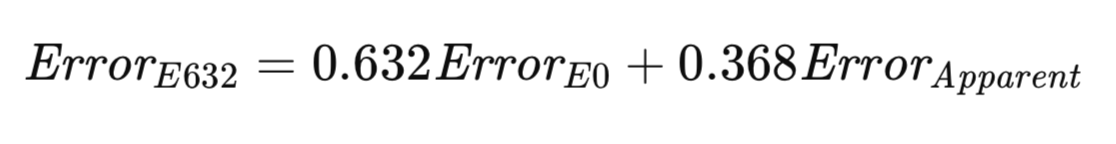
Реализация алгоритма E632 представлена в виде метода efrons_632(), что и показано ниже.

//+------------------------------------------------------------------+
//| estimate error variance using efron's E632 bootstrap             |
//+------------------------------------------------------------------+
bool CErrorVar::efrons_632(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   double apparent;

   if(!efrons_0(nboot,predictors,targets,model,out_err))
      return false;


   if(!model.train(predictors,targets))
     {
      Print(__FUNCTION__," failed to train model ");
      return false;
     }

   apparent = 0.0;
   
   vector predicted(predictors.Rows());

   for(ulong i=0; i<predictors.Rows(); i++)
     {
      predicted[i] = model.forecast(predictors.Row(i));
      apparent+= error_fun(targets[i][0],predicted[i]);
     }

   apparent/=double(predictors.Rows());

   out_err = 0.632*out_err + 0.368*apparent;

   return true;
  }

Все обсуждавшиеся до сих пор в этой статье алгоритмы реализованы как члены класса CErrorVar. Кроме того, этот класс определяет метод error_fun(), используемый для вычисления ошибки между прогнозируемым значением, представленным как второй параметр, и соответствующим целевым значением, предоставленным как первый параметр метода.

//+------------------------------------------------------------------+
//|  class for estimating error variance                             |
//+------------------------------------------------------------------+
class CErrorVar
  {
public:
                     CErrorVar(void);
                    ~CErrorVar(void);

   virtual double    error_fun(const double truevalue,const double predictedvalue);
   virtual bool      cross_validation(matrix &predictors, matrix &targets, IModel & model,double &out_err);
   virtual bool      boot_strap(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err);
   virtual bool      efrons_0(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err);
   virtual bool      efrons_632(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err);
  };
//+------------------------------------------------------------------+
//| constructor                                                      |
//+------------------------------------------------------------------+
CErrorVar::CErrorVar(void)
  {
  }
//+------------------------------------------------------------------+
//| destructor                                                       |
//+------------------------------------------------------------------+
CErrorVar::~CErrorVar(void)
  {
  }
//+------------------------------------------------------------------+
//| calculate the error                                              |
//+------------------------------------------------------------------+
double CErrorVar::error_fun(const double truevalue,const double predictedvalue)
  {
   return pow(truevalue-predictedvalue,2.0);
  }

В следующем разделе продемонстрировано использование этих алгоритмов для оценки ошибки обученной модели с использованием только обучающего набора данных.

Сравнительный анализ блоков оценки ошибок прогнозирования

В настоящем тексте представлен набор методик оценки ошибки генеральной совокупности для прогностической модели. Следует отметить следующие основные соображения:

• Перекрестная проверка: этот способ характеризуется простотой реализации и вычислительной эффективностью. Он демонстрирует широкие возможности применения к моделям различных классов и обеспечивает практически беспристрастную оценку. Однако он подвержен высокой изменчивости, особенно в сценариях, связанных с нестабильными процедурами обучения. Следовательно, перекрестная проверка обычно не рекомендуется в качестве основного метода, за исключением случаев, когда альтернативные подходы недоступны. Хотя они и эффективны, этот вариант не считается оптимальным.
• Прямой бутстрап: этот метод обычно считается наименее желательным вариантом. Он несовместим с моделями, которые не могут учитывать повторяющиеся обучающие наблюдения, или моделями, качество которых снижено из-за наличия в обучающем наборе тестовых наблюдений. Более того, он демонстрирует значительное смещение в сторону недооценки истинной ошибки генеральной совокупности. Следовательно, неоспоримых преимуществ у него нет.
• Блок оценки E0: в сценариях, где процесс обучения допускает дублирование наблюдений, блок оценки E0 обычно является предпочтительным вариантом. Возможности его применения распространяются на широкий спектр моделей, поскольку он позволяет избежать оценки обучающих наблюдений. Он демонстрирует устойчивость в присутствии нестабильных условий обучения, например в моделях со стохастическими процедурами обучения. Эмпирически его дисперсия приближается к дисперсии перекрестной проверки в стабильных средах обучения, а в нестабильных средах он демонстрирует существенно меньшую дисперсию. Более того, он эффективен с вычислительной точки зрения, учитывая, что мнимую ошибку, необходимую для оценки E632, можно вычислять одновременно с оценкой E0. Однако важно признать, что практикующие специалисты могут отдавать предпочтение сдержанному смещению E0 по сравнению с потенциально более высокой дисперсией, связанной с блоком оценки E632, смещенным в меньшей степени.

Для эмпирического исследования этих блоков оценок был проведен модельный анализ с использованием искусственных данных, полученных в соответствии с моделью, заданной как y = x_1 - x_2 + ошибка. В этой модели предикторные переменные x_1 и x_2 следуют стандартному нормальному распределению, а компонент ошибки также распределен нормально, причем среднее значение равно нулю, а дисперсия задана пользователем. Обычная линейная модель была согласована с набором данных, а среднеквадратическая ошибка генеральной совокупности оценивалась с использованием представленных в этой статье алгоритмов. Кроме того, подогнанная модель получила количественную оценку на основе данных независимых испытаний для определения ее истинной ошибки. Этот процесс повторялся для указанного пользователем количества попыток, после чего рассчитывались среднее значение и стандартное отклонение оценок ошибок. Это реализовано в скрипте ErrorVarianceEstimation_NumericalPredictionDemo.mq5.

//+------------------------------------------------------------------+
//|              ErrorVarianceEstimation_NumericalPredictionDemo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<error_variance_estimation.mqh>
#include<OLS.mqh>
//--- input parameters
input ulong      NumSamples=15;
input ulong      NumBootStraps = 1000;
input ulong      NumReplications = 100;
input double     Variance = 1.0;
//---
//+------------------------------------------------------------------+
//|  normal(rngstate)                                                |
//+------------------------------------------------------------------+
double normal(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndNormal(state);
  }
//+------------------------------------------------------------------+
//|   unifrand(rngstate)                                             |
//+------------------------------------------------------------------+
double unifrand(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndUniformR(state);
  }
//+------------------------------------------------------------------+
//| ordinary least squares class                                     |
//+------------------------------------------------------------------+
class COrdReg:public IModel
  {
private:
   OLS*              m_ols;
public:
                     COrdReg(void)
     {
      m_ols = new OLS();
     }
                    ~COrdReg(void)
     {
      if(CheckPointer(m_ols) == POINTER_DYNAMIC)
         delete m_ols;
     }
   bool              train(matrix &predictors,matrix& targets)
     {
      return m_ols.Fit(targets.Col(0),predictors);
     }
   double            forecast(vector &predictors)
     {
      return m_ols.Predict(predictors);
     }
  };
//---
ulong nreplications, itry, nsamps, nboots, divisor, ndone;
vector computed_err_cv, computed_err_boot, predictions;
vector computed_err_E0, computed_err_E632 ;
double temperr,sum_observed_error, mean_computed_err, var_computed_err,dfactor,dif;
matrix xdata, testdata,trainpreds,traintargs,testpreds,testtargs;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CHighQualityRandStateShell rngstate;
   CHighQualityRand::HQRndRandomize(rngstate.GetInnerObj());
//---
   nboots = NumBootStraps;
   nsamps = NumSamples ;
   nreplications = NumReplications ;
   dfactor = Variance ;

   if((nsamps <= 3)  || (nreplications <= 0) || (dfactor < 0.0) || nboots<=0)
     {
      Alert(" Invalid inputs ");
      return;
     }

   double std = sqrt(dfactor) ;

   divisor = 1000000 / (nsamps * nboots) ;  // This is for progress reports only
   if(divisor < 2)
      divisor = 2 ;

   xdata = matrix::Zeros(nsamps,3);

   sum_observed_error = mean_computed_err = var_computed_err = 0.0;
   computed_err_cv = vector::Zeros(nreplications);
   computed_err_E0 = vector::Zeros(nreplications);
   computed_err_E632 = vector::Zeros(nreplications);
   computed_err_boot = vector::Zeros(nreplications);

   testdata = matrix::Zeros(nsamps*10,3);
   predictions = vector::Zeros(nsamps*10);

   CErrorVar errorvar;
   COrdReg regmodel;

   for(ulong irep = 0; irep<nreplications; irep++)
     {
      ndone = irep + 1 ;

      for(ulong i =0; i<nsamps; i++)
        {
         xdata[i][0] = normal(rngstate);
         xdata[i][1] = normal(rngstate);
         xdata[i][2] = xdata[i][0] - xdata[i][1] + std * normal(rngstate);
        }


      for(ulong j =0; j<testdata.Rows(); j++)
        {
         testdata[j][0] = normal(rngstate);
         testdata[j][1] = normal(rngstate);
         testdata[j][2] = testdata[j][0] - testdata[j][1] + std *normal(rngstate);
        }

      trainpreds = np::sliceMatrixCols(xdata,0,2);
      traintargs = np::sliceMatrixCols(xdata,2);

      if(!regmodel.train(trainpreds,traintargs))
        {
         Print(" fitting first model failed ");
         return;
        }

      testpreds=np::sliceMatrixCols(testdata,0,2);
      testtargs=np::sliceMatrixCols(testdata,2);
      temperr = 0.0;
      for(ulong i = 0;i<testpreds.Rows(); i++)
        {
         predictions[i] = regmodel.forecast(testpreds.Row(i));
         temperr += errorvar.error_fun(testtargs[i][0],predictions[i]);
        }

      sum_observed_error += temperr/double(10*nsamps);

      if(!errorvar.cross_validation(trainpreds,traintargs,regmodel,computed_err_cv[irep]) ||
         !errorvar.boot_strap(nboots,trainpreds,traintargs,regmodel,computed_err_boot[irep]) ||
         !errorvar.efrons_0(nboots,trainpreds,traintargs,regmodel,computed_err_E0[irep]) ||
         !errorvar.efrons_632(nboots,trainpreds,traintargs,regmodel,computed_err_E632[irep])
        )
        {
         Print(" error variance calculation failed ");
         return;
        }
      //---
     }
//---
   PrintFormat("Number of Iterations %d   Observed error = %.5lf",ndone, sum_observed_error / double(ndone)) ;
//---
   PrintFormat("CV: computed error  mean=%10.5lf      std=%10.5lf",computed_err_cv.Mean(), computed_err_cv.Std()) ;
//---
   PrintFormat("BOOT: computed error  mean=%10.5lf      std=%10.5lf",computed_err_boot.Mean(), computed_err_boot.Std()) ;
//---
   PrintFormat("E0: computed error  mean=%10.5lf      std=%10.5lf",computed_err_E0.Mean(), computed_err_E0.Std()) ;
//---
   PrintFormat("E632: computed error  mean=%10.5lf      std=%10.5lf",computed_err_E632.Mean(), computed_err_E632.Std()) ;
  }
//+------------------------------------------------------------------+

Использовались: дисперсия 1.0, размер выборки 15 наблюдений и 1000 бутстрап-итераций. Результаты были следующими:

MJ      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    Number of Iterations 100   Observed error = 1.18380
RF      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    CV: computed error  mean=   1.18825      std=   0.53117
PK      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    BOOT: computed error  mean=   1.12521      std=   0.48780
IR      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E0: computed error  mean=   1.38168      std=   0.63579
NO      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E632: computed error  mean=   1.18647      std=   0.52380

Как и предполагалось, стандартный бутстрап-метод продемонстрировал недооценку истинной оценки. Напротив, блок оценки E0 значительно переоценил ошибку. Хотя эта переоценка может восприниматься как ограничение, важно отметить, что блок оценки E0 также показал самое высокое стандартное отклонение. Такая степень переоценки в первую очередь объясняется малым размером выборки. Однако решение относительно его приемлемости остается субъективным. Для дальнейшей количественной оценки производительности блоков оценки ошибок был повторно проведен модельный анализ с увеличенным размером выборки в 100 наблюдений, что является более репрезентативным сценарием для многих сфер практического применения. Вот пример результата:

KG      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    CV: computed error  mean=   1.01810      std=   0.24132
LH      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    BOOT: computed error  mean=   1.01672      std=   0.14194
PS      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E0: computed error  mean=   1.01989      std=   0.14441
IP      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E632: computed error  mean=   1.01855      std=   0.14099

Результаты этого эксперимента демонстрируют удовлетворительную производительность по всем четырем методикам. Примечательно, что блок оценки E0 показал небольшое завышение ошибки. Остальные три алгоритма продемонстрировали незначительную недооценку. Хотя блок оценки E0 поддерживал самое высокое значение стандартного отклонения, разница была минимальной. В сценариях, которые характеризуются высоким общим качеством оценки, незначительная переоценка ошибки, полученная с помощью блока оценки E0, вероятно, будет предпочтительнее небольшой недооценки, наблюдаемой в других методах, особенно учитывая последствия недооценки для выбора и количественной оценки модели.

Предыдущий пример проиллюстрировал некоторые различия между несколькими методами оценки ошибки генеральной совокупности. Однако он мог непреднамеренно создать впечатление, что перекрестная проверка последовательно сопоставима с другими методами с точки зрения эффективности. Такое восприятие объясняется использованием сглаженной функции ошибок, в частности среднеквадратической ошибки простой модели, что способствует созданию стабильной среды обучения.

Задачи категоризации, напротив, обычно характеризуются внутренней нестабильностью. Незначительные возмущения в данных могут спровоцировать резкие и существенные колебания уровня ошибок. В этом разделе представлен пример, в котором разбирается это явление. Алгоритмы, применяемые для оценки ошибки генеральной совокупности, остаются такими же, что обсуждались выше. Главные изменения касаются определения функции ошибки прогноза и структуры основной программы, используемой для сравнительной количественной оценки.

Тестовый скрипт ErrorVarianceEstimation_ClassificationDemo.mq5 генерирует двумерные данные, демонстрирующие умеренную положительную корреляцию.

//+------------------------------------------------------------------+
//|                   ErrorVarianceEstimation_ClassificationDemo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<error_variance_estimation.mqh>
#include<OLS.mqh>
//--- input parameters
input ulong      NumSamples=15;
input ulong      NumBootStraps = 1000;
input ulong      NumReplications = 100;
input double     PredictionDifficultyLevel = 0.0;
//---
//+------------------------------------------------------------------+
//|  normal(rngstate)                                                |
//+------------------------------------------------------------------+
double normal(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndNormal(state);
  }
//+------------------------------------------------------------------+
//|   unifrand(rngstate)                                             |
//+------------------------------------------------------------------+
double unifrand(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndUniformR(state);
  }
//+------------------------------------------------------------------+
//| ordinary least squares class                                     |
//+------------------------------------------------------------------+
class COrdReg:public IModel
  {
private:
   OLS*              m_ols;
public:
                     COrdReg(void)
     {
      m_ols = new OLS();
     }
                    ~COrdReg(void)
     {
      if(CheckPointer(m_ols) == POINTER_DYNAMIC)
         delete m_ols;
     }
   bool              train(matrix &predictors,matrix& targets)
     {
      return m_ols.Fit(targets.Col(0),predictors);
     }
   double            forecast(vector &predictors)
     {
      return m_ols.Predict(predictors);
     }
  };
//+------------------------------------------------------------------+
//| error variance for classification models                         |
//+------------------------------------------------------------------+
class CErrorVarC:public CErrorVar
  {
public:
                     CErrorVarC(void)
     {
     }
                    ~CErrorVarC(void)
     {
     }

   virtual double    error_fun(const double truevalue,const double predictedvalue)
     {
      if(truevalue*predictedvalue>0.0)
         return 0.0;
      else
         return 1.0;
     }


  };
//---
ulong nreplications, itry, nsamps, nboots, divisor, ndone;
vector computed_err_cv, computed_err_boot, predictions;
vector computed_err_E0, computed_err_E632 ;
double temperr,sum_observed_error, mean_computed_err, var_computed_err,dfactor,dif;
matrix xdata, testdata,trainpreds,traintargs,testpreds,testtargs;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CHighQualityRandStateShell rngstate;
   CHighQualityRand::HQRndRandomize(rngstate.GetInnerObj());
//---
   nboots = NumBootStraps;
   nsamps = NumSamples ;
   nreplications = NumReplications ;
   dfactor = PredictionDifficultyLevel ;

   if((nsamps <= 3)  || (nreplications <= 0) || (dfactor < 0.0) || nboots<=0)
     {
      Alert(" Invalid inputs ");
      return;
     }

   double std = sqrt(dfactor) ;

   divisor = 1000000 / (nsamps * nboots) ;  // This is for progress reports only
   if(divisor < 2)
      divisor = 2 ;

   xdata = matrix::Zeros(nsamps,3);

   sum_observed_error = mean_computed_err = var_computed_err = 0.0;
   computed_err_cv = vector::Zeros(nreplications);
   computed_err_E0 = vector::Zeros(nreplications);
   computed_err_E632 = vector::Zeros(nreplications);
   computed_err_boot = vector::Zeros(nreplications);

   testdata = matrix::Zeros(nsamps*10,3);
   predictions = vector::Zeros(nsamps*10);

   CErrorVarC errorvar;
   COrdReg olsmodel;

   for(ulong irep = 0; irep<nreplications; irep++)
     {
      ndone = irep + 1 ;

      for(ulong i =0; i<nsamps; i++)
        {
         xdata[i][0] = normal(rngstate);
         xdata[i][1] = 0.7071 * xdata[i][0]  +  0.7071 * normal(rngstate);
         if(CAlglib::HQRndUniformR(rngstate)>0.5)
           {
            xdata[i][0] -=dfactor;
            xdata[i][1] +=dfactor;
            xdata[i][2] = 1.0;
           }
         else
           {
            xdata[i][0] +=dfactor;
            xdata[i][1] -=dfactor;
            xdata[i][2] = -1.0;
           }
        }


      for(ulong j =0; j<testdata.Rows(); j++)
        {
         testdata[j][0] = normal(rngstate);
         testdata[j][1] = 0.7071 * testdata[j][0]  +  0.7071 * normal(rngstate);
         if(CAlglib::HQRndUniformR(rngstate)>0.5)
           {
            testdata[j][0] -=dfactor;
            testdata[j][1] +=dfactor;
            testdata[j][2] = 1.0;
           }
         else
           {
            testdata[j][0] +=dfactor;
            testdata[j][1] -=dfactor;
            testdata[j][2] = -1.0;
           }
        }

      trainpreds = np::sliceMatrixCols(xdata,0,2);
      traintargs = np::sliceMatrixCols(xdata,2);

      if(!olsmodel.train(trainpreds,traintargs))
        {
         Print(" fitting first model failed ");
         return;
        }

      testpreds=np::sliceMatrixCols(testdata,0,2);
      testtargs=np::sliceMatrixCols(testdata,2);
      temperr = 0.0;
      for(ulong i = 0;i<testpreds.Rows(); i++)
        {
         predictions[i] = olsmodel.forecast(testpreds.Row(i));
         temperr += errorvar.error_fun(testtargs[i][0],predictions[i]);
        }

      sum_observed_error += temperr/double(10*nsamps);

      if(!errorvar.cross_validation(trainpreds,traintargs,olsmodel,computed_err_cv[irep]) ||
         !errorvar.boot_strap(nboots,trainpreds,traintargs,olsmodel,computed_err_boot[irep]) ||
         !errorvar.efrons_0(nboots,trainpreds,traintargs,olsmodel,computed_err_E0[irep]) ||
         !errorvar.efrons_632(nboots,trainpreds,traintargs,olsmodel,computed_err_E632[irep])
        )
        {
         Print(" error variance calculation failed ");
         return;
        }
     }

   PrintFormat("Number of Iterations %d   Observed error = %.5lf",ndone, sum_observed_error / double(ndone)) ;
//---
   PrintFormat("CV: computed error  mean=%10.5lf      std=%10.5lf",computed_err_cv.Mean(), computed_err_cv.Std()) ;
//---
   PrintFormat("BOOT: computed error  mean=%10.5lf    std=%10.5lf",computed_err_boot.Mean(), computed_err_boot.Std()) ;
//---
   PrintFormat("E0: computed error  mean=%10.5lf      std=%10.5lf",computed_err_E0.Mean(), computed_err_E0.Std()) ;
//---
   PrintFormat("E632: computed error  mean=%10.5lf    std=%10.5lf",computed_err_E632.Mean(), computed_err_E632.Std()) ;
  }
//+--------------------------------------------------------------------+

Диаграмма рассеивания данных для заданного уровня сложности прогнозирования PredictionDifficultyLevel 1.0, покажет эллиптическое распределение, причем его главная ось ориентирована по диагонали вверх и вправо. Параметр PredictionDifficultyLevel в скрипте контролирует степень разделения кластерами, что упрощает идентификацию классов. Чем ниже этот параметр, тем сложнее для модели определить принадлежность к классу.

Генерируются два отдельных класса, соответствующие им распределения данных смещены приблизительно перпендикулярно главной оси на указанную пользователем величину. Линейная модель подстраивается под данные, при этом прогнозируемой переменной присваивается значение −1.0 для одного класса и +1.0 для другого. Ошибка прогнозирования определяется как 0.0, если у истинного и прогнозируемого значений одинаковые знаки, и как 1.0, если у них противоположные знаки. Эта двоичная метрика ошибок отражает внутреннюю природу проблем категоризации.

Были проведены две отдельные экспериментальные оценки. В первом эксперименте использовались выборка размером 15 наблюдений, 1000 повторений бутстрапа, 100 испытаний и нулевое разделение. Такая конфигурация эффективно смоделировала сценарий без какой-либо различающей информации, поскольку два класса демонстрировали одинаковые распределения. Как и предполагалось, наблюдаемая средняя ошибка составила около 0.5. Далее представлены результаты этого эксперимента:

OO      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) Number of Iterations 100   Observed error = 0.50267
PS      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) CV: computed error  mean=   0.50267      std=   0.18389
KM      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) BOOT: computed error  mean=   0.45214    std=   0.11748
EQ      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E0: computed error  mean=   0.50517      std=   0.10845
RF      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E632: computed error  mean=   0.45196    std=   0.09941

И снова перекрестная проверка продемонстрировала свой практически беспристрастный характер. В этом сценарии такой результат ожидаем, поскольку отсутствие у модели способностей к прогнозированию приводит к 50% вероятности ошибочной классификации для каждого данного наблюдения. Аналогичные рассуждения применимы к блоку оценки E0. Хотя обычно ожидается, что E0 будет демонстрировать смещение в сторону пессимистичного сценария, эта характеристика проявляется только тогда, когда модель обладает некоторой степенью эффективности. В этом примере принудительное исключение E0 из тестовых наблюдений из обучающего набора оказывает нейтральное воздействие.

Однако такая нейтральность распространяется и на блок оценки E632. Из-за сочетания действительно беспристрастного компонента и компонента, сильно смещенного в сторону оптимистичного сценария, E632 демонстрирует заметную предвзятость в сторону оптимистичного сценария. Такая потенциальная предвзятость требует тщательного рассмотрения. Кроме того, этот эксперимент подчеркивает главный недостаток перекрестной проверки — ее высокую дисперсию. Стандартное отклонение оценки перекрестной проверки существенно выше, чем у блока оценок E0. Как часто показывают наблюдения, блок оценки E632 характеризуется наименьшим стандартным отклонением. Однако это преимущество нивелируется сильным уклоном в оптимистическую сторону, характерным для E632.

Кроме того, был проведен второй эксперимент, в котором модель обладала некоторой способностью к прогнозированию (параметр PredictionDifficultyLevel был увеличен до 1.0). Результаты этого эксперимента представлены ниже:

GM      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) Number of Iterations 100   Observed error = 0.00747
NM      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) CV: computed error  mean=   0.00533      std=   0.01909
RO      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) BOOT: computed error  mean=   0.00716    std=   0.01766
OG      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E0: computed error  mean=   0.01012      std=   0.01878
FD      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E632: computed error  mean=   0.00820    std=   0.01869

Этот эксперимент демонстрирует, что блок оценки E632 — наиболее эффективный. Он демонстрирует низкий уровень предвзятости и самое низкое стандартное отклонение. Однако блок оценок E0 сохраняет несколько более высокое стандартное отклонение и демонстрирует характерное для него и часто желательное смещение в сторону пессимистичного сценария. Учитывая результаты предыдущего эксперимента, этот фактор следует тщательно оценить при выборе между блоками ошибок E0 и E632. Опять же, перекрестная проверка демонстрирует самое высокое стандартное отклонение, а прямой метод бутстрап показывает потенциально опасное смещение в сторону оптимистичного сценария.

Примечание об использовании представленных алгоритмов для оценки эффективности классификации. Существует значительное ограничение, связанное с генерацией наборов классификационных данных методом бутстрап. Иногда множество бутстрап-выборок может содержать в конечном итоге экземпляры одного класса, что приводит к проблемам в алгоритме классификации или (в некоторых случаях) к полному нарушению работоспособности. Читатели, желающие использовать описанные способы, должны знать о подобных потенциальных подводных камнях.

Заключение

Беглое изучение содержания этой статьи может привести к представлению, что методы повторной выборки для оценки ошибки генеральной совокупности модели интересны с концептуальной точки зрения, но чрезмерно сложны и имеют лишь ограниченную практическую ценность. Это был бы неудачный вывод, поскольку представленные здесь методики повторной выборки обладают существенными преимуществами и заслуживают серьезного рассмотрения.

В частности, эти методы решают фундаментальную проблему количественной оценки модели: необходимость наличия независимого набора данных. Традиционный подход требует получения отдельного набора данных, что зачастую оказывается обременительным с точки зрения логистики, а в некоторых случаях — неосуществимым.

Способы повторной выборки, обсуждаемые в этом тексте, устраняют такое требование. Весь набор данных можно использовать как для обучения модели, так и для оценки ее будущей эффективности, обеспечивая тем самым максимальное использование данных. Эта возможность представляет собой значительный методологический прогресс, и ее не следует недооценивать.

Название файла	Описание файла
MQL5/include/error_variance_estimation.mqh	Заголовочный файл, содержащий определения описанных в этой статье алгоритмов оценки ошибок.
MQL5/include/imodel.mqh	Заголовочный файл включает в себя определение интерфейсов, используемых для взаимодействия с моделями машинного обучения.
MQL5/include/np.mqh	Заголовочный файл различных векторных и матричных вспомогательных функций.
MQL5/include/OLS.mqh	Включаемый файл задает класс OLS, который реализует обычные модели наименьших квадратов.
MQL5/scripts/ErrorVarianceEstimation_NumericalPredictionDemo.mq5	Демонстрационный скрипт, который показывает пользу алгоритмов оценки ошибки в численном прогнозировании.
MQL5/scripts/ErrorVarianceEstimation_ClassificationDemo.mq5	Демонстрационный скрипт, который показывает пользу алгоритмов оценки ошибки при классификации данных.