Нейросети в трейдинге: Распутывание структурных компонентов (SCNN)

Введение

Прогнозирование многомерных временных рядов — фундаментальная задача в машинном обучении. Именно через её призму можно рассматривать широкий спектр прикладных задач: от оценки спроса и прогнозов трафика до распознавания поведения участников рынка и движения котировок. Для финансовой сферы это особенно актуально — ведь практически любой актив, будь то акция, валюта или сырьё, представляет собой комплексный временной ряд с множеством взаимосвязанных факторов: объёмы, цены, индикаторы, макроэкономические данные, поведенческие сигналы и так далее.

Главная сложность таких прогнозов — это улавливание пространственно-временных закономерностей. Пространственные аспекты проявляются в особенностях внешней среды: различия в ликвидности, торговых сессиях, региональной активности. Временные же закономерности связаны с ритмами самих рынков — торговыми циклами, новостными импульсами, периодичностью макроданных. На практике финансовые ряды крайне далеки от стационарности. Они подвержены резким изменениям, сдвигам распределения и сложным переходам между фазами — трендами, флетом, паникой и ажиотажем. Кроме того, автокорреляционные зависимости нестабильны: то, что работает сегодня, может не иметь никакой силы завтра.

Современные методы на базе нейросетей такие, как трансформеры, рекуррентные сети и сверточные архитектуры, не требуют предпосылки стационарности и доказали свою эффективность в задачах краткосрочного прогнозирования. Однако в условиях реального рынка они чаще всего демонстрируют устойчивость лишь к знакомым паттернам. Столкнувшись же с внезапными сдвигами, будь то крах ликвидности или смена поведенческой модели участников, их точность резко снижается. Кроме того, такие модели остаются по сути чёрными ящиками с высокой вычислительной нагрузкой и ограниченной интерпретируемостью.

В связи с этим всё больше внимания привлекает идея декомпозиции временных рядов — то есть разделения их на тренд, сезонность и остаточные колебания. Такой подход позволяет упростить структуру задачи, повысить адаптивность модели и дать более ясное понимание того, на чём основан прогноз. Даже простые линейные модели, использующие декомпозицию, в ряде случаев превосходят сложные нейросети по точности и стабильности.

Однако стоит признать, что и у таких методов есть ограничения. Многие из них фокусируются исключительно на долгосрочных и сезонных компонентах, игнорируя краткосрочные или волатильные фрагменты, в которых как раз и заключаются ключевые рыночные сигналы. Кроме того, раздельная обработка разных компонент без взаимного обмена информацией между ними мешает уловить высокоуровневые и нелинейные взаимодействия. А использование статических параметров оказывается неэффективным на фоне динамичной автокорреляции, ведь оптимальные настройки модели должны гибко меняться в зависимости от текущего состояния рынка.

Для преодоления этих трудностей в работе "Disentangling Structured Components: Towards Adaptive, Interpretable and Scalable Time Series Forecasting" была представлена новая архитектура — Structured Component Neural Network (SCNN). Она представляет собой первую в своём роде нейросеть, целиком построенную на структурной декомпозиции временных рядов. Основная идея SCNN — стратегически разложить данные на несколько разнородных компонентов: не только на долгосрочные тренды и сезонные колебания, но и на быстро изменяющиеся волатильные фрагменты. Каждая группа обрабатывается специализированной подсетью, настроенной под свою собственную динамику. Благодаря этому подходу, модель становится более чувствительной к изменению рыночных условий, а её работа — более понятной и прозрачной.

Особое отличие SCNN в том, что процессы декомпозиции и сборки интегрированы в саму структуру нейросети, а не ограничиваются только этапами входа и выхода. Такая архитектура позволяет не только глубоко декомпозировать данные, но и выявлять сложные взаимодействия между компонентами, включая перекрёстные связи и латентные зависимости. Более того, каждый модуль сети построен по двухветвевой схеме: одна ветвь динамически адаптирует параметры модели под текущие рыночные условия, а вторая — использует эти параметры для обработки скрытых признаков. По сути, модель на лету перенастраивает саму себя, подстраиваясь под текущую структуру автокорреляции.

Чтобы дополнительно повысить устойчивость и обобщающую способность SCNN, авторы фреймворка интегрировали специальный механизм структурной регуляризации. Это помогает модели акцентировать внимание на тех компонентах временного ряда, которые менее подвержены шуму и искажениям. Таким образом, даже в условиях нестабильной рыночной среды, где одни закономерности быстро теряют силу, а другие появляются внезапно, SCNN сохраняет высокую точность и надёжность.

Подтверждением служат результаты обширной экспериментальной проверки, проведенной авторами фреймворка на трёх независимых датасетах. SCNN стабильно демонстрировала превосходство над конкурентами, особенно в условиях резких сдвигов распределения и аномалий в данных. Что особенно важно — всё это достигается при разумной вычислительной нагрузке, что делает модель применимой и для локальных расчётов, и для интеграции в торговые системы.

Алгоритм SCNN

В своей работе авторы фреймворка SCNN исходят из предположения, что временной ряд формируется поэтапно — от случайных возмущений к сложным рыночным структурам.

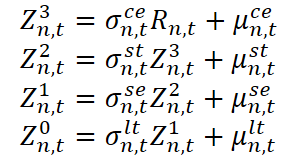
Здесь Z⁰n,t — исходное значение наблюдаемого временного ряда (например, цена или объём сделки), а Zⁱn,t для i = 1, 2, 3 — промежуточные представления на разных уровнях структуры. Rn,t — остаточная компонента, включающая шумы или неожиданные выбросы. Каждая стадия включает как мультипликативный коэффициент σ, отражающий масштабное влияние, так и аддитивный сдвиг µ, соответствующий абсолютным корректировкам.

Чтобы интуитивно понять эту конструкцию, обратимся к аналогии с анализом рыночных данных. Представим себе динамику цены актива. Долгосрочная компонента отражает фундаментальные сдвиги. Это может быть влияние процентных ставок или структурные изменения в экономике. Сезонная — это повторяющиеся паттерны, связанные с квартальной отчётностью, налоговыми периодами или привычками крупных игроков. Краткосрочная компонента улавливает локальные колебания, вызванные, скажем, выходом новостей, повышенной торговой активностью или временным дефицитом ликвидности. Совместно эволюционирующий слой моделирует синхронные рыночные события — к примеру, если сразу несколько акций из одного сектора реагируют на общую макроэкономическую новость. Остаточная компонента — это белый шум или выбросы, вызванные, скажем, единичными ордерами большого объёма или ошибками котирования.

Важно понимать, что в реальных рыночных условиях границы между этими слоями весьма подвижны. Например, резкий рост объёма торгов в определённой акции может поначалу восприниматься как выброс, но если он продолжается, это уже краткосрочный тренд. А если он сохраняется неделями, то со временем становится частью долгосрочной структуры. Такая эволюция паттернов требует от моделей гибкости и способности адаптироваться к меняющейся структуре данных.

В рамках данной структуры каждая компонента обладает как мультипликативным, так и аддитивным воздействием. Мультипликативный эффект позволяет моделировать пропорциональные изменения. Аддитивный эффект, напротив, отражает постоянные сдвиги такие, как устойчивое влияние корпоративных дивидендов или сезонных сборов, не зависящих от текущего уровня цены. Именно совмещение этих двух типов воздействий позволяет моделировать рыночные данные максимально реалистично. Ведь в одних случаях ключевым оказывается относительное изменение, а в других — абсолютная величина.

Долгосрочная компонента служит для выявления устойчивых структурных паттернов временного ряда, таких как стабильный рост объёмов торговли или расширение рыночной активности на фоне экономического подъёма. Под паттерном мы понимаем не просто хронологическую последовательность, а именно форму распределения агрегированных данных — без привязки к конкретным временным точкам. Таким образом, долгосрочная структура определяется статистическим профилем данных, собранных за длительный период, охватывающий несколько циклов сезонности.

Идея проста: если объединить наблюдения за разные сезоны, можно нивелировать краткосрочные колебания и получить более чистую, слабо зашумлённую оценку устойчивых тенденций. Подобный подход позволяет избежать переобучения на временные аномалии такие, как разовые всплески объёмов или кратковременные коррекции, и сфокусироваться на фундаментальной рыночной динамике.

Для реализации этого подхода используется скользящее окно длиной ∆, которое позволяет динамически отбирать наблюдения на каждом шаге времени. Затем рассчитываются два ключевых статистических параметра: среднее значение (или центр распределения) и стандартное отклонение (характеризующее масштаб колебаний). Оба параметра используются совместно, чтобы сформировать представление о долгосрочной компоненте. После этого каждый новый анализируемый фрагмент нормализуется — из него вычитается долгосрочное среднее и результат делится на стандартное отклонение. Это приводит все фрагменты к единому масштабу, устраняя долгосрочные смещения и готовя данные к следующему этапу декомпозиции.

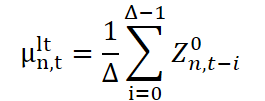
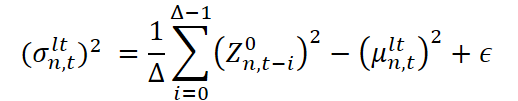
Здесь μˡᵗn,t и σˡᵗn,t — соответственно долгосрочное среднее и масштаб (стандартное отклонение), полученные из данных за окно ∆. А Z¹n,t — нормализованное значение, очищенное от долгосрочной компоненты, которое передаётся на следующий уровень обработки, где будет выделяться сезонность.

Этот этап можно интерпретировать как выровненное представление рынка, где учтены устойчивые структурные тренды. Это особенно важно в финансовом прогнозировании, где краткосрочные стратегии (например, внутридневные) нуждаются в данных, очищенных от долгосрочных сдвигов, чтобы выявить локальные возможности без искажений от глобальных тенденций.

Сезонная компонента отвечает за выявление повторяющихся циклических паттернов временного ряда. В контексте финансовых рынков такими паттернами могут быть, например, внутридневные пики торговой активности: утренние всплески, затишье в обеденное время, вечерний разгон перед закрытием сессии. Это может быть и недельная цикличность: снижение волатильности в пятницу или рост объёмов по понедельникам, а также квартальные и годовые сезонные эффекты, связанные с отчётностью или макроэкономическими публикациями.

Предполагается, что длина сезонного цикла остаётся постоянной во времени — это упрощённое, но практичное допущение. Тем не менее, для сценариев с переменной длиной цикла авторы фреймворка предлагают интегрировать автоматическую оценку сезонности с помощью FFT (быстрого преобразования Фурье).

Технически извлечение сезонной компоненты организовано схожим образом с долгосрочной нормализацией, но с важным отличием: используется разреженное окно (dilated window), шаг которого соответствует длине цикла. Пусть τ — размер окна, а m — коэффициент разрежения (фактически — длина цикла). Это позволяет просматривать данные через интервалы, соответствующие сезонной структуре.

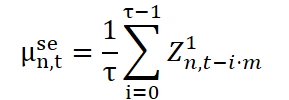
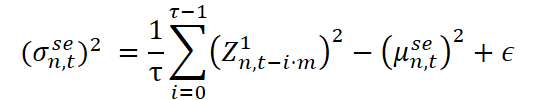
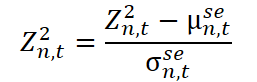
Здесь Z²n,t — нормализованные данные, очищенные от сезонности, которые передаются на следующий этап обработки.

Краткосрочная компонента отвечает за улавливание локальных и нерегулярных отклонений, которые не объясняются ни долгосрочными трендами, ни сезонными паттернами. В условиях финансового рынка такие эффекты могут быть вызваны внезапной реакцией на новостной вброс, техническими сбоями, спекулятивными всплесками ликвидности или резкой сменой настроений трейдеров на фоне волатильности. Это — своего рода пульсация рынка, отражающая его чувствительность к внешним раздражителям на очень коротких интервалах времени.

В отличие от долгосрочной нормализации, здесь используется малое окно сглаживания, чтобы избежать размытия кратковременных колебаний. Пусть δ — длина этого окна. На его основе рассчитываются стандартные статистические характеристики — центр и масштаб выборки, после чего данные нормализуются.

Полученное значение Z³n,t представляет собой промежуточное представление, очищенное от кратковременных флуктуаций, и направляется далее — на финальный этап нормализации.

Однако у такой компоненты есть свои ограничения. Во-первых, она не может мгновенно отреагировать на внезапные, резкие изменения — модель демонстрирует инерционность. Во-вторых, если изменение длится всего два-три шага по времени, оно может остаться незамеченным, особенно в условиях высокой дисперсии. Это напоминает ситуацию на рынке, когда кратковременная волатильность на одной акции может быть проигнорирована общей системой, если её значение теряется в агрегированном шуме.

Для сглаживания этого эффекта и повышения чувствительности модели к краткосрочным сигналам, в SCNN предусмотрено использование сопряжённых (co-evolving) временных рядов. То есть, если наблюдается отклонение на одном инструменте, модель проверяет синхронные сигналы по другим активам, таким как производные инструменты, индексы или объёмы. Таким образом, краткосрочная компонента становится не только реактивной, но и контекстуальной — что особенно важно в условиях высокочастотной и алгоритмической торговли.

Сопряжённая компонента занимает особое место в общей структуре модели. В отличие от предыдущих трёх компонент, которые анализируют поведение каждого временного ряда изолированно, эта часть модели опирается на пространственные корреляции и позволяет улавливать мгновенные изменения, проявляющиеся синхронно в нескольких временных рядах. Если два или более временных ряда демонстрируют схожую динамику в одни и те же моменты времени, это с высокой вероятностью указывает на наличие общего генеративного процесса. В таком случае можно получить его оценку путём агрегирования соответствующих наблюдений.

Однако для реализации такого подхода необходимо решить ключевую задачу — определить, какие именно ряды участвуют в этом совместном процессе. Это сводится к измерению корреляции между временными рядами. Здесь возможны два подхода: можно либо зафиксировать матрицу корреляций заранее, основываясь на экспертных знаниях, либо обучать её напрямую по данным. Авторы фреймворка выбрали второй путь — более гибкий и универсальный, особенно в условиях отсутствия априорной информации о структуре данных.

Для каждой пары временных рядов n и n' рассчитывается индивидуальный коэффициент внимания, который затем нормализуется с помощью SoftMax-функции. Это гарантирует, что сумма весов для каждого ряда будет равна единице.

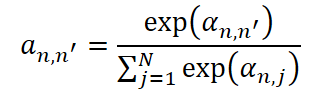
Используя эти веса, рассчитываем параметры сопряжённой компоненты. Сначала вычисляется среднее значение, отражающее локальную центровку с учётом взаимосвязей.

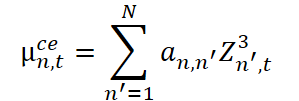
Затем оценивается масштаб (стандартное отклонение) с добавлением стабилизирующей константы ϵ.

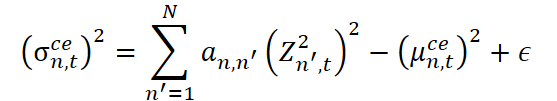
На этом основании формируется нормализованный остаток.

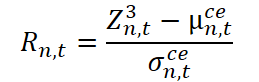
Этот остаток Rn,t представляет собой ту часть сигнала, которая не объясняется ни одной из ранее выделенных компонент. Он отражает остаточную неопределённость, структурный шум или же уникальные, не формализуемые отклонения конкретного ряда от общей динамики.

При работе с большим числом временных рядов можно дополнительно повысить масштабируемость модели. Для этого предлагается использовать модуль обучения матрицы смежности, позволяющий гибко регулировать архитектуру внимания и оптимизировать расчёты.

На заключительном этапе все промежуточные представления объединяются в один вектор признаков.

Параллельно формируется вспомогательный вектор параметров нормализации.

Таким образом, временной ряд перестаёт быть просто набором чисел, фиксированных во времени. Он превращается в многокомпонентное представление, где каждая часть отвечает за определённый тип динамики: структурный тренд, повторяющиеся сезонные колебания, локальные краткосрочные флуктуации или коллективные синхронные изменения. Это даёт возможность более точно анализировать данные, строить интерпретируемые модели и разрабатывать устойчивые алгоритмы прогнозирования.

Поскольку каждая компонента демонстрирует свою собственную динамику с различной степенью предсказуемости, возникает естественная необходимость моделировать их поведение раздельно. Это особенно актуально при краткосрочном прогнозировании, когда долгосрочные и сезонные компоненты, как правило, сохраняют устойчивый характер и изменяются по достаточно регулярным законам. В подобных условиях их можно продолжать экстраполировать напрямую, без необходимости вводить дополнительные параметры или усложнённые модели.

Так, для долгосрочной компоненты применяется самый простой приём: предполагается, что её значения остаются неизменными на всём горизонте прогнозирования. То есть, если текущие оценки параметров этой компоненты известны, мы просто копируем их в будущее.

Сезонная компонента, напротив, опирается на периодичность и требует чуть более тонкого подхода. Поскольку цикличность сохраняется, мы повторно используем значения параметров из прошлых временных точек, находящихся в той же фазе цикла, что и прогнозируемая точка. Иначе говоря, значения сезонной компоненты для момента t+i берутся из момента t-m+i, где m — длина цикла.

Такой метод обеспечивает сохранение сезонного ритма и позволяет с высокой точностью продолжать поведение компоненты без дополнительной нагрузки на модель.

В отличие от долгосрочной и сезонной составляющих, короткосрочная компонента, сопряженные зависимости и остаточные представления обладают гораздо большей стохастичностью. Их динамика значительно менее регулярна, что делает невозможным использование фиксированных эвристик или жёстко заданных законов экстраполяции. В связи с этим, для каждой из этих трёх компонент авторы фреймворка применяют параметризованную модель, построенную на авторегрессии — это позволяет учесть их сложные и непредсказуемые колебания.

Для каждой временной точки прогнозного горизонта планирования i, значения соответствующих компонент вычисляются на основе предыдущих δ значений, с помощью линейной модели с обучаемыми весами. Процедура экстраполяции одинакова для короткосрочной, сопряженной и остаточной составляющих, и выражается следующим образом:

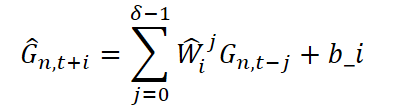
где G ∈ {Zˡn,t+i, μ^stn,t+i, σ^stn,t+i,μ^cen,t+i, σ^cen,t+i} — экстраполируемые параметры, соответствующие различным компонентам; Ŵ^ji ∈ R^{dz · dz} — обучаемые матрицы весов, отражающие вклад прошлых значений; bi — смещение (bias), также подлежащее обучению.

После экстраполяции все компонентs объединяются в два вектора:

• Ĥn, t+i — совокупность статистических параметров;
• Źn, t+i — совокупность нормализованных представлений.

Чтобы смоделировать взаимодействие между этими двумя множествами признаков, применяется операция попарного перемножения (поэлементное произведение) двух линейных проекций, каждая из которых формируется на основе обучаемой матрицы параметров.

Таким образом, формируется финальное представление прогноза, обобщающее все статистически значимые аспекты изучаемого процесса.

Реализация средствами MQL5

После детального рассмотрения теоретических основ фреймворка SCNN, мы переходим к его практической реализации. В этом разделе будет представлен один из рабочих вариантов переноса ключевых идей модели на прикладной уровень средствами MQL5. Мы продемонстрируем, как можно реализовать декомпозицию временного ряда на структурные компоненты, а также построить прогнозную часть модели, сохранив её интерпретируемость и модульность. Такой подход открывает путь к созданию наглядных, гибких и адаптивных торговых стратегий на базе сложных нейросетевых архитектур.

На первом этапе реализации фреймворка SCNN мы сосредоточим внимание на построении базового блока — алгоритма извлечения статистических характеристик и нормализации входных данных по фиксированным временным периодам. Этот этап играет ключевую роль в декомпозиции временного ряда, поскольку именно здесь формируются долгосрочные и краткосрочные компоненты, на которых позже будет основано всё дальнейшее прогнозирование.

Алгоритм реализован в виде OpenCL-кернела PeriodNorm, который отвечает за вычисление статистических характеристик и нормализацию данных внутри скользящих окон временного ряда. Реализация основывается на идее параллельной обработки, при которой данные по всем переменным и временным окнам обрабатываются одновременно.

__kernel void PeriodNorm(__global const float* inputs,
                         __global float2* mean_stdevs,
                         __global float* outputs,
                         const int total_inputs
                        )
  {
   const size_t i = get_global_id(0);
   const size_t p = get_local_id(1);
   const size_t v = get_global_id(2);
   const size_t windows = get_global_size(0);
   const size_t period = get_local_size(1);
   const size_t variable = get_global_size(2);

Функция принимает массив входных значений inputs, а также массивы для записи нормализованных значений outputs и рассчитанных статистических параметров (средние значения и стандартное отклонения) mean_stdevs. Также передаётся параметр total_inputs, определяющий длину временного ряда на одну переменную.

Организация потоков операций трёхмерная: первая координата отвечает за номер окна (временной сегмент), вторая — за позицию внутри окна, третья — индекс переменной. Таким образом, каждый поток отвечает за один конкретный элемент ряда внутри конкретного окна и для конкретной переменной.

Сначала рассчитываются индексы, необходимые для корректного доступа к данным в памяти. Переменная shift_i определяет положение текущей точки относительно начала временного ряда, shift_v — смещение по переменным, а shift_ms — позицию в массиве статистик.

   __local float Temp[LOCAL_ARRAY_SIZE];
   const int shift_i = i * period + p;
   const int shift_v = v * total_inputs;
   const int shift_ms = v * windows + i;

После этого значение временного ряда извлекается из исходного массива с помощью проверки на недопустимые значения: если встречаются NaN или бесконечности, они заменяются на ноль.

//---
   float val = 0;
   if((shift_i) < total_inputs)
      val = IsNaNOrInf(inputs[shift_v + shift_i], 0);

Следующий шаг — вычисление среднего значения в пределах текущего окна. Для этого используется вспомогательная функция LocalSum, позволяющая суммировать значения элементов из потоков локальной группы, что существенно повышает производительность.

   float mean = IsNaNOrInf(LocalSum(val, 1, Temp) / period, 0);
   val -= mean;
   BarrierLoc;

Полученное среднее значение затем вычитается из текущего наблюдения, и на этой основе рассчитывается стандартное отклонение как корень из среднего квадрата отклонений. Все этапы сопровождаются встроенными проверками числовой стабильности, чтобы избежать деления на ноль и накопления ошибок.

   float stdev = LocaSum(val * val, 1, Temp) / period;
   stdev = IsNaNOrInf(sqrt(stdev), 1);

Результаты сохраняются в двух формах: во-первых, статистики по каждому окну и переменной записываются в массив mean_stdevs, а во-вторых, нормализованные значения возвращаются в массив outputs.

   mean_stdevs[shift_ms] = (float2)(mean, stdev);
   if((shift_i) < total_inputs)
      outputs[shift_v + shift_i] = IsNaNOrInf(val / stdev, 0);
  }

Нормализация выполняется по классической формуле Z-преобразования, при этом в качестве нормы используется рассчитанное на лету стандартное отклонение.

Кернел написан так, чтобы легко масштабироваться: можно изменить размер окна, количество переменных или глубину временного ряда без изменения логики. В частности, при увеличении длины окна нормализация становится чувствительной к долгосрочным тенденциям и может использоваться для выделения тренда. Напротив, уменьшение окна позволяет более точно фиксировать краткосрочные отклонения и аномалии.

Для реализации модели с полным циклом обучения, включающим обратное распространение ошибки, нам необходимо обеспечить возможность передачи градиента от выходов нейросетевой архитектуры к её входам. Несмотря на то, что в кернеле PeriodNorm нет обучаемых параметров (все вычисления строго статистические и основаны на данных входного ряда) градиенты должны быть рассчитаны, если нормализация выполняется как часть вычислительного графа. Поэтому мы дополняем архитектуру вторым кернелом — PeriodNormGrad.

__kernel void PeriodNormGrad(__global const float* inputs,
                             __global float* inputs_gr,
                             __global const float2* mean_stdevs,
                             __global const float2* mean_stdevs_gr,
                             __global const float* outputs,
                             __global const float* outputs_gr,
                             const int total_inputs
                            )
  {
   const size_t i = get_global_id(0);
   const size_t p = get_local_id(1);
   const size_t v = get_global_id(2);
   const size_t windows = get_global_size(0);
   const size_t period = get_local_size(1);
   const size_t variable = get_global_size(2);

В отличие от классических блоков с обучаемыми параметрами, алгоритм, реализованный в кернеле PeriodNormGrad, направлен на корректную обратную передачу ошибки через слой, который сам по себе не содержит нейронов или весов. Прежде всего, внутри кернела организуется точечный доступ к каждому временному окну ряда для каждой переменной. Индексы рассчитываются так же, как в прямом проходе:

• i — номер окна,
• p — позиция внутри окна,
• v — номер переменной.

Получив таким образом координаты, мы извлекаем все необходимые данные — исходное значение (inp), его нормализованную версию (out), градиент ошибки по нормализованному значению (out_gr), а также заранее рассчитанные среднее и стандартное отклонение в окне (mean_stdev) и градиенты по ним (mean_stdev_gr), которые могут быть дополнительно получены при многократном использовании значений. В частности, фреймворком SCNN предполагается их использование для экстраполяции данных. Все значения проходят проверку на корректность — выбрасываются NaN и бесконечности, чтобы не испортить расчёты.

   __local float Temp[LOCAL_ARRAY_SIZE];
   const int shift_i = i * period + p;
   const int shift_v = v * total_inputs;
   const int shift_ms = v * windows + i;
//---
   float inp = 0;
   float inp_gr = 0;
   float out = 0;
   float out_gr = 0;
   const float2 mean_stdev = means_stdevs[shift_ms];
   const float2 mean_stdev_gr = means_stdevs_gr[shift_ms];
   if((shift_i) < total_inputs)
     {
      inp = IsNaNOrInf(inputs[shift_v + shift_i], 0);
      out = IsNaNOrInf(outputs[shift_v + shift_i], 0);
      out_gr = IsNaNOrInf(outputs_gr[shift_v + shift_i], 0);
     }

Дальше — самое интересное. Чтобы понять, как сильно каждое исходное значение повлияло на итоговую ошибку модели, мы должны рассчитать, как изменится ошибка, если немного изменить это значение. В статистике нормализация осуществляется вычитанием среднего и делением на стандартное отклонение. А значит, любое изменение входа повлияет как на числитель (отклонение от среднего), так и на знаменатель (размер разброса в окне). Поэтому нужно рассчитать градиенты по обоим параметрам — и по среднему, и по стандартному отклонению.

   float mean_gr = LocalSum(out_gr, 1, Temp) / period + IsNaNOrInf(mean_stdev.x, 0);
   BarrierLoc;
   float stdev_gr = out * LocalSum(IsNaNOrInf(out * out_gr, 0), 1, Temp) / period +
                                                        IsNaNOrInf(mean_stdev.y, 0);

Для этого сначала берётся сумма всех градиентов на уровне результатов слоя out_gr по текущему окну и усредняется — это и есть вклад в градиент по среднему (mean_gr). Обратите внимание, что здесь мы не просто передаём градиент напрямую: мы учитываем, как изменение среднего влияет на нормализованные значения по всему окну.

Далее, расчёт градиента по стандартному отклонению (stdev_gr) чуть сложнее — здесь мы используем произведение усредненного значения на его градиент ошибки, затем усредняем его, и тем самым получаем чувствительность ошибки к разбросу данных.

Теперь, имея оба этих градиента, можно переходить к расчёту основного результата — градиента по самому входу. Мы комбинируем градиент от out_gr с производными по среднему и стандартному отклонению. Итоговая формула сбалансирована и позволяет точно отразить вклад каждого входного значения в общую ошибку модели, учитывая его положение в окне и влияние на среднестатистические характеристики.

   inp_gr = (out_gr - mean_gr - stdev_gr) / IsNaNOrInf(mean_stdev.y, 1);
//---
   if((shift_i) < total_inputs)
      inpurs_gr[shift_v + shift_i] = IsNaNOrInf(inp_gr, 0);
  }

В конце, как обычно, полученное значение записывается обратно в массив градиентов по входу (inputs_gr). Всё делается с учётом границ: если текущий индекс выходит за пределы массива, никакие операции не проводятся.

Таким образом, PeriodNormGrad — это не просто формальная реализация градиентов, а важный функциональный мост между классической статистикой и современными методами обучения моделей. Он позволяет статистическим операциям быть полноправными участниками вычислительного графа и участвовать в обучении, корректно передавая информацию об ошибке туда, где она возникла.

На стороне основной программы создадим специализированный класс CNeuronPeriodNorm, предназначенный для инкапсуляции логики работы с OpenCL-кернерами нормализации по периодам, как для прямого, так и обратного прохода. Он наследуется от базового класса CNeuronBaseOCL, что указывает на его принадлежность к иерархии компонентов вычислительной модели. Структура нового объекта представлена ниже.

class CNeuronPeriodNorm :  public CNeuronBaseOCL
  {
protected:
   uint                    iPeriod;
   uint                    iVariables;
   uint                    iCount;
   CNeuronBaseOCL          cMeanSTDevs;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return true; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronPeriodNorm(void) : iPeriod(-1), iVariables(1) {};
                    ~CNeuronPeriodNorm(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint units_count, uint period, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(const int file_handle) override;
   virtual bool      Load(const int file_handle) override;
   //---
   virtual int       Type(void) override const  {  return defNeuronPeriodNorm; }
   virtual void      SetOpenCL(COpenCLMy *obj) override;
//---
   CNeuronBaseOCL*   GetMeanSTDevs(void) { return cMeanSTDevs.AsObject(); }
   virtual uint      GetPeriod(void) const { return iPeriod; }
   virtual uint      GetVariables(void) const { return iVariables; }
   virtual uint      GetUnits(void) const { return iCount; }
  };

Внутренние поля класса отражают ключевые параметры конфигурации. В частности, переменная iPeriod задаёт длину окна, в пределах которого производится статистическая обработка — расчёт среднего и стандартного отклонения. Параметр iVariables определяет количество обрабатываемых переменных (или признаков), а iCount — число независимых окон для каждой унитарной последовательности.

Кроме того, внутри класса содержится объект cMeanSTDevs, который представляет собой промежуточный буфер для хранятся значения средних и стандартных отклонений, рассчитанных на этапе прямого прохода. Этот буфер также участвует в обратной передаче градиентов, как это было реализовано в кернеле PeriodNormGrad.

Метод Init играет роль конструктора инициализации — он получает на вход все параметры, и на их основе подготавливает внутренние структуры и связывает объект с необходимыми ресурсами OpenCL.

Методы прямого и обратного прохода по своей сути выполняют роль служебных обёрток. Их задача — не пересчитывать данные вручную, а подготовить всё необходимое для корректной постановки соответствующих OpenCL-кернелов в очередь исполнения.

Обратите внимание на функцию GetMeanSTDevs — она предоставляет доступ к буферу с рассчитанными статистиками, который может быть использован другими компонентами модели, например, для визуализации или дальнейшей обработки.

Таким образом, класс CNeuronPeriodNorm представляет собой полностью автономный и гибкий компонент, который не просто выполняет нормализацию, но и обеспечивает корректную интеграцию в структуру вычислительной модели с поддержкой обучения. Всё сделано строго по канонам архитектуры нейросетевых фреймворков, но с сохранением чёткой логики, характерной для систем с ручным управлением вычислениями, таких как MQL5 + OpenCL.

Полный код данного класса, включая его методы, представлен во вложении для самостоятельного изучения.

Сегодня мы проделали серьёзную и продуктивную работу. Материал получился насыщенным и требует времени на осмысление. Самое время сделать небольшую паузу, перевести дух — и с новыми силами продолжить работу в следующей статье.

Заключение

В данной статье мы познакомились с теоретическими аспектами фреймворка SCNN, который предлагает оригинальный и концептуально стройный подход к декомпозиции временных рядов на интерпретируемые компоненты: долгосрочную, сезонную, краткосрочную и остаточную. Такая структура позволяет не только повысить точность прогнозирования, но и значительно улучшает прозрачность модели, делая её поведение более предсказуемым и адаптивным к изменяющимся рыночным условиям.

Особый акцент делается на различии в характере динамики каждой из компонент, что обуславливает использование специализированных методов интерполяции: для долгосрочной и сезонной составляющих применяются простые повторяющиеся паттерны, в то время как краткосрочные и остаточные колебания моделируются обучаемыми авторегрессионными структурами.

В практической части статьи мы начали реализацию собственного видения предложенных подходов и построили один из базовых элементов модели — алгоритм нормализации периодических сегментов временного ряда. Мы рассмотрели детали реализации вычислений на стороне OpenCL, в том числе прямой и обратный проходы, что позволит впоследствии встроить данный механизм в обучаемую нейросетевую архитектуру. Этот шаг стал важным звеном в практической адаптации фреймворка под задачи трейдинга в среде MQL5.

В следующей статье мы продолжим развивать эту реализацию, добавляя новые компоненты модели и постепенно приближаясь к полноценной системе анализа и прогнозирования временных рядов на основе фреймворка SCNN.

Ссылки

• Disentangling Structured Components: Towards Adaptive, Interpretable and Scalable Time Series Forecasting
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Study.mq5	Советник	Советник офлайн обучения моделей
2	StudyOnline.mq5	Советник	Советник онлайн обучения моделей
3	Test.mq5	Советник	Советник для тестирования модели
4	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
5	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
6	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы