Нейросети в трейдинге: Распутывание структурных компонентов (Энкодер)

MetaTrader 5 — Торговые системы | 29 июля 2025, 14:18

Введение

Продолжаем работу по реализации собственного видения подходов, представленных авторами фреймворка SCNN. Напомним, что SCNN (Structured Component Neural Network) предлагает концептуально иной подход: вместо того, чтобы пытаться охватить весь временной ряд единым универсальным механизмом, он разделяет его на пять ключевых компонент — долгосрочную, сезонную, краткосрочную, сопряженную и остаточную. Каждая из этих компонент моделируется и экстраполируется отдельно, что даёт нам не только гибкость, но и возможность получить интерпретируемый результат на каждом этапе.

Главное преимущество такой архитектуры — прозрачность. В отличие от традиционных чёрных ящиков, SCNN позволяет аналитикам и трейдерам видеть, какая именно часть модели отвечает за тот или иной участок прогноза, и насколько уверенно модель себя ведёт в текущих условиях. Это особенно важно при работе с финансовыми данными, где доверие к модели должно подкрепляться объяснимостью и контролируемостью. Кроме того, индивидуальный подход к экстраполяции каждой компоненты даёт возможность использовать как статистические эвристики (для долгосрочных и сезонных паттернов), так и обучаемые нейросетевые модули (для моделирования краткосрочных аномалий или взаимозависимостей между активами).

Фреймворк также учитывает сложные зависимости во времени, включая автокорреляционные связи, которые часто игнорируются в упрощённых моделях. Это особенно актуально для задач, связанных с внутридневным трейдингом или прогнозированием на границе между торговыми сессиями. SCNN позволяет динамически подстраиваться под смещение статистики в реальном времени, а также выявлять аномальные точки, в которых прогноз может быть ненадёжен.

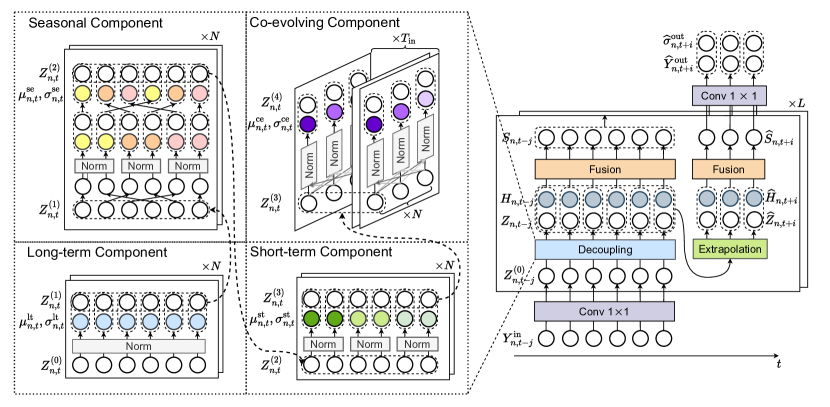
Авторская визуализация фреймворка SCNN представлена ниже.

Авторская визуализация фреймворка SCNN

В практической части предыдущей работы мы разработали объект CNeuronPeriodNorm, предназначенный для выделения периодических компонент временного ряда. Этот компонент стал первым шагом к реализации фреймворка SCNN в среде MQL5 и будет применяться для извлечения долгосрочных и краткосрочных составляющих. Благодаря использованию OpenCL-кернелов, обеспечивается эффективная параллельная обработка данных и поддержка механизма обратного распространения ошибки, что делает данный модуль пригодным для использования внутри обучаемых нейросетевых конструкций.

Позже мы покажем, что благодаря нескольким несложным преобразованиям данных, CNeuronPeriodNorm может быть адаптирован и для выделения сезонной составляющей, что придаёт ему дополнительную универсальность. А сегодня мы сделаем следующий шаг — начнём построение объекта, отвечающего за извлечение сопряжённой компоненты, отражающей взаимосвязанные изменения между несколькими переменными временного ряда. Этот модуль сыграет ключевую роль в моделировании синхронизированных колебаний и аномальных совместных движений, что особенно актуально в условиях мультивариативного рыночного анализа.

Выделение сопряженной компоненты

Полученный нами практический опыт говорит, что для корректной реализации модели недостаточно одного лишь временного анализа. Важно учитывать также пространственные зависимости — то есть связи между различными переменными в каждый конкретный момент времени. Именно этим и занимается механизм выделения сопряжённой компоненты, который помогает улавливать сонаправленные или противонаправленные движения между сигналами отдельных унитарных последовательностей анализируемого мультимодального временного ряда. Такая соэволюция может быть как устойчивой, так и динамически изменяющейся, и потому требует адаптивного подхода к нормализации.

В рамках фреймворка SCNN, эта задача решается через внедрение пространственно-взвешенной нормализации с использованием механизма внимания. Мы переходим к следующему шагу реализации, в котором представим собственное видение предложенного алгоритма с опорой на практические потребности финансового моделирования. Основную часть вычислений, включая взвешенное усреднение и адаптивную стандартизацию, мы, как обычно, делегируем стороне OpenCL-контекста. Это позволяет не только ускорить обработку, но и сохранить гибкость в настройке архитектуры.

Для этой цели мы создадим новый кернел AdaptSpatialNorm. Алгоритм кернела реализует адаптивную нормализацию исходных данных с учётом внимания между переменными, обеспечивая более точную и чувствительную обработку пространственных взаимосвязей. Идея заключается в том, чтобы для каждой временной точки рассчитать среднее значение и стандартное отклонение, взвешенные по маске внимания. Это позволяет не просто усреднять по всем переменным, а учитывать их относительную значимость — то есть влияние каждой переменной на конкретную точку в пространственно-временном контексте.

__kernel void AdaptSpatialNorm(__global const float* inputs,
                               __global const float* attention,
                               __global float2* mean_stdevs,
                               __global float* outputs
                              )
  {
   const size_t i = get_global_id(0);
   const size_t a = get_local_id(1);
   const size_t v = get_global_id(2);
   const size_t total_inputs = get_global_size(0);
   const size_t total_local = get_local_size(1);
   const size_t variables = get_global_size(2);

В вычислительном ядре расчёты организованы по трём измерениям: по времени, по переменным и по локальным потокам. Каждый поток отвечает за обработку конкретного значения — одной переменной в определённый момент времени. Сначала определяется смещение индексов, которое позволяет каждому потоку корректно обращаться к нужным участкам памяти.

   __local float Temp[LOCAL_ARRAY_SIZE];
   const int shift_v = v * total_inputs;
   const int shift_out = shift_v + i;

Затем начинается основная часть работы, где по всем переменным извлекаются значения исходного массива и соответствующие коэффициенты внимания. Каждое значение умножается на свой вес, после чего, происходит локальное суммирование — сначала для расчёта среднего, затем для определения дисперсии.

   float mean = 0, stdev = 0;
   for(uint l = 0; l < variables; l += total_local)
     {
      const int shift_at = v * variables + (a + l);
      float val = IsNaNOrInf(inputs[(a + l) * total_inputs + i], 0);
      float att = IsNaNOrInf(attention[shift_at], 0);
      mean += LocalSum(val * att, 1, Temp);
      BarrierLoc;
      stdev += LocalSum(val * val * att, 1, Temp);
      BarrierLoc;
     }

Для обеспечения корректности параллельных вычислений между потоками используется барьер синхронизации, что позволяет избежать конфликтов доступа при работе с общей памятью.

Здесь стоит обратить особое внимание на техническую сторону организации вычислений. Для корректного выполнения операций суммирования значений, поступающих от разных потоков, в рамках OpenCL создаются так называемые рабочие группы. Потоки внутри этих групп могут обмениваться данными через локальную память, которая, в отличие от глобальной, работает значительно быстрее и позволяет эффективно реализовывать коллективные операции, такие как свёртка или суммирование.

Однако у этой архитектуры есть естественное ограничение — размер рабочей группы не может превышать определённый аппаратный предел, установленный видеокартой или другим вычислительным устройством. На практике это означает, что количество потоков, одновременно обрабатывающих переменные в одной группе, ограничено и далеко не всегда соответствует размерности обрабатываемого входного массива.

Для обхода этого ограничения в теле кернела реализован специальный цикл, который позволяет поэтапно перебрать все переменные, даже если их количество существенно превышает размер рабочей группы. Общее пространство признаков разбивается на блоки, обрабатываемые порциями, и значения последовательно агрегируются. Такой подход сохраняет эффективность вычислений и обеспечивает корректное выполнение всех математических операций, независимо от количества переменных, задействованных в модели.

Этот технический приём делает реализацию устойчивой к масштабированию и универсальной для запуска на различных устройствах с разными характеристиками, а саму модель — более гибкой и переносимой.

Когда все значения обработаны, только один поток в каждой локальной группе берёт на себя задачу финальной нормализации. Он вычисляет дисперсию, вычитая квадрат среднего из суммы квадратов значений, и затем извлекает квадратный корень, получая стандартное отклонение. Чтобы избежать деления на ноль, предусмотрена защита: при слишком малом значении дисперсия заменяется на единицу.

   if(a == 0)
     {
      stdev -= mean * mean;
      stdev = IsNaNOrInf(sqrt(stdev), 1);
      if(stdev <= 0)
         stdev = 1;
      mean_stdevs[shift_out] = (float2)(mean, stdev);
      outputs[shift_out] = IsNaNOrInf((inputs[shift_out] - mean) / stdev, 0);
     }
  }

После этого рассчитывается нормализованное значение входа, которое и записывается в выходной массив. Параллельно сохраняются вычисленные среднее и стандартное отклонение — они будут полезны в дальнейшем.

Реализованная логика сочетает в себе агрегацию информации о пространственном распределении данных и нормализацию по данному распределению. Это позволяет модели чувствительно реагировать на скрытые зависимости между переменными, а значит — более точно улавливать динамику сложных временных процессов, что особенно актуально в финансовом прогнозировании.

Для полноценного обучения модели необходим не только прямой проход с вычислением нормализованных значений, но и корректный обратный проход, обеспечивающий передачу градиентов ошибки обратно к исходным данным и параметрам. В контексте нашего кернела AdaptSpatialNorm, для пространственно-взвешенной нормализации следующий логичный шаг — реализация кернела обратного прохода AdaptSpatialNormGrad, который отвечает за распределение градиентов ошибки по исходным данным и коэффициентам внимания.

__kernel void AdaptSpatialNormGrad(__global const float* inputs,
                                   __global float* inputs_gr,
                                   __global const float* attention,
                                   __global float* attention_gr,
                                   __global const float2* mean_stdevs,
                                   __global const float2* mean_stdevs_gr,
                                   __global const float* outputs_gr,
                                   const uint total_inputs
                                  )
  {
   const size_t i = get_global_id(0);              // main
   const size_t loc = get_local_id(1);             // local to sum
   const size_t v = get_global_id(2);              // variable
   const size_t total_main = get_global_size(0);   // total
   const size_t total_loc = get_local_size(1);     // local dimension
   const size_t variables = get_global_size(2);    // total variables
//---
   __local float Temp[LOCAL_ARRAY_SIZE];

В основе алгоритма лежит распределение вычислительной нагрузки по потокам, где каждый поток обрабатывает конкретную комбинацию индексов, отвечающих за временной срез и переменную. Для хранения промежуточных значений используется локальная память, что ускоряет процессы суммирования и агрегирования данных внутри рабочих групп.

Сначала происходит вычисление градиентов по исходным данным. Для каждого элемента входного массива берутся соответствующие параметры внимания и выходных градиентов. Далее рассчитывается градиент, учитывающий частные производные по параметрам нормализации (среднему и стандартному отклонению), которые также участвуют в обратном распространении ошибки. Все частные суммы аккумулируются, после чего результат записывается в массив градиентов входных данных.

//--- Inputs gradient
     {
      if(i < total_inputs)
        {
         float grad = 0;
         int shift_in = v * total_inputs + i;
         float x = IsNaNOrInf(inputs[shift_in], 0);
         for(int l = 0; l < variables; l += total_loc)
           {
            if((l + loc) >= variables)
               break;
            int shift_out = i + (l + loc) * total_inputs;
            float att = IsNaNOrInf(attention[(l + loc) * variables + v], 0);
            float out_gr = IsNaNOrInf(outputs_gr[shift_out], 0);
            float2 ms = mean_stdevs[shift_out];
            float2 ms_gr = mean_stdevs_gr[shift_out];
            float dy = (1 - att) * (1 / ms.y - (x - ms.x) * att * x / pow(ms.y, 3.0f));
            float dmean = IsNaNOrInf(ms_gr.x * att, 0);
            float dstd = IsNaNOrInf(ms_gr.y * x * (att - att * att) / ms.y, 0);
            grad += IsNaNOrInf(dy * out_gr + dmean + dstd, 0);
           }
         grad = LocalSum(grad, 1, Temp);
         if(loc == 0)
            inputs_gr[shift_in] = grad;
        }
      BarrierLoc;
     }

Забегая немного вперёд, стоит отметить важную деталь: сохранённые нами параметры нормализации (среднее значение и стандартное отклонение) не являются побочным продуктом вычислений. Напротив, они активно участвуют в последующих операциях фреймворка SCNN, формируя своеобразную вспомогательную ветвь обработки данных. Поэтому градиент ошибки, накопленный на этих параметрах в ходе более поздних стадий прямого прохода, необходимо также спустить до уровня исходных данных.

Это означает, что в процессе обратного прохода мы не ограничиваемся только основным информационным потоком — дополнительно учитываем вклад, связанный с производными по сохранённым статистикам нормализации, и прибавляем его к итоговому градиенту входа. Такой подход обеспечивает целостность вычислительного графа и позволяет модели эффективно корректировать все параметры, влияющие на результат, включая те, что косвенно связаны с входом через механизмы нормализации.

Затем вычисляются градиенты по параметрам внимания. Для каждого элемента весов внимания алгоритм перебирает все соответствующие временные точки, используя значения исходных данных и уже вычисленных градиентов по выходу. Вычисления также учитывают влияние внимания на нормализацию через среднее и стандартное отклонение. Итоговые значения аккумулируются с использованием локальной памяти и сохраняются в соответствующем массиве градиентов для внимания.

//--- Attention gradient
     {
      if(i < variables)
        {
         float grad = 0;
         int shift_att = v * variables + i;
         float att = IsNaNOrInf(attention[shift_att], 0);
         for(int l = 0; l < total_inputs; l += total_loc)
           {
            if((l + loc) >= total_inputs)
               break;
            int shift_out = (l + loc) + v * total_inputs;
            int shift_in = (l + loc) + i * total_inputs;
            float x = IsNaNOrInf(inputs[shift_in], 0);
            float out_gr = IsNaNOrInf(outputs_gr[shift_out], 0);
            float2 ms = mean_stdevs[shift_out];
            float2 ms_gr = mean_stdevs_gr[shift_out];
            float dy = -x / ms.y - (x - ms.x) * x * x * (1 - 2 * att) / (2 * pow(ms.y, 3.0f));
            float dmean = IsNaNOrInf(ms_gr.x * x, 0);
            float dstd = IsNaNOrInf(ms_gr.y * x * x * (1 - 2 * att) / (2 * ms.y), 0);
            grad += IsNaNOrInf(dy * out_gr + dmean + dstd, 0);
           }
         grad = LocalSum(grad, 1, Temp);
         if(loc == 0)
            attention_gr[shift_att] = grad;
        }
     }
  }

Важно отметить, что реализация учитывает возможность некорректных числовых значений, таких как NaN или бесконечности, и защищает от их распространения, что повышает устойчивость алгоритма.

Общий подход с циклической обработкой данных и использованием локальной памяти обеспечивает масштабируемость и эффективность, позволяя обрабатывать большие наборы переменных и временных шагов, даже если их размер превышает размеры рабочих групп.

Таким образом, кернел AdaptSpatialNormGrad обеспечивает точное и эффективное вычисление градиентов для ключевых параметров нормализации с учётом пространственных весов внимания, что позволяет интегрировать данный механизм в сложные модели с обучением посредством обратного распространения ошибки.

Для интеграции описанного выше алгоритма пространственно-взвешенной нормализации в общую архитектуру, на стороне основной программы создаётся специализированный объект CNeuronAdaptSpatialNorm. Этот класс наследует базовые интерфейсы от CNeuronBaseOCL, что позволяет ему органично встраиваться в иерархию нейронных компонентов. Основная задача объекта — обеспечить правильную организацию вычислений как прямого, так и обратного прохода, а также корректно обрабатывать все вспомогательные компоненты, связанные с механизмом внимания.

Структура нового класса представлена ниже.

class CNeuronAdaptSpatialNorm :  public CNeuronBaseOCL
  {
protected:
   uint                    iVariables;
   uint                    iCount;
   //---
   CParams                 cEn;
   CNeuronTransposeOCL     cEnT;
   CNeuronBaseOCL          cEnEnT;
   CNeuronSoftMaxOCL       cAttan;
   CNeuronBaseOCL          cMeanSTDevs;
   //---
   virtual bool      AdaptSpatialNorm(CNeuronBaseOCL *NeuronOCL);
   virtual bool      AdaptSpatialNormGrad(CNeuronBaseOCL *NeuronOCL);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronAdaptSpatialNorm(void) : iCount(0), iVariables(1) {};
                    ~CNeuronAdaptSpatialNorm(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint units_count, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(const int file_handle) override;
   virtual bool      Load(const int file_handle) override;
   //---
   virtual int       Type(void) override const  {  return defNeuronAdaptSpatialNorm; }
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   CNeuronBaseOCL*   GetMeanSTDevs(void) { return cMeanSTDevs.AsObject(); }
   virtual uint      GetVariables(void) const { return iVariables; }
   virtual uint      GetUnits(void) const { return iCount; }
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
  };

Внутри класса мы видим ряд защищённых членов, каждый из которых играет важную роль в функционировании компонента. Переменные iVariables и iCount задают размеры тензора исходных данных и определяют пространственные границы обработки. Внутренние объекты cEn, cEnT, cEnEnT и cAttan последовательно формируют и обучают матрицу внимания. Компонент cMeanSTDevs замыкает эту цепочку, отвечая за хранение и обновление параметров нормализации, которые используются для масштабирования исходных данных с учётом рассчитанных весов внимания.

Все внутренние объекты объявлены статически, что позволяет существенно упростить управление памятью и инициализацией. Благодаря этому, решение становится более надёжным и предсказуемым в поведении: отсутствует необходимость вручную выделять или освобождать ресурсы. Конструктор и деструктор класса остаются пустыми, так как объекты уже существуют на момент создания экземпляра класса и автоматически уничтожаются при завершении его жизненного цикла.

Инициализация всех внутренних компонентов класса осуществляется централизованно в методе Init. Этот метод получает на входе ключевые параметры, позволяющие однозначно определить архитектуру создаваемого объекта, включая размерность входных данных. Весь процесс разворачивается последовательно и логично, с чёткой привязкой к внутренней структуре модели.

bool CNeuronAdaptSpatialNorm::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                   uint units_count, uint variables,
                                   ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, units_count * variables, optimization_type, batch))
      return false;

На первом этапе вызывается одноименный метод родительского класса CNeuronBaseOCL, в котором происходит первичная инициализация нейронного узла. Размер буфера результатов рассчитывается как произведение числа переменных на длину последовательности. Если инициализация базового уровня прошла успешно, задаются параметры тензора исходных данных сохраняются в локальные переменные iVariables и iCount.

   iVariables = variables;
   iCount = units_count;
//---
   uint dimension = (iVariables + 1) / 2;
   uint index = 0;
   if(!cEn.Init(0, index, OpenCL, iVariables * dimension, optimization, iBatch))
      return false;
   cEn.SetActivationFunction(None);

Далее, начинается последовательная настройка внутренних компонентов, отвечающих за формирование матрицы внимания. Объект cEn инициализируется первым. Он представляет собой тензор обучаемых праметров. Его размерность задаётся как произведение количества переменных на половину их количества. Это сжатие позволяет выделить наиболее существенные признаки для последующей обработки. Активационная функция здесь явно отключается, так как на этом этапе требуется чистая линейная трансформация без искажения выходного сигнала.

Следом инициализируется объект транспонирования cEnT, который позволяет получить транспонированную копию тензора обучаемых параметров.

   index++;
   if(!cEnT.Init(0, index, OpenCL, iVariables, dimension, optimization, iBatch))
      return false;
   cEnT.SetActivationFunction(None);
   index++;
   if(!cEnEnT.Init(0, index, OpenCL, iVariables * iVariables, optimization, iBatch))
      return false;
   cEnEnT.SetActivationFunction(None);

Объект cEnEnT играет ключевую роль в построении механизма внимания внутри фреймворка SCNN. Он предназначен для хранения результатов матричного умножения тензора обучаемых параметров на его транспонированную копию. Такая операция формирует симметричную матрицу, которая отражает взаимные зависимости и силу корреляции между переменными в пределах одного временного шага. Полученная структура позволяет явно зафиксировать, какие из анализируемых признаков оказывают наибольшее влияние друг на друга.

Объект cAttan завершает построение механизма внимания. Он принимает на вход матрицу корреляции и применяет к ней SoftMax-нормализацию, распределяя внимание по переменным. Количество голов внимания соответствует числу строк в матрице корреляции, что позволяет гибко адаптироваться к структуре данных.

   index++;
   if(!cAttan.Init(0, index, OpenCL, iVariables * iVariables, optimization, iBatch))
      return false;
   cAttan.SetHeads(iVariables);

В завершение настраивается объект cMeanSTDevs, предназначенный для хранения пар значений: среднее и стандартное отклонение, рассчитанные по пространственно-взвешенной нормализации. Размерность этого объекта — удвоенное количество нейронов на выходе, так как на каждый элемент результатов требуется сохранить два параметра.

   index++;
   if(!cMeanSTDevs.Init(0, index, OpenCL, 2 * Neurons(), optimization, iBatch))
      return false;
   cMeanSTDevs.SetActivationFunction(None);
//---
   return true;
  }

Таким образом, метод Init создаёт и конфигурирует все необходимые компоненты для корректной работы механизма пространственно-взвешенной нормализации в рамках SCNN. Структура кода отражает строгость и модульность архитектуры, где каждый блок имеет своё чёткое назначение и взаимодействует с другими в заданной последовательности.

После успешной инициализации всех внутренних компонентов переходим к построению механизма прямого прохода, реализованного в методе feedForward. Здесь начинается ключевой этап работы слоя, в котором формируется матрица внимания и осуществляется пространственно-взвешенная нормализация входных данных.

bool CNeuronAdaptSpatialNorm::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(bTrain)
     {
      if(!cEn.FeedForward())
         return false;
      if(!cEnT.FeedForward(cEn.AsObject()))
         return false;
      if(!MatMul(cEn.getOutput(), cEnT.getOutput(), cEnEnT.getOutput(),
                 iVariables, cEnT.GetWindow(), iVariables, 1, false))
         return false;
      if(!cAttan.FeedForward(cEnEnT.AsObject()))
         return false;
     }
//---
   return AdaptSpatialNorm(NeuronOCL);
  }

Здесь стоит особо подчеркнуть важный архитектурный момент: формирование параметров внимания выполняется исключительно в режиме обучения. Это сделано намеренно, поскольку сама матрица внимания является статичным компонентом модели — она не адаптируется под конкретные исходные данные в ходе эксплуатации. Другими словами, мы обучаем универсальные весовые коэффициенты, которые отражают устойчивые взаимосвязи между переменными внутри временного ряда. Благодаря этому подходу достигается стабильность поведения модели на новых данных, а расчёт внимания в ходе инференса можно опустить, существенно ускоряя работу без потери качества нормализации.

Далее в цепочке прямого прохода вызывается метод AdaptSpatialNorm, выполняющий роль обёртки одноимённого кернела. Именно этот шаг передаёт управление в OpenCL-контекст, где и происходят основные вычисления: нормализация исходных данных с учётом весов внимания.

Несколько слов стоит сказать об организации работы метода-обёртки для OpenCL-кернела. Хотя общая логика алгоритма осталась прежней, в реализацию были внесены конструктивные улучшения, направленные на повышение читаемости и надёжности кода. В первую очередь это касается оформления вызовов OpenCL-функций.

Были введены макросы-подстановки, позволяющие упростить и стандартизировать установку аргументов кернела и его запуск. Например, макрос setBuffer оборачивает вызов OpenCL.SetArgumentBuffer с автоматической обработкой ошибки и выводом отладочной информации, включая имя кернела, код ошибки и строку, где возник сбой. Аналогично работает setArgument для установки скалярных значений.

#define setBuffer(kernel, id, buffer)  if(!OpenCL.SetArgumentBuffer(kernel, id, buffer)) { \
                                          printf("Error of set parameter kernel %s: %d; line %d",
                                                 OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); \
                                          return false; }
#define setArgument(kernel, id, value) if(!OpenCL.SetArgument(kernel, id, value)) { \
                                          printf("Error of set parameter kernel %s: %d; line %d",
                                                 OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); \
                                          return false; }

Запуск кернела осуществляется через макросы kernelExecute и kernelExecuteLoc, которые скрывают всю техническую обвязку, связанную с инициализацией сетки потоков, и в случае сбоя, автоматически выводят подробное текстовое описание ошибки с привязкой к имени вызываемой функции.

#define kernelExecute(kernel,offset,global)  if(!OpenCL.Execute(kernel, global.Size(), offset, global)) { \
                                                string error; \
                                                CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error); \
                                                printf("Error of execution kernel %s %s: %s", __FUNCSIG__,
                                                        OpenCL.GetKernelName(kernel), error); \
                                                return false; }
#define kernelExecuteLoc(kernel,offset,global,local)  if(!OpenCL.Execute(kernel, global.Size(), offset,
                                                                         global, local)) {  string error; \
                                                         CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION,
                                                                                                          error); \
                                                         printf("Error of execution kernel %s %s: %s", __FUNCSIG__,
                                                                 OpenCL.GetKernelName(kernel), error); \
                                                         return false; }

Благодаря такой структуре, код метода становится компактнее, логически яснее и легче масштабируется при добавлении новых кернелов или параметров.

Кроме того, как уже упоминалось при описании кернелов, перед их запуском необходимо учитывать технические ограничения вычислительного устройства — в частности, максимальный размер рабочей группы, поддерживаемый платформой OpenCL. Эти параметры варьируются в зависимости от модели графического адаптера и могут существенно повлиять на корректность выполнения кода.

В теле метода AdaptSpatialNorm это реализуется через вызов CLGetDeviceInfo, с помощью которого запрашивается допустимый размер рабочей группы по каждой размерности. Возвращаемые значения сохраняются в структуре union sizes, что позволяет удобно обращаться к ним как к массиву целых чисел, не заботясь об особенностях внутреннего представления данных.

bool CNeuronAdaptSpatialNorm::AdaptSpatialNorm(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || !NeuronOCL)
      return false;
   uint global_work_offset[3] = { 0 };
   union sizes
     {
      long data[3];
      uchar cdata[24];
     } max_workgroup_size;
   uint size = 0;
   if(!CLGetDeviceInfo(OpenCL.GetContext(), CL_DEVICE_MAX_WORK_ITEM_SIZES, max_workgroup_size.cdata, size))
      return false;

После получения этих параметров, мы формируем массив global_work_size, определяющий общую сетку вычислений. Причём по второй размерности (которая и задаёт ширину локальной группы) мы явно ограничиваемся минимальным значением между числом переменных iVariables и максимальным размером, разрешённым устройством. Это гарантирует, что цикл, организованный в кернеле, будет корректно отрабатывать даже при большом объёме данных.

   uint global_work_size[] = { iCount, MathMin(iVariables, uint(max_workgroup_size.data[1])), iVariables};
   uint local_work_size[] = { 1, global_work_size[1], 1};
//---
   uint kernel = def_k_AdaptSpatialNorm;
   setBuffer(kernel, def_k_asn_inputs, NeuronOCL.getOutputIndex())
   setBuffer(kernel, def_k_asn_mean_stdevs, cMeanSTDevs.getOutputIndex())
   setBuffer(kernel, def_k_asn_attention, cAttan.getOutputIndex())
   setBuffer(kernel, def_k_asn_outputs, getOutputIndex())
   kernelExecuteLoc(kernel, global_work_offset, global_work_size, local_work_size)
//---
   return true;
  }

Параллельно с этим формируется массив local_work_size, в котором жёстко задаётся количество потоков по второй размерности. Такой подход позволяет эффективно использовать локальную память при обработке векторов признаков.

Далее мы последовательно устанавливаем буферы аргументов кернела с помощью ранее определённых макросов setBuffer, что обеспечивает единообразную и безопасную инициализацию параметров. Завершает работу макрос kernelExecuteLoc, который запускает кернел AdaptSpatialNorm с учётом всех ранее заданных ограничений и структуры вычислительной сетки.

Таким образом, мы реализуем не только обёртку для вызова кернела, но и гибкий механизм адаптации алгоритма к конкретным техническим возможностям целевого оборудования, обеспечивая совместимость и устойчивость работы на широком спектре устройств.

Следующим важным этапом является распределение градиента ошибки, реализованное в методе calcInputGradients. Именно здесь происходит обратное распространение сигнала по внутренним объектам. Накопленные ошибки последовательно трансформируются, возвращаясь к обучаемым параметрам исходного уровня. Эта часть алгоритма особенно важна, поскольку позволяет обновить веса на основе актуальной информации о расхождении между прогнозными и истинными значениями.

bool CNeuronAdaptSpatialNorm::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!AdaptSpatialNormGrad(NeuronOCL))
      return false;

Работа начинается с вызова метода AdaptSpatialNormGrad, который, как и его собрат для прямого прохода, представляет собой обёртку соответствующего OpenCL-кернела. Он отвечает за распространение градиента от выходов блока нормализации вниз к исходным данным и обучаемым параметрам матрицы внимания.

Алгоритм построения метода AdaptSpatialNormGrad практически полностью повторяет структуру, ранее использованную при постановке кернела прямого прохода в очередь выполнения. Мы также формируем глобальные и локальные размеры работы, настраиваем буферы с помощью макросов, и передаём параметры кернелу в нужном порядке. Однако здесь есть важное отличие, которое вытекает из самой природы операции обратного распространения ошибки.

Если при прямом проходе каждый элемент обрабатывался независимо, то при вычислении градиентов ситуация меняется: для каждого элемента на уровне исходных данных необходимо агрегировать вклад градиента от всех унитарных последовательностей — через веса внимания. Это требует одновременного доступа ко множеству различных компонент выходного тензора, а значит — более сложной схемы суммирования.

Особый подход требуется и для коэффициентов внимания. Здесь необходимо аккуратно интегрировать градиент по временному измерению, то есть собрать информацию по всем позициям последовательности, в которых соответствующий коэффициент был применён. Это довольно ресурсоёмкая операция, особенно в случае больших исходных тензоров, поэтому особое внимание уделяется размеру рабочей группы.

В результате, для корректной и эффективной постановки задачи размер рабочей группы берётся по максимуму среди осей, вдоль которых необходимо агрегировать градиенты, но при этом обязательно учитывается ограничение по максимально допустимому значению, поддерживаемому конкретным OpenCL-устройством. Такой подход позволяет не только соблюсти технические требования, но и оптимизировать производительность, избежав ненужных переполнений и конфликтов доступа к памяти.

После завершения вычислений на стороне OpenCL, метод продолжает работу в более привычном стиле. Мы последовательно спускаем градиент ошибки по объектам формирования матрицы внимания.

   if(!cEnEnT.CalcHiddenGradients(cAttan.AsObject()))
      return false;
   if(!MatMulGrad(cEn.getOutput(), cEn.getPrevOutput(),
                  cEnT.getOutput(), cEnT.getGradient(),
                  cEnEnT.getGradient(), iVariables,
                  cEnT.GetWindow(), iVariables, 1, false))
      return false;
   if(!cEn.CalcHiddenGradients(cEnT.AsObject()) ||
      !SumAndNormilize(cEn.getGradient(), cEn.getPrevOutput(), cEn.getGradient(),
                       cEnT.GetWindow(), false, 0, 0, 0, 1))
      return false;
   if(cEn.Activation() != None)
      if(!DeActivation(cEn.getOutput(), cEn.getGradient(), cEn.getGradient(), cEn.Activation()))
         return false;
//---
   return true;
  }

Таким образом, весь метод calcInputGradients представляет собой чётко выстроенную цепочку шагов, обеспечивающих последовательное и корректное распространение ошибки назад по сети.

Метод оптимизации параметров реализован здесь максимально лаконично, но вместе с тем — предельно целенаправленно. Вся задача сводится к передаче управления лишь одному внутреннему объекту — cEn, который и содержит обучаемые параметры внимания. Этот объект представляет собой ядро параметрического блока, на основе которого строится матрица корреляции. Он один несёт на себе всю ответственность за обучаемую часть модуля.

bool CNeuronAdaptSpatialNorm::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   return cEn.UpdateInputWeights();
  }

Полный код класса CNeuronAdaptSpatialNorm и всех его методов представлен во вложении для самостоятельного изучения.

SCNN Энкодер

После того, как мы построили объекты, отвечающие за выделение отдельных компонент временного ряда, следующим логическим шагом становится их интеграция в единую согласованную структуру — SCNN-Энкодер. На этом этапе предварительно сформированные блоки сшиваются в чётко определённую последовательность, обеспечивающую надёжную, устойчивую и в то же время гибкую обработку анализируемых данных.

Ключевая особенность SCNN-Энкодера заключается в его модульной архитектуре. В её основе — четыре параллельные ветви, каждая из которых отвечает за собственный масштаб анализа. Одна улавливает долгосрочные тренды, другая — сезонные закономерности, третья — краткосрочные флуктуации, а четвёртая адаптивно нормализует данные, усиливая взаимосвязи между отдельными признаками.

Все эти алгоритмы аккуратно реализуются в рамках специализированного объекта CNeuronSCNNEncoder. Его структура воплощает описанную логику и закладывает фундамент для формирования обобщённого представления последовательности — сжатого, осмысленного и пригодного для дальнейшего прогнозирования.

class CNeuronSCNNEncoder   :  public CNeuronTransposeOCL
  {
protected:
   CNeuronPeriodNorm       cLongNorm;
   CNeuronTransposeVRCOCL  cSeasonTransp;
   CNeuronPeriodNorm       cSeasonNorm;
   CNeuronTransposeVRCOCL  cUnSeasonTransp;
   CNeuronPeriodNorm       cShortNorm;
   CNeuronAdaptSpatialNorm cAdaptSpatNorm;
   CNeuronBaseOCL          cConcatenated;
   CNeuronSwiGLUOCL        cProjection;
   CNeuronTransposeOCL     cTranspose;
   CNeuronConvOCL          caFusion[2];
   CNeuronBaseOCL          cFusionOut;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)  override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL)  override;

public:
                     CNeuronSCNNEncoder(void) {};
                    ~CNeuronSCNNEncoder(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint units_count, uint variables, uint forecast,
                          uint season_period, uint short_period,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(const int file_handle) override;
   virtual bool      Load(const int file_handle) override;
   //---
   virtual int       Type(void) override const  {  return defNeuronGinAR; }
   virtual void      TrainMode(bool flag) override;
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
  };

В структуре нового класса мы наблюдаем целый ряд внутренних объектов, каждый из которых выполняет строго определённую функцию в составе Энкодера. С их назначением мы познакомимся чуть позже, по мере раскрытия логики алгоритма. Сейчас же стоит подчеркнуть важный архитектурный момент: все эти компоненты объявлены статически. Это означает, что память под них выделяется заранее, а их жизненный цикл строго соответствует жизненному циклу самого объекта CNeuronSCNNEncoder. Это решение позволяет обойтись без лишней обработки — конструктор и деструктор класса остаются пустыми.

Инициализация всех объявленных и унаследованных внутренних объектов реализована в методе Init, в параметрах которого мы получаем все константы, определяющие архитектуру объекта.

bool CNeuronSCNNEncoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                              uint units_count, uint variables, uint forecast,
                              uint season_period, uint short_period,
                              ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronTransposeOCL::Init(numOutputs, myIndex, open_cl, units_count + forecast, variables,
                                                                       optimization_type, batch))
      return false;
   SetActivationFunction(None);

Начинается всё с вызова базового одноименного метода родительского класса, где задаются ключевые параметры архитектуры. После успешной инициализации активируется нейтральная функция активации, исключающая внесение нелинейных искажений на этом этапе.

Далее последовательно создаются модули, отвечающие за предварительную обработку временного ряда. Сначала запускается блок нормализации долгосрочной компоненты.

   uint index = 0;
   if(!cLongNorm.Init(0, index, OpenCL, 1, units_count, variables, optimization, iBatch))
      return false;
   cLongNorm.SetActivationFunction(None);

Следующим важным этапом становится выделение сезонной компоненты. В оригинальной концепции авторов фреймворка SCNN этот шаг интерпретируется, как нормализация данных с шагом, соответствующим периоду сезонности. На первый взгляд может показаться, что для этого требуется некий специализированный модуль. Однако мы подошли к решению задачи более рационально, в духе классических принципов системной инженерии.

Мы разработали универсальный объект нормализации, предназначенный для обработки данных по фиксированным периодам. Сам по себе он не содержит информации о сезонной структуре — она появляется, как только мы меняем представление анализируемого массива. Стоит лишь транспонировать последовательность временных шагов на величину периода сезонности, как данные автоматически группируются в последовательности с нужным интервалом. Эти вновь сформированные последовательности идеально подходят под формат, который ожидает наш модуль нормализации по периодам.

Таким образом, при минимальных усилиях мы получаем мощный механизм выделения сезонной компоненты, не внося дополнительных изменений в структуру самого нормализующего объекта. Всё, что требуется — грамотно перестроить входные данные, а дальше уже работает проверенный и отлаженный алгоритм.

   index++;
   if(!cSeasonTransp.Init(0, index, OpenCL, variables, units_count / season_period, season_period,
                                                                            optimization, iBatch))
      return false;
   cSeasonTransp.SetActivationFunction(None);
   index++;
   if(!cSeasonNorm.Init(0, index, OpenCL, cSeasonTransp.GetCount(), season_period, variables,
                                                                       optimization, iBatch))
      return false;
   cSeasonNorm.SetActivationFunction(None);
   index++;
   if(!cUnSeasonTransp.Init(0, index, OpenCL, variables, season_period, cSeasonTransp.GetCount(),
                                                                           optimization, iBatch))
      return false;
   index++;

После выделения сезонной компоненты мы возвращаем данные в исходное представление путем обратного транспонирования и активируем блок краткосрочной нормализации.

   if(!cShortNorm.Init(0, index, OpenCL, units_count / short_period, short_period, variables, optimization, iBatch))
      return false;
   cSeasonNorm.SetActivationFunction(None);
   index++;
   if(!cAdaptSpatNorm.Init(0, index, OpenCL, units_count, variables, optimization, iBatch))
      return false;
   cAdaptSpatNorm.SetActivationFunction(None);

Затем — адаптивная пространственная нормализация, учитывающая взаимосвязи между переменными во входной последовательности.

После завершения подготовки данных из различных источников, создаётся модуль объединения, аккумулирующий выходы всех нормализующих блоков в единую матрицу признаков. Размер этого модуля вычисляется динамически, с учётом как основных выходов, так и статистических значений, сопровождающих каждый блок нормализации.

   index++;
   uint concatSize = units_count * variables;                                         //inputs
   concatSize += cLongNorm.Neurons() + cLongNorm.GetMeanSTDevs().Neurons();           // long term
   concatSize += cSeasonNorm.Neurons() + cSeasonNorm.GetMeanSTDevs().Neurons();       // seasons
   concatSize += cShortNorm.Neurons() + cShortNorm.GetMeanSTDevs().Neurons();         // short term
   concatSize += cAdaptSpatNorm.Neurons() + cAdaptSpatNorm.GetMeanSTDevs().Neurons(); // spatial
   if(!cConcatenated.Init(0, index, OpenCL, concatSize, optimization, iBatch))
      return false;
   cConcatenated.SetActivationFunction(None);

Следующим логическим элементом становится проекционный блок, позволяющий эффективно сжать и реструктурировать многомерное пространство признаков.

   index++;
   if(!cProjection.Init(0, index, OpenCL, concatSize / variables, concatSize / variables, 
                             units_count + forecast, 1, variables, optimization, iBatch))
      return false;

Его выход передаётся в транспонирующий модуль, осуществляющий преобразование данных между представлениями времени и признаков — в зависимости от требований последующей обработки.

   index++;
   if(!cTranspose.Init(0, index, OpenCL, variables, units_count + forecast, optimization, iBatch))
      return false;
   index++;
   if(!caFusion[0].Init(0, index, OpenCL, variables, variables, variables, units_count + forecast,
                                                                            optimization, iBatch))
      return false;
   caFusion[0].SetActivationFunction(TANH);
   index++;
   if(!caFusion[1].Init(0, index, OpenCL, variables, variables, variables, units_count + forecast,
                                                                            optimization, iBatch))
      return false;
   caFusion[1].SetActivationFunction(SIGMOID);
   index++;
   if(!cFusionOut.Init(0, index, OpenCL, caFusion[0].Neurons(), optimization, iBatch))
      return false;
//---
   return true;
  }

Заключительный этап включает два параллельных сверточных слоя, реализующих различные механизмы фильтрации сигнала. Один из них использует гиперболический тангенс, придавая выходу плавную насыщенность, другой — сигмоиду, обеспечивая логистическое ограничение значений. Их результаты сходятся в модуле итоговой свертки, который завершает построение архитектуры.

Мы проделали значительную работу, и объём статьи заметно вырос. Впереди нас ждёт рассмотрение непростого алгоритма прямого и обратного проходов нашего Энкодера — этап, требующий особого внимания и сосредоточенности. Поэтому логично сделать небольшой перерыв, чтобы было время усвоить и осмыслить уже изложенный материал. В следующей статье мы продолжим работу, доведём её до логического завершения и проведём проверку эффективности реализованных решений на реальных исторических данных.

Заключение

В данной статье мы подробно рассмотрели следующий этап реализации фреймворка SCNN — построение и интеграцию объекта адаптивной пространственной нормализации, а также объединение основных компонент в единый Энкодер. Мы показали, как грамотно выстроенная архитектура и использование современных вычислительных технологий OpenCL позволяют эффективно выделять структурные составляющие временных рядов и обеспечивать качественную подготовку данных для дальнейшего прогнозирования.

В следующей статье мы продолжим исследование, сфокусировавшись на тестировании и практической оценке работы фреймворка SCNN на реальных данных, что позволит оценить прикладную значимость реализованных методов и их эффективность в задачах финансового прогнозирования.

Ссылки

Программы, используемые в статье

#	Имя	Тип	Описание
1	Study.mq5	Советник	Советник офлайн обучения моделей
2	StudyOnline.mq5	Советник	Советник онлайн обучения моделей
3	Test.mq5	Советник	Советник для тестирования модели
4	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
5	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
6	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы

Прикрепленные файлы |

Загрузить ZIP

MQL5.zip (2931.75 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Отправка сообщений из MQL5 в Discord, создание бота Discord-MetaTrader 5

Подобно Telegram, Discord способен получать информацию и сообщения в формате JSON, используя свои коммуникационные API. В настоящей статье мы рассмотрим, как можно использовать API Discord для отправки торговых сигналов и обновлений из MetaTrader 5 в ваше торговое сообщество Discord.

Торгуем опционы без опционов (Часть 2): Использование в реальной торговле

В статье рассматриваются простые опционные стратегии и их реализация на MQL5. Пишем базовый эксперт, который будет модернизироваться и усложняться.

Особенности написания экспертов

Написание и тестирование экспертов в торговой системе MetaTrader 4.

Передовые алгоритмы исполнения ордеров на MQL5: TWAP, VWAP и ордера Iceberg

Фреймворк MQL5, предоставляющий розничным трейдерам алгоритмы исполнения институционального уровня (TWAP, VWAP, Iceberg) с помощью унифицированного менеджера исполнения и анализатора эффективности для более плавного и точного разделения ордеров и аналитики.