Нейросети в трейдинге: Сквозная многомерная модель прогнозирования временных рядов (Основные компоненты)

MetaTrader 5 — Торговые системы | 18 июля 2025, 13:51

450

Dmitriy Gizlyk

Введение

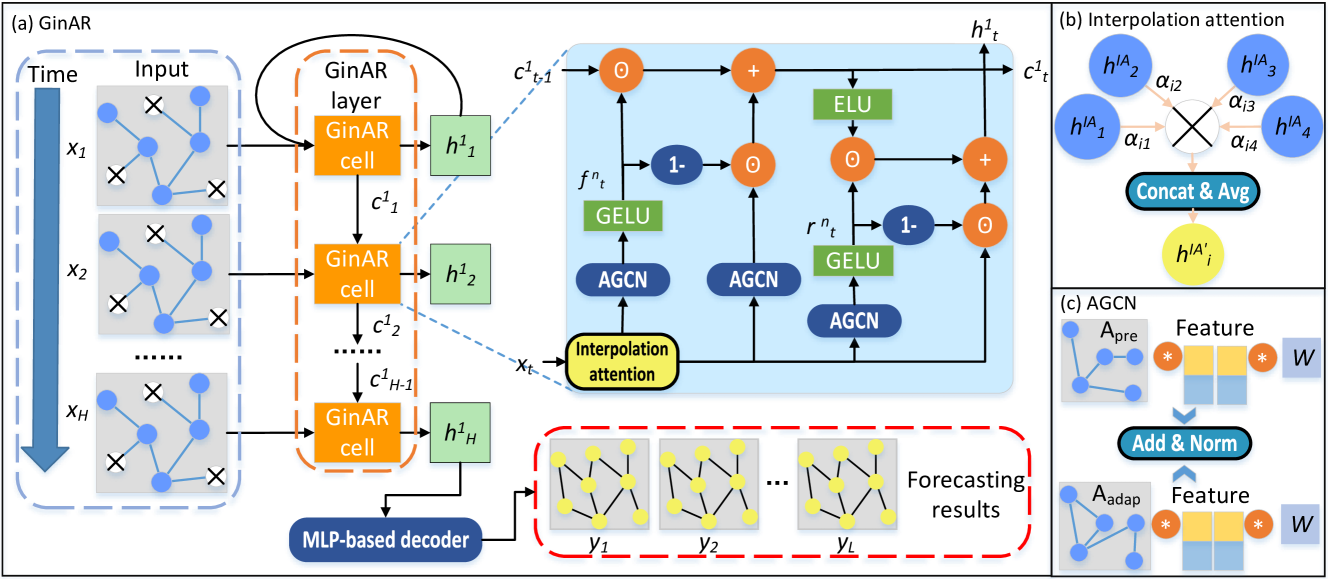
В предыдущей статье мы подробно рассмотрели фреймворк GinAR — современную архитектуру для работы с временными рядами, сочетающую преимущества графовых нейросетей с возможностью обучения на асинхронных, неполных и гетерогенных данных. Основная идея подхода заключается в том, чтобы интерпретировать временной ряд не как плоскую последовательность наблюдений, а как графовую структуру, где отдельные переменные или временные точки могут быть связаны между собой произвольными, обучаемыми взаимозависимостями. Такой взгляд особенно актуален для задач финансового моделирования, где данные нередко бывают нерегулярными, с пропусками и сложными латентными связями.

GinAR был предложен как универсальный инструмент для решения подобных задач. Его модульная структура включает в себя несколько ключевых компонентов:

механизм Interpolation Attention, позволяющий восстанавливать пропущенные значения путём агрегирования информации от наблюдаемых переменных;
графовые слои с индивидуальными обучаемыми весами;
адаптивные функции нормализации, обеспечивающие устойчивость модели к выбросам и нестабильности масштаба.

Кроме того, в фреймворке реализован особый способ обработки отсутствующих значений через построение условно-зависимых весовых матриц, позволяющий выстраивать осмысленную реконструкцию на основе скрытых взаимосвязей в данных.

Центральное место в архитектуре занимает механизм Interpolation Attention — это не классическое Self-Attention ядро, а полноценный адаптивный модуль, способный учитывать как глобальные зависимости между переменными, так и локальный контекст наблюдений. Практически это означает, что модель способна, например, прогнозировать значение финансового индикатора, даже в случае отсутствия его последних измерений, используя при этом структуру соседних индикаторов и общую рыночную картину. Такой подход критически важен в реальных условиях, где данные часто приходят с задержкой, неравномерно или с большими пропусками.

Особенность GinAR — в способности динамически перестраивать графовую структуру во время обучения. В отличие от большинства моделей на графах, где структура фиксирована заранее, здесь она формируется в процессе обучения. Это позволяет учитывать изменение рыночных условий, корреляций и скрытых факторов. Модель самостоятельно решает, какие переменные следует связать между собой, какие — ослабить, а какие — выделить в качестве ключевых для текущего контекста. Таким образом, создаётся гибкая архитектура, способная адаптироваться к рыночным режимам и динамике.

Авторская визуализация фреймворка GinAR представлена ниже.

Авторская визуализация фреймворка GinAR

В практической части предыдущей статьи мы проделали значительный объём работы, заложив основу для вычислений на стороне OpenCL-программы. Были реализованы все ключевые функции — от локальных редукций и вычисления SoftMax до прямого и обратного прохода в модуле Interpolation Attention. Особое внимание было уделено корректной обработке локальной памяти, синхронизации потоков и числовой устойчивости, что особенно важно при работе с неполными временными рядами в условиях параллельных вычислений.

Эта подготовка открывает нам путь к следующему этапу — интеграции ядра модели в основную программу. Именно здесь алгоритм начнёт оживать: данные будут поступать из торговой среды, обрабатываться с помощью OpenCL-устройств, проходить через модель и возвращаться в виде прогнозов и торговых решений. Такой мост между высокоуровневой логикой и низкоуровневыми ускоренными вычислениями является фундаментальной частью всей нашей реализации архитектуры GinAR.

Interpolation Attention

Сегодня нам предстоит выполнить большой объём практической работы, связанной с реализацией ключевых компонентов фреймворка GinAR. Поэтому долго задерживаться на теории не будем — переходим сразу к делу.

Первым шагом станет создание важнейшего модуля — Interpolation Attention, который мы оформим в виде отдельного класса CNeuronInterpolationAttention. Этот класс наследуется от базового объекта нейронных слоев в нашей библиотеке CNeuronBaseOCL и реализует всю требуемую логику, позволяющую эффективно использовать подготовленные ранее OpenCL-ядра в полном цикле прямого и обратного проходов.

class CNeuronInterpolationAttention :  public CNeuronBaseOCL
  {
protected:
   //---
   uint                 iCount;
   uint                 iDimension;
   //---
   CParams              cW;
   CParams              cA;
   CParams              cGL;
   //---
   CNeuronBaseOCL       cH;
   CNeuronBaseOCL       cAdj;
   CNeuronBaseOCL       cAttention;
   //---
   virtual bool      InterpolationAttention(CNeuronBaseOCL *NeuronOCL);
   virtual bool      InterpolationAttentionGrad(CNeuronBaseOCL *NeuronOCL);
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronInterpolationAttention(void) { activation = None; }
                    ~CNeuronInterpolationAttention(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint units_count, uint dimension,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(const int file_handle) override;
   virtual bool      Load(const int file_handle) override;
   //---
   virtual int       Type(void) override const {  return defNeuronInterpolationAttention; }
   virtual void      TrainMode(bool flag) override;
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetActivationFunction(ENUM_ACTIVATION value) override {};
  };

Класс содержит набор внутренних переменных, среди которых iCount и iDimension отвечают за количество элементов в тензоре исходных данных, а объекты cW, cA и cGL представляют собой параметры обучаемых матриц. Отдельно определены промежуточные объекты для хранения промежуточных результатов скрытых представлений, графа смежности и весов внимания.

Основная вычислительная логика инкапсулирована в методах InterpolationAttention и InterpolationAttentionGrad, отвечающих за прямой и обратный проход модели соответственно. В них осуществляется процесс подготовки и постановки в очередь выполнения соответствующих кернелов OpenCL-программы, которые нами были созданы в рамках практической работы предыдущей статьи. В них используется уже знакомый нам алгоритм, поэтому в рамках данной статьи не будем на них останавливаться. Полный код данных методов представлен во вложении для самостоятельного изучения.

Все внутренние объекты класса CNeuronInterpolationAttention объявлены статически, что упрощает управление жизненным циклом экземпляра. Благодаря этому, можно оставить конструктор и деструктор класса пустыми — они не требуют явной инициализации или освобождения ресурсов. Вся необходимая настройка, включая инициализацию собственных членов и унаследованных компонентов родительского класса, выполняется централизованно в методе Init. Это обеспечивает чистую и предсказуемую структуру инициализации, позволяя избежать дублирования кода и повысить надёжность при повторном использовании модуля в различных конфигурациях модели.

bool CNeuronInterpolationAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                         uint units_count, uint dimension,
                                         ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, units_count * dimension,
                                                        optimization_type, batch))
      return false;

В теле метода мы сначала осуществляем вызов одноименного метода родительского класса CNeuronBaseOCL. При этом размер слоя пересчитывается с учётом пространственной размерности исходного сигнала.

Далее сохраняются ключевые параметры модели (количество переменных и размерность представления) для использования в вычислениях и управлении внутренними буферами. Эти параметры определяют размер всех остальных векторов и матриц, которые будут использоваться в ходе прямого и обратного проходов.

iCount = units_count;
iDimension = dimension;

Следующий блок кода — инициализация параметров и промежуточных тензоров, задействованных в механизме Interpolation Attention. Сначала создаются обучаемые веса cW, которые представляют индивидуальную матрицу взаимодействия между переменными. Это квадратная матрица dimension × dimension.

int index = 0;
if(!cW.Init(0, index, OpenCL, iDimension * iDimension, optimization, iBatch))
   return false;

Затем инициализируются параметры cA, которые отвечают за агрегацию внимания между узлами.

index++;
if(!cA.Init(0, index, OpenCL, 2 * iDimension, optimization, iBatch))
   return false;
index++;
if(!cGL.Init(0, index, OpenCL, iDimension * iDimension, optimization, iBatch))
   return false;

После этого создаётся объект cGL, представляющий латентные векторы переменных. Он тоже имеет размерность dimension × dimension.

После инициализации всех обучаемых параметров, начинается конфигурация вспомогательных объектов, отвечающих за хранение промежуточных результатов. Буфер cH представляет матрицу линейных преобразований исходного сигнала, полученную путём перемножения входа с весами. Её размерность — units_count × dimension.

index++;
if(!cH.Init(0, index, OpenCL, iCount * iDimension, optimization, iBatch))
   return false;

Далее следует объект cAdj, в котором сохраняются значения скорректированной корреляции между переменными.

   index++;
   if(!cAdj.Init(0, index, OpenCL, iDimension * iDimension, optimization, iBatch))
      return false;
   index++;
   if(!cAttention.Init(0, index, OpenCL, iDimension * iDimension, optimization, iBatch))
      return false;
//---
   return true;
  }

И наконец, cAttention — тензор финальных значений внимания, полученных после нормализации через SoftMax.

Каждая инициализация сопровождается проверкой на успешность. В случае сбоя на любом этапе, метод немедленно возвращает false, обеспечивая надёжную защиту от ошибок в конфигурации.

Если все объекты успешно сконфигурированы и размещены в памяти OpenCL-устройства, метод завершает работу, возвращая true. Это означает, что слой полностью готов к запуску и может быть использован в составе модели.

После завершения работы по инициализации объекта, переходим к организации процесса прямого прохода, который реализуем в методе feedForward. Его задача — корректно подготовить все исходные данные и запустить основное вычисление с использованием OpenCL-кернела, разработанного ранее. Алгоритм достаточно компактный, но включает в себя несколько ключевых этапов, каждый из которых выполняет важную функцию в общей схеме работы слоя.

bool CNeuronInterpolationAttention::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(bTrain)
     {
      if(!cW.FeedForward())
         return false;
      if(!cA.FeedForward())
         return false;
      if(!cGL.FeedForward())
         return false;
     }
   if(!InterpolationAttention(NeuronOCL))
      return false;
//---
   return true;
  }

Прежде всего метод проверяет, активен ли флаг bTrain, означающий, что слой находится в режиме обучения. Это критично, поскольку обучаемые параметры модели в таком случае должны быть предварительно прогнаны через собственные методы FeedForward. Этот вызов необходим, чтобы актуализировать их значения и обеспечить их участие в текущем вычислительном цикле. Все три вызова сопровождаются проверкой успешности и, при малейшем сбое, метод немедленно прекращает выполнение, возвращая false. Это позволяет избежать ситуации, при которой неинициализированные или некорректные параметры попадут в дальнейшие вычисления.

После завершения всех подготовительных шагов выполняется вызов основного метода InterpolationAttention. Именно он инициализирует запуск OpenCL-кернела, ответственного за вычисление внимания, агрегацию значений и формирование выходного представления слоя.

Метод завершает свою работу, возвращая логический результат выполнения операций вызывающей программе.

Метод calcInputGradients реализован в предельно лаконичном виде, поскольку вся логика обратного распространения ошибки уже была вынесена в соответствующий OpenCL-кернел. Здесь мы просто вызываем функцию-обёртку InterpolationAttentionGrad, отвечающую за запуск кернела и передачу необходимых буферов. И возвращаем логический результат выполнения операций вызывающей программе.

bool CNeuronInterpolationAttention::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!InterpolationAttentionGrad(NeuronOCL))
      return false;
//---
   return true;
  }

Такая реализация полностью сохраняет общую структуру работы нейронных слоёв, позволяя использовать данный модуль наравне с другими типами слоёв, без каких-либо изменений в логике обучения. Это подчёркивает архитектурную гибкость системы и делает интеграцию новых решений максимально простой и безопасной.

Обновление обучаемых параметров в модуле реализовано максимально компактно и логично. Все веса, участвующие в расчётах — это внутренние объекты класса (cW, cA, cGL), каждый из которых инкапсулирует собственный алгоритм обновления. Метод updateInputWeights лишь вызывает для них соответствующие функции, обеспечивая модульность и чистоту архитектуры.

bool CNeuronInterpolationAttention::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cW.UpdateInputWeights())
      return false;
   if(!cA.UpdateInputWeights())
      return false;
   if(!cGL.UpdateInputWeights() ||
      !Normilize(cGL.getWeightsParams(), 2 * iDimension))
      return false;
//---
   return true;
  }

Особое внимание уделено тензору cGL, который после обновления дополнительно нормализуется при помощи функции Normilize. Это необходимо, поскольку cGL содержит веса корреляционных связей между переменными, и стабильность этих коэффициентов напрямую влияет на устойчивость всего модуля внимания. Нормализация позволяет сгладить возможные выбросы и сохранить интерпретируемость весов. Таким образом, данный метод полностью завершает цикл обучения, не требуя дополнительных вмешательств или настроек.

С полным кодом класса CNeuronInterpolationAttention, а также реализацией всех его методов можно ознакомиться во вложении. Мы сознательно не перегружаем статью техническими деталями, чтобы сохранить живость изложения, однако рекомендуем изучить исходный код, для полного понимания логики работы модуля и его интеграции в общий фреймворк GinAR.

AGNC

Следующим логическим шагом в построении фреймворка GinAR является реализация механизма адаптивной графовой свёртки (AGCN). Это важнейший элемент фреймворка, позволяющий учитывать сложные взаимосвязи между временными рядами, представляемыми в виде узлов графа. В отличие от традиционных подходов, где структура графа задаётся заранее и остаётся неизменной в ходе обучения, адаптивная свёртка позволяет модели самостоятельно формировать и изменять топологию связей в зависимости от текущего состояния данных. Такая гибкость критически важна при работе с динамичными финансовыми временными рядами, структура которых подвержена постоянным колебаниям, скрытым взаимосвязям и внешним возмущениям.

Для реализации этой идеи был разработан отдельный модуль, представленный в виде класса CNeuronAGCN. Этот класс наследуется от базового полносвязного слоя CNeuronBaseOCL и служит инкапсуляцией всей логики, необходимой для выполнения адаптивной свёртки с использованием OpenCL-ускорения. Его внутренняя структура выстроена так, чтобы на каждом этапе обработки обеспечивалась максимальная эффективность и точность вычислений, включая выделение признаков, формирование матрицы связей, нормализацию, агрегацию и обучение весов графа.

Особенностью данного модуля является то, что в процессе обработки информации он не опирается на фиксированную матрицу смежности, а вычисляет её в режиме реального времени. Для этого исходные данные проходят через последовательность трансформаций, в результате которых формируется латентное представление каждого узла. Эти представления используются для вычисления сходства между узлами, на основе которого и строится матрица адаптивных связей. Таким образом, модель как бы смотрит на каждый временной ряд и сама решает, с какими другими рядами его стоит связать — и с какой интенсивностью. В итоге получаем гибкий механизм внимания, где каждый узел способен адаптировать своё поведение в зависимости от контекста.

Структура нового класса представлена ниже.

class CNeuronAGCN    :  public CNeuronBaseOCL
  {
protected:
   CParams              cEa;
   CNeuronSwiGLUOCL     cWx;
   CNeuronSwiGLUOCL     cWe;
   CNeuronBaseOCL       cWconcat_ex;
   CNeuronConvOCL       cEn;
   CNeuronTransposeOCL  cEnT;
   CNeuronBaseOCL       cEnEnT;
   CNeuronSoftMaxOCL    cAadapt;
   CNeuronBaseOCL       cAadaptX;
   CNeuronBaseOCL       cApreX;
   CNeuronSwiGLUOCL     cWadapt;
   CNeuronSwiGLUOCL     cWpre;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *second) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL,
                                        CBufferFloat *SecondInput,
                                        CBufferFloat *SecondGradient,
                                        ENUM_ACTIVATION SecondActivation = None) override;

public:
                     CNeuronAGCN(void) {activation = None;}
                    ~CNeuronAGCN(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint units_count, uint dimension,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(const int file_handle) override;
   virtual bool      Load(const int file_handle) override;
   //---
   virtual int       Type(void) override const  {  return defNeuronAGCN; }
   virtual void      TrainMode(bool flag) override;
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   //---
   virtual uint      GetWindow(void) const      { return cWx.GetWindow(); }
   virtual uint      GetUnits(void) const       { return cWx.GetUnits(); }
   virtual void      SetActivationFunction(ENUM_ACTIVATION value) override {};
  };

Вся вычислительная цепочка организована внутри одного объекта, но включает в себя множество вспомогательных слоёв и операций. Логика разбита на этапы, с которыми мы познакомимся в процессе реализации методов класса. Полученные на выходе признаки можно интерпретировать как результат согласованной фильтрации по адаптированному графу — с учётом содержательной информации и топологических соотношений между временными рядами.

Как и в случае с предыдущим слоем, все внутренние компоненты класса CNeuronAGCN были объявлены статически. Такой подход позволяет нам оставить пустыми конструктор и деструктор класса, сосредоточив всю логику инициализации в одном методе — Init. Это обеспечивает компактность реализации, а также облегчает контроль за жизненным циклом объектов внутри слоя.

bool CNeuronAGCN::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                       uint units_count, uint dimension,
                       ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl,
                            units_count * dimension, optimization_type, batch))
      return false;

Инициализация начинается с вызова одноименного метода родительского класса, где выполняется первичная настройка интерфейсов и общих параметров слоя. После этого пошагово настраиваются все ключевые компоненты адаптивной свёртки.

На первом этапе создаётся объект cEa, который будет использоваться для кодирования дополнительной информации о структуре данных.

//---
   int index = 0;
   if(!cEa.Init(0, index, OpenCL, Neurons(), optimization, iBatch))
      return false;
   cEa.SetActivationFunction(None);

Далее инициализируются два важных слоя — cWx и cWe, отвечающие за извлечение признаков из исходных данных и ранее выученной структуры временного ряда. Оба слоя реализованы на основе механизма SwiGLU и обучаются параллельно.

index++;
if(!cWx.Init(0, index, OpenCL, dimension, dimension, dimension, units_count,
                                                   1, optimization, iBatch))
   return false;
index++;
if(!cWe.Init(0, index, OpenCL, dimension, dimension, dimension, units_count,
                                                   1, optimization, iBatch))
   return false;

За ними следует буфер cWconcat_ex, обеспечивающий объединение представлений в латентном пространстве.

index++;
if(!cWconcat_ex.Init(0, index, OpenCL, 2 * Neurons(), optimization, iBatch))
   return false;
cWconcat_ex.SetActivationFunction(None);

Следующим элементом инициализации становится слой cEn, выполняющий линейное преобразование объединённых признаков. Он дополняется транспонирующим модулем cEnT, который подготавливает данные для формирования предварительной матрицы внимания.

index++;
if(!cEn.Init(0, index, OpenCL, 2 * dimension, 2 * dimension, dimension, units_count,
                                                           1, optimization, iBatch))
   return false;
cEn.SetActivationFunction(None);
index++;
if(!cEnT.Init(0, index, OpenCL, units_count, dimension, optimization, iBatch))
   return false;
index++;
if(!cEnEnT.Init(0, index, OpenCL, units_count * units_count, optimization, iBatch))
   return false;
cEnEnT.SetActivationFunction(GELU);

После этапа транспонирования подготовленные данные направляются в операцию матричного умножения, где происходит скалярное свёртывание исходного представления с его транспонированной версией. В результате формируется симметричная матрица взаимосвязей, которая помещается в объект cEnEnT. Именно в этом блоке выполняется активация полученных значений с использованием функции GELU — она позволяет мягко подавлять отрицательные корреляции, не обнуляя их полностью, но одновременно снижая их вклад в итоговое представление.

Такой подход способствует выделению наиболее значимых паттернов и латентных связей между узлами графа, что критически важно при формировании адаптивной матрицы внимания. В конечном итоге, благодаря этой операции, модель получает возможность улавливать более глубокие структурные закономерности внутри графа и корректно взвешивать межузловые взаимодействия.

Затем наступает ключевой этап — нормализация полученных значений. Для этого используется функция SoftMax, применяемая внутри объекта cAadapt. Эта операция преобразует необработанные весовые коэффициенты в вероятностное распределение, где каждой связи между узлами графа присваивается определённая степень значимости. Таким образом, слабые и шумовые зависимости подавляются, а сильные и информативные — усиливаются. В результате получается полноценная адаптивная матрица внимания, отражающая индивидуальные паттерны взаимодействия между компонентами входного сигнала.

index++;
if(!cAadapt.Init(0, index, OpenCL, units_count * units_count, optimization, iBatch))
   return false;
cAadapt.SetHeads(units_count);

Следующей логической операцией становится применение адаптивных весов к исходным данным. Этот этап реализуется путём взвешивания входных признаков на соответствующие коэффициенты внимания. Результат сохраняется в буфере cAadaptX, который представляет собой уже обновлённое, контекстно обогащённое представление входного сигнала. По сути, это — перенормированная проекция исходной информации с учётом выявленных взаимосвязей между отдельными узлами графа.

index++;
if(!cAadaptX.Init(0, index, OpenCL, Neurons(), optimization, iBatch))
   return false;
cAadaptX.SetActivationFunction(None);
index++;
if(!cApreX.Init(0, index, OpenCL, Neurons(), optimization, iBatch))
   return false;
cApreX.SetActivationFunction(None);

Дополнительным этапом обработки становится адаптация исходных данных с учётом заранее определённой структуры графа. Этот шаг направлен на усиление влияния известных, априорных связей между узлами, полученных вне рамок обучающей модели — например, на основе фундаментальных связей, топологии или экспертных правил. Механизм здесь аналогичен предыдущему: к исходному тензору применяются веса, но уже не из адаптивной матрицы внимания, а из внешней матрицы коэффициентов. Результат сохраняется в буфере cApreX. Таким образом, модель получает сразу два независимых канала информации — один основан на самообучении и выявленных закономерностях, второй — на структурной априорной информации. Их объединение позволяет достичь большего баланса между гибкостью и устойчивостью модели.

Наконец, в заключительной части инициализации создаются два слоя свёртки: cWadapt и cWpre. Оба используют архитектуру SwiGLU, выступая в роли фильтров, адаптирующих признаки к структуре сформированной матрицы связей.

   index++;
   if(!cWadapt.Init(0, index, OpenCL, dimension, dimension, dimension, units_count,
                                                          1, optimization, iBatch))
      return false;
   cWadapt.SetActivationFunction(None);
   index++;
   if(!cWpre.Init(0, index, OpenCL, dimension, dimension, dimension, units_count, 1,
                                                              optimization, iBatch))
      return false;
   cWpre.SetActivationFunction(None);
   SetActivationFunction(None);
//---
   return true;
  }

По завершении всех этих этапов принудительно отключаем функцию активации слоя, так как нелинейности применяются внутри внутренних блоков и нет необходимости в их дублировании на выходе.

Таким образом, весь метод Init представляет собой тщательно организованную последовательность шагов, в ходе которой создаются и настраиваются все элементы адаптивной свёртки. Каждый компонент отвечает за определённую часть вычислений и вписывается в общую архитектуру слоя, создавая основу для дальнейшей работы модели.

Следующий этап нашей работы — метод feedForward, который реализует полный цикл прямого прохода адаптивной графовой свёртки с учётом как обучаемых, так и внешне заданных структурных связей. Алгоритм достаточно насыщенный, поэтому разберём его поэтапно, с акцентом на смысловую логику каждого блока.

bool CNeuronAGCN::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
   if(!SecondInput || SecondInput.Total() < cAadapt.Neurons())
      return false;

Перед началом выполнения алгоритма производится обязательная проверка корректности входных данных: если матрица предопределенных коэффициентов корреляции SecondInput отсутствует, или её размер недостаточен для выполнения матричных операций — выполнение немедленно прерывается.

Затем, если модель находится в режиме обучения, запускается цикл подготовки параметров для ветки, отвечающей за адаптивный контекст узлов. Сначала производится прямой проход по объекту cEa, который содержит обучаемые параметры для вычисления эмбеддингов рёбер. Полученный результат передаётся в cWe, где происходит формирование матрицы весов внешнего взаимодействия, отражающих контекст связей между узлами на текущем шаге обучения.

if(bTrain)
  {
   if(!cEa.FeedForward())
      return false;
   if(!cWe.FeedForward(cEa.AsObject()))
      return false;
  }

Параллельно с этим активируется главная ветка — та, что работает с основной последовательностью признаков. В ней вызывается метод прямого прохода cWx, формируя представление текущего состояния узлов.

if(!cWx.FeedForward(NeuronOCL))
   return false;
if(!Concat(cWx.getOutput(), cWe.getOutput(), cWconcat_ex.getOutput(), 
             cWx.GetWindowOut(), cWe.GetWindowOut(), cWx.GetUnits()))
   return false;

После этого, оба вектора выходов (cWx и cWe) конкатенируются в разрезе отдельных элементов последовательности, что позволяет модели учитывать структурную и контекстную информацию при последующих операциях. Полученный результат используется в cEn, который реализует линейную свёртку, уменьшающую размерность и усиливающую значимые признаки.

if(!cEn.FeedForward(cWconcat_ex.AsObject()))
   return false;
if(!cEnT.FeedForward(cEn.AsObject()))
   return false;
if(!MatMul(cEn.getOutput(), cEnT.getOutput(), cEnEnT.getOutput(),
             cEnT.GetCount(), cEnT.GetWindow(), cEnT.GetCount()))
   return false;
if(cEnEnT.Activation() != None)
   if(!Activation(cEnEnT.getOutput(), cEnEnT.getOutput(), cEnEnT.Activation()))
      return false;

Далее происходит ключевая операция — транспонирование полученной матрицы и перемножение её с исходной, что позволяет сформировать симметричную корреляционную матрицу в объекте cEnEnT. Если к этому объекту применена функция активации (в нашем случае — GELU), происходит её вызов, смягчающий влияние шумов и отрицательных корреляций.

После этого полученная матрица передаётся в объект cAadapt, где применяется механизм SoftMax с использованием многоголовой структуры внимания. Он нормализует веса по строкам и возвращает матрицу внимания, адаптированную к текущей структуре данных. Для усиления диагональных связей вызывается функция IdentSum, добавляющая единичную диагональную матрицу к результату, что обеспечивает устойчивость графа к разреженным входам.

if(!cAadapt.FeedForward(cEnEnT.AsObject()))
   return false;
if(!IdentSum(cAadapt.getOutput(), cAadapt.getOutput(), cAadapt.Heads()))
   return false;

Далее модель рассчитывает два параллельных потока умножения матриц. Первый поток работает с внешними данными SecondInput, перемножая их с текущими выходами нейронного слоя — результат сохраняется в буфере cApreX. Второй поток аналогично работает с матрицей внимания cAadapt и текущими выходами, сохраняя результат в cAadaptX.

if(!MatMul(SecondInput, NeuronOCL.getOutput(), cApreX.getOutput(),
           cWpre.GetUnits(), cWpre.GetUnits(), cWpre.GetWindow()))
   return false;
if(!MatMul(cAadapt.getOutput(), NeuronOCL.getOutput(), cAadaptX.getOutput(),
           cWadapt.GetUnits(), cWadapt.GetUnits(), cWadapt.GetWindow()))
   return false;

Финальный этап — пропуск обоих потоков через обучаемые свёрточные блоки cWpre и cWadapt. Это позволяет модели уточнить полученные данные с точки зрения локальных признаков.

   if(!cWpre.FeedForward(cApreX.AsObject()))
      return false;
   if(!cWadapt.FeedForward(cAadaptX.AsObject()))
      return false;
   if(!SumAndNormilize(cWadapt.getOutput(), cWpre.getOutput(), Output, cWadapt.GetWindowOut(), true))
      return false;
//---
   return true;
  }

После этого вызывается функция SumAndNormilize, объединяющая оба потока и приводящая результат к требуемому виду на выходе слоя.

Таким образом, метод реализует сразу несколько мощных механизмов: адаптивное внимание, извлечение признаков, структурную интеграцию и свёрточное преобразование. Всё это превращает модуль в полноценный блок графовой обработки, способный учитывать и внутренние зависимости между узлами, и внешние ограничения структуры.

После завершения прямого прохода в адаптивной графовой свёртке (AGCN) наступает один из наиболее ответственных этапов — распространение градиентов ошибки от выхода слоя к его обучаемым компонентам. В рамках этого процесса реализуется обратное распространение (backpropagation), которое позволяет точно определить вклад каждого объекта в итоговый результат и скорректировать параметры, минимизируя ошибку. Весь алгоритм организован внутри метода calcInputGradients.

bool CNeuronAGCN::calcInputGradients(CNeuronBaseOCL *NeuronOCL,
                                     CBufferFloat *SecondInput,
                                     CBufferFloat *SecondGradient,
                                     ENUM_ACTIVATION SecondActivation = -1)
  {
   if(!NeuronOCL || !SecondInput || !SecondGradient ||
      SecondInput.Total() < cAadapt.Neurons() ||
      SecondGradient.Total() < cAadapt.Neurons())
      return false;

На первом этапе происходит стандартная проверка валидности входных данных: если полученные указатели не инициализированы, или размер входных буферов недостаточен для выполнения матричных операций — выполнение метода останавливается. Далее начинается фактическое распределение ошибок.

Обратное распространение в блоке AGCN начинается с самого конца, а именно с выхода слоя, где уже сформирован итоговый результат. В нашем случае — это сумма выходов двух ключевых компонент: cWadapt и cWpre. Именно они, напомню, участвуют в построении финального представления, обобщающего как внимание, так и статическую структуру графа.

Так как выход блока является обычной суммой двух тензоров, то и градиент ошибки, полученный от последующего слоя, необходимо передать в равной степени обоим модулям — без каких-либо дополнительных весовых коэффициентов. Однако перед тем, как запустить вычисление градиентов по внутренним связям каждого из модулей, мы обязаны скорректировать этот градиент с учётом применённых в прямом проходе функций активации. Для этого вызывается метод DeActivation — по сути, он умножает полученный градиент на производную функции активации, применённой к выходу cWadapt и cWpre. Это ключевой шаг, без которого обратное распространение через нелинейные преобразования будет некорректным.

if(!DeActivation(cWadapt.getOutput(), cWadapt.getGradient(), Gradient, cWadapt.Activation()))
   return false;
if(!DeActivation(cWpre.getOutput(), cWpre.getGradient(), Gradient, cWpre.Activation()))
   return false;

После этого ошибка распределяется по их входам: вызываются методы CalcHiddenGradients для объектов cAadaptX и cApreX, через которые проходили потоки, сформированные с учётом матриц адаптивных и предопределенных связей между узлами соответственно.

if(!cApreX.CalcHiddenGradients(cWpre.AsObject()))
   return false;
if(!cAadaptX.CalcHiddenGradients(cWadapt.AsObject()))
   return false;

Далее, с помощью MatMulGrad выполняется обратное распространение через операцию умножения: вычисляется вклад каждой части в итоговую ошибку. В случае использования функции активации, осуществляется её обратная трансформация с помощью DeActivation, что позволяет восстановить истинную ошибку до её нормализации.

   if(!MatMulGrad(SecondInput, SecondGradient,
                  NeuronOCL.getOutput(), NeuronOCL.getGradient(),
                  cApreX.getGradient(), cWpre.GetUnits(),
                  cWpre.GetUnits(), cWpre.GetWindow()))
      return false;
   if(SecondActivation != None)
      if(!DeActivation(SecondInput, SecondGradient,
                       SecondGradient, SecondActivation))
         return false;
//---
   if(!MatMulGrad(cAadapt.getOutput(), cAadapt.getGradient(),
                  NeuronOCL.getOutput(), PrevOutput,
                  cAadaptX.getGradient(),  cWadapt.GetUnits(),
                  cWadapt.GetUnits(), cWadapt.GetWindow()))
      return false;
   if(!SumAndNormilize(NeuronOCL.getGradient(), PrevOutput,
                       PrevOutput, cWx.GetWindow(), false))
      return false;
   if(NeuronOCL.Activation() != None)
      if(!DeActivation(NeuronOCL.getOutput(), PrevOutput,
                       PrevOutput, NeuronOCL.Activation()))
         return false;

Обратите внимание, что в обеих операциях матричного умножения при прямом проходе использовались исходные данные основного информационного потока. Следовательно, нам предстоит собрать градиент ошибки по обеим магистралям. Для накопления значений используем временный буфер PrevOutput. Если NeuronOCL использует какую-либо функцию активации, то её производная применяется для корректного пересчёта градиента с учётом нелинейности.

Следующий ключевой этап — обратное распространение через корреляционную матрицу cEnEnT, полученную ранее на шаге прямого прохода. Сначала происходит расчёт скрытых градиентов, затем — деактивация на выходе, если использовалась функция GELU.

if(!cEnEnT.CalcHiddenGradients(cAadapt.AsObject()))
   return false;
if(cEnEnT.Activation() != None)
   if(!DeActivation(cEnEnT.getOutput(), cEnEnT.getGradient(),
                    cEnEnT.getGradient(), cEnEnT.Activation()))
      return false;

После этого вызывается MatMulGrad, реализующая обратное распространение градиента через операцию умножения признаков и их транспонированной копии.

if(!MatMulGrad(cEn.getOutput(), cEn.getPrevOutput(),
               cEnT.getOutput(), cEnT.getGradient(),
               cEnEnT.getGradient(), cEnT.GetCount(),
               cEnT.GetWindow(), cEnT.GetCount()))
   return false;

Дополнительно транспонированные ошибки передаются в слой cEn, где они суммируются с ранее полученными значениями и осуществляется деактивация, если использовалась функция активации.

if(!cEn.CalcHiddenGradients(cEnT.AsObject()))
   return false;
if(!SumAndNormilize(cEn.getGradient(), cEn.getPrevOutput(),
                    cEn.getGradient(), cEnT.GetWindow(), false))
   return false;
if(cEn.Activation() != None)
   if(!DeActivation(cEn.getOutput(), cEn.getGradient(),
                    cEn.getGradient(), cEn.Activation()))
      return false;

Сразу после этого градиенты поступают в cWconcat_ex, где начинается обратная процедура разделения признаков (вспомним, что на прямом проходе они объединялись).

if(!cWconcat_ex.CalcHiddenGradients(cEn.AsObject()))
   return false;
if(!DeConcat(cWx.getGradient(), cWe.getGradient(), cWconcat_ex.getGradient(),
             cWx.GetWindowOut(), cWe.GetWindowOut(), cWx.GetUnits()))
   return false;
if(cWx.Activation() != None)
   if(!DeActivation(cWx.getOutput(), cWx.getGradient(),
                    cWx.getGradient(), cWx.Activation()))
      return false;
if(cWe.Activation() != None)
   if(!DeActivation(cWe.getOutput(), cWe.getGradient(),
                    cWe.getGradient(), cWe.Activation()))
      return false;

Функция DeConcat корректно разделяет градиенты на две части — для cWx и cWe. В каждом из этих модулей отдельно вызывается DeActivation, восстанавливая чистый градиент. Затем происходит обратное распространение по сети: сначала на уровень исходных данных через `cWx`, потом в cEa через cWe.

   if(!NeuronOCL.CalcHiddenGradients(cWx.AsObject()))
      return false;
   if(!SumAndNormilize(NeuronOCL.getGradient(), PrevOutput,
                       NeuronOCL.getGradient(), cWx.GetWindow(), false))
      return false;
   if(!cEa.CalcHiddenGradients(cWe.AsObject()))
      return false;
//---
   return true;
  }

Обратите внимание, что на уровень исходных данных основной магистрали мы уже передавали градиент ошибки, поэтому полученные значения суммируем с ранее накопленными.

Особое внимание стоит уделить тому, что в методе реализована строгая последовательность всех шагов. Это необходимо, так как ошибка должна отматываться строго в порядке, обратном тому, в каком происходил прямой проход. Каждый шаг аккуратно компенсирует влияние свёрток, нормализаций, активаций и транспонирований. И лишь в конце, после полного расчёта градиентов, модель готова к обновлению весов, сохраняя точность на каждом этапе обучения.

Метод обновления параметров реализован в предельно прямолинейной, но при этом элегантной и надёжной форме. Здесь нет сложных условий или дополнительных вычислений — всё сводится к аккуратной передаче управления внутренним объектам, которые непосредственно содержат обучаемые веса. Каждый из них реализует собственный механизм обновления на основе накопленных градиентов и выбранной схемы оптимизации.

bool CNeuronAGCN::updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *second)
  {
   if(!cEa.UpdateInputWeights())
      return false;
   if(!cWe.UpdateInputWeights(cEa.AsObject()))
      return false;
   if(!cWx.UpdateInputWeights(NeuronOCL))
      return false;
   if(!cEn.UpdateInputWeights(cWconcat_ex.AsObject()))
      return false;
   if(!cWpre.UpdateInputWeights(cApreX.AsObject()))
      return false;
   if(!cWadapt.UpdateInputWeights(cAadaptX.AsObject()))
      return false;
//---
   return true;
  }

Каждый метод вызывается с передачей нужного входного объекта, полученного в ходе прямого прохода, что позволяет сохранить корректность вычислений в условиях графовой топологии.

Такой подход делает структуру кода не только читабельной, но и легко масштабируемой.

Для удобства читателя и обеспечения полной технической прозрачности, весь исходный код данного класса, включая определения всех методов, представлен во вложении.

Ячейка GinAR

Двигаемся к завершающему этапу — созданию полноценной вычислительной ячейки GinAR, в которой объединяются все ранее рассмотренные компоненты в единую согласованную структуру. Именно здесь, в классе CNeuronGinARCell, сходятся механизмы интерполяционного внимания, адаптивной графовой свёртки и управляющих элементов памяти, образуя гибкую, но при этом строго структурированную архитектуру.

class CNeuronGinARCell  :  public CNeuronBaseOCL
  {
protected:
   CNeuronInterpolationAttention cX_IA;
   CNeuronAGCN                   cX_AGNC;
   CNeuronAGCN                   cForgetGate;
   CNeuronAGCN                   cResetGate;
   CNeuronBaseOCL                cContext;
   CBufferFloat                  bTemp;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *second) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, 
                                        CBufferFloat *SecondInput, 
                                        CBufferFloat *SecondGradient, 
                                        ENUM_ACTIVATION SecondActivation = None) override;

public:
                     CNeuronGinARCell(void) { activation = None;}
                    ~CNeuronGinARCell(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint units_count, uint dimension,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(const int file_handle) override;
   virtual bool      Load(const int file_handle) override;
   //---
   virtual int       Type(void) override const  {  return defNeuronGinARCell; }
   virtual void      TrainMode(bool flag) override;
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetActivationFunction(ENUM_ACTIVATION value) override {};
  };

В представленной выше структуре нового объекта видно, что CNeuronGinARCell наследует базовый интерфейс от CNeuronBaseOCL. Это обеспечивает совместимость с остальными слоями и модулями фреймворка. Однако, в отличие от простых блоков, здесь собраны сразу несколько функциональных компонентов:

cX_IA — блок интерполяционного внимания, отвечающий за сглаживание и корректировку входных временных рядов;
cX_AGNC — основной модуль графовой адаптивной свёртки, формирующий обобщённое представление входных признаков с учётом их связей;
cForgetGate и cResetGate — две дополнительные графовые подсистемы, реализующие механизмы забывания и сброса по аналогии с GRU-ячейками;
cContext — внутренний буфер, хранящий накопленное состояние скрытой памяти;
bTemp — временный буфер, используемый в промежуточных вычислениях.

Класс реализует стандартный цикл работы нейронного слоя. Метод Init выполняет поэтапную инициализацию всех компонентов ячейки CNeuronGinARCell. Здесь задаются основные параметры модели: количество выходов, размерность признакового пространства, тип оптимизации и размер батча.

bool CNeuronGinARCell::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                            uint units_count, uint dimension,
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl,
                            units_count * dimension, optimization_type, batch))
      return false;

Затем, по очереди инициализируются внутренние блоки ячейки. Сначала cX_IA, отвечающий за интерполяционное внимание.

int index = 0;
if(!cX_IA.Init(0, index, OpenCL, units_count, dimension, optimization, iBatch))
   return false;

Следующим инициализируется основной модуль графовой свёртки cX_AGNC, за которым следуют управляющие шлюзы cForgetGate и cResetGate. Каждый из них получает свой уникальный индекс.

index++;
if(!cX_AGNC.Init(0, index, OpenCL, units_count, dimension, optimization, iBatch))
   return false;
index++;
if(!cForgetGate.Init(0, index, OpenCL, units_count, dimension, optimization, iBatch))
   return false;
index++;
if(!cResetGate.Init(0, index, OpenCL, units_count, dimension, optimization, iBatch))
   return false;

Отдельным пунктом инициализируется модуль cContext, который играет роль накопителя внутреннего состояния. Его выход явно заполняется нулями, чтобы избежать случайного шума на старте, а функция активации отключается, позволяя использовать его как чистую память.

   index++;
   if(!cContext.Init(0, index, OpenCL, units_count * dimension, optimization, iBatch))
      return false;
   if(!cContext.getPrevOutput().Fill(0))
      return false;
   cContext.SetActivationFunction(None);
   bTemp.BufferFree();
   if(!bTemp.BufferInit(units_count * units_count, 0) ||
      !bTemp.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

В завершение создаётся временный буфер bTemp, необходимый для выполнения промежуточных операций. Размер буфера выбирается квадратично units_count * units_count. При этом, если ранее буфер уже создавался, он предварительно освобождается, что гарантирует корректную работу и экономию ресурсов.

После выполнения всех операций модуль завершает работу, предварительно вернув логический результат вызывающей программе.

Алгоритм прямого прохода в методе, построенный в методе feedForward, реализует ключевую логику работы ячейки CNeuronGinARCell, объединяя механизмы внимания, графовых свёрток и управления памятью через ворота забывания и сброса.

bool CNeuronGinARCell::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
   if(!cX_IA.FeedForward(NeuronOCL))
      return false;

На первом этапе активируется модуль cX_IA, выполняющий интерполяционное преобразование исходных данных NeuronOCL. Полученное представление используется как основа для трёх параллельных блоков — главного графового сверточного модуля cX_AGNC, а также модулей cForgetGate и cResetGate, которые отвечают за формирование управляющих масок.

if(!cX_AGNC.FeedForward(cX_IA.AsObject(), SecondInput))
   return false;
if(!cForgetGate.FeedForward(cX_IA.AsObject(), SecondInput))
   return false;
if(!cResetGate.FeedForward(cX_IA.AsObject(), SecondInput))
   return false;
if(!Activation(cForgetGate.getOutput(), cForgetGate.getOutput(), GELU))
   return false;
if(!Activation(cResetGate.getOutput(), cResetGate.getOutput(), GELU))
   return false;

Каждый из этих трёх блоков принимает дополнительно второй вход SecondInput, содержащий, графовую или структурную информацию — матрицу смежности или данные о соседних узлах. После прохождения через слои, выходы ворот cForgetGate и cResetGate активируются функцией GELU, что позволяет создать сглаженные и более гибкие маски, снижающие влияние резких переходов и отрицательных значений.

Затем обновляется внутренний контекст. Здесь стоит обратить внимание, что при прямом проходе сразу переписываются значения контекста, необходимые нам для операций обратного прохода. Для предотвращения этого мы используем карусель буферов — вызываем метод SwapOutputs, который переставляет указатели буферов Output и PrevOutput.

//--- Context
   if(!cContext.SwapOutputs())
      return false;
   if(!GateElementMult(cContext.getPrevOutput(), cX_AGNC.getOutput(), 
                       cForgetGate.getOutput(), cContext.getOutput()))
      return false;

Далее формируется новый вектор контекста — через поэлементное перемножение предыдущего состояния cContext и результатов cX_AGNC, взвешенных маской забывания cForgetGate. Это позволяет гибко контролировать, какие элементы памяти стоит сохранить, а какие — обнулить.

Новый вектор контекста проходит через функцию активации ELU, адаптированную для работы с отрицательными значениями, что повышает стабильность градиентов.

//--- Output
   if(!Activation(cContext.getOutput(), cContext.getPrevOutput(), ELU))
      return false;
   if(!GateElementMult(cContext.getPrevOutput(), cX_IA.getOutput(), cResetGate.getOutput(), Output))
      return false;
//---
   return true;
  }

Наконец, итоговый выход блока в буфере Output формируется поэлементным умножением обновлённого контекста, тензора результатов cX_IA и маски cResetGate. Этот шаг объединяет долгосрочную память, текущее входное состояние и маску сброса, отвечающую за передачу релевантных признаков на выход.

Если на любом этапе возникает ошибка или неудача при выполнении операции, метод возвращает false. В случае успешного завершения всех операций — true, подтверждая корректное прохождение данных через всю структуру ячейки.

Алгоритм обратного распространения ошибки устроен не так просто, как может показаться на первый взгляд. Его основная сложность заключается в необходимости аккуратно суммировать и нормализовать градиенты от нескольких источников — ведь исходные данные обеих магистралей используются сразу в нескольких местах: в основном потоке (cX_AGNC) и во вспомогательных путях через управляющие ворота cForgetGate и cResetGate. А потому, каждый из этих потребителей генерирует собственный вклад в итоговый градиент, и все они должны быть корректно объединены.

bool CNeuronGinARCell::calcInputGradients(CNeuronBaseOCL *NeuronOCL,
                                          CBufferFloat *SecondInput,
                                          CBufferFloat *SecondGradient,
                                          ENUM_ACTIVATION SecondActivation = -1)
  {
   if(!NeuronOCL || !SecondInput || !SecondGradient)
      return false;
//--- Output
   if(!GateElementMultGrad(cContext.getPrevOutput(), cContext.getGradient(),
                           cX_IA.getOutput(), cX_IA.getPrevOutput(),
                           cResetGate.getOutput(), cResetGate.getGradient(),
                           Gradient, ELU, cX_IA.Activation(), GELU))
      return false;

Первым делом распределяется градиент итогового выхода ячейки между контекстом cContext, результатом интерполяционного внимания cX_IA и вратами сброса cResetGate. При этом учитываются все производные по соответствующим функций активации.

Следом восстанавливается градиент внутреннего состояния памяти cContext. Поскольку оно формируется из результатов умножения выхода основного сверточного модуля cX_AGNC и маски cForgetGate, используется аналогичная операция обратного распространения. Здесь уже участвуют другие функции активации и другие градиенты, а результат аккумулируется в объекте cContext.

//--- Context
   if(!GateElementMultGrad(cContext.getOutput(), cContext.getPrevOutput(),
                           cX_AGNC.getOutput(), cX_AGNC.getGradient(),
                           cForgetGate.getOutput(), cForgetGate.getGradient(),
                           cContext.getGradient(), None,
                           cX_AGNC.Activation(), GELU))
      return false;

Затем наступает один из самых ответственных моментов — передача градиентов обратно в модуль интерполяционного внимания cX_IA. Он был общим предшественником для трёх веток, поэтому требуется провести три независимых вызова CalcHiddenGradients, один для каждого пути: основной (cX_AGNC), ворота забывания (cForgetGate) и ворота сброса (cResetGate).

//--- Gradient to Interposition Attention
   if(!cX_IA.CalcHiddenGradients(cX_AGNC.AsObject(), SecondInput,
                                 SecondGradient, SecondActivation) ||
      !SumAndNormilize(cX_IA.getGradient(), cX_IA.getPrevOutput(), 
                       cX_IA.getPrevOutput(), cForgetGate.GetWindow(), false, 0, 0, 0, 1))
      return false;
   if(!cX_IA.CalcHiddenGradients(cForgetGate.AsObject(), SecondInput, 
                                 GetPointer(bTemp), SecondActivation) ||
      !SumAndNormilize(cX_IA.getGradient(), cX_IA.getPrevOutput(), 
                       cX_IA.getPrevOutput(), cForgetGate.GetWindow(), false, 0, 0, 0, 1) ||
      !SumAndNormilize(SecondGradient, GetPointer(bTemp), 
                       SecondGradient, cForgetGate.GetUnits(), false, 0, 0, 0, 1))
      return false;
   if(!cX_IA.CalcHiddenGradients(cResetGate.AsObject(), SecondInput, 
                                 GetPointer(bTemp), SecondActivation) ||
      !SumAndNormilize(cX_IA.getGradient(), cX_IA.getPrevOutput(), 
                       cX_IA.getPrevOutput(), cForgetGate.GetWindow(), false, 0, 0, 0, 1) ||
      !SumAndNormilize(SecondGradient, GetPointer(bTemp), SecondGradient, 
                       cForgetGate.GetUnits(), false, 0, 0, 0, 1))
      return false;

После каждого вызова результат суммируется в буфере bTemp и аккуратно возвращается в SecondGradient, обеспечивая накопление всех вкладов в один выходной поток.

В завершение вызывается расчёт скрытого градиента у объекта исходных данных NeuronOCL, связанного с cX_IA. Это завершает цепочку распространения ошибки и гарантирует, что вся информация о том, как изменение исходных данных влияет на выход, аккуратно донесена обратно до начала модели.

//---
   if(!NeuronOCL.CalcHiddenGradients(cX_IA.AsObject()))
      return false;
//---
   return true;
  }

Таким образом, метод реализует последовательный и взвешенный механизм агрегации и передачи градиентов во всех направлениях. Это обеспечивает корректное обучение сложной многокомпонентной структуры, такой как GinAR, где каждый выход влияет сразу на несколько веток вычислений.

Полный код данного класса и всех его методов представлен во вложении для самостоятельного изучения. При необходимости вы сможете легко проследить цепочку вычислений, структуру зависимостей между компонентами и логику передачи данных на всех этапах — от прямого прохода до обратного распространения ошибки и обновления весов.

Позади остался внушительный объём работы — шаг за шагом мы разобрали архитектуру, методы и внутреннюю логику ключевых компонентов, заложив прочный фундамент для дальнейших шагов. Предлагаю сделать небольшую паузу, перевести дух и дать мыслям улечься. А уже в следующей статье мы доведём начатое до логического завершения: перейдём от теории к практике и оценим реальную эффективность реализованных решений на рыночных данных.

Заключение

В данной статье мы провели глубокий анализ архитектуры ключевых компонентов фреймворка GinAR. Мы поэтапно рассмотрели процесс инициализации компонентов, реализацию прямого прохода, а также детализировали алгоритмы обратного распространения ошибки. Особое внимание было уделено механизму взаимодействия модулей внимания, графовых свёрток и управляющих гейтов, что позволило создать гибкую и выразительную структуру.

Такая модульность не только упрощает масштабирование, но и открывает путь к интеграции более сложных управляющих блоков — будь то в контексте обучения с подкреплением, или для задач прогнозирования с переменными зависимостями.

Ссылки

Программы, используемые в статье

#	Имя	Тип	Описание
1	Study.mq5	Советник	Советник офлайн обучения моделей
2	StudyOnline.mq5	Советник	Советник онлайн обучения моделей
3	Test.mq5	Советник	Советник для тестирования модели
4	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
5	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
6	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы

Прикрепленные файлы |

Загрузить ZIP

MQL5.zip (2912.14 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Гауссовcкие процессы в машинном обучении (Часть 1): Модель классификации в MQL5

В данной статье мы рассмотрим модель классификации гауссовских процессов. Мы начнём с изучения её теоретических принципов, а затем перейдём к практической разработке библиотеки ГП на MQL5.

Разработка инструментария для анализа движения цен (Часть 3): Советник Analytics Master

Переход от простого торгового скрипта к полнофункциональному советнику может значительно улучшить ваш торговый опыт. Представьте себе систему, которая автоматически отслеживает графики, выполняет основные вычисления в фоновом режиме и предоставляет регулярные обновления каждые два часа. Советник способен анализировать ключевые показатели, имеющие решающее значение для принятия обоснованных торговых решений, гарантируя вам доступ к самой актуальной информации для эффективной корректировки ваших стратегий.

Трейдинг с экономическим календарем MQL5 (Часть 4): Обновление новостей в панели управления в реальном времени

В этой статье мы расширим возможности нашей панели экономического календаря, внедрив обновления новостей в реальном времени для поддержания актуальности рыночной информации. Мы интегрируем методы извлечения данных в реальном времени в MQL5 для непрерывного обновления событий на панели управления и повышения отзывчивости интерфейса. Это обновление обеспечивает нам доступ к последним экономическим новостям непосредственно с панели управления, оптимизируя торговые решения на основе самых свежих данных.

Возможности Мастера MQL5, которые вам нужно знать (Часть 50): Осциллятор Awesome

Осциллятор Awesome — еще один индикатор Билла Вильямса, используемый для измерения импульса. Он может генерировать несколько сигналов. Как и в предыдущих статьях, мы рассмотрим его на основе паттернов, используя классы и сборку Мастера MQL5.