Нейросети в трейдинге: Сквозная многомерная модель прогнозирования временных рядов (Окончание)

Введение

В предыдущих статьях мы прошли путь от знакомства с теоретическими аспектами до практической реализации предложенных подходов, шаг за шагом раскрывая архитектуру и логику GinAR — оригинального нейросетевого фреймворка, разработанного специально для анализа и прогнозирования временных рядов в условиях структурной неопределённости и высокого уровня шумов. Основанный на многослойной и многокомпонентной архитектуре, GinAR уверенно сочетает принципы внимания, графовых преобразований и рекуррентной динамики, обретая тем самым способность не просто видеть структуру данных, но и адаптироваться к ней в реальном времени.

Мы подошли к самой ответственной и, пожалуй, самой интересной части — оценке работы фреймворка GinAR в реальных условиях. Позади остались этапы проектирования архитектуры, реализации ключевых компонентов и построения алгоритмов прямого и обратного прохода. Все элементы системы были детально проработаны, проверены и адаптированы к специфике финансовых временных рядов. Теперь пришло время объединить их воедино и, что называется, вывести на трассу — проверить, насколько эффективно GinAR справляется с практическими задачами анализа и прогнозирования.

В данной статье мы не просто завершаем разработку — мы подводим черту под концепцией, на реализацию которой ушло немало усилий. Основной упор будет сделан на обучение и тестирование модели в условиях, приближенных к боевым.

Прежде чем перейти к оценке, кратко напомним, как устроен сам фреймворк GinAR. В его основе — оригинальная ячейка GinARCell, сочетающая в себе сразу несколько ключевых компонентов:

• Interpolation Attention (IA) — механизм контекстного внимания, предварительно обрабатывающий входной поток и акцентирующий модель на релевантных элементах. Это своеобразный фильтр первичного восприятия, позволяющий выделить значимые закономерности и восстановить недостающие элементы до основного преобразования.
• AGCN-блоки (Adaptive Graph Convolution Network) — три модуля, один из которых отвечает за основную обработку (cX_AGNC), а два других — за управляющие сигналы (ForgetGate и ResetGate). Их задача — извлекать структурную и топологическую информацию, а также моделировать поток на основе временных и структурных зависимостей.
• Контекстный блок (Context) — хранилище временного состояния, обеспечивающее глубокую память и непрерывность в потоке обработки. Его обновление происходит по взвешенному принципу, основанному на взаимодействии с управляющими воротами (гейтами).
• Двойной механизм контроля — ForgetGate и ResetGate, которые работают по принципу отсеивания и перезаписи контекста. Они реализованы как самостоятельные AGCN-ячейки, что позволяет гибко управлять внутренним состоянием модели.

Результат работы ячейки формируется на основе активации ELU и множителей контекстного внимания, что обеспечивает мягкий, но чувствительный переход между временными интервалами.

Такое сочетание делает GinAR по-настоящему уникальным. В отличие от классических рекуррентных сетей, он не просто помнит прошлое — он умеет его структурировать. В отличие от стандартных GCN-моделей, он не оперирует фиксированной топологией, а обучает её на лету. И наконец, в отличие от обобщённых трансформеров, GinAR сохраняет локальность и динамическую адаптацию — две черты, жизненно важные для анализа финансовых временных рядов.

Авторская визуализация фреймворка GinAR представлена ниже.

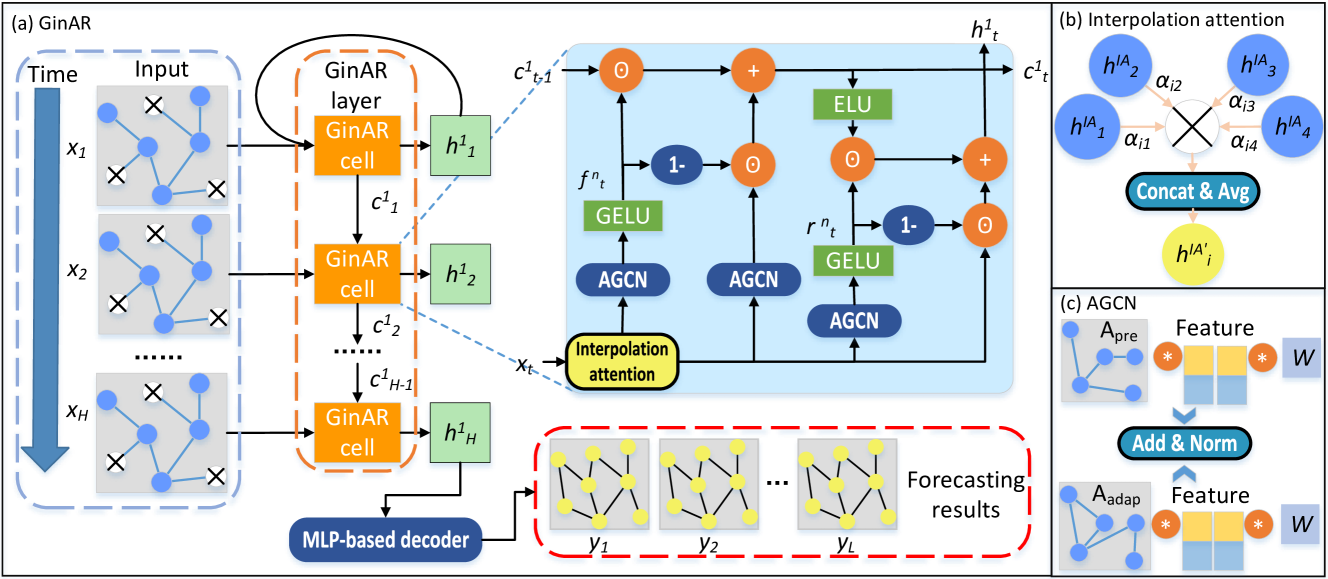
Данная статья служит не только завершением технической части, но и своеобразной демонстрацией зрелости всей конструкции. Мы увидим, как фреймворк ведёт себя на практике, какие возникают узкие места, какова точность и устойчивость модели на новых данных. И, что особенно важно, — оценим, действительно ли он способен дать трейдеру то самое преимущество, за которым стоит вся эта архитектурная сложность.

Блок GinAR

Архитектура GinAR организована по иерархическому принципу. Она состоит из нескольких последовательных слоёв GinAR и завершается Декодером, построенным на базе многослойного персептрона (MLP). Каждый слой GinAR, в свою очередь, содержит набор ячеек GinARCell, которые выполняют пошаговую обработку временной последовательности, аналогично тому, как кадры фильма формируют непрерывную сцену.

На выходе каждого слоя сохраняется только финальное скрытое состояние последней ячейки. Эти состояния объединяются в один итоговый тензор hⁿₐₗₗ, содержащий сжатое и максимально информативное представление всей анализируемой последовательности. Именно этот тензор поступает на вход MLP-декодера, состоящего из двух полносвязных слоёв с функцией активации ReLU между ними.

Стоит обратить особое внимание на важный архитектурный момент, связанный с организацией потока данных в многослойной структуре GinAR. Само по себе последовательное применение нескольких слоёв, где каждый следующий получает на вход выход предыдущего, является вполне стандартной практикой и хорошо укладывается в логику линейной модели.

Однако в оригинальной модели GinAR используется более сложная схема: после последовательной обработки несколькими слоями, результатом становится не просто выход последнего слоя, а объединённое представление, полученное в результате конкатенации выходов всех слоёв. Такой подход позволяет Декодеру использовать сразу весь спектр внутренних признаков, сформированных на разных уровнях абстракции — что, безусловно, усиливает модель. Но вместе с тем он нарушает линейную структуру передачи данных, которая лежит в основе наших реализаций, и требует дополнительной логики сбора и объединения данных из разных слоёв.

Используемый нами верхнеуровневый объект построения моделей изначально не предусматривал операций слияния выходов нескольких слоёв в один тензор, что делает невозможным прямое внедрение этой части оригинальной архитектуры GinAR. С целью обхода этого ограничения мы разработали специальный GinAR-блок, который управляет последовательной обработкой исходных данных с помощью набора ячеек CNeuronGinARCell, а затем аккумулирует результаты всех ячеек в единый тензор. Этот итоговый тензор передаётся на вход Декодеру, воспроизводя ключевую особенность оригинальной модели — интеграцию признаков, полученных на разных уровнях абстракции.

Переходя к рассмотрению архитектуры GinAR-блока, стоит подчеркнуть одно важное отличие от оригинальной модели. Помимо базовой структуры, мы добавили обучаемую матрицу предопределённых зависимостей между компонентами анализируемых данных. В её основу положен механизм адаптивного обучения, аналогичный тому, что используется в матрицах структурных зависимостей внутри каждой ячейки GinARCell. Однако ключевое отличие заключается в области применения. Если адаптивные матрицы формируются отдельно в каждой ячейке, отражая локальные закономерности, то введённая нами матрица имеет глобальный характер и является общей для всех ячеек в пределах одного GinAR-блока. Это позволяет зафиксировать устойчивые, повторяющиеся корреляции между переменными на протяжении всего анализа, тем самым усиливая структурную согласованность модели.

Для реализации GinAR-блока в рамках нашей архитектуры был построен специальный класс CNeuronGinAR, унаследованный от CNeuronSwiGLUOCL. Эта иерархия позволяет сохранить совместимость с остальной частью модели и использовать преимущества свёрточной активации с гибкой нелинейностью SwiGLU. Однако, ключевые функциональные элементы и логика работы были существенно расширены и переопределены. Структура нового объекта представлена ниже.

class CNeuronGinAR   :  public CNeuronSwiGLUOCL
  {
protected:
   CParams              cEa;
   CNeuronSwiGLUOCL     cWx;
   CNeuronSwiGLUOCL     cWe;
   CNeuronBaseOCL       cWconcat_ex;
   CNeuronConvOCL       cEn;
   CNeuronTransposeOCL  cEnT;
   CNeuronBaseOCL       cEnEnT;
   CNeuronSoftMaxOCL    cApre;
   CNeuronGinARCell     caCells[4];
   CNeuronBaseOCL       cConcat;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronGinAR(void) {};
                    ~CNeuronGinAR(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint units_count, uint dimension,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(const int file_handle) override;
   virtual bool      Load(const int file_handle) override;
   //---
   virtual int       Type(void) override const  {  return defNeuronGinAR; }
   virtual void      TrainMode(bool flag) override;
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   //---
   virtual bool      Clear(void) override;
  };

Класс CNeuronGinAR представляет собой полноценный блок фреймворка GinAR, реализованный в среде MQL5 с использованием OpenCL. Он предназначен для обработки временных рядов и извлечения сложных закономерностей на основе иерархии линейных взаимосвязей. Внутри класса сосредоточено сразу несколько ключевых компонентов, ответственных за генерацию и интерпретацию глобальной матрицы структурных зависимостей, а также массив ячеек CNeuronGinARCell, реализующих последовательную обработку исходных данных. Их результаты впоследствии конкатенируются, формируя итоговое представление анализируемой последовательности.

Структура класса построена на принципах модульности и повторного использования. Все внутренние элементы объявлены статично. Это означает, что управление их жизненным циклом (создание, уничтожение и очистка памяти) осуществляется автоматически, без необходимости явного вмешательства со стороны конструктора или деструктора.

Для настройки всех внутренних компонентов используется метод Init, играющий роль единой точки входа в процесс инициализации. Он принимает параметры, задающие архитектуру объекта и тип оптимизации параметров.

bool CNeuronGinAR::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                        uint units_count, uint dimension,
                        ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronSwiGLUOCL::Init(numOutputs, myIndex, open_cl, caCells.Size()*dimension,
                              caCells.Size()*dimension, dimension, units_count, 1,
                              optimization_type, batch))
      return false;

Сначала вызывается одноименный метод родительского класса CNeuronSwiGLUOCL, который в нашей реализации формирует агрегированные представления результатов работы ячеек GinARCell. После этого последовательно инициализируются вновь объявленные компоненты, входящие в архитектуру блока.

Первой идет обучаемая матрица глобальных структурных зависимостей между переменными временного ряда.

int index = 0;
if(!cEa.Init(0, index, OpenCL, Neurons(), optimization, iBatch))
   return false;
cEa.SetActivationFunction(None);

В отличие от оригинального подхода, где предопределённая ковариационная матрица формируется на основе априорных знаний или предварительного анализа структуры прогнозируемой последовательности, в нашей реализации используется обучаемая матрица структурных зависимостей, единая для всех ячеек GinARCell внутри одного блока. Такой подход позволяет отказаться от ручной настройки или внешнего анализа данных и обеспечивает более гибкую, адаптивную настройку взаимосвязей между переменными на этапе обучения.

Затем инициализируем линейные преобразователи cWx и cWe. Их задача — привести исходные данные и матрицу ковариации к общей размерности перед объединением в единый тензор cWconcat_ex.

   index++;
   if(!cWx.Init(0, index, OpenCL, dimension, dimension, dimension, units_count, 1,
                                                            optimization, iBatch))
      return false;
   index++;
   if(!cWe.Init(0, index, OpenCL, dimension, dimension, dimension, units_count, 1,
                                                            optimization, iBatch))
      return false;
   if(!cWconcat_ex.Init(0, index, OpenCL, 2 * Neurons(), optimization, iBatch))
      return false;
   cWconcat_ex.SetActivationFunction(None);

Сверточный слой cEn предназначен для осуществления глубокого смешивания признаков и их зависимостей.

   index++;
   if(!cEn.Init(0, index, OpenCL, 2 * dimension, 2 * dimension, dimension, units_count,
                                                              1, optimization, iBatch))
      return false;
   cEn.SetActivationFunction(None);
   index++;
   if(!cEnT.Init(0, index, OpenCL, units_count, dimension, optimization, iBatch))
      return false;
   index++;
   if(!cEnEnT.Init(0, index, OpenCL, units_count * units_count, optimization, iBatch))
      return false;
   cEnEnT.SetActivationFunction(GELU);

Полученные данные сначала транспонируем, а затем перемножаем исходное и транспонированное представление для получения симметричной матрицы взаимозависимостей между переменными cEnEnT. Для активации используется функция GELU, усиливающая значимые взаимосвязи.

Далее нормализуем матрицу зависимостей с помощью функции SoftMax, переводя данные в вероятностное распределение.

   index++;
   if(!cApre.Init(0, index, OpenCL, units_count * units_count, optimization, iBatch))
      return false;
   cApre.SetHeads(units_count);

Следующим шагом производится инициализация массива ячеек CNeuronGinARCell, каждая из которых отвечает за обработку анализируемой последовательности на своём уровне иерархии. Несмотря на логическую независимость, все ячейки обладают идентичной архитектурой, что позволяет упростить процедуру их инициализации — достаточно одного аккуратного цикла.

   for(uint i = 0; i < caCells.Size(); i++)
     {
      index++;
      if(!caCells[i].Init(0, index, OpenCL, units_count, dimension, optimization, iBatch))
         return false;
     }
   index++;
   if(!cConcat.Init(0, index, OpenCL, GetWindow()*units_count, optimization, iBatch))
      return false;
//---
   return true;
  }

Результаты работы ячеек агрегируются в объекте cConcat. А после успешной инициализации всех внутренних компонентов, мы возвращаем логический результат выполнения операций вызывающей программе.

Важно подчеркнуть, что метод Init не управляет жизненным циклом перечисленных объектов. Его задача — строго сконфигурировать параметры и выстроить архитектуру слоя, передав управление в рабочий цикл модели. Такой подход обеспечивает высокую стабильность, предсказуемость поведения и эффективное использование памяти.

После завершения этапа инициализации все компоненты блока CNeuronGinAR готовы к работе в рамках прямого прохода. Именно здесь проявляется взаимодействие между структурными модулями, скрытыми состояниями ячеек и обучаемой матрицей зависимостей. Метод feedForward отвечает за выполнение полного цикла обработки исходной последовательности, включая построение матрицы структурных зависимостей и генерацию финального выходного тензора, который будет передан следующему уровню нейронной архитектуры.

bool CNeuronGinAR::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- Calculate Apre
   if(bTrain)
     {
      if(!cEa.FeedForward())
         return false;
      if(!cWe.FeedForward(cEa.AsObject()))
         return false;
     }

На первом этапе происходит построение обучаемой матрицы зависимостей. Если модель находится в режиме обучения (bTrain == true), то сначала активируется тензор глобальных структурных зависимостей, за которым следует обработка его выхода с помощью слоя линейной проекции.

Параллельно обрабатывается и основной информационный поток исходных данных, проходя через слой линейной проекции cWx.

//---
   if(!cWx.FeedForward(NeuronOCL))
      return false;
   if(!Concat(cWx.getOutput(), cWe.getOutput(), cWconcat_ex.getOutput(), 
              cWx.GetWindowOut(), cWe.GetWindowOut(), cWx.GetUnits()))
      return false;

Далее результаты обоих направлений объединяются в один тензор с помощью операции Concat, результат которой поступает на сверточный слой cEn.

   if(!cEn.FeedForward(cWconcat_ex.AsObject()))
      return false;
   if(!cEnT.FeedForward(cEn.AsObject()))
      return false;
   if(!MatMul(cEn.getOutput(), cEnT.getOutput(), cEnEnT.getOutput(), cEnT.GetCount(),
                                                  cEnT.GetWindow(), cEnT.GetCount()))
      return false;
   if(cEnEnT.Activation() != None)
      if(!Activation(cEnEnT.getOutput(), cEnEnT.getOutput(), cEnEnT.Activation()))
         return false;

Следом производится транспонирование полученного тензора (cEnT), и затем осуществляется матричное перемножение оригинала с его транспонированной версией. На этом этапе фактически формируется ковариационная матрица, к которой, при необходимости, добавляется нелинейность с использованием заданной функции активации.

Финальная матрица ковариации строится в слое cApre, где данные переводятся в вероятностное представление с помощью функции SoftMax.

if(!cApre.FeedForward(cEnEnT.AsObject()))
   return false;
if(!IdentSum(cApre.getOutput(), cApre.getOutput(), cApre.Heads()))
   return false;

Для обеспечения устойчивости и базового уровня самозависимости (self-connection), эта матрица дополняется единичной диагональной матрицей. То есть, каждая переменная получает не только информацию о взаимосвязях с другими, но и сохраняет базовую ориентацию на саму себя. В результате получается сбалансированная структура весов внимания, способная учитывать как глобальные зависимости, так и локальную значимость каждого элемента. Именно эта итоговая матрица затем передаётся на вход каждой из ячеек GinARCell, выступая в роли универсального механизма селективного усиления сигналов.

Далее начинается основная обработка исходной последовательности через массив ячеек. На вход первой ячейки подаются анализируемые данные, полученная от внешней программы. А каждая последующая ячейка анализирует результаты работы предыдущей, повышая уровень детализации латентного представления. Таким образом, формируется последовательность скрытых представлений, отражающая иерархическую природу анализа временного ряда.

//--- GimAR Cells
   CNeuronBaseOCL *temp = NeuronOCL;
   for(uint i = 0; i < caCells.Size(); i++)
     {
      if(!caCells[i].FeedForward(temp, cApre.getOutput()))
         return false;
      temp = caCells[i].AsObject();
     }
//---
   if(!Concat(caCells[0].getOutput(), caCells[1].getOutput(), caCells[2].getOutput(),
              caCells[3].getOutput(), cConcat.getOutput(), GetWindow() / 4,
              GetWindow() / 4, GetWindow() / 4, GetWindow() / 4, GetUnits()))
      return false;
//---
   return CNeuronSwiGLUOCL::feedForward(cConcat.AsObject());
  }

Завершающим этапом работы метода является объединение выходов всех ячеек в один общий тензор (cConcat), который затем подаётся на вход одноименному методу родительского класса CNeuronSwiGLUOCL для дальнейшей обработки. Эта структура обеспечивает согласованное и эффективное прохождение информации сквозь блок GinAR, максимально приближая поведение системы к оригинальной архитектуре, несмотря на архитектурные ограничения используемого фреймворка.

После завершения прямого прохода и вычисления результатов работы блока, мы переходим ко второму ключевому этапу — распространению градиента ошибки (Backpropagation). Именно здесь начинается истинная обратная инженерия прогнозирования: ошибка от Декодера возвращается к каждому элементу архитектуры с целью точной корректировки весов и оптимизации модели.

Метод calcInputGradients отвечает за реализацию полного обратного прохода по всей архитектуре блока, начиная с выхода и заканчивая исходными данными. Поскольку структура блока сложная, и состоит как из последовательных операций, так и из операций ветвления и слияния тензоров, обратный проход требует поэтапного и строго согласованного выполнения.

bool CNeuronGinAR::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;
//---
   if(!CNeuronSwiGLUOCL::calcInputGradients(cConcat.AsObject()))
      return false;
   if(!DeConcat(caCells[0].getPrevOutput(), caCells[1].getPrevOutput(),
                caCells[2].getPrevOutput(), caCells[3].getGradient(),
                cConcat.getGradient(), GetWindow() / 4,
                GetWindow() / 4, GetWindow() / 4,
                GetWindow() / 4, GetUnits()))
      return false;

Метод начинается с вызова одноименного метода родительского класса CNeuronSwiGLUOCL, который передаёт градиент на конкатенированный тензора результатов работы внутренних ячеек — cConcat. Поскольку в процессе прямого прохода данный тензор формировался путём конкатенации выходов четырёх GinAR-ячеек, теперь необходимо корректно распределить градиент обратно по четырем информационным потокам. С помощью метода DeConcat мы передаем каждой ячейке градиент ошибки в соответствии с её влиянием на итоговый результат.

Следует особо подчеркнуть один важный момент, касающийся логики распространения градиента ошибки внутри GinAR-блока. Несмотря на внешнюю симметрию ячеек, их функциональная нагрузка в процессе обучения не одинакова.

Во-первых, лишь последняя ячейка используется только для формирования итогового тензора результатов блока путём конкатенации. Все предыдущие ячейки имеют двойное назначение: их выходы не только участвуют в конкатенации, но и служат исходными данными для следующей по иерархии GinARCell. Это означает, что градиент ошибки должен поступить в каждую такую ячейку из двух источников. Следовательно, при расчёте градиента для первых трёх ячеек мы собираем градиент по двум направлениям использования данных и корректно их суммируем. Это обеспечивает непрерывность потока ошибки и точную обратную связь на каждом уровне иерархии.

//--- GimAR Cells
   cApre.getGradient().Fill(0);
   for(uint i = caCells.Size() - 1; i > 0; i--)
      if(!caCells[i - 1].CalcHiddenGradients(caCells[i].AsObject(), cApre.getOutput(),
                                             cApre.getPrevOutput(),
                                             (ENUM_ACTIVATION)cApre.Activation()) ||
         !SumAndNormilize(caCells[i - 1].getGradient(), caCells[i - 1].getPrevOutput(),
                          caCells[i - 1].getGradient(), cWx.GetWindow(), false, 0, 0, 0, 1) ||
         !SumAndNormilize(cApre.getGradient(), cApre.getPrevOutput(),
                          cApre.getGradient(), GetUnits(), false, 0, 0, 0, 1))
         return false;
   if(!NeuronOCL.CalcHiddenGradients(caCells[0].AsObject(), cApre.getOutput(),
                                     cApre.getPrevOutput(), (ENUM_ACTIVATION)cApre.Activation()) ||
      !SumAndNormilize(cApre.getGradient(), cApre.getPrevOutput(),
                       cApre.getGradient(), GetUnits(), false, 0, 0, 0, 1))
      return false;

Во-вторых, ещё более тонкая ситуация возникает при расчёте градиента для глобальной матрицы ковариации, представленной в объекте cApre. Эта матрица была передана одновременно всем четырём GinARCell. Следовательно, в процессе обратного прохода её градиент должен аккумулировать информацию из четырёх независимых направлений — от каждой ячейки. Это требует поочерёдного добавления всех поступающих градиентов с сохранением согласованной формы и масштаба. Ошибки в этой части могут привести к резким скачкам в весах и, как следствие, к нестабильности обучения.

Далее начинается обратное распространение через блок формирования матрицы зависимостей. Сначала рассчитывается градиент для cEnEnT, после чего значения корректируются на производную соответствующей функции активации.

//---
   if(!cEnEnT.CalcHiddenGradients(cApre.AsObject()))
      return false;
   if(cEnEnT.Activation() != None)
      if(!DeActivation(cEnEnT.getOutput(), cEnEnT.getGradient(),
                       cEnEnT.getGradient(), cEnEnT.Activation()))
         return false;
   if(!MatMulGrad(cEn.getOutput(), cEn.getPrevOutput(),
                  cEnT.getOutput(), cEnT.getGradient(),
                  cEnEnT.getGradient(), cEnT.GetCount(),
                  cEnT.GetWindow(), cEnT.GetCount()))
      return false;
   if(!cEn.CalcHiddenGradients(cEnT.AsObject()))
      return false;
   if(!SumAndNormilize(cEn.getGradient(), cEn.getPrevOutput(),
                       cEn.getGradient(), cEnT.GetWindow(), false, 0, 0, 0, 1))
      return false;
   if(cEn.Activation() != None)
      if(!DeActivation(cEn.getOutput(), cEn.getGradient(),
                       cEn.getGradient(), cEn.Activation()))
         return false;

Затем производится вычисление градиента для операции матричного умножения MatMulGrad, распределяя ошибку между сверточным слоем cEn и его транспонированной копией cEnT. При этом градиент ошибки транспонированного представления мы так же спускаем до уровня сверточного слоя и суммируем значения, полученные по двум информационным потокам. Подобная схема позволяет собрать полное дифференцируемое представление симметричной ковариационной матрицы, тем самым сохранив точность и целостность передачи ошибки даже в рамках сложной топологии.

Полученные значения спускаем до уровня тензора cWconcat_ex.

if(!cWconcat_ex.CalcHiddenGradients(cEn.AsObject()))
   return false;
if(!DeConcat(cWx.getGradient(), cWe.getGradient(), cWconcat_ex.getGradient(),
             cWx.GetWindowOut(), cWe.GetWindowOut(), cWx.GetUnits()))
   return false;

Выход cWconcat_ex был сформирован из результатов cWx и cWe. Теперь их градиенты раскладываются обратно, проходя через возможную деактивацию. После этого инициируется обратный проход от cWx к объекту исходных данных NeuronOCL.

Однако здесь следует вспомнить, что на уровень исходных данных ранее уже был передан градиент ошибки от первой ячейки. Поэтому мы воспользуемся фокусом с подменой указателей на буфера данных с последующим суммированием значений, полученных из двух информационных потоков.

   if(cWx.Activation() != None)
      if(!DeActivation(cWx.getOutput(), cWx.getGradient(),
                       cWx.getGradient(), cWx.Activation()))
         return false;
   if(cWe.Activation() != None)
      if(!DeActivation(cWe.getOutput(), cWe.getGradient(),
                       cWe.getGradient(), cWe.Activation()))
         return false;
   CBufferFloat* temp = NeuronOCL.getGradient();
   if(!NeuronOCL.SetGradient(NeuronOCL.getPrevOutput(), false))
      return false;
   if(!NeuronOCL.CalcHiddenGradients(cWx.AsObject()))
      return false;
   if(!SumAndNormilize(NeuronOCL.getGradient(), temp,
                       NeuronOCL.getGradient(), cWx.GetWindow(), false, 0, 0, 0, 1))
      return false;
   if(!NeuronOCL.SetGradient(temp, false))
      return false;

Завершается метод передачей градиента ошибки на уровень матрицы глобальных зависимостей cEa.

   if(!cEa.CalcHiddenGradients(cWe.AsObject()))
      return false;
//---
   return true;
  }

А после успешного выполнения всех итераций, мы возвращаем логический результат работы метода вызывающей программе.

Таким образом, метод calcInputGradients обеспечивает корректное распространение градиента по всей структуре GinAR-блока. Архитектура обратного прохода в точности отражает структуру прямого — как в зеркале, что особенно важно при использовании сложных механизмов внимания и вложенных компонентов.

Полный код данного класса и всех его методов представлен во вложении и доступен для самостоятельного изучения.

Архитектура модели

После создания всех компонентов, необходимых для построения фреймворка GinAR, мы переходим к следующему этапу — описанию архитектуры обучаемых моделей. Здесь логика построения выходит далеко за рамки простого прогнозирования временных рядов: наша задача — построить полноценного торгового агента, в котором фреймворк GinAR выполняет роль Энкодера состояния окружающей среды.

Каждый компонент модели отвечает за строго определённую функцию. Энкодер отвечает за извлечение и обобщение информации из исторических данных. Модули прогнозирования, разделённые на три параллельные модели, осуществляют прогнозирование на разных временных горизонтах. Далее следуют Actor и Critic, блоки, соответствующие архитектуре Reinforcement Learning: первый вырабатывает торговые действия, второй — оценивает ожидаемую эффективность поведения модели в текущем состоянии рынка.

Для описания архитектуры используется метод CreateDescriptions, который формирует конфигурации для всех модулей. На первом этапе метод инициализирует контейнеры под каждую модель: Энкодер, прогнозные модули, Actor и Critic. Эти контейнеры реализуются как массивы объектов — описаний нейронных слоёв.

bool CreateDescriptions(CArrayObj *&encoder,
                        CArrayObj *&forecast1,
                        CArrayObj *&forecast2,
                        CArrayObj *&forecast3,
                        CArrayObj *&actor,
                        CArrayObj *&critic
                       )
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
   if(!forecast1)
     {
      forecast1 = new CArrayObj();
      if(!forecast1)
         return false;
     }
   if(!forecast2)
     {
      forecast2 = new CArrayObj();
      if(!forecast2)
         return false;
     }
   if(!forecast3)
     {
      forecast3 = new CArrayObj();
      if(!forecast3)
         return false;
     }
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!critic)
     {
      critic = new CArrayObj();
      if(!critic)
         return false;
     }

После инициализации начинается формирование структуры моделей. Энкодер начинает с базового полносвязного слоя, который просто получает на вход модели исторические данные.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   uint prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormWithNoise;
   descr.count = prev_count;
   descr.batch = BatchSize;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Далее следует слой пакетной нормализации с добавлением шума, задача которых — стабилизировать распределение исходных данных и ввести в систему аугментацию представлений для повышения устойчивости модели к переобучению.

После этого, добавляются каналы дифференциальных признаков между соседними барами. Это позволяет системе фиксировать не только абсолютные значения, но так же направление и интенсивность изменений. Это особенно важно в условиях высокочастотного и нерегулярного поведения рынка.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatDiff;
   prev_count = descr.count = HistoryBars;
   descr.layers = BarDescr;
   descr.step = 1;
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Следующий слой отвечает за обогащение представлений гармониками временных меток.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defMamba4CastEmbeding;
   prev_count = descr.count = HistoryBars;
   descr.window = 2 * BarDescr;
   uint prev_out = descr.window_out = NSkills;
     {
      uint temp[] = {PeriodSeconds(PERIOD_H1), PeriodSeconds(PERIOD_D1)};
      if(ArrayCopy(descr.windows, temp) < (int)temp.Size())
         return false;
     }
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Подготовленные данные затем проходят через транспонирующий слой, который меняет оси представления: временные последовательности превращаются в пространственные характеристики и подаются на вход свёрточному фильтру. Свёрточный слой с активацией tanh выделяет ключевые паттерны и структурные зависимости в эмбеддингах, получая тем самым сжатое и концентрированное представление скрытых рыночных закономерностей.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = prev_count;
   prev_count = descr.window = prev_out;
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
   prev_out = descr.count;
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = prev_count;
   descr.window = prev_out;
   descr.variables = 1;
   prev_out = descr.window_out = EmbeddingSize;
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   descr.activation = TANH;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Кульминацией энкодера является слой, реализующий фреймворк GinAR. Именно здесь объединяются все ранее полученные признаки, и происходит их интерпретация с помощью иерархии GinAR-ячеек. Они работают синхронно, используя общую обучаемую матрицу ковариаций для моделирования скрытых структурных связей в данных. Этот слой не просто передаёт информацию дальше — он формирует активное представление рыночного состояния, которое уже можно считать готовым к использованию для принятия торговых решений.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronGinAR;
   descr.count = prev_count;
   descr.window = prev_out;
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Таким образом, подходы фреймворка GinAR встраиваются в архитектуру модели последовательно, логично и без излишеств. Итоговое скрытое состояние, сформированное Энкодером, представляет собой высокоуровневое описание рыночной ситуации, пригодное как для прогнозирования, так и для генерации торговых решений.

Для обучения Энкодера состояния окружающей среды применяется стратегия сквозного распространения градиента ошибки от сразу нескольких независимых подсистем. В первую очередь — это три модели прогнозирования, каждая из которых специализируется на продолжении временного ряда на своём горизонте планирования. Эти модули анализируют одно и то же скрытое состояние, сформированное Энкодером, но интерпретируют его по-разному в зависимости от заданного горизонта планирования. Благодаря этому достигается многомасштабное понимание текущей рыночной ситуации.

Дополнительно к ним подключается Actor — компонент, отвечающий за выработку торгового решения. Он опирается на то же сжатое представление состояния окружающей среды и интерпретирует его уже как руководство к действию. Таким образом, Энкодер оказывается под давлением сразу с четырёх сторон — его выход должен быть одновременно информативным для прогнозирования и пригодным для практического применения в условиях рыночной неопределённости.

Важно подчеркнуть, что архитектура всех этих моделей полностью заимствована из предыдущей работы. Поэтому в рамках текущего исследования мы не будем останавливаться на её детальном описании. Всё внимание сосредоточено на новой части — интеграции фреймворка GinAR в состав обучаемой системы.

Полный код всех компонентов, включая конфигурации слоёв, приведён во вложении.

Обучение

Завершив построение всех компонентов и настройку архитектуры обучаемых моделей, мы переходим к финальному и, пожалуй, самому ответственному этапу — обучению моделей. В рамках нашей системы мы используем комбинированный подход, сочетающий достоинства офлайн- и онлайн-режимов обучения. Это позволяет не только обеспечить устойчивую начальную подготовку модели, но и адаптировать её поведение под конкретные торговые условия, включая смену рыночной фазы, уровня волатильности и частоты появления торговых сигналов.

Процесс обучения, как и в предыдущих работах, реализован в два этапа. Первый этап — это офлайн-обучение. Здесь модели тренируются на исторических данных. Причём мы используем подход без предварительного сбора обучающей выборки. Вместо этого, формируем состояние окружающей среды непосредственно по историческим данным терминала и параллельно моделируем состояние счета. Такой подход обеспечивает высокую гибкость и позволяет использовать произвольные исторические отрезки без необходимости ручной подготовки датасетов.

Второй этап — онлайн-настройка. Он проходит уже в условиях, максимально приближенных к реальной торговле в тестере стратегий MetaTrader 5. Модель продолжает обучение, сталкиваясь с новыми, ранее не встречавшимися рыночными сценариями, и адаптируется к ним в реальном времени. Эта фаза позволяет устранить остаточные рассогласования, накопленные во время офлайн-обучения, и подготовить систему к полноценному автономному использованию на реальном счёте.

Важно отметить, что двухэтапное обучение — не новая концепция в рамках наших исследований. Мы успешно применяли эту стратегию и в предыдущих работах. Однако в текущем проекте, на стадии офлайн-обучения, были внесены принципиально важные изменения, обусловленные как теоретическими соображениями, так и практическим опытом реализации прежних моделей.

Вы, вероятно, заметили, что в текущей архитектуре отсутствует компонент под названием Режиссёр. Напомним, в ряде последних работ Режиссёр использовался как дополнительная оценочная модель, работающая параллельно Критику. Его основная функция заключалась в бинарной классификации действий Агента на прибыльные и убыточные. Такой жёсткий способ обратной связи хорошо зарекомендовал себя на ранних стадиях обучения, помогая ускорить начальную адаптацию политики.

Тем не менее в сегодняшней реализации мы пошли иным путём. И решили объединить два обучающих подхода (обучение с подкреплением и обучение с учителем) непосредственно в фазе офлайн-обучения. Это решение оказалось более элегантным и в то же время эффективным, с точки зрения качества и направленности обратной связи.

Суть изменения заключается в следующем: параллельно с оценкой текущих действий Агента, которая осуществляется Критиком, мы предоставляем Актёру эталонные действия, сформированные на основе анализа будущего ценового движения. Поскольку в фазе офлайн-обучения у нас есть доступ к полному отрезку временного ряда, включая последующее движение цен, мы можем вычислить так называемую почти идеальную траекторию действий. Эти действия, сформированные постфактум, не просто указывают направление — они становятся своеобразным эталоном, к которому стремится политика Актёра.

Таким образом, мы реализуем механизм, где Агент учится как на собственных ошибках, так и на примере заранее просчитанных выгодных стратегий. Это позволяет отказаться от резкой бинарной обратной связи Режиссёра, не теряя при этом её обучающего эффекта. Напротив, качество направляющего сигнала становится выше, а процесс выработки прибыльной политики — более управляемым и устойчивым.

Предложенный подход реализован в методе Train советника "…\MQL5\Experts\GinAR\Study.mq5". Алгоритм метода представляет собой центральный этап офлайн-обучения, в котором сочетаются методы обучения с подкреплением и обучение с учителем. В его основе — последовательная имитация рыночных ситуаций, основанная на исторических данных, и обучение торговой стратегии на основе анализа как текущих состояний, так и идеализированных траекторий торговых решений.

Всё начинается с подготовки обучающей выборки: из истории котировок выбирается заданный пользователем диапазон, и для каждого временного отрезка рассчитываются анализируемые технические индикаторы. При этом мы контролируем, чтобы все индикаторы были рассчитаны и готовы к использованию, иначе процесс прерывается.

void Train(void)
  {
   int start = iBarShift(Symb.Name(), TimeFrame, Start);
   int end = iBarShift(Symb.Name(), TimeFrame, End);
   int bars = CopyRates(Symb.Name(), TimeFrame, 0, start, Rates);
//---
   if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) ||
      !ATR.BufferResize(bars) || !MACD.BufferResize(bars))
     {
      PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
      ExpertRemove();
      return;
     }
//---
   int count = -1;
   bool calculated = false;
   do
     {
      count++;
      calculated = (RSI.BarsCalculated() >= bars &&
                    CCI.BarsCalculated() >= bars &&
                    ATR.BarsCalculated() >= bars &&
                    MACD.BarsCalculated() >= bars
                   );
      Sleep(100);
      count++;
     }
   while(!calculated && count < 100);
   if(!calculated)
     {
      PrintFormat("%s -> %d The training data has not been loaded", __FUNCTION__, __LINE__);
      ExpertRemove();
      return;
     }
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();
//---
   if(!ArraySetAsSeries(Rates, true))
     {
      PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
      ExpertRemove();
      return;
     }
   bars -= end + HistoryBars + NForecast;
   if(bars < 0)
     {
      PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
      ExpertRemove();
      return;
     }

Формируются буферы, которые будут использоваться для хранения исходных состояний, временных меток и целевых значений.

Далее начинается основной цикл обучения. Обучение организовано в виде серии эпох — полных проходов по выбранной истории. Внутри каждой эпохи осуществляется последовательная симуляция рыночных ситуаций.

//---
   vector<float> result, target, neg_target;
   bool Stop = false;
//---
   uint ticks = GetTickCount();
//---
   for(int epoch = 0; (epoch < Epochs && !IsStopped() && !Stop); epoch ++)
     {
      if(!cEncoder.Clear())
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         ExpertRemove();
         return;
        }
      for(int posit = start - HistoryBars - NForecast - 1; posit >= end; posit--)
        {
         if(!CreateBuffers(posit, GetPointer(bState), GetPointer(bTime), Result))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            ExpertRemove();
            return;
           }
         const vector<float> account = SampleAccount(GetPointer(bState), datetime(bTime[0]));
         const vector<float> target_action = OraculAction(account, Result);
         if(!bAccount.AssignArray(account))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            ExpertRemove();
            return;
           }

На каждом шаге формируется текущее состояние рынка, представленное в виде числового вектора, и определяется соответствующая ему временная шкала. Эти данные подаются на вход Энкодеру, который преобразует состояние в компактное скрытое представление — своего рода квинтэссенцию рыночной картины.

//--- Feed Forward
if(!cEncoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false,
                                   (CBufferFloat*)GetPointer(bTime)))
  {
   PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
   Stop = true;
   break;
 }

Полученный латентный вектор используется сразу по трем направлениям. С одной стороны, он передаётся в три модели прогнозирования, каждая из которых отвечает за свой горизонт планирования: краткосрочное, среднесрочное и долгосрочное. Эти модели выдают свои прогнозы на ближайшие периоды.

for(uint f = 0; f < caForecast.Size(); f++)
   if(!caForecast[f].feedForward(GetPointer(cEncoder), -1, (CBufferFloat*)NULL))
     {
      PrintFormat("%s -> %d - Forecast %d", __FUNCTION__, __LINE__, f);
      Stop = true;
      break;
     }

С другой стороны, то же скрытое представление поступает Актеру, ответственному за принятие торгового решения. На основании рыночного состояния и текущего состояния счёта она формирует тензор действий.

if(!cActor.feedForward(GetPointer(bAccount), 1, false, GetPointer(cEncoder), LatentLayer))
  {
   PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
   Stop = true;
   break;
  }

Принятое решение оценивается Критиком, который определяет насколько разумным является оно в данных условиях.

if(!cCritic.feedForward(GetPointer(cActor), -1, GetPointer(cEncoder), LatentLayer))
  {
   PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
   Stop = true;
   break;
  }

После осуществления прямого прохода нам необходимо дать обратную связь моделям. Сначала корректируются параметры моделей-прогнозирования.

//--- Study
for(uint f = 0; f < caForecast.Size(); f++)
   if(!caForecast[f].backProp(Result, (CBufferFloat*)NULL) ||
     !cEncoder.backPropGradient((CBufferFloat*)NULL))
     {
     PrintFormat("%s -> %d - Forecast %d", __FUNCTION__, __LINE__, f);
      Stop = true;
      break;
     }

Оценка действий Актера строится на основе расчёта вознаграждения: изменения капитала, нормализованного к эталонному балансу. В случае убытка, штраф удваивается, чтобы сделать обратную связь жёстче и убедительнее. Полученное вознаграждение передаем Критику. А от него спускаем градиент ошибки до Актера и Энкодера.

//---
cActor.getResults(Action);
double equity = bAccount[2] * bAccount[0] * EtalonBalance / (1 + bAccount[1]);
double reward = CheckAction(Action, equity, posit - NForecast + 1) / EtalonBalance;
if(reward < 0)
   reward *= 2;
Result.Clear();
if(!Result.Add(float(reward)))
  {
   PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
   Stop = true;
   break;
  }
if(!cCritic.backProp(Result, GetPointer(cEncoder), LatentLayer) ||
  !cActor.backPropGradient(GetPointer(cEncoder), LatentLayer, -1, false) ||
  !cEncoder.backPropGradient((CBufferFloat*)NULL, NULL, LatentLayer, true))
 {
   PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
   Stop = true;
  break;
  }

Так происходит первое обучение: на основе фактической реакции рынка на выбранное действие.

Но на этом процесс не заканчивается. В дело вступает вторая часть подхода — обучение с учителем. Вместо того, чтобы ориентироваться только на реальный отклик рынка, система использует информацию, которая в реальной торговле недоступна: знание будущего. Для каждого состояния вычисляется почти идеальная эталонная траектория — действие, которое привело бы к наилучшему результату, если судить по последующему движению цены. Это действие передаётся Актеру, и он сравнивает его с собственной политикой. Таким образом, мы обучаем стратегию не только методом проб и ошибок, но и даём ей чёткий ориентир, на что следует равняться. Такая двухслойная схема (фактический и идеализированный контроль) ускоряет обучение и делает поведение модели более устойчивым и рациональным.

//--- Oracul
if(!Action.AssignArray(target_action))
  {
   PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
   Stop = true;
   break;
  }
reward = CheckAction(Action, equity, posit - NForecast + 1) / EtalonBalance;
if(!cActor.backProp(Action, GetPointer(cEncoder), LatentLayer) ||
   !cEncoder.backPropGradient((CBufferFloat*)NULL, NULL, LatentLayer, true))
  {
   PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
   Stop = true;
   break;
  }

Использование эталонного действия не ограничивается обучением Актера. Мы также передаём это действие на вход Критику, который, в отличие от первого прохода, оценивает заведомо правильное поведение. После прямого прохода, с этим идеализированным действием осуществляется обратное распространение ошибки до Энкодера. Это позволяет Критику более точно уловить структуру функции вознаграждения, получить дополнительную информацию о тех участках пространства состояний, где поведение Агента должно быть особенно чётким, и, как следствие, повысить свою эффективность при последующем обучении Актера.

if(!cCritic.feedForward(Action, 1, false, GetPointer(cEncoder), LatentLayer))
  {
   PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
   Stop = true;
   break;
  }
if(!Result.Update(0, float(reward)))
  {
   PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
   Stop = true;
   break;
  }
if(!cCritic.backProp(Result, GetPointer(cEncoder), LatentLayer) ||
   !cEncoder.backPropGradient((CBufferFloat*)NULL, NULL, LatentLayer, true))
  {
   PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
   Stop = true;
   break;
  }
//---

Таким образом, завершается полный цикл обучения для одного состояния. Причём обучение идёт сразу по двум траекториям: через реальное поведение и через эталонное. Такой двойной контур позволяет не только быстрее снижать ошибку, но и формировать внутренние представления, устойчивые к рыночному шуму и локальным флуктуациям.

По ходу всей процедуры, с заданной частотой, в терминале обновляется визуальный отчёт. На экране отображаются средние ошибки всех моделей. Эти данные дают разработчику возможность в реальном времени следить за прогрессом обучения, оценивать стабильность процесса и выявлять возможные сбои или аномалии.

    if(GetTickCount() - ticks > 500)
      {
       double percent = (epoch + 1.0 - double(posit - end) / 
                        (start - end - HistoryBars - NForecast))
                        / Epochs * 100.0;
       string str = "";
       for(uint f = 0; f < caForecast.Size(); f++)
          str += StringFormat("%-12s%d %6.2f%% -> Error %15.8f\n", "Forecast", f,
                                 percent, caForecast[f].getRecentAverageError());
       str += StringFormat("%-12s %6.2f%% -> Error %15.8f\n", "Actor", percent, 
                                                 cActor.getRecentAverageError());
       str += StringFormat("%-12s %6.2f%% -> Error %15.8f\n", "Critic", percent, 
                                                cCritic.getRecentAverageError());
       Comment(str);
       ticks = GetTickCount();
      }
   }
}

Когда обучение по всем эпохам завершено, алгоритм подводит итоги — показывает усреднённую ошибку каждой из моделей. После этого советник отключается.

   Comment("");
//---
   for(uint f = 0; f < caForecast.Size(); f++)
      PrintFormat("%s -> %d -> %-15s%d %10.7f", __FUNCTION__, __LINE__, "Forecast", f, 
                                               caForecast[f].getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", 
                                                      cActor.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, 
                                            "Critic",cCritic.getRecentAverageError());
   ExpertRemove();
//---
  }

В итоге метод Train демонстрирует, как можно построить обучение торговой стратегии, опираясь одновременно на реальные результаты действий и на идеальные эталоны, полученные из будущего. Такая архитектура обеспечивает не просто адаптацию к прошлым данным, а направленное движение в сторону потенциальной прибыли.

Полный код данного советника, как и всех программ, используемых при подготовке статьи, представлен во вложении.

Тестирование

Как уже упоминалось, весь процесс обучения модели был выстроен в два последовательных этапа. На первом из них мы использовали офлайн-обучение, проведённое на исторических данных валютной пары EURUSD с таймфреймом H1 за весь 2024 год. Этот период, охватывает широкий спектр рыночных сценариев — от протяжённых боковиков до стремительных трендовых движений, от вялых, сонных периодов до взрывных всплесков волатильности. Такое разнообразие позволило модели познакомиться с типовыми и нетипичными ситуациями, что критически важно для надёжности и универсальности.

В процессе обучения Энкодер научился вычленять в рыночной информации повторяющиеся закономерности, сжимать их в компактное, но насыщенное признаками представление. Это внутреннее состояние рынка стало основой, на которой Актёр, используя обратную связь от Критика, формировал устойчивую стратегию, способную эффективно работать в разных условиях. В дополнение к этому, на этапе офлайн-обучения ему предоставлялись так называемые почти идеальные траектории — эталонные действия, сформированные на основе знания будущего ценового движения. Эти подсказки не только направляли политику в сторону увеличения прибыли, но и обеспечивали надёжный ориентир при формировании стратегии, особенно на начальных этапах обучения, когда собственный опыт модели ещё ограничен.

После завершения офлайн-обучения мы перешли ко второму этапу — тонкой онлайн-настройке, проводимой уже в условиях, приближённых к реальному рынку. Обучение велось в тестере стратегий MetaTrader 5, где модель шаг за шагом, свеча за свечой, анализировала рынок в потоковом режиме. Это не только позволило протестировать устойчивость модели к шуму, рыночным искажениям и случайным колебаниям, но и стало важным инструментом адаптации: модель не просто запоминала, а действительно училась работать в реальных, непредсказуемых условиях. Такой подход существенно повысил её живучесть, снизил переобучение и улучшил обобщающую способность.

Финальным шагом стало тестирование модели на полностью новых данных — котировках за период с Января по Март 2025 года. Все параметры и внутренние настройки, используемые в ходе обучения, были сохранены без изменений. Таким образом, полученные результаты позволяют объективно оценить не только точность, но и прикладную надёжность предложенного подхода.

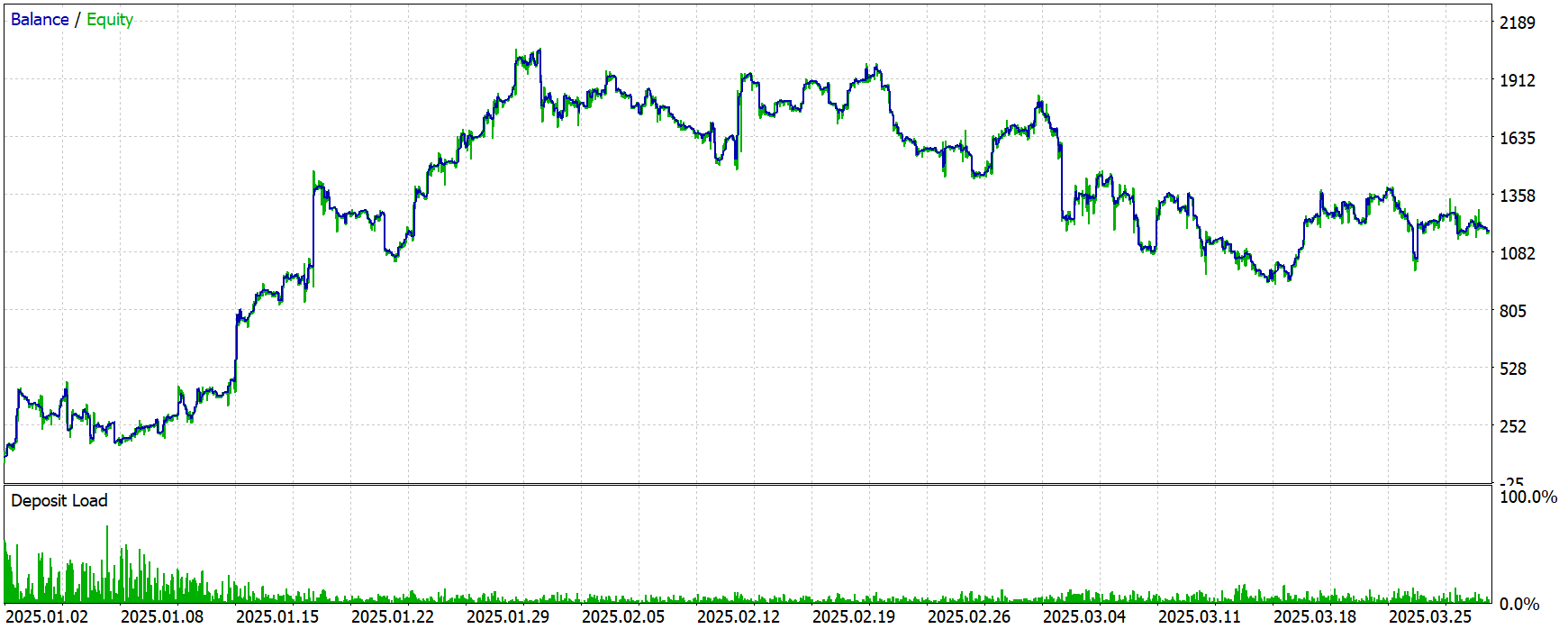
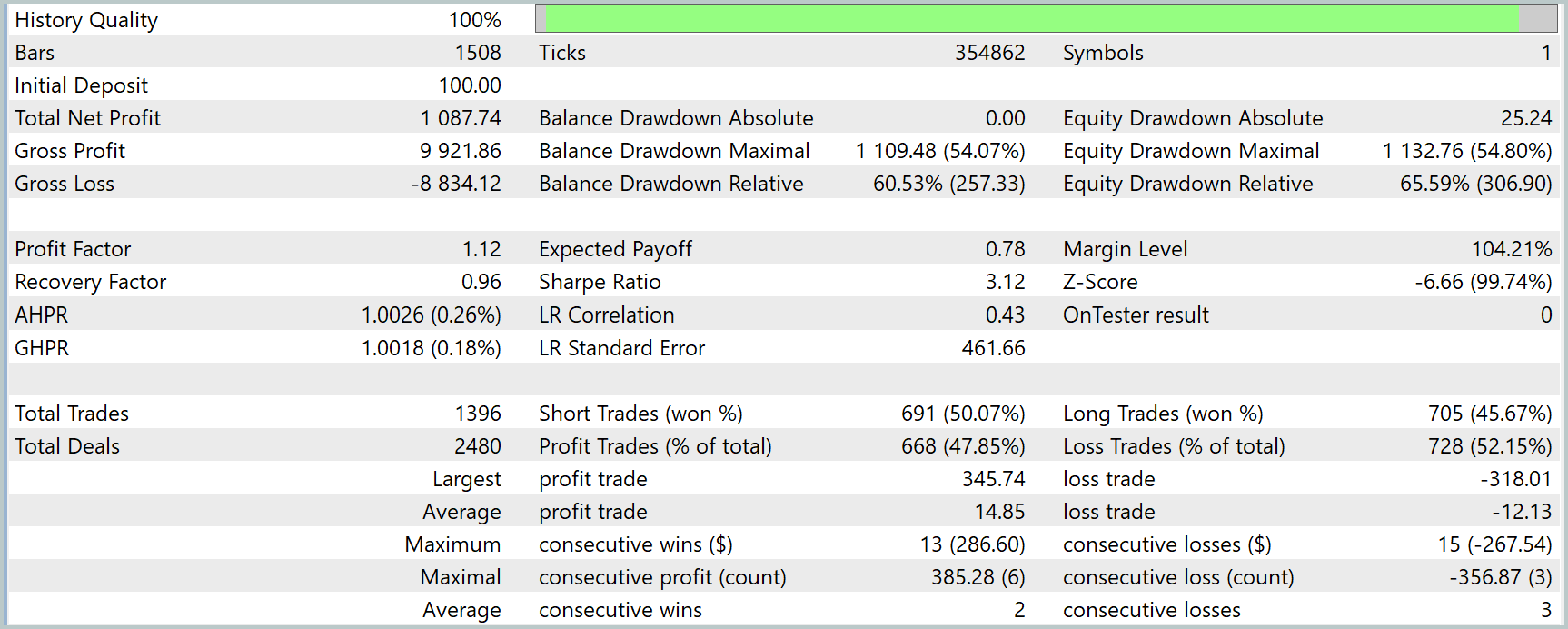
Результаты тестирования модели позволяют получить объективное представление о её реальной эффективности и устойчивости вне обучающей выборки. Начальный депозит в $100 был увеличен до $1087.74, что эквивалентно приросту капитала более чем в 10 раз — результат на первый взгляд впечатляющий. Однако, если копнуть глубже, становится заметна характерная особенность: модель демонстрирует высокую эффективность в начале тестового периода, а затем — с отдалением от обучающей выборки — её результативность начинает снижаться.

График баланса чётко отражает этот эффект. Первая треть периода сопровождается быстрым ростом, почти эталонной траекторией с минимальными просадками и стабильным приростом. Однако, начиная с середины февраля и особенно в марте, кривая выходит на плато и даже демонстрирует признаки ухудшения — растут колебания, увеличиваются серии убыточных сделок, и заметно снижается темп прибыли.

Этот эффект подтверждается и числовыми метриками. Коэффициент восстановления (Recovery Factor) составляет менее 1 (0.96), что говорит о неидеальном соотношении прибыли к глубине просадки. Относительная просадка по equity достигает 65.59% — это довольно высокий уровень риска, особенно с учётом того, что абсолютная просадка в начале теста была близка к нулю. Фактор прибыли (Profit Factor) равен 1.12 — минимально допустимое значение для стратегии, которая претендует на устойчивую работу. Равновесие между прибыльными и убыточными сделками также смещено не в пользу модели: доля прибыльных трейдов составляет менее 48%.

Такое поведение логично объясняется ограниченностью обучающей выборки. Модель тренировалась на данных только за 2024 год, и хотя в них были представлены разные рыночные фазы, рынок остаётся живым и изменчивым организмом. По мере удаления от известного периода, модель всё чаще сталкивается с ситуациями, которые ей не знакомы. Без дополнительных обучающих эпизодов её поведение становится всё менее релевантным, особенно в новых волатильных условиях.

Одним из очевидных путей решения этой проблемы является расширение обучающей выборки. Включение данных за предыдущие годы — например, с 2020 или даже с 2015 года — может позволить модели охватить гораздо более широкий спектр рыночных сценариев. Это обеспечит не только большую обобщающую способность, но и лучшее понимание редких, но критически важных паттернов поведения цены. Альтернативой также может стать постепенное онлайн-обучение с периодическим обновлением весов модели по мере поступления новых данных, что позволит сохранить её актуальность без полного переобучения.

Заключение

В ходе работы мы продемонстрировали практическую применимость фреймворка GinAR в условиях реального рынка. От построения архитектуры и поэтапного обучения до финального тестирования — весь процесс подтвердил жизнеспособность предложенного подхода.

Несмотря на высокие показатели в начале тестового периода, дальнейшая динамика выявила естественные ограничения модели, связанные с узкой обучающей выборкой. Это подчёркивает фундаментальный принцип работы с временными рядами: устойчивость стратегии напрямую зависит от её способности обобщать знания за пределами обучающего контекста.

Полученные результаты дают прочную основу для дальнейших исследований и доработок. В частности, очевидным направлением развития становится расширение объёма обучающих данных и внедрение механизма непрерывного обучения. Всё это открывает перспективы для построения действительно адаптивных и интеллектуальных торговых систем, способных не просто выживать, но и стабильно зарабатывать в сложных рыночных условиях.

Ссылки

• GinAR: An End-To-End Multivariate Time Series Forecasting Model Suitable for Variable Missing
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Study.mq5	Советник	Советник офлайн обучения моделей
2	StudyOnline.mq5	Советник	Советник онлайн обучения моделей
3	Test.mq5	Советник	Советник для тестирования модели
4	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
5	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
6	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы