Нейросети в трейдинге: Вероятностное прогнозирование временных рядов (Окончание)

MetaTrader 5 — Торговые системы | 11 июля 2025, 14:25

163

Dmitriy Gizlyk

Введение

Финансовые временные ряды остаются одним из самых трудно поддающихся типов данных для анализа. Их поведение сложно назвать стабильным: здесь нет чётких закономерностей, а присутствует комбинация трендов, циклов, шума и неожиданных структурных сдвигов. По этой причине традиционные модели линейной регрессии или скользящих средних, несмотря на простоту и скорость, в большинстве случаев оказываются недостаточными. С другой стороны, современные нейросетевые решения, обладающие колоссальной выразительной способностью, часто страдают от переобучения, нестабильности и отсутствия интерпретируемости.

В таких условиях особенно интересны гибридные подходы, сочетающие проверенные временем математические конструкции с гибкостью нейросетей. Именно на этом балансе построен фреймворк K²VAE — система, созданная для анализа и прогнозирования временных рядов, с учётом их реалий. Ключевым достоинством данного фреймворка является способность улавливать скрытую динамику системы, обучаясь на последовательностях рыночных состояний и корректируя свои выводы по мере поступления новых данных.

Фреймворк базируется на трёх фундаментальных идеях, каждая из которых дополняет другую и компенсирует её слабые стороны. Первая — это представление Купмана, суть которого заключается в том, чтобы перевести поведение нелинейной системы в линейное подпространство. Эта трансформация, пусть и приближённая, даёт мощный инструмент для описания и прогнозирования, позволяя работать с временными рядами не на уровне поверхностных статистик, а через реконструкцию глубинной динамики.

Вторая идея — использование фильтра Калмана, но не в его канонической форме, а в стабилизированной, подходящей для применения в стохастических нейросетевых архитектурах. Фильтр Калмана здесь выполняет функцию адаптивного корректора: он уточняет оценки, полученные из модуля KoopmanNet, опираясь на новые наблюдения, и одновременно даёт информацию о степени уверенности в каждом прогнозе. Это особенно ценно, когда речь идёт не просто о прогнозировании цен, а об оценке вероятности определённых сценариев.

Третья идея — интеграция вариационного автоэнкодера. Он позволяет строить не точечные, а вероятностные прогнозы: вместо одного возможного сценария мы получаем целое распределение, в котором отражены и основной тренд, и возможные отклонения.

Таким образом, K²VAE становится не просто очередной моделью в арсенале анализа, а системой, способной количественно описывать неопределённость, принимать во внимание альтернативные сценарии и адаптироваться к новым рыночным условиям.

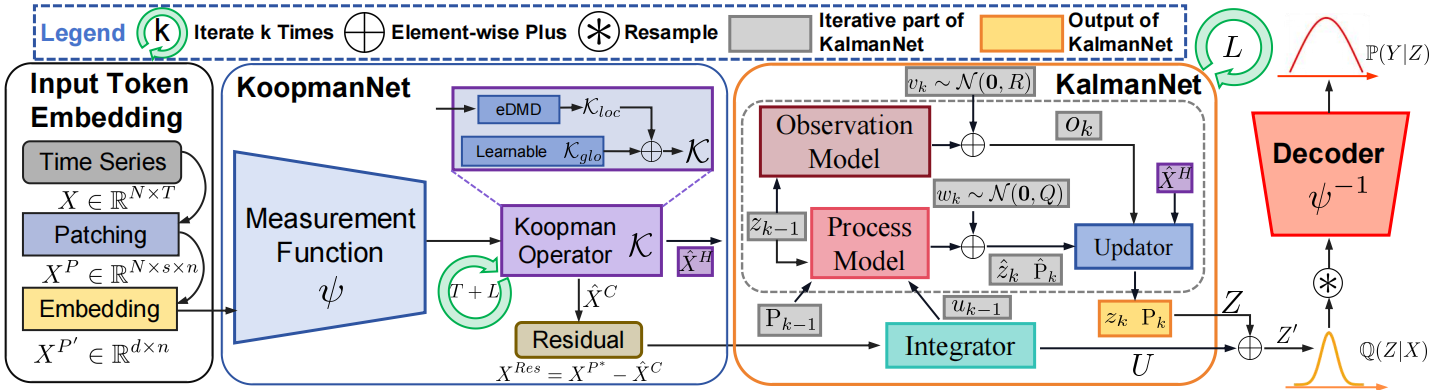
Авторская визуализация фреймворка K²VAE

В предыдущих работах мы уже подробно рассмотрели ключевые компоненты этого фреймворка. Было описано, как работает KoopmanNet, как формируется латентное представление, каким образом фильтр Калмана интегрируется в архитектуру, и как происходит совместное обучение всех элементов. Особое внимание было уделено стабильности вычислений и механике распространения информации внутри модели.

Архитектура модели

После поэтапного построения отдельных компонентов, составляющих архитектурную основу фреймворка K²VAE, мы переходим к следующей логической стадии — интеграции всех элементов в единую функциональную систему.

Следует подчеркнуть, что, как и в предыдущих работах, наша цель не заключается в построении прогностической модели в её классическом, изолированном виде. Прогноз здесь — лишь побочный продукт, вторичный по отношению к более фундаментальной задаче: созданию выразительного и устойчивого латентного представления текущего состояния среды. Это представление не просто обобщает поступающую информацию, но и служит ключевым входом для принятия торгового решения со стороны обучаемого Агента.

Таким образом, фреймворк K²VAE мы рассматриваем не как самостоятельную модель прогнозирования, а как продвинутый Энкодер состояния окружающей среды, встроенный в ранее реализованную архитектуру на основе подхода Actor–Director–Critic. Здесь VAE-компонент становится механизмом генерации вероятностного описания будущих сценариев, KoopmanNet отвечает за линейную динамику в скрытом пространстве, а фильтр Калмана выполняет корректировку и уточнение с учётом поступающих наблюдений. Всё это работает на одну цель — дать Агенту такую репрезентацию внешней среды, которая содержит максимум полезной информации для принятия взвешенных, статистически обоснованных торговых решений.

Внедрение компонентов K²VAE в архитектуру Actor–Director–Critic позволяет придать системе необходимую глубину и устойчивость. Благодаря этому, латентное состояние, формируемое Энкодером, несёт в себе информацию не только о текущем положении дел, но и о вероятных траекториях его изменения. Это качественно улучшает поведение Агента: он не просто реагирует на текущие сигналы, а действует с учётом возможных вариантов развития событий, что особенно важно в условиях высокой волатильности и непредсказуемости рынка.

Здесь на сцену выходит метод CreateDescriptions. Именно он отвечает за сборку всех архитектурных описаний — от Энкодера и модулей прогнозирования до компонентов принятия решений. Этот метод создаёт фундамент для будущего обучения, определяя, какие слои и в каком порядке будут использоваться внутри каждого компонента нашей системы.

bool CreateDescriptions(CArrayObj *&encoder,
                        CArrayObj *&forecast1,
                        CArrayObj *&forecast2,
                        CArrayObj *&forecast3,
                        CArrayObj *&actor,
                        CArrayObj *&director,
                        CArrayObj *&critic
                       )
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
   if(!forecast1)
     {
      forecast1 = new CArrayObj();
      if(!forecast1)
         return false;
     }
   if(!forecast2)
     {
      forecast2 = new CArrayObj();
      if(!forecast2)
         return false;
     }
   if(!forecast3)
     {
      forecast3 = new CArrayObj();
      if(!forecast3)
         return false;
     }
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!director)
     {
      director = new CArrayObj();
      if(!director)
         return false;
     }
   if(!critic)
     {
      critic = new CArrayObj();
      if(!critic)
         return false;
     }

В параметрах метода мы получаем указатели на ряд динамических массивов — по одному для каждой из моделей. Это контейнеры, в которые будет записано архитектурное описание нейросетевых блоков. Прежде чем переходить к их наполнению, мы выполняем обязательную проверку корректности полученных указателей. При отсутствии нужного объекта, мы не пытаемся работать с висячей памятью, а аккуратно создаём новый экземпляр массива. Этот шаг может показаться технической рутиной, но на практике именно он закладывает стабильность всей дальнейшей работы.

После этого начинается основная часть — наполнение каждого массива соответствующими слоями и связями, формирующими полную конфигурацию нейросети. Начнём с центрального элемента системы — Энкодера состояния окружающей среды. Именно в этот компонент мы интегрируем основные идеи, заложенные в фреймворке K²VAE. Напомним, что задача Энкодера — не просто собрать информацию о рыночной ситуации, а создать выразительное и информативное латентное представление, способное послужить надёжной основой для принятия торговых решений Агентом.

Сырые исходные данные, поступающие напрямую от терминала передаём в полносвязный слой. Здесь он выполняет роль интерфейса между внешним миром и внутренней логикой модели.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   uint prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormWithNoise;
   descr.count = prev_count;
   descr.batch = BatchSize;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Далее данные передаются на этап первичной обработки — слой пакетной нормализации. Именно здесь разнородные входные признаки, различающиеся по масштабу, диапазону или физическому смыслу, приводятся к сопоставимому виду. Этот шаг важен не только с точки зрения числовой стабильности, но и с позиции обучения всей модели: нормализованные данные позволяют нейросети быстрее сходиться и более точно улавливать зависимости между признаками.

Пакетная нормализация в данном контексте действует как фильтр, сглаживающий статистический шум и выравнивающий распределения отдельных компонент входного сигнала. Это создаёт устойчивую и предсказуемую среду для дальнейших преобразований, минимизируя искажения на начальном этапе обработки.

После нормализации данные готовы к следующему важному этапу — пространственному разделению или патчингу. Авторы оригинального фреймворка K²VAE предлагают делить подготовленные исходные данные на неперекрывающиеся патчи, каждый из которых представляет собой фрагмент общего потока информации. При этом значения из различных каналов смешиваются внутри одного патча, что позволяет модели естественным образом обучаться выявлению перекрёстных зависимостей между признаками.

Однако в нашей реализации мы пошли дальше и решили не ограничиваться стандартной схемой патчинга, а внедрили более сложную структуру, вдохновлённую рядом современных архитектур, ранее рассмотренных в наших статьях. Вначале дополнительно обогащаем входной массив признаков — добавляем производные, отражающие пошаговые отклонения значений каждого канала. Это позволяет учесть краткосрочную динамику сигналов и усилить чувствительность модели к изменениям структуры рынка, сохраняя при этом устойчивость к шуму.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatDiff;
   prev_count = descr.count = HistoryBars;
   descr.layers = BarDescr;
   descr.step = 1;
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Затем к данным добавляются временные метки — важный элемент, позволяющий модели учитывать не только значения признаков, но и их положение во времени. Эти метки предоставляют нейросети контекст о фактическом моменте наступления события, будь то минута, час, день недели или иной масштаб. Благодаря этому, модель получает возможность выявлять повторяющиеся паттерны и сезонные колебания, характерные для финансовых временных рядов. Введение такой временной информации особенно важно при работе с историческими котировками, где цикличность играет ключевую роль в формировании торговых стратегий.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defMamba4CastEmbeding;
   prev_count = descr.count = HistoryBars;
   descr.window = 2 * BarDescr;
   uint prev_out = descr.window_out = NSkills;
     {
      uint temp[] = {PeriodSeconds(PERIOD_H1), PeriodSeconds(PERIOD_D1)};
      if(ArrayCopy(descr.windows, temp) < (int)temp.Size())
         return false;
     }
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = prev_count;
   prev_count = descr.window = prev_out;
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
   prev_out = descr.count;

Здесь стоит особо подчеркнуть важный момент: разные каналы входной информации могут обладать различной внутренней ритмикой, то есть демонстрировать отличающиеся по периоду циклы. В таких условиях простое механическое объединение значений из всех каналов в единый поток может нивелировать скрытые сезонные зависимости и исказить динамику сигналов.

Чтобы избежать потери этих особенностей, мы внедрили механизм адаптивной свёртки. Его задача — анализировать характер каждой временной последовательности и формировать патчи с учётом индивидуальных особенностей канала. Таким образом, каждому каналу обеспечивается одинаковое количество представлений в латентном пространстве, и при этом сохраняется чувствительность к его уникальной цикличности.

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronAdaptConv;
   descr.count = Segments;
   descr.window = 2 * prev_out / Segments;
   descr.variables = prev_count;
   prev_out = descr.window_out = EmbeddingSize;
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
   prev_count = descr.count;
   uint prev_var = descr.variables;

К сформированным патчам мы добавляем RoPE-кодирование (Rotary Positional Encoding), которое обеспечивает модели знание относительного положения каждого элемента во временной последовательности. В отличие от классических позиционных кодировок, RoPE внедряет информацию о позиции через вращение вектора признаков в латентном пространстве. Это позволяет сохранять временную структуру данных при последующей обработке трансформерными слоями, а также эффективно передавать информацию о расстояниях между событиями. Такой подход особенно важен в задачах анализа временных рядов, где порядок и интервал между событиями играют критическую роль.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRoPE;
   descr.count = prev_count;
   descr.window = prev_out;
   descr.variables = prev_var;
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Далее мы выполняем транспонирование полученного трёхмерного тензора, представляющего собой патчи независимых каналов, в формат временной последовательности смешанных патчей. Это преобразование позволяет перейти от структуры вида [Каналы × Патчи × Признаки] к более подходящей для обработки последовательной модели форме [Патчи × Каналы × Признаки], где каждый патч теперь представляет собой временной срез, содержащий данные со всех каналов одновременно. Таким образом, мы подготавливаем данные к последующей обработке в K²VAE-энкодере, фокусируя внимание модели на взаимосвязях между признаками в рамках общего временного потока.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeRCDOCL;
   descr.count = prev_var;
   descr.window = prev_count;
   descr.step = prev_out;
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Подобное представление данных полностью соответствует ключевым идеям, заложенным авторами фреймворка K²VAE, в частности — стремлению к интеграции разнородной информации в едином латентном пространстве. Однако, в отличие от базовой реализации, мы сохранили важные свойства структуры временных рядов, в частности — цикличность отдельных каналов, что критически важно для финансовых данных. Более того, за счёт расширенного патчинга, пошаговых отклонений и временных меток мы обогатили входное представление, усилив способность модели распознавать устойчивые шаблоны и сезонные зависимости, не теряя при этом нюансов индивидуальных источников данных.

Сформированные патчи, содержащие обогащённую и структурированную информацию о текущем состоянии среды, передаются в K²VAE-энкодер. На этом этапе происходит вероятностное кодирование: каждая входная последовательность трансформируется в распределение эмбеддингов на выходе блока. Каждый отдельный эмбеддинг в этом распределении представляет собой компактное, но выразительное, сжатое описание одного из возможных сценариев развития анализируемого временного ряда. Таким образом, модель формирует не просто точечную оценку будущего состояния, а множество вероятностных гипотез, отражающих разнообразие потенциальных траекторий. Это особенно важно в условиях высокой неопределённости, присущей финансовым рынкам.

//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronK2VAEEncoder;
     {
      uint temp[] = {prev_count,                        // units in
                     NScenarios,                        // Scenarios
                     NExperts,                          // MoE
                     TopK                               // Top K
                    };
      if(ArrayCopy(descr.units, temp) < int(temp.Size()))
         return false;
     }
   descr.step = NHeads;
     {
      uint temp[] = {prev_out * prev_var,               // window
                     prev_out * prev_var / descr.step,  // dimension Key
                     2 * prev_out*prev_var / NExperts   // dimension MoE
                    };
      if(ArrayCopy(descr.windows, temp) < int(temp.Size()))
         return false;
     }
   descr.layers = 3;
   descr.variables = 1;
   descr.batch = BatchSize;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Здесь следует обратить внимание, что именно распределение в латентном пространстве, полученное на выходе K²VAE-энкодера, и будет передаваться Агенту для последующего принятия торгового решения. Однако, чтобы обеспечить выразительность и практическую ценность этого латентного состояния, а именно его способность содержать информацию о наиболее вероятных сценариях будущего поведения временного ряда, нам необходимо выстроить полноценный поток прогнозирования внутри модели.

Как уже отмечалось ранее, целью нашего фреймворка не является создание точного прогноза в его классическом понимании. Тем не менее, нам необходимо организовать поток обучения так, чтобы градиент ошибки мог распространяться от финального результата обратно к каждому элементу вероятностного распределения эмбеддингов. Для этого мы добавляем специализированный слой TimeMoEAttention.

Этот слой выполняет важную функцию: он агрегирует вероятностные эмбеддинги, формируя на их основе единое представление, и тем самым создаёт необходимую видимость традиционной модели прогнозирования. Такое решение позволяет нам совместить вероятностную природу латентного пространства с требованиями обучаемости и оптимизации, обеспечив полноценное обучение распределения с опорой на финальный результат.

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTimeMoEAttention;
   descr.window_out = EmbeddingSize;
     {
      uint temp[] = {prev_out, prev_out, 8, TopK};               //Window Main, Window Cross, Experts dimension, TopK
      if(ArrayCopy(descr.windows, temp) < ArraySize(temp))
         return false;
     }
     {
      uint temp[] = {prev_var, prev_var * NScenarios, NExperts}; //Units Main, Units Cross, Experts
      if(ArrayCopy(descr.units, temp) < ArraySize(temp))
         return false;
     }
   descr.layers = 3;
   descr.step = NHeads;                                          // Attention heads
   descr.batch = BatchSize;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }//---
   CLayerDescription *latent = descr;

Далее переходим к формированию архитектуры трёх классических моделей прогнозирования, каждая из которых отвечает за предсказание на своём горизонте планирования — краткосрочном, среднем и дальнем. Эти модели выполняют важную роль: они разворачивают полученное латентное представление, сформированное в энкодере, обратно в пространство наблюдаемых данных. Таким образом, каждое состояние получает интерпретацию в терминах реальных величин, отражающих возможные сценарии будущего поведения временного ряда.

Следует отметить, что архитектуры этих моделей прогнозирования были подробно рассмотрены в наших предыдущих работах. Они доказали свою эффективность на практике, и именно по этой причине были напрямую заимствованы без изменений. В рамках текущей статьи мы не будем углубляться в технические детали их построения.

Следующим логическим шагом становится построение архитектуры торгового Актера — центрального элемента системы принятия решений. Его задача — на основе доступной информации выбрать наилучшее торговое действие. В отличие от классических предсказательных моделей, Актер не пытается напрямую прогнозировать будущее поведение рынка, а использует вероятностное описание возможных сценариев, предоставленное Энкодером, для оценки потенциальной эффективности каждого из возможных действий.

Модель Актера получает на вход два источника информации. Первый — это текущее состояние баланса, включая активные позиции, капитал и другую служебную информацию. Второй — распределение латентных представлений, полученное из K²VAE-энкодера, где каждое представление описывает один из возможных вариантов развития рыночной ситуации в будущем. Это распределение не только несёт информацию о наиболее вероятных траекториях, но и передаёт уровень неопределённости модели относительно этих сценариев.

В качестве первого, как и ранее, мы используем полносвязный слой, выполняющий роль внешнего интерфейса модели. Именно через него Актер получает на вход информацию о состоянии баланса.

//--- Actor
   latent = encoder.At(LatentLayer);
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = AccountDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = AccountDescr;
   descr.batch = BatchSize;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Полученные на вход данные приводятся в сопоставимый вид с помощью слоя пакетной нормализации. Это позволяет устранить масштабные различия между признаками и обеспечить стабильную работу последующих слоёв модели, вне зависимости от исходных величин и природы данных.

После приведения данных о состоянии счёта к сопоставимому виду, они передаются в модуль кросс-внимания, который рассматривает эту информацию в контексте вероятностного распределения последующих состояний среды.

Здесь важно отметить одно ключевое отличие от классических моделей: Актёр не просто реагирует на текущую ситуацию, а оценивает риски принятия решения с учётом ширины и формы распределения будущих сценариев. Чем выше уверенность Энкодера в прогнозе (а это выражается в более узком и сконцентрированном распределении), тем меньший разброс сценариев получает Актёр. В таком случае он может действовать более решительно — например, повышать объём позиции или использовать более агрессивные параметры сделки. Таким образом, стратегия адаптивно подстраивается под изменяющуюся степень неопределённости рынка.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronCrossDMHAttention;
     {
      uint temp[] = {AccountDescr,           // Inputs window
                     latent.windows[0]       // Cross window
                    };
      if(ArrayCopy(descr.windows, temp) < (int)temp.Size())
         return false;
     }
     {
      uint temp[] = {1,                      // Inputs units
                     latent.units[1]         // Cross units
                    };
      if(ArrayCopy(descr.units, temp) < (int)temp.Size())
         return false;
     }
   descr.step = NHeads;                      // Heads
   descr.window_out = 8;
   descr.batch = 1e4;
   descr.layers = 2;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Затем, обработанная информация поступает в трёхслойную полносвязную нейросеть (MLP), которая завершает цепочку обработки и формирует итоговое торговое решение. Именно на этом этапе происходит интеграция всех признаков: текущего состояния счёта, вероятностного представления будущего и контекста, выявленного с помощью механизма внимания. Модель анализирует совокупность этих факторов и определяет направление сделки и её параметры. Эта структура, несмотря на кажущуюся простоту, играет решающую роль в обеспечении гибкости и адаптивности всей торговой системы.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.batch = BatchSize;
   descr.activation = TANH;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = TANH;
   descr.batch = BatchSize;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 2 * NActions;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

На выходе Актёра используется стохастическая голова генерации торгового решения, реализованная через слой CNeuronVAEOCL.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronVAEOCL;
   descr.count = NActions;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = NActions / 3;
   descr.window = 3;
   descr.step = 3;
   descr.window_out = 3;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

На первый взгляд, подобное решение может показаться чрезмерно рискованным: объединение вероятностного распределения будущих сценариев с вероятностной же природой головы Актёра действительно увеличивает долю случайности в процессе принятия решений. И в контексте реальных рыночных условий это вызывает закономерные опасения.

Однако суть подхода заключается в том, что стохастическая природа Актера проявляется в полной мере лишь на ранних этапах обучения модели. В этот период Актёр активно исследует возможные варианты поведения, обучаясь на широком спектре реакций среды. По мере накопления опыта и переоценки полученных результатов, распределение выходов становится всё более концентрированным вокруг наилучших стратегий, а разброс — уменьшается. В результате, поведение Актёра стабилизируется, приобретая направленность и фокус, необходимые для уверенного принятия решений в условиях реального рынка.

Оценочные модели Режиссёра и Критика во многом повторяют архитектуру Актёра, сохраняя общий каркас и принципы обработки данных. Главное отличие заключается в источнике основного потока исходных данных: вместо состояния баланса, они принимают на вход тензор действий, сгенерированных Актёром. Это позволяет им оценивать каждое действие более предметно и детально.

При этом стохастическая голова принятия решений, характерная для Актёра, здесь отсутствует. Вместо вероятностного распределения действий, Режиссёр и Критик формируют конкретные оценки и сигналы качества для каждого действия. Такая детализированная обратная связь помогает Актёру уточнять свои стратегии и повышать эффективность торговых решений.

Полный исходный код, описывающий архитектурное решение всех моделей, представлен во вложении.

Обучение

После завершения этапа построения архитектуры всех компонентов модели, мы переходим к следующему шагу — процессу обучения. Как и в предыдущих работах, процесс организован в два этапа. На первом этапе мы проводим офлайн-обучение на исторических данных, доступных непосредственно из терминала. Особенность подхода заключается в том, что обучение осуществляется без необходимости в заранее подготовленной обучающей выборке. Вместо этого, мы внедряем внутрь самой обучающей процедуры механизм оценки действий — благодаря этому значительно расширяется охват исторических данных, доступных для начального этапа обучения, и снимается ограничение на ручную разметку или формирование специализированных датасетов.

Здесь стоит обратить особое внимание на один важный момент, выявленный в ходе предыдущих экспериментов. При использовании модели оценки действий Актера на ограниченном горизонте прогнозируемых состояний, наблюдается устойчивое негативное поведение. Модель склонна формировать чрезмерно амбициозные уровни стоп-лосса и тейк-профита, которые не успевают реализоваться в рамках заданного окна оценки. Это приводит к систематическому пересиживанию убытков, когда убыточные позиции удерживаются слишком долго, без достаточных оснований для разворота или выхода из рынка. Такое поведение становится доминирующим, и модель фактически теряет способность реагировать на краткосрочные изменения рынка, сводя стратегию к пассивному следованию за глобальным трендом.

Для борьбы с этим эффектом были внесены два ключевых изменения в процедуру обучения. Во-первых, мы существенно снизили коэффициент дисконтирования (Discount Factor), сместив акцент в сторону получения быстрой прибыли. Это решение позволяет модели фокусироваться на ближайших результатах своих действий, придавая больший вес краткосрочным последствиям. Ведь текущие убытки в рамках такого подхода оказывают более значительное влияние на итоговое вознаграждение, чем потенциальная прибыль в далёком будущем, даже если последняя и выглядит более внушительно. Таким образом, модель начинает избегать стратегий, основанных на пассивном ожидании разворота рынка, и снижает склонность к нежелательному пересиживанию убытков, повышая свою адаптивность к реальной рыночной динамике.

Второе, уже конструктивное решение было реализовано в методе CheckAction. Здесь мы отказались от оценки действий в пределах ограниченного горизонта прогнозирования и перешли к подходу, при котором оценка производится на всём доступном историческом отрезке. Такой шаг позволяет значительно повысить точность обратной связи, ведь в подавляющем большинстве случаев мы точно знаем, какой из торговых уровней (стоп-лосс или тейк-профит) будет достигнут в рамках этой расширенной истории. Это, в свою очередь, даёт более объективную оценку каждому действию и позволяет обучающей системе чётче различать эффективные и неэффективные решения.

double CheckAction(CBufferFloat *action, double equity, uint start_position)
  {
   if(!action || start_position >= Rates.Size())
      return 0;

В параметрах метода мы получаем:

action — тензор торгового действия: объёмы, уровни SL/TP;
equity — текущее состояние Эквити, используемое для оценки максимальной просадки;
start_position — индекс состояния открытия позиции в массиве рыночных данных Rates.

Метод начинается с проверки актуальности указателя на объект action и индекса стартовой позиции, который не должен выходить за пределы массива котировок.

Далее происходит извлечение параметров сделки.

double buy_lot = MathMax(double(action[0] - action[3]), 0);
double sell_lot = MathMax(double(action[3] - action[0]), 0);

Таким образом, система поддерживает раздельную подачу объёма по направлению. Например, если action[0] > action[3], предполагается открытие buy-позиции, в противном случае — sell.

Затем вычисляется маржинальное обеспечение по текущей цене, рассчитывается стоимость одного пункта движения (point_cost), и в случае недостаточного объёма (меньше минимально допустимого), метод возвращает ожидаемый убыток (недополученную прибыль), основанный на амплитуде свечи.

double marg = 0;
if(!OrderCalcMargin(ORDER_TYPE_BUY, Symb.Name(), 1, Symb.Ask(), marg))
   return 0;
double point_cost = Symb.TickValue() / Symb.TickSize();
if(MathMax(buy_lot, sell_lot) < Symb.LotsMin())
  {
   double loss = -MathMax(Rates[start_position].high - Rates[start_position].open,
                          Rates[start_position].open - Rates[start_position].low) *
                 point_cost * equity / (2 * marg);
   return loss;
  }
if((marg * MathMax(buy_lot, sell_lot)) >= equity)
  {
   double loss = -MathMax(Rates[start_position].high - Rates[start_position].open,
                          Rates[start_position].open - Rates[start_position].low) *
                 point_cost * MathMax(buy_lot, sell_lot);
   return loss;
  }
point_cost *= MathAbs(buy_lot - sell_lot);

Аналогичная ситуация в случае завышенного объёма, не покрываемого доступными средствами (marg * lot > equity). Это стимулирует модель к совершению сделок в пределах допустимых средств, исключая бездействие.

Далее переходим к проверке эффективности предложенных действий. Сначала поверяем длинные позиции.

//---
  double tp = 0, sl = 0, profit = 0, reward = 0;
  int stops = MathMax(Symb.StopsLevel(), 10);
  int spread = Symb.Spread();
  if(buy_lot > 0)
    {
     tp = action[1] * MaxTP;
     sl = action[2] * MaxSL;
     if(int(tp) < stops || int(sl) < (stops + spread))
       {
        double loss = -MathMax(Rates[start_position].high - Rates[start_position].open,
                               Rates[start_position].open - Rates[start_position].low) *
                      point_cost * buy_lot;
        return loss;
       }
     tp = (tp + spread) * Symb.Point() + Rates[start_position].open;
     sl = Rates[start_position].open - (sl + spread) * Symb.Point();
     reward = profit = -spread * Symb.Point() * point_cost;

Извлекаются уровни TakeProfit и StopLoss из элементов тензора action. После чего они масштабируются и проверяются на соответствие уровню стопов брокера.

Если условия допустимы, TP и SL преобразуются в абсолютные ценовые значения. В противном случае рассчитываем размер недополученной прибыли.

Далее происходит симуляция движения цены на отрезке исторических данных. Для этого организовываем цикл перебора исторических данных в хронологической последовательности.

Здесь следует обратить внимание, что массив Rates является таймсерией. Поэтому для сохранения исторической последовательности, перебор данных осуществляется в обратном порядке.

for(uint i = start_position; i >=0; i--)
  {
   if(sl >= Rates[i].low)
     {
      double p = (Rates[i].open - sl) * point_cost;
      profit -= p;
      reward -= p * MathPow(DiscFactor, float(i - start_position));
      break;
     }

В теле цикла реализуется строго риск-ориентированный подход: приоритет в проверке отдаётся уровню стоп-лосса. Это решение продиктовано здравым смыслом — убытки на рынке, как правило, наступают внезапно и гораздо быстрее, чем накапливается прибыль. В случае достижения уровня стопа, определяется размер убытка в денежном выражении и с учетом фактора дисконтирования.

Применение фактора дисконтирования позволяет гибко балансировать между быстрыми и отложенными результатами, обучая модель выбирать действия, ведущие к стабильной доходности. Чем выше фактор, тем сильнее модель ориентирована на долгосрочные выгоды, и наоборот. Однако у этой гибкости есть оборотная сторона: использование дисконтирования затрудняет корректную оценку глубокой просадки. Убытки, наступающие через значительное количество шагов, подвергаются серьёзному обесцениванию и могут быть восприняты моделью как малозначимые. В результате модель склонна пересиживать убыточные позиции в надежде на разворот, что в условиях реального рынка может привести к фатальной просадке до уровня StopOut. Чтобы избежать подобного поведения, помимо дисконтированной оценки применяется контроль абсолютной просадки.

Аналогичным образом проверяется достижения уровня тейк-профита.

if(tp <= Rates[i].high)
  {
   double p = (tp - Rates[i].open) * point_cost;
   profit += p;
   reward += p * MathPow(DiscFactor, float(i - start_position));
   break;
  }

Если ни один из торговых уровней не достигнут, то текущая прибыль/убыток фиксируются по цене открытия последующей свечи.

double p = (Rates[i - 1].open - Rates[i].open) * point_cost;
profit += p;
reward += p * MathPow(DiscFactor, float(i - start_position));

Здесь особенно важно подчеркнуть использование именно цены открытия следующего бара, а не цены закрытия текущего. Хотя в большинстве случаев эти значения совпадают или различаются несущественно, мы обязаны учитывать особенности рыночной динамики. Наша модель принимает торговое решение на открытии нового бара, и потому корректно учитывать именно эту цену при фиксации результатов незакрытых позиций.

Такой подход позволяет сохранить реалистичность симуляции и не игнорировать вероятность появления ценовых разрывов — гэпов, характерных для высоковолатильных участков рынка или моментов выхода значимых новостей. Использование цены открытия следующего бара также акцентирует внимание на последовательности торговых событий, подчеркивая причинно-следственную логику между принятым решением и его реализацией в условиях реального рынка.

Далее мы сравниваем накопленные убытки без учета фактора дисконтирования с уровнем Эквити на момент открытия позиции. Такой подход позволяет контролировать достаточность средств для выполнения торговой операции. Если убытки превышают доступный капитал — то есть происходит слив депозита — мы увеличиваем штраф в функции вознаграждения и немедленно завершаем процесс симуляции. Это имитирует реальную ситуацию на рынке, когда недостаток средств приводит к остановке торговой деятельности, и обеспечивает более точную и безопасную оценку торговой стратегии в процессе обучения модели.

    if(-profit >= equity)
      {
       reward-=1000;
       break;
      }
   }
}

Аналогичным образом проводим оценку короткой позиции.

   if(sell_lot > 0)
     {
      tp = action[4] * MaxTP;
      sl = action[5] * MaxSL;
      if(int(tp) < stops || int(sl) < (stops + spread))
        {
         double loss = -MathMax(Rates[start_position].high - Rates[start_position].open,
                                Rates[start_position].open - Rates[start_position].low) *
                       point_cost * sell_lot;
         return loss;
        }
      tp = Rates[start_position].open - (tp + spread) * Symb.Point();
      sl = Rates[start_position].open + (sl - spread) * Symb.Point();
      for(uint i = start_position; i >=0; i--)
        {
         if(sl <= Rates[i].high)
           {
            double p = (sl - Rates[i].open) * point_cost;
            profit -= p;
            reward -= p * MathPow(DiscFactor, float(i - start_position));
            break;
           }
         if(tp >= Rates[i].low)
           {
            double p = (Rates[i].open - tp) * point_cost;
            profit += p;
            reward += p * MathPow(DiscFactor, float(i - start_position));
            break;
           }
         double p = (Rates[i - 1].open - Rates[i].open) * point_cost;
         profit -= p;
         reward -= p  * MathPow(DiscFactor, float(i - start_position));
         if(-profit >= equity)
           {
            reward-=1000;
            break;
           }
        }
     }
//---
   return reward;
  }

После чего, завершаем работу метода, вернув накопленное вознаграждение с учетом фактора дисконтирования вызывающей программе.

Полный код советника офлайн-обучения модели "…\Experts\K2VAE\Study.mq5" представлен во вложении. Там же представлены все программы, используемые при подготовке статьи.

Тестирование

Как уже упоминалось, обучение модели осуществляется в два последовательных этапа. Сначала мы провели офлайн-обучение на 15-летней истории пары EURUSD с таймфреймом H1. Этот массив данных охватывает все типы рыночных ситуаций: от длительных боковиков до резких трендов, от спокойных периодов до всплесков волатильности. Благодаря этому, модель смогла изучить разнообразие рыночного поведения. Энкодер научился выделять ключевые закономерности и преобразовывать состояние рынка в компактное, но информативное представление, которое стало основой для принятия решений Агентом. Актёр же, используя обратную связь от Критика и Режиссёра, формировал устойчивую стратегию, способную эффективно работать в разных условиях.

Далее последовал второй этап — онлайн-обучение на данных 2024 года, организованному в тестере стратегий MetaTrader 5. Здесь модель работала в режиме, приближенном к реальному времени, анализируя рынок свеча за свечой. Она сталкивалась с шумами, случайными колебаниями и искажениями, характерными для живого рынка. Такой подход позволил не просто дообучить модель, но и адаптировать её поведение к реальной динамике, улучшить стратегию и повысить устойчивость при неопределённости.

По завершении обучения, мы провели тестирование на новых данных — котировках за Январь–Март 2025 года, с сохранением всех параметров, используемых при обучении. Результаты тестирования приведены ниже.

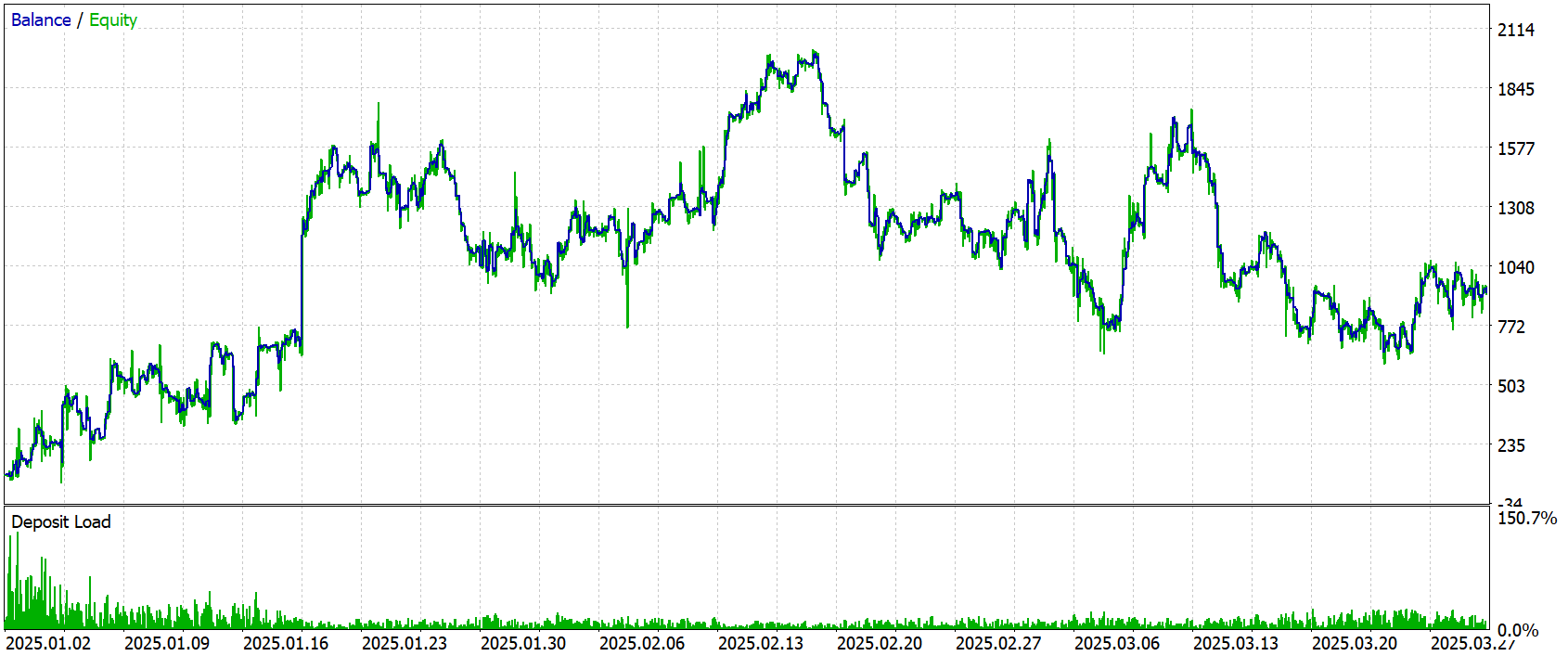
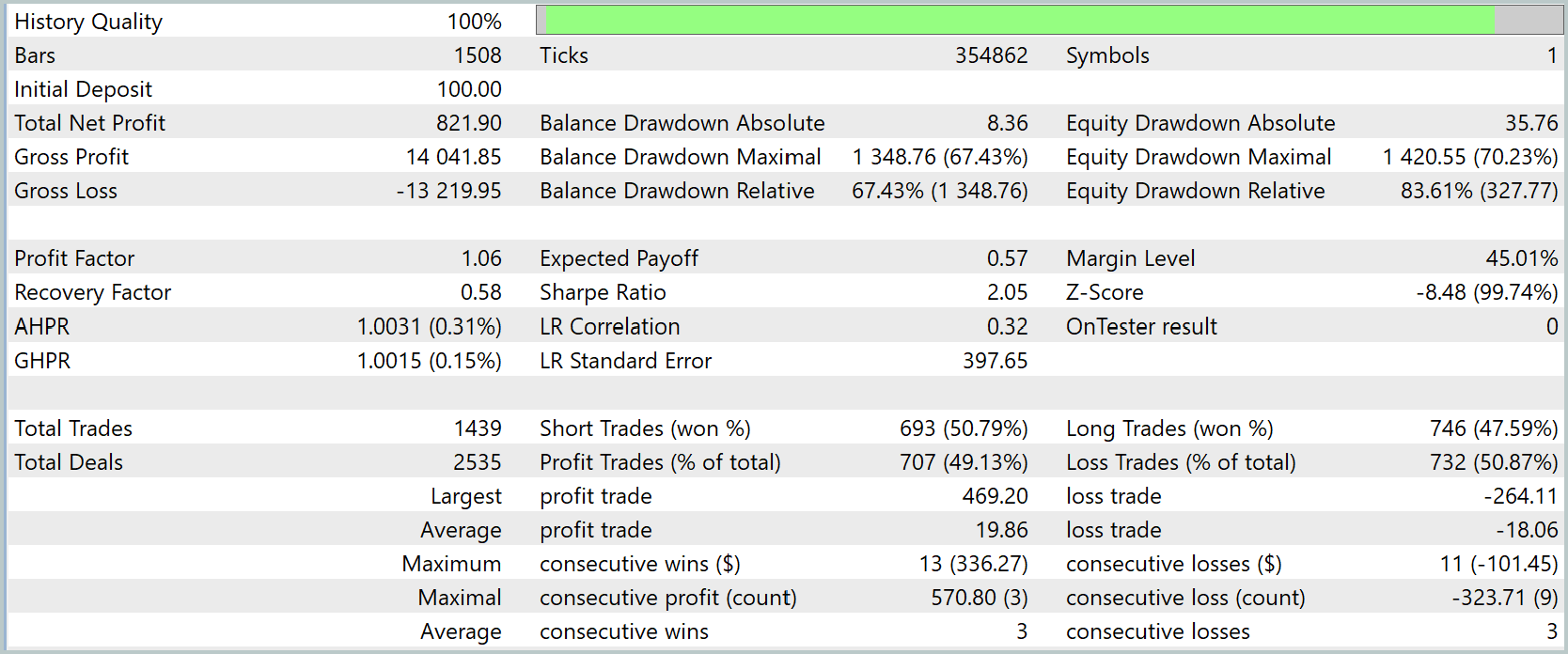
Результаты тестирования

Результаты тестирования показывают, что модель продемонстрировала положительную прибыль на выбранном историческом периоде. Общий чистый доход составил $821.90 при начальном депозите $100.0, что говорит о росте капитала. При этом следует отметить, что коэффициент прибыльности (Profit Factor) находится на уровне 1.06 — это указывает на незначительное превосходство прибыли над убытками.

Из торговых показателей видно, что количество прибыльных сделок примерно равно количеству убыточных — около 49% и 51% соответственно, что говорит о балансе между выигрышными и проигрышными позициями.

На графике видно, что кривая баланса в целом растет, несмотря на заметные просадки и периоды снижения. Особое внимание обращает явная тенденция к росту баланса в Январе и первой половине Февраля. При этом Март месяц выглядит явно убыточным. Это может свидетельствовать о необходимости дообучения модели на более длительном отрезке истории.

Заключение

В заключение отметим, что предложенный фреймворк K²VAE в составе нашего торгового агента доказал свою работоспособность и получил подтверждение в условиях реальной исторической выборки. Модель сочетает в себе глубокое понимание скрытой динамики рынка, адаптивную корректировку рисков и генерацию вероятностных сценариев, что позволило добиться роста капитала. Вместе с тем, снижение эффективности на длительном отрезке тестирования говорит о необходимости поиска путей повышения обобщающей способности модели.

Ссылки

Программы, используемые в статье

#	Имя	Тип	Описание
1	Study.mq5	Советник	Советник офлайн обучения моделей
2	StudyOnline.mq5	Советник	Советник онлайн обучения моделей
3	Test.mq5	Советник	Советник для тестирования модели
4	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
5	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
6	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы

Прикрепленные файлы |

Загрузить ZIP

MQL5.zip (2916.14 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Оценка качества торговли спредами по факторам сезонности на рынке Форекс в терминале MetaTrader 5

В статье рассматривается оценка качества сезонного торгового подхода на дневном таймфрейме — как для отдельных символов, так и для спредов. Особое внимание уделяется выявлению повторяющихся месячных циклов и возможностям их применения в торговле в рамках текущего года.

Создание торговой панели администратора на MQL5 (Часть VII): Доверенный пользователь, восстановление и криптография

Подсказки безопасности, например те, которые появляются каждый раз при обновлении графика, добавлении новой пары в чат с панелью администратора советника или перезапуске терминала, могут стать утомительными. В этом обсуждении мы рассмотрим и реализуем функцию, которая отслеживает количество попыток входа в систему для идентификации доверенного пользователя. После определенного количества неудачных попыток приложение перейдет к расширенной процедуре входа в систему, которая также облегчает восстановление пароля для пользователей, которые могли его забыть. Кроме того, мы рассмотрим, как можно эффективно интегрировать криптографию в панель администратора для повышения безопасности.

Особенности написания экспертов

Написание и тестирование экспертов в торговой системе MetaTrader 4.

Разрабатываем мультивалютный советник (Часть 28): Добавляем менеджер закрытия позиций

При параллельной работе многих стратегий может возникнуть желание время от времени закрывать все открытые позиции и начинать работу стратегий заново. Уже написанный код позволяет реализовать такое поведение только вместе с ручными манипуляциями. Попробуем автоматизировать эту часть.