MetaTrader 5 / Торговые системы
English 中文 Español Deutsch 日本語 Português
preview
Машинное обучение и Data Science (Часть 13): Анализируем финансовый рынок с помощью метода главных компонент (PCA)

Машинное обучение и Data Science (Часть 13): Анализируем финансовый рынок с помощью метода главных компонент (PCA)

MetaTrader 5 — Торговые системы | 11 мая 2023, 15:23
1 094 0
Omega J Msigwa
Omega J Msigwa

Метод главных компонент — это фундаментальный метод анализа данных и машинного обучения, который широко используется в самых различных приложениях, начиная от обработки изображений и сигналов и заканчивая финансами и социальными науками. 

Введение

Метод главных компонент — это метод уменьшения размерности, который часто используется для уменьшения размерности больших датасетов путем преобразования большого набора переменных в меньший, который по-прежнему содержит большую часть информации из большого набора.

Уменьшение количества переменных в выборке обычно происходит за счет уменьшения точности, но хитрость в уменьшении размерности заключается в том, чтобы немного пожертвовать точностью ради упрощения. Мы с вами знаем, что небольшое количество переменных в датасете легче исследовать и визуализировать, а сам анализ данных становится намного проще и быстрее для алгоритмов машинного обучения. Лично я не считаю, что выбор простоты в обмен на точность — это плохо, если речь идет об области торговли. Точность не обязательно означает прибыль.

pca article image

Основная идея метода проста: уменьшить количество переменных в наборе данных, сохраняя при этом как можно больше информации. Давайте посмотрим, из каких шагов состоит алгоритм метода главных компонент.


Шаги алгоритма метода PCA

  1. Стандартизация данных
  2. Вычисление ковариационной матрицы
  3. Вычисление собственных векторов и собственных значений
  4. Вычисление оценок PCA и их стандартизация
  5. Получение компонент

Сразу начнем со стандартизации данных.


1. Стандартизация данных

Цель стандартизации состоит в том, чтобы привести все переменные к одному масштабу, чтобы их можно было сравнивать и анализировать на общей основе. При анализе данных часто бывает, что мы имеем дело с переменными, имеющими разные единицы измерения или шкалы измерения, что может привести к некорректным результатам и неверным выводам. Например, скользящее значение имеет диапазон значений такой же, как и цены на рынке, а индикатор RSI обычно имеет значения от 0 до 100. Эти две переменные невозможно сравнить при совместном использовании в любой модели. То есть их в чистом виде сочетать или использовать для сравнения нельзя.

Стандартизация данных представляет собой преобразование каждой переменной таким образом, чтобы она имела среднее значение равное нулю, а в качестве стандартного отклонения — единицу. Это гарантирует, что каждая переменная имеет одинаковый масштаб и распределение, что делает их сопоставимыми. Стандартизация данных также может помочь повысить точность и стабильность моделей машинного обучения, особенно когда переменные имеют разные величины или отклонения.

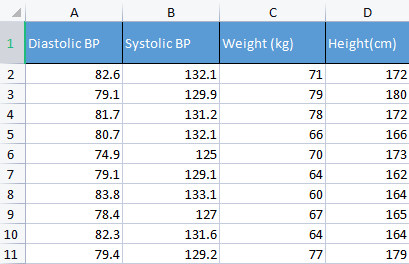
Чтобы продемонстрировать этот момент, будем использовать данные по артериальному давлению. Обычно я использую различные не относящиеся к теме данные, просто чтобы лучше понять основы. Например, как сейчас, данные, связанные с человеком, которые легче понять и отладить.

   matrix Matrix = matrix_utiils.ReadCsv("bp data.csv");

   pre_processing = new CPreprocessing(Matrix, NORM_STANDARDIZATION);

До и после:

CS      0       10:17:31.956    PCA Test (NAS100,H1)    Non-Standardized data
CS      0       10:17:31.956    PCA Test (NAS100,H1)    [[82.59999999999999,132.1,71,172]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [79.09999999999999,129.9,79,180]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [81.7,131.2,78,172]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [80.7,132.1,66,166]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [74.90000000000001,125,70,173]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [79.09999999999999,129.1,64,162]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [83.8,133.1,60,164]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [78.40000000000001,127,67,165]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [82.3,131.6,64,164]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [79.40000000000001,129.2,77,179]]
CS      0       10:17:31.956    PCA Test (NAS100,H1)    Standardized data
CS      0       10:17:31.956    PCA Test (NAS100,H1)    [[0.979632638610581,0.8604038253411385,0.2240645398825688,0.3760399462363875]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.4489982926965129,-0.0540350228475094,1.504433339211528,1.684004976623816]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.6122703991316175,0.4863152056275964,1.344387239295408,0.3760399462363875]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.2040901330438764,0.8604038253411385,-0.5761659596980309,-0.6049338265541837]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-2.163355410265021,-2.090739730176784,0.06401843996644889,0.539535575034816]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.4489982926965129,-0.3865582403706605,-0.8962581595302708,-1.258916341747898]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [1.469448957915872,1.276057847245071,-1.536442559194751,-0.9319250841510407]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.7347244789579271,-1.259431686368917,-0.416119859781911,-0.7684294553526122]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.8571785587842599,0.6525768143891719,-0.8962581595302708,-0.9319250841510407]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.326544212870186,-0.3449928381802696,1.184341139379288,1.520509347825387]]

В контексте метода главных компонент стандартизация данных является важным шагом, поскольку метод основан на ковариационной матрице, которая чувствительна к различиям в масштабе и разнице между переменными. Стандартизация данных перед запуском метода гарантирует, что в полученных главных компонентах не будут преобладать переменные с большей величиной или дисперсией, что может исказить анализ и привести к ошибочным выводам.


2. Вычисление ковариационной матрицы

Ковариационная матрица — это матрица, которая содержит измерение того, насколько случайные переменные влияют на изменение вместе. Она используется для вычисления ковариации между каждым столбцом матрицы данных. Ковариация между двумя совместно распределенными действительными случайными величинами X и Y с конечными вторыми моментами определяется как:

Ничего страшного, если вы не понимаете эту формулу. Уже есть готовая функция в стандартной библиотеке языка MQL5. 

   matrix Cova = Matrix.Cov(false);

   Print("Covariances\n", Cova);  

Результат

CS      0       10:17:31.957    PCA Test (NAS100,H1)    Covariances
CS      0       10:17:31.957    PCA Test (NAS100,H1)    [[1.111111111111111,1.05661579634328,-0.2881675653452953,-0.3314539233600543]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [1.05661579634328,1.111111111111111,-0.2164241126576326,-0.2333966556085017]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.2881675653452953,-0.2164241126576326,1.111111111111111,1.002480628180182]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.3314539233600543,-0.2333966556085017,1.002480628180182,1.111111111111111]]

Напомню, что ковариация представляет собой квадратную матрицу со значениями 1 по диагонали. При вызове этого метода матрицы ковариации нужно установить для входа rowval значение false.

matrix matrix::Cov( 
  const bool    rowvar=true  // rows or cols vectors of observations 
);

потому нам нужно, чтобы наша квадратная матрица была единичной матрицей на основе столбцов, которые мы задаем этой функции, и у нас есть 4 столбца. На выходе будет матрица 4x4, иначе это была бы матрица 8x8.


3. Вычисление собственных векторов и собственных значений

Собственные векторы представляют собой специальные векторы, связанные с квадратной матрицей. Собственный вектор матрицы — это ненулевой вектор, который при умножении на матрицу дает скалярное число, кратное самому себе, называемое собственным числом (значением).

Формально, если A — это квадратная матрица, то ненулевой вектор v является собственным вектором A, если существует скаляр λ, называемый собственным значением, чтобы Аv = λv. Подробнее можно почитать здесь.

Как и прежде, не обязательно знать и понимать формулу расчета — можно воспользоваться функцией из стандартной библиотеки.

   if (!Cova.Eig(component_matrix, eigen_vectors))
      Print("Failed to get the Component matrix matrix & Eigen vectors");

Если посмотреть на метод Eig внимательнее

bool matrix::Eig( 
  matrix&  eigen_vectors,     // matrix of eigenvectors  
  vector&  eigen_values       // vector of eigenvalues  
   );

Можно заметить, что первая входная матрица eigen_vectors возвращает собственные векторы. Но этот собственный вектор можно также отнести к компонентной матрице. Поэтому я храню эти собственные векторы в матрице компонент, так как название их собственными векторами может запутывать, учитывая, что по стандартам языка MQL5 на самом деле это матрица.

Print("\nComponent matrix\n",component_matrix,"\nEigen Vectors\n",eigen_vectors);

Результат

CS      0       10:17:31.957    PCA Test (NAS100,H1)    Component matrix
CS      0       10:17:31.957    PCA Test (NAS100,H1)    [[-0.5276049902734494,0.459884739531444,0.6993704635263588,-0.1449826035480651]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.4959779194731578,0.5155907011803843,-0.679399121133044,0.1630612352922813]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.4815459137666799,0.520677926282417,-0.1230090303369406,-0.6941734714553853]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.4937128827246101,0.5015643052337933,0.184842006606018,0.6859404272536788]]
CS      0       10:17:31.957    PCA Test (NAS100,H1)    Eigen Vectors
CS      0       10:17:31.957    PCA Test (NAS100,H1)    [2.677561590453738,1.607960239905343,0.04775016337426833,0.1111724507110918]


5. Вычисление оценок PCA

Найти результаты метода главных компонент очень просто, и для этого требуется всего одна строка кода.

 pca_scores = Matrix.MatMul(component_matrix);

Чтобы найти оценки метода, нудно нормализованную матрицу умножить на матрицу компонентов.

Результат

CS      0       10:17:31.957    PCA Test (NAS100,H1)    PCA SCORES
CS      0       10:17:31.957    PCA Test (NAS100,H1)    [[-0.6500472384886967,1.199407986803537,0.1425145462368588,0.1006701620494091]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [1.819562596624738,1.393614599196321,-0.1510888243020112,0.1670753033981925]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.2688014256048517,1.420914385142756,0.001937917070391801,-0.6847663538666366]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-1.110534258768705,-0.06593596223641518,-0.4827665581567511,0.09571954869438426]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [2.475561333978323,-1.768915328424386,-0.0006861487484489809,0.2983796568520111]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.6245145789301378,-1.503882637300733,-0.1738415909335406,-0.2393186981373224]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-2.608156175249579,0.0662886285379769,0.1774740257067155,0.4223436077935874]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.4325302694103054,-1.589321053467977,0.2509606394263523,-0.337079680008286]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-1.667608250048573,-0.2034163217366656,0.09411419638842802,-0.03495245015036286]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [1.664404875867474,1.051245703485609,0.1413817973120564,0.2119289033750197]]

После получения оценок метода их нужно стандартизировать.

   pre_processing = new CPreprocessing(pca_scores_standardized, NORM_STANDARDIZATION);

Результат

CS      0       10:17:31.957    PCA Test (NAS100,H1)    PCA SCORES | STANDARDIZED
CS      0       10:17:31.957    PCA Test (NAS100,H1)    [[-0.4187491401035159,0.9970295470975233,0.68746486754918,0.3182591681100855]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [1.172130620033975,1.15846730049564,-0.7288256625700642,0.528192723531639]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.1731572094549987,1.181160740523977,0.009348167869829477,-2.164823873278453]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.715386880184365,-0.05481045923432144,-2.328780161211247,0.3026082735855334]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [1.594713612332284,-1.470442808583469,-0.003309859736641006,0.9432989819176616]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.4023014443028848,-1.250129598312728,-0.8385809690405054,-0.7565833632510734]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-1.68012890598631,0.05510361946569121,0.8561031894464458,1.335199254045385]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.2786284867625921,-1.321151824538665,1.210589566461227,-1.06564543418136]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-1.074244269325531,-0.1690934905926844,0.4539901733759543,-0.1104988556867913]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [1.072180711318756,0.8738669736790375,0.6820006878558206,0.6699931252073736]]


6. Получение компонент метода

И последнее, но не менее важное: нам нужно получить главные компоненты, что, собственно, и является главной целью всех тех шагов, которые мы делали до этого.

Чтобы получить компоненты, нам нужно сначала вычислить коэффициенты нестандартизированных оценок метода. Ведь теперь у нас есть две оценки метода: стандартизированная и нестандартизированная.

Коэффициенты каждой оценки метода — это просто дисперсия каждого столбца в столбце оценок.

   pca_scores_coefficients.Resize(cols);
   vector v_row;
   
   for (ulong i=0; i<cols; i++)
     {
       v_row = pca_scores.Col(i);
       
       pca_scores_coefficients[i] = v_row.Var(); //variance of the pca scores
     }  

Результат

2023.02.25 10:17:31.957 PCA Test (NAS100,H1)    SCORES COEFF [2.409805431408367,1.447164215914809,0.04297514703684173,0.1000552056399828]

Для извлечения компонент нужно рассмотреть критерии:

  1. Критерий собственного значения: этот критерий включает в себя выбор основных компонент с наибольшими собственными значениями. Идея состоит в том, что самые большие собственные числа соответствуют главным компонентам, которые охватывают наибольшую дисперсию данных.
  2. Критерий пропорции дисперсии: этот критерий включает в себя выбор основных компонент, которые объясняют определенную долю общей дисперсии данных. В этой библиотеке я установлю значение выше 90%.
  3. Критерий отсеивания: этот критерий включает в себя изучение графика, который показывает собственные значения каждой основной компоненты в порядке убывания. Точка, в которой кривая начинает выравниваться, используется в качестве порога для выбора основных компонент, которые необходимо сохранить.
  4. Критерий Кайзера: этот критерий предполагает сохранение только главных компонент с собственными значениями, превышающими среднее значение коэффициентов. Другими словами, это главная компонента с коэффициентами больше единицы.
  5. Критерий перекрестной проверки: этот критерий включает в себя оценку производительности модели на валидационной выборке и выбор основных компонент, обеспечивающих наилучшую точность прогнозирования.

В этой библиотеке реализованы три критерия, которые я считаю лучшими и самыми эффективными с точки зрения вычислений. Это доля дисперсии, график Кайзера и график отсеивания. Выбрать подходящий из них можно из перечисления:

enum criterion
  {
    CRITERION_VARIANCE,
    CRITERION_KAISER,
    CRITERION_SCREE_PLOT
  };

Ниже приведена полная функция для извлечения основных компонент:

matrix Cpca::ExtractComponents(criterion CRITERION_)
 {

  vector vars = pca_scores_coefficients;   
  vector vars_percents = (vars/(double)vars.Sum())*100.0;
  
//--- for Kaiser
  double vars_mean = pca_scores_coefficients.Mean();

//--- for scree 
   double x[], y[];
   
//---
  matrix PCAS = {};
  
  double sum=0;
  ulong  max;
  vector v_cols = {};
   
   switch(CRITERION_)
     {
      case  CRITERION_VARIANCE:       
       #ifdef DEBUG_MODE
        Print("vars percentages ",vars_percents);       
       #endif  
     
         for (int i=0, count=0; i<(int)cols; i++)
           { 
             count++;
             
              max = vars_percents.ArgMax();
              sum += vars_percents[max];
              
              vars_percents[max] = 0; 
              
              v_cols.Resize(count);
              v_cols[count-1] = (int)max;
                   
              if (sum >= 90.0)
		 break;
           }
         
         PCAS.Resize(rows, v_cols.Size());
         
         for (ulong i=0; i<v_cols.Size(); i++)
            PCAS.Col(pca_scores.Col((ulong)v_cols[i]), i);
         
        break;
      case  CRITERION_KAISER:
      
      #ifdef DEBUG_MODE
         Print("var ",vars," scores mean ",vars_mean);
      #endif 
      
       vars = pca_scores_coefficients;
        for (ulong i=0, count=0; i<cols; i++)
           if (vars[i] > vars_mean)
             {
               count++;
       
               PCAS.Resize(rows, count);
               
               PCAS.Col(pca_scores.Col(i), count-1);
             }           
           
        break;
      case  CRITERION_SCREE_PLOT:        
         v_cols.Resize(cols);     
         for (ulong i=0; i<v_cols.Size(); i++)
             v_cols[i] = (int)i+1;
             
         
          vars = pca_scores_coefficients;          
          SortAscending(vars); //Make sure they are in ascending first order
          ReverseOrder(vars);  //Set them to descending order
          
          VectorToArray(v_cols, x);
          VectorToArray(vars, y);
          
          plt.ScatterCurvePlots("Scree plot",x,y,"variance","PCA","Variance");

//---
       vars = pca_scores_coefficients;
        for (ulong i=0, count=0; i<cols; i++)
           if (vars[i] > vars_mean)
             {
               count++;       
               PCAS.Resize(rows, count);       
               PCAS.Col(pca_scores.Col(i), count-1);
             }    
             
        break;
     } 
   return (PCAS);
 }

Критерий Кайзера настроен на выбор основных компонентов с коэффициентами, объясняющими более 90% всех отклонений. Поэтому пришлось преобразовать отклонения в проценты:

  vector vars = pca_scores_coefficients;   
  vector vars_percents = (vars/(double)vars.Sum())*100.0;

Ниже приведены результаты использования каждого метода.

CRITERION KAISER:

CS      0       12:03:49.579    PCA Test (NAS100,H1)    PCA'S
CS      0       12:03:49.579    PCA Test (NAS100,H1)    [[-0.6500472384886967,1.199407986803537]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [1.819562596624738,1.393614599196321]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [0.2688014256048517,1.420914385142756]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [-1.110534258768705,-0.06593596223641518]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [2.475561333978323,-1.768915328424386]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [-0.6245145789301378,-1.503882637300733]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [-2.608156175249579,0.0662886285379769]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [0.4325302694103054,-1.589321053467977]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [-1.667608250048573,-0.2034163217366656]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [1.664404875867474,1.051245703485609]]

CRITERION VARIANCE:

CS      0       12:03:49.579    PCA Test (NAS100,H1)    PCA'S
CS      0       12:03:49.579    PCA Test (NAS100,H1)    [[-0.6500472384886967,1.199407986803537]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [1.819562596624738,1.393614599196321]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [0.2688014256048517,1.420914385142756]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [-1.110534258768705,-0.06593596223641518]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [2.475561333978323,-1.768915328424386]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [-0.6245145789301378,-1.503882637300733]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [-2.608156175249579,0.0662886285379769]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [0.4325302694103054,-1.589321053467977]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [-1.667608250048573,-0.2034163217366656]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [1.664404875867474,1.051245703485609]]

CRITERION SCREE PLOT:

scree plot

Отлично, теперь у нас есть две главные компоненты. Говоря простым языком, набор данных сокращается с 4 до 2 переменных. Далее эти переменные можно использовать в любом проекте, над которым вы работали.


Метод главных компонент в MetaTrader

Теперь пришло время использовать метод главных компонент для того, для чего мы все здесь собрались — для сферы трейдинга.

Для этого я взял 10 осцилляторов. Поскольку все они являются осцилляторами, я решил проверить их, чтобы доказать, что если у вас есть 10 индикаторов одного типа, можно использовать метод главных компонент, чтобы уменьшить их, чтобы в итоге получить несколько переменных, с которыми легко работать.

Я запустил 10 индикаторов на одном графике: ATR, Bears Power, MACD, Chaikin Oscillator, Commodity Channel Index, De marker, индекс силы, Momentum, RSI, процентный диапазон Вильямса.

   handles[0] = iATR(Symbol(),PERIOD_CURRENT, period);
   handles[1] = iBearsPower(Symbol(), PERIOD_CURRENT, period);
   handles[2] = iMACD(Symbol(),PERIOD_CURRENT,12, 26,9,PRICE_CLOSE);
   handles[3] = iChaikin(Symbol(), PERIOD_CURRENT,12,26,MODE_SMMA,VOLUME_TICK);
   handles[4] = iCCI(Symbol(),PERIOD_CURRENT,period, PRICE_CLOSE);
   handles[5] = iDeMarker(Symbol(),PERIOD_CURRENT,period);
   handles[6] = iForce(Symbol(),PERIOD_CURRENT,period,MODE_EMA,VOLUME_TICK);
   handles[7] = iMomentum(Symbol(),PERIOD_CURRENT,period, PRICE_CLOSE);
   handles[8] = iRSI(Symbol(),PERIOD_CURRENT,period,PRICE_CLOSE);
   handles[9] = iWPR(Symbol(),PERIOD_CURRENT,period);
   
   
   for (int i=0; i<10; i++)
    {
      matrix_utiils.CopyBufferVector(handles[i],0,0,bars,buff_v);
      ind_Matrix.Col(buff_v, i); //store each indicator in ind_matrix columns
    }

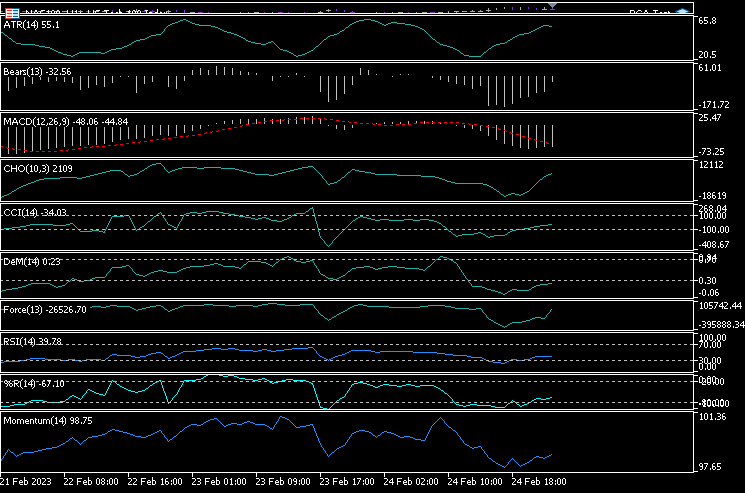
Все эти индикаторы я визуализировал на одном графике. Вот как они выглядят:

осцилляторы

Почему же все они все выглядят почти одинаково? Давайте посмотрим на их матрицу корреляции:

    Print("Oscillators Correlation Matrix\n",ind_Matrix.CorrCoef(false));  

Результат

CS      0       18:03:44.405    PCA Test (NAS100,H1)    Oscillators Correlation Matrix
CS      0       18:03:44.405    PCA Test (NAS100,H1)    [[1,0.01772984879133655,-0.01650305145071043,0.03046861668248528,0.2933315924162302,0.09724971519249033,-0.054459564042778,-0.0441397473782667,0.2171969726706487,0.3071254662907512]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [0.01772984879133655,1,0.6291675928958272,0.2432064602541826,0.7433991440764224,0.7857575973967624,0.8482060554701495,0.8438879842180333,0.8287766948950483,0.7510097635884428]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [-0.01650305145071043,0.6291675928958272,1,0.80889919514547,0.3583185473647767,0.79950773673123,0.4295059398014639,0.7482107564439531,0.8205910850439753,0.5941794310595322]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [0.03046861668248528,0.2432064602541826,0.80889919514547,1,0.03576792595345671,0.436675349452699,0.08175026884450357,0.3082792264724234,0.5314362133025707,0.2271361556104472]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [0.2933315924162302,0.7433991440764224,0.3583185473647767,0.03576792595345671,1,0.6368513319457978,0.701918992559641,0.6677393692960837,0.7952832674277922,0.8844891719743937]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [0.09724971519249033,0.7857575973967624,0.79950773673123,0.436675349452699,0.6368513319457978,1,0.6425071357003039,0.9239712092224102,0.8809179254503203,0.7999862160768584]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [-0.054459564042778,0.8482060554701495,0.4295059398014639,0.08175026884450357,0.701918992559641,0.6425071357003039,1,0.7573281438252102,0.7142333470379938,0.6534102287503526]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [-0.0441397473782667,0.8438879842180333,0.7482107564439531,0.3082792264724234,0.6677393692960837,0.9239712092224102,0.7573281438252102,1,0.8565660350098397,0.8221821793990941]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [0.2171969726706487,0.8287766948950483,0.8205910850439753,0.5314362133025707,0.7952832674277922,0.8809179254503203,0.7142333470379938,0.8565660350098397,1,0.8866871375902136]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [0.3071254662907512,0.7510097635884428,0.5941794310595322,0.2271361556104472,0.8844891719743937,0.7999862160768584,0.6534102287503526,0.8221821793990941,0.8866871375902136,1]]

Глядя на матрицу корреляции, можно заметить, что лишь несколько показателей коррелируют с некоторыми другими, но таких меньшинство, так что все-таки они не одинаковые. Давайте применим метод главных компонент к этой матрице и посмотрим, что он нам даст.

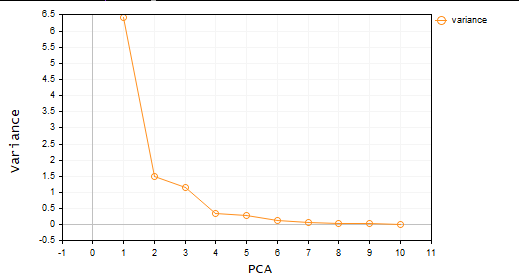
    pca = new Cpca(ind_Matrix);
    matrix pca_matrix = pca.ExtractComponents(ENUM_CRITERION);

Я выбрал критерий графика Scree:

График отсеивания осцилляторов

По графику понятно, что выбраны были только три главные компоненты, ниже показано, как они выглядят:

CS      0       15:03:30.992    PCA Test (NAS100,H1)    PCA'S
CS      0       15:03:30.992    PCA Test (NAS100,H1)    [[-2.297373513063062,0.8489493134565058,0.02832445955171548]
CS      0       15:03:30.992    PCA Test (NAS100,H1)     [-2.370488225540198,0.9122356709081817,-0.1170316144060158]
CS      0       15:03:30.992    PCA Test (NAS100,H1)     [-2.728297784013197,1.066014896296926,-0.2859442064697605]
CS      0       15:03:30.992    PCA Test (NAS100,H1)     [-1.818906988827231,1.177846546204641,-0.748128826146959]
...
...
CS      0       15:03:30.992    PCA Test (NAS100,H1)     [-3.26602969252589,0.4816995789189212,-0.7408982990360158]
CS      0       15:03:30.992    PCA Test (NAS100,H1)     [-3.810781495417407,0.4426824869307094,-0.5737277071364888…]

Только с 10 переменных остались только 3!

Вот почему очень важно быть не только трейдером, но и аналитиком. Я так часто видел трейдеров с большим количеством индикаторов на графике, а иногда даже и в советниках. Думаю, использование этого способа сокращения переменных стоит того с точки зрения уменьшения вычислительных затрат. Кстати, не воспринимайте это как торговый совет. Если то, что вы делаете, работает, и вы удовлетворены, то вам не о чем беспокоиться.

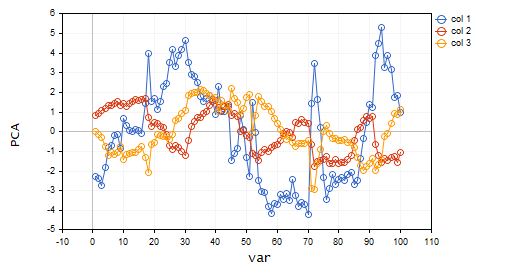
Давайте визуализируем эти главные компоненты, чтобы увидеть, как они выглядят на одной оси.

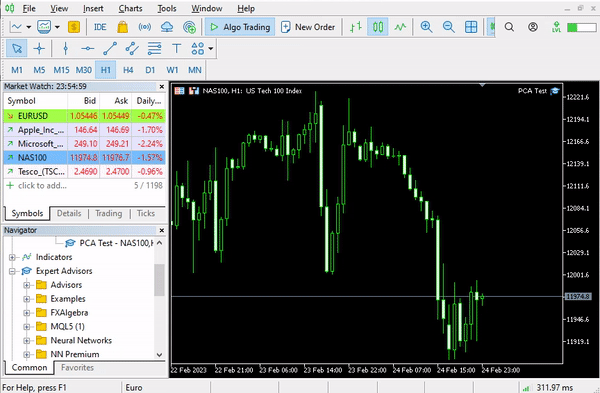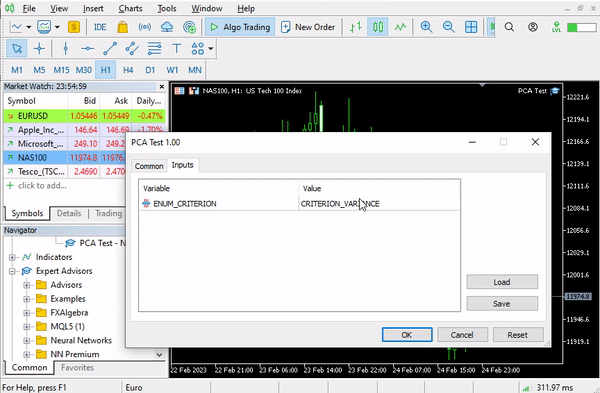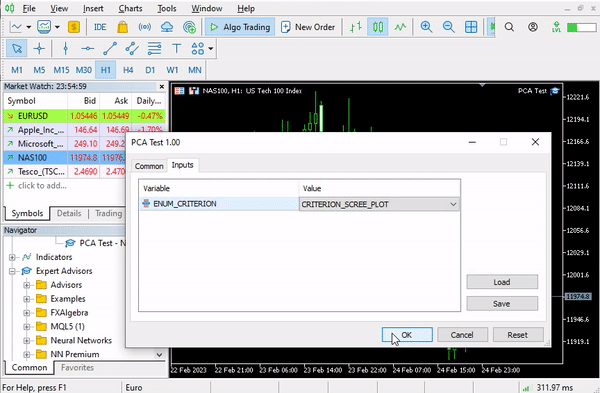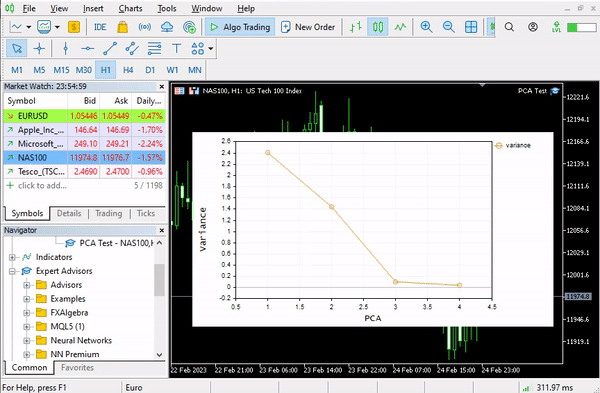
       plt.ScatterCurvePlotsMatrix("pca's ",pca_matrix,"var","PCA");

Результат

Главные компоненты


Преимущества метода главных компонент

  1. Снижение размерности: этот метод может эффективно уменьшить количество переменных в наборе данных, сохраняя при этом наиболее важную информацию. Это может упростить анализ и визуализацию данных, снизить вычислительную сложность и повысить производительность модели.
  2. Сжатие данных: метод можно использовать для эффективного сжатия больших датасетов до меньшего числа главных компонент, что может сэкономить место, требуемое для хранения, и сократить время передачи данных.
  3. Избавление от шумовых данных: метод может удалить шум или случайные отклонения в данных, чтобы сосредоточиться на наиболее значимых закономерностях или тенденциях. Как вы только что видели, у 10 осцилляторов было достаточно много шума.
  4. Интерпретируемые результаты: получаемые главные компоненты можно легко интерпретировать и визуализировать, что полезно для понимания структуры данных. 
  5. Нормализация данных: метод стандартизирует данные, масштабируя их до единичной дисперсии, чтобы избавиться от влияния различий в масштабах переменных и повысить точность моделей.

    Недостатки метода главных компонент.

    1. Потеря данных: метод может отбросить слишком много главных компонент или оставить те, которые не охватывают все разнообразие данных.
    2. Интерпретация результатов может быть сложной, потому что сложно понять, что это за переменные, особенно когда исходные переменные сильно коррелированы или когда получается много главных компонент.
    3. Чувствительность к выбросам: как и многие методы ML, выбросы могут исказить алгоритм и привести к необъективным результатам.
    4. Требует больших вычислительных ресурсов. В большом наборе данных метод главных компонент может создать ту же проблему, которую он пытается решить.
    5. Метод предполагает, что данные линейно связаны, а главные компоненты не коррелированы, что на самом деле не всегда верно. И если это не так, результаты будут недостоверными


    Заключительные замечания

    В заключение скажу, что метод главных компонент (PCA) — это мощный метод, который можно использовать для уменьшения размерности данных при сохранении наиболее важной информации. Определив главные компоненты датасета, мы можем получить представление об основных структурах рынка. Метод широко применяется за пределами трейдинга, например в инженерии и биологии. Хотя это математически интенсивный метод, его преимущества делают его достойным внимания. При правильном подходе и подходящих данных метод может помочь найти новые идеи и принимать обоснованные торговые решения на основе полученных данных.

    Следите за развитием темы в моем репозитории GitHub https://github.com/MegaJoctan/MALE5

    Файл Описание
    matrix_utils.mqh  Содержит дополнительные матричные функции
    pca.mqh  Основная библиотека метода главных компонент
    plots.mqh   Содержит класс для помощи в рисовании векторов
    preprocessing.mqh  Библиотека для подготовки и масштабирования данных для алгоритмов ML
     PCA Test.mqh  Советник для тестирования алгоритма и всего, что обсуждается в этой статье 

    Статьи по теме:




    Перевод с английского произведен MetaQuotes Ltd.
    Оригинальная статья: https://www.mql5.com/en/articles/12229

    Прикрепленные файлы |
    Загрузить ZIP
    PCA_Attachments.zip (12.8 KB)
    Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

    Другие статьи автора

    Перейти к обсуждению на форуме трейдеров
    Понимание и эффективное использование OpenCL API путем воссоздания встроенной поддержки в виде DLL в Linux (Часть 2): Реализация OpenCL Simple DLL Понимание и эффективное использование OpenCL API путем воссоздания встроенной поддержки в виде DLL в Linux (Часть 2): Реализация OpenCL Simple DLL
    В продолжение первой части создадим простую DLL и протестируем ее с помощью MetaTrader 5. Это хорошо подготовит нас к разработке полноценной поддержки OpenCL в виде DLL в следующей части.
    Машинное обучение и Data Science (Часть 12): Можно ли выигрывать на рынке с помощью самообучающихся нейронных сетей? Машинное обучение и Data Science (Часть 12): Можно ли выигрывать на рынке с помощью самообучающихся нейронных сетей?
    Наверняка многим надоели постоянные попытки предсказать фондовый рынок. Хотели бы вы иметь хрустальный шар, который бы помогал принимать более обоснованные инвестиционные решения? Самообучающиеся нейронные сети могут стать таким решением. В этой статье мы посмотрим, могут ли такие мощные алгоритмы помочь «оседлать волну» и перехитрить фондовый рынок. Анализируя огромные объемы данных и выявляя закономерности, самообучающиеся нейронные сети могут делать прогнозы, которые зачастую более точны, чем прогнозы от трейдеров. Давайте посмотрим, можно ли использовать эти передовые технологии, чтобы принимать разумные инвестиционные решения и зарабатывать больше.
    Оборачиваем ONNX-модели в классы Оборачиваем ONNX-модели в классы
    Объектно-ориентированное программирование позволяет создавать более компактный код, который легко читать и модифицировать. Представляем пример для трёх ONNX-моделей.
    Нейросети — это просто (Часть 40): Подходы к использованию Go-Explore на большом объеме данных Нейросети — это просто (Часть 40): Подходы к использованию Go-Explore на большом объеме данных
    В данной статье обсуждается применение алгоритма Go-Explore на протяжении длительного периода обучения, так как стратегия случайного выбора действий может не привести к прибыльному проходу с увеличением времени обучения.