Datenwissenschaft und maschinelles Lernen (Teil 13): Verbessern Sie Ihre Finanzmarktanalyse mit der Principal Component Analysis (PCA)
„PCA ist eine grundlegende Technik der Datenanalyse und des maschinellen Lernens und wird in vielen Bereichen eingesetzt, von der Bild- und Signalverarbeitung bis zu den Finanz- und Sozialwissenschaften.“
David J. Sheskin
Einführung
Die Hauptkomponentenanalyse (PCA) ist eine Methode zur Dimensionalitätsreduktion, die häufig zur Verringerung der Dimensionalität großer Datensätze verwendet wird, indem eine große Menge von Variablen in eine kleinere Menge umgewandelt wird, die immer noch den Großteil der Informationen in der großen Menge enthält.
Die Verringerung der Anzahl der Variablen im Datensatz geht in der Regel auf Kosten der Genauigkeit, aber der Trick bei der Dimensionalitätsreduktion besteht darin, geringe Genauigkeit gegen Einfachheit einzutauschen. Wir beide wissen, dass einige wenige Variablen im Datensatz einfacher zu erforschen und zu visualisieren sind und die Analyse der Daten für Algorithmen des maschinellen Lernens wesentlich einfacher und schneller machen. Ich persönlich denke nicht, dass es eine schlechte Sache ist, Einfachheit gegen Genauigkeit einzutauschen, denn wir befinden uns im Handelsbereich. Genauigkeit bedeutet nicht unbedingt Gewinne.
Die Grundidee der PCA ist im Kern sehr einfach: Reduzieren der Anzahl der Variablen in einem Datensatz und dem Bewahren von so viel Information wie möglich. Schauen wir uns die einzelnen Schritte des Algorithmus der Hauptkomponentenanalyse an.
Die Schritte des Algorithmus der Hauptkomponentenanalyse
- Standardisierung der Daten
- Ermittlung der Kovarianz der Matrix
- Suche nach Eigenvektoren und Eigenwerten
- Ermittlung der PCA-Werte und deren Standardisierung
- Beschaffung der Komponenten
Beginnen wir also mit der Standardisierung der Daten.
01: Standardisierung der Daten
Der Zweck der Standardisierung der Daten besteht darin, alle Variablen auf dieselbe Skala zu bringen, damit sie auf gleicher Basis verglichen und analysiert werden können. Bei der Analyse von Daten kommt es häufig vor, dass die Variablen unterschiedliche Maßeinheiten oder Skalen haben, was zu verzerrten Ergebnissen oder falschen Schlussfolgerungen führen kann. Der gleitende Durchschnittsindikator beispielsweise hat die gleiche Preisspanne wie der Marktwert, während der RSI-Indikator Werte zwischen 0 und 100 aufweist. Diese beiden Variablen sind nicht vergleichbar, wenn sie zusammen in einem Modell verwendet werden. Sie können nicht sinnvoll zusammen verwendet werden.
Bei der Standardisierung der Daten wird jede Variable so transformiert, dass sie einen Mittelwert von Null und eine Standardabweichung von Eins aufweist . Dadurch wird sichergestellt, dass jede Variable die gleiche Skala und Verteilung hat, sodass sie direkt vergleichbar sind. Die Standardisierung der Daten kann auch dazu beitragen, die Genauigkeit und Stabilität von Modellen des maschinellen Lernens zu verbessern, insbesondere wenn die Variablen unterschiedliche Größen oder Varianzen haben.
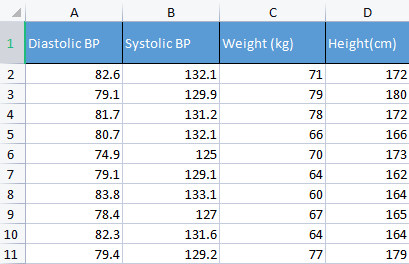
Um einen Punkt zu demonstrieren, werde ich Blutdruckdaten verwenden. Normalerweise verwende ich verschiedene Arten von irrelevanten Daten, um Dinge aufzubauen, weil diese Art von Daten mit Menschen in Verbindung gebracht werden können, was es einfacher macht, Dinge zu verstehen und zu debuggen.
matrix Matrix = matrix_utiils.ReadCsv("bp data.csv"); pre_processing = new CPreprocessing(Matrix, NORM_STANDARDIZATION);
Vorher und nachher:
CS 0 10:17:31.956 PCA Test (NAS100,H1) Non-Standardized data CS 0 10:17:31.956 PCA Test (NAS100,H1) [[82.59999999999999,132.1,71,172] CS 0 10:17:31.956 PCA Test (NAS100,H1) [79.09999999999999,129.9,79,180] CS 0 10:17:31.956 PCA Test (NAS100,H1) [81.7,131.2,78,172] CS 0 10:17:31.956 PCA Test (NAS100,H1) [80.7,132.1,66,166] CS 0 10:17:31.956 PCA Test (NAS100,H1) [74.90000000000001,125,70,173] CS 0 10:17:31.956 PCA Test (NAS100,H1) [79.09999999999999,129.1,64,162] CS 0 10:17:31.956 PCA Test (NAS100,H1) [83.8,133.1,60,164] CS 0 10:17:31.956 PCA Test (NAS100,H1) [78.40000000000001,127,67,165] CS 0 10:17:31.956 PCA Test (NAS100,H1) [82.3,131.6,64,164] CS 0 10:17:31.956 PCA Test (NAS100,H1) [79.40000000000001,129.2,77,179]] CS 0 10:17:31.956 PCA Test (NAS100,H1) Standardized data CS 0 10:17:31.956 PCA Test (NAS100,H1) [[0.979632638610581,0.8604038253411385,0.2240645398825688,0.3760399462363875] CS 0 10:17:31.957 PCA Test (NAS100,H1) [-0.4489982926965129,-0.0540350228475094,1.504433339211528,1.684004976623816] CS 0 10:17:31.957 PCA Test (NAS100,H1) [0.6122703991316175,0.4863152056275964,1.344387239295408,0.3760399462363875] CS 0 10:17:31.957 PCA Test (NAS100,H1) [0.2040901330438764,0.8604038253411385,-0.5761659596980309,-0.6049338265541837] CS 0 10:17:31.957 PCA Test (NAS100,H1) [-2.163355410265021,-2.090739730176784,0.06401843996644889,0.539535575034816] CS 0 10:17:31.957 PCA Test (NAS100,H1) [-0.4489982926965129,-0.3865582403706605,-0.8962581595302708,-1.258916341747898] CS 0 10:17:31.957 PCA Test (NAS100,H1) [1.469448957915872,1.276057847245071,-1.536442559194751,-0.9319250841510407] CS 0 10:17:31.957 PCA Test (NAS100,H1) [-0.7347244789579271,-1.259431686368917,-0.416119859781911,-0.7684294553526122] CS 0 10:17:31.957 PCA Test (NAS100,H1) [0.8571785587842599,0.6525768143891719,-0.8962581595302708,-0.9319250841510407] CS 0 10:17:31.957 PCA Test (NAS100,H1) [-0.326544212870186,-0.3449928381802696,1.184341139379288,1.520509347825387]]
Im Zusammenhang mit der Hauptkomponentenanalyse (PCA) ist die Standardisierung der Daten ein wesentlicher Schritt, da die PCA auf der Kovarianzmatrix basiert, die empfindlich auf Unterschiede in Skala und Varianz zwischen den Variablen reagiert. Die Standardisierung der Daten vor der Durchführung der PCA stellt sicher, dass die resultierenden Hauptkomponenten nicht von den Variablen mit größerer Größe oder Varianz dominiert werden, was die Analyse verzerren und zu falschen Schlussfolgerungen führen könnte.
02: Ermittlung der Kovarianz der Matrix
Die Kovarianzmatrix ist eine Matrix, die angibt, wie stark sich die Zufallsvariablen gemeinsam verändern. Sie wird zur Berechnung der Kovarianz zwischen den einzelnen Spalten der Datenmatrix verwendet. Die Kovarianz zwischen zwei gemeinsam verteilten reellwertigen Zufallsvariablen X und Y mit endlichen zweiten Momenten ist definiert als:
![]()
Sie müssen sich jedoch keine Gedanken über das Verständnis dieser Formel machen, da die Standardbibliothek über diese Funktion verfügt.
matrix Cova = Matrix.Cov(false); Print("Covariances\n", Cova);
Ausgaben:
CS 0 10:17:31.957 PCA Test (NAS100,H1) Covariances CS 0 10:17:31.957 PCA Test (NAS100,H1) [[1.111111111111111,1.05661579634328,-0.2881675653452953,-0.3314539233600543] CS 0 10:17:31.957 PCA Test (NAS100,H1) [1.05661579634328,1.111111111111111,-0.2164241126576326,-0.2333966556085017] CS 0 10:17:31.957 PCA Test (NAS100,H1) [-0.2881675653452953,-0.2164241126576326,1.111111111111111,1.002480628180182] CS 0 10:17:31.957 PCA Test (NAS100,H1) [-0.3314539233600543,-0.2333966556085017,1.002480628180182,1.111111111111111]]
Beachten Sie, dass die Kovarianz eine quadratische Matrix mit Werten von 1 auf der Diagonalen ist. Beim Aufruf dieser Kovarianzmatrix-Methode müssen Sie die Eingabe rowvar auf false setzen:
matrix matrix::Cov( const bool rowvar=true // rows or cols vectors of observations );
weil wir wollen, dass unsere quadratische Matrix eine Identitätsmatrix ist, die auf den Spalten basiert, die wir dieser Funktion geben, da wir 4 Spalten haben. Die Ausgabe ist eine 4x4-Matrix, sonst wäre es eine 8x8-Matrix gewesen.
03: Ermittlung von Eigenvektoren und Eigenwerten
Eigenvektoren, auch Eigenvektoren genannt, sind spezielle Vektoren, die einer quadratischen Matrix zugeordnet sind. Ein Eigenvektor einer Matrix ist ein von Null verschiedener Vektor, der, wenn er mit der Matrix multipliziert wird, ein skalares Vielfaches von sich selbst ergibt, Eigenwert genannt.
Wenn A eine quadratische Matrix ist, dann ist ein Vektor v, der nicht Null ist, ein Eigenvektor von A, wenn es einen Skalar λ gibt, der als Eigenwert bezeichnet wird, sodass Av = λv. Für weitere Informationen
Sie müssen sich auch keine Gedanken über das Verständnis der Formeln dafür machen, da diese ebenfalls in der Standardbibliothek enthalten sind.
if (!Cova.Eig(component_matrix, eigen_vectors)) Print("Failed to get the Component matrix matrix & Eigen vectors");
Wenn man sich diese Methode Eig genauer ansieht.
bool matrix::Eig( matrix& eigen_vectors, // matrix of eigenvectors vector& eigen_values // vector of eigenvalues );
Sie werden feststellen, dass die erste Eingabematrix eigen_vectors Eigenvektoren liefert, genau wie angegeben. Dieser Eigenvektor kann aber auch als Komponentenmatrix bezeichnet werden. Daher speichere ich diese Eigenvektoren in der Komponentenmatrix, da ich es verwirrend finde, sie als Eigenvektor zu bezeichnen, wenn es sich in Wirklichkeit um eine Matrix handelt, entsprechend den MQL5-Sprachstandards.
Print("\nComponent matrix\n",component_matrix,"\nEigen Vectors\n",eigen_vectors);
Ausgaben:
CS 0 10:17:31.957 PCA Test (NAS100,H1) Component matrix CS 0 10:17:31.957 PCA Test (NAS100,H1) [[-0.5276049902734494,0.459884739531444,0.6993704635263588,-0.1449826035480651] CS 0 10:17:31.957 PCA Test (NAS100,H1) [-0.4959779194731578,0.5155907011803843,-0.679399121133044,0.1630612352922813] CS 0 10:17:31.957 PCA Test (NAS100,H1) [0.4815459137666799,0.520677926282417,-0.1230090303369406,-0.6941734714553853] CS 0 10:17:31.957 PCA Test (NAS100,H1) [0.4937128827246101,0.5015643052337933,0.184842006606018,0.6859404272536788]] CS 0 10:17:31.957 PCA Test (NAS100,H1) Eigen Vectors CS 0 10:17:31.957 PCA Test (NAS100,H1) [2.677561590453738,1.607960239905343,0.04775016337426833,0.1111724507110918]
05: Auffinden der PCA-Werte.
Die Ermittlung der Ergebnisse der Hauptkomponentenanalyse ist sehr einfach und erfordert nur eine einzige Codezeile.
pca_scores = Matrix.MatMul(component_matrix);
Die PCA-Scores können durch Multiplikation der normalisierten Matrix mit der Komponentenmatrix ermittelt werden.
Ausgaben:
CS 0 10:17:31.957 PCA Test (NAS100,H1) PCA SCORES CS 0 10:17:31.957 PCA Test (NAS100,H1) [[-0.6500472384886967,1.199407986803537,0.1425145462368588,0.1006701620494091] CS 0 10:17:31.957 PCA Test (NAS100,H1) [1.819562596624738,1.393614599196321,-0.1510888243020112,0.1670753033981925] CS 0 10:17:31.957 PCA Test (NAS100,H1) [0.2688014256048517,1.420914385142756,0.001937917070391801,-0.6847663538666366] CS 0 10:17:31.957 PCA Test (NAS100,H1) [-1.110534258768705,-0.06593596223641518,-0.4827665581567511,0.09571954869438426] CS 0 10:17:31.957 PCA Test (NAS100,H1) [2.475561333978323,-1.768915328424386,-0.0006861487484489809,0.2983796568520111] CS 0 10:17:31.957 PCA Test (NAS100,H1) [-0.6245145789301378,-1.503882637300733,-0.1738415909335406,-0.2393186981373224] CS 0 10:17:31.957 PCA Test (NAS100,H1) [-2.608156175249579,0.0662886285379769,0.1774740257067155,0.4223436077935874] CS 0 10:17:31.957 PCA Test (NAS100,H1) [0.4325302694103054,-1.589321053467977,0.2509606394263523,-0.337079680008286] CS 0 10:17:31.957 PCA Test (NAS100,H1) [-1.667608250048573,-0.2034163217366656,0.09411419638842802,-0.03495245015036286] CS 0 10:17:31.957 PCA Test (NAS100,H1) [1.664404875867474,1.051245703485609,0.1413817973120564,0.2119289033750197]]
Sobald wir die PCA-Werte haben, müssen wir sie standardisieren.
pre_processing = new CPreprocessing(pca_scores_standardized, NORM_STANDARDIZATION); Ausgaben:
CS 0 10:17:31.957 PCA Test (NAS100,H1) PCA SCORES | STANDARDIZED CS 0 10:17:31.957 PCA Test (NAS100,H1) [[-0.4187491401035159,0.9970295470975233,0.68746486754918,0.3182591681100855] CS 0 10:17:31.957 PCA Test (NAS100,H1) [1.172130620033975,1.15846730049564,-0.7288256625700642,0.528192723531639] CS 0 10:17:31.957 PCA Test (NAS100,H1) [0.1731572094549987,1.181160740523977,0.009348167869829477,-2.164823873278453] CS 0 10:17:31.957 PCA Test (NAS100,H1) [-0.715386880184365,-0.05481045923432144,-2.328780161211247,0.3026082735855334] CS 0 10:17:31.957 PCA Test (NAS100,H1) [1.594713612332284,-1.470442808583469,-0.003309859736641006,0.9432989819176616] CS 0 10:17:31.957 PCA Test (NAS100,H1) [-0.4023014443028848,-1.250129598312728,-0.8385809690405054,-0.7565833632510734] CS 0 10:17:31.957 PCA Test (NAS100,H1) [-1.68012890598631,0.05510361946569121,0.8561031894464458,1.335199254045385] CS 0 10:17:31.957 PCA Test (NAS100,H1) [0.2786284867625921,-1.321151824538665,1.210589566461227,-1.06564543418136] CS 0 10:17:31.957 PCA Test (NAS100,H1) [-1.074244269325531,-0.1690934905926844,0.4539901733759543,-0.1104988556867913] CS 0 10:17:31.957 PCA Test (NAS100,H1) [1.072180711318756,0.8738669736790375,0.6820006878558206,0.6699931252073736]]
06: Gewinnung der PCA-Komponenten
Zu guter Letzt müssen wir die Hauptkomponenten ermitteln, was der Zweck all dieser Schritte ist.
Um die Komponenten zu erhalten, müssen wir die Koeffizienten der nicht standardisierten PCA-Scores finden, denn wir haben jetzt zwei PCA-Scores, den standardisierten und den nicht standardisierten.
Die Koeffizienten der einzelnen PCA-Scores sind lediglich die Varianz jeder Spalte in der Spalte PCA-Scores.
pca_scores_coefficients.Resize(cols); vector v_row; for (ulong i=0; i<cols; i++) { v_row = pca_scores.Col(i); pca_scores_coefficients[i] = v_row.Var(); //variance of the pca scores }
Ausgaben:
2023.02.25 10:17:31.957 PCA Test (NAS100,H1) SCORES COEFF [2.409805431408367,1.447164215914809,0.04297514703684173,0.1000552056399828]
Um die Hauptkomponenten zu extrahieren, gibt es eine Reihe von Kriterien, die wir berücksichtigen müssen:
- Eigenwertkriterium: Dieses Kriterium beinhaltet die Auswahl der Hauptkomponenten mit den größten Eigenwerten. Die Idee ist, dass die größten Eigenwerte den Hauptkomponenten entsprechen, die die größte Varianz in den Daten erfassen.
- Das Kriterium des Anteils der Varianz: Bei diesem Kriterium werden die Hauptkomponenten ausgewählt, die einen bestimmten Anteil der Gesamtvarianz der Daten erklären. In dieser Bibliothek werde ich den Wert auf mehr als 90 % setzen.
- Kriterium des Scree Plots: Dieses Kriterium beinhaltet die Untersuchung des Scree Plots, in dem die Eigenwerte jeder Hauptkomponente in absteigender Reihenfolge dargestellt sind. Der Punkt, an dem sich die Kurve abflacht, wird als Schwellenwert für die Auswahl der zu behaltenden Hauptkomponenten verwendet.
- Kaiser-Kriterium: Bei diesem Kriterium werden nur die Hauptkomponenten beibehalten, deren Eigenwerte größer sind als der Mittelwert der Koeffizienten. Mit anderen Worten: die Hauptkomponente mit Koeffizienten größer als eins.
- Kriterium der Kreuzvalidierung: Bei diesem Kriterium wird die Leistung des PCA-Modells anhand eines Validierungssatzes bewertet, und es werden die Hauptkomponenten ausgewählt, die die beste Vorhersagegenauigkeit bieten.
In dieser Bibliothek habe ich für drei Kriterien kodiert, die ich für besser und rechnerisch effizienter halte. Es handelt sich dabei um den Anteil der Varianz, Kaiser und Scree-Plot. Sie können jede von ihnen mit Hilfe der unten stehenden Enumeration auswählen;
enum criterion
{
CRITERION_VARIANCE,
CRITERION_KAISER,
CRITERION_SCREE_PLOT
};
Nachstehend finden Sie die vollständige Funktion zur Extraktion der Hauptkomponenten:
matrix Cpca::ExtractComponents(criterion CRITERION_) { vector vars = pca_scores_coefficients; vector vars_percents = (vars/(double)vars.Sum())*100.0; //--- for Kaiser double vars_mean = pca_scores_coefficients.Mean(); //--- for scree double x[], y[]; //--- matrix PCAS = {}; double sum=0; ulong max; vector v_cols = {}; switch(CRITERION_) { case CRITERION_VARIANCE: #ifdef DEBUG_MODE Print("vars percentages ",vars_percents); #endif for (int i=0, count=0; i<(int)cols; i++) { count++; max = vars_percents.ArgMax(); sum += vars_percents[max]; vars_percents[max] = 0; v_cols.Resize(count); v_cols[count-1] = (int)max; if (sum >= 90.0) break; } PCAS.Resize(rows, v_cols.Size()); for (ulong i=0; i<v_cols.Size(); i++) PCAS.Col(pca_scores.Col((ulong)v_cols[i]), i); break; case CRITERION_KAISER: #ifdef DEBUG_MODE Print("var ",vars," scores mean ",vars_mean); #endif vars = pca_scores_coefficients; for (ulong i=0, count=0; i<cols; i++) if (vars[i] > vars_mean) { count++; PCAS.Resize(rows, count); PCAS.Col(pca_scores.Col(i), count-1); } break; case CRITERION_SCREE_PLOT: v_cols.Resize(cols); for (ulong i=0; i<v_cols.Size(); i++) v_cols[i] = (int)i+1; vars = pca_scores_coefficients; SortAscending(vars); //Make sure they are in ascending first order ReverseOrder(vars); //Set them to descending order VectorToArray(v_cols, x); VectorToArray(vars, y); plt.ScatterCurvePlots("Scree plot",x,y,"variance","PCA","Variance"); //--- vars = pca_scores_coefficients; for (ulong i=0, count=0; i<cols; i++) if (vars[i] > vars_mean) { count++; PCAS.Resize(rows, count); PCAS.Col(pca_scores.Col(i), count-1); } break; } return (PCAS); }
Da das Kaiser-Kriterium so eingestellt ist, dass die Hauptkomponenten mit Koeffizienten ausgewählt werden, die mehr als 90 % aller Varianzen erklären. Ich musste die Abweichungen in Prozentsätze umrechnen:
vector vars = pca_scores_coefficients; vector vars_percents = (vars/(double)vars.Sum())*100.0;
Im Folgenden sind die Ergebnisse der einzelnen Methoden aufgeführt.
KRITERIUM KAISER:
CS 0 12:03:49.579 PCA Test (NAS100,H1) PCA'S CS 0 12:03:49.579 PCA Test (NAS100,H1) [[-0.6500472384886967,1.199407986803537] CS 0 12:03:49.579 PCA Test (NAS100,H1) [1.819562596624738,1.393614599196321] CS 0 12:03:49.579 PCA Test (NAS100,H1) [0.2688014256048517,1.420914385142756] CS 0 12:03:49.579 PCA Test (NAS100,H1) [-1.110534258768705,-0.06593596223641518] CS 0 12:03:49.579 PCA Test (NAS100,H1) [2.475561333978323,-1.768915328424386] CS 0 12:03:49.579 PCA Test (NAS100,H1) [-0.6245145789301378,-1.503882637300733] CS 0 12:03:49.579 PCA Test (NAS100,H1) [-2.608156175249579,0.0662886285379769] CS 0 12:03:49.579 PCA Test (NAS100,H1) [0.4325302694103054,-1.589321053467977] CS 0 12:03:49.579 PCA Test (NAS100,H1) [-1.667608250048573,-0.2034163217366656] CS 0 12:03:49.579 PCA Test (NAS100,H1) [1.664404875867474,1.051245703485609]]
KRITERIUM VARIANZ:
CS 0 12:03:49.579 PCA Test (NAS100,H1) PCA'S CS 0 12:03:49.579 PCA Test (NAS100,H1) [[-0.6500472384886967,1.199407986803537] CS 0 12:03:49.579 PCA Test (NAS100,H1) [1.819562596624738,1.393614599196321] CS 0 12:03:49.579 PCA Test (NAS100,H1) [0.2688014256048517,1.420914385142756] CS 0 12:03:49.579 PCA Test (NAS100,H1) [-1.110534258768705,-0.06593596223641518] CS 0 12:03:49.579 PCA Test (NAS100,H1) [2.475561333978323,-1.768915328424386] CS 0 12:03:49.579 PCA Test (NAS100,H1) [-0.6245145789301378,-1.503882637300733] CS 0 12:03:49.579 PCA Test (NAS100,H1) [-2.608156175249579,0.0662886285379769] CS 0 12:03:49.579 PCA Test (NAS100,H1) [0.4325302694103054,-1.589321053467977] CS 0 12:03:49.579 PCA Test (NAS100,H1) [-1.667608250048573,-0.2034163217366656] CS 0 12:03:49.579 PCA Test (NAS100,H1) [1.664404875867474,1.051245703485609]]
KRITERIUM SCREE PLOT:
Toll, jetzt haben wir also zwei Hauptkomponenten. Einfach ausgedrückt, wird der Datensatz von 4 Variablen auf nur 2 Variablen reduziert. Sie können diese Variablen dann in dem Projekt verwenden, an dem Sie gerade arbeiten.
Hauptkomponentenanalyse im MetaTrader
Nun ist es an der Zeit, die Hauptkomponentenanalyse auf das anzuwenden, was Sie sehen wollen, nämlich das Handelsumfeld.
Zu diesem Zweck habe ich 10 Oszillatoren ausgewählt. Da es sich um Oszillatoren handelt, beschloss ich, ihnen eine Chance zu geben, um zu beweisen, dass man 10 Indikatoren desselben Typs mit PCA so reduzieren kann, dass man am Ende nur noch wenige Variablen hat, mit denen man leicht arbeiten kann.
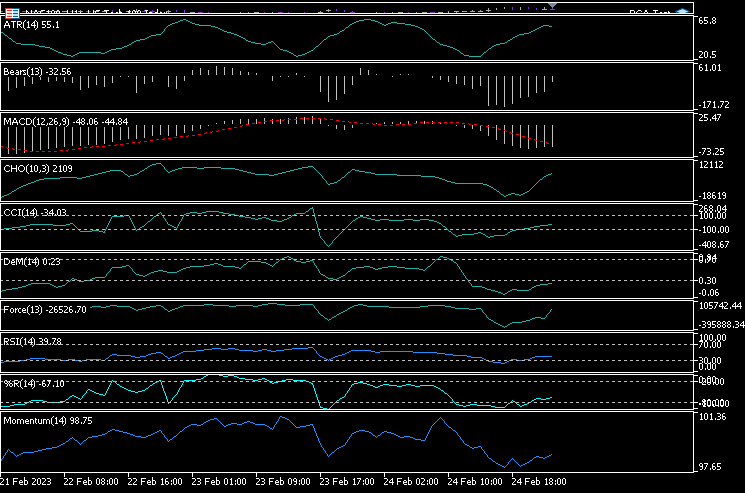
Ich habe 10 Indikatoren zu einem einzelnen Chart hinzugefügt, und zwar: ATR, Bears Power, MACD, Chaikin Oscillator, Commodity Channel Index, De Marker, Force Index, Momentum, RSI, Williams Percent Range.
handles[0] = iATR(Symbol(),PERIOD_CURRENT, period); handles[1] = iBearsPower(Symbol(), PERIOD_CURRENT, period); handles[2] = iMACD(Symbol(),PERIOD_CURRENT,12, 26,9,PRICE_CLOSE); handles[3] = iChaikin(Symbol(), PERIOD_CURRENT,12,26,MODE_SMMA,VOLUME_TICK); handles[4] = iCCI(Symbol(),PERIOD_CURRENT,period, PRICE_CLOSE); handles[5] = iDeMarker(Symbol(),PERIOD_CURRENT,period); handles[6] = iForce(Symbol(),PERIOD_CURRENT,period,MODE_EMA,VOLUME_TICK); handles[7] = iMomentum(Symbol(),PERIOD_CURRENT,period, PRICE_CLOSE); handles[8] = iRSI(Symbol(),PERIOD_CURRENT,period,PRICE_CLOSE); handles[9] = iWPR(Symbol(),PERIOD_CURRENT,period); for (int i=0; i<10; i++) { matrix_utiils.CopyBufferVector(handles[i],0,0,bars,buff_v); ind_Matrix.Col(buff_v, i); //store each indicator in ind_matrix columns }
Ich habe beschlossen, alle diese Indikatoren in einem Chart darzustellen. Nachstehend sehen Sie, wie sie aussehen:
Wie kann es sein, dass sie alle fast gleich aussehen? Sehen wir uns ihre Korrelationsmatrix an:
Print("Oscillators Correlation Matrix\n",ind_Matrix.CorrCoef(false));
Ausgaben:
CS 0 18:03:44.405 PCA Test (NAS100,H1) Oscillators Correlation Matrix CS 0 18:03:44.405 PCA Test (NAS100,H1) [[1,0.01772984879133655,-0.01650305145071043,0.03046861668248528,0.2933315924162302,0.09724971519249033,-0.054459564042778,-0.0441397473782667,0.2171969726706487,0.3071254662907512] CS 0 18:03:44.405 PCA Test (NAS100,H1) [0.01772984879133655,1,0.6291675928958272,0.2432064602541826,0.7433991440764224,0.7857575973967624,0.8482060554701495,0.8438879842180333,0.8287766948950483,0.7510097635884428] CS 0 18:03:44.405 PCA Test (NAS100,H1) [-0.01650305145071043,0.6291675928958272,1,0.80889919514547,0.3583185473647767,0.79950773673123,0.4295059398014639,0.7482107564439531,0.8205910850439753,0.5941794310595322] CS 0 18:03:44.405 PCA Test (NAS100,H1) [0.03046861668248528,0.2432064602541826,0.80889919514547,1,0.03576792595345671,0.436675349452699,0.08175026884450357,0.3082792264724234,0.5314362133025707,0.2271361556104472] CS 0 18:03:44.405 PCA Test (NAS100,H1) [0.2933315924162302,0.7433991440764224,0.3583185473647767,0.03576792595345671,1,0.6368513319457978,0.701918992559641,0.6677393692960837,0.7952832674277922,0.8844891719743937] CS 0 18:03:44.405 PCA Test (NAS100,H1) [0.09724971519249033,0.7857575973967624,0.79950773673123,0.436675349452699,0.6368513319457978,1,0.6425071357003039,0.9239712092224102,0.8809179254503203,0.7999862160768584] CS 0 18:03:44.405 PCA Test (NAS100,H1) [-0.054459564042778,0.8482060554701495,0.4295059398014639,0.08175026884450357,0.701918992559641,0.6425071357003039,1,0.7573281438252102,0.7142333470379938,0.6534102287503526] CS 0 18:03:44.405 PCA Test (NAS100,H1) [-0.0441397473782667,0.8438879842180333,0.7482107564439531,0.3082792264724234,0.6677393692960837,0.9239712092224102,0.7573281438252102,1,0.8565660350098397,0.8221821793990941] CS 0 18:03:44.405 PCA Test (NAS100,H1) [0.2171969726706487,0.8287766948950483,0.8205910850439753,0.5314362133025707,0.7952832674277922,0.8809179254503203,0.7142333470379938,0.8565660350098397,1,0.8866871375902136] CS 0 18:03:44.405 PCA Test (NAS100,H1) [0.3071254662907512,0.7510097635884428,0.5941794310595322,0.2271361556104472,0.8844891719743937,0.7999862160768584,0.6534102287503526,0.8221821793990941,0.8866871375902136,1]]
Wenn Sie sich die Korrelationsmatrix ansehen, werden Sie feststellen, dass nur einige wenige Indikatoren mit einigen anderen korrelieren, aber diese sind in der Minderheit, sodass sie doch nicht gleich aussehen. Wenden wir die PCA auf diese Matrix an und sehen wir uns an, was dieser Algorithmus für uns bereithält.
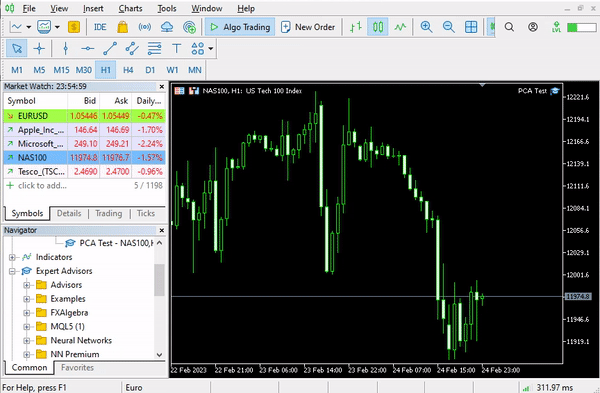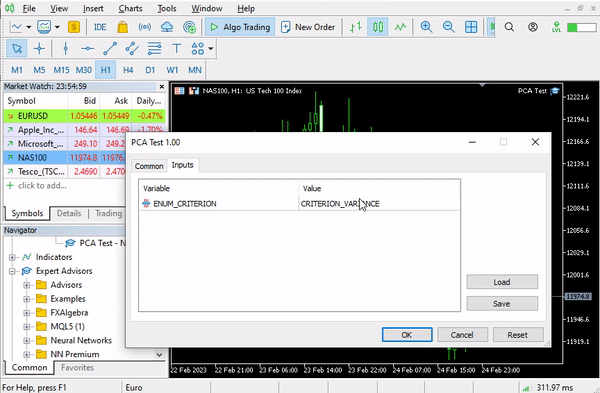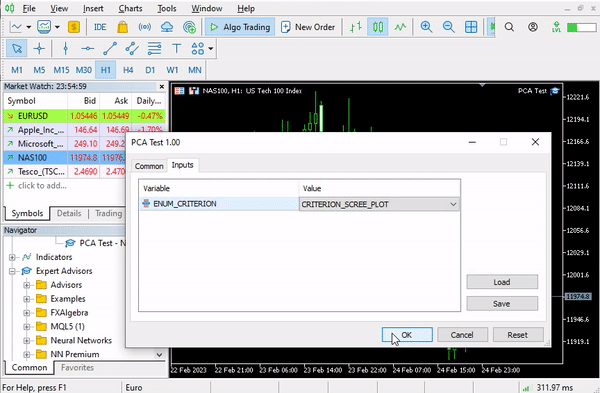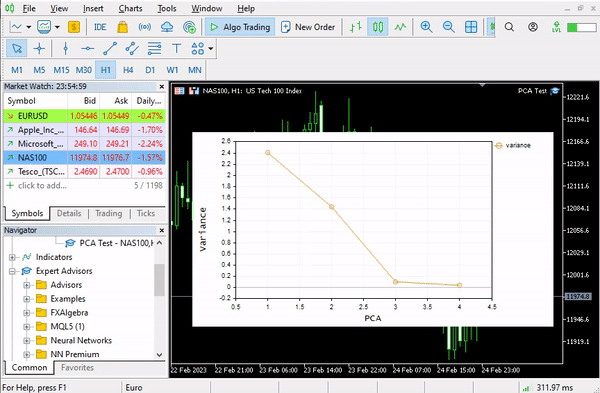
pca = new Cpca(ind_Matrix); matrix pca_matrix = pca.ExtractComponents(ENUM_CRITERION);Ich habe mich für das Kriterium des Scree Plots entschieden (siehe Abbildung):
Ein Blick auf den Scree Plot zeigt, dass nur 3 PCA(s) ausgewählt wurden, die im Folgenden dargestellt werden;
CS 0 15:03:30.992 PCA Test (NAS100,H1) PCA'S CS 0 15:03:30.992 PCA Test (NAS100,H1) [[-2.297373513063062,0.8489493134565058,0.02832445955171548] CS 0 15:03:30.992 PCA Test (NAS100,H1) [-2.370488225540198,0.9122356709081817,-0.1170316144060158] CS 0 15:03:30.992 PCA Test (NAS100,H1) [-2.728297784013197,1.066014896296926,-0.2859442064697605] CS 0 15:03:30.992 PCA Test (NAS100,H1) [-1.818906988827231,1.177846546204641,-0.748128826146959] ... ... CS 0 15:03:30.992 PCA Test (NAS100,H1) [-3.26602969252589,0.4816995789189212,-0.7408982990360158] CS 0 15:03:30.992 PCA Test (NAS100,H1) [-3.810781495417407,0.4426824869307094,-0.5737277071364888…]
Von 10 Variablen auf nur noch 3 Variablen!!!
Deshalb ist es sehr wichtig, ein Datenanalytiker und ein Händler zu sein, denn ich habe Händler gesehen, die viele Indikatoren auf dem Chart und manchmal auf Expert Advisors haben. Ich denke, dass es sich lohnt, auf diese Weise die Variablen zu reduzieren, um die Berechnungskosten für unsere Programme zu senken, übrigens ist dies kein Handelsratschlag, wenn das, was Sie getan haben, für Sie funktioniert und Sie zufrieden sind, dann gibt es keinen Grund zur Sorge.
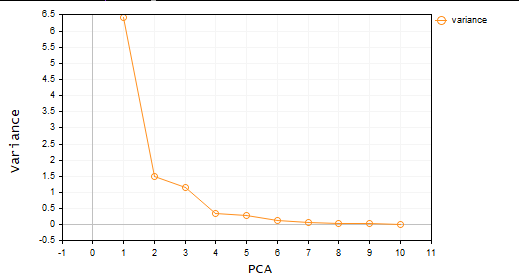
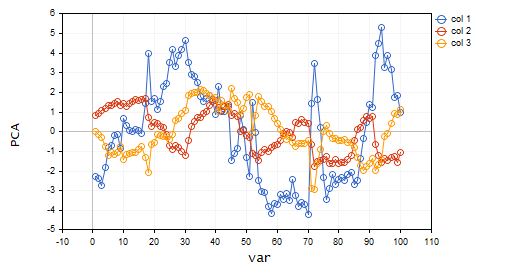
Lassen Sie uns diese Hauptkomponenten visualisieren, um zu sehen, wie sie auf derselben Achse aussehen.
plt.ScatterCurvePlotsMatrix("pca's ",pca_matrix,"var","PCA");
Ausgaben:
Vorteile der Principal Component Analysis
- Dimensionalitätsreduktion: Die PCA kann die Anzahl der Variablen im Datensatz wirksam reduzieren, während die wichtigsten Informationen erhalten bleiben. Dies kann die Datenanalyse und -visualisierung vereinfachen, die Komplexität der Berechnungen verringern und die Modellleistung verbessern.
- Datenkompression: Mit der PCA lassen sich große Datensätze effektiv auf eine geringere Anzahl von Hauptkomponenten komprimieren, was Speicherplatz spart und die Datenübertragungszeiten verkürzt.
- Rauschreduktion: Die PCA kann Rauschen oder zufällige Schwankungen in den Daten entfernen, indem sie sich auf die wichtigsten Muster oder Trends konzentriert. Wie Sie gerade gesehen haben, hatten 10 Oszillatoren eine Menge Rauschen.
- Interpretierbare Ergebnisse: Die PCA erzeugt Hauptkomponenten, die leicht interpretiert und visualisiert werden können, was zum Verständnis der Datenstruktur beitragen kann.
- Normalisierung der Daten: Die PCA standardisiert die Daten durch Skalierung auf eine Einheitsvarianz, wodurch die Auswirkungen von Unterschieden in den Variablenskalen verringert und die Genauigkeit der statistischen Modelle verbessert werden können.
Nachteile der Principal Component Analysis.
- Verlust von Informationen: Die PCA kann zu einem Informationsverlust führen, wenn zu viele Hauptkomponenten verworfen werden oder wenn die verbleibenden Komponenten nicht alle relevanten Variationen in den Daten erfassen.
- Die Interpretation der Ergebnisse kann lästig sein: Die Interpretation von Hauptkomponenten kann schwierig sein, weil man keine Ahnung hat, was diese Variablen eigentlich sind, insbesondere wenn die ursprünglichen Variablen stark korreliert sind oder wenn die Anzahl der Hauptkomponenten groß ist.
- Empfindlich gegenüber Ausreißern: Wie bei vielen ML-Techniken können Ausreißer diesen Algorithmus verzerren und zu verzerrten Ergebnissen führen.
- Sehr rechenintensiv: Bei großen Datensätzen kann der PCA-Algorithmus das gleiche Problem verursachen, das er zu lösen versucht.
- Modellannahmen: Bei diesem Algorithmus wird davon ausgegangen, dass die Daten in einem linearen Zusammenhang stehen und die Hauptkomponenten unkorreliert sind, was in der Praxis nicht immer der Fall ist. Ein Verstoß gegen diese Annahmen kann zu schlechten Ergebnissen führen
Bemerkungen am Ende
Zusammenfassend lässt sich sagen, dass die Hauptkomponentenanalyse (PCA) eine leistungsstarke Technik ist, mit der die Dimensionalität von Daten reduziert werden kann, wobei die wichtigsten Informationen erhalten bleiben. Durch die Identifizierung der Hauptkomponenten eines Datensatzes können wir Einblicke in die zugrunde liegenden Strukturen des Marktes gewinnen. PCA hat eine breite Palette von Anwendungen außerhalb des Handelsbereichs, z. B. in den Bereichen Technik und Biologie. Obwohl es sich um eine mathematisch intensive Technik handelt, ist sie aufgrund ihrer Vorteile einen Versuch wert. Mit dem richtigen Ansatz und den richtigen Daten kann die PCA uns helfen, neue Erkenntnisse zu gewinnen und fundierte Handelsentscheidungen auf der Grundlage der uns zur Verfügung stehenden Daten zu treffen.
Verfolgen Sie die Entwicklung und Änderungen an diesem Algorithmus auf meinem GitHub Repo: https://github.com/MegaJoctan/MALE5
| Datei | Beschreibungen |
|---|---|
| matrix_utils.mqh | Enthält zusätzliche Funktionen zur Matrixmanipulation |
| pca.mqh | Die Hauptbibliothek für die Hauptkomponentenanalyse |
| plots.mqh | Enthält die Klasse zur Unterstützung beim Zeichnen von Vektoren |
| preprocessing.mqh | Bibliothek zur Vorbereitung und Skalierung der Daten für ML-Algorithmen |
| PCA Test.mqh | Der EA zum Testen des Algorithmus und alles, was in diesem Artikel besprochen wird |
Referenzartikel:
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/12229
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.

Fragen: Welche Indikatoren weisen eine umgekehrte Korrelation auf? Kann dieser Indikator je nach Asset und Parameter variieren? Können Sie in diesem Programm weitere Indikatoren in den Handler einfügen, damit wir sie gemeinsam auswerten können? Ihre Artikel sind großartig! Herzlichen Dank!
Zweifeln: 1 - Was sind die 3 Indikatoren? Sie sind umgekehrt zueinander korreliert. Ist das richtig? 2 - Können Sie das Programm ändern, um weitere Indikatoren einzufügen? Trendindikatoren wie gleitender Durchschnitt und Volumenindikator in das Programm? 3 - Ändert sich das Ergebnis der 3 Indikatoren für jeden Vermögenswert, Zeitrahmen und die jeweiligen Parameter?
Danke, dass Sie meinen Artikel gelesen haben. Es gibt viele Ideen und Indikatoren, mit denen man in diesem Programm spielen kann. Ich kann nicht alle von ihnen erkunden tbh Ich würde vorschlagen, das Programm herunterladen und spielen mit ihm, wie ich glaube, der Artikel ist sehr klar. Kein Körper kann die Arbeit für Sie tun, vor allem für Sie, vor allem für frei.