Redes neuronales en el trading: Estudio de la estructura local de datos

MetaTrader 5 — Sistemas comerciales | 7 mayo 2025, 05:16

131

Dmitriy Gizlyk

Introducción

La tarea de detección de objetos en una nube de puntos atrae cada vez más atención de los especialistas. Y la eficacia de la resolución de este problema depende en gran medida de la información sobre la estructura de las zonas locales. Sin embargo, la naturaleza dispersa e irregular de las nubes de puntos con frecuencia hace que la estructura local resulte incompleta y ruidosa.

La detección de objetos por convolución tradicional se basa en núcleos fijos, y todos los puntos vecinos se procesan de la misma manera. Por lo tanto, resulta inevitable considerar los puntos no conectados o ruidosos de otros objetos.

El Transformer ha demostrado su eficacia en diversas tareas. En comparación con la convolución, el mecanismo de Self-Attention es capaz de excluir de forma adaptativa los puntos ruidosos o irrelevantes. Sin embargo, el Transformer vainilla utiliza una única función para transformar todos los elementos de una secuencia. Este trabajo isótropo ignora la información de la estructura local en las relaciones espaciales y no considera la dirección y la distancia del punto central hasta sus vecinos. Si intercambiamos las posiciones de los puntos, el resultado del Transformer seguirá siendo el mismo. Y esto creará problemas para reconocer la dirección de los objetos, lo que resulta importante para detectar patrones de precios.

Los autores del artículo "SEFormer: Structure Embedding Transformer for 3D Object Detection" tratan de combinar lo mejor de los dos enfoques, desarrollando un nuevoStructure-Embedding transFormer ( SEFormer), capaz de codificar la estructura local orientada según la dirección y la distancia. El SEFormer propuesto explora diferentes transformaciones para puntos Value desde diferentes direcciones y distancias. En consecuencia, los cambios en la estructura espacial local pueden codificarse en los resultados del trabajo del modelo, lo que ofrecerá pistas para reconocer con precisión las direcciones de los objetos.

Basándose en el módulo de SEFormer propuesto, en el artículo anterior se propone una red multiescala para la detección de objetos 3D.

1. El algoritmo SEFormer

La localidad y la invarianza espacial de la convolución se adaptan bien al desplazamiento inductivo de las imágenes. Otra ventaja importante de la convolución es que puede codificar la información estructural de los datos. Los autores del método SEFormer descomponen la convolución como un operador de dos pasos: transformación y agregación. Durante la transformación, cada punto se multiplicará por el núcleo w correspondienteδ. Dichas puntuaciones se sumarán simplemente con un factor de agregación fijo α=1. En la convolución, los núcleos se entrenan de forma diferente, según sus direcciones y distancias hasta el centro del núcleo. Por consiguiente, la convolución puede codificar la estructura espacial local. No obstante, en la convolución, todos los puntos vecinos en el proceso de agregación son iguales (α=1). El operador de convolución básico usa un núcleo estático y rígido, pero la nube de puntos suele ser irregular e incluso incompleta. En consecuencia, la convolución incluye inevitablemente puntos irrelevantes o ruidosos en la característica resultante.

En comparación con la convolución, el mecanismo de Self-Attention del Transformer propone un método más eficaz para preservar las formas irregulares y los límites de los objetos en una nube de puntos. Para una nube de puntos de N elementos 𝒑=[p1,…, pN], el Transformer calcula la respuesta de cada punto de la forma siguiente:

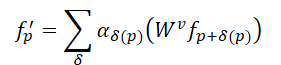
Aquí αδ representa los coeficientes de autointeracción entre puntos de la región vecina, mientras que 𝑾v denota la transformación de Value. En comparación con el α=1 estático de la convolución, los coeficientes de autointeracción permiten una selección adaptativa de los puntos de agregación y eliminan la influencia de los puntos no relacionados. No obstante, la misma transformación para Value resulta común a todos los puntos del Transformer. Esto significa que no hay posibilidad de codificar una estructura que posee convolución.

Considerando lo anterior, los autores de SEFormer han descubierto que la convolución tiene la capacidad de codificar la estructura de los datos, mientras que el Transformer puede preservar bien la estructura. Por consiguiente, una idea sencilla sería desarrollar un nuevo operador que tenga las ventajas de la convolución y el Transformer. Así, proponen el SEFormer, que puede formularse como:

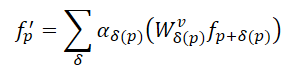
La mayor diferencia entre SEFormer y el Transformer vainilla es la función de transformación para los puntos Value, que se entrena usando como base la posición mutua entre puntos.

Dada la irregularidad de la nube de puntos, los autores del método SEFormer siguen el paradigma del Point Transformer para muestrear independientemente los puntos vecinos alrededor de cada punto Query antes de importarlos al Transformer. En este caso, los autores del método han decidido utilizar la interpolación de cuadrículas para generar puntos clave. Alrededor del punto analizado se generan varios puntos virtuales, dispuestos en una cuadrícula. La distancia entre dos elementos de la cuadrícula es una d predefinida.

A continuación, los puntos virtuales se interpolan con sus elementos vecinos más próximos de la nube de puntos analizada. En comparación con el muestreo tradicional, como KNN, la ventaja del muestreo de cuadrícula reside en la capacidad de seleccionar a la fuerza puntos de diferentes direcciones. La interpolación de cuadrículas ofrece una mejor descripción de la estructura local. Sin embargo, se utiliza una distancia fija d para la interpolación de la cuadrícula, por lo que los autores del método emplean una estrategia de radios múltiples para aumentar la flexibilidad del muestreo.

SEFormer construye un pool de memoria que contiene múltiples matrices de transformación para Value (𝑾v). Los puntos clave interpolados buscarán su 𝑾v correspondiente en función de su coordenada relativa respecto al punto original. Entonces sus signos se transformarán de forma distinta. De esta manera, SEFormer tiene la capacidad de codificar la estructura que falta en el Transformer vainilla.

En el modelo de detección de objetos propuesto por los autores del método, primero se construye una línea troncal basada en la convolución 3D para extraer características de vóxel multiescala y generar frases primarias. El proceso de convolución transforma primero los datos de origen en una serie de características de vóxel utilizando disminuciones de 1×, 2×, 4× y 8× en el tamaño de muestreo. Estos objetos de diferentes tamaños tienen capas de profundidad distintas. Tras la extracción de características, el volumen de elementos 3D se comprimirá a lo largo del eje Z y se convertirá en un mapa de características 2D "a vista de pájaro". A partir de los mapas resultantes, se realizará una predicción inicial de los lugares candidatos.

A continuación, la estructura de modulación espacial propuesta agrega los objetos multiescala [𝑭1, 𝑭2, 𝑭3, 𝑭4] en varias incorporaciones al nivel del punto 𝑬. A partir de 𝑬init, los puntos clave de cada elemento analizado se interpolan a partir de la función de escala más pequeña 𝑭1. Los autores del método utilizan m distancias de cuadrícula diferentes d para generar conjuntos de características clave multiescala en forma de 𝑭1,1, 𝑭2,1,…, 𝑭m,1 Esta estrategia de radios múltiples permite gestionar mejor la distribución dispersa e irregular de las nubes de puntos. Así, se aplican m bloques SEFormer paralelos que generan m incorporaciones actualizadas 𝑬1,1, 𝑬2,1,…, 𝑬m,1. Las incorporaciones resultantes se concatenan y se transforman en una incorporación 𝑬1 utilizando el Transformer vainilla. A continuación, 𝑬1 repite el proceso descrito anteriormente y agrega [𝑭2, 𝑭3, 𝑭4] a la incorporación 𝑬final. En comparación con las funciones de vóxel 𝑭 originales, la incorporación de 𝑬final contiene una descripción estructural más detallada del área local.

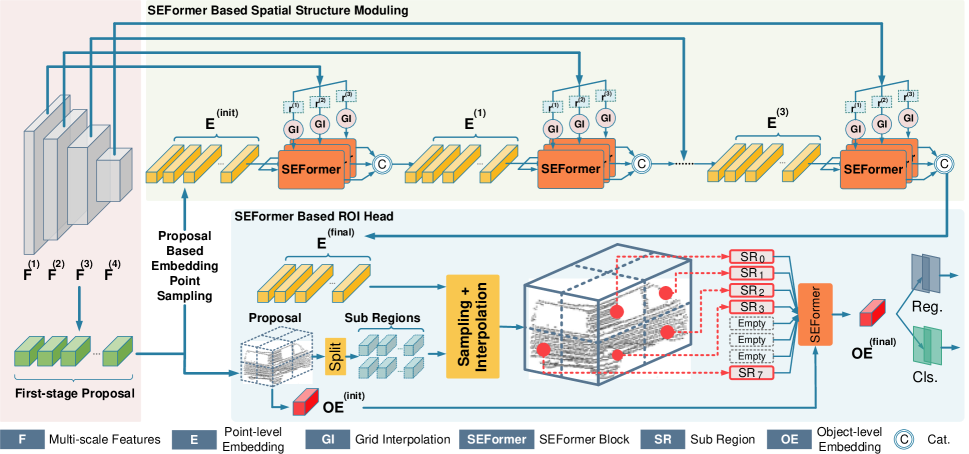
A partir de las incorporaciones obtenidas, en el nivel de puntos 𝑬final, la cabeza de modelo propuesta por los autores del método los agrega en varias incorporaciones de objetos para crear frases finales. Para ser más precisos, primero dividiremos cada frase de la primera etapa en varias subáreas cúbicas e interpolaremos cada subzona con los objetos de incorporación circundantes a nivel de puntos. Dada la escasa densidad de la nube de puntos, algunas zonas suelen estar vacías. El enfoque tradicional consiste simplemente en sumar las características de las regiones no vacías. En cambio, el SEFormer propuesto puede usar la información tanto de las zonas llenas como de las vacías. Una mayor capacidad de incorporación de estructuras en SEFormer puede ofrecer una mejor descripción de la estructura a nivel de objeto y, a continuación, generar sugerencias más precisas.

A continuación le mostramos la visualización del método por parte del autor.

2. Implementación con MQL5

Tras repasar los aspectos teóricos del método SEFormer propuesto, pasaremos a la parte práctica de nuestro artículo, donde haremos realidad nuestra visión de los enfoques propuestos. Y ahora debemos pensar en la arquitectura de nuestro futuro modelo.

Para la extracción inicial de características, los autores del método proponen utilizar la convolución de vóxeles en 3D. En nuestro caso, sin embargo, el vector de características de una sola barra puede contener muchas más características, así que este enfoque no parece del todo eficaz. Por ello, le propongo centrarnos en el enfoque de agregación de características que utilizamos anteriormente mediante un bloque de atención dispersa con distintos niveles de enfoque.

El segundo punto sobre el que me gustaría llamar la atención es la construcción de la cuadrícula alrededor del punto estudiado. En este caso, los autores del método pueden permitirse comprimir los datos de altura y analizar los objetos en mapas planos al resolver el problema de detección de objetos en 3D. Sin embargo, en nuestro caso con la representación multidimensional de datos, cada dimensión puede tener un impacto clave en un punto u otro, y no podemos permitirnos comprimir los datos en ninguna dimensión. Por ello, construir una "cuadrícula" en un espacio multidimensional puede suponer todo un reto. En este caso, el número de elementos aumentará exponencialmente con el incremento del número de características analizadas. Y en mi opinión, en tal situación, resulta más eficiente hacer que el modelo aprenda los puntos centroides más óptimos en el espacio multidimensional.

Dicho esto, le propongo construir nuestro nuevo objeto heredando la funcionalidad principal de la clase CNeuronPointNetNet2OCL. A continuación le mostramos la estructura general de la nueva clase CNeuronSEFormer.

class CNeuronSEFormer   :    public CNeuronPointNet2OCL
  {
protected:
   uint              iUnits;
   uint              iPoints;
   //---
   CLayer            cQuery;
   CLayer            cKey;
   CLayer            cValue;
   CLayer            cKeyValue;
   CArrayInt         cScores;
   CLayer            cMHAttentionOut;
   CLayer            cAttentionOut;
   CLayer            cResidual;
   CLayer            cFeedForward;
   CLayer            cCenterPoints;
   CLayer            cFinalAttention;
   CNeuronMLCrossAttentionMLKV SEOut;
   CBufferFloat      cbTemp;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      AttentionOut(CBufferFloat *q, CBufferFloat *kv, int scores, CBufferFloat *out);
   virtual bool      AttentionInsideGradients(CBufferFloat *q, CBufferFloat *q_g,
                                              CBufferFloat *kv, CBufferFloat *kv_g,
                                              int scores, CBufferFloat *gradient);
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   //---

public:
                     CNeuronSEFormer(void) {};
                    ~CNeuronSEFormer(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint output, bool use_tnets,
                          uint center_points, uint center_window,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronSEFormer; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

En la estructura presentada anteriormente, podemos observar la ya familiar lista de métodos redefinidos y una serie de objetos anidados. Los nombres de algunos de ellos pueden recordarnos a la arquitectura del Transformer. Y esto no es casualidad, porque los autores del método SEFormer han intentado mejorar el algoritmo del Transformer vainilla. Pero lo primero es lo primero.

Hemos declarado todos los objetos internos de nuestra clase de forma estática, lo cual nos permitirá dejar el constructor y el destructor de la clase "vacíos". La inicialización de los objetos declarados y heredados se realizará en el método Init, en cuyos parámetros, como ya sabe, obtendremos las constantes principales que definen la arquitectura del objeto a crear.

bool CNeuronSEFormer::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                           uint window, uint units_count, uint output, bool use_tnets,
                           uint center_points, uint center_window,
                           ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronPointNet2OCL::Init(numOutputs, myIndex, open_cl, window, units_count, output, use_tnets,
                                 optimization_type, batch))
      return false;

A los parámetros ya conocidos añadiremos aquí el número de centroides entrenados y el tamaño de su vector de descripción de estados.

Aquí cabe señalar que la arquitectura de nuestro bloque está construida de tal manera que el tamaño del vector de descripción del centroide pueda diferir del número de características de descripción de una barra analizada.

En el cuerpo del método, como es habitual, llamaremos directamente al método homónimo de la clase padre, que ya este implementará los mecanismos de control de los parámetros recibidos y de inicialización de los objetos heredados. Solo comprobaremos el resultado lógico de las operaciones del método de la clase padre.

Después guardaremos algunos parámetros de la arquitectura creada que necesitaremos durante la ejecución directa de las operaciones del algoritmo que estamos construyendo.

   iUnits = units_count;
   iPoints = MathMax(center_points, 9);

Como array de objetos internos, hemos utilizado objetos CLayer. Para que funcionen correctamente, transmitiremos el puntero a un objeto de contexto OpenCL.

   cQuery.SetOpenCL(OpenCL);
   cKey.SetOpenCL(OpenCL);
   cValue.SetOpenCL(OpenCL);
   cKeyValue.SetOpenCL(OpenCL);
   cMHAttentionOut.SetOpenCL(OpenCL);
   cAttentionOut.SetOpenCL(OpenCL);
   cResidual.SetOpenCL(OpenCL);
   cFeedForward.SetOpenCL(OpenCL);
   cCenterPoints.SetOpenCL(OpenCL);
   cFinalAttention.SetOpenCL(OpenCL);

Para entrenar la representación de los centroides, crearemos un pequeño MLP de dos capas consecutivas totalmente conectadas.

//--- Init center points
   CNeuronBaseOCL *base = new CNeuronBaseOCL();
   if(!base)
      return false;
   if(!base.Init(iPoints * center_window * 2, 0, OpenCL, 1, optimization, iBatch))
      return false;
   CBufferFloat *buf = base.getOutput();
   if(!buf || !buf.BufferInit(1, 1) || !buf.BufferWrite())
      return false;
   if(!cCenterPoints.Add(base))
      return false;
   base = new CNeuronBaseOCL();
   if(!base.Init(0, 1, OpenCL, iPoints * center_window * 2, optimization, iBatch))
      return false;
   if(!cCenterPoints.Add(base))
      return false;

Tenga en cuenta que estamos creando dos veces más centroides del número dado. De esta forma crearemos dos conjuntos de centroides, simulando la construcción de una cuadrícula con diferentes escalas.

Y luego crearemos un ciclo en el que inicializaremos los objetos internos según el número de capas de escalado de las características.

Recordemos que en la clase padre, agregaremos los datos de origen con dos coeficientes de atención. En consecuencia, nuestro ciclo contendrá dos iteraciones.

//--- Inside layers
   for(int i = 0; i < 2; i++)
     {
      //--- Interpolation
      CNeuronMVCrossAttentionMLKV *cross = new CNeuronMVCrossAttentionMLKV();
      if(!cross ||
         !cross.Init(0, i * 12 + 2, OpenCL, center_window, 32, 4, 64, 2, iPoints, iUnits, 
                                                         2, 2, 2, 1, optimization, iBatch))
         return false;
      if(!cCenterPoints.Add(cross))
         return false;

Para interpolar los centroides, utilizaremos un bloque de atención cruzada en el que asignaremos la representación actual de los centroides al conjunto de datos de origen analizados. La idea principal de este proceso consiste en encontrar un conjunto de centroides que dividan los datos de origen en regiones locales de la forma más correcta y eficaz posible. De este modo, estudiaremos la estructura de los datos de origen.

A continuación, procederemos a inicializar los objetos del método del bloque SEFormter propuesto por los autores. En este bloque se presupone el enriquecimiento de la incorporación de los puntos analizados con datos de la estructura de la nube. Técnicamente, usaremos un algoritmo para atribuir de forma cruzada los puntos analizados a nuestros centroides enriquecidos con información sobre la estructura de la nube de puntos.

Aquí utilizaremos la capa de convolución para generar una entidad Query basada en las incorporaciones de los puntos analizados.

      //--- Query
      CNeuronConvOCL *conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0, i * 12 + 3, OpenCL, 64, 64, 64, iUnits, optimization, iBatch))
         return false;
      if(!cQuery.Add(conv))
         return false;

Del mismo modo, generaremos las entidades Key, pero a partir de la representación del centroide.

      //--- Key
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0, i * 12 + 4, OpenCL, center_window, center_window, 32, iPoints, 2, optimization, iBatch))
         return false;
      if(!cKey.Add(conv))
         return false;

Pero para generar la entidad Value, los autores del método SEFormer sugieren usar una matriz de transformación individual para cada elemento de la secuencia. Por lo tanto, utilizaremos una capa convolucional similar, solo que en los elementos de la secuencia indicaremos 1. En este caso, transferiremos el número completo de centroides al parámetro de las variables analizadas. Este planteamiento nos permitirá obtener los resultados deseados.

      //--- Value
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0, i * 12 + 5, OpenCL, center_window, center_window, 32, 1, iPoints * 2,
                                                                       optimization, iBatch))
         return false;
      if(!cValue.Add(conv))
         return false;

No obstante, conviene recordar que todos nuestros kernels creados por el algoritmo de atención cruzada se crearon para trabajar con el tensor de entidades Key-Value concatenado. Y para no introducir cambios en el programa OpenCL, simplemente añadiremos la concatenación de los tensores especificados.

      //--- Key-Value
      base = new CNeuronBaseOCL();
      if(!base ||
         !base.Init(0, i * 12 + 6, OpenCL, iPoints * 2 * 32 * 2, optimization, iBatch))
         return false;
      if(!cKeyValue.Add(base))
         return false;

La matriz de coeficientes de dependencia solo se utilizará en el contexto OpenCL y se recalculará en cada pasada directa. Por lo tanto, crear este búfer en la memoria principal no tiene sentido: solo lo crearemos en la memoria contextual OpenCL.

      //--- Score
      int s = int(iUnits * iPoints * 4);
      s = OpenCL.AddBuffer(sizeof(float) * s, CL_MEM_READ_WRITE);
      if(s < 0 || !cScores.Add(s))
         return false;

Aquí también crearemos una capa para registrar los datos de la atención multicabeza.

      //--- MH Attention Out
      base = new CNeuronBaseOCL();
      if(!base ||
         !base.Init(0, i * 12 + 7, OpenCL, iUnits * 64, optimization, iBatch))
         return false;
      if(!cMHAttentionOut.Add(base))
         return false;

Y añadiremos una capa de convolución de escalado de los resultados obtenidos.

      //--- Attention Out
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0, i * 12 + 8, OpenCL, 64, 64, 64, iUnits, 1, optimization, iBatch))
         return false;
      if(!cAttentionOut.Add(conv))
         return false;

Según el algoritmo del Transformer, los resultados de Self-Attention obtenidos se sumarán con los datos de origen y se normalizarán.

      //--- Residual
      base = new CNeuronBaseOCL();
      if(!base ||
         !base.Init(0, i * 12 + 9, OpenCL, iUnits * 64, optimization, iBatch))
         return false;
      if(!cResidual.Add(base))
         return false;

A continuación, añadiremos 2 capas del bloque FeedForward.

      //--- Feed Forward
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0, i * 12 + 10, OpenCL, 64, 64, 256, iUnits, 1, optimization, iBatch))
         return false;
      conv.SetActivationFunction(LReLU);
      if(!cFeedForward.Add(conv))
         return false;
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0, i * 12 + 11, OpenCL, 256, 64, 64, iUnits, 1, optimization, iBatch))
         return false;
      if(!cFeedForward.Add(conv))
         return false;

Y el objeto para organizar el enlace residual.

      //--- Residual
      base = new CNeuronBaseOCL();
      if(!base ||
         !base.Init(0, i * 12 + 12, OpenCL, iUnits * 64, optimization, iBatch))
         return false;
      if(!base.SetGradient(conv.getGradient(), true))
         return false;
      if(!cResidual.Add(base))
         return false;

Nótese que, en este caso, sustituiremos el búfer de gradiente de error en la capa de organización de enlace residual. Esto nos permitirá excluir la operación de copiado de los datos del gradiente de error de la capa de enlace residual a la última capa del bloque de pasada directa.

Para completar el módulo SEFormer, los autores del método sugieren usar el Ttransformer vainilla. Yo, en cambio, he decidido aprovechar una arquitectura más compleja e insertar un módulo de atención condicionada por la escena.

      //--- Final Attention
      CNeuronMLMHSceneConditionAttention *att = new CNeuronMLMHSceneConditionAttention();
      if(!att ||
         !att.Init(0, i * 12 + 13, OpenCL, 64, 16, 4, 2, iUnits, 2, 1, optimization, iBatch))
         return false;
      if(!cFinalAttention.Add(att))
         return false;
     }

En este punto, hemos inicializado todos los objetos de la capa interna, y pasaremos a la siguiente iteración del ciclo.

Una vez completadas las iteraciones del ciclo de inicialización de objetos de la capa interna, deberemos prestar atención al hecho de que no utilizamos los resultados de cada capa interna. Y probablemente sería lógico concatenarlos en un único tensor y luego transmitir el tensor común para generar una incorporación global de la nube de puntos mediante la clase padre. Por supuesto, tendremos que escalar previamente el tensor resultante al tamaño requerido. Pero en este caso, he decidido tomar una ruta alternativa. Simplemente usaremos el bloque de atención cruzada y enriqueceremos los datos de menor escala con información de la mayor.

   if(!SEOut.Init(0, 26, OpenCL, 64, 64, 4, 16, 4, iUnits, iUnits, 4, 1, optimization, iBatch))
      return false;

Y al final del método inicializaremos el búfer auxiliar de almacenamiento temporal de datos.

   if(!cbTemp.BufferInit(buf_size, 0) ||
      !cbTemp.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Después, devolveremos el resultado lógico de las operaciones del método al programa que realiza la llamada.

En este punto, hemos completado el método de inicialización del objeto de clase. Ahora construiremos el algoritmo de pasada directa en el método feedForward. Como ya sabrá, en los parámetros de este método obtendremos el puntero al objeto de datos de origen.

bool CNeuronSEFormer::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//---
   CNeuronBaseOCL *neuron = NULL, *q = NULL, *k = NULL, *v = NULL, *kv = NULL;

En el cuerpo del método, primero declararemos varias variables locales para almacenar temporalmente los punteros a los objetos internos. Y luego generaremos una representación de centroides.

//--- Init Points
   if(bTrain)
     {
      neuron = cCenterPoints[1];
      if(!neuron ||
         !neuron.FeedForward(cCenterPoints[0]))
         return false;
     }

Tenga en cuenta que solo generaremos la representación del centroide durante el entrenamiento del modelo. Durante el funcionamiento, los puntos del centroide serán estáticos. Y no necesitaremos generarlos en cada pasada.

A continuación, organizaremos un ciclo para enumerar las capas internas,

//--- Inside Layers
   for(int l = 0; l < 2; l++)
     {
      //--- Segmentation Inputs
      if(l > 0 || !cTNetG)
        {
         if(!caLocalPointNet[l].FeedForward((l == 0 ? NeuronOCL : GetPointer(caLocalPointNet[l - 1]))))
            return false;
        }
      else
        {
         if(!cTurnedG)
            return false;
         if(!cTNetG.FeedForward(NeuronOCL))
            return false;
         int window = (int)MathSqrt(cTNetG.Neurons());
         if(IsStopped() ||
            !MatMul(NeuronOCL.getOutput(), cTNetG.getOutput(), cTurnedG.getOutput(), 
                                      NeuronOCL.Neurons() / window, window, window))
            return false;
         if(!caLocalPointNet[0].FeedForward(cTurnedG.AsObject()))
            return false;
        }

en cuyo cuerpo segmentaremos primero los datos de origen (el algoritmo se tomará prestado de la clase padre). Y luego enriquecemos los centroides con los datos obtenidos.

      //--- Interpolate center points
      neuron = cCenterPoints[l + 2];
      if(!neuron ||
         !neuron.FeedForward(cCenterPoints[l + 1], caLocalPointNet[l].getOutput()))
         return false;

A continuación, pasaremos al módulo de atención con la codificación de la estructura de datos. Primero extraeremos las capas interiores correspondientes de los arrays.

      //--- Structure-Embedding Attention
      q = cQuery[l];
      k = cKey[l];
      v = cValue[l];
      kv = cKeyValue[l];

Y, a continuación, generaremos secuencialmente todas las entidades necesarias.

      //--- Query
      if(!q || !q.FeedForward(GetPointer(caLocalPointNet[l])))
         return false;
      //--- Key
      if(!k || !k.FeedForward(cCenterPoints[l + 2]))
         return false;
      //--- Value
      if(!v || !v.FeedForward(cCenterPoints[l + 2]))
         return false;

Después concatenaremos los resultados de la generación de Keys y Values en un único tensor.

      if(!kv ||
         !Concat(k.getOutput(), v.getOutput(), kv.getOutput(), 32 * 2, 32 * 2, iPoints))
         return false;

Y luego podremos utilizaremos los métodos de la Self-Attention Multicabeza clásica.

      //--- Multi-Head Attention
      neuron = cMHAttentionOut[l];
      if(!neuron ||
         !AttentionOut(q.getOutput(), kv.getOutput(), cScores[l], neuron.getOutput()))
         return false;

Los datos resultantes se escalarán al tamaño de los datos de origen.

      //--- Scale
      neuron = cAttentionOut[l];
      if(!neuron || !neuron.FeedForward(cMHAttentionOut[l]))
         return false;

A continuación, sumaremos los dos flujos de información y normalizaremos los datos resultantes.

      //--- Residual
      q = cResidual[l * 2];
      if(!q ||
         !SumAndNormilize(caLocalPointNet[l].getOutput(), neuron.getOutput(), q.getOutput(), 64, true,
                                                                                           0, 0, 0, 1))
         return false;

De forma similar al codificador del Transformer vainilla, utilizaremos un bloque FeedForward seguido de un enlace residual y la normalización de datos.

      //--- Feed Forward
      neuron = cFeedForward[l * 2];
      if(!neuron || !neuron.FeedForward(q))
         return false;
      neuron = cFeedForward[l * 2 + 1];
      if(!neuron || !neuron.FeedForward(cFeedForward[l * 2]))
         return false;
      //--- Residual
      k = cResidual[l * 2 + 1];
      if(!k ||
         !SumAndNormilize(q.getOutput(), neuron.getOutput(), k.getOutput(), 64, true, 0, 0, 0, 1))
         return false;

Luego pasaremos los resultados obtenidos por un bloque de atención específico para cada escena. Y pasaremos a la siguiente iteración del ciclo.

      //--- Final Attention
      neuron = cFinalAttention[l];
      if(!neuron || !neuron.FeedForward(k))
         return false;
     }

Una vez realizadas con éxito las operaciones de todas las capas internas, enriqueceremos las incorporaciones de puntos de menor escala con información de gran escala.

//--- Cross scale attention
   if(!SEOut.FeedForward(cFinalAttention[0], neuron.getOutput()))
      return false;

Y transmitiremos el resultado obtenido para formar una incorporación global de la nube de puntos analizada.

//--- Global Point Cloud Embedding
   if(!CNeuronPointNetOCL::feedForward(SEOut.AsObject()))
      return false;
//--- result
   return true;
  }

Y al finalizar el método de pasada directa, retornaremos el resultado lógico de las operaciones realizadas al programa que realiza la llamada.

Como podemos ver, en el proceso de aplicación del algoritmo de pasada directa, hemos organizado una estructura de flujo de información bastante compleja, que dista mucho de ser lineal. Aquí vemos los enlaces residuales. Algunos objetos utilizan dos fuentes de datos. Además, algunos flujos de información están entrelazados. Y obviamente, esto ha dejado una huella en el algoritmo de pasada inversa que implementamos en el método calcInputGradients.

bool CNeuronSEFormer::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

En los parámetros del método, obtendremos el puntero al objeto de la capa anterior. En la pasada directa, este nos daba los datos de origen. Y ahora tendremos que transmitirle el gradiente de error que se corresponde con la influencia de los datos de entrada en el resultado final del modelo.

En el cuerpo del método comprobaremos directamente la relevancia del puntero obtenido, porque de lo contrario todas las operaciones posteriores carecerán de sentido.

También declararemos una serie de variables locales para almacenar temporalmente los punteros a los objetos internos.

   CNeuronBaseOCL *neuron = NULL, *q = NULL, *k = NULL, *v = NULL, *kv = NULL;
   CBufferFloat *buf = NULL;

Después, haremos descender el gradiente de error desde la incorporación global de la nube de puntos a nuestras capas interiores.

//--- Global Point Cloud Embedding
   if(!CNeuronPointNetOCL::calcInputGradients(SEOut.AsObject()))
      return false;

Nótese que en la pasada directa, hemos obtenido el resultado final llamando al método de la clase padre. Por lo tanto, necesitaremos utilizar el método correspondiente de la clase padre para obtener también el gradiente de error.

A continuación, distribuiremos el gradiente de error en flujos de diferentes escalas.

//--- Cross scale attention
   neuron = cFinalAttention[0];
   q = cFinalAttention[1];
   if(!neuron.calcHiddenGradients(SEOut.AsObject(), q.getOutput(), q.getGradient(), (
                                                    ENUM_ACTIVATION)q.Activation()))
      return false;

Y organizaremos un ciclo para volver a pasar por las capas interiores.

   for(int l = 1; l >= 0; l--)
     {
      //--- Final Attention
      neuron = cResidual[l * 2 + 1];
      if(!neuron || !neuron.calcHiddenGradients(cFinalAttention[l]))
         return false;

Aquí, primero bajaremos el gradiente de error a la capa de enlace residual.

Recordemos que al inicializar los objetos internos, hemos sustituido el búfer de gradiente de error de la capa de enlace residual por un búfer de capa similar del bloque FeedForward. Así que ahora podremos omitir la operación redundante de copiado de datos y pasar inmediatamente el gradiente de error al nivel inferior.

      //--- Feed Forward
      neuron = cFeedForward[l * 2];
      if(!neuron || !neuron.calcHiddenGradients(cFeedForward[l * 2 + 1]))
         return false;

A continuación, bajaremos el gradiente de error hasta la capa de enlace residual del bloque de atención.

      neuron = cResidual[l * 2];
      if(!neuron || !neuron.calcHiddenGradients(cFeedForward[l * 2]))
         return false;

Y aquí sumaremos el gradiente de error de los dos flujos de información y transmitiremos el valor sumado a la unidad de atención.

      //--- Residual
      q = cResidual[l * 2 + 1];
      k = neuron;
      neuron = cAttentionOut[l];
      if(!neuron ||
         !SumAndNormilize(q.getGradient(), k.getGradient(), neuron.getGradient(), 64, false, 0, 0, 0, 1))
         return false;

Después, distribuiremos el gradiente de error entre las cabezas de atención.

      //--- Scale
      neuron = cMHAttentionOut[l];
      if(!neuron || !neuron.calcHiddenGradients(cAttentionOut[l]))
         return false;

Y utilizando los algoritmos del Transformer vainilla, bajaremos el gradiente de error al nivel de las entidades Query, Key y Value.

      //--- MH Attention
      q = cQuery[l];
      kv = cKeyValue[l];
      k = cKey[l];
      v = cValue[l];
      if(!AttentionInsideGradients(q.getOutput(), q.getGradient(), kv.getOutput(), kv.getGradient(),
                                                                   cScores[l], neuron.getGradient()))
         return false;

Como resultado de esta operación, hemos obtenido dos tensores de gradiente de error: un tensor al nivel de Query y un tensor concatenado Key-Value. Luego distribuiremos los gradientes de error de Key y Value a los búferes de las capas internas correspondientes.

      if(!DeConcat(k.getGradient(), v.getGradient(), kv.getGradient(), 32 * 2, 32 * 2, iPoints))
         return false;

Y además podemos bajar el gradiente de error desde el tensor Query hasta el nivel de segmentación de los datos de origen. No obstante, deberemos considerar un pequeño detalle: Para la última capa, esta operación no resultará especialmente difícil. Pero para la primera capa, el búfer de gradiente ya almacenará la información del error de la capa de segmentación posterior. Y deberemos mantenerlo. Por consiguiente, comprobaremos el índice de la capa actual y sustituiremos los punteros a los búferes de datos, si es necesario.

      if(l == 0)
        {
         buf = caLocalPointNet[l].getGradient();
         if(!caLocalPointNet[l].SetGradient(GetPointer(cbTemp), false))
            return false;
        }

A continuación, haremos descender el gradiente de error.

      if(!caLocalPointNet[l].calcHiddenGradients(q, NULL))
         return false;

Y si es necesario, sumaremos los datos de los dos flujos de información con el retorno posterior del puntero tomado del búfer de datos.

      if(l == 0)
        {
         if(!SumAndNormilize(buf, GetPointer(cbTemp), buf, 64, false, 0, 0, 0, 1))
            return false;
         if(!caLocalPointNet[l].SetGradient(buf, false))
            return false;
        }

Y luego añadiremos el gradiente de error de enlace residual del bloque de atención.

      neuron = cAttentionOut[l];
      //--- Residual
      if(!SumAndNormilize(caLocalPointNet[l].getGradient(), neuron.getGradient(), 
                          caLocalPointNet[l].getGradient(), 64, false, 0, 0, 0, 1))
         return false;

El siguiente paso consistirá en distribuir el gradiente de error hasta el nivel de nuestros centroides. Aquí tendremos que distribuir el gradiente de error tanto desde la entidad Key como desde la entidad Value. Y también utilizaremos la sustitución de punteros en los búferes de datos.

      //--- Interpolate Center points
      neuron = cCenterPoints[l + 2];
      if(!neuron)
         return false;
      buf = neuron.getGradient();
      if(!neuron.SetGradient(GetPointer(cbTemp), false))
         return false;

A continuación, omitiremos el primer gradiente de error de la entidad Key.

      if(!neuron.calcHiddenGradients(k, NULL))
         return false;

Sin embargo, será el primero solo para la última capa, pero para la primera ya contendrá información sobre el gradiente de error a partir de la influencia de la capa posterior en el resultado. Por lo tanto, comprobaremos el índice de la capa interna analizada y, si es necesario, sumaremos los datos de los dos flujos de información.

      if(l == 0)
        {
         if(!SumAndNormilize(buf, GetPointer(cbTemp), buf, 1, false, 0, 0, 0, 1))
            return false;
        }
      else
        {
         if(!SumAndNormilize(GetPointer(cbTemp), GetPointer(cbTemp), buf, 1, false, 0, 0, 0, 0.5f))
            return false;
        }

Del mismo modo, ejecutaremos el gradiente de error de la entidad Value y sumaremos los datos de los dos flujos de información.

      if(!neuron.calcHiddenGradients(v, NULL))
         return false;
      if(!SumAndNormilize(buf, GetPointer(cbTemp), buf, 1, false, 0, 0, 0, 1))
         return false;

A continuación, retornaremos el puntero tomado anteriormente al búfer de gradiente de error.

      if(!neuron.SetGradient(buf, false))
         return false;

Después distribuiremos el gradiente de error entre la capa centroide anterior y los datos segmentados de la capa actual.

      neuron = cCenterPoints[l + 1];
      if(!neuron.calcHiddenGradients(cCenterPoints[l + 2], caLocalPointNet[l].getOutput(), 
                                     GetPointer(cbTemp), (ENUM_ACTIVATION)caLocalPointNet[l].Activation()))
         return false;

Para preservar este gradiente de error en particular, realizaremos la sustitución de los búferes en la capa centroide anterior. Además, cabe señalar que el búfer de gradiente de error de la capa de segmentación de datos ya almacena la mayor parte de la información. Por consiguiente, en esta etapa, escribiremos el gradiente de error en un búfer de datos temporal. Y luego sumaremos los datos de los dos flujos de información.

      if(!SumAndNormilize(caLocalPointNet[l].getGradient(), GetPointer(cbTemp), 
                          caLocalPointNet[l].getGradient(), 64, false, 0, 0, 0, 1))
         return false;

En esta etapa, hemos distribuido el gradiente de error entre todos los objetos internos recién declarados. Pero queda por distribuir el gradiente de error a través de las capas de segmentación de datos. Tomaremos prestado este algoritmo al completo del método de la clase padre.

      //--- Local Net
      neuron = (l > 0 ? GetPointer(caLocalPointNet[l - 1]) : NeuronOCL);
      if(l > 0 || !cTNetG)
        {
         if(!neuron.calcHiddenGradients(caLocalPointNet[l].AsObject()))
            return false;
        }
      else
        {
         if(!cTurnedG)
            return false;
         if(!cTurnedG.calcHiddenGradients(caLocalPointNet[l].AsObject()))
            return false;
         int window = (int)MathSqrt(cTNetG.Neurons());
         if(IsStopped() ||
            !MatMulGrad(neuron.getOutput(), neuron.getGradient(), cTNetG.getOutput(), cTNetG.getGradient(), 
                                        cTurnedG.getGradient(), neuron.Neurons() / window, window, window))
            return false;
         if(!OrthoganalLoss(cTNetG, true))
            return false;
         //---
         CBufferFloat *temp = neuron.getGradient();
         neuron.SetGradient(cTurnedG.getGradient(), false);
         cTurnedG.SetGradient(temp, false);
         //---
         if(!neuron.calcHiddenGradients(cTNetG.AsObject()))
            return false;
         if(!SumAndNormilize(neuron.getGradient(), cTurnedG.getGradient(), neuron.getGradient(), 1, false, 
                                                                                               0, 0, 0, 1))
            return false;
        }
     }
//---
   return true;
  }

Y después de ejecutar todas las iteraciones de nuestro ciclo de capa interna, retornaremos el resultado lógico de las operaciones del método al programa que realiza la llamada.

Arriba, hemos implementado los algoritmos para la pasada directa y la distribución del gradiente de error a través de los objetos internos de nuestra nueva clase. Queda por implementar el método de actualización de los parámetros entrenados de la clase updateInputWeights. En este caso, todos los parámetros entrenados estarán contenidos en objetos anidados. En consecuencia, para actualizar los parámetros de nuestra clase, bastará con llamar sistemáticamente a los métodos homónimos de los objetos internos. Este algoritmo es bastante simple, así que le sugiero que lo estudie por su cuenta.

Como recordatorio, encontrará el código completo de la nueva clase CNeuronSEFormer y todos sus métodos en el archivo adjunto. Allí también encontrará el código de los métodos que ofrecen servicio a esta clase, y que han sido declarados anteriormente para su redefinición.

Asimismo, debemos decir que la arquitectura de los modelos se ha tomado casi por completo del artículo anterior. Solo hemos reemplazado una capa en el Codificador de estado de entorno.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSEFormer;
     {
      int temp[] = {BarDescr, 8};                  // Variables, Center embedding
      if(ArrayCopy(descr.windows, temp) < (int)temp.Size())
         return false;
     }
     {
      int temp[] = {HistoryBars, 27};              // Units, Centers
      if(ArrayCopy(descr.units, temp) < (int)temp.Size())
         return false;
     }
   descr.window_out = LatentCount;                 // Output Dimension
   descr.step = int(true);                         // Use input and feature transformation
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Lo mismo ocurre con todos los programas de interacción con el entorno y de entrenamiento de modelos, que hemos tomado al completo del documento anterior. Así que no nos detendremos en ellos. En el archivo adjunto figura el código completo de todos los programas usados en la elaboración de este artículo.

3. Simulación

Y así, después de mucho trabajo, hemos llegado a la parte final y probablemente más emocionante: el entrenamiento de los modelos y la prueba de la política del Actor resultante con datos históricos reales.

Al igual que antes, para entrenar los modelos utilizaremos datos históricos reales del instrumento EURUSD para todo el año 2023 y el marco temporal H1. Los parámetros de todos los indicadores analizados se han usado por defecto.

El algoritmo de entrenamiento del modelo lo hemos tomado prestado de artículos anteriores, junto con los programas utilizados en el entrenamiento y las pruebas de los modelos.

Para probar la política del Actor entrenada, hemos usado datos históricos reales para enero de 2024 con todos los demás parámetros intactos. Ahora le presentamos los resultados de las mismas.

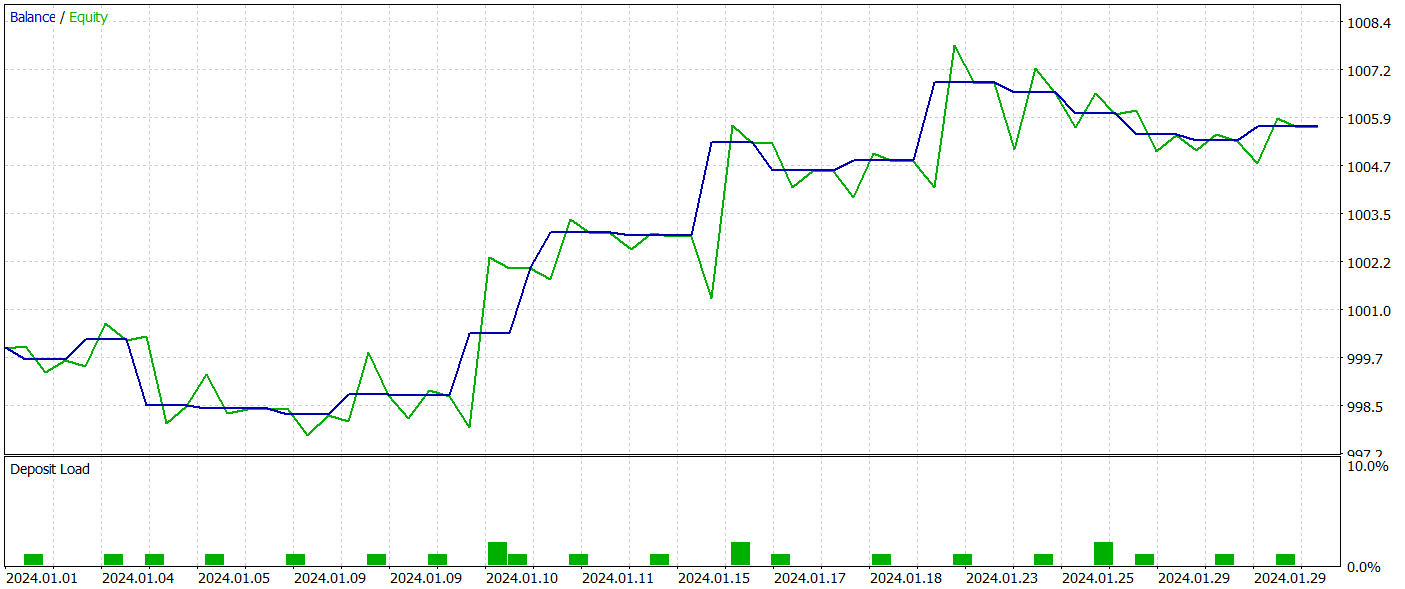
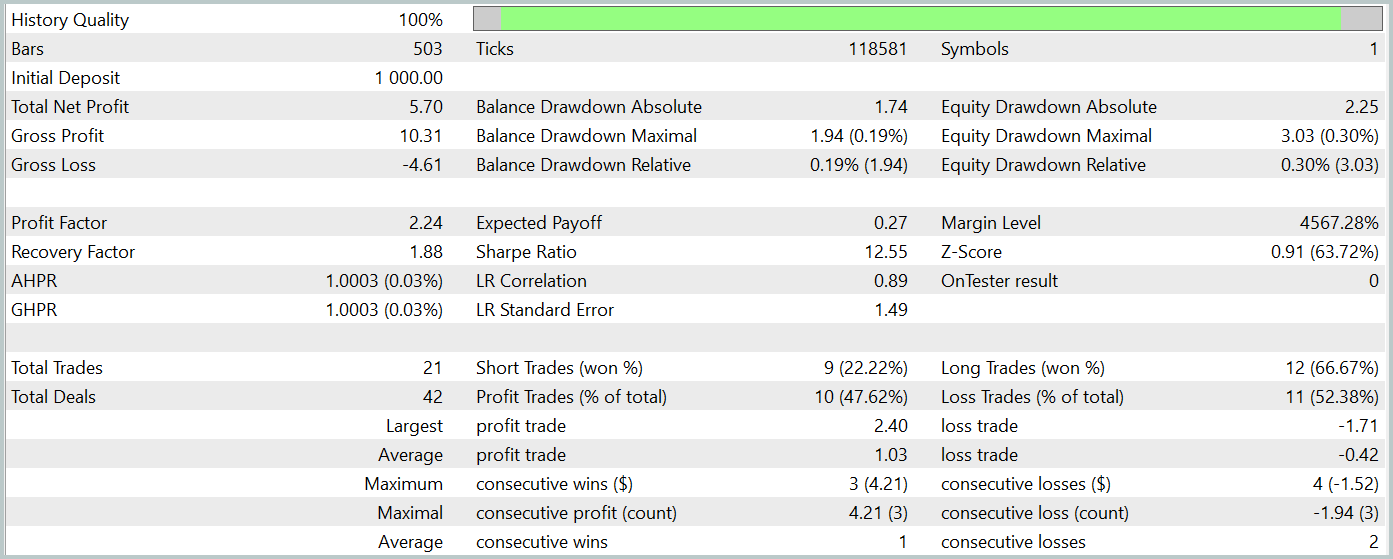
Durante el periodo de prueba, el modelo entrenado ha realizado 21 transacciones, algo más del 47% de las cuales se han cerrado con beneficio. Aquí cabe señalar que las posiciones largas se caracterizan por rendimientos significativamente más elevados (el 66% frente al 22%). Obviamente, deberemos realizar un entrenamiento adicional del modelo. Sin embargo, la media de transacciones rentables es 2,5 veces superior a la de transacciones perdedoras similares, lo cual ha permitido al modelo obtener un beneficio general según los resultados de las pruebas.

En mi opinión subjetiva, el modelo ha resultado bastante pesado. Probablemente esto tenga que ver con el uso de un algoritmo de atención basado en escenas. Sin embargo, usando un enfoque similar en HyperDet3D se han obtenido mejores resultados a un coste menor.

No obstante, el reducido número de transacciones y el breve periodo de prueba en ambos casos no nos permiten juzgar la eficacia de los métodos a lo largo de un periodo de tiempo más prolongado.

Conclusión

El método SEFormer ha sido adaptado para el análisis de nubes de puntos y puede identificar eficazmente las dependencias locales en el ruido, que es un factor clave para obtener predicciones precisas. Esto descubre perspectivas considerables para prever con mayor precisión los movimientos del mercado y mejorar las estrategias de toma de decisiones.

En la parte práctica de este artículo, hemos implementado nuestra visión de los enfoques propuestos utilizando MQL5. Asimismo, hemos entrenado y probado el modelo con datos históricos reales. Los resultados obtenidos demuestran el potencial del método propuesto. Sin embargo, antes de usar el modelo en condiciones comerciales reales, deberemos entrenarlo en un periodo histórico más largo con la consiguiente prueba exhaustiva de la política entrenada.

Enlaces

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15882

Archivos adjuntos |

Descargar ZIP

MQL5.zip (1823.3 KB)

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores

Características del Wizard MQL5 que debe conocer (Parte 40): SAR parabólico

El SAR parabólico (Stop-and-Reversal, SAR) es un indicador de confirmación de tendencia y de puntos de finalización de tendencia. Debido a que es un rezagado en la identificación de tendencias, su propósito principal ha sido posicionar trailing stop loss en posiciones abiertas. Sin embargo, exploramos si realmente podría usarse como una señal de Asesor Experto, gracias a clases de señales personalizadas de Asesores Expertos ensamblados por un asistente.

Características del Wizard MQL5 que debe conocer (Parte 39): Índice de fuerza relativa

El Índice de fuerza relativa (Relative Strength Index, RSI) es un oscilador de momento popular que mide el ritmo y el tamaño del cambio de precio reciente de un valor para evaluar situaciones de sobrevaloración y subvaloración en el precio del valor. Estos conocimientos sobre velocidad y magnitud son clave para definir puntos de reversión. Ponemos este oscilador a trabajar en otra clase de señal personalizada y examinamos las características de algunas de sus señales. Sin embargo, comenzaremos resumiendo lo que comenzamos anteriormente sobre las Bandas de Bollinger.

Del básico al intermedio: Recursividad

En este artículo, veremos un concepto de programación muy interesante y bastante divertido, aunque debe ser tratado con extremo respeto, ya que un mal uso o un mal entendimiento del mismo convierte programas relativamente simples en algo innecesariamente complicado. Aunque, el buen uso y la perfecta adecuación en situaciones igualmente adecuadas convierten la recursividad en un gran aliado para resolver cuestiones que, de otra forma, serían mucho más trabajosas y demoradas. El contenido expuesto aquí tiene un propósito puramente didáctico. En ningún caso debe ser considerado como una aplicación cuya finalidad no sea el aprendizaje y el estudio de los conceptos mostrados.

Del básico al intermedio: Unión (II)

Este será un artículo muy divertido y bastante curioso, en varios aspectos. Abordará la unión, para resolver un problema discutido anteriormente. Además, exploraremos algunas situaciones inusuales que pueden surgir al usar una unión en aplicaciones. El contenido expuesto aquí tiene, pura y simplemente, una finalidad didáctica. En ningún caso debe considerarse como una aplicación cuya finalidad no sea el aprendizaje y el estudio de los conceptos mostrados.