Redes neurais em trading: Transformer para nuvens de pontos (Pointformer)
Introdução
A detecção de objetos em nuvens de pontos é de grande importância para diversas aplicações práticas. Em comparação com imagens, as nuvens de pontos podem fornecer uma geometria detalhada e capturar a estrutura da cena. Por outro lado, as nuvens de pontos são irregulares, o que cria um grande desafio para o estudo eficiente de características.
Os modelos baseados na arquitetura Transformer alcançaram grande sucesso no campo do processamento de linguagem natural. Eles são bastante eficazes para aprender representações contextuais e capturar dependências de longo alcance na sequência inicial. O Transformer e o mecanismo de Self-Attention associado não apenas atendem ao requisito de invariância a permutações, como também se mostraram altamente expressivos. No entanto, a aplicação direta do Transformer às nuvens de pontos é extremamente cara, pois o custo computacional cresce quadraticamente com o tamanho dos dados brutos.
Esse problema foi abordado pelos autores do método Pointformer, apresentado no trabalho "3D Object Detection with Pointformer". O método permite estudar características de maneira eficiente ao aproveitar a superioridade dos modelos Transformer em dados estruturados em conjuntos. O Pointformer é uma estrutura U-Net com blocos Pointformer multiescalares. O bloco Pointformer é composto por módulos baseados no Transformer, que são simultaneamente expressivos e adequados para a tarefa de detecção de objetos.
a solução arquitetônica, os autores do método utilizam 3 módulos Transformer:
- O Local Transformer (LT) é utilizado para modelar interações entre pontos em uma região local. Ele estuda as características contextuais da região no nível do objeto.
- O Local-Global Transformer (LGT) permite integrar funções locais e globais com maior resolução.
- O Global Transformer (GT) é projetado para estudar representações contextuais no nível da cena.
Como resultado, o Pointformer consegue capturar tanto dependências locais quanto globais, aumentando o desempenho do aprendizado de funções para cenas com múltiplos objetos aglomerados.
1. Algoritmo Pointformer
Ao estudar nuvens de pontos, é necessário levar em consideração sua natureza irregular e desordenada, bem como seu tamanho variável. Os autores do método Pointformer desenvolveram módulos baseados no Transformer para trabalhar com conjuntos de pontos. Esses módulos não apenas aumentam a expressividade na extração de características locais, como também incluem informações globais nas representações dos pontos.
O bloco Pointformer é composto por três módulos: Local Transformer (LT), Local-Global Transformer (LGT) e Global Transformer (GT). Inicialmente, o LT recebe os dados brutos do bloco anterior (alta resolução) e extrai características para um novo conjunto com um número reduzido de elementos (baixa resolução). Em seguida, o LGT utiliza um mecanismo de atenção cruzada multinível para integrar as funções de alta e baixa resolução. Por fim, o GT é usado para capturar representações contextuais. Quanto ao bloco de aumento de amostragem, os autores do método utilizam o módulo de propagação de funções PointNet++.
Para construir uma representação hierárquica da cena da nuvem de pontos, os autores do Pointformer empregam uma metodologia de alto nível que organiza blocos de aprendizado de características em diferentes resoluções. Inicialmente, para selecionar um subconjunto de pontos, é utilizada a amostragem dos pontos mais distantes (FPS) como um conjunto de centroides. Para cada centroide, são selecionados pontos da região local dentro de um raio especificado. Em seguida, esses objetos são agrupados ao redor dos centroides e passados como uma sequência de pontos para a camada Transformer. O bloco Transformer geral é aplicado a todas as regiões locais. À medida que mais camadas Transformer são sobrepostas no bloco Pointformer, a expressividade do módulo aumenta, permitindo a extração de representações mais detalhadas.
Além disso, são levadas em consideração as correlações entre características de pontos vizinhos. Em algumas circunstâncias, os pontos vizinhos podem ser mais informativos do que o ponto do centroide. Dessa forma, ao utilizar a transmissão de informações entre todos os pontos, os objetos na região local são considerados de maneira equitativa, tornando o módulo de extração de características locais mais eficiente.
A amostragem dos pontos mais distantes (FPS) é amplamente utilizada em muitos sistemas de nuvem de pontos, pois permite gerar amostras quase uniformes enquanto mantém a forma original. Isso garante que a maior parte dos pontos possa ser coberta por um número limitado de centroides. No entanto, o FPS apresenta duas principais limitações:
- É sensível a valores atípicos, o que resulta em alta instabilidade, especialmente ao trabalhar com nuvens de pontos reais.
- Os pontos amostrados pelo FPS são um subconjunto da nuvem de pontos original, o que dificulta a recuperação da informação geométrica original em casos em que os objetos estão parcialmente sobrepostos ou quando um número insuficiente de pontos do objeto foi capturado.
Considerando que os pontos geralmente são fixados na superfície dos objetos, o segundo problema pode se tornar mais relevante, uma vez que as propostas são geradas com base na amostragem de pontos, o que leva a uma discrepância natural entre a proposta e a precisão.
Para superar essas limitações, os autores do método Pointformer propõem um módulo de refinamento das coordenadas dos pontos utilizando mapas de Self-Attention. Inicialmente, os mapas de Self-Attention da última camada do bloco Transformer são extraídos para cada cabeça de atenção. Em seguida, calcula-se o valor médio dos mapas de atenção. Após isso, as coordenadas refinadas dos centroides são calculadas ponderando os valores de todos os pontos na região local pelos respectivos coeficientes médios dos mapas de Self-Attention. Com o módulo de refinamento proposto, os centroides são adaptativamente deslocados para mais próximo dos centros dos objetos.
Informações globais, que representam os contextos da cena e a correlação das bordas entre diferentes objetos, também são valiosas para tarefas de detecção. O Pointformer utiliza as capacidades dos módulos Transformer para modelar relações não locais. Em particular, o módulo Global Transformer é projetado para transmitir informações por toda a nuvem de pontos. Todos os pontos são agrupados em uma única unidade e servem como dados brutos para o módulo GT.
O uso de Transformer no nível da cena permite capturar representações contextuais e facilita a troca de informações entre diferentes objetos. Além disso, as representações globais podem ser especialmente úteis para detectar objetos com um número muito pequeno de pontos.
O Local-Global Transformer também é um módulo essencial para integrar as funções locais e globais extraídas pelos módulos LT e GT. O LGT utiliza um módulo de atenção cruzada multiescalar e gera relações entre os centroides de baixa resolução e os pontos de alta resolução. Formalmente, o mecanismo de atenção cruzada do Transformer é aplicado aqui. Os resultados do LT servem como Query, enquanto os dados do GT com maior resolução (do nível anterior) são usados como Key e Value.
A codificação posicional é uma parte integrante dos modelos Transformer. É o único mecanismo que codifica informações de posição para cada token na sequência inicial. Ao adaptar Transformers para dados de nuvens de pontos, a codificação posicional desempenha um papel ainda mais importante, pois as coordenadas das nuvens de pontos são características valiosas que indicam estruturas locais.
Abaixo, é apresentada a visualização do método Pointformer pelos autores.

2. Implementação utilizando MQL5
Após analisarmos os aspectos teóricos do método Pointformer, partimos para a parte prática deste artigo, na qual implementamos nossa visão dos conceitos propostos usando MQL5.
Ao examinar detalhadamente os métodos apresentados, é possível notar certa semelhança com o PointNet++. Ambos os algoritmos utilizam a amostragem dos pontos mais distantes para formar os centroides. Além disso, as operações principais de ambos os métodos são baseadas na agrupação de pontos ao redor dos centroides. Por esse motivo, decidiu-se usar o objeto CNeuronPointNet2OCL como classe base para construir a nova classe CNeuronPointFormer, cuja estrutura é apresentada a seguir.
class CNeuronPointFormer : public CNeuronPointNet2OCL { protected: CNeuronMLMHSparseAttention caLocalAttention[2]; CNeuronMLCrossAttentionMLKV caLocalGlobalAttention[2]; CNeuronMLMHAttentionMLKV caGlobalAttention[2]; CNeuronLearnabledPE caLocalPE[2]; CNeuronLearnabledPE caGlobalPE[2]; CNeuronBaseOCL cConcatenate; CNeuronConvOCL cScale; //--- CBufferFloat *cbTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override ; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronPointFormer(void) {}; ~CNeuronPointFormer(void) { delete cbTemp; } //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, uint output, bool use_tnets, ENUM_OPTIMIZATION optimization_type, uint batch) override; //--- virtual int Type(void) override const { return defNeuronPointFormer; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
No CNeuronPointNet2OCL, utilizamos 2 níveis de escalas para extrair características locais. Na nova classe, manteremos o mesmo nível de escalonamento, mas elevaremos a qualidade da extração de características para um novo patamar, graças aos módulos de atenção propostos. Isso é evidenciado pelos arrays das camadas internas de neurônios, cuja finalidade será explorada durante a implementação dos métodos da nova classe CNeuronPointFormer.
Entre os objetos internos, existe apenas um buffer dinâmico declarado, que será removido no destrutor da classe. Enquanto isso, o construtor da classe será deixado vazio. A inicialização de todos os objetos internos será realizada no método Init, cujos parâmetros foram transferidos sem alterações da classe base.
bool CNeuronPointFormer::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, uint output, bool use_tnets, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronPointNet2OCL::Init(numOutputs, myIndex, open_cl, window, units_count, output, use_tnets, optimization_type, batch)) return false;
No corpo do método, como de costume, começamos chamando o método homônimo da classe base, onde ocorre o controle dos parâmetros recebidos e a inicialização dos objetos herdados.
Aqui, vale lembrar que, na classe base, criamos 2 camadas internas de subamostragem local. Na saída dessas camadas, obtemos um vetor de 64 elementos para cada ponto da nuvem analisada.
Após cada camada de discretização local, adicionaremos os módulos de atenção propostos pelos autores do método Pointformer. A arquitetura dos módulos das duas camadas será a mesma. Portanto, a inicialização dos objetos será realizada em um laço.
for(int i = 0; i < 2; i++) { if(!caLocalAttention[i].Init(0, i*5, OpenCL, 64, 16, 4, units_count, 2, optimization, iBatch)) return false;
Primeiro, inicializamos o módulo de atenção local, cuja função será desempenhada pelo bloco de atenção esparsa CNeuronMLMHSparseAttention.
Vale dizer que aqui nos desviamos um pouco do algoritmo proposto pelos autores do método Pointformer. Porém, mantemos, em nossa opinião, a lógica de funcionamento. No módulo de atenção local, os autores enriqueceram os pontos da área local com características globais, o que permite focar a atenção no objeto de generalização. É evidente que pontos pertencentes ao mesmo objeto apresentam maiores dependências entre si. O uso do bloco de atenção esparsa permite não se limitar a uma área local específica, mas sim focar nos elementos com dependências significativas. Isso pode ser comparado à definição de níveis de suporte e resistência, nos quais o preço se chocou várias vezes em diferentes partes do intervalo histórico analisado.
Em seguida, inicializamos o bloco de atenção local-global, no qual complementamos as informações dos objetos locais com nuances dos dados brutos.
if(!caLocalGlobalAttention[i].Init(0, i*5+1, OpenCL, 64, 16, 4, 64, 2, units_count, units_count, 2, 2, optimization, iBatch)) return false;
O bloco de atenção global, por sua vez, é projetado para identificar representações contextuais no nível da cena.
if(!caGlobalAttention[i].Init(0, i*5+2, OpenCL, 64, 16, 4, 2, units_count, 2, 2, optimization, iBatch)) return false;
E, claro, adicionamos camadas internas de codificação posicional treinável. Aqui utilizamos codificações posicionais separadas para as representações local e global.
if(!caLocalPE[i].Init(0, i*5+3, OpenCL, 64*units_count, optimization, iBatch)) return false; if(!caGlobalPE[i].Init(0, i*5+4, OpenCL, 64*units_count, optimization, iBatch)) return false; }
Vale mencionar que não utilizamos o bloco de refinamento das coordenadas dos centroides proposto pelos autores do método Pointformer. Em primeiro lugar, ao implementar o algoritmo PointNet++, determinamos que cada ponto da nuvem seria o centroide da área local. Portanto, alterar as coordenadas dos pontos poderia distorcer a cena como um todo. Por outro lado, a função de refinamento das posições dos centroides é parcialmente desempenhada pelas camadas de codificação posicional treinável.
Algumas palavras sobre o escalonamento da extração de características. Os objetos inicializados anteriormente não indicam diretamente diferenças no escalonamento da extração de características. Contudo, há dois pontos a considerar. Na classe base, utilizamos diferentes raios para a discretização local. Aqui, adicionaremos diferentes níveis de esparsidade à atenção local.
caLocalAttention[0].Sparse(0.1f); caLocalAttention[1].Sparse(0.3f);
Os resultados dos dois níveis de atenção global são concatenados em um único tensor.
if(!cConcatenate.Init(0, 10, OpenCL, 128 * units_count, optimization, iBatch)) return false;
Depois, reduzimos sua dimensionalidade ao nível dos dados brutos do bloco de extração de descritor global da nuvem de pontos, inicializado no método da classe base.
if(!cScale.Init(0, 11, OpenCL, 128, 128, 64, units_count, 1, optimization, iBatch)) return false;
Ao final do método de inicialização, adicionamos a criação de um buffer para armazenar dados intermediários.
if(!!cbTemp) delete cbTemp; cbTemp = new CBufferFloat(); if(!cbTemp || !cbTemp.BufferInit(caGlobalAttention[0].Neurons(), 0) || !cbTemp.BufferCreate(OpenCL)) return false; //--- return true; }
Depois disso, retornamos à função chamadora o resultado lógico da execução das operações e encerramos o método.
O próximo passo do nosso trabalho é a construção do algoritmo de propagação para frente no método feedForward. E, aqui, diferentemente do método de inicialização, não podemos utilizar plenamente o método correspondente da classe base. No novo método, precisaremos combinar operações com objetos herdados e adicionados.
Nos parâmetros do método de propagação para frente, como antes, recebemos um ponteiro para o objeto dos dados brutos. No corpo do método, salvamos imediatamente o ponteiro recebido em uma variável local.
bool CNeuronPointFormer::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- LocalNet CNeuronBaseOCL *inputs = NeuronOCL;
Na maioria dos casos, não salvamos o ponteiro recebido em uma variável local, pois isso não faz sentido. No entanto, neste método, precisamos implementar um algoritmo de operação sequencial de dois blocos aninhados para extrair características em diferentes escalas. No corpo do laço, é mais conveniente trabalharmos com uma variável local, à qual podemos atribuir ponteiros para diferentes objetos.
Em seguida, criamos imediatamente o ciclo mencionado acima.
for(int i = 0; i < 2; i++) { if(!cTNetG || i > 0) { if(!caLocalPointNet[i].FeedForward(inputs)) return false; }
No corpo do ciclo, primeiro realizamos as operações de discretização local, cujos objetos foram declarados e inicializados na classe base.
Lembro que o algoritmo da classe base prevê a possibilidade de projeção dos dados brutos no espaço canônico. Essa operação é realizada somente antes da primeira camada de discretização local. Por isso, primeiro verificamos se há necessidade de projetar os dados brutos e, caso não haja, realizamos diretamente a operação de discretização local.
Caso contrário, primeiro geramos a matriz de projeção.
else { if(!cTurnedG) return false; if(!cTNetG.FeedForward(inputs)) return false;
Realizamos a operação de projeção dos dados brutos.
int window = (int)MathSqrt(cTNetG.Neurons()); if(IsStopped() || !MatMul(NeuronOCL.getOutput(), cTNetG.getOutput(), cTurnedG.getOutput(), NeuronOCL.Neurons() / window, window, window)) return false;
E somente após isso, realizamos a discretização dos dados locais.
if(!caLocalPointNet[i].FeedForward(cTurnedG.AsObject())) return false; }
As informações são transmitidas do bloco de discretização local para o módulo de atenção local.
//--- Local Attention if(!caLocalAttention[i].FeedForward(caLocalPointNet[i].AsObject())) return false;
Observe que os dados são enviados ao módulo de atenção local sem codificação posicional. Quero lembrá-lo de que o algoritmo de Self-Attention é invariante à sequência dos objetos analisados. Assim, no bloco de atenção local, identificamos objetos com alto grau de influência mútua, independentemente de suas coordenadas.
"Análise no bloco de atenção local sem referência às coordenadas" pode soar um pouco contraditório. Afinal, o termo "atenção local" parece sugerir uma limitação nas coordenadas analisadas. Mas vejamos isso de outra forma. Existe um gráfico de preços. Dividimos as informações sobre o preço em duas categorias: coordenadas e características. A coordenada, neste caso, é o tempo, e o nível de preço é a característica. Se removermos as coordenadas (dados sobre o tempo), obteremos uma nuvem de pontos no espaço das características. E no nível em que o preço do ativo foi mais frequente, haverá maior concentração de pontos. Esses pontos podem estar significativamente separados no tempo. No entanto, essas áreas frequentemente representam níveis de suporte e resistência. Consequentemente, nosso módulo de atenção local opera no espaço local das características.
Depois disso, adicionaremos codificação posicional tanto ao resultado do módulo de atenção local quanto ao resultado da camada de discretização local dos dados.
//--- Position Encoder if(!caLocalPE[i].FeedForward(caLocalAttention[i].AsObject())) return false; if(!caGlobalPE[i].FeedForward(caLocalPointNet[i].AsObject())) return false;
No próximo passo, no módulo de atenção local-global, enriquecemos os dados provenientes da atenção local com informações do contexto global, levando em consideração as coordenadas dos objetos.
//--- Local to Global Attention if(!caLocalGlobalAttention[i].FeedForward(caLocalPE[i].AsObject(), caGlobalPE[i].getOutput())) return false;
Como parte final do nosso ciclo, utilizamos o módulo de atenção global, que enriquece as informações dos objetos com o contexto geral da cena.
//--- Global Attention if(!caGlobalAttention[i].FeedForward(caLocalGlobalAttention[i].AsObject())) return false; inputs = caGlobalAttention[i].AsObject(); }
Antes de avançar para a próxima iteração do ciclo, não nos esquecemos de atualizar o ponteiro para o objeto dos dados brutos na variável local.
Após a execução bem-sucedida de todas as iterações do nosso ciclo de processamento sequencial das camadas internas, concatenamos os resultados de todos os módulos de atenção global em um único tensor. Isso nos permite levar em consideração as características de objetos em diferentes escalas.
if(!Concat(caGlobalAttention[0].getOutput(), caGlobalAttention[1].getOutput(), cConcatenate.getOutput(), 64, 64, cConcatenate.Neurons() / 128)) return false;
Reduzimos ligeiramente o tamanho do tensor concatenado utilizando uma camada de escalonamento.
if(!cScale.FeedForward(cConcatenate.AsObject())) return false;
Em seguida, transmitimos os dados obtidos para o método de propagação para frente da classe CNeuronPointNetOCL, que é a ancestral da nossa classe base. Este método implementa o mecanismo de geração de um descritor global para a nuvem de pontos.
if(!CNeuronPointNetOCL::feedForward(cScale.AsObject())) return false; //--- return true; }
Não se esqueça de controlar o processo de execução das operações em cada etapa. E, após a execução bem-sucedida de todas as operações do método, retornamos seu resultado lógico para o programa chamador.
A seguir, passamos à construção dos algoritmos de propagação reversa. Aqui, como você sabe, precisamos implementar dois métodos:
- calcInputGradients — distribuição do gradiente do erro para todos os objetos, de acordo com sua influência no resultado geral;
- updateInputWeights — atualização dos parâmetros treináveis do modelo.
Para construir o algoritmo do segundo método, podemos simplesmente utilizar o método de propagação para frente apresentado anteriormente. Mantemos nele apenas a hierarquia de chamadas dos métodos dos objetos com parâmetros treináveis e substituímos a chamada do método de propagação para frente pelo método de atualização dos parâmetros. O resultado obtido pode ser consultado na documentação anexa.
Já com o algoritmo do método de distribuição do gradiente do erro, calcInputGradients, precisamos trabalhar. Como anteriormente, o algoritmo do método segue completamente o fluxo das operações de propagação para frente, mas em ordem inversa. No entanto, existem nuances relacionadas à paralelização dos fluxos de informação.
Nos parâmetros do método, recebemos um ponteiro para o objeto da camada anterior, no qual precisamos transmitir o gradiente do erro, de acordo com a influência dos dados brutos no resultado final do modelo.
bool CNeuronPointFormer::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
No corpo do método, imediatamente verificamos a validade do ponteiro recebido. Afinal, se ele for inválido, toda a execução das operações subsequentes perde o sentido.
Vale dizer que o gradiente do erro nos resultados da nossa camada, no momento em que este método é chamado, já está armazenado no buffer de dados correspondente. Nós o propagamos até o nível da camada interna de escalonamento chamando o método correspondente da classe ancestral.
if(!CNeuronPointNetOCL::calcInputGradients(cScale.AsObject())) return false;
Em seguida, propagamos o gradiente do erro até o nível da camada de dados concatenados.
if(!cConcatenate.calcHiddenGradients(cScale.AsObject())) return false;
Depois, distribuímos o gradiente pelos módulos de atenção global correspondentes.
if(!DeConcat(caGlobalAttention[0].getGradient(), caGlobalAttention[1].getGradient(), cConcatenate.getGradient(), 64, 64, cConcatenate.Neurons() / 128)) return false;
Agora, precisamos propagar o gradiente do erro sequencialmente por todos os módulos das camadas internas. Para isso, criamos um ciclo de iteração reversa.
CNeuronBaseOCL *inputs = caGlobalAttention[0].AsObject(); for(int i = 1; i >= 0; i--) { //--- Global Attention if(!caLocalGlobalAttention[i].calcHiddenGradients(caGlobalAttention[i].AsObject())) return false;
No ciclo, começamos determinando o gradiente do erro no nível do módulo de atenção local-global. Em seguida, o distribuímos pelas camadas de codificação posicional treinável.
if(!caLocalPE[i].calcHiddenGradients(caLocalGlobalAttention[i].AsObject(), caGlobalPE[i].getOutput(), caGlobalPE[i].getGradient(), (ENUM_ACTIVATION)caGlobalPE[i].Activation())) return false;
Após isso, transmitimos o gradiente do erro das camadas de codificação posicional ao módulo de atenção local e à camada de discretização local.
if(!caLocalAttention[i].calcHiddenGradients(caLocalPE[i].AsObject())) return false; if(!caLocalPointNet[i].calcHiddenGradients(caGlobalPE[i].AsObject())) return false;
Aqui, é importante notar que o módulo de atenção local também utiliza os resultados da camada de discretização local como dados brutos. Assim, ele deve transmitir sua parte do gradiente de erro a esse objeto. Entretanto, o buffer de dados correspondente já contém o gradiente do erro proveniente da camada de codificação posicional, e não queremos perder essas informações. Por isso, antes de transmitir o gradiente do erro do módulo de atenção local, é necessário salvar as informações existentes em um buffer temporário.
Nesse ponto, é relevante destacar que criamos conscientemente um ponteiro dinâmico para o objeto do buffer de armazenamento de dados. Além disso, criamos esse buffer com o mesmo tamanho do buffer de gradientes do erro da camada de discretização local. Isso nos permite, em vez de copiar os dados, simplesmente realizar uma troca de ponteiros entre os objetos.
CBufferFloat *temp = caLocalPointNet[i].getGradient();
caLocalPointNet[i].SetGradient(cbTemp, false);
cbTemp = temp;
Agora, podemos tranquilamente transmitir o gradiente do erro do módulo de atenção local sem risco de perder os dados previamente armazenados.
if(!caLocalPointNet[i].calcHiddenGradients(caLocalAttention[i].AsObject())) return false; if(!SumAndNormilize(caLocalPointNet[i].getGradient(), cbTemp, caLocalPointNet[i].getGradient(), 64, false, 0, 0, 0, 1)) return false;
Depois disso, somamos os gradientes do erro provenientes dos dois fluxos de informação.
O próximo passo é transmitir o gradiente do erro até o nível dos dados brutos. No entanto, aqui surge mais uma nuance. Dependendo da iteração do ciclo, nós transmitimos o gradiente do erro para o módulo de atenção global da camada interna anterior ou para o objeto de dados brutos recebido nos parâmetros do método. No último caso, o algoritmo é idêntico ao método da classe base. No primeiro caso, devemos lembrar que, anteriormente, já havíamos salvo o gradiente do erro durante a desconcatenação dos dados provenientes do módulo de geração do descritor global da nuvem de pontos analisada. Nesse caso, também substituímos os ponteiros para os buffers de dados. Afinal, eles foram projetados intencionalmente com o mesmo tamanho.
if(i > 0) { temp = inputs.getGradient(); inputs.SetGradient(cbTemp, false); cbTemp = temp; }
Em seguida, verificamos se é necessário ajustar o gradiente do erro para a projeção no espaço canônico. Se essa necessidade não existir, transmitimos o gradiente diretamente para o objeto correspondente.
if(!cTNetG || i > 0) { if(!inputs.calcHiddenGradients(caLocalPointNet[i].AsObject())) return false; }
No entanto, se a projeção para o espaço canônico foi realizada durante a propagação para frente, primeiro transmitimos o gradiente do erro ao nível do módulo da camada de projeção.
else { if(!cTurnedG) return false; if(!cTurnedG.calcHiddenGradients(caLocalPointNet[i].AsObject())) return false;
Depois, distribuímos o gradiente do erro entre os dados brutos e a matriz de projeção.
int window = (int)MathSqrt(cTNetG.Neurons()); if(IsStopped() || !MatMulGrad(inputs.getOutput(), inputs.getGradient(), cTNetG.getOutput(), cTNetG.getGradient(), cTurnedG.getGradient(), inputs.Neurons() / window, window, window)) return false;
Corrigimos o gradiente da matriz de projeção para levar em conta o erro de desvio em relação à matriz ortogonal.
if(!OrthoganalLoss(cTNetG, true)) return false;
Aqui, também executamos operações de substituição dos buffers de dados para preservar os gradientes de erro provenientes dos dois fluxos de informação.
CBufferFloat *temp = inputs.getGradient(); inputs.SetGradient(cTurnedG.getGradient(), false); cTurnedG.SetGradient(temp, false);
Transmitimos o gradiente do erro do módulo de geração da matriz de projeção no espaço canônico para o nível dos dados brutos.
if(!inputs.calcHiddenGradients(cTNetG.AsObject())) return false;
E somamos o gradiente do erro no nível dos dados brutos provenientes dos dois fluxos de informação.
if(!SumAndNormilize(inputs.getGradient(), cTurnedG.getGradient(), inputs.getGradient(), 1, false, 0, 0, 0, 1)) return false; }
Depois, verificamos mais uma vez se é necessário somar o gradiente do erro de outros fluxos de informação e atualizamos o ponteiro na variável local para o objeto dos dados brutos. Em seguida, avançamos para a próxima iteração do ciclo.
if(i > 0) { if(!SumAndNormilize(inputs.getGradient(), cbTemp, inputs.getGradient(), 64, false, 0, 0, 0, 1)) return false; inputs = caGlobalAttention[i - 1].AsObject(); } else inputs = NeuronOCL; } //--- return true; }
Após completar todas as iterações do nosso ciclo de iteração reversa das camadas internas, retornamos ao programa chamador o valor lógico do resultado das operações do nosso método de distribuição do gradiente do erro e finalizamos sua execução.
Com isso, encerramos a análise dos algoritmos de construção dos métodos da nossa nova classe de implementação dos conceitos propostos pelos autores do método Pointformer, a CNeuronPointFormer. O código completo dessa classe e de todos os seus métodos está disponível na documentação anexa.
Normalmente, o próximo passo é descrever a arquitetura do modelo no qual integramos a nova classe. Desta vez, isso é bastante simples. Assim como anteriormente, integramos a nova classe no modelo do Codificador de estado do ambiente. Usamos como base a arquitetura do modelo descrita no artigo anterior. A arquitetura do modelo permanece praticamente inalterada. Apenas substituímos o tipo de camada da classe base pelo novo tipo, preservando todos os outros parâmetros. Essas alterações não exigem modificações na arquitetura dos modelos Ator e Crítico, nem nos algoritmos de treinamento ou na interação com o ambiente. Esses componentes também foram transferidos sem alterações. Por isso, neste artigo, não nos deteremos a esses aspectos. A arquitetura completa de todos os modelos pode ser consultada na documentação anexa, onde também está disponível o código completo de todos os programas utilizados na preparação deste artigo.
3. Testes
Realizamos um grande trabalho de implementação da nossa visão dos conceitos propostos pelos autores do método Pointformer utilizando os recursos do MQL5.
Gostaria de destacar que a implementação apresentada neste artigo difere do algoritmo descrito no trabalho original dos autores. Portanto, os resultados obtidos podem diferir, em maior ou menor grau, dos resultados alcançados pelo algoritmo original.
Agora é o momento de analisarmos os resultados do nosso trabalho. Assim como anteriormente, utilizamos dados históricos reais de 2023 do instrumento financeiro EURUSD no time frame H1 para treinar os modelos. Os parâmetros de todos os indicadores analisados foram mantidos como padrão.
Inicialmente, treinamos os modelos offline iterativamente por meio da execução do EA “...\PointFormer\Study.mq5” no modo de tempo real. Esse EA não realiza operações de trading. Seu algoritmo se limita ao treinamento dos modelos.
As primeiras iterações de treinamento foram realizadas com os dados de passagens coletados durante o treinamento dos modelos em publicações anteriores. A estrutura e os parâmetros dos dados analisados permaneceram inalterados.
Em seguida, atualizamos os dados do conjunto de treinamento para que fiquem o mais próximos possível da política de ações atual do Ator. Isso permite uma avaliação mais precisa de suas ações durante o treinamento, além de corrigir adequadamente a direção da otimização da política. Para isso, no testador de estratégias, ativamos o modo de otimização lenta para o EA de interação com o ambiente “...\PointFormer\Research.mq5”.


Posteriormente, repetimos o processo de treinamento dos modelos.
O treinamento dos modelos e a atualização do conjunto de treinamento são realizados de maneira iterativa várias vezes. Um bom indicativo para encerrar o processo de treinamento é alcançar resultados satisfatórios em todas as passagens da última iteração de atualização do conjunto de treinamento.
É importante observar que pequenas diferenças nos resultados de passagens individuais são aceitáveis. Isso ocorre devido ao uso de uma política estocástica do Ator, que implica certa aleatoriedade nas ações dentro do intervalo aprendido. À medida que os modelos são treinados, a estocasticidade das ações diminui. Contudo, algum grau de variação nas ações é admissível, desde que não altere significativamente a rentabilidade da política.
Após várias iterações de treinamento dos modelos e atualizações do conjunto de treinamento, conseguimos desenvolver uma política capaz de gerar lucros tanto no conjunto de treinamento quanto no conjunto de testes.
O teste do modelo treinado foi realizado no testador de estratégias do MetaTrader 5, utilizando os dados históricos de janeiro de 2024 e mantendo todos os outros parâmetros inalterados. Os resultados do teste estão apresentados abaixo.

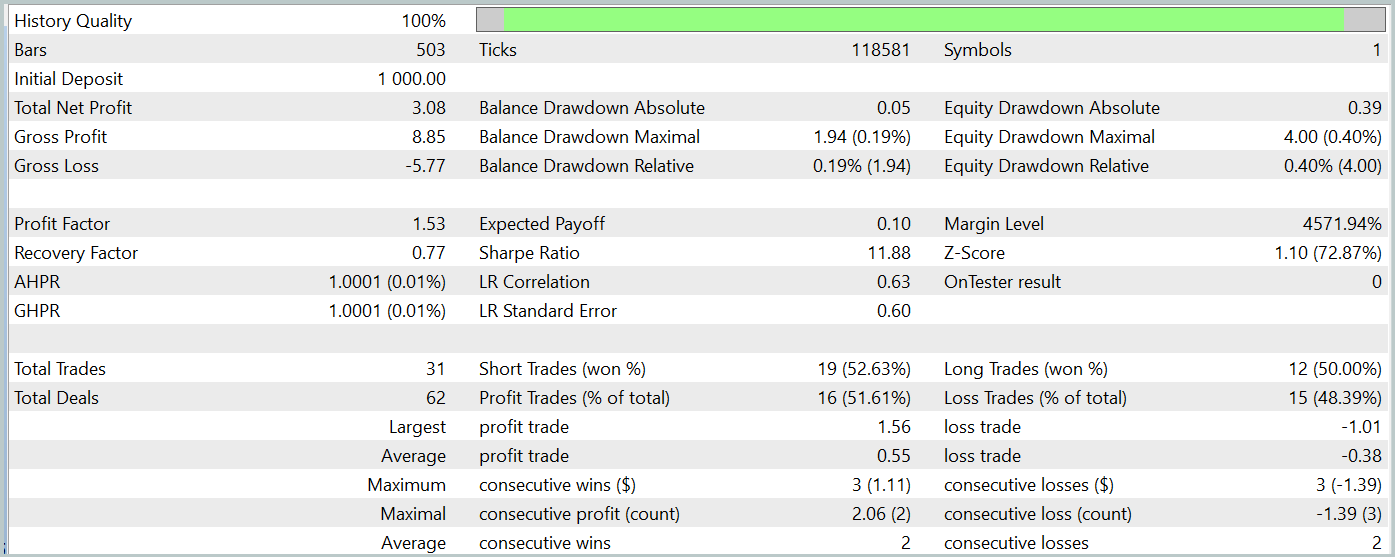
Durante o período de teste, o modelo treinado realizou um total de 31 operações de negociação, das quais metade foi encerrada com lucro. O fato de o valor máximo e o lucro médio das operações vencedoras terem superado em quase 50% os mesmos indicadores das operações perdedoras resultou em um fator de lucro de 1,53. No entanto, apesar de a curva do saldo mostrar uma tendência de crescimento, o número reduzido de operações realizadas não nos permite tirar conclusões definitivas sobre a eficácia do modelo em um período prolongado.
Considerações finais
Neste artigo, exploramos o método Pointformer, que propõe uma nova arquitetura para trabalhar com nuvens de pontos. O algoritmo apresentado combina Transformers locais e globais, permitindo a extração eficiente de padrões espaciais tanto locais quanto globais a partir de dados multidimensionais. O Pointformer utiliza mecanismos de atenção para processar informações considerando o contexto espacial e suporta o aprendizado levando em conta a relevância de cada ponto.
Na parte prática, implementamos nossa visão dos métodos propostos utilizando MQL5. Realizamos o treinamento e o teste do modelo com os algoritmos sugeridos. Os resultados obtidos demonstram o potencial do método para a análise de estruturas de dados complexas.
No entanto, é importante destacar que, para um entendimento mais completo das capacidades do Pointformer no contexto de dados financeiros, são necessários mais estudos e otimizações.
Referências
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA para coleta de exemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA para coleta de exemplos pelo método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA para treinamento de Modelos |
| 4 | Test.mq5 | Expert Advisor | EA para teste do modelo |
| 5 | Trajectory.mqh | Biblioteca de classe | Estrutura de descrição do estado do sistema |
| 6 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criar uma rede neural |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código do programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/15820
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Soluções simples para trabalhar com indicadores
Soluções simples para trabalhar com indicadores
 Simulação de mercado (Parte 08): Sockets (II)
Simulação de mercado (Parte 08): Sockets (II)
 Reimaginando Estratégias Clássicas (Parte II): Rompimentos das Bandas de Bollinger
Reimaginando Estratégias Clássicas (Parte II): Rompimentos das Bandas de Bollinger
 Redes neurais em trading: Aprendizado hierárquico de características em nuvens de pontos
Redes neurais em trading: Aprendizado hierárquico de características em nuvens de pontos
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
em dados históricos de janeiro de 2024.
Por que somente janeiro, se já não estamos em setembro? Ou está implícito que é preciso treinar novamente todos os meses?
Por que somente em janeiro, se já estamos em setembro? Ou está implícito que é preciso fazer um novo treinamento todo mês?
Não é possível treinar um modelo com 1 ano de dados e esperar um desempenho estável no mesmo período de tempo ou em um período mais longo. Para obter um desempenho estável do modelo por 6 a 12 meses, você precisa de um histórico muito mais longo para treinar. Consequentemente, será necessário mais tempo e custo para treinar o modelo.