Técnicas do MQL5 Wizard que você deve conhecer (Parte 51): Aprendizado por Reforço com SAC

Introdução

Soft Actor Critic (SAC) é mais um algoritmo de aprendizado por reforço que estamos considerando, tendo já analisado alguns que incluíram proximal policy optimization, deep-Q-networks, SARSA e outros. Este algoritmo, contudo, assim como alguns que já analisamos, usa redes neurais, mas com uma ressalva importante. O número total de redes utilizadas é três, sendo elas: 2 redes críticas e 1 rede ator. As duas redes críticas fazem previsões de recompensa (Q-Values) quando recebem como entrada uma ação e um estado de ambiente, e o mínimo das saídas dessas 2 redes é usado na modulação da função de perda utilizada para treinar a rede ator.

As entradas da rede de atores são coordenadas do estado do ambiente, sendo a saída binária. Um vetor de médias e um vetor de log-desvio-padrão. Usando o processo Gaussiano, esses dois vetores são usados para derivar uma distribuição de probabilidade para as possíveis ações disponíveis ao ator. Assim, enquanto as 2 redes críticas podem ser treinadas tradicionalmente, a rede ator claramente é um caso à parte. Há bastante a abordar aqui, então vamos reiterar os fundamentos antes de prosseguir. As duas redes críticas recebem como entrada o estado atual do ambiente e uma ação. Sua saída é uma estimativa do retorno esperado (valor Q) para executar aquela ação naquele estado. O uso de duas redes críticas ajuda a reduzir o viés de superestimação, um problema comum no Q-learning.

A rede ator possui o estado atual do ambiente como sua entrada. Sua saída é efetivamente uma distribuição de probabilidade sobre as ações possíveis, sendo essa distribuição estocástica para incentivar a exploração. Uso o termo “efetivamente” porque as saídas reais da rede ator são dois vetores que precisam ser alimentados em uma distribuição de probabilidade Gaussiana para obter os pesos de cada ação. Em MQL5, realizamos isso da seguinte forma:

//+------------------------------------------------------------------+
// Function to compute the Gaussian probability distribution and log
// probabilities
//+------------------------------------------------------------------+
vectorf CSignalSAC::LogProbabilities(vectorf &Mean, vectorf &Log_STD)
{  vectorf _log_probs;
   // Compute standard deviations from log_std
   vectorf _std = exp(Log_STD);
   // Sample actions and compute log probabilities
   float _z = float(rand() % USHORT_MAX / USHORT_MAX); // Generate N(0, 1) sample
   // Sample action using reparameterization trick: action = mean + std * N(0, 1)
   vectorf _actions = Mean + (_std * _z);
   // Compute log probability of the sampled action
   vectorf _variance = _std * _std;
   vectorf _diff = _actions - Mean;
   _log_probs = -0.5f * (log(2.0f * M_PI * _variance) + (_diff * _diff) / _variance);
   return(_log_probs);
}

Como o SAC Funciona

Dito isso, SAC funciona como a maioria dos algoritmos de aprendizado por reforço. Primeiro ocorre a seleção de ação, onde o ator amostra uma ação a partir da distribuição de probabilidade das saídas da rede ator. Isso é seguido pela “interação com o ambiente”, onde o agente executa a ação amostrada no ambiente e observa seu próximo estado e recompensa. Isso é então seguido pela atualização dos críticos, onde as duas redes críticas são atualizadas por uma função de perda que utiliza a comparação entre valores Q previstos e valores Q alvo. No entanto, como já mencionado acima, a atualização da rede ator é uma novidade, pois é atualizada usando um gradiente de política que visa maximizar o retorno esperado, levando em consideração a entropia da distribuição de política. Isso tem como objetivo incentivar a exploração e evitar uma convergência prematura para soluções subótimas.

A entropia da distribuição de política no SAC mede a aleatoriedade ou incerteza. No SAC, entropias mais altas correspondem a ações mais exploratórias, enquanto entropias mais baixas significam ênfase em escolhas mais determinísticas. As saídas da rede ator no SAC são, por natureza, uma política estocástica parametrizada por uma distribuição de probabilidade, que em nosso caso (para este artigo) é a distribuição Gaussiana. A entropia dessa distribuição descreve o panorama das ações que um agente pode tomar quando exposto a um estado específico (as entradas).

A importância disso é incentivar a exploração do agente, como é típico na maioria dos algoritmos de aprendizado por reforço, reduzindo o risco de convergência prematura para políticas subótimas. Isso, portanto, cria um equilíbrio entre exploração e aproveitamento. SAC incorpora um termo de entropia em seu objetivo de otimização de política para maximizar tanto a recompensa esperada quanto a entropia. A equação objetivo é a seguinte:

Onde:

• α: Temperatura de entropia, equilibrando maximização de recompensa e exploração.
• logπ(a∣s): Log-probabilidade da ação (a saída da nossa função cujo código foi compartilhado acima), que depende tanto de μ quanto de log(σ).
• Q(s,a): É o valor-Q mínimo entre as duas saídas das redes críticas.

Entropia mais alta tende a gerar tomada de decisão mais robusta em ambientes com informações incompletas, pois evita overfitting a cenários específicos. Portanto, maximizar entropia é algo positivo no SAC. Além da exploração aprimorada, já que o agente é incentivado a tentar uma gama maior de ações, ou evitar políticas subótimas que impedem ficar preso em ótimos locais, a entropia também funciona como uma forma de regularização ao prevenir políticas excessivamente determinísticas que podem falhar em cenários imprevistos. Também, ajustes graduais de entropia costumam levar a atualizações de política mais suaves, garantindo treinamento estável e convergência.

O parâmetro de controle da temperatura é muito sensível à entropia e ao processo de aprendizado da rede ator, e vale mencionar o porquê. Para nossos propósitos estamos fixando isso em 0.5, como pode ser visto na função de Logaritmo das probabilidades, cujo código MQL5 foi compartilhado acima. Entretanto, o parâmetro de temperatura alpha dita quanto peso é dado à energia no objetivo. Valores mais altos de alpha incentivam a exploração, enquanto valores menores promovem políticas determinísticas ou exploração intensiva. Então, definir isso como 0.5, para nossos propósitos, de fato produz uma forma de equilíbrio.

É comum, no entanto, que SAC utilize um mecanismo automático de ajuste de entropia que adapta alfa dinamicamente para manter um nível-alvo de entropia, ajustando o equilíbrio entre exploração e exploração intensiva. As implicações práticas disso são: aprendizado robusto entre tarefas; criação de políticas generalizáveis e aptas a lidar com informações incompletas (políticas estocásticas); e fornecimento de uma base para aprendizado contínuo. Os possíveis trade-offs disso são majoritariamente dois. Excesso de exploração e custo computacional.

Entropia excessiva pode levar a aprendizado ineficiente ao enfatizar demais ações exploratórias em detrimento da exploração intensiva de estratégias de alta recompensa já conhecidas. Isso sempre vem acompanhado do cálculo e otimização dos termos de entropia, que adicionam sobrecarga computacional comparado a algoritmos que focam apenas em maximização de recompensa. A rede ator produz dois vetores, MU e Log-STD, como mencionado acima, então como eles afetam essa entropia?

MU representa a tendência central da distribuição de ações da política. Ela não afeta diretamente a entropia, porém define o comportamento médio da política. O Log-STD, por outro lado, controla a dispersão ou incerteza da distribuição de ações e influencia diretamente a entropia. Um Log-STD mais alto significa uma distribuição de ações mais ampla e incerta, enquanto um Log-STD mais baixo indica o oposto. O que então a magnitude de uma determinada ação no Log-STD tem a ver com a probabilidade de seleção?

Os detalhes são determinados pelo processo Gaussiano, como já mencionado, contudo um Log-STD baixo frequentemente implica que a rede ator está confiante sobre a ação ótima, MU. Isso normalmente implica menor variabilidade nas ações amostradas. As ações amostradas ficarão mais concentradas ao redor do valor correspondente de MU para essa ação com leitura baixa de Log-STD, o que incentiva mais exploração intensiva de políticas ao redor dessa ação. Portanto, embora leituras baixas de Log-STD não tornem diretamente uma ação mais provável, elas, em essência, estreitam o escopo de ações possíveis, aumentando assim a chance de ações próximas a MU serem escolhidas.

Também existem alguns ajustes práticos que são frequentemente aplicados à entropia. Primeiro, como Log-STD determina diretamente a entropia, para um treinamento estável o SAC normalmente limita log(σ) dentro de um intervalo para evitar entropia extremamente alta ou baixa. Isso é feito com o parâmetro ‘z’ mostrado na nossa função de Log Probabilities acima. Segundo, o ajuste de alpha (que definimos como 0.5f na nossa função de Log Probabilities) é crucial para atingir o equilíbrio entre exploração e exploração intensiva, como mencionado. Para esse fim, frequentemente o ajuste automático de alpha é usado como meio de atingir dinamicamente esse equilíbrio.

Isso é alcançado usando um alvo de entropia H. A equação abaixo define isso:

Onde:

• alpha (α t ): É a temperatura atual que controla o peso do termo de entropia no objetivo, com valores maiores incentivando exploração, enquanto valores menores tendem à exploração intensiva.

• alpha (αt+1 ): É o parâmetro de temperatura atualizado após o feedback da entropia atual em relação ao alvo ter sido incluído.

• lambda (λ): É a taxa de aprendizado para o processo de ajuste de alpha, que controla a velocidade com que alpha se adapta a desvios do alvo de entropia H.

• E (E a~π ): É a expectativa de ações amostradas da política atual.

• Log(a|s): É a Log-probabilidade da ação-a no estado-s sob a política atual. Quantifica a incerteza da seleção de ações da política.

• H target : Serve como o valor-alvo de entropia da política. É frequentemente atribuído com base na dimensionalidade do espaço de ações (número e escopo das ações disponíveis) em casos em que as ações são discretas, como as implementações (comprar, vender, manter) que consideramos até aqui; também pode ser escalado se as ações forem contínuas (por exemplo, se tivermos ordens de mercado bidimensionais ambas escaladas de 0.01 a 0.10 para dimensionamento de posição de dois ativos comprados simultaneamente com valores sendo uma porcentagem da margem livre).

Portanto, o uso de ajuste automático de alpha, embora não explorado em nossa implementação neste artigo, garante que o agente se adapte dinamicamente às mudanças no ambiente, elimina a necessidade de ajuste manual de alpha e promove aprendizado eficiente pela manutenção de um equilíbrio pré-definido entre exploração e exploração intensiva.

SAC vs comparação com DQN

Consideramos até agora outro algoritmo de aprendizado por reforço que usa uma única rede neural, nomeadamente o Deep-Q-Networks, então quais vantagens, se existirem, justificam usar SAC com suas múltiplas redes? Para defender o SAC, consideremos um cenário de uso de uma tarefa de manipulação robótica. Então, aqui está a tarefa: um braço robótico precisa segurar e mover objetos para locais-alvo específicos. As juntas de seus braços seriam atribuídas a espaços de ação contínuos que quantificam o torque necessário, ajustes de ângulo etc.

Os desafios do uso de um DQN nesse caso são que, primeiro, DQN é mais adequado para espaços de ação discretos. Tentar estendê-lo para acomodar um espaço contínuo levaria a um crescimento exponencial no número de ações discretas disponíveis para espaços de ação de maior dimensionalidade, tornando o treinamento caro e ineficiente. DQNs também dependem de estratégias epsilon-greedy para equilibrar exploração e exploração intensiva, e essas podem ter dificuldades para funcionar de forma eficiente em espaços discretizados de alta dimensão. Finalmente, DQN é propenso a viés de superestimação, o que pode gerar instabilidade no treinamento, especialmente em ambientes complexos com alta variabilidade de recompensa.

SAC seria mais adequado nesse caso, principalmente por seu suporte a espaços de ação contínuos. Isso se manifesta na forma como SAC otimiza políticas estocásticas sobre espaços de ação contínuos, eliminando a necessidade de discretização (ou classificação) de ações. Isso leva a um controle suave e preciso do braço do robô. As três redes no SAC trabalham em sinergia, onde a rede ator gera uma política estocástica que define a distribuição (ponderação probabilística) das ações contínuas. Isso promove eficiência enquanto evita exploração prematura.

Por sua vez, as redes críticas empregam um método de estimativa de valor Q duplo que ajuda a evitar o viés de superestimação ao encaminhar o valor mínimo na retropropagação para a rede ator. Isso estabiliza o treinamento e garante resultados mais precisos. Em resumo, o objetivo aumentado por entropia, que incentiva mais exploração (especialmente quando combinado com ajuste automático de temperatura como discutido acima com alpha), além da robustez e estabilidade oferecidas pela capacidade do SAC de lidar com espaços de ação de alta dimensionalidade, claramente o colocam um passo à frente do DQN. Para esse fim, exemplos de desempenho divulgados das tarefas Reacher e Fetch do OpenAI Gym indicam claramente que DQN tem dificuldade para produzir movimentos suaves de braço devido às suas saídas discretizadas e exploração deficiente, com políticas convergindo frequentemente para estratégias subótimas. Por outro lado, SAC gera ações precisas e suaves, com uma política estocástica que leva a conclusão mais rápida das tarefas, menos colisões e melhor adaptação à mudança de posição dos objetos ou dos locais-alvo, novamente graças à abordagem estocástica.

Python and TensorFlow

Para este artigo, ao contrário das peças anteriores de aprendizado de máquina, estamos aprofundando em TensorFlow do Python. MQL5, a linguagem principal da MetaQuotes, obviamente continua relevante, pois os Expert Advisors montados pelo wizard dependem muito dele. Para novos leitores, existem guias aqui e aqui sobre como usar o código anexado ao final deste artigo para montar um Expert Advisor. Python, porém, certamente está avançando sobre a relevância e dominância do MQL5 como linguagem de programação principal no desenvolvimento de modelos financeiros. Um rápido reconhecimento pode indicar que a MetaQuotes precisa simplesmente lançar mais bibliotecas em python para acompanhar o ritmo da inovação e continuar reafirmando sua liderança. 

Entretanto, sou suficientemente velha para lembrar a introdução do MetaTrader 5 em 09(?). E a adoção dolorosamente lenta que eles receberam de seus clientes, apesar de todas as vantagens oferecidas. Portanto, consigo entender por que eles seriam hesitantes em lançar e manter bibliotecas ativas em python. Dito isso, as inovações sendo apresentadas aqui vêm majoritariamente dos “clientes” (ou seja, da comunidade python) e não da MetaQuotes, como foi o caso com o MetaTrader 5 onde posições em vez de ordens estavam sendo introduzidas. Então talvez eles precisem atender isso com certa urgência? O tempo dirá, mas, enquanto isso, os benefícios de eficiência ao usar não apenas TensorFlow, mas também PyTorch ao desenvolver e principalmente treinar redes são, de fato, gigantescos.

Na minha opinião, a MetaQuotes pode explorar patrocínios corporativos, tornar-se contribuidora, ou mesmo criar forks para as principais bibliotecas python como Pandas, NumPy e Sci-Kit; e, entre outras coisas, permitir a leitura de seus formatos de arquivo altamente comprimidos *.*hcc e *.*tkc. Mas essas são considerações gerais; voltando ao TensorFlow, ele oferece capacidades avançadas de deep learning essencialmente em duas frentes. Na frente de software e na frente de hardware/GPU.  

MQL5 suporta OpenCL, então pode-se argumentar que as duas linguagens poderiam competir, porém o mesmo certamente não pode ser dito sobre as bibliotecas e ferramentas avançadas do Python para construir, treinar e otimizar modelos de deep learning. Essas bibliotecas incluem suporte para arquiteturas complexas como SAC via TensorFlow Agents.

Ele também apresenta um ecossistema rico com ferramentas pré-construídas, como stable-baseline para avançar aprendizado por reforço (além de tensor-agents); permite flexibilidade e experimentação, já que é possível prototipar e testar rapidamente uma ampla variedade de implementações de modelos; é altamente reproduzível e facilmente depurável (especialmente ao usar ferramentas como TensorBoard para visualização e treinamento de matrizes/kernels); oferece interoperabilidade com formatos exportáveis como ONNX; e possui uma comunidade vastíssima e crescente com atualizações regulares.

SAC pode ser implementado em python de várias formas. Para fins de ilustração dos princípios centrais, focaremos em duas abordagens. A primeira define manualmente as três redes principais do SAC e, usando iterações via for loop, treina e testa o modelo SAC. A segunda usa os já mencionados tensor-agents que vêm com a biblioteca python e são especificamente destinados a auxiliar no aprendizado por reforço.

Os passos na abordagem iterativa manual são: projetar os componentes SAC em TensorFlow/Keras, onde para a rede ator isso envolve definir uma rede neural que produza uma política estocástica para Amostragem Gaussiana; para as redes críticas isso significa construir 2 redes de valor-Q para aprendizado Q duplo e gerenciamento do viés de superestimação; e a definição de um regime de regularização de entropia para exploração eficiente. Para nossos propósitos, como mencionado acima, nossa entropia está utilizando um valor fixo de alpha em 0.5. A fonte de abertura que cobre isso é a seguinte:

import numpy as np
import pandas as pd

from sklearn.model_selection import train_test_split

import tensorflow as tf

print("Num GPUs Available: ", len(tf.config.list_physical_devices('GPU')))

from tensorflow.keras import optimizers
from tensorflow.keras.layers import Input
from tensorflow.keras import layers
from tensorflow import keras
import tf2onnx
import onnx

import os

# Define the actor network
def ActorNetwork(state_dim, action_dim, hidden_units=256):
    """
    Creates a simple SAC actor network.
    
    :param state_dim: The dimension of the state space.
    :param action_dim: The dimension of the action space.
    :param hidden_units: The number of hidden units in each layer.
    :return: A Keras model representing the actor network.
    """
    # Input layer
    state_input = layers.Input(shape=(state_dim, ))
    
    # Hidden layers (Dense layers with ReLU activation)
    x = layers.Dense(hidden_units, activation='relu')(state_input)
    x = layers.Dense(hidden_units, activation='relu')(x)
    
    # Output layer: output means (mu) and log standard deviation (log_std) for Gaussian distribution
    
    output_size = action_dim + action_dim
    stacked_mean_logs = layers.Dense(output_size)(x)
    
    # Create the model

    actor_model = tf.keras.Model(inputs=state_input, outputs=stacked_mean_logs)
    
    return actor_model

# Define the critic network
def CriticNetwork(state_dim, action_dim, hidden_units=256):
    """
    Creates a simple SAC critic network (Q-value approximation).
    
    :param state_dim: The dimension of the state space.
    :param action_dim: The dimension of the action space.
    :param hidden_units: The number of hidden units in each layer.
    :return: A Keras model representing the critic network.
    """
    
    input_size = state_dim + action_dim
    state_action_inputs = layers.Input(shape=(None, input_size, 1))  # Concatenate state and action
    
    # Hidden layers (Dense layers with ReLU activation)
    x = layers.Dense(hidden_units, activation='relu')(state_action_inputs)
    x = layers.Dense(hidden_units, activation='relu')(x)
    
    # Output layer: Q-value for the given state-action pair
    q_value_output = layers.Dense(1)(x)  # Single output for Q-value
    
    # Create the model 
    critic_model = tf.keras.Model(inputs=state_action_inputs, outputs=q_value_output)
    
    return critic_model

Depois disso, precisaríamos treinar o modelo SAC em TensorFlow/Keras. Isso normalmente envolveria usar uma biblioteca antiga do MetaTrader 5 para importar dados do MetaTrader 5 a partir do terminal MetaTrader e, em seguida, dividir esses dados em dados de teste e treinamento. Estamos usando uma proporção de dois terços para treinamento, o que deixa um terço para testes. Simulamos a configuração de negociações do MetaTrader 5 em um loop for tedioso e altamente ineficiente que, como esperado, é dimensionado para um número de épocas e para o tamanho dos dados de treinamento. Além disso, buscamos otimizar as redes ator e críticas com a função objetivo SAC, incluindo o termo de entropia. O código envolvido nisso é compartilhado abaixo:

# Filter the DataFrame to keep only the '<state>' column
df = pd.read_csv(name_csv)

states = df.filter(['<STATE>']).astype(int).values
# Extract the '<state>' column as an integer array
rewards = df.filter(['<REWARD>']).values

states_size = int(len(states)*(2.0/3.0))
actor_x_train = states[0:states_size,:]
actor_x_test = states[states_size:,:1]
rewards_size = int(len(rewards)*(2.0/3.0))
critic_y_train = rewards[0:rewards_size,:]
critic_y_test = rewards[rewards_size:,:1]

# Initialize networks and optimizers
input_dim = 1  # 2 states, of 3 gradations are flattened into a single index
output_dim = 3  # possible actions buy, sell, hold
actor = ActorNetwork(input_dim, output_dim)
critic1 = CriticNetwork(input_dim, output_dim)  # Input paired with action
critic2 = CriticNetwork(input_dim, output_dim)  # Input paired with action

critic_optimizer_1 = tf.keras.optimizers.Adam(learning_rate=0.001)
critic_optimizer_2 = tf.keras.optimizers.Adam(learning_rate=0.001)
actor_optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)

# Training loop
for e in range(epoch_size):
    train_critic_loss1 = 0
    train_critic_loss2 = 0
    train_actor_loss = 0
    
    for i in range(actor_x_train.shape[0]):
        input_state = tf.expand_dims(actor_x_train[i], axis=0)  # Select a single sample and maintain batch dim
        target_q = tf.expand_dims(critic_y_train[i], axis=0)

        # Actor forward pass and sampling
        with tf.GradientTape(persistent=True) as tape:

            actor_output = actor(input_state)
            # Split the vector into mean and log_std
            mu = actor_output[:, :output_dim]     # First 3 values
            log_std = actor_output[:, output_dim:]  # Last 3 values
            std = tf.exp(log_std)
            sampled_action = tf.random.normal(shape=mu.shape, mean=mu, stddev=std)  # Sample action from Gaussian

            # Concatenate the state and action tensors
            in_state = tf.convert_to_tensor(tf.cast(input_state, dtype=tf.float32), dtype=tf.float32)  # Ensure it's a tensor
            in_action = tf.convert_to_tensor(tf.cast(sampled_action, dtype=tf.float32), dtype=tf.float32)
            
            # Concatenate along the last axis
            critic_raw_input = tf.concat([in_state, in_action], axis=-1)  # Ensure correct axis
            critic_input = tf.reshape(critic_raw_input, [-1, 1, 4, 1])  # -1 infers the batch size dynamically

            q_value1 = critic1(critic_input)
            q_value2 = critic2(critic_input)

            # Critic loss (mean squared error)
            critic_loss1 = tf.reduce_mean((tf.cast(q_value1, tf.float32) - tf.cast(target_q, tf.float32)) ** 2)
            critic_loss2 = tf.reduce_mean((tf.cast(q_value2, tf.float32) - tf.cast(target_q, tf.float32)) ** 2)

            # Actor loss (maximize expected Q-value based on minimum critic output)
            min_q_value = tf.minimum(q_value1, q_value2)  # Take the minimum Q-value
            actor_loss = tf.reduce_mean(min_q_value)  # Maximize expected Q-value (negative for minimization)

        # Backpropagation
        critic_gradients1 = tape.gradient(critic_loss1, critic1.trainable_variables)
        critic_gradients2 = tape.gradient(critic_loss2, critic2.trainable_variables)
        actor_gradients = [-grad for grad in tape.gradient(actor_loss, actor.trainable_variables)]

        del tape  # Free up resources from persistent GradientTape
        
        critic_optimizer_1.apply_gradients(zip(critic_gradients1, critic1.trainable_variables))
        critic_optimizer_2.apply_gradients(zip(critic_gradients2, critic2.trainable_variables))
        actor_optimizer.apply_gradients(zip(actor_gradients, actor.trainable_variables))
        
        # Accumulate losses for epoch summary
        train_critic_loss1 += critic_loss1.numpy()
        train_critic_loss2 += critic_loss2.numpy()
        train_actor_loss += actor_loss.numpy()

    print(f"  Epoch {e + 1}/{epoch_size}:")
    print(f"  Train Critic Loss 1: {train_critic_loss1 / actor_x_train.shape[0]:.4f}")
    print(f"  Train Critic Loss 2: {train_critic_loss2 / actor_x_train.shape[0]:.4f}")
    print(f"  Train Actor Loss: {train_actor_loss / actor_x_train.shape[0]:.4f}")
    print("-" * 40)

critic2.summary()
critic1.summary()
actor.summary()

Após o treinamento, estaríamos aptos a exportar nosso modelo, que compreende três redes, para ONNX. ONNX, que é uma abreviação de Open Neural Network Exchange, fornece um padrão aberto para interoperabilidade de machine learning, no qual modelos treinados em python usando várias bibliotecas como PyTorch ou SciKit-Learn podem ser exportados para esse formato para uso em uma variedade maior de plataformas e linguagens de programação, incluindo MQL5. Essa compatibilidade elimina a necessidade de replicar lógica complexa de machine learning, o que economiza tempo e reduz erros.

A importação de ONNX como recurso permite a compilação de um único arquivo ex5 que inclui o modelo ONNX de machine learning e a lógica de execução de trades em MQL5, para que os traders não precisem lidar com vários arquivos. Dito isso, o processo de exportação de Python para ONNX tem: Várias opções, uma das quais é o tf2onnx, mas não é a única, pois existem: onnxmltools, skl2onnx, transformers.onnx (para Hugging Face) e mxnet.contrib.onnx. O que é crucial na etapa de exportação, no entanto, é garantir que os formatos das camadas de entrada e saída de cada rede sejam registrados e gravados corretamente, pois em MQL5 essa informação é crucial para inicializar com precisão os respectivos identificadores ONNX para cada rede. Fazemos isso da seguinte forma:

# Check input and output layer shapes for importing ONNX
import onnxruntime as ort

session_critic2 = ort.InferenceSession(path_critic2_onnx)
session_critic1 = ort.InferenceSession(path_critic1_onnx)
session_actor = ort.InferenceSession(path_actor_onnx)

for i in session_critic2.get_inputs():
    print(f"in critic2 Name: {i.name}, Shape: {i.shape}, Type: {i.type}")

for i in session_critic1.get_inputs():
    print(f"in critic1 Name: {i.name}, Shape: {i.shape}, Type: {i.type}")

for i in session_actor.get_inputs():
    print(f"in actor Name: {i.name}, Shape: {i.shape}, Type: {i.type}")
    

for o in session_critic2.get_outputs():
    print(f"out critic2 Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

for o in session_critic1.get_outputs():
    print(f"out critic1 Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

for o in session_actor.get_outputs():
    print(f"out actor Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

O desempenho do código python com essa implementação que usa loops for como indicado acima está longe de ser eficiente, na verdade é muito semelhante ao MQL5, porque o uso de tensores/gráficos não é devidamente aproveitado. No entanto, isso é necessário, dado que a função fit do TensorFlow, que geralmente é usada para aproveitar a eficiência de treinamento do TensorFlow, não seria aplicável neste caso, visto que na retropropagação as saídas das 2 redes críticas (os valores Q) são usadas para treinar a rede ator. A rede ator não possui vetores-alvo ou um dataset-alvo como as redes críticas ou a maioria das redes neurais típicas.

A segunda abordagem para implementar isso usa tensor-agents, que são bibliotecas internas para lidar com aprendizado por reforço dentro do TensorFlow e python. Analisaremos isso com profundidade em artigos futuros, mas basta dizer que a inicialização não abrange apenas as redes constituintes, mas também considera o ambiente e os agentes. Aspectos cruciais do aprendizado por reforço que podem ser negligenciados se houver foco excessivo na eficiência de treinamento das redes.

Combinando com MQL5

Importamos nossos modelos ONNX exportados para os recursos do MQL5, o que nos apresenta o seguinte cabeçalho para o arquivo da nossa classe de sinal personalizado.

//+------------------------------------------------------------------+
//|                                                    SignalSAC.mqh |
//|                   Copyright 2009-2017, MetaQuotes Software Corp. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#include <Expert\ExpertSignal.mqh>
#include <My\Cql.mqh>
#resource "Python/EURUSD_H1_D1_critic2.onnx" as uchar __CRITIC_2[]
#resource "Python/EURUSD_H1_D1_critic1.onnx" as uchar __CRITIC_1[]
#resource "Python/EURUSD_H1_D1_actor.onnx" as uchar __ACTOR[]
#define  __ACTIONS 3
#define  __ENVIONMENTS 3

Os dados que exportamos para python foram do símbolo EURUSD no período gráfico de uma hora, de 2023.12.12 a 2024.12.12. O treinamento foi para dois terços desse período, o que corresponde a oito meses, significando que treinamos de 2023.12.12 a 2024.08.12. Assim, podemos executar testes a partir de 2024.08.12. Isso resulta em um período pouco superior a 4 meses, o que não é tão longo, mas como estamos usando o período de 1 hora, pode ser significativo.

Como a retropropagação já foi feita em python, não estamos incluindo parâmetros especiais de entrada para otimização nesses testes de forward walk. Nossa interface de classe, portanto, é a seguinte:

//+------------------------------------------------------------------+
//| SACs CSignalSAC.                                                 |
//| Purpose: Soft Actor Critic for Reinforcement-Learning.           |
//|            Derives from class CExpertSignal.                     |
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalSAC   : public CExpertSignal
{
protected:

   long                          m_critic_2_handle;
   long                          m_critic_1_handle;
   long                          m_actor_handle;

public:
   void                          CSignalSAC(void);
   void                          ~CSignalSAC(void);

   //--- methods of setting adjustable parameters

   //--- method of verification of arch
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);

protected:
   vectorf           GetOutput();
   vectorf           LogProbabilities(vectorf &Mean, vectorf &Log_STD);
};

Inicializamos e validamos os tamanhos das camadas de entrada e saída de cada modelo ONNX como segue:

//+------------------------------------------------------------------+
//| Validation arch protected data.                                  |
//+------------------------------------------------------------------+
bool CSignalSAC::ValidationSettings(void)
{  if(!CExpertSignal::ValidationSettings())
      return(false);
//--- initial data checks
   if(m_period > PERIOD_H1)
   {  Print(" time frame too large ");
      return(false);
   }
   ResetLastError();
   if(m_critic_2_handle == INVALID_HANDLE)
   {  Print("Crit 2 OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   if(m_critic_1_handle == INVALID_HANDLE)
   {  Print("Crit 1 OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   if(m_actor_handle == INVALID_HANDLE)
   {  Print("Actor OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   // Set input shapes
   const long _critic_in_shape[] = {1, 4, 1};
   const long _actor_in_shape[] = {1};
   // Set output shapes
   const long _critic_out_shape[] = {1, 4, 1, 1};
   const long _actor_out_shape[] = {1, 6};
   if(!OnnxSetInputShape(m_critic_2_handle, ONNX_DEFAULT, _critic_in_shape))
   {  Print("Crit 2  OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_critic_2_handle, 0, _critic_out_shape))
   {  Print("Crit 2  OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetInputShape(m_critic_1_handle, ONNX_DEFAULT, _critic_in_shape))
   {  Print("Crit 1 OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_critic_1_handle, 0, _critic_out_shape))
   {  Print("Crit 1 OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetInputShape(m_actor_handle, ONNX_DEFAULT, _actor_in_shape))
   {  Print("Actor OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_actor_handle, 0, _actor_out_shape))
   {  Print("Actor OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
//read best weights
//--- ok
   return(true);
}

Sobre os formatos das camadas, é importante notar que tivemos que fazer mudanças que facilitaram nossa exportação para ONNX, mesmo indo contra a lógica base do SAC. Primeiro, a rede ator deve exportar 2 vetores: vetores de média e um vetor de log-desvio-padrão. Definir esses elementos no formato de camadas ONNX teria sido suscetível a erros, então combinamos ambos em um único vetor dentro do python, conforme indicado no código do loop for acima. Além disso, as entradas das redes críticas são 2: o estado do ambiente e a distribuição de probabilidade da ação fornecida pela rede ator. Isso também pode ser definido normalmente como 2 tensores, mas, por simplicidade, também os combinamos em um único vetor de tamanho 4. Nossa função get output é a seguinte:

//+------------------------------------------------------------------+
//| This function calculates the next actions to be selected from    |
//| the Reinforcement Learning Cycle.                                |
//+------------------------------------------------------------------+
vectorf CSignalSAC::GetOutput()
{  vectorf _out;
   int _load = 1;
   static vectorf _x_states(1);
   _out.Init(__ACTIONS);
   _out.Fill(0.0);
   vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(_load) &&
      _in_row.CopyRates(m_symbol.Name(), PERIOD_H1, 8, 0, _load) &&
      _in_row.Size() == _load
      &&
      _in_row_old.Init(_load) &&
      _in_row_old.CopyRates(m_symbol.Name(), PERIOD_H1, 8, 1, _load) &&
      _in_row_old.Size() == _load
      &&
      _in_col.Init(_load) &&
      _in_col.CopyRates(m_symbol.Name(), PERIOD_D1, 8, 0, _load) &&
      _in_col.Size() == _load
      &&
      _in_col_old.Init(_load) &&
      _in_col_old.CopyRates(m_symbol.Name(), PERIOD_D1, 8, 1, _load) &&
      _in_col_old.Size() == _load
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      Cql *QL;
      Sql _RL;
      _RL.actions  = __ACTIONS;//buy, sell, do nothing
      _RL.environments = __ENVIONMENTS;//bullish, bearish, flat
      QL = new Cql(_RL);
      vector _e(_load);
      QL.Environment(_in_row, _in_col, _e);
      delete QL;
      _x_states[0] = float(_e[0]);
      static matrixf _y_mu_logstd(6, 1);
//--- run the inference
      ResetLastError();
      if(!OnnxRun(m_actor_handle, ONNX_NO_CONVERSION, _x_states, _y_mu_logstd))
      {  Print("Actor OnnxConversion error ", GetLastError());
         return(_out);
      }
      else
      {  vectorf _mu(__ACTIONS), _logstd(__ACTIONS);
         _mu.Fill(0.0); _logstd.Fill(0.0);
         for(int i=0;i<__ACTIONS;i++)
         {  _mu[i] = _y_mu_logstd[i][0];
            _logstd[i] = _y_mu_logstd[i+__ACTIONS][0];
         }
         _out = LogProbabilities(_mu, _logstd);
      }
   }
   return(_out);
}

Continuamos com o mesmo modelo que usamos até aqui, com 9 estados de ambiente e 3 ações possíveis. Para processar a distribuição de probabilidade das ações, precisamos da função de log-probabilidades cujo código foi compartilhado no início deste artigo. Compilar com o wizard e realizar um teste para os 4 meses restantes da janela de dados nos apresenta o seguinte relatório:

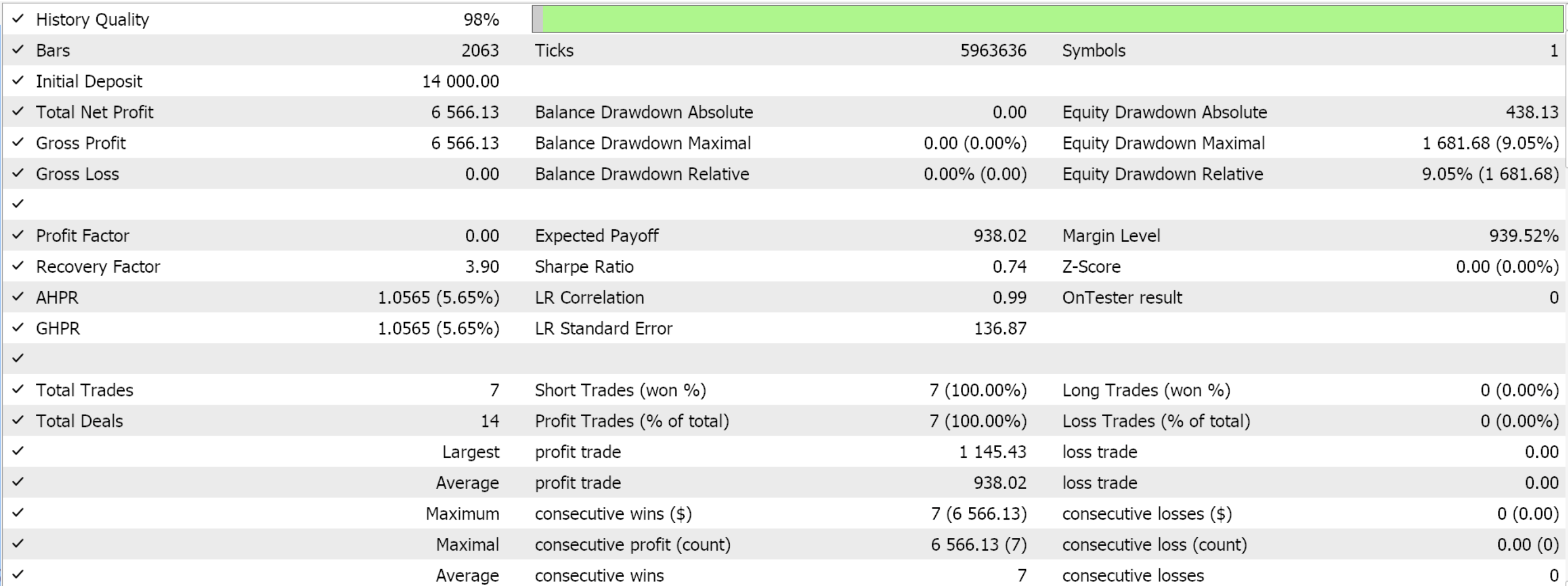
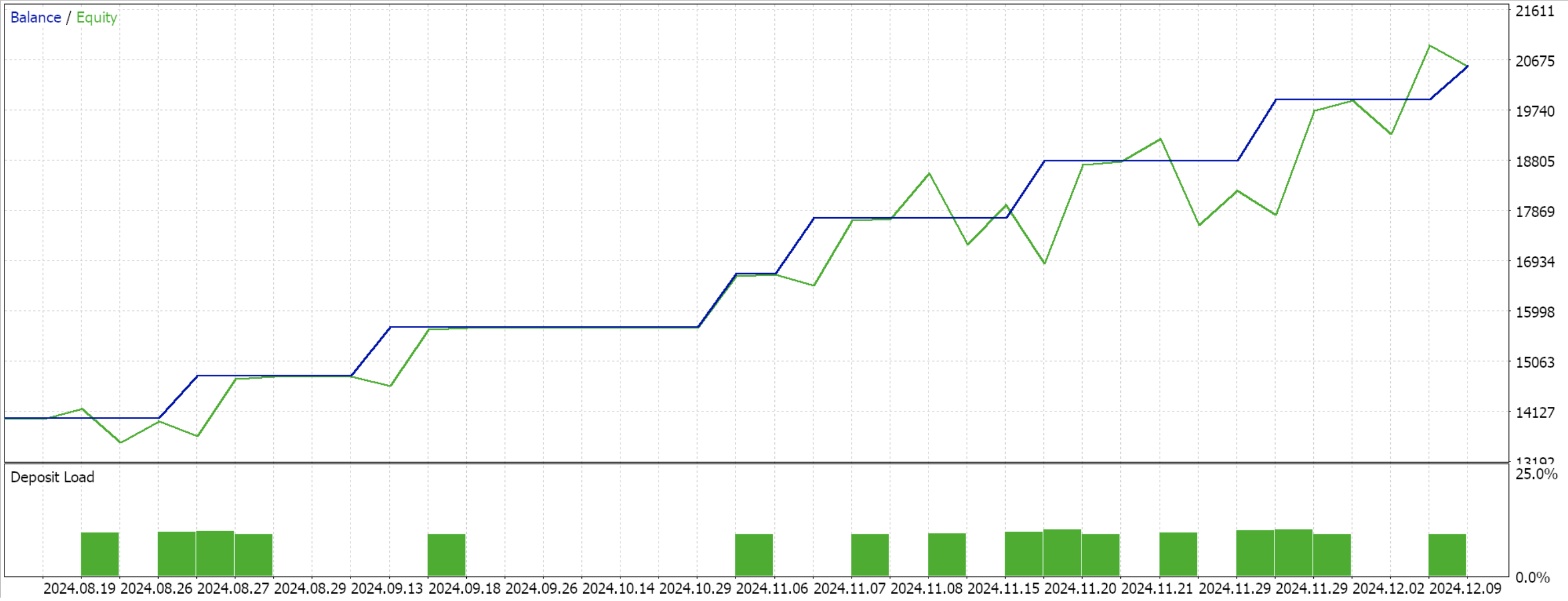
Conclusão

Analisamos um cenário de implementação muito básico do SAC em python, que não utilizou a biblioteca tensor-agent e, portanto, não fez uso das eficiências que ela proporciona. Essa abordagem expõe os fundamentos do SAC e destaca por que a retropropagação é um pouco prolongada, já que envolve o pareamento de múltiplas redes e uma delas não possui um dataset típico de treinamento. SAC, em princípio, destina-se a promover exploração mais segura por meio da entropia, modulada pelo parâmetro alpha (que aplicamos na Distribuição Gaussiana). O leitor é, portanto, convidado a explorar isso mais a fundo, considerando um alpha não fixo, como o ajuste automático que possui um valor-alvo de entropia. Também deveremos abordar exemplos disso em artigos futuros.

Nome do Arquivo	Descrição
WZ_51.mq5	Expert Advisor montado pelo Wizard cujo cabeçalho mostra os arquivos utilizados
SignalWZ_51.mqh	Arquivo de Classe de Sinal Personalizada
EURUSD_H1_D1_critic2.onnx	Rede Crítica 2 ONNX
EURUSD_H1_D1_critic1.onnx	Rede Crítica 1 ONNX
EURUSD_H1_D1_actor.onnx	Rede Ator