
Características del Wizard MQL5 que debe conocer (Parte 37): Regresión de procesos gaussianos con núcleos Matérn y lineales
Introducción
Continuamos esta serie sobre las diferentes formas en las que se pueden implementar las clases de componentes clave de los Asesores Expertos ensamblados por el asistente considerando dos núcleos de proceso gaussianos. El núcleo lineal y el núcleo Matérn. El primero es tan simple que no se puede encontrar su página de Wikipedia, sin embargo el segundo tiene una página de referencia aquí.
Si vamos a hacer un resumen de lo que cubrimos anteriormente sobre los núcleos de procesos gaussianos (Gaussian Process, GP), son modelos no paramétricos capaces de mapear relaciones complejas entre conjuntos de datos (normalmente en forma vectorial) sin ningún conocimiento funcional o previo sobre el par de conjuntos de datos involucrados. Esto los hace ideales para manejar situaciones donde los conjuntos de datos involucrados son no lineales o incluso ruidosos. Esta flexibilidad, además, los hace un poco ideales para series de tiempo financieras que pueden ser a menudo volátiles, ya que los GP tienden a dar resultados matizados. Proporcionan una estimación de pronóstico más un intervalo de confianza. Los GP ayudan a determinar la similitud entre dos conjuntos de datos y, dado que hay varios tipos de kernels para usar en la regresión del proceso gaussiano, siempre es clave identificar el kernel apropiado o tener en cuenta las deficiencias del kernel seleccionado, particularmente en los casos en que se utilizan kernels para extrapolar un pronóstico.
A continuación se muestra una tabla resumen que cubre los núcleos introducidos hasta ahora en estas series y algunas de sus características:
| Tipo de núcleo | Ideales para la capturar | Explicación |
|---|---|---|
| Núcleo lineal | Tendencias | Captura tendencias lineales a lo largo del tiempo; ideal para activos que muestran movimientos de precios ascendentes o descendentes a largo plazo. Simple y computacionalmente eficiente, pero supone una relación lineal. |
| Núcleo de función de base radial (Radial Basis Function, RBF) | Tendencias y volatilidad | Ideal para capturar tendencias suaves a largo plazo con cambios de precios graduales. Proporciona estimaciones suaves y es bueno para patrones continuos. Sin embargo, tiene dificultades ante transiciones bruscas o volatilidad extrema. |
| Núcleo Matérn | Tendencias, volatilidad, ciclos | Puede capturar tendencias más toscas y menos suaves y cambios repentinos en la volatilidad. El parámetro ν controla la suavidad, por lo que un ν más bajo captura una volatilidad aproximada, mientras que un ν más alto suaviza las tendencias. |
Dependiendo de la serie temporal que se esté extrapolando, será necesario seleccionar el kernel apropiado en función de sus fortalezas. Las series temporales financieras a menudo pueden mostrar un comportamiento periódico o cíclico y núcleos como el Matérn que presentamos a continuación pueden ayudar a mapear estas relaciones. Además, la cuantificación de la incertidumbre, como vimos con la función de base radial en este artículo inicial, puede ser de gran ayuda cuando los operadores se enfrentan a mercados planos o con fluctuaciones. Los núcleos como el RBF no sólo proporcionan estimaciones puntuales, sino también intervalos de confianza, lo que puede ser beneficioso en estas situaciones. Esto se debe a que el intervalo de confianza puede ayudar a descartar las señales débiles y, al mismo tiempo, poner de relieve los principales puntos de inflexión en entornos inciertos.
Los conjuntos de datos con inversión de la media también pueden tratarse con núcleos especiales, como el Ornstein-Uhlenbeck, que trataremos en un próximo artículo. Otro aspecto interesante que podríamos estudiar en el futuro es que las GP permiten la composición de núcleos, en la que se pueden apilar múltiples núcleos, como un núcleo lineal y un núcleo RBF, para modelar relaciones más complejas entre conjuntos de datos. Esto podría incluir emparejamientos como los patrones de acción de precios a corto plazo y las tendencias a largo plazo, donde un modelo es capaz de colocar las salidas de las posiciones abiertas en los puntos óptimos al tiempo que capitaliza cualquier acción subyacente a largo plazo que un valor pueda estar teniendo.
Los GP ofrecen varias ventajas y usos adicionales, como la gestión y reducción del ruido, la adaptación a los cambios de régimen y muchas otras. Sin embargo, como traders, queremos aprovechar estos beneficios, así que veamos un kernel lineal muy básico.
Núcleos lineales
El uso principal de los núcleos lineales es trazar relaciones lineales simples entre conjuntos de datos en un proceso gaussiano. Por ejemplo, consideremos un par de conjuntos de datos muy sencillos, el coste de envío de un contenedor a EE.UU. desde China, y el precio de la ETF de envío BOAT. En circunstancias normales, esperaríamos que los altos costos de envío reflejaran el poder de fijación de precios de las compañías navieras, de modo que sus ganancias y, por lo tanto, sus ingresos reflejaran esto, lo que llevaría a una apreciación en el precio de sus acciones. En este escenario, un comerciante que busca comprar compañías navieras a lo largo del tiempo o incluso simplemente comprar ETF, estaría interesado en modelar sus precios de acciones esperados y los costos de envío actuales, con un kernel lineal.
Es relativamente simple y no complejo, lo que hace que requiera menos recursos computacionales entre todos los kernels. También requiere sólo un único parámetro constante 'c' en su fórmula. Esta fórmula se comparte a continuación:
![]()
Donde:
- x y x′ son vectores de entrada.
- x⊤x′ es el producto punto del vector transpuesto x y x′.
- c es una constante.
El requisito de sólo este parámetro c lo hace rápido y muy eficiente en conjuntos de datos grandes. Su papel es fundamentalmente cuádruple. En primer lugar, ayuda en el ajuste de sesgo, lo que significa que, en el caso de que el conjunto de datos o el gráfico no pasen por el origen, la constante proporciona un desplazamiento que desplaza el hiperplano y permite que el núcleo represente mejor el modelo subyacente. Sin esta constante, el núcleo asumiría que todos los puntos de datos están centrados alrededor del origen. Esta constante no es optimizable per se, pero se puede ajustar en pasos de validación cruzada preestablecidos.
En segundo lugar, la constante permite una separación más personalizable entre las dos clases de conjuntos de datos al controlar este margen de diferencia. Esto es particularmente importante cuando este núcleo se utiliza con máquinas de vectores de soporte (Support Vector Machines, SVM) y también en situaciones donde hay conjuntos de datos más grandes que no se pueden separar linealmente fácilmente. En tercer lugar, esta constante permite una homogeneidad no lineal, que podría estar presente en ciertos conjuntos de datos. Sin esta constante, si todas las entradas se escalan por un factor, la salida del núcleo se escalará por el mismo factor. Ahora bien, si bien algunos conjuntos de datos presentan estas características, no todos son así. Es por eso que la adición de esta constante c agrega cierto sesgo inherente y garantiza que el modelo no asuma automáticamente la linealidad.
Por último, se argumenta que proporciona estabilidad numérica a los productos puntuales que podrían resultar en valores muy pequeños, que sesgarían la matriz del kernel. En el caso de que los vectores de entrada tengan valores muy pequeños, el producto escalar sin una constante también sería muy pequeño, lo que afectaría el proceso de optimización. Por tanto, la constante proporciona cierta estabilidad para una mejor optimización.
El kernel lineal ha encontrado aplicaciones en la extrapolación y el pronóstico de tendencias ya que, como veremos a continuación, extrapola tendencias más allá de los datos observados. Por lo tanto, el núcleo lineal puede ser útil, sobre todo en casos en los que se cuestiona la tasa (rate) de revalorización lineal de un activo a lo largo del tiempo. Además, la ponderación de las características del producto escalar hace que el modelo de núcleo lineal sea más interpretable. La interpretabilidad es útil cuando uno tiene un vector de datos de entrada y necesita saber la importancia relativa o significancia de cada uno de los puntos de datos de entrada en este vector. Para ilustrar esto, imagine que tiene un kernel que utiliza para pronosticar el precio de las casas. Este kernel tiene un vector de entrada de datos de tamaño 4 que incluye: el área de la casa (en pies cuadrados), el número de habitaciones de la casa, el ingreso medio en su área y el año en que fue construida. El precio previsto de nuestro kernel vendría dado por la siguiente fórmula:
Donde:
- b es la constante que añadimos al producto punto vectorial, cuyo papel ya se ha destacado anteriormente (denominada c).
- w 1 a w 4 son los pesos que se optimizan con el entrenamiento.
- x 1 a x 4 son los datos de entrada que hemos mencionado anteriormente.
Después del entrenamiento, obtendrá valores para w1 a w4 y con esta configuración de kernel lineal simple, cuanto mayor sea el peso, más importante será la característica o el punto de datos para el próximo precio de la propiedad. Lo mismo es cierto si el peso w4 dice ser el más pequeño, ya que implicaría que x4 (el año en que se compró la propiedad) es el menos importante para el siguiente precio. Sin embargo, el uso del núcleo lineal en este contexto no es lo que estamos cubriendo aquí, sino más bien el uso de núcleos lineales con regresión de proceso gaussiano. Esto significa que si uno necesita inferir la importancia de una característica, no podría hacerlo tan simplemente como lo mostramos anteriormente, porque el resultado de nuestro producto escalar anterior es un escalar y, sin embargo, en nuestra aplicación es una matriz. Las alternativas, sin embargo, para obtener una idea de la importancia relativa de los datos de entrada, incluyen determinación automática de relevancia, análisis de sensibilidad (donde se ajustan los datos de entrada seleccionados y se observa su impacto en la previsión) y probabilidad marginal e hiperparámetros (donde la magnitud de los hiperparámetros, como en la normalización por lotes, puede inferir la importancia relativa de los datos de entrada).
Implementamos el kernel lineal, para su uso dentro de la Regresión del Proceso Gaussiano (Gaussian Process Regression, GPR), en MQL5 de la siguiente manera:
//+------------------------------------------------------------------+ // Linear Kernel Function //+------------------------------------------------------------------+ matrix CSignalGauss::Linear_Kernel(vector &Rows, vector &Cols) { matrix _linear, _c; _linear.Init(Rows.Size(), Cols.Size()); _c.Init(Rows.Size(), Cols.Size()); for(int i = 0; i < int(Rows.Size()); i++) { for(int ii = 0; ii < int(Cols.Size()); ii++) { _linear[i][ii] = Rows[i] * Cols[ii]; } } _c.Fill(m_constant); _linear += _c; return(_linear); }
Las entradas aquí son 2 vectores como ya se indicó en la fórmula, uno de ellos denominado 'Filas' para implicar la transposición de este vector antes de que se aplique en el producto escalar. Por lo tanto, los núcleos lineales, por simples que sean, además de las cosas buenas que hemos mencionado anteriormente, sirven como base para la comparación de modelos con otros núcleos más complejos porque son los más fáciles de configurar y probar. Al comenzar con ellos, se puede ir ampliando gradualmente, dependiendo de si se justifica la complejidad adicional de los otros núcleos. Esto es importante particularmente porque a medida que los núcleos se vuelven más complejos, también aumentan los costos de procesamiento, lo cual es fundamental cuando se trabaja con conjuntos de datos y núcleos muy grandes. Sin embargo, los núcleos lineales capturan las dependencias a largo plazo, se pueden combinar con otros núcleos para definir relaciones más complejas y pueden actuar como una forma de regularización en los casos en los que los conjuntos de datos comparados tienen una fuerte relación lineal.
Núcleos de Matérn
El kernel de Matérn también es una función de covarianza común utilizada en procesos gaussianos debido a su suavidad ajustable y su capacidad para capturar dependencias de datos. Su suavidad está controlada por el parámetro de entrada ν (que se pronuncia nyoo). Este parámetro puede ajustar su suavidad de tal manera que el núcleo Matérn se puede mapear como el núcleo exponencial irregular cuando ν es ½ o hasta un núcleo de función de base radial cuando este parámetro tiende a∞. Su fórmula, a partir de primeros principios, viene dada como:
Donde:
- ∥x-x′∥ es la distancia euclídea entre los dos puntos.
- ν es el parámetro que controla la suavidad.
- l es el parámetro de escala de longitud (similar al del núcleo RBF).
- Γ(ν) es la función Gamma.
- K ν es la función de Bessel modificada del segundo tipo.
La función gamma y la función de Bessel son un poco torpes, y no vamos a entrar en ellas, sin embargo para nuestros propósitos tenemos ν como 3/2 lo que hace que nuestro kernel esté, casi, a medio camino entre un kernel exponencial y el Kernel de la Función de Base Radial. Cuando hacemos eso, nuestra fórmula para el núcleo de Matérn se simplifica a:
Donde:
- Las representaciones son similares a la primera fórmula compartida anteriormente.
Casos especiales:
- Para ν=1/2, el núcleo de Matérn se convierte en el Núcleo exponencial.
- Para ν→∞, se convierte en el núcleo RBF.
La suavidad de este núcleo es muy sensible al parámetro ν, y normalmente se le asigna 1/2 o 3/2 o 5/2 . Cada uno de estos valores de parámetro implica un grado diferente de suavidad, y un valor mayor conlleva una mayor suavidad.
Cuando v es 1/2 el kernel es equivalente al kernel exponencial como se mencionó y esto lo hace adecuado para modelar conjuntos de datos donde los cambios bruscos o discontinuidades son comunes. Desde la perspectiva de un comerciante, esto generalmente indica valores o pares de divisas muy volátiles. Esta configuración del kernel supone un proceso irregular y, por lo tanto, tiende a producir resultados menos fluidos y posiblemente más sensibles a los cambios inmediatos. Cuando v es 3/ 2, que es la configuración que estamos adoptando para este artículo al probar el Asesor Experto montado por el asistente, su suavidad suele calificarse como intermedia. Es un compromiso ya que puede manejar tanto datos ligeramente volátiles como conjuntos de datos con tendencias moderadas. Se podría argumentar que este tipo de configuración hace que el kernel sea adecuado para determinar puntos de inflexión en una serie temporal o puntos de oscilación en el mercado. La configuración 5/2 y cualquier otra superior hace que el kernel se ajuste mejor a los entornos de tendencia, especialmente cuando la tasa está en cuestión.
Por lo tanto, los datos ruidosos o los conjuntos de datos que tienen saltos o discontinuidades se benefician mejor de valores ν más pequeños, mientras que los conjuntos de datos que son más graduales y tienen cambios suaves funcionarían bien con valores v más altos. Como nota al margen, la diferenciabilidad o el número de veces que se puede diferenciar la función kernel, aumenta con el parámetro v. Esto, a su vez, se correlaciona con recursos computacionales con valores de parámetro ν más altos, lo que consume más recursos computacionales. Implementamos el kernel Matérn en MQL5 de la siguiente manera:
//+------------------------------------------------------------------+ // Matern Kernel Function //+------------------------------------------------------------------+ matrix CSignalGauss::Matern_Kernel(vector &Rows,vector &Cols) { matrix _matern; _matern.Init(Rows.Size(), Cols.Size()); for(int i = 0; i < int(Rows.Size()); i++) { for(int ii = 0; ii < int(Cols.Size()); ii++) { _matern[i][ii] = (1.0 + (sqrt(3.0) * fabs(Rows[i] - Cols[ii]) / m_next)) * exp(-1.0 * sqrt(3.0) * fabs(Rows[i] - Cols[ii]) / m_next); } } return(_matern); }
Por lo tanto, en comparación con los núcleos lineales, los núcleos Matérn son más flexibles y más adecuados para capturar relaciones de datos complejas y no lineales. Al modelar una gran cantidad de fenómenos y datos del mundo real, claramente tiene una ventaja sobre los núcleos lineales porque, como hemos visto anteriormente, un ligero ajuste del parámetro v lo hace capaz no solo de manejar conjuntos de datos de tendencia sino también datos volátiles y discontinuos.
La clase de señal
Creamos una clase de señal personalizada que reúne los dos núcleos como dos opciones de implementación en la clase de señal. Nuestra función de obtención de salida también está recodificada para atender la elección de selección de kernel a partir de la entrada del Asesor Experto. La nueva función es la siguiente:
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CSignalGauss::GetOutput(double BasisMean, vector &Output) { ... matrix _k_s; matrix _k_ss; _k_s.Init(_next_time.Size(), _past_time.Size()); _k_ss.Init(_next_time.Size(), _next_time.Size()); if(m_kernel == KERNEL_LINEAR) { _k_s = Linear_Kernel(_next_time, _past_time); _k_ss = Linear_Kernel(_next_time, _next_time); } else if(m_kernel == KERNEL_MATERN) { _k_s = Matern_Kernel(_next_time, _past_time); _k_ss = Matern_Kernel(_next_time, _next_time); } ... }
Los pasos a seguir para interpolar los próximos cambios de precios, una vez seleccionado el núcleo adecuado, son idénticos a los que cubrimos en este artículo anterior. El procesamiento de la condición larga y de la condición corta tampoco es muy diferente, y su código se comparte aquí para completar:
//+------------------------------------------------------------------+ //| "Voting" that price will grow. | //+------------------------------------------------------------------+ int CSignalGauss::LongCondition(void) { int result = 0; vector _o; GetOutput(0.0, _o); if(_o[_o.Size()-1] > _o[0]) { result = int(round(100.0 * ((_o[_o.Size()-1] - _o[0])/(_o.Max() - _o.Min())))); } //printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0); return(result); } //+------------------------------------------------------------------+ //| "Voting" that price will fall. | //+------------------------------------------------------------------+ int CSignalGauss::ShortCondition(void) { int result = 0; vector _o; GetOutput(0.0, _o); if(_o[_o.Size()-1] < _o[0]) { result = int(round(100.0 * ((_o[0] - _o[_o.Size()-1])/(_o.Max() - _o.Min())))); } //printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0); return(result); }
Las condiciones, como en el artículo enlazado, se basan en si el cambio de precio previsto va a ser positivo o negativo. Luego, estos cambios se normalizan para que estén en el rango de números enteros de 0 a 100, como se espera de todas las instancias de clase de señal personalizada. El montaje de este archivo de señal en un Asesor Experto a través del asistente MQL5 se cubre en artículos separados aquí y aquí para los lectores que son nuevos.
Informes del probador de estrategias
Realizamos algunas optimizaciones, sobre el par GBPJPY, en el marco temporal diario para el año 2023 con el kernel lineal y con el kernel Matérn. Los resultados de cada uno, que simplemente demuestran la utilidad del Asesor Experto pero de ninguna manera apuntan al rendimiento futuro, se indican a continuación:
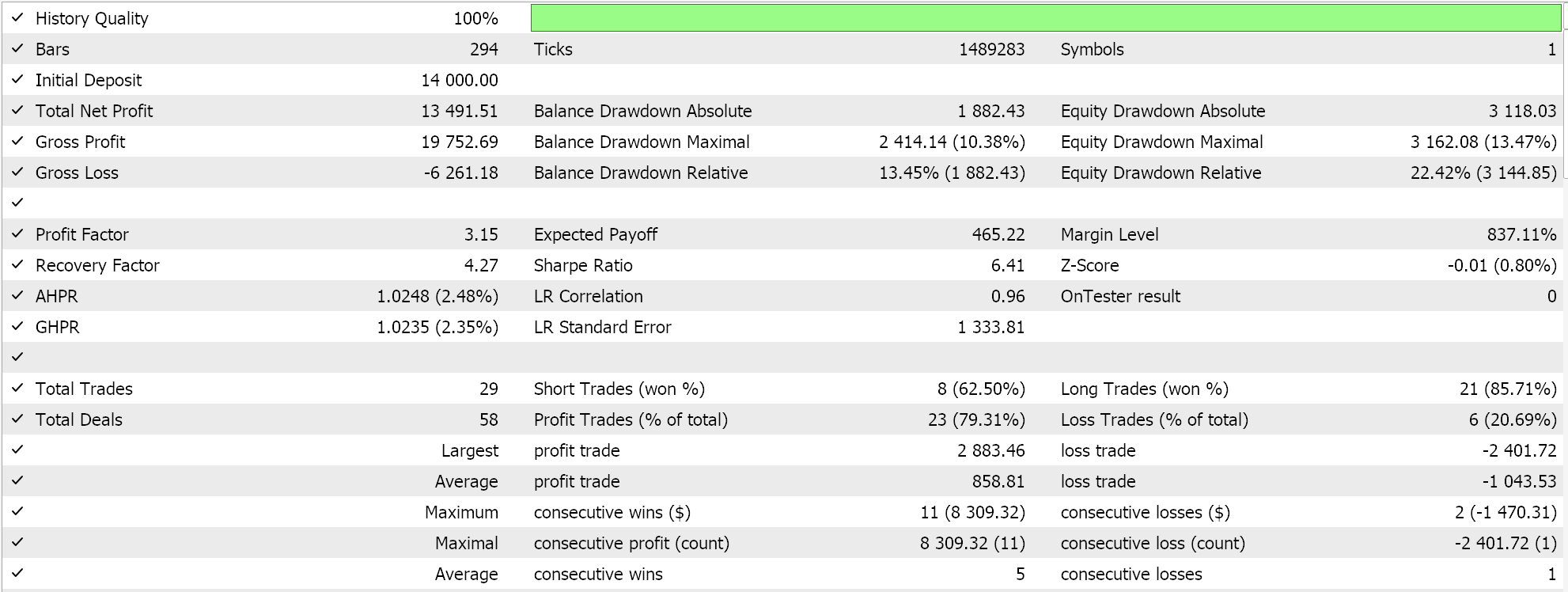
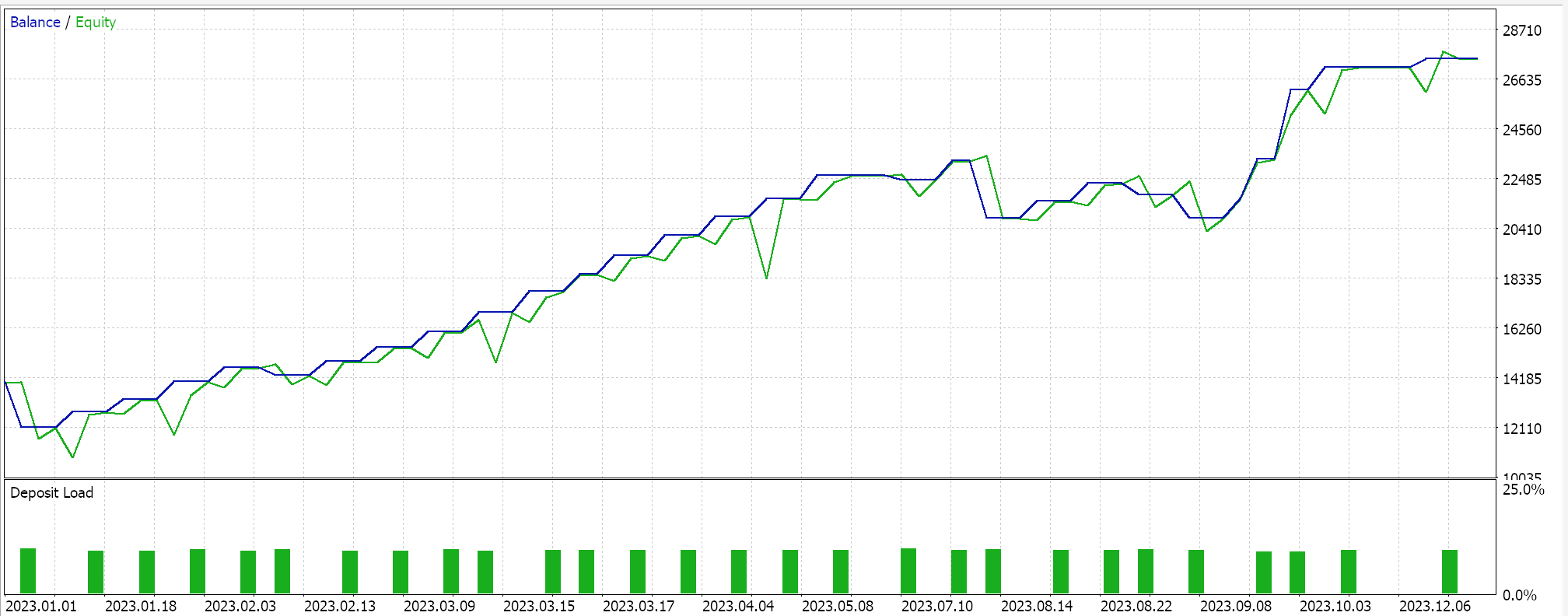
Y los resultados para el kernel Matérn son:
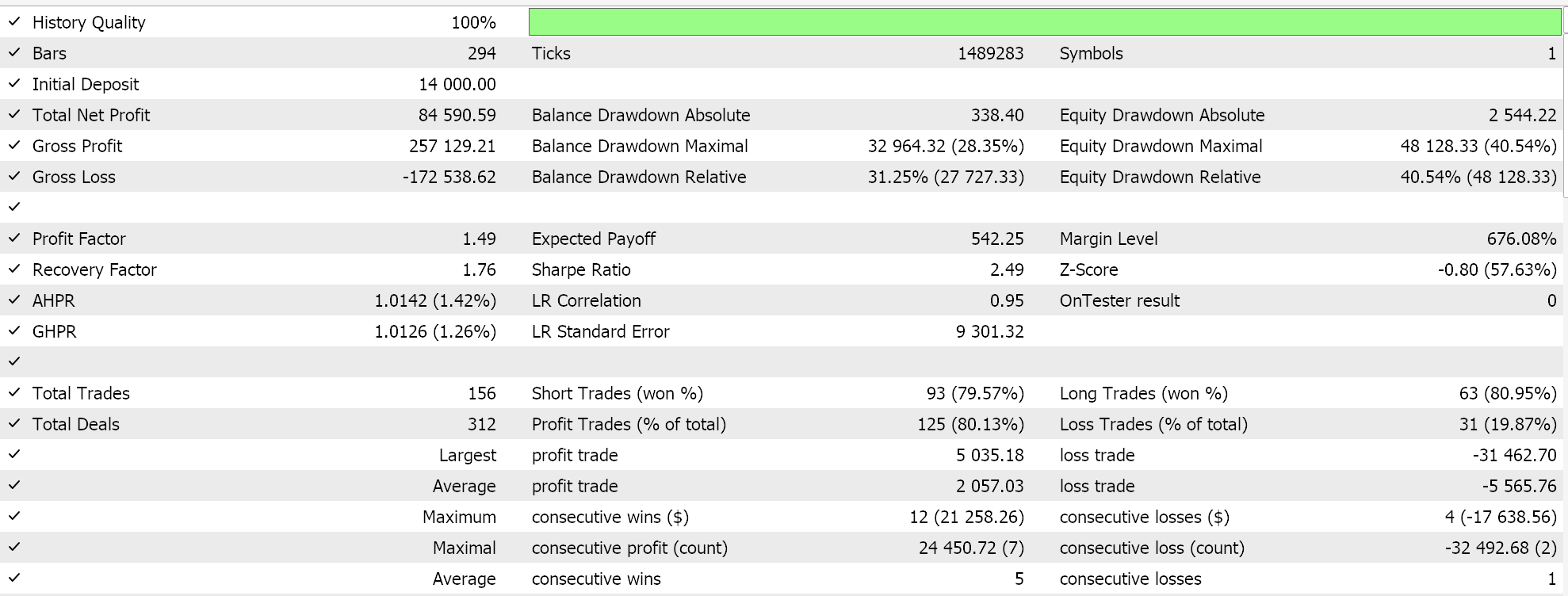
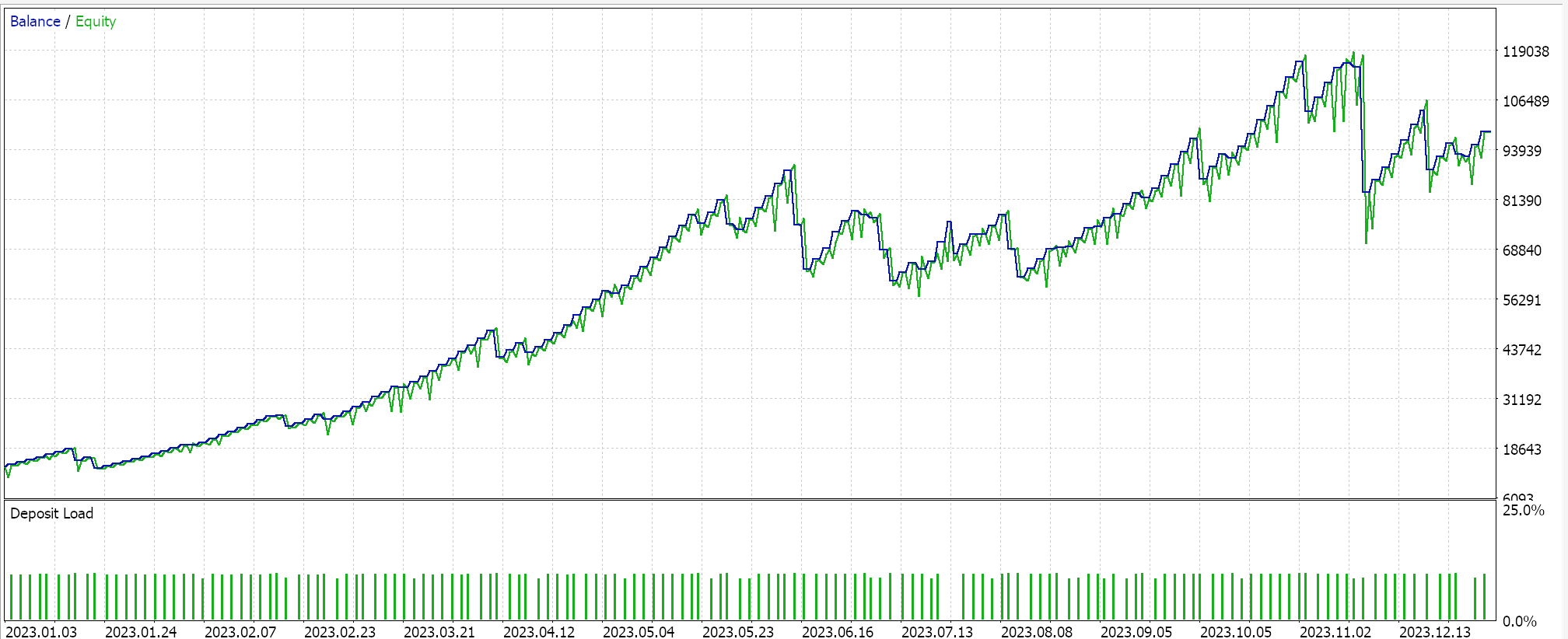
Una implementación alternativa de ambos núcleos también puede ser con una clase de gestión de dinero personalizada. Esto también, al igual que la señal, se puede ensamblar en el asistente MQL5 con la diferencia de que solo se selecciona una instancia personalizada de administración de dinero. Para utilizar la regresión del proceso gaussiano como lo hicimos con la clase de señal, idealmente tendríamos una clase de anclaje común a la que hagan referencia tanto la clase de señal personalizada como la clase de administración de dinero personalizada. Esto minimizaría la duplicidad en la codificación de las mismas funciones que realizan tareas muy similares en las dos clases personalizadas.
Sin embargo, en la clase de administración de dinero, tenemos algunos cambios leves en el tipo de datos que se introducen en los núcleos del proceso gaussiano. Mientras que teníamos cambios de precios cercanos como conjunto de datos de entrada para la clase de señal personalizada, para esta clase de administración de dinero tenemos cambios en el indicador ATR como entradas a nuestro kernel. La salida de nuestro kernel está entrenada para ser el próximo cambio en el ATR. Esta clase personalizada también es una adaptación de la clase común optimizada para el tamaño del dinero que, para aquellos que no estén familiarizados, está diseñada para reducir el tamaño de la posición si un Asesor Experto sufre una racha de pérdidas. La proporción de reducción en el tamaño de los lotes es proporcional a la cadena de pérdidas sufridas. Adoptamos esta clase y hacemos algunos cambios que regulan cuándo se produce la reducción de lotes.
Con nuestras modificaciones, sólo reducimos los lotes si el Asesor Experto sufre pérdidas y existe una proyección de subida del ATR a través de los valores de previsión.El número de estos valores de previsión se establece mediante el parámetro 'm_next', tal y como se comenta en el artículo ya enlazado, que introdujo la Regresión del Proceso Gaussiano en estas series. Estos cambios junto con la mayor parte del código original para optimizar el tamaño de la posición se comparten a continuación:
//+------------------------------------------------------------------+ //| Optimizing lot size for open. | //+------------------------------------------------------------------+ double CMoneyGAUSS::Optimize(int Type, double lots) { double lot = lots; //--- calculate number of losses orders without a break if(m_decrease_factor > 0) { //--- select history for access HistorySelect(0, TimeCurrent()); //--- int orders = HistoryDealsTotal(); // total history deals int losses = 0; // number of consequent losing orders //-- int size = 0; matrix series; series.Init(fmin(m_series_size, orders), 2); series.Fill(0.0); //-- CDealInfo deal; //--- for(int i = orders - 1; i >= 0; i--) { deal.Ticket(HistoryDealGetTicket(i)); if(deal.Ticket() == 0) { Print("CMoneySizeOptimized::Optimize: HistoryDealGetTicket failed, no trade history"); break; } //--- check symbol if(deal.Symbol() != m_symbol.Name()) continue; //--- check profit double profit = deal.Profit(); //-- series[size][0] = profit; size++; //-- if(size >= m_series_size) break; if(profit < 0.0) losses++; } //-- double _cond = 0.0; //-- vector _o; GetOutput(0.0, _o); //--- //decrease lots on rising ATR if(_o[_o.Size()-1] > _o[0]) lot = NormalizeDouble(lot - lot * losses / m_decrease_factor, 2); } //--- normalize and check limits double stepvol = m_symbol.LotsStep(); lot = stepvol * NormalizeDouble(lot / stepvol, 0); //--- double minvol = m_symbol.LotsMin(); if(lot < minvol) lot = minvol; //--- double maxvol = m_symbol.LotsMax(); if(lot > maxvol) lot = maxvol; //--- return(lot); }
También se puede adoptar un enfoque similar al crear una clase de seguimiento personalizada que utilice núcleos de proceso gaussiano, como hemos demostrado anteriormente. Hay una variedad de indicadores para elegir, además del fácil acceso a los precios que ofrecen los tipos de datos vectoriales y matriciales.
Conclusión
Para concluir, hemos continuado nuestra investigación sobre la regresión del proceso gaussiano considerando otro conjunto de kernels que se pueden utilizar con esta forma de regresión al realizar pronósticos con series de tiempo financieras. El núcleo lineal y el núcleo Matérn son casi opuestos no sólo en los tipos de conjuntos de datos para los que son adecuados sino también en su flexibilidad. Si bien el núcleo lineal solo puede manejar un tipo determinado de conjunto de datos, a menudo resulta práctico comenzar a modelar con él, especialmente en casos en los que las muestras del conjunto de datos podrían ser de tamaño pequeño al inicio de un estudio. Con el tiempo, una vez que la muestra del conjunto de datos aumenta y los datos se vuelven más complejos, o incluso ruidosos, se puede utilizar un núcleo más robusto como el núcleo Matérn, no solo para manejar los datos ruidosos o las brechas o discontinuaciones, sino también conjuntos de datos que podrían ser muy uniformes. Esto se debe a que la capacidad de ajuste de su parámetro de entrada clave v le permite asumir diferentes roles dependiendo de los desafíos que presente el conjunto de datos, y es por eso que posiblemente sea más adecuado para la mayoría de los entornos de datos.
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/15767
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Optimización del búfalo africano - African Buffalo Optimization (ABO)
Optimización del búfalo africano - African Buffalo Optimization (ABO)
 Redes neuronales en el trading: Segmentación guiada (Final)
Redes neuronales en el trading: Segmentación guiada (Final)
 Introducción a MQL5 (Parte 9): Comprensión y uso de objetos en MQL5
Introducción a MQL5 (Parte 9): Comprensión y uso de objetos en MQL5
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
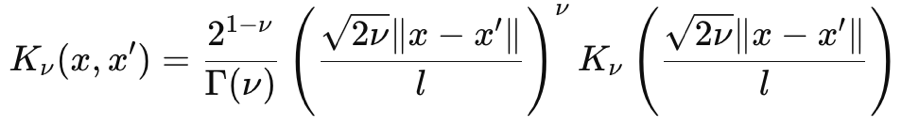

Estoy recibiendo un error crítico
índice fuera de rango en 'MoneyWZ_37.mqh' (197,17)
relativo a la línea
serie[tamaño][0] = beneficio;
índice fuera de rango en 'MoneyWZ_37.mqh' (197,17)
relativo a la línea
serie[tamaño][0] = beneficio;
Hola,
Acabo de hacer cambios en el código adjunto y reenviado para su publicación.