
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 37): Gaußsche Prozessregression mit linearen und Matérn-Kernel
Einführung
Wir setzen diese Serie über die verschiedenen Möglichkeiten fort, wie die Schlüsselkomponenten von Expert Advisors mit Assistenten implementiert werden können, indem wir 2 Gaußsche Prozesskernel betrachten. Der lineare Kernel und der Matérn-Kernel. Ersterer ist so einfach, dass man seine Wikipedia-Seite nicht finden kann, aber letzterer hat hier seine Referenzseite.
Wenn wir noch einmal rekapitulieren wollen, was wir zuvor über Gaußsche Prozesskernel (GPs) gesagt haben, handelt es sich um nichtparametrische Modelle, die komplexe Beziehungen zwischen Datensätzen (in der Regel in Vektorform) abbilden können, ohne dass eine Funktion oder ein Vorwissen über das betreffende Datensatzpaar erforderlich ist. Dadurch eignen sie sich ideal für Situationen, in denen die betroffenen Datensätze nichtlinear oder sogar verrauscht sind. Diese Flexibilität macht sie außerdem zu einem idealen Instrument für finanzielle Zeitreihen, die oft volatil sind, da GPs dazu neigen, nuancierte Ergebnisse zu liefern. Sie liefern eine Prognoseschätzung und ein Konfidenzintervall. GPs helfen dabei, die Ähnlichkeit zwischen zwei Datensätzen zu bestimmen, und da es mehrere Arten von Kerneln gibt, die in der Gaußschen Prozessregression verwendet werden können, ist es immer wichtig, den geeigneten Kernel zu identifizieren oder die Unzulänglichkeiten des von Ihnen gewählten Kernels zu beachten, insbesondere in Fällen, in denen Kernel zur Extrapolation einer Prognose verwendet werden.
Nachfolgend finden Sie eine zusammenfassende Tabelle mit den bisher in dieser Reihe vorgestellten Kernen und einigen ihrer Eigenschaften:
| Kernel-Typ | Ideal zum Erfassen | Erklärung |
|---|---|---|
| Linearer Kernel | Trends | Erfasst lineare Trends im Zeitverlauf; ideal für Vermögenswerte, die langfristige Kursbewegungen nach oben oder unten aufweisen. Einfach und rechnerisch effizient, geht aber von einer linearen Beziehung aus. |
| Radiale Basisfunktion (RBF) Kernel | Trends und Volatilität | Am besten geeignet für die Erfassung gleichmäßiger, langfristiger Trends mit allmählichen Preisänderungen. Sie liefert gleichmäßige Schätzungen und eignet sich gut für kontinuierliche Muster. Es hat jedoch Probleme mit scharfen Übergängen oder extremer Volatilität. |
| Matérn Kernel | Trends, Volatilität, Zyklen | Kann gröbere, weniger glatte Trends und plötzliche Veränderungen der Volatilität erfassen. Der Parameter ν steuert die Glättung, sodass ein niedrigeres ν die grobe Volatilität erfasst, während ein höheres ν die Trends glättet. |
Je nach der Zeitreihe, die man extrapoliert, muss der geeignete Kernel auf der Grundlage seiner Stärken ausgewählt werden. Finanzielle Zeitreihen können oft ein periodisches oder zyklisches Verhalten aufweisen, und Kernel wie der Matérn-Kernel, den wir im Folgenden vorstellen, können bei der Abbildung dieser Beziehungen helfen. Darüber hinaus ist die Quantifizierung der Unsicherheit, wie wir das mit der Radialbasisfunktion in diesem ersten Artikel gesehen haben, kann ein großer Segen sein, wenn Händler mit flachen oder schwankenden Märkten konfrontiert sind. Kernel wie das RBF liefern nicht nur Punktschätzungen, sondern auch Konfidenzintervalle, was in diesen Situationen von Vorteil sein kann. Der Grund dafür ist, dass das Konfidenzintervall dazu beitragen kann, schwache Signale herauszufiltern und gleichzeitig wichtige Wendepunkte in einem unsicheren Umfeld hervorzuheben.
Mittelwertumkehrende Datensätze können auch mit speziellen Kerneln wie dem Ornstein-Uhlenbeck-Kernel behandelt werden, den wir in einem späteren Artikel behandeln werden. Ein weiterer interessanter Aspekt, mit dem wir uns in Zukunft befassen könnten, ist die Tatsache, dass GPs eine Kernel-Zusammensetzung ermöglichen, bei der mehrere Kernel wie das Stapeln eines linearen Kernels und eines RBF-Kernels verwendet werden können, um komplexere Beziehungen zwischen Datensätzen zu modellieren. Dies könnte Paarungen wie kurzfristige Preisaktionsmuster und langfristige Trends umfassen, bei denen ein Modell in der Lage ist, Ausstiege aus offenen Positionen zu optimalen Zeitpunkten zu platzieren und gleichzeitig von einer zugrunde liegenden langfristigen Aktion eines Wertpapiers zu profitieren.
GPs bieten eine Reihe zusätzlicher Vorteile und Verwendungszwecke, wie z. B. den Umgang mit und die Verringerung von Lärm sowie die Anpassung an Regimewechsel und vieles mehr. Als Händler wollen wir jedoch von diesen Vorteilen profitieren, also lassen Sie uns einen sehr einfachen linearen Kernel betrachten.
Lineare Kernel
Lineare Kernel werden in erster Linie verwendet, um einfache lineare Beziehungen zwischen Datensätzen in einem Gauß-Prozess abzubilden. Betrachten wir zum Beispiel ein sehr einfaches Paar von Datensätzen, die Kosten für den Versand eines Containers von China in die USA und den ETF BOAT für den Versandkosten per Schiff. Unter normalen Umständen würden wir erwarten, dass hohe Schifffahrtskosten die Preissetzungsmacht der Schifffahrtsunternehmen widerspiegeln, sodass ihre Gewinne und damit ihre Einnahmen dies widerspiegeln würden, was zu einem Anstieg ihres Aktienkurses führen würde. In diesem Szenario wäre ein Händler, der im Laufe der Zeit Schifffahrtsunternehmen oder auch nur die ETFs kaufen möchte, daran interessiert, seine erwarteten Aktienkurse und die aktuellen Schifffahrtskosten mit einem linearen Kernel zu modellieren.
Er ist relativ einfach und wenig komplex, sodass er von allen Kernels die wenigsten Rechenressourcen benötigt. Außerdem benötigt sie nur einen einzigen konstanten Parameter c in ihrer Formel. Diese Formel wird im Folgenden erläutert:
![]()
Wo:
- x und x′ sind Eingangsvektoren
- x⊤x′ ist das Punktprodukt des transponierten Vektors x und x′
- c ist eine Konstante
Da nur dieser eine Parameter c benötigt wird, ist es schnell und sehr effizient bei großen Datensätzen. Sie hat vor allem eine vierfache Aufgabe. Erstens hilft sie bei der Bias-Anpassung, d. h. für den Fall, dass der Datensatz oder das Diagramm nicht durch den Ursprung verläuft, liefert die Konstante einen Offset, der die Hyperebene verschiebt und es dem Kernel ermöglicht, das zugrunde liegende Modell besser darzustellen. Ohne diese Konstante würde der Kernel davon ausgehen, dass alle Datenpunkte um den Ursprung zentriert sind. Diese Konstante ist nicht per se optimierbar, sondern kann in vorgegebenen Kreuzvalidierungsschritten eingestellt werden.
Zweitens ermöglicht die Konstante eine besser anpassbare Trennung zwischen den beiden Datensatzklassen, indem sie diesen Randabstand kontrolliert. Dies ist besonders wichtig, wenn dieser Kernel mit Support Vector Machines verwendet wird, und auch in Situationen, in denen es größere Datensätze gibt, die nicht einfach linear trennbar sind. Drittens ermöglicht diese Konstante eine nicht-lineare Homogenität, die in bestimmten Datensätzen vorhanden sein könnte. Ohne diese Konstante wird, wenn alle Eingaben um einen Faktor skaliert werden, die Ausgabe des Kernels um denselben Faktor skaliert. Nun weisen zwar einige Datensätze diese Merkmale auf, aber nicht alle. Deshalb wird durch die Hinzufügung dieser Konstante c eine gewisse Verzerrung hinzugefügt und sichergestellt, dass das Modell nicht automatisch von Linearität ausgeht.
Schließlich wird argumentiert, dass es numerische Stabilität für Punktprodukte bietet, die zu sehr kleinen Werten führen könnten, die die Kernelmatrix verzerren würden. Falls die Eingangsvektoren sehr kleine Werte haben, wäre das Punktprodukt ohne Konstante ebenfalls sehr klein, was den Optimierungsprozess beeinträchtigen würde. Die Konstante bietet daher eine gewisse Stabilität für eine bessere Optimierung.
Der lineare Kernel findet Anwendung in der Extrapolation und Trendvorhersage, da er, wie wir weiter unten sehen werden, Trends über die beobachteten Daten hinaus extrapoliert. Insbesondere in Fällen, in denen es beispielsweise um die Rate der linearen Wertsteigerung eines Vermögenswerts im Laufe der Zeit geht. Auch die Gewichtung der Merkmale aus dem Punktprodukt macht das Linear-Kernel-Modell besser interpretierbar. Interpretierbarkeit ist nützlich, wenn man einen Vektor von Eingabedaten hat und die relative Bedeutung oder Signifikanz jedes der Eingabedatenpunkte in diesem Vektor kennen muss. Zur Veranschaulichung: Stellen Sie sich vor, Sie haben einen Kernel, den Sie für die Vorhersage von Hauspreisen verwenden. Dieser Kernel hat einen Daten-Eingabevektor der Größe 4, der Folgendes umfasst: die Fläche des Hauses (in Quadratfuß), die Anzahl der Schlafzimmer im Haus, das Medianeinkommen in der Gegend und das Baujahr. Der von unserem Kernel prognostizierte Preis würde sich aus der folgenden Formel ergeben:
Wobei
- b ist die Konstante, die wir zum Vektorpunktprodukt hinzufügen, deren Rolle bereits oben hervorgehoben wurde (bezeichnet als c)
- w1 bis w4 sind die Gewichte, die durch Training optimiert werden
- x1 bis x4 ist die oben erwähnte Dateneingabe
Nach dem Training erhält man Werte für w1 bis w4, und bei diesem einfachen linearen Kernel-Setup gilt: Je größer das Gewicht, desto wichtiger ist das Merkmal oder der Datenpunkt für den nächsten Preis der Immobilie. Das Gleiche gilt, wenn das Gewicht w4 das kleinste ist, da dies bedeuten würde, dass x4 (das Jahr, in dem die Immobilie gekauft wurde) für den nächsten Preis am wenigsten wichtig ist. Die Verwendung des linearen Kerns in dieser Umgebung ist jedoch nicht das, was wir hier behandeln, sondern vielmehr die Verwendung linearer Kernel mit Gaußscher Prozessregression. Das bedeutet, dass man, wenn man die Bedeutung eines Merkmals ableiten muss, dies nicht so einfach tun kann, wie wir es oben gezeigt haben, weil das Ergebnis unseres Punktprodukts oben ein Skalar ist, in unserer Anwendung aber eine Matrix ist. Die Alternativen, um ein Gefühl für die relative Bedeutung der Eingabedaten zu bekommen, umfassen jedoch die automatische Relevanzbestimmung, die Sensitivitätsanalyse (bei der ausgewählte Eingaben angepasst werden und ihre Auswirkungen auf die Vorhersage beobachtet werden) sowie Grenzwahrscheinlichkeit und Hyperparameter (wobei die Größe der Hyperparameter wie bei der Stapelnormalisierung auf die relative Bedeutung der Eingabedaten schließen lässt).
Wir implementieren den linearen Kernel zur Verwendung in der Gaußschen Prozessregression in MQL5 wie folgt:
//+------------------------------------------------------------------+ // Linear Kernel Function //+------------------------------------------------------------------+ matrix CSignalGauss::Linear_Kernel(vector &Rows, vector &Cols) { matrix _linear, _c; _linear.Init(Rows.Size(), Cols.Size()); _c.Init(Rows.Size(), Cols.Size()); for(int i = 0; i < int(Rows.Size()); i++) { for(int ii = 0; ii < int(Cols.Size()); ii++) { _linear[i][ii] = Rows[i] * Cols[ii]; } } _c.Fill(m_constant); _linear += _c; return(_linear); }
Die Eingaben sind hier 2 Vektoren, wie bereits in der Formel angegeben, wobei einer von ihnen mit „Zeilen“ beschriftet ist, um die Transponierung dieses Vektors zu implizieren, bevor sie im Punktprodukt angewendet wird. Lineare Kernel, so einfach sie auch sind, dienen also zusätzlich zu den oben genannten Vorteilen als Grundlage für den Modellvergleich mit anderen, komplexeren Kerneln, da sie am einfachsten einzurichten und zu testen sind. Wenn man mit ihnen beginnt, kann man schrittweise aufsteigen, je nachdem, ob die zusätzliche Komplexität der anderen Kernel gerechtfertigt ist. Dies ist vor allem deshalb wichtig, weil mit zunehmender Komplexität der Kernel auch die Rechenkosten ansteigen, was bei sehr großen Datensätzen und Kerneln kritisch ist. Lineare Kernel erfassen jedoch langfristige Abhängigkeiten, sind mit anderen Kerneln kombinierbar, um komplexere Beziehungen zu definieren, und sie können als eine Form von Regularisierung in Fällen, in denen die verglichenen Datensätze eine starke lineare Beziehung aufweisen.
Matérn-Kernel
Der Matérn-Kernel ist auch eine gängige Kovarianzfunktion, die in Gauß-Prozessen verwendet wird, da er eine einstellbare Glätte aufweist und in der Lage ist, Datenabhängigkeiten zu erfassen. Seine Glätte wird durch den Eingabeparameter ν (ausgesprochen: nyoo) gesteuert. Mit diesem Parameter kann die Glätte so eingestellt werden, dass der Matérn-Kernel als gezackter Exponential-Kernel abgebildet werden kann, wenn ν gleich ½ ist, oder bis zu einem Radialbasisfunktionskern, wenn dieser Parameter gegen ∞ tendiert. Seine Formel lautet nach den ersten Prinzipien wie folgt:
Wobei:
- ∥x-x′∥ ist der euklidische Abstand zwischen den beiden Punkten
- ν ist der die Glätte steuernde Parameter
- l ist der Längenskalenparameter (ähnlich dem des RBF-Kerns)
- Γ(ν) ist die Gamma-Funktion
- K ν ist die modifizierte Besselfunktion der zweiten Art
Die Gammafunktion und die Besselfunktion sind etwas kompliziert, und wir werden uns nicht mit ihnen befassen, aber für unsere Zwecke nehmen wir ν als 3/2, was unseren Kernel fast auf halbem Weg zwischen einem Exponentialkernel und dem Radialbasisfunktionskernel macht. Wenn wir das tun, vereinfacht sich unsere Formel für den Matérn-Kernel zu:
Wobei
- Die Darstellungen sind ähnlich wie bei der ersten Formel oben.
Besondere Fälle:
- Für ν=1/2 wird der Matérn-Kernel zum Exponential-Kernel.
- Für ν→∞ wird daraus der RBF-Kernel.
Die Glattheit dieses Kernels ist sehr empfindlich gegenüber dem Parameter ν, und typischerweise wird er entweder 1/2 oder 3/2 oder 5/2 zugeordnet. Jeder dieser Parameterwerte impliziert einen anderen Grad an Glätte, wobei ein größerer Wert zu mehr Glätte führt.
Wenn v gleich 1/2 ist, entspricht der Kernel dem bereits erwähnten Exponentialkernel und eignet sich daher für die Modellierung von Datensätzen, bei denen starke Veränderungen oder Diskontinuitäten häufig vorkommen. Aus der Sicht eines Händlers deutet dies in der Regel auf sehr volatile Wertpapiere oder Devisenpaare hin. Diese Kernel-Einstellung geht von einem zerklüfteten Prozess aus und führt daher tendenziell zu Ergebnissen, die weniger glatt sind und wohl eher auf unmittelbare Änderungen reagieren. Wenn v 3/2 ist, was die Einstellung ist, die wir für diesen Artikel annehmen, wenn wir den mit dem Assistenten zusammengestellten Expert Advisor testen, wird seine Glattheit oft als mittelmäßig eingestuft. Sie stellt einen Kompromiss dar, da sie sowohl mit leicht volatilen Daten als auch mit leicht trendigen Datensätzen umgehen kann. Diese Art von Einstellung, so könnte man argumentieren, macht den Kernel geeignet für die Bestimmung von Wendepunkten in einer Zeitreihe oder von Schwungpunkten auf dem Markt. Mit der Einstellung 5/2 und höher eignet sich der Kernel besser für Trendumgebungen, insbesondere wenn der Kurs in Frage steht.
Für verrauschte Daten oder Datensätze, die Sprünge oder Diskontinuitäten aufweisen, sind kleinere ν-Werte besser geeignet, während für Datensätze mit allmählichen und gleichmäßigen Veränderungen höhere v-Werte besser geeignet sind. Nebenbei bemerkt: Die Differenzierbarkeit bzw. die Anzahl der Differenzierungen der Kernel-Funktion nimmt mit dem Parameter v zu. Dies wiederum korreliert mit Rechenressourcen mit höheren ν-Parameterwerten, die mehr Rechenleistung verbrauchen. Wir implementieren den Matérn-Kernel in MQL5 wie folgt:
//+------------------------------------------------------------------+ // Matern Kernel Function //+------------------------------------------------------------------+ matrix CSignalGauss::Matern_Kernel(vector &Rows,vector &Cols) { matrix _matern; _matern.Init(Rows.Size(), Cols.Size()); for(int i = 0; i < int(Rows.Size()); i++) { for(int ii = 0; ii < int(Cols.Size()); ii++) { _matern[i][ii] = (1.0 + (sqrt(3.0) * fabs(Rows[i] - Cols[ii]) / m_next)) * exp(-1.0 * sqrt(3.0) * fabs(Rows[i] - Cols[ii]) / m_next); } } return(_matern); }
Im Vergleich zu linearen Kerneln sind Matérn-Kernel daher flexibler und besser geeignet, komplexe, nicht-lineare Datenbeziehungen zu erfassen. Bei der Modellierung vieler realer Phänomene und Daten ist er eindeutig im Vorteil gegenüber linearen Kerneln, da er, wie wir oben gesehen haben, durch eine geringfügige Anpassung des v-Parameters nicht nur in der Lage ist, tendenzielle Datensätze zu verarbeiten, sondern auch unbeständige und diskontinuierliche Daten.
Die Signalklasse
Wir erstellen eine nutzerdefinierte Signalklasse, die die beiden Kernel als zwei Implementierungsoptionen in der Signalklasse zusammenführt. Unsere Funktion GetOutput ist ebenfalls neu kodiert, um die Auswahl des Kernels aus der Eingabe des Expert Advisors zu berücksichtigen. Die neue Funktion lautet wie folgt:
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CSignalGauss::GetOutput(double BasisMean, vector &Output) { ... matrix _k_s; matrix _k_ss; _k_s.Init(_next_time.Size(), _past_time.Size()); _k_ss.Init(_next_time.Size(), _next_time.Size()); if(m_kernel == KERNEL_LINEAR) { _k_s = Linear_Kernel(_next_time, _past_time); _k_ss = Linear_Kernel(_next_time, _next_time); } else if(m_kernel == KERNEL_MATERN) { _k_s = Matern_Kernel(_next_time, _past_time); _k_ss = Matern_Kernel(_next_time, _next_time); } ... }
Die Schritte zur Interpolation der nächsten Preisänderungen, sobald der geeignete Kernel ausgewählt wurde, sind identisch mit denen, die wir in diesem, früheren Artikel behandelt haben. Die Verarbeitung der langen und der kurzen Bedingung unterscheidet sich ebenfalls nicht wesentlich, und ihr Code wird hier der Vollständigkeit halber gemeinsam verwendet:
//+------------------------------------------------------------------+ //| "Voting" that price will grow. | //+------------------------------------------------------------------+ int CSignalGauss::LongCondition(void) { int result = 0; vector _o; GetOutput(0.0, _o); if(_o[_o.Size()-1] > _o[0]) { result = int(round(100.0 * ((_o[_o.Size()-1] - _o[0])/(_o.Max() - _o.Min())))); } //printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0); return(result); } //+------------------------------------------------------------------+ //| "Voting" that price will fall. | //+------------------------------------------------------------------+ int CSignalGauss::ShortCondition(void) { int result = 0; vector _o; GetOutput(0.0, _o); if(_o[_o.Size()-1] < _o[0]) { result = int(round(100.0 * ((_o[0] - _o[_o.Size()-1])/(_o.Max() - _o.Min())))); } //printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0); return(result); }
Die Bedingungen wie im verlinkten Artikel basieren darauf, ob die prognostizierte Preisänderung positiv oder negativ sein wird. Diese Änderungen werden dann so normalisiert, dass sie im ganzzahligen Bereich von 0 bis 100 liegen, wie es von allen nutzerdefinierten Signalklasseninstanzen erwartet wird. Die Zusammenstellung dieser Signaldatei zu einem Expert Advisor über den MQL5-Assistenten wird in separaten Artikeln hier und hier für Leser, die neu sind, behandelt.
Berichte des Strategie-Testers
Wir führen einige Optimierungen für das Paar GBPJPY auf dem täglichen Zeitrahmen für das Jahr 2023 mit dem linearen Kernel und mit dem Matérn-Kernel durch. Die jeweiligen Ergebnisse, die lediglich die Nutzerfreundlichkeit des Expert Advisors demonstrieren, aber in keiner Weise auf die künftige Leistung schließen lassen, sind im Folgenden aufgeführt:
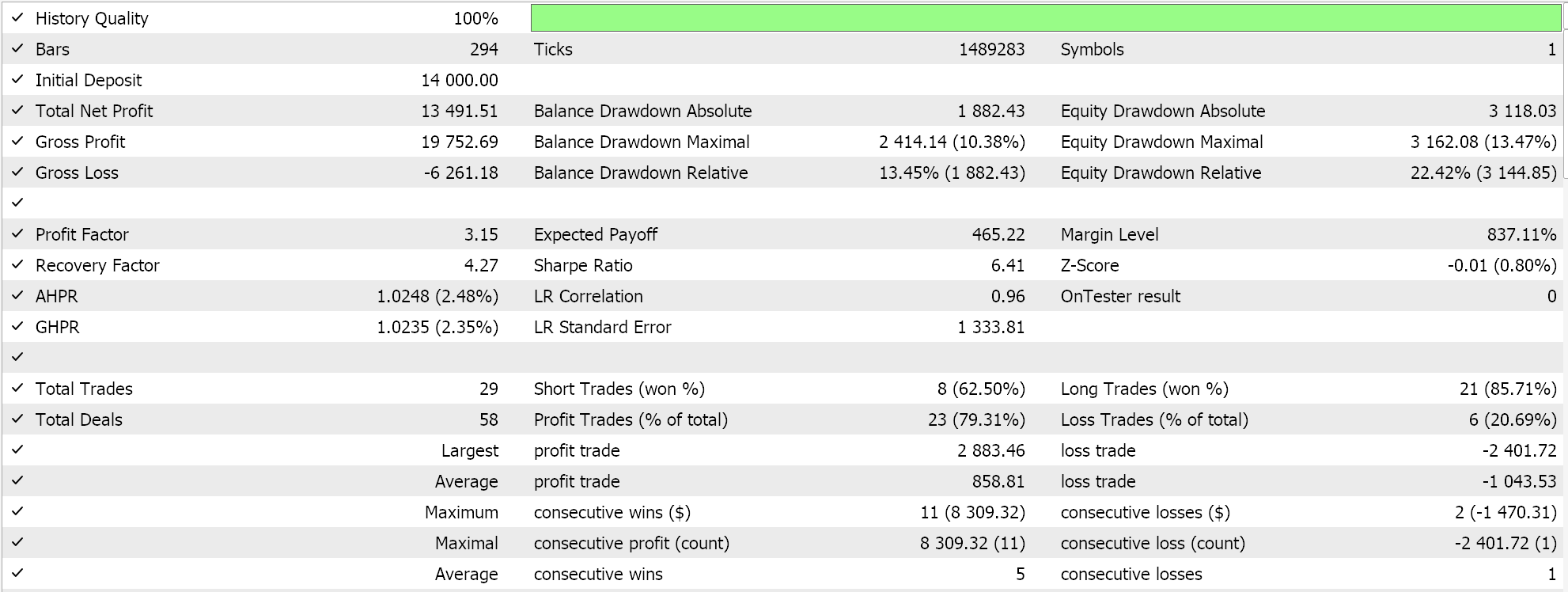
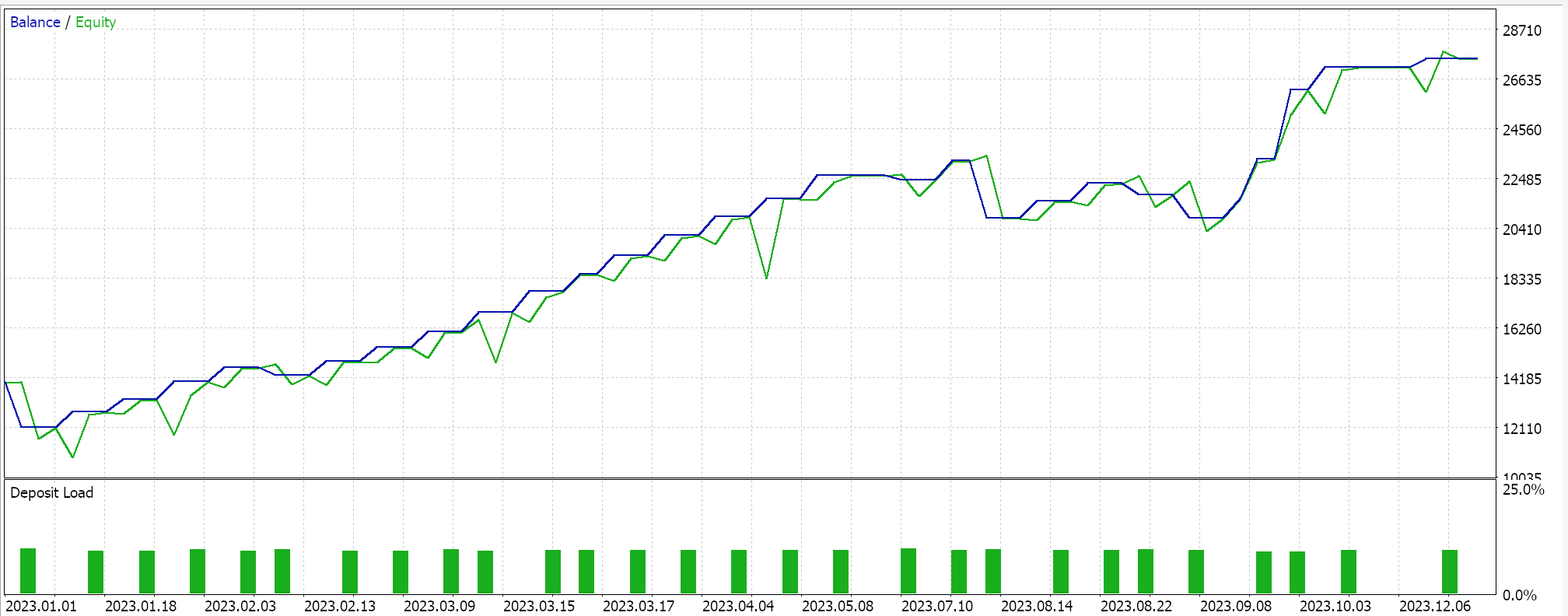
Und die Ergebnisse für den Matérn-Kernel sind:
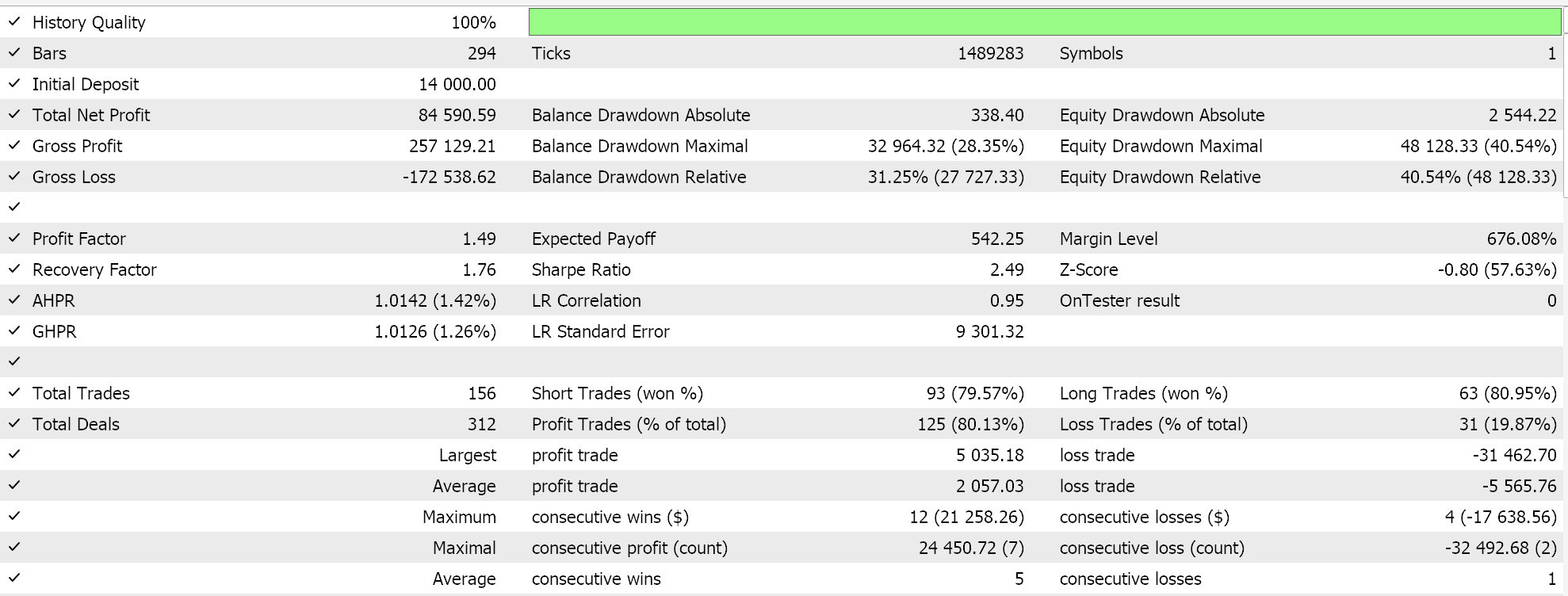
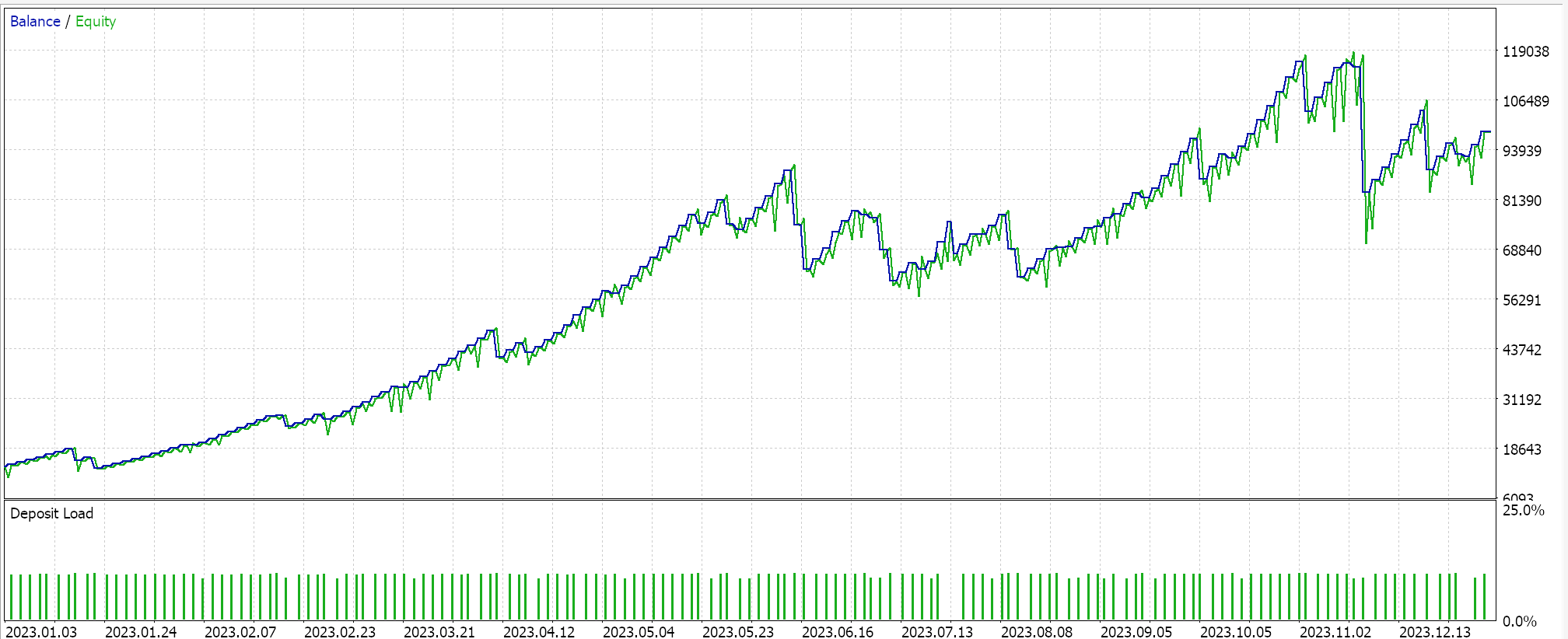
Eine alternative Implementierung beider Kernel kann auch mit einer eigenen Geldverwaltungsklasse erfolgen. Dies kann auch wie das Signal im MQL5-Assistenten zusammengestellt werden, mit dem Unterschied, dass nur eine nutzerdefinierte Instanz der Geldverwaltung ausgewählt wird. Um die Gaußsche Prozessregression wie bei der Signalklasse zu verwenden, wäre es ideal, eine gemeinsame Ankerklasse zu haben, auf die sowohl die nutzerdefinierte Signalklasse als auch die nutzerdefinierte Geldmanagementklasse verweisen. Dies würde die Duplizität der Codierung derselben Funktionen, die in den beiden nutzerdefinierten Klassen sehr ähnliche Aufgaben erfüllen, minimieren.
In der Geldmanagement-Klasse gibt es jedoch einige leichte Änderungen bei der Art der Daten, die den Kerneln des Gauß-Prozesses zugeführt werden. Während wir für die nutzerdefinierte Signalklasse die Änderungen der Close-Preis als Eingabedatensatz hatten, haben wir für diese Geldmanagementklasse Änderungen im ATR-Indikator als Eingaben für unseren Kernel. Die Ausgabe für unseren Kernel wird so trainiert, dass sie die nächste Änderung der ATR zeigt. Diese nutzerdefinierte Klasse ist ebenfalls eine Anpassung an die übliche Klasse zur Optimierung der Geldmenge, die dazu dient, die Positionsgröße zu reduzieren, wenn ein Expert Advisor eine Reihe von Verlusten erleidet, falls diese nicht bekannt sind. Der Anteil der Verringerung der Losgrößen ist proportional zu der Anzahl der erlittenen Verluste. Wir übernehmen diese Klasse und nehmen einige Änderungen vor, die regeln, wann die Reduzierung der Lose erfolgt.
Mit unseren Änderungen reduzieren wir die Lots nur dann, wenn der Expert Advisor Verluste erleidet und ein Anstieg der ATR über die Prognosewerte prognostiziert wird. Die Anzahl dieser Prognosewerte wird durch den Parameter „m_next“ festgelegt, wie in dem bereits verlinkten Artikel erläutert, in dem die Gaußsche Prozessregression für diese Reihen eingeführt wurde. Diese Änderungen sowie der größte Teil des ursprünglichen Codes zur Optimierung der Positionsgröße sind im Folgenden aufgeführt:
//+------------------------------------------------------------------+ //| Optimizing lot size for open. | //+------------------------------------------------------------------+ double CMoneyGAUSS::Optimize(int Type, double lots) { double lot = lots; //--- calculate number of losses orders without a break if(m_decrease_factor > 0) { //--- select history for access HistorySelect(0, TimeCurrent()); //--- int orders = HistoryDealsTotal(); // total history deals int losses = 0; // number of consequent losing orders //-- int size = 0; matrix series; series.Init(fmin(m_series_size, orders), 2); series.Fill(0.0); //-- CDealInfo deal; //--- for(int i = orders - 1; i >= 0; i--) { deal.Ticket(HistoryDealGetTicket(i)); if(deal.Ticket() == 0) { Print("CMoneySizeOptimized::Optimize: HistoryDealGetTicket failed, no trade history"); break; } //--- check symbol if(deal.Symbol() != m_symbol.Name()) continue; //--- check profit double profit = deal.Profit(); //-- series[size][0] = profit; size++; //-- if(size >= m_series_size) break; if(profit < 0.0) losses++; } //-- double _cond = 0.0; //-- vector _o; GetOutput(0.0, _o); //--- //decrease lots on rising ATR if(_o[_o.Size()-1] > _o[0]) lot = NormalizeDouble(lot - lot * losses / m_decrease_factor, 2); } //--- normalize and check limits double stepvol = m_symbol.LotsStep(); lot = stepvol * NormalizeDouble(lot / stepvol, 0); //--- double minvol = m_symbol.LotsMin(); if(lot < minvol) lot = minvol; //--- double maxvol = m_symbol.LotsMax(); if(lot > maxvol) lot = maxvol; //--- return(lot); }
Ein ähnlicher Ansatz kann auch bei der Erstellung einer nutzerdefinierten Trailing-Klasse gewählt werden, die Gauß'sche Prozess-Kernel verwendet, wie wir oben gezeigt haben. Neben dem einfachen Zugriff auf die Preise, der durch die Vektor- und Matrix-Datentypen ermöglicht wird, steht eine Vielzahl von Indikatoren zur Auswahl.
Schlussfolgerung
Abschließend haben wir uns weiter mit der Gauß'schen Prozessregression beschäftigt, indem wir eine weitere Gruppe von Kerneln betrachtet haben, die mit dieser Form der Regression bei der Erstellung von Prognosen für finanzielle Zeitreihen verwendet werden können. Der lineare Kernel und der Matérn-Kernel sind nicht nur in Bezug auf die Art der Datensätze, für die sie geeignet sind, sondern auch in Bezug auf ihre Flexibilität nahezu gegensätzlich. Obwohl der lineare Kernel nur eine bestimmte Art von Datensätzen verarbeiten kann, ist es oft praktisch, die Modellierung mit ihm zu beginnen, insbesondere in Fällen, in denen die Stichproben der Datensätze zu Beginn einer Studie klein sein könnten. Mit der Zeit, wenn die Stichprobe des Datensatzes zunimmt und die Daten komplexer oder sogar verrauscht werden, kann ein robusterer Kernel wie der Matérn-Kernel verwendet werden, um nicht nur die verrauschten Daten oder Lücken oder Diskontinuitäten zu verarbeiten, sondern auch Datensätze, die sehr glatt sein könnten. Dies liegt daran, dass die Anpassungsfähigkeit des wichtigsten Eingabeparameters v es ermöglicht, je nach den Herausforderungen des Datensatzes verschiedene Rollen zu übernehmen, und deshalb ist es wohl für die meisten Datenumgebungen besser geeignet.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/15767
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Erstellen eines integrierten MQL5-Telegram Expert Advisors (Teil 5): Senden von Befehlen von Telegram an MQL5 und Empfangen von Antworten in Echtzeit
Erstellen eines integrierten MQL5-Telegram Expert Advisors (Teil 5): Senden von Befehlen von Telegram an MQL5 und Empfangen von Antworten in Echtzeit
 Einführung in MQL5 (Teil 9): Verstehen und Verwenden von Objekten in MQL5
Einführung in MQL5 (Teil 9): Verstehen und Verwenden von Objekten in MQL5
 Neuinterpretation klassischer Strategien in MQL5 (Teil II): FTSE100 und britische Staatsanleihen
Neuinterpretation klassischer Strategien in MQL5 (Teil II): FTSE100 und britische Staatsanleihen
 Erstellen eines Administrator-Panels für den Handel in MQL5 (Teil III): Verbesserung der grafischen Nutzeroberfläche mit visuellem Styling (I)
Erstellen eines Administrator-Panels für den Handel in MQL5 (Teil III): Verbesserung der grafischen Nutzeroberfläche mit visuellem Styling (I)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
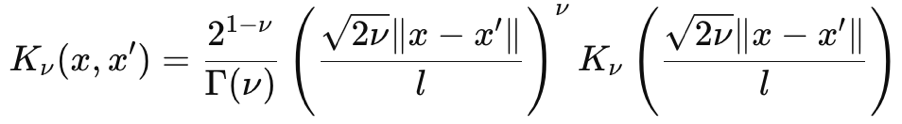
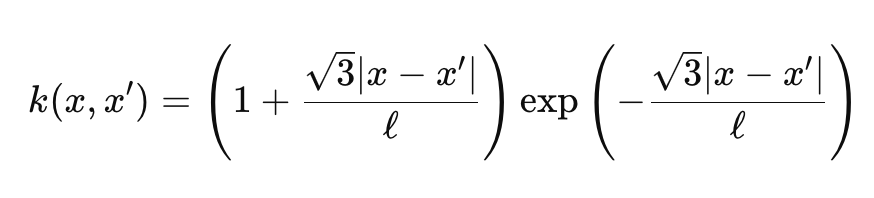
Ich erhalte einen kritischen Fehler.
Index außerhalb des Bereichs in 'MoneyWZ_37.mqh' (197,17)
bezogen auf die Zeile
Serie[Größe][0] = Gewinn;
Index außerhalb des Bereichs in 'MoneyWZ_37.mqh' (197,17)
bezogen auf die Zeile
Serie[Größe][0] = Gewinn;
Hallo!
Ich habe gerade Änderungen am angehängten Code vorgenommen und zur Veröffentlichung erneut gesendet.