Recursos do Assistente MQL5 que você precisa conhecer (Parte 47): Aprendizado por reforço (algoritmo de diferenças temporais)

Introdução

Vamos analisar em que o TD difere de outros algoritmos, como Monte Carlo, Q-learning e SARSA. O objetivo do artigo é esclarecer as dificuldades relacionadas ao treinamento com TD, destacando sua habilidade única de atualizar gradualmente as estimativas de valores com base em informações parciais dos episódios, sem precisar esperar a conclusão dos episódios, como acontece nos métodos de Monte Carlo. Essa diferença torna o treinamento TD uma ferramenta poderosa, especialmente em situações em que o ambiente é dinâmico e exige atualização imediata da política de aprendizado.

No artigo anterior sobre aprendizado supervisionado estudamos o algoritmo de Monte Carlo, que coletava informações de recompensas ao longo de vários ciclos antes de realizar uma única atualização para cada episódio. TD implica aprendizado a partir de episódios parciais e incompletos, de forma bastante semelhante aos algoritmos Q-learning e SARSA, que já analisamos aqui aqui e aqui.

Abaixo está uma tabela resumida com as principais diferenças entre TD, Q-learning e SARSA.

Resumindo, pode-se dizer que a fórmula para pares "estado-ação" com atualização dentro da política, como no caso do SARSA, é a seguinte:

	Aprendizado TD	Q-learning	SARSA
Tipos de valores	Valores de estado V(s)	Valores de ação Q(s,a)	Valores de ação Q(s,a)
Abordagem de aprendizado	Estimativas de valores futuros de estado	Fora da política	Dentro da política
Tipo de política	Não depende de uma política específica	Aprende a política ótima	Aprende a política de comportamento atual
Atualização do objetivo	Próximo valor de estado V(s′)	Máximo Q(s′,a′)	Valor real Q(s′,a′)
Pesquisa	Frequentemente requer uma política separada	Assume que o agente busca a política ótima	Mais conservadora
Comportamento	Move-se em direção ao valor do próximo estado	Greedy; prefere o caminho ótimo	Segue o caminho real de exploração

Em resumo, podemos dizer que as atualizações de política significam que os pares "estado-ação" atualizados são os atuais, e não necessariamente os ótimos ou com os maiores valores Q. Se quisermos atualizar os pares "estado-ação" com os maiores valores Q, isso já seria uma abordagem fora da política. Essas atualizações em MQL5 nós realizamos da seguinte forma:

//+------------------------------------------------------------------+
// Update using On-policy
//+------------------------------------------------------------------+
void Cql::SetOnPolicy(double Reward, vector &E)
{  Action(E);
//where 'act' index 1 represents the current Q_SA-action from Q_SA-Map
   double _sa = Q_SA[transition_act][e_row[1]][e_col[1]];
   double _v = Q_V[e_row[1]][e_col[1]];
   if(THIS.use_markov)
   {  int _old_index = GetMarkov(e_row[1], e_col[1]);
      int _new_index = GetMarkov(e_row[0], e_col[0]);
      _sa *= markov[_old_index][_new_index];
      _v *= markov[_old_index][_new_index];
   }
   for (int i = 0; i < THIS.actions; i++)
   {  Q_SA[i][e_row[1]][e_col[1]] += THIS.alpha * ((Reward + (THIS.gamma * _sa)) - Q_SA[i][e_row[1]][e_col[1]]);
   }
   Q_V[e_row[1]][e_col[1]] += THIS.alpha * ((Reward + (THIS.gamma * _v)) - Q_V[e_row[1]][e_col[1]]);
}

//+------------------------------------------------------------------+
// Update using Off-policy
//+------------------------------------------------------------------+
void Cql::SetOffPolicy(double Reward, vector &E)
{  Action(E);
//where 'act' index 0 represents highest valued Q_SA-action from Q_SA-Map
//as determined from Action() function above.
   double _sa = Q_SA[transition_act][e_row[0]][e_col[0]];
   double _v = Q_V[e_row[0]][e_col[0]];
   if(THIS.use_markov)
   {  int _old_index = GetMarkov(e_row[1], e_col[1]);
      int _new_index = GetMarkov(e_row[0], e_col[0]);
      _sa *= markov[_old_index][_new_index];
      _v *= markov[_old_index][_new_index];
   }
   for (int i = 0; i < THIS.actions; i++)
   {  Q_SA[i][e_row[0]][e_col[0]] += THIS.alpha * ((Reward + (THIS.gamma * _sa)) - Q_SA[i][e_row[0]][e_col[0]]);
   }
   Q_V[e_row[0]][e_col[0]] += THIS.alpha * ((Reward + (THIS.gamma * _v)) - Q_V[e_row[0]][e_col[0]]);
}

Em nossas funções modificadas e revisadas foram incluídas atualizações com a adição de um novo objeto Q_V, que apresentamos como uma matriz para facilitar a correspondência com os estados do ambiente. No entanto, poderíamos facilmente representá-lo como um vetor, já que as coordenadas do estado do ambiente podem ser associadas a um único índice inteiro. O antigo mapa Q foi renomeado para Q_SA. Essa nova denominação corresponde ao novo rastreamento dos objetos de valores do mapa Q de forma independente das ações, que é justamente o foco do TD, enquanto o renomear do antigo mapa Q para Q_SA enfatiza seus pares "estado-ação", que são atualizados a cada chamada da função. Nossas implementações em MQL5, apresentadas acima, são derivadas da seguinte fórmula para TD (que pode ser ativada ou desativada):

onde:

• V(s) - estado atual s
• V(s′) - próximo estado s′
• α - taxa de aprendizado (o quanto ajustamos o valor atual)
• r - recompensa pela execução da ação
• γ - fator de desconto (importância das recompensas futuras)
• A fórmula atualiza a estimativa do valor do estado V(s) com base na recompensa recebida e na estimativa do valor do próximo estado V(s′).

Resumindo, pode-se dizer que a fórmula para pares "estado-ação" com atualização dentro da política, como no caso do SARSA, é a seguinte:

onde:

• Q(s, a) - valor Q do par estado-ação atual (s, a)
• Q(s′, a′) - valor Q do próximo par estado-ação (s′, a′), onde a′ é a ação escolhida pela política atual no próximo estado s′
• α - taxa de aprendizado
• r - recompensa pela execução da ação a
• γ - fator de desconto

Da mesma forma, a fórmula para atualizações fora da política é a seguinte:

onde:

• Q(s, a) - valor Q do par estado-ação atual (s, a)
• max a′Q(s′, a′) - valor máximo de Q do próximo estado s′ entre todas as ações possíveis a′ (assume-se que será executada a melhor ação em s′)
• α - taxa de aprendizado
• r - recompensa pela execução da ação a
• γ - fator de desconto

A partir das duas últimas fórmulas fica claro que as atualizações relacionadas a ações específicas contribuem de maneira direta para a escolha da próxima ação. No entanto, no caso da atualização TD, como ela agrega valores de todas as ações e apenas os atribui ao estado correspondente do ambiente, a influência desse processo sobre a ação escolhida não é bem definida.

É por isso que, ao usar TD, é necessário contar com um modelo adicional, que no nosso caso é uma rede neural de política para controlar a escolha da próxima ação do ator. Esse modelo pode assumir diversas formas, mas para nossos propósitos trata-se simplesmente de um perceptron multicamadas (MLP) com estrutura 3-9-3, onde a camada de saída fornece a distribuição de probabilidades para cada uma das três ações possíveis, que em nosso caso continuam sendo compra, venda e manter. Assim, esse MLP será um classificador e não um regressor. A seguir, mostramos o código de declaração dessa classe na interface da classe de sinal do usuário, como indicado abaixo:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalTD   : public CExpertSignal
{
protected:

   int                           m_actions;           // LetMarkov possible actions
   int                           m_environments;      // Environments, per matrix axis
   int                           m_scale;             // Environments, row-to-col scale
   bool                          m_use_markov;        // Use Markov
   double                        m_epsilon;           // Epsilon
   bool                          m_policy;            // On Policy
   
public:
   void                          CSignalTD(void);
   void                          ~CSignalTD(void);

   //--- methods of setting adjustable parameters
   void                          QL_Scale(int value)
   {  m_scale = value;
   }
   void                          QL_Markov(bool value)
   {  m_use_markov = value;
   }
   void                          QL_Epsilon(bool value)
   {  m_epsilon = value;
   }
   void                          QL_Policy(bool value)
   {  m_policy = value;
   }

   //--- method of verification of arch
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);

protected:
   int               GetOutput(Cql *QL, CNeuralNetwork &PN);
   Sql               RL;
   Cql               *QL_BUY, *QL_SELL;
   CNeuralNetwork    POLICY_NETWORK_BUY,POLICY_NETWORK_SELL;
};

O código-fonte completo da nossa classe personalizada de sinais está anexado no final e é destinado à criação de um EA com a ajuda do Assistente MQL5. Guias para iniciantes podem ser encontrados aqui e aqui. Com o nosso código-fonte, o leitor pode facilmente modificar a estrutura do MLP, alterando não apenas o número de camadas, mas também o tamanho delas. No entanto, em nossa construção, a camada de entrada com número 3 é projetada para receber como dados de entrada as coordenadas do ambiente no eixo X, os valores de transição ou a leitura atual da matriz Q_V e as leituras do ambiente no eixo Y. O valor de transição é obtido da matriz Q_V, que atualizamos nos parâmetros da política de ativação e desativação, como já foi indicado no código-fonte acima. Essa escolha do valor de transição é tratada na função de ação revisada, conforme mostrado abaixo:

//+------------------------------------------------------------------+
// Choose an action using epsilon-greedy approach
//+------------------------------------------------------------------+
void Cql::Action(vector &E)
{  int _best_act = 0;
   if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon)
   {  // Explore: Choose random action
      _best_act = (rand() % THIS.actions);
   }
   else
   {  // Exploit: Choose best action
      double _best_value = Q_SA[0][e_row[0]][e_col[0]];
      for (int i = 1; i < THIS.actions; i++)
      {  if (Q_SA[i][e_row[0]][e_col[0]] > _best_value)
         {  _best_value = Q_SA[i][e_row[0]][e_col[0]];
            _best_act = i;
         }
      }
   }
//update last action
   act[1] = act[0];
   act[0] = _best_act;
//markov decision process
   e_row[1] = e_row[0];
   e_col[1] = e_col[0];
   LetMarkov(e_row[1], e_col[1], E);
   int _next_state = 0;
   for (int i = 0; i < int(markov.Cols()); i++)
   {  if(markov[int(E[0])][i] > markov[int(E[0])][_next_state])
      {  _next_state = i;
      }
   }
   int _next_row = 0, _next_col = 0;
   SetMarkov(_next_state, _next_row, _next_col);
   e_row[0] = _next_row;
   e_col[0] = _next_col;
   transition_value = Q_V[_next_row][_next_col];
   policy_history[1][0] = policy_history[0][0];
   policy_history[1][1] = policy_history[0][1];
   policy_history[1][2] = policy_history[0][2];
   policy_history[0][0] = _next_row;
   policy_history[0][1] = transition_value;
   policy_history[0][2] = _next_col;
   transition_act = 1;
   for (int i = 0; i < THIS.actions; i++)
   {  if(Q_SA[i][_next_row][_next_col] > Q_SA[transition_act][_next_row][_next_col])
      {  transition_act = i;
      }
   }
   //if(transition_act!=1)printf(__FUNCSIG__+ " act is : %i ",transition_act);
}

Assim, a tese fundamental da nossa rede de política, o MLP mencionado acima, é que a ação apropriada que deve ser escolhida em seguida é uma função apenas do estado atual do ambiente e de seu valor Q. Isso difere do que utilizamos até agora, quando o processo de decisão de Markov (Markov Decision Process, MDP) era usado para selecionar a ação adequada a partir do mapa Q, que renomeamos neste artigo (código anexado) como Q_SA. Em todos os casos, utilizamos o MDP sem memória, calculando o buffer das últimas sequências de estados do ambiente. Essas sequências do ambiente, graças à função de Markov, que será abordada a seguir, nos fornecem a projeção do próximo estado do ambiente.

//+------------------------------------------------------------------+
// Function to update markov matrix
//+------------------------------------------------------------------+
void Cql::LetMarkov(int OldRow, int OldCol, vector &E)  //
{  matrix _transitions;  // Count the transitions
   _transitions.Init(markov.Rows(), markov.Cols());
   _transitions.Fill(0.0);
   vector _states;  // Count the occurrences of each state
   _states.Init(markov.Rows());
   _states.Fill(0.0);
// Count transitions from state i to state ii
   for (int i = 0; i < int(E.Size()) - 1; i++)
   {  int _old_state = int(E[i]);
      int _new_state = int(E[i + 1]);
      _transitions[_old_state][_new_state]++;
      _states[_old_state]++;
   }
// Reset prior values to zero.
   markov.Fill(0.0);
// Compute probabilities by normalizing transition counts
   for (int i = 0; i < int(markov.Rows()); i++)
   {  for (int ii = 0; ii < int(markov.Cols()); ii++)
      {  if (_states[i] > 0)
         {  markov[i][ii] = double(_transitions[i][ii] / _states[i]);
         }
         else
         {  markov[i][ii] = 0.0;  // No transitions from this state
         }
      }
   }
}

Esse processo de determinação dos próximos estados por meio do MDP ainda é realizado com o TD, mas a diferença aqui é que não podemos utilizar essas coordenadas projetadas do próximo estado isoladamente para definir a próxima ação. Antes, quando usávamos o Q_SA, tratava-se de ler a ação com a maior probabilidade, ponderando as coordenadas do próximo estado para descobrir o que o agente deveria fazer. No entanto, agora nossa matriz equivalente Q_V nos fornece apenas valores para quaisquer coordenadas de estado fornecidas, e ainda assim a determinação da próxima ação do ator continua sendo um elemento crucial no ciclo de aprendizado por reforço.

É por isso que introduzimos a rede de política, o MLP, que para os nossos objetivos projetamos simplesmente como 3-9-3, contendo uma camada oculta com 9 neurônios, recebendo como entrada os 3 parâmetros mencionados acima — duas coordenadas do ambiente e seu valor Q — e gerando um vetor de saída de 3 elementos, destinado a capturar a distribuição de probabilidades entre as 3 possíveis ações: comprar, vender e manter. O valor que obtiver a maior pontuação nesse vetor será a ação recomendada.

Vantagens e objetivo do TD

O TD atualiza seus valores Q com mais frequência do que o Monte Carlo, o que traz vantagens evidentes em mercados financeiros voláteis e em rápida mudança. Mas o que o diferencia, por exemplo, do SARSA ou do Q-learning em termos de benefícios? Tentaremos responder a essa questão com alguns exemplos práticos.

Por definição, a principal diferença entre TD e SARSA/Q-learning está no fato de que o TD se concentra mais no aprendizado baseado em valores, onde apenas os valores dos estados são estudados e atualizados, enquanto os outros dois algoritmos focam no pareamento estado-ação para realizar atualizações semelhantes.

Cenário A

Suponha que em um armazém exista um sistema de gestão de estoques, responsável por monitorar os níveis de estoque de diversos produtos. O objetivo desse sistema seria exclusivamente controlar os níveis de estoque e evitar tanto a escassez quanto o excesso de mercadorias.

Nessa situação, o TD teria uma vantagem sobre o SARSA ou o Q-learning simplesmente por seu foco em pares estado-valor, e não estado-ação. Aqui, o sistema precisaria apenas prever o "valor" de cada estado (por exemplo, os níveis gerais de estoque), sem avaliar cada ação específica (como o pedido para cada SKU). Assim, nesse caso, sem necessidade de uma rede de política MLP, o aprendizado TD poderia atualizar a função de valor para o estado (níveis de estoque) sem calcular cada possível decisão de pedido para cada produto.

Além disso, a gestão de estoques pode ser caracterizada por mudanças graduais, em vez de pares "estado-ação" bruscos que oferecem uma resposta imediata sob a forma de recompensa. Como o aprendizado TD lida com o recebimento gradual de feedback, isso o torna adequado para ambientes com transições suaves, onde compreender o estado geral é mais importante do que conhecer cada resultado específico de estado-ação. Por fim, em ambientes com múltiplas ações e grandes espaços de estados e ações, como a gestão de estoques, que é mais complexa (onde seria necessário associar um curso de ação a cada estado de nível de estoque), o Q-learning e o SARSA, embora aplicáveis, inevitavelmente exigiriam custos computacionais que o TD nunca enfrenta, devido à sua aplicação mais simples e global.

Cenário B

Consideremos um sistema inteligente de edifício que regula os parâmetros de aquecimento, ventilação e ar-condicionado (HVAC) de forma a minimizar o consumo de energia e, ao mesmo tempo, garantir conforto aos ocupantes. Assim, seus objetivos de equilibrar ganhos de curto prazo com metas de longo prazo coincidem tanto com a redução das contas de eletricidade quanto com a manutenção de uma temperatura e qualidade do ar ideais no edifício.

Nesse caso, o TD se adequa melhor do que o SARSA ou o Q-learning, pois os níveis de consumo de energia ou o conforto dos usuários são indicadores absolutos que não estão diretamente vinculados a ações específicas em função de seus valores. Nesse cenário em particular, para equilibrar recompensas de curto e longo prazo, é possível treinar dois ciclos de aprendizado por reforço para prever ambos os resultados em paralelo. As atualizações graduais do TD a cada ciclo (e não por episódio, como vimos no caso do Monte Carlo) também o tornam ideal para esse sistema inteligente de edifício, já que as condições ambientais, como temperatura, ocupação e qualidade do ar, se alteram de forma gradual. Isso permite que o TD forneça um mecanismo de ajuste contínuo.

Por fim, como mencionado anteriormente, o equivalente em SARSA ou Q-learning apresentaria requisitos adicionais de processamento e memória, já que seriam necessárias ações específicas para "corrigir" eventuais deficiências ou excessos nos valores dos estados do ambiente.  

 

Cenário C

Um sistema de previsão e controle de fluxo de tráfego, cujo objetivo é minimizar congestionamentos em vários cruzamentos por meio da previsão do tráfego e da consequente adaptação dos sinais de semáforo. O TD também é vantajoso nessa situação em comparação ao SARSA ou ao Q-learning, pois a principal tarefa está no entendimento e na previsão do estado geral do tráfego (como os níveis de congestionamento), e não na otimização de cada ação individual do semáforo. O aprendizado TD permite que o sistema aprenda o "valor" global do estado do tráfego, em vez do impacto de cada alteração específica no sinal.

Além disso, como o tráfego é, por natureza, dinâmico e muda constantemente ao longo do dia, ele também contribui para as atualizações passo a passo do TD. Trata-se de um algoritmo muito mais flexível em comparação ao Monte Carlo, que precisa esperar o fim do episódio antes de executar atualizações. Nesse caso, também é relevante destacar a redução da carga computacional e do consumo de memória com o TD, especialmente se considerarmos o quão entrelaçados e interconectados podem ser os cruzamentos viários mesmo em uma cidade relativamente pequena. Os custos de processamento e memória certamente se tornarão um fator crítico na implementação de um sistema de previsão de tráfego, e o TD trará uma contribuição significativa para a solução desse problema.

Cenário D

A manutenção preditiva na indústria representa nosso último caso de uso do TD como algoritmo preferencial em relação a outros algoritmos de aprendizado por reforço que discutimos até aqui. Vejamos o exemplo de uma fábrica que busca prever quando suas máquinas precisarão de manutenção para evitar paradas inesperadas. Assim como no caso do sistema "edifício inteligente", essa solução precisa equilibrar ganhos de curto prazo (economia de custos ao adiar inspeções) com benefícios de longo prazo (prevenção de falhas). O aprendizado TD seria adequado aqui, pois pode atualizar continuamente o valor geral da condição operacional da máquina ao longo do tempo, com base em feedback parcial, em vez de rastrear ações específicas (reparo ou substituição), como fazem o SARSA ou o Q-learning.

O algoritmo TD também se mostra mais vantajoso porque a deterioração do estado da máquina acontece de forma gradual, e o TD pode atualizar facilmente o valor de condição operacional de forma contínua a partir de dados adicionais de sensores, sem precisar esperar longos períodos, o que poderia trazer riscos adicionais. Além disso, em uma fábrica com várias máquinas, o aprendizado TD consegue escalar bem conforme o número de máquinas aumenta ou diminui, já que ele se concentra apenas no rastreamento do estado/condição de cada máquina e não exige o armazenamento e a atualização de pares específicos "estado-ação" para cada uma delas.

Esses são apenas alguns exemplos fora do contexto do trading financeiro e dos mercados, portanto, vamos agora examinar como podemos aplicar especificamente o algoritmo como uma classe de sinais personalizados.

Estruturação da classe personalizada de sinais usando o algoritmo TD

A classe personalizada de sinais que criamos para implementar o TD se baseia em duas classes adicionais. Como se trata de um algoritmo de aprendizado por reforço, uma dessas classes é a classe CQL. Já utilizamos ou mencionamos essa classe em todos os artigos anteriores. Sua interface é novamente apresentada abaixo:

//+------------------------------------------------------------------+
//| Q_SA-Learning Class Interface.                                      |
//+------------------------------------------------------------------+
class Cql
{
protected:
   matrix            markov;
   void              LetMarkov(int OldRow, int OldCol, vector &E);

   vector            acts;
   matrix            environment;
   matrix            Q_SA[];
   matrix            Q_V;

public:
   void              Action(vector &E);
   void              Environment(vector &E_Row, vector &E_Col, vector &E);

   void              SetOffPolicy(double Reward, vector &E);
   void              SetOnPolicy(double Reward, vector &E);

   double            GetReward(double MaxProfit, double MaxLoss, double Float);
   vector            SetTarget(vector &Rewards, vector &TargetOutput);

   void              SetMarkov(int Index, int &Row, int &Col);
   int               GetMarkov(int Row, int Col);


   Sql               THIS;

   int               act[2];

   int               e_row[2];
   int               e_col[2];

   int               transition_act;
   double            transition_value;
   
   matrix            policy_history;

   vector            Q_Loss()
   {  vector _loss;
      _loss.Init(THIS.actions);
      _loss.Fill(0.0);
      for(int i = 0; i < THIS.actions; i++)
      {  _loss[i] = Q_SA[e_row[0]][e_col[0]][i];
      }
      return(_loss);
   }


   void              Cql(Sql &RL)
   {  //
      if(RL.actions > 0 && RL.environments > 0)
      {  policy_history.Init(2,2+1);
         policy_history.Fill(0.0);
         acts.Init(RL.actions);
         ArrayResize(Q_SA, RL.actions);
         for(int i = 0; i < RL.actions; i++)
         {  acts[i] = i + 1;
            Q_SA[i].Init(RL.environments, RL.environments);
         }
         Q_V.Init(RL.environments, RL.environments);
         environment.Init(RL.environments, RL.environments);
         for(int i = 0; i < RL.environments; i++)
         {  for(int ii = 0; ii < RL.environments; ii++)
            {  environment[i][ii] = ii + (i * RL.environments) + 1;
            }
         }
         markov.Init(RL.environments * RL.environments, RL.environments * RL.environments);
         markov.Fill(0.0);
         THIS = RL;
         ArrayFill(e_row, 0, 2, 0);
         ArrayFill(e_col, 0, 2, 0);
         ArrayFill(act, 0, 2, 1);
         transition_act = 1;
      }
   };
   void              ~Cql(void) {};
};

Esse é o principal classe de aprendizado por reforço, e alguns de seus métodos, que definem atualizações dentro e fora da política, já foram apresentados acima. Além disso, essa classe costuma ser suficiente para implementar aprendizado por reforço em uma classe personalizada de sinais, mas no caso do TD, como não usamos nem dependemos exclusivamente dos valores do ambiente para tomar decisões de trading e decidimos continuar prevendo ações adequadas, como fazíamos antes, precisamos de um modelo para gerar tais previsões.

É por isso que, para definir esse modelo como uma rede neural ou MLP, utilizamos uma classe adicional — a CNeuralNetwork. Da mesma forma, sua interface de classe está apresentada abaixo:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CNeuralNetwork
{
protected:
   
   matrix               TransposeToCol(vector &V);
   matrix               TransposeToRow(vector &V);
   
public:
   CLayer               *layers[];
   double               m_learning_rate;
   ENUM_LOSS_FUNCTION   m_loss;
   void                 AddDenseLayer(ulong Neurons, ENUM_ACTIVATION_FUNCTION AF = AF_RELU, ulong LastNeurons = 0)
   {  ArrayResize(layers, layers.Size() + 1);
      layers[layers.Size() - 1] = new CLayer(Neurons, AF);
      if(LastNeurons  != 0)
      {  layers[layers.Size() - 1].AddWeights(LastNeurons);
      }
      else if(layers.Size() - 1 > 0)
      {  layers[layers.Size() - 1].AddWeights(layers[layers.Size() - 2].activations.Size());
      }
   };
   void                 Init(double LearningRate, ENUM_LOSS_FUNCTION LF)
   {  m_loss = LF;
      m_learning_rate = LearningRate;
   };
   
   vector               Forward(vector& Data);
   void                 Backward(vector& LabelAnswer);
   
   void                 CNeuralNetwork(){};
   void                 ~CNeuralNetwork()
   {  if(layers.Size() > 0)
      {  for(int i = 0; i < int(layers.Size()); i++)
         {  delete layers[i];
         }
      }
   };
};

Fizemos algumas alterações notáveis em relação à última classe CMLP, que desempenhava função semelhante. O foco principal foi a eficiência, embora essa ainda seja uma versão beta, apesar de já ter conseguido entregar alguns resultados para os nossos objetivos. Além das melhorias de eficiência, que afetaram principalmente a função de propagação reversa (Backward) e ainda estão em desenvolvimento, introduzimos uma classe de camadas, além de termos modificado a forma de construção da rede. A inicialização da classe personalizada de sinais agora tem o seguinte formato: 

//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
void CSignalTD::CSignalTD(void) :    m_scale(5),
   m_use_markov(true),
   m_policy(true)

{
//--- initialization of protected data
   m_used_series = USE_SERIES_OPEN + USE_SERIES_HIGH + USE_SERIES_LOW + USE_SERIES_CLOSE + USE_SERIES_SPREAD + USE_SERIES_TIME;
   //
   RL.actions  = 3;//buy, sell, do nothing
   RL.environments = 3;//bullish, bearish, flat
   RL.use_markov = m_use_markov;
   RL.epsilon = m_epsilon;
   QL_BUY = new Cql(RL);
   QL_SELL = new Cql(RL);
   //
   POLICY_NETWORK_BUY.AddDenseLayer(9, AF_SIGMOID, 3);
   POLICY_NETWORK_BUY.AddDenseLayer(3, AF_SOFTMAX);
   POLICY_NETWORK_BUY.Init(0.0004,LOSS_BCE);
   //
   POLICY_NETWORK_SELL.AddDenseLayer(9, AF_SIGMOID, 3);
   POLICY_NETWORK_SELL.AddDenseLayer(3, AF_SOFTMAX);
   POLICY_NETWORK_SELL.Init(0.0004,LOSS_BCE);
}

Além das duas classes CQL para processar o aprendizado por reforço nos lados de compra e venda, agora temos também duas redes de política, que podem prever ações nos lados de compra e venda, respectivamente. A função get output continua funcionando como nas versões anteriores, sendo que a principal mudança é que a instância da classe de rede neural agora é usada como uma de suas entradas, atuando como rede de política. O novo trecho de código é o seguinte:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int CSignalTD::GetOutput(Cql *QL, CNeuralNetwork &PN)
{  int _td_act = 1;
   vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale+1) &&
      _in_row.Size() == m_scale+1
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale+1) &&
      _in_row_old.Size() == m_scale+1
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale+1) &&
      _in_col.Size() == m_scale+1
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale+1) &&
      _in_col_old.Size() == m_scale+1
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      _in_row.Resize(m_scale);
      _in_col.Resize(m_scale);
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = _in_row[m_scale - 1];
      double _reward_max = _in_row.Max();
      double _reward_min = _in_row.Min();
      double _reward = QL.GetReward(_reward_max, _reward_min, _reward_float);
      if(m_policy)
      {  QL.SetOnPolicy(_reward, _in_e);
      }
      else if(!m_policy)
      {  QL.SetOffPolicy(_reward, _in_e);
      }
      PN.Forward(QL.policy_history.Row(1));
      vector _label;
      _label.Init(3);
      _label.Fill(0.0);
      if(_in_row[m_scale-1] > 0.0)
      {  _label[0] = 1.0;
      }
      else if(_in_row[m_scale-1] < 0.0)
      {  _label[2] = 1.0;
      }
      else if(_in_row[m_scale-1] == 0.0)
      {  _label[1] = 1.0;
      }
      PN.Backward(_label);
      vector _td_output = PN.Forward(QL.policy_history.Row(0));
      if(_td_output[0] >= _td_output[1] && _td_output[0] >= _td_output[2])
      {  _td_act = 0;
      }
      else if(_td_output[2] >= _td_output[0] && _td_output[2] >= _td_output[1])
      {  _td_act = 2;
      }
   }
   return(_td_act);
}

Usando a rede de política como uma das entradas, agora é possível realizar aprendizado online ou aprendizado passo a passo, já que antes da previsão não treinamos sobre um lote de dados, mas apenas sobre os dados mais recentes de uma coluna. Deve haver apenas uma execução da propagação reversa e uma execução da propagação para frente, mas como precisamos carregar a informação do preço atual da barra em nossa rede neural antes de realizar a propagação reversa, fazemos uma execução da propagação para frente com os dados da barra anterior, de modo a carregar essa informação. Nossa função Forward também foi modificada para retornar o vetor de saída de classificação da propagação para frente. Esse vetor tem tamanho três, onde cada valor em seu respectivo índice fornece a "probabilidade" ou o limiar de probabilidade de venda, manutenção ou compra, se seguirmos a ordem de indexação 0, 1, 2, respectivamente.

Então, resumindo o que foi dito acima, mantemos o mesmo ambiente simples de aprendizado por reforço e a configuração de ações com 3 estados e 3 ações. A escolha da atualização de política pode ser otimizada, como na última parte sobre aprendizado por reforço, em que analisamos o método Monte Carlo. No entanto, aqui, ao realizar as atualizações, apenas os valores Q da nova matriz Q_V introduzida são atualizados. Isso contrasta com o que fazíamos anteriormente, quando atualizávamos os valores Q em todo o mapa do ambiente para cada ação. A atualização dos valores de cada ação era útil para a escolha da próxima ação, pois, após a aplicação do processo de decisão de Markov para determinar as coordenadas do próximo estado do ambiente, bastava ler a ação com o maior valor Q e escolhê-la como a próxima ação.

Com o uso do TD, nossa matriz de ambiente Q_V não possui ações associadas a valores Q, mas apenas valores atribuídos a um estado específico do ambiente. Isso significa que, para selecionar ou definir o próximo curso de ação, utilizamos a rede de política (no nosso caso, o MLP) para gerar essas previsões, sendo suas entradas o valor do estado atual do ambiente (que, na prática, é a soma de todos os valores Q das ações aplicáveis nesse estado) e as coordenadas do estado do ambiente. Como já foi mencionado, o resultado é uma "distribuição de probabilidades" entre as três possíveis ações, indicando qual delas será a mais adequada, considerando a situação atual e seu valor.

Assim, essa classe personalizada de sinais é montada com a ajuda do Assistente MQL5 em um EA, e após uma breve otimização para o ano de 2022 no timeframe de 1 hora e no símbolo GBPUSD, uma das configurações favoráveis desse período nos fornece o seguinte relatório:

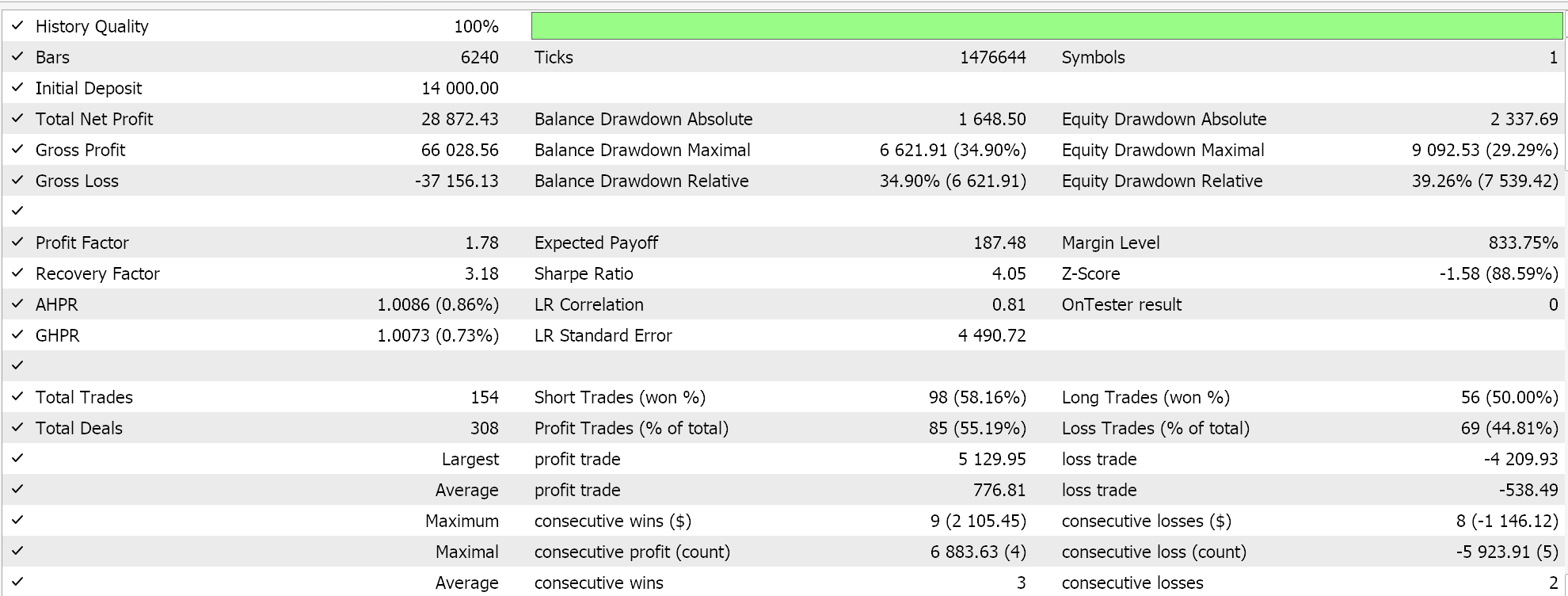
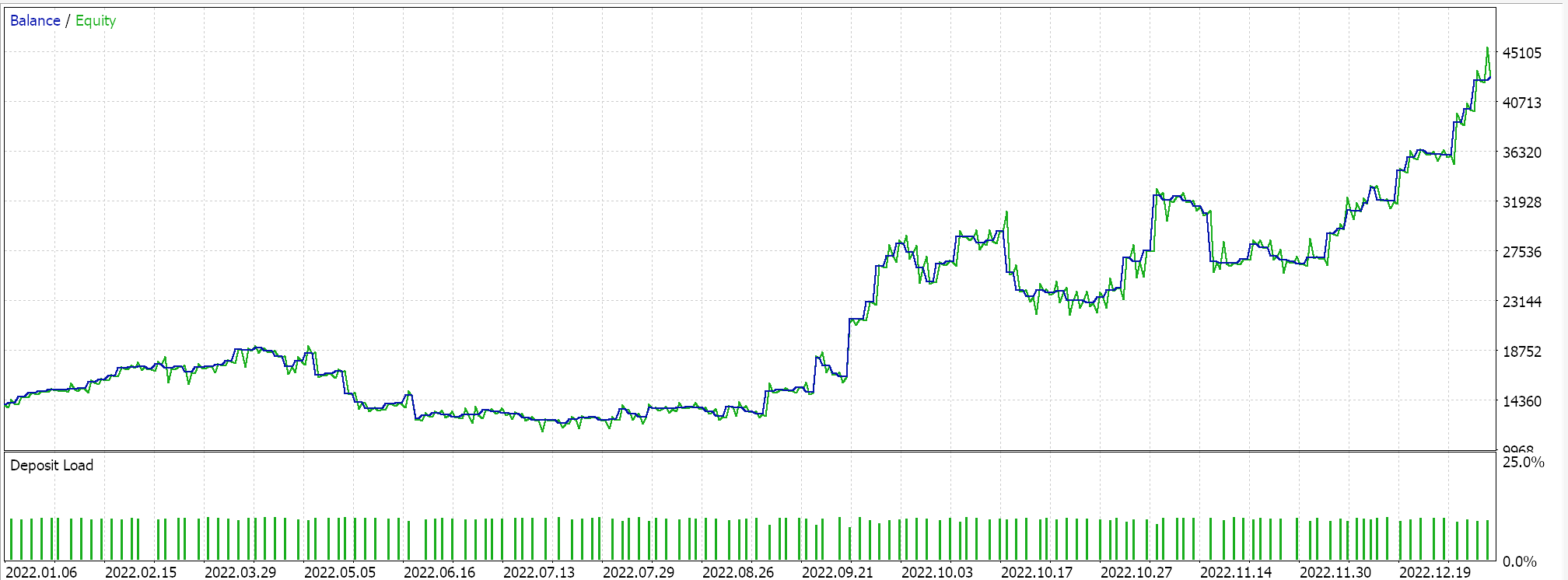
Esses resultados talvez indiquem o potencial da nossa classe personalizada de sinais, mas, sem diminuir sua relevância, é importante observar que sempre é recomendável realizar validação cruzada das configurações de qualquer EA antes de decidir se ele deve ou não ser implantado em um ambiente real. A validação cruzada e os testes adicionais por um período mais longo do que o que fizemos aqui ficam a critério do leitor.

Otimização e configuração da classe de sinais com aprendizado TD

Em nossos testes descritos acima, otimizamos exclusivamente o valor de epsilon, a necessidade de utilizar coeficientes de ponderação de Markov no processo de atualização e a necessidade de realizar atualizações dentro ou fora da política. Naturalmente, também havia outros parâmetros típicos não relacionados ao TD, como os limites de abertura e fechamento para posições longas e curtas, o nível de take-profit, bem como o limite de preço de entrada em pontos.

No entanto, no TD e no aprendizado por reforço, existem diversos parâmetros que deixamos de lado e utilizamos com valores pré-definidos. Esses incluem alpha e gamma, definidos em 0,1 e 0,5 respectivamente. Esses dois parâmetros são fundamentais para as atualizações de política e podem ter grande impacto no desempenho geral da classe de sinais. Outros parâmetros importantes que também negligenciamos ao implementar nossa classe de sinais, fixando-os em valores constantes, são as configurações das redes de política. Optamos por uma rede 3-9-3, na qual todas as funções de ativação em cada camada foram definidas antecipadamente, assim como a taxa de aprendizado. Cada um desses fatores, e possivelmente todos em conjunto, podem influenciar significativamente os resultados e a performance da classe personalizada de sinais.

Considerações finais

Exploramos o algoritmo de diferenças temporais no aprendizado por reforço e buscamos destacar os cenários em que seu uso se diferencia de outros algoritmos analisados. Um aspecto que não abordamos, mas que é relevante para o aprendizado por reforço em geral, é o decaimento da pesquisa ao longo do tempo. A possível razão para isso é que, à medida que o modelo de aprendizado por reforço evolui, a necessidade de explorar novas alternativas ou continuar aprendendo se reduz significativamente; torna-se mais importante a intensificação. Esse é um ponto que os leitores podem considerar ao decidirem ajustar o código anexado para usos futuros.

Outro aspecto a ser considerado é transformar epsilon em uma variável dinâmica, e não apenas reduzi-lo, como o decaimento descrito acima sugere. A essência dessa abordagem está no fato de que o aprendizado por reforço precisa ser altamente dinâmico e adaptativo, em contraste com os modelos de aprendizado supervisionado, que dependem de dados estáticos. Dessa forma, a estrutura de aprendizado por reforço com TD pode interagir de forma ativa com um ambiente em constante mudança. Já analisamos métodos de taxa de aprendizado dinâmica na artigo anterior, e pode-se argumentar que o mesmo pode ser feito com o epsilon, de modo que o decaimento não seja a única forma de preservar o aprendizado por reforço em sua essência.