Técnicas do MQL5 Wizard que você deve conhecer (Parte 41): Deep-Q-Networks

Introdução

Deep-Q-Networks (DQN) são outro algoritmo de aprendizado por reforço, além do Q-Learning que analisamos neste artigo, mas eles, ao contrário do Q-Learning, utilizam redes neurais para prever o valor-Q (q-value) e a próxima ação a ser tomada pelo agente. Ele é semelhante/relacionado ao Q-Learning no sentido de que ainda envolve uma Q-Table, onde o conhecimento cumulativo sobre ações e estados de “episódios” anteriores é armazenado. De fato, compartilha a mesma página da Wikipédia que o Q-Learning, como pode ser visto nos links, onde é definido essencialmente como uma variante do Q-Learning.

A classe de sinal, juntamente com a classe de trailing stop e a classe de gerenciamento de dinheiro (money management), são os três módulos principais que precisam ser definidos ao construir um Expert Advisor montado pelo Wizard. Reunir tudo isso via o assistente do MQL5 pode ser feito seguindo os guias que estão aqui e aqui, para novos leitores. O código-fonte anexado ao final deste artigo deve ser usado seguindo os guias de montagem do assistente compartilhados nesses links. Estamos, mais uma vez, definindo uma classe de sinal personalizada para uso em um Expert Advisor montado pelo assistente.

Esta não é, porém, a única forma de examinarmos DQN, já que também podem ser feitas e testadas implementações para uma classe de trailing personalizada ou uma classe de gerenciamento de capital personalizada. Estamos focando na classe de sinal porque determinar as condições de compra (long) e venda (short) nesses Expert Advisors é crítico e, em muitos casos, demonstra melhor o potencial de um setup de trade. Este artigo se baseia em artigos anteriores desta série, nos quais abordamos técnicas ou diferentes arranjos que podem ser usados no desenvolvimento de Expert Advisors personalizados montados pelo assistente; portanto, para novos leitores, uma revisão dos artigos anteriores é uma boa ideia, especialmente se buscam diversificar sua abordagem. Esses artigos cobrem não apenas uma variedade de sinais personalizados, mas também implementações personalizadas da classe de trailing e da classe de gerenciamento de capital.

A configuração de DQN, como vimos no artigo sobre Q-Learning, é implementada como um suporte à função de perda, porque estamos encarando estritamente o aprendizado por reforço como uma 3^rd forma de treinamento além de supervisionado e não supervisionado. Isso, como mencionado no artigo de Q-Learning, não significa que ele não possa ser implementado como um modelo independente para uso no treinamento, sem um MLP subordinado. Essa forma alternativa de usar aprendizado por reforço será explorada em artigos futuros, nos quais não haverá um MLP subordinado e as previsões de ações do agente, em vez disso, informarão as condições de compra e venda.

Recapitulação sobre Aprendizado por Reforço

Antes de começarmos, pode ser uma boa ideia fazer um rápido resumo do que é aprendizado por reforço. Trata-se de uma forma alternativa de treinamento em aprendizado de máquina que, em sua essência, foca nas interações agente-ambiente. O agente é a entidade que toma decisões, cujo objetivo é aprender as melhores ações para maximizar as recompensas cumulativas. O ambiente é tudo “fora” do agente que atua como hospedeiro de um crítico/observador e fornece feedback ao agente na forma de novos estados e recompensas (recompensas por projeções corretas do agente). O ciclo, portanto, começa com o agente observando o estado atual do ambiente, fazendo previsões de mudanças nesse estado e, então, selecionando uma ação apropriada para esse estado.

Os estados são representações da situação/condição do ambiente. Uma vez que o agente seleciona ou executa uma ação, ocorre uma transição nos estados do ambiente, previamente/ao mesmo tempo, de modo que suas ações são avaliadas quanto à adequação a esse novo ambiente. Essa avaliação é quantificada como as “recompensas”. Uma matriz de Cadeia de Markov (sem memória) foi usada para ponderar o processo de decisão do agente ao prever o próximo estado, mas as transições reais são determinadas pelo ambiente, que, no caso daquele artigo, foi modelado por uma tabela cruzada entre a direção do mercado e o horizonte de timeframe. As ações tomadas pelo agente, embora possam ser contínuas (ou de faixa infinita de possibilidades), muitas vezes são discretas, ou seja, assumem um conjunto predefinido de opções que, no nosso caso, eram vender, comprar ou não fazer nada. Essa lista, entretanto, no nosso caso, poderia ter sido expandida para seguir, por exemplo, o formato de ordens do mercado, de modo que não apenas ordens a mercado fossem consideradas, mas também ordens pendentes entrassem em jogo.

Da mesma forma, nossa métrica de recompensas, que era reavaliada a cada nova barra — já que a perda ou o lucro da ação ou ordem anterior podia ser “atualizado” — poderia quantificar excursões favoráveis versus desfavoráveis como uma razão ou qualquer outra métrica híbrida. Essa métrica de recompensa, juntamente com o estado atual e a ação previamente selecionada, é usada para atualizar a Q-table; a fonte para isso foi compartilhada na função “Critic Source” da classe CQL. Como já mencionado acima, estamos encarando estritamente o aprendizado por reforço como uma alternativa ao aprendizado supervisionado e não supervisionado, de modo que ele sirva estritamente para quantificar nossa função de perda. No entanto, há casos em que o aprendizado por reforço é aplicado fora desse cenário “definitivo” e é usado como um modelo independente para fazer previsões, em que as ações do agente são aplicadas fora do treinamento — esses cenários não são considerados aqui, mas podem ser analisados em artigos futuros 

Introdução ao algoritmo Deep Q-Network

O DQN se fundamenta no Q-Learning — o primeiro algoritmo de aprendizado por reforço que analisamos — e seu objetivo principal, que continua sendo o do DQN, é prever valores-Q. Esses, como recapitulamos acima, são pontos de dados que classificam vários estados do ambiente e são registrados em uma Q-table. A diferença em relação ao algoritmo Q-Learning está no uso de redes neurais para prever o próximo valor-Q, em vez de depender de um Q-Map ou tabela, como usado pelo Q-Learning, conforme demonstrado em nosso primeiro artigo de aprendizado por reforço. Além disso, há o experience replay (repetição de experiências) e uma rede-alvo (target network), conforme descrito nas seções abaixo. A política epsilon-greedy que anteriormente era aplicada sobre o Q-Map deixa de ser aplicável com DQNs, já que entram em cena redes neurais.

O DQN, portanto, mapeia as recompensas futuras para cada ação possível em todos os estados aplicáveis com o auxílio de uma rede neural. Esse mapeamento de estados — que os traders podem encarar como várias ponderações para cada ação possível (comprar-vender-manter) em diversas condições de mercado (altista-baixista-lateral) — de fato fornece ponderações, e essas ponderações determinam a posição de trade. Os DQNs são hábeis em lidar com ambientes de alta complexidade e alta dimensionalidade, que fazem parte das principais características dos mercados financeiros. Os mercados financeiros são dinâmicos e não lineares, com fatores altamente variáveis e independentes, como mudanças de preço, indicadores macroeconômicos e sentimento de mercado.

O Q-Learning tradicional tende a ter dificuldades com isso, pois utiliza Q-Tables discretas com um número finito e gerenciável de estados, o que contrasta com o DQN, que é muito mais apto dado o uso de redes neurais. Os DQNs também são bons em capturar dependências não lineares nos mercados, entre várias classes de ativos, que também servem como sinais de entrada em certas estratégias de trade — por exemplo, o yen carry trade. Além disso, o uso de DQNs permite melhor generalização, na qual a rede pode se adaptar melhor a novos dados e condições de mercado, porque redes neurais tendem a ser mais flexíveis do que as q-tables. Isso é crucial nos mercados financeiros, onde as condições podem mudar rapidamente, e o agente deve se adaptar a situações desconhecidas. Os DQNs também são mais resilientes ao ruído de mercado do que o Q-Learning tradicional. Nos mercados financeiros, as ações do agente muitas vezes têm recompensas atrasadas (por exemplo, manter uma posição que só pode gerar lucro após vários dias ou semanas). O uso, pelo DQN, da equação de Bellman com um fator de desconto (gamma) permite avaliar as recompensas imediatas e de longo prazo, de modo que a rede aprende a equilibrar entre lucros rápidos e ganhos de longo prazo — algo essencial na tomada de decisão estratégica para portfólios financeiros.

Previsão de valores-Q com DQN

Estamos usando o DQN para normalizar a função de perda de um MLP, já que, neste artigo, como já mencionado, estamos encarando estritamente o DQN como uma abordagem alternativa de treinamento e não como um modelo independente que possa fazer suas próprias previsões como um MLP típico. Esse uso de DQN no cenário “rudimentar” de aprendizado por reforço significa que estamos praticamente aderindo à abordagem que usamos neste artigo anterior. Isso implica, portanto, que temos uma instância de um MLP que atua como o agente, ao qual nos referimos como “DQN_ONLINE” na interface da nossa classe de sinal, que é resumida abaixo:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalDQN   : public CExpertSignal
{
protected:

   int                           m_actions;           // LetMarkov possible actions
   int                           m_environments;      // Environments, per matrix axis


   int                           m_train_set;                       //
   int                           m_epochs;                              // Epochs
   double                        m_learning_rate;                       // Alpha

   Elearning                     m_learning_type;

   double                        m_train_deposit;
   double                        m_train_criteria;

   double                        m_initial_weight;
   double                        m_initial_bias;
   
   int                           m_state_lag;
   int                           m_target_counts;
   int                           m_target_counter;

   Smlp                          m_mlp;
   Smlp                          m_dqn;
   Slearning                     m_learning;

public:
   void                          CSignalDQN(void);
   void                          ~CSignalDQN(void);

   //--- methods of setting adjustable parameters



...



...


protected:
   void                          GetOutput(int &Output);

   Cmlp                          *MLP,*DQN_ONLINE,*DQN_TARGET;
};

Essa rede recebe como entrada o estado atual e produz um vetor de valores-Q para cada uma das ações possíveis. Sua arquitetura, que pode ser ajustada ou refinada pelo leitor, segue uma topologia 2-6-3, em que 2 é o tamanho da camada de entrada. Seu tamanho é 2 porque, como compartilhado em nosso artigo anterior, os estados, embora passíveis de serem “achatados” em um único índice, são, estritamente falando, um par de índices ou coordenadas. Uma coordenada mede o tipo de tendência no curto prazo, enquanto a outra observa a tendência no longo prazo.

A camada oculta é simplesmente definida com tamanho 6; porém, como dito, esse tamanho e a adição de camadas ocultas adicionais podem ser personalizados em relação ao que usamos aqui. Escolhemos 6 a partir de “tamanho de entrada × tamanho de saída”. Assim, nosso tamanho de saída é 3, como no artigo de Q-Learning, onde isso representa o número de ações possíveis que um agente pode tomar. Recapitulando: essas ações são comprar, vender ou manter. O fato de a saída ser um vetor de probabilidades para a tomada de cada uma dessas ações implica que o DQN é uma rede classificadora. Essa saída do DQN (de aprendizado por reforço) serve como valor-alvo para a rede MLP “mãe”. Uma vez que temos essa saída, então podemos treinar o MLP. Não se deve ignorar, porém, o treinamento do próprio DQN — e isso não acontece da mesma forma que outras redes. Em vez de recorrer a outro conjunto onipresente de dados de estados e valores-Q, usamos outra rede neural, que denominamos “DQN_TARGET”, para fornecer vetores-alvo para treinar a rede “DQN_ONLINE”. Vejamos isso a seguir.

O papel de uma rede-alvo (target network)

A rede-alvo, assim como a rede online (o DQN acima que fornece o alvo ao MLP), também recebe como entrada um estado do ambiente e produz um vetor de valores-Q para cada ação possível. A principal diferença em relação à rede online é que as entradas de estado do ambiente dizem respeito ao estado que sucede o estado atual. Além disso, sendo outra rede neural, poder-se-ia esperar que ela fosse treinada por retropropagação (backpropagation), mas, em vez disso, em um intervalo predefinido, ela apenas copia a rede online. A rede-alvo fornece valores-alvo mais estáveis ao calcular a diferença temporal, o que reduz o risco de oscilações e divergência durante o treinamento.

Sem uma rede-alvo independente, o MLP principal e a rede online teriam valores-alvo mudando constantemente em um comportamento oscilante e instável. Isso ocorre porque ambas as redes seriam atualizadas simultaneamente. Ao usar a rede-alvo, o processo de aprendizagem se estabiliza, pois ambos os algoritmos divergem/oscilam menos. Como mencionado acima, a rede-alvo não é retropropagada como um MLP regular; ela copia a rede online em intervalos definidos. Esses intervalos são tipicamente da ordem de 10.000 passos e nosso parâmetro de entrada para modular isso é chamado de “m_target_counts”, atribuído por padrão a apenas 65! Isso porque estamos testando no timeframe diário por apenas um ano, então temos 260 barras de preço para o teste. Esse é um parâmetro ajustável; assim, com um período de teste mais longo ou um timeframe menor, os 10.000 passos são factíveis. O cálculo do valor-Q alvo é obtido pela seguinte fórmula:

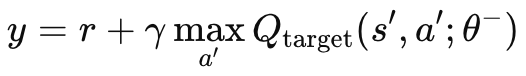
Onde:

• y: o valor-Q alvo, que representa o retorno estimado (recompensa futura) a partir do estado atual s, tomando a ação a e, então, seguindo a política ótima daí em diante.
• r: a recompensa imediata recebida após tomar a ação a no estado s.
• γ: o fator de desconto, que determina a importância das recompensas futuras. É um valor entre 0 e 1.
• max a′ Qtarget(s′,a′;θ−): o valor-Q máximo previsto para o próximo estado s′, considerando todas as ações possíveis a′, estimado pela rede-alvo com parâmetros θ−.

• Qtarget(s′,a′;θ−): O valor Q para o próximo par estado-ação (s′,a′)(s', a')(s′,a′), previsto pela rede alvo.
• θ−: os parâmetros (pesos) da rede-alvo, que são atualizados periodicamente a partir dos parâmetros da rede principal.
• 
  

Essa fórmula é implementada em MQL5 por meio da função crítica de alvo (target), que anexamos à classe CQL já usada em nosso artigo introdutório sobre aprendizado por reforço. Essa função está listada abaixo:

//+------------------------------------------------------------------+
// Critic Target for DQN
//+------------------------------------------------------------------+
vector Cql::CriticTarget(vector &Rewards, vector &TargetOutput)
{  vector _target = Rewards + (THIS.gamma * TargetOutput);
   return(_target);
}

Há um problema de bootstrapping. No Q-learning tradicional, como vimos no artigo anterior sobre aprendizado por reforço, a rede atualiza os valores-Q com base em suas próprias previsões, o que pode levar a uma cascata de erros (mais comumente chamada de erro de bootstrapping) caso as previsões estejam incorretas. Isso ocorre porque os valores-Q de um estado dependem dos valores-Q de estados subsequentes, o que pode potencialmente resultar em amplificação de erros.

O papel da target network é, portanto, mitigar isso, fornecendo um alvo de atualização mais lento. Como os parâmetros da target network são atualizados com menor frequência (normalmente a cada poucas dezenas de milhares de passos), ela muda mais gradualmente do que a online network. Isso desacelera a taxa com que os erros podem se propagar, ajudando assim a gerenciar o problema de bootstrapping.

Em situações nas quais temos dinâmicas não lineares, como nos ambientes complexos dos mercados financeiros ou mesmo em outros, como jogos eletrônicos, as relações entre estados e recompensas tendem a ser altamente não lineares. A estabilidade introduzida pela target network é, portanto, fundamental para que o DQN aprenda de forma eficaz nesses cenários. Sem essa target network, a online network (DQN) tem mais chances de divergir quando enfrenta ambientes complexos ou de rápida mudança, devido às atualizações rápidas tanto dos valores-Q quanto das metas (targets).

Além disso, a target network pode ser aprimorada com a adição de uma extensão frequentemente chamada de “double DQN”, que aborda o viés de superestimação. Isso é implementado usando as redes online e target separadamente para selecionar e avaliar ações. É um desacoplamento dos processos de seleção e avaliação de ações entre as redes online e target. A online network é usada para selecionar a ação, enquanto a target network a avalia.

Experience Replay e seu papel no treinamento

Experience replay é uma técnica de armazenamento em que um agente DQN de aprendizado por reforço guarda suas “experiências” de estado, ação, recompensa e próximo estado em um replay buffer. Essas experiências são então amostradas aleatoriamente durante o treinamento para atualizar os pesos e vieses (biases) do DQN do agente. Essa abordagem, como era de se esperar, é útil para quebrar a correlação sequencial resultante de considerar apenas pontos de dados consecutivos e, portanto, pode ser mais adequada para cenários do mundo real, como os mercados financeiros. Nos mercados financeiros, pontos de dados consecutivos — sejam eles de preço, volume de contratos ou volatilidade — tendem a ser altamente correlacionados, já que todos são influenciados por condições de mercado e comportamentos de participantes semelhantes. Treinar um agente DQN em dados sequencialmente correlacionados tende a levar ao overfitting e à falta de generalização, já que o agente se acostuma a explorar padrões específicos que não se aplicam bem a diferentes condições de mercado.

Para quebrar essas correlações temporais, normalmente o DQN é treinado em mini-batches de pontos de dados de experiência amostrados aleatoriamente do replay buffer. A amostragem aleatória, em particular, ajuda a quebrar as correlações temporais, fazendo com que o agente aprenda uma melhor distribuição de experiências, aproximando mais fielmente as dinâmicas subjacentes do mercado. Além de uma melhor generalização, o processo de treinamento a longo prazo se torna mais estável e também converge melhor. Isso ocorre porque o experience replay reduz a variância das atualizações durante o treinamento.

Sem experience replay, as atualizações de pesos da rede ocorreriam em rajadas de amostras consecutivas altamente correlacionadas, apenas para serem interrompidas por uma atualização totalmente diferente de outras condições de ambiente, o que tenderia a tornar todo o processo de atualização muito volátil, podendo levar à instabilidade no aprendizado. Ao amostrar aleatoriamente de um conjunto diverso de experiências, o agente DQN realiza atualizações mais suaves e estáveis, melhorando a convergência para uma política ótima.

O uso eficiente de dados históricos também é algo que o experience replay possibilita, pois o agente reaprende a partir de experiências várias vezes (devido à seleção aleatória), o que é particularmente valioso em mercados financeiros, onde obter grandes quantidades de dados diversificados e representativos em um determinado momento é um desafio. Na essência, isso permite que o DQN aprenda com eventos raros ou significativos, como quedas ou altas acentuadas do mercado, mesmo que eles não estejam acontecendo no momento. Isso torna o agente mais preparado e robusto para esses eventos, caso eles ocorram.

O experience replay também aumenta o potencial de exploração no aprendizado por reforço, em oposição ao simples aproveitamento (exploitation). Ele reduz a probabilidade de “esquecimento catastrófico”, pois o agente amostra repetidamente de seu replay buffer, permitindo reforçar o conhecimento de estratégias antigas e evitando que elas sejam sobrescritas por experiências mais recentes; e, por fim, possibilita até instâncias mais especializadas de experience replay, como o prioritized experience replay, no qual amostras de dados com erros maiores na função de perda são priorizadas, dado seu maior potencial de aprendizado, tornando o aprendizado mais eficiente e direcionado.

Mencionamos o experience replay neste artigo porque ele é um princípio fundamental no DQN; no entanto, demonstraremos sua aplicação no MQL5 em artigos futuros, onde o DQN será mais do que apenas uma função de perda híbrida, passando a ser o principal modelo de previsão da nossa classe de sinais.

Tomada de decisão temporal

Muitas vezes, decisões tomadas — mesmo fora do contexto de negociações, em áreas como robótica ou jogos — têm efeitos retardados nos resultados futuros, que não são necessariamente imediatos, mas se desenrolam ao longo de horizontes temporais maiores. Para traders, vêm à mente divulgações econômicas e comunicados de empresas, mas essa relação estabelece uma dependência temporal. Essa relação temporal é considerada na equação do valor-Q mencionada acima por meio do fator gamma. O gamma permite equilibrar recompensas de curto e longo prazo, conferindo aos valores-Q do DQN a capacidade de olhar mais à frente e estimar o impacto cumulativo das ações ao longo do tempo. Argumenta-se que o efeito disso é que algumas recompensas são retardadas e o gamma garante que o agente não ignore recompensas de longo prazo, mantendo, ao mesmo tempo, atenção às imediatas, o que pode ser essencial ao negociar. Por exemplo, posições abertas com base em decisões importantes sobre taxas de juros nem sempre geram ganhos favoráveis imediatamente. Os períodos de excursão adversa geralmente marcam essas posições e, portanto, a capacidade de ter e usar sinais que considerem isso — como os DQNs — pode ser uma vantagem.

Alterações em nosso código anterior

Para utilizar nosso DQN dentro de uma função de perda híbrida, precisamos primeiro adicionar nossa enumeração personalizada de perda para que fique assim:

//+------------------------------------------------------------------+
//| Custom Loss-Function Enumerator                                  |
//+------------------------------------------------------------------+
enum Eloss
{  LOSS_TYPICAL = -1,
   LOSS_SVR = 1,
   LOSS_QL = 2,
   LOSS_DQN = 3
};

Adicionamos uma nova enumeração ‘LOSS_DQN’ a ser selecionada quando a função de perda utilizar DQN. Alterações adicionais que precisamos fazer, como no primeiro artigo sobre aprendizado por reforço, são na função de retropropagação, onde a seleção do tipo de perda adequado determina o valor usado no cálculo dos deltas. Essas alterações são as seguintes:

//+------------------------------------------------------------------+
//| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON.              |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Run-time Validation of learning rate, decay rates and epoch     |
//|  index is performed as these are optimisable inputs.             |
//+------------------------------------------------------------------+
void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network arch! ");
      return;
   }


....

//COMPUTE DELTAS
   vector _last, _last_derivative;
   _last.Init(inputs.Size());
   if(hidden_layers == 0)
   {  _last = weights[hidden_layers].MatMul(inputs);
   }
   else if(hidden_layers > 0)
   {  _last = weights[hidden_layers].MatMul(hidden_outputs[hidden_layers - 1]);
   }
   _last.Derivative(_last_derivative, THIS.activation);
   vector _last_loss = output.LossGradient(label, THIS.loss_typical);
   if(THIS.loss_custom == LOSS_SVR)
   {  _last_loss = SVR_Loss();
   }
   else if(THIS.loss_custom == LOSS_QL)
   {  

....

   }
   else if(THIS.loss_custom == LOSS_DQN)
   {  double _reward = QL.CriticReward(Learning.ql_reward_max, Learning.ql_reward_min, Learning.ql_reward_float);
      vector _rewards;
      _rewards.Init(Learning.dqn_target.Size());
      _rewards.Fill(0.0);
      if(_reward > 0.0)
      {  _rewards[0] = 1.0;
      }
      else if(_reward == 0.0)
      {  _rewards[1] = 1.0;
      }
      else if(_reward < 0.0)
      {  _rewards[2] = 1.0;
      }
      vector _target = QL.CriticTarget(_rewards, Learning.dqn_target);
      _last_loss = output.LossGradient(_target, THIS.loss_typical);
   }
   
....


}

Adicionamos uma nova enumeração ‘LOSS_DQN’ a ser selecionada quando a função de perda utilizar DQN. Alterações adicionais que precisamos fazer, como no primeiro artigo sobre aprendizado por reforço, são na função de retropropagação, onde a seleção do tipo de perda adequado determina o valor usado no cálculo dos deltas. Essas alterações são as seguintes:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalDQN::GetOutput(int &Output)
{  m_learning.rate = m_learning_rate;
   for(int i = m_epochs; i >= 1; i--)
   {  MLP.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  int _states = 2;
         vector _in, _in_old, _in_row, _in_row_old, _in_col, _in_col_old;
         if
         (
            _in_row.Init(_states) &&
            _in_row.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, _states) &&
            _in_row.Size() == _states
            &&
            _in_row_old.Init(_states) &&
            _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, ii + 1 + 1, _states) &&
            _in_row_old.Size() == _states
            &&
            _in_col.Init(_states) &&
            _in_col.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, _states) &&
            _in_col.Size() == _states
            &&
            _in_col_old.Init(_states) &&
            _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_state_lag + ii + 1, _states) &&
            _in_col_old.Size() == _states
         )
         {  _in_row -= _in_row_old;
            _in_col -= _in_col_old;
            //
            m_learning.ql_reward_max = _in_row.Max();
            m_learning.ql_reward_min = _in_row.Min();
            if(m_learning.ql_reward_max == m_learning.ql_reward_min)
            {  m_learning.ql_reward_max += m_symbol.Point();
            }
            MLP.Set(_in_row);
            MLP.Forward();
            //
            MLP.QL.THIS.environments = m_environments;
            //
            vector _in_e;
            _in_e.Init(1);
            MLP.QL.Environment(_in_row, _in_col, _in_e);
            //
            int _row = 0, _col = 0;
            MLP.QL.SetMarkov(int(_in_e[_states - 1]), _row, _col);
            _in.Init(2);
            _in[0] = _row;
            _in[1] = _col;
            DQN_ONLINE.Set(_in);
            DQN_ONLINE.Forward();
            //
            MLP.QL.SetMarkov(int(_in_e[_states - 2]), _row, _col);
            _in_old.Init(2);
            _in_old[0] = _row;
            _in_old[1] = _col;
            DQN_TARGET.Set(_in_old);
            DQN_TARGET.Forward();
            m_learning.dqn_target = DQN_TARGET.output;
            if(ii > 0)
            {  vector _target, _target_data, _target_data_old;
               if
               (
                  _target_data.Init(2) &&
                  _target_data.CopyRates(m_symbol.Name(), m_period, 8, ii, 2) &&
                  _target_data.Size() == 2
                  &&
                  _target_data_old.Init(2) &&
                  _target_data_old.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, 2) &&
                  _target_data_old.Size() == 2
               )
               {  _target.Init(__MLP_OUTPUTS);
                  _target.Fill(0.0);
                  _target_data -= _target_data_old;
                  double _type = _target_data[1] - _in_row[1];
                  int _index = (_type < 0.0 ? 0 : (_type > 0.0 ? 2 : 1));
                  _target[_index] = 1.0;
                  MLP.Get(_target);
                  if(i == m_epochs && ii == m_train_set)
                  {  DQN_ONLINE.Backward(m_learning, i);
                     if(m_target_counter >= m_target_counts)
                     {  DQN_TARGET = DQN_ONLINE;
                        m_target_counter = 0;
                     }
                     MLP.Backward(m_learning, i);
                  }
               }
            }
            Output = (MLP.output.Max()==MLP.output[0]?0:(MLP.output.Max()==MLP.output[1]?1:2));
         }
      }
   }
}

Como já mencionado acima, temos 2 redes DQN: a online network e a target network. Além disso, é claro, está a MLP principal, que recebe mudanças no preço de fechamento como entradas, assim como no artigo sobre Q-learning. Não deveríamos nos referir à classe QL, exceto para chamar a função crítica de target para obter os valores-Q do DQN, como mencionado anteriormente. No entanto, como a classe QL nos permite acessar as coordenadas de estado do ambiente (quando fornecido um índice), bem como compor um índice a partir de coordenadas de estado, estamos nos referindo a ela para obter as entradas para as duas redes DQN. Como mencionado, não estamos usando o q-map para nossas previsões, mas confiando na online network do DQN, que é treinada pela target network. Tanto a online quanto a target network DQN simplesmente recebem estados de ambiente (antigo e novo, respectivamente) e são treinadas para prever um vetor de valores-Q (para cada ação do agente).

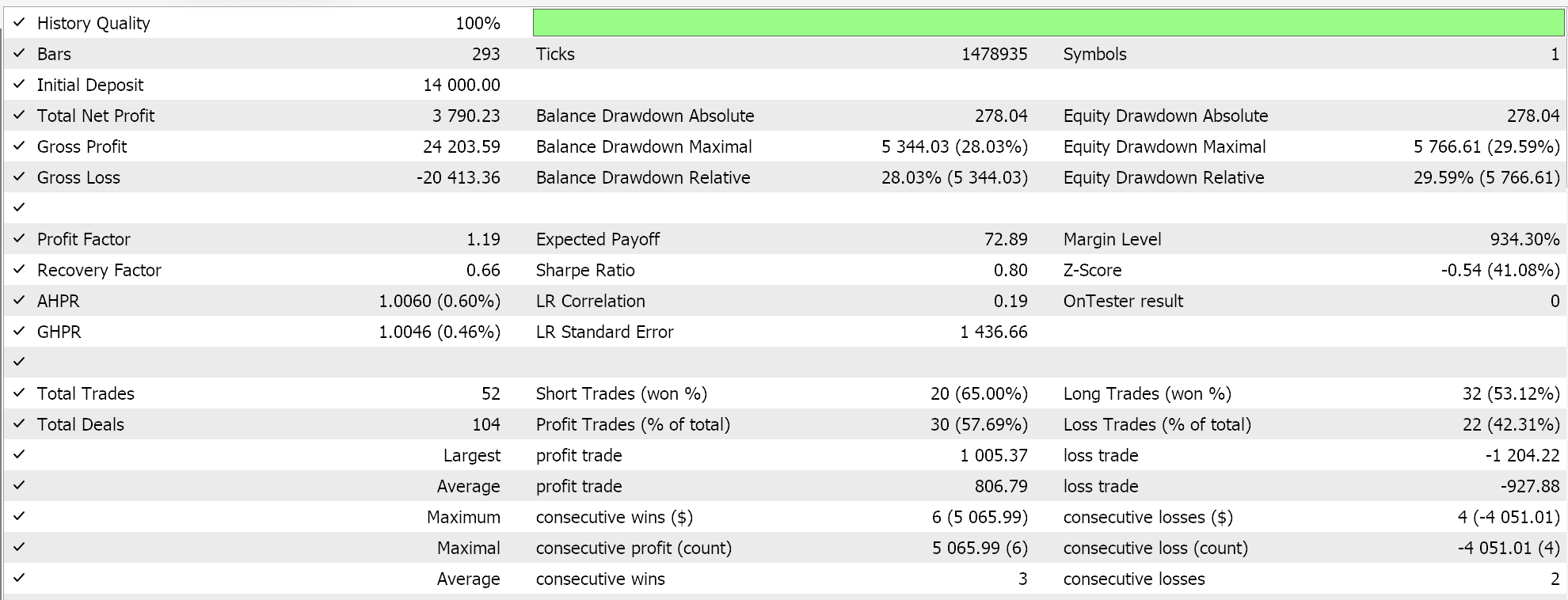
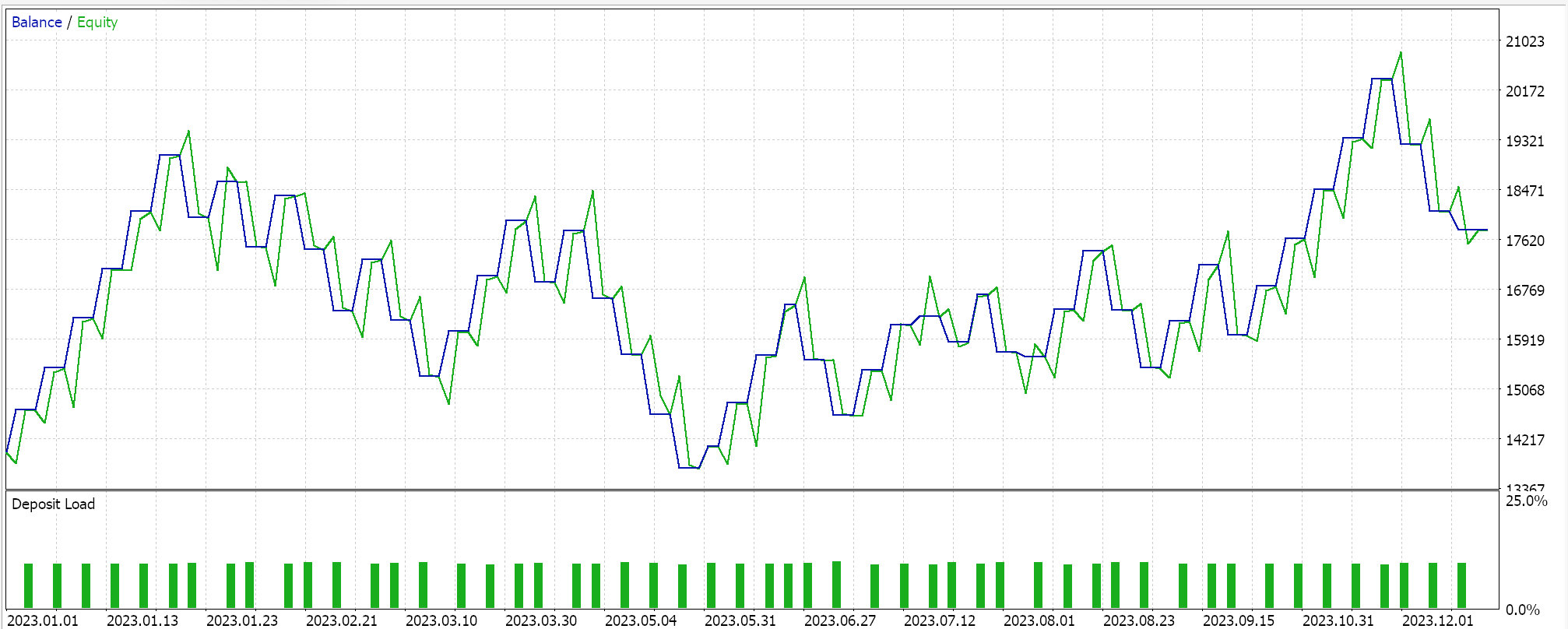
Relatórios do Strategy Tester:

Testamos essa MLP com treinamento por aprendizado por reforço via Deep-Q-networks no EURGBP para o ano de 2023 no timeframe diário. A seguir, apresentamos nossos resultados, que têm o objetivo de demonstrar estritamente a negociabilidade, e não necessariamente a replicação em ações futuras do mercado.

Conclusão

Analisamos a implementação e o teste de um algoritmo alternativo ao aprendizado por reforço (reinforcement learning) chamado Deep-Q-Networks em Expert Advisors montados via wizard. O aprendizado por reforço (reinforcement learning) é o 3^º método de treinamento em aprendizado de máquina, além do aprendizado supervisionado (supervised learning) e não supervisionado (unsupervised learning), e embora seja, tecnicamente falando, uma abordagem diferente de treinamento dentro do aprendizado de máquina, em artigos subsequentes consideraremos cenários nos quais ele pode, de fato, atuar como o modelo principal e gerador de sinais.