As modificações mais conhecidas do algoritmo de busca cooperativa artificial (Artificial Cooperative Search, ACSm)

Conteúdo:

1. Introdução
2. Implementação do algoritmo
3. Resultados dos testes

1. Introdução

No artigo anterior, apresentamos um algoritmo de otimização interessante e promissor, conhecido como algoritmo de busca cooperativa artificial (ACS). Este algoritmo é inspirado por observações da interação e cooperação entre organismos vivos na natureza, onde eles se unem para alcançar objetivos comuns e obter benefícios mútuos. A ideia principal do ACS é modelar essas relações mutualísticas entre "predadores" e "presas" para otimizar tarefas complexas e multidimensionais.

Agora que já estamos familiarizados com a versão básica do ACS, vamos tentar expandir suas capacidades com variantes modificadas do algoritmo. Essas versões aprimoradas do ACS utilizarão mecanismos adicionais, inspirados em observações de ecossistemas naturais, para aumentar a eficiência da busca por soluções ótimas.

O estudo de versões modificadas conhecidas do ACS nos permitirá compreender mais profundamente como os princípios de cooperação e coexistência mutuamente benéfica entre organismos vivos podem ser adaptados com sucesso para resolver problemas complexos de otimização, além de abrir novas perspectivas na área de inteligência artificial e inspirar futuros desenvolvimentos neste campo fascinante.

2. Implementação do algoritmo

A primeira e insignificante modificação do algoritmo ACS (Modified Artificial Cooperative Search Algorithms) inclui duas mudanças principais:

1. Uso de formas aumentadas das matrizes (populações) "A" e "B":
   - Nesta modificação, as matrizes "A" e "B" têm colunas adicionais. Cada linha da matriz contém N variáveis e uma coluna adicional, onde o valor da função é armazenado, calculado com base nas primeiras N variáveis. Isso facilita o acompanhamento dos valores das funções e melhora a precisão das soluções.

2. Alteração do método de criação da matriz binária "M":
   - No algoritmo original, a matriz "M" é preenchida com valores "0", e então alguns elementos são escolhidos e configurados como "1". Essa alteração resulta em uma pequena melhoria na precisão das soluções, pelo menos para as funções de teste em que os experimentos foram realizados.

Assim, essas mudanças na primeira e insignificante modificação do algoritmo ACS visam melhorar a precisão das soluções e a eficiência do algoritmo na resolução de problemas de otimização. Em vez de adicionar uma coluna adicional para armazenar os valores de adaptabilidade dos indivíduos, como sugerem os autores, usaremos o já familiar campo "f" na estrutura dos agentes, que descrevem os indivíduos na população.

A segunda e significativa modificação do algoritmo ACS inclui as seguintes alterações, que se diferenciam da versão original:

1. Alteração da abordagem para o preenchimento das matrizes "Predator" e "Prey":
   - Nesta modificação, cada linha nas matrizes aumentadas "A" e "B" é classificada com base no valor da função de adaptabilidade. Em seguida, as linhas das matrizes classificadas "A" e "B" são comparadas, e com base nessa comparação, é determinado quais linhas irão para as matrizes "Predator" e "Prey". Essa abordagem permite escolher candidatos para atualização com base em seu mérito (valor da função), ao invés de uma seleção aleatória.

2. Comparações aleatórias para atualização das matrizes "A" e "B":
   - No final de cada iteração do ciclo principal, nesta modificação, a atualização das matrizes "A" e "B" ocorre mediante comparações aleatórias. Isso significa que ambas as matrizes têm a mesma probabilidade de serem atualizadas. Essa abordagem permite atualizar uniformemente ambas as populações e melhora a diversidade na busca pela solução ideal.

Assim, a segunda modificação do algoritmo ACS aprimora o processo de seleção de candidatos e a atualização das populações "A" e "B", tornando-as mais eficientes e diversificadas na busca pela solução ótima. Ela difere da versão original do algoritmo na forma de formação das populações "Predator" e "Prey" e no uso de comparações aleatórias para a atualização das matrizes.

A terceira e significativa modificação do algoritmo ACS apresenta uma abordagem completamente diferente para a formação das matrizes "Predator" e "Prey". Descrição detalhada das mudanças feitas na terceira modificação:

1. População "Pop":
   - Nesta modificação, é criada uma nova matriz "Pop", que une as matrizes aumentadas "A" e "B". "Pop" contém todas as linhas das matrizes "A" e "B", e depois é classificada pelos valores da função de fitness. As primeiras "popSize" linhas de "Pop" tornam-se a população "Predator", e as últimas "popSize" linhas tornam-se a população "Prey".

2. Atualização de "Predator" e "Prey":
   - Após a formação das populações "Predator" e "Prey", o algoritmo continua a atualização com base na adaptabilidade dos indivíduos. A preferência é dada às melhores soluções, selecionadas como "Predator", o que contribui para melhorar a precisão e a velocidade de convergência do algoritmo.

3. Uso de comparações aleatórias:
   - De forma similar à segunda modificação, no final de cada iteração do ciclo principal, a atualização das matrizes "A" e "B" ocorre por meio de comparações aleatórias. Essa abordagem garante chances iguais de atualização para ambas as populações e contribui para a diversidade na busca pela solução ótima.

Assim, a terceira modificação do algoritmo ACS se concentra no uso da adaptabilidade para a formação das populações "Predator" e "Prey". Ela representa uma abordagem mais avançada e eficiente para a seleção de candidatos e a atualização das populações no processo de busca pela solução ideal.

Após explorar as possíveis modificações da versão básica do algoritmo (ACS), estamos agora prontos para passar à implementação da primeira versão aprimorada deste promissor método de otimização. Nosso objetivo é aumentar a eficiência na busca por soluções ótimas. Passo a passo, vamos introduzir novos elementos na estrutura básica do ACS, analisando cuidadosamente seu impacto no desempenho e na convergência do algoritmo.

Vamos começar a implementação da primeira versão modificada do algoritmo e explorar seu potencial. Em cada versão subsequente do algoritmo, as partes do código que diferem da versão anterior serão destacadas em verde.

Descrição do código da classe C_AO_ACSm1:

1. C_AO_ACSm1 é uma classe que herda da classe base "C_AO".
2. A classe possui um construtor e destrutor públicos.
3. No construtor, os seguintes membros de dados são inicializados:

• ao_name, ao_desc, ao_link - strings descritivas sobre o algoritmo
• popSize - tamanho da população
• bioProbab - probabilidade de interação biológica
• params - matriz de parâmetros do algoritmo, neste caso, dois parâmetros: "popSize" e "bioProbab"

4. SetParams() - método que define os valores de "popSize" e "bioProbab" com base nos parâmetros da matriz "params".
5. Init() - método que recebe intervalos e passos de busca, além do número de épocas, e retorna um valor booleano indicando o sucesso da inicialização.
6. Moving() e Revision() - métodos que contêm a lógica principal do algoritmo para mover agentes e realizar revisões.
7. Os membros de dados privados incluem matrizes de estruturas do tipo "S_AO_Agent" e "S_C", bem como variáveis "Key" e "phase", usadas no algoritmo.
8. ArrayShuffle() - método privado que embaralha os elementos de uma matriz.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACSm1 : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ACSm1 () { }
  C_AO_ACSm1 ()
  {
    ao_name = "ACS";
    ao_desc = "Artificial Cooperative Search m1";
    ao_link = "https://www.mql5.com/ru/articles/15014";

    popSize   = 1;   //population size
    bioProbab = 0.9; //biological interaction probability

    ArrayResize (params, 2);

    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "bioProbab"; params [1].val = bioProbab;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    bioProbab = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double bioProbab; //biological interaction probability

  private: //-------------------------------------------------------------------
  S_AO_Agent A        [];
  S_AO_Agent B        [];
  S_AO_Agent Predator [];
  S_AO_Agent Prey     [];

  S_C M               [];

  int Key;
  int phase;

  void ArrayShuffle (double &arr []);
};
//——————————————————————————————————————————————————————————————————————————————

O método "Init" da classe "C_AO_ACSm1" realiza a inicialização do objeto:

1. Init() - declaração do método. Ele recebe quatro argumentos: o intervalo mínimo de busca "rangeMinP", intervalo máximo de busca "rangeMaxP", passo de busca "rangeStepP" e o número de épocas "epochsP", que por padrão é "0".
2. if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false - chamada da função "StandardInit", que realiza a inicialização padrão da classe base. Se "StandardInit" retornar "false", então o método "Init" é imediatamente encerrado e retorna "false".
3. No laço "for (int i = 0; i < popSize; i++)", cada elemento das matrizes "A", "B", "Predator", "Prey" e "M" é inicializado com o método "Init".
4. "ArrayResize (A, popSize)" e linhas semelhantes redimensionam as matrizes "A", "B", "Predator", "Prey" e "M" para o tamanho "popSize".
5. No laço aninhado "for (int j = 0; j < coords; j++)", cada elemento "c" (coordenadas dos indivíduos) de cada objeto nas matrizes "A" e "B" é inicializado com um valor aleatório dentro do intervalo especificado.
6. "phase = 0" define o valor da variável "phase" como 0.
7. O método retorna "true" em caso de inicialização bem-sucedida.

Este código é responsável pela configuração inicial e preparação dos dados necessários para o funcionamento do algoritmo. Ele cria matrizes de objetos, inicializa seus valores e define o estado inicial do algoritmo.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ACSm1::Init (const double &rangeMinP [], //minimum search range
                       const double &rangeMaxP  [], //maximum search range
                       const double &rangeStepP [], //step search
                       const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (A,        popSize);
  ArrayResize (B,        popSize);
  ArrayResize (Predator, popSize);
  ArrayResize (Prey,     popSize);

  ArrayResize (M,         popSize);

  for (int i = 0; i < popSize; i++)
  {
    A        [i].Init (coords);
    B        [i].Init (coords);
    Predator [i].Init (coords);
    Prey     [i].Init (coords);

    M        [i].Init (coords);
  }

  // Initialization
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      A [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      B [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
    }
  }

  phase = 0;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

O método "Moving" da classe "C_AO_ACSm1" implementa a lógica principal de movimentação dos indivíduos no algoritmo:

1. "if (phase == 0)" - nesta fase, ocorre a cópia dos indivíduos da população "A" para a matriz "a" (a matriz "a" é usada para passar os indivíduos para o cálculo da função de fitness).

• Para cada elemento no laço "for (int i = 0; i < popSize; i++)", as coordenadas dos indivíduos da matriz "A" são copiadas para a matriz "a".
• Em seguida, o valor da variável "phase" é incrementado em 1, e o método retorna.

2. "if (phase == 1)" - nesta fase, os valores de adaptabilidade são atribuídos aos indivíduos da população "A" e os indivíduos são copiados da população "B".

• Para cada elemento no laço "for (int i = 0; i < popSize; i++)", o valor de adaptabilidade "a [i].f" é copiado para "A [i].f".
• Em seguida, para cada elemento no laço "for (int i = 0; i < popSize; i++)", as coordenadas dos indivíduos da matriz "B" são copiadas para a matriz "a" para o cálculo posterior da adaptabilidade dos indivíduos.
  
• O valor "phase" é incrementado em 1, e o método retorna.

3. "if (phase == 2)" - nesta fase, a adaptabilidade dos indivíduos da população "B" é retornada.

• Para cada elemento no laço "for (int i = 0; i < popSize; i++)", o valor de adaptabilidade "a [i].f" é copiado para "B [i].f".
  
• O valor "phase" é incrementado em 1, e a lógica do algoritmo continua.

4. "Selection" - neste bloco ocorre a operação de seleção.

• Se o número aleatório "u.RNDprobab()" for menor que 0.5, para cada elemento no laço "for (int i = 0; i < popSize; i++)", o indivíduo "A [i]" é copiado para "Predator [i]" e "Key" é definido como 1.
• Caso contrário, para cada elemento no laço "for (int i = 0; i < popSize; i++)", o indivíduo "B [i]" é copiado para "Predator [i]" e "Key" é definido como 2.
• De forma similar, a seleção é realizada para a matriz "Prey".

5. "Permutation of Prey" - neste bloco ocorre a operação de permutação aleatória das coordenadas em cada indivíduo da população "Prey".

• Para cada indivíduo no laço "for (int i = 0; i < popSize; i++)", executa-se "ArrayShuffle (Prey [i].c)", embaralhando as coordenadas dos indivíduos (as coordenadas de cada indivíduo são embaralhadas separadamente, mas não entre os indivíduos).

6. "Mutation" e "Crossover" - nestes blocos ocorrem as operações de mutação e cruzamento.

• O valor de "R" é calculado com base em um número aleatório.
• A matriz binária "M" é preenchida com uns.
• Operações adicionais são realizadas na matriz "M", alterando alguns de seus elementos para 0 ou 1, dependendo da probabilidade de interação biológica "bioProbab".
• Para cada indivíduo no laço "for (int i = 0; i < popSize; i++)", a mutação e o cruzamento são realizados, atualizando os valores na matriz da população "a".

7. "Boundary control" - neste bloco ocorre o controle de limites, onde as coordenadas dos indivíduos da população "a" que ultrapassam os limites do intervalo de parâmetros otimizáveis são substituídas por valores aleatórios dentro desse intervalo.

Este método implementa as principais operações do algoritmo, como seleção, mutação, cruzamento e controle de limites, que são aplicadas à população de indivíduos para a busca da solução ótima.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm1::Moving ()
{
  //----------------------------------------------------------------------------
  if (phase == 0)
  {
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 1)
  {
    for (int i = 0; i < popSize; i++) A [i].f = a [i].f;
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 2)
  {
    for (int i = 0; i < popSize; i++) B [i].f = a [i].f;

    phase++;
  }

  //----------------------------------------------------------------------------
  // Selection
  if (u.RNDprobab () < 0.5)
  {
    for (int i = 0; i < popSize; i++)
    {
      Predator [i] = A [i];                                                       
    }

    Key = 1;
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      Predator [i] = B [i];                             
    }

    Key = 2;
  }

  if (u.RNDprobab () < 0.5)
  {
    for (int i = 0; i < popSize; i++)
    {
      Prey [i] = A [i];                                 
    }
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      Prey [i] = B [i];                                 
    }
  }

  // Permutation of Prey
  for (int i = 0; i < popSize; i++)
  {
    ArrayShuffle (Prey [i].c);
  }

  double R;

  if (u.RNDprobab () < 0.5)
  {
    R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0);
  }
  else R = 1 / MathExp (4 * MathRand () / 32767.0);

  // Fill binary matrix M with 0s
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      M [i].c [j] = 0;
    }
  }

  // Additional operations with matrix M
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    int sum = 0;

    for (int c = 0; c < coords; c++) sum += M [i].c [c];

    if (sum == coords)
    {
      int j = MathRand () % coords;
      M [i].c [j] = 0;
    }
  }

  // Mutation
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]);

      // Crossover
      if (M [i].c [j] > 0)
      {
        a [i].c [j] = Predator [i].c [j];
      }

      // Boundary control
      if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j])
      {
        a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      }
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Agora, vamos analisar o código do método "Revision" da classe "C_AO_ACSm1". Ele realiza as seguintes operações:

1. Verifica se a fase de preparação das populações "phase" já foi concluída "phase >= 3". Se esta condição não for atendida, o método retorna sem realizar outras ações.

2. Atualiza a seleção de indivíduos "Selection update":

• Para cada indivíduo na população "a", verifica-se se o valor de adaptabilidade "f" excede o valor correspondente na matriz "Predator". Se sim, o valor em "Predator" é atualizado.
• Dependendo do valor da variável "Key", os indivíduos da população "Predator" são copiados para a população "A" ou "B".

3. Determina o melhor valor de adaptabilidade "Ybest" e seu índice "Ibest" na matriz "Predator":

• Percorre a matriz "Predator" e encontra o valor máximo de adaptabilidade e seu índice.

4. Atualiza a melhor solução global "fB":

• Se "Ybest" for maior que o valor atual de "fB", então "fB" é atualizado, e os elementos correspondentes das matrizes "a" e "cB" são copiados da matriz "Predator".

Este método realiza a atualização da seleção de indivíduos, a determinação da melhor solução e a atualização da melhor solução global no contexto do algoritmo de otimização.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm1::Revision ()
{
  if (phase < 3) return;

  // Selection update
  for (int i = 0; i < popSize; i++)
  {
    double d = a [i].f;

    if (d > Predator [i].f)
    {                      
      Predator [i] = a [i];
    }                                    
  }

  if (Key == 1)
  {
    for (int i = 0; i < popSize; i++)
    {
      A [i] = Predator [i];
    }
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      B [i] = Predator [i];
    }
  }

  double Ybest = -DBL_MAX;
  int Ibest = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (Predator [i].f > Ybest)
    {
      Ybest = Predator [i].f;
      Ibest = i;
    }
  }

  if (Ybest > fB)
  {
    fB = Ybest;
    ArrayCopy (a [Ibest].c, Predator [Ibest].c);
    ArrayCopy (cB, Predator [Ibest].c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "ArrayShuffle" da classe "C_AO_ACS", utilizado em todas as três modificações, realiza o embaralhamento aleatório dos elementos em uma matriz:

1. Determina o tamanho da matriz "arr" usando a função "ArraySize".
2. Percorre a matriz "arr" em ordem reversa, começando do último elemento.
3. Para cada elemento "i", gera um índice aleatório "j" entre 0 e "i".
4. Troca os elementos "arr[i]" e "arr[j]" usando uma variável temporária "tmp".

Como resultado deste método, os elementos da matriz "arr" são embaralhados em ordem aleatória.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm1::ArrayShuffle (double &arr [])
{
  int n = ArraySize (arr);
  for (int i = n - 1; i > 0; i--)
  {
    int j = MathRand () % (i + 1);
    double tmp = arr [i];
    arr [i] = arr [j];
    arr [j] = tmp;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Agora vamos revisar o código da segunda modificação do algoritmo ACS. O código do método "Moving" da classe "C_AO_ACSm2" conforme as alterações:

1. "Fase 0":

• Se a fase for "0", para cada indivíduo na população "a", os valores são copiados da população "A".
• O valor da fase é incrementado, e o método retorna.

2. "Fase 1":

• Se a fase for "1", para cada indivíduo na população "a", os valores de adaptabilidade "f" são copiados para a população "A".
• Para cada indivíduo na população "a", os valores são copiados da população "B".
• O valor da fase é incrementado, e o método retorna.

3. "Fase 2":

• Se a fase for "2", para cada indivíduo na população "B", os valores de adaptabilidade "f" são copiados da população "a".
• O valor da fase é incrementado, e a lógica do algoritmo continua.

4. "Selection":

• Para cada indivíduo nas populações "A" e "B", os valores de adaptabilidade "f" são comparados.
• Se o valor de "f" em "A" for maior do que em "B", então o indivíduo de "A" é copiado para "Predator", e o indivíduo de "B" é copiado para "Prey". Caso contrário, o oposto ocorre (na prática, os indivíduos mais adaptados são designados como "predadores", e os menos adaptados como "presas").

5. "Permutação de Prey":

• Para cada indivíduo na população "Prey", suas coordenadas são embaralhadas usando a função "ArrayShuffle".

6. "Mutação" e "Crossover":

• Determina-se o valor de "R", dependendo de um número aleatório.
• A matriz binária "M" é preenchida com zeros.
• Operações adicionais são realizadas na matriz "M", onde alguns elementos são definidos como "1" dependendo da probabilidade "bioProbab".

   Para cada indivíduo na população "a":

• A mutação é realizada: o elemento "a[i].c[j]" é calculado como a soma do elemento "Predator[i].c[j]" e o produto de "R" pela diferença entre "Prey[i].c[j]" e "Predator[i].c[j]".
• O cruzamento é realizado: se o elemento "M[i].c[j]" for igual a "1", o elemento "a[i].c[j]" é substituído pelo elemento "Predator[i].c[j]".
• O controle de limites é realizado: se o elemento "a[i].c[j]" sair do intervalo entre "rangeMin[j]" e "rangeMax[j]", ele é substituído por um valor aleatório dentro desse intervalo.

7. "Verificação de Coordenadas":

• Para cada indivíduo na população "a", a verificação das coordenadas é realizada usando a função "SeInDiSp".
  

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm2::Moving ()
{
  //----------------------------------------------------------------------------
  if (phase == 0)
  {
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 1)
  {
    for (int i = 0; i < popSize; i++) A [i].f = a [i].f;
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 2)
  {
    for (int i = 0; i < popSize; i++) B [i].f = a [i].f;

    phase++;
  }

  //----------------------------------------------------------------------------
  // Selection                     
  for (int i = 0; i < popSize; i++)
  {                                
    if (A [i].f > B [i].f)         
    {                              
      Predator [i] = A [i];        
      Prey     [i] = B [i];        
    }                              
    else                           
    {                              
      Predator [i] = B [i];        
      Prey     [i] = A [i];        
    }                              
  }                                

  // Permutation of Prey
  for (int i = 0; i < popSize; i++)
  {
    ArrayShuffle (Prey [i].c);
  }

  double R;

  if (u.RNDprobab () < 0.5)
  {
    R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0);
  }
  else R = 1 / MathExp (4 * MathRand () / 32767.0);

  // Fill binary matrix M with 0s
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      M [i].c [j] = 0;
    }
  }

  // Additional operations with matrix M
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    int sum = 0;

    for (int c = 0; c < coords; c++) sum += M [i].c [c];

    if (sum == coords)
    {
      int j = MathRand () % coords;
      M [i].c [j] = 0;
    }
  }

  // Mutation
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]);

      // Crossover
      if (M [i].c [j] > 0)
      {
        a [i].c [j] = Predator [i].c [j];
      }

      // Boundary control
      if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j])
      {
        a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      }
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Não iremos considerar o método "Revision" da segunda modificação do algoritmo, pois ele não sofreu alterações.

Agora que concluímos a segunda modificação, vamos prosseguir para a terceira. Na definição da classe da terceira modificação "C_AO_ACSm3", que é derivada da classe base "C_AO", surgiram as seguintes alterações:

Houve mudanças na lista de membros de dados:

• "bioProbab" - probabilidade de interação biológica.
• "A[]", "B[]", "Predator[]", "Prey[]", "Pop[]", "pTemp[]" - matrizes que armazenam várias populações de indivíduos.
• "M[]" - matriz que armazena dados adicionais relacionados aos indivíduos.
• "phase" - fase atual do algoritmo.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACSm3 : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ACSm3 () { }
  C_AO_ACSm3 ()
  {
    ao_name = "ACS";
    ao_desc = "Artificial Cooperative Search m3";
    ao_link = "https://www.mql5.com/ru/articles/15014";

    popSize   = 10;   //population size
    bioProbab = 0.9; //biological interaction probability

    ArrayResize (params, 2);

    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "bioProbab"; params [1].val = bioProbab;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    bioProbab = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double bioProbab; //biological interaction probability

  private: //-------------------------------------------------------------------
  S_AO_Agent A        [];
  S_AO_Agent B        [];
  S_AO_Agent Predator [];
  S_AO_Agent Prey     [];
  S_AO_Agent Pop      [];
  S_AO_Agent pTemp    [];

  S_C M               [];

  int phase;

  void ArrayShuffle (double &arr []);
};
//——————————————————————————————————————————————————————————————————————————————

No método de inicialização "Init" da classe "C_AO_ACSm3", surgiram as seguintes alterações:

1. A memória é alocada para as matrizes "A", "B", "Predator", "Prey", "Pop", "pTemp" e "M" com tamanho "popSize" ou "popSize * 2".

2. Cada elemento das matrizes "A", "B", "Predator", "Prey", "Pop" e "M" é inicializado com o método "Init".

Vale notar que os autores da versão original do algoritmo não dividiram a lógica em fases. Para implementar o algoritmo no estilo que adotamos para todos os algoritmos populacionais, foi adicionado esse particionamento em fases. Isso era necessário, pois no ACS é utilizado o cálculo prévio da adaptabilidade dos agentes para as duas populações "А" e "B", e essas operações precisam ser realizadas sequencialmente nos métodos.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ACSm3::Init (const double &rangeMinP [], //minimum search range
                       const double &rangeMaxP  [], //maximum search range
                       const double &rangeStepP [], //step search
                       const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (A,        popSize);
  ArrayResize (B,        popSize);
  ArrayResize (Predator, popSize);
  ArrayResize (Prey,     popSize);
  ArrayResize (Pop,      popSize * 2);
  ArrayResize (pTemp,    popSize * 2);

  ArrayResize (M,        popSize);

  for (int i = 0; i < popSize; i++)
  {
    A        [i].Init (coords);
    B        [i].Init (coords);
    Predator [i].Init (coords);
    Prey     [i].Init (coords);

    M        [i].Init (coords);
  }

  for (int i = 0; i < popSize * 2; i++) Pop [i].Init (coords);

  // Initialization
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      A [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      B [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
    }
  }

  phase = 0;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Agora, vamos examinar o código do método "Moving" da classe "C_AO_ACSm3" da terceira modificação. As mudanças afetaram as seguintes partes do código:

• Unificação das populações "A" e "B" em uma única população "Pop".
• Ordenação da população "Pop" com base nos valores de adaptabilidade dos indivíduos.
• Preenchimento das populações "Predator" e "Prey" a partir do array ordenado "Pop", onde a melhor metade da população torna-se "Predadores", e a segunda metade "Presas", respectivamente.
• Preenchimento da matriz binária "M" com uns.
• Operações adicionais com a matriz "M", onde alguns elementos são alterados para "0" ou "1", dependendo de um número aleatório e da probabilidade de interação biológica "bioProbab".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm3::Moving ()
{
  //----------------------------------------------------------------------------
  if (phase == 0)
  {
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 1)
  {
    for (int i = 0; i < popSize; i++) A [i].f = a [i].f;
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 2)
  {
    for (int i = 0; i < popSize; i++) B [i].f = a [i].f;

    phase++;
  }

  //----------------------------------------------------------------------------
  // Merge matrices A and B to create matrix Pop      
  for (int i = 0; i < popSize; i++)                   
  {                                                   
    Pop [i]           = A [i];                        
    Pop [i + popSize] = B [i];                        
  }                                                   
                                                      
  // Sort matrix Pop using column N as sort key values
  u.Sorting (Pop, pTemp, popSize * 2);                
                                                      
  // Populate Predator and Prey matrices              
  for (int i = 0; i < popSize; i++)                   
  {                                                   
    Predator [i] = Pop [i];                           
    Prey     [i] = Pop [i + popSize];                 
  }                                                   

  // Permutation of Prey
  for (int i = 0; i < popSize; i++)
  {
    ArrayShuffle (Prey [i].c);
  }

  double R;

  if (u.RNDprobab () < 0.5)
  {
    R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0);
  }
  else R = 1 / MathExp (4 * MathRand () / 32767.0);

  // Fill binary matrix M with 1s
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      M [i].c [j] = 1;                
    }
  }

  // Additional operations with matrix M
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 0;              
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        if (u.RNDprobab() < bioProbab)
        {                             
          M[i].c[j] = 1;              
        }                             
        else                          
        {                             
          M[i].c[j] = 0;              
        }                             
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    int sum = 0;

    for (int c = 0; c < coords; c++) sum += M [i].c [c];

    if (sum == coords)
    {
      int j = MathRand () % coords;
      M [i].c [j] = 0;
    }
  }

  // Mutation
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]);

      // Crossover
      if (M [i].c [j] > 0)
      {
        a [i].c [j] = Predator [i].c [j];
      }

      // Boundary control
      if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j])
      {
        a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      }
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Resultados dos testes

Analisamos cuidadosamente todas as versões conhecidas deste algoritmo. Agora é hora de focar nos resultados práticos e nas conclusões que podemos tirar. Sugiro que analisemos detalhadamente como cada modificação impactou o desempenho, a precisão e a eficiência. Isso nos permitirá compreender melhor quais mudanças foram mais bem-sucedidas e em que direção devemos avançar.

Assim, a primeira versão da modificação apresentou resultados aproximadamente comparáveis no escore geral, mas os resultados melhoraram significativamente na função Hilly com 1000 variáveis e na função Forest com 50 e 1000 variáveis.

ACS|Artificial Cooperative Search m1|1.0|0.7|
=============================
5 Hilly's; Func runs: 10000; result: 0.7130880902279995
25 Hilly's; Func runs: 10000; result: 0.7565145335137569
500 Hilly's; Func runs: 10000; result: 0.31899537529427235
=============================
5 Forest's; Func runs: 10000; result: 0.9999999999866176
25 Forest's; Func runs: 10000; result: 0.9555551824899264
500 Forest's; Func runs: 10000; result: 0.24186829565864398
=============================
5 Megacity's; Func runs: 10000; result: 0.6607692307692307
25 Megacity's; Func runs: 10000; result: 0.5038461538461539
500 Megacity's; Func runs: 10000; result: 0.13922307692307825
=============================
All score: 5.28986 (58.78%)

A segunda versão do algoritmo mostrou uma melhoria notável nos resultados em todas as funções de teste com 50 e 1000 variáveis. No entanto, os resultados pioraram significativamente na função Megacity com 10 variáveis (com uma variação extremamente grande nos resultados) em comparação com a versão básica. Isso indica que o avanço nessa direção é promissor (apesar de alguns pontos controversos), e vale a pena continuar trabalhando em novas modificações para aprimorar o algoritmo.

ACS|Artificial Cooperative Search m2|2.0|0.7|
=============================
5 Hilly's; Func runs: 10000; result: 0.7682797921658492
25 Hilly's; Func runs: 10000; result: 0.7664893907210706
500 Hilly's; Func runs: 10000; result: 0.31831672493319296
=============================
5 Forest's; Func runs: 10000; result: 0.9999997349437437
25 Forest's; Func runs: 10000; result: 0.9534110489423269
500 Forest's; Func runs: 10000; result: 0.24425762117784502
=============================
5 Megacity's; Func runs: 10000; result: 0.6176923076923077
25 Megacity's; Func runs: 10000; result: 0.5384615384615385
500 Megacity's; Func runs: 10000; result: 0.14057692307692446
=============================
All score: 5.34749 (59.42%)

Infelizmente, a terceira modificação, que parecia ser a mais promissora, não atendeu às expectativas e apresentou um resultado geral um pouco inferior à versão básica do algoritmo. No entanto, vale destacar que os resultados melhoraram significativamente na função suave Hilly com 10 variáveis, com o algoritmo demonstrando maior precisão de convergência especificamente em funções suaves com um pequeno número de variáveis.

ACS|Artificial Cooperative Search m3|10.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.8836798635515516
25 Hilly's; Func runs: 10000; result: 0.715438105666966
500 Hilly's; Func runs: 10000; result: 0.3011611038405591
=============================
5 Forest's; Func runs: 10000; result: 0.9893902762645717
25 Forest's; Func runs: 10000; result: 0.7954795408759185
500 Forest's; Func runs: 10000; result: 0.21910399769909533
=============================
5 Megacity's; Func runs: 10000; result: 0.6315384615384615
25 Megacity's; Func runs: 10000; result: 0.49876923076923074
500 Megacity's; Func runs: 10000; result: 0.12683076923077044
=============================
All score: 5.16139 (57.35%)

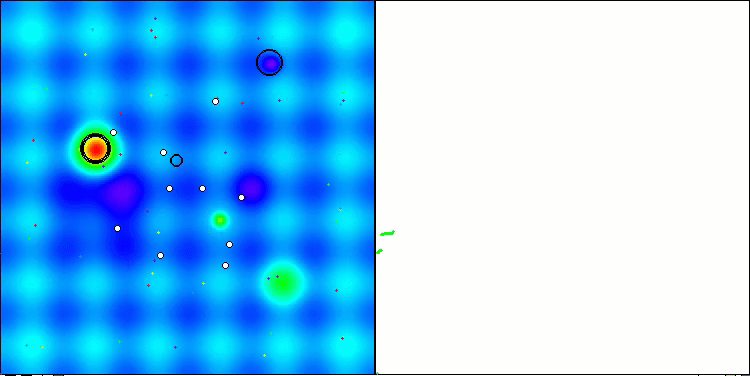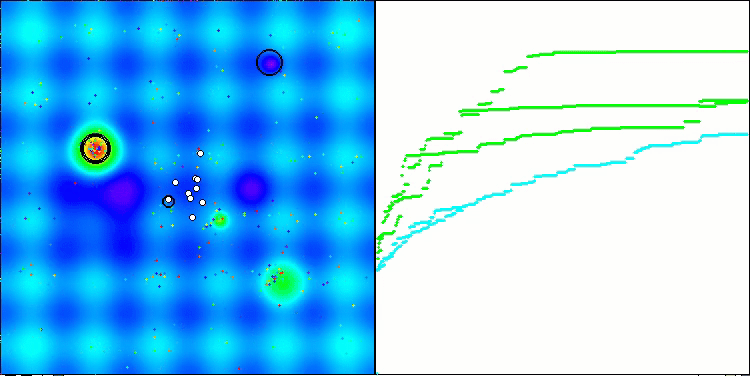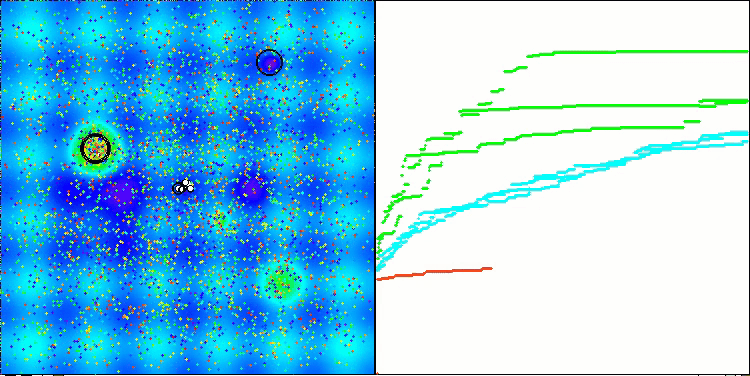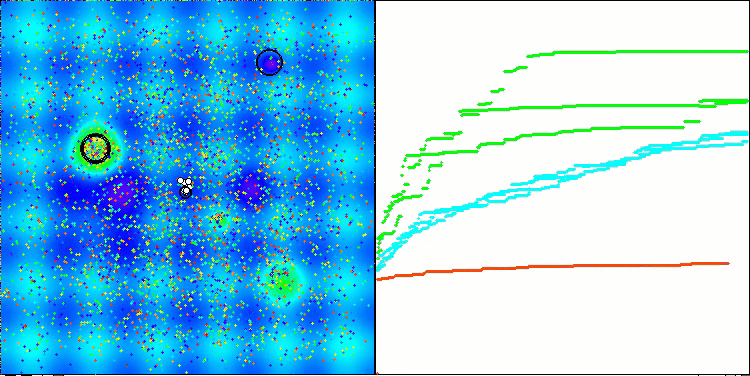
Visualização da segunda modificação do algoritmo. Com um pequeno número de variáveis, há uma dispersão bastante grande nos resultados das funções Hilly e Megacity, enquanto o algoritmo apresenta excelente desempenho na função suave e pontiaguda Forest.

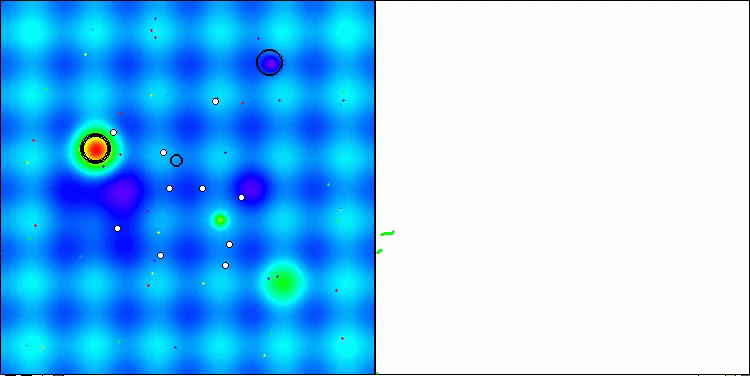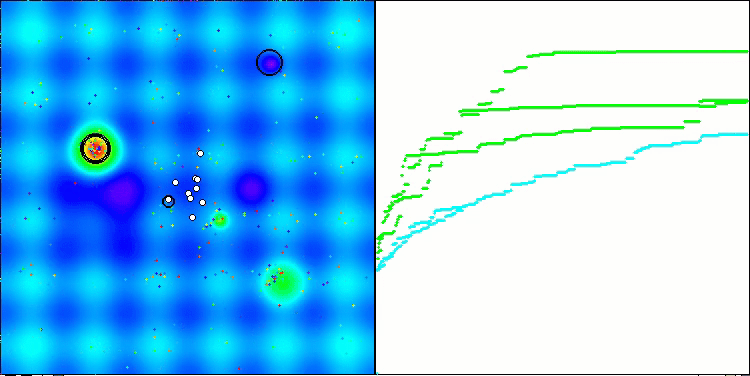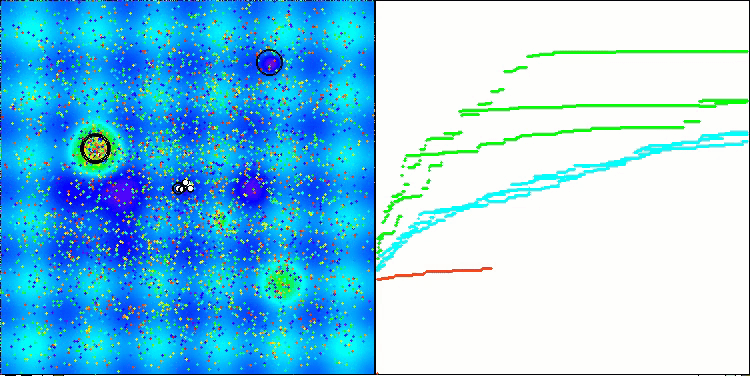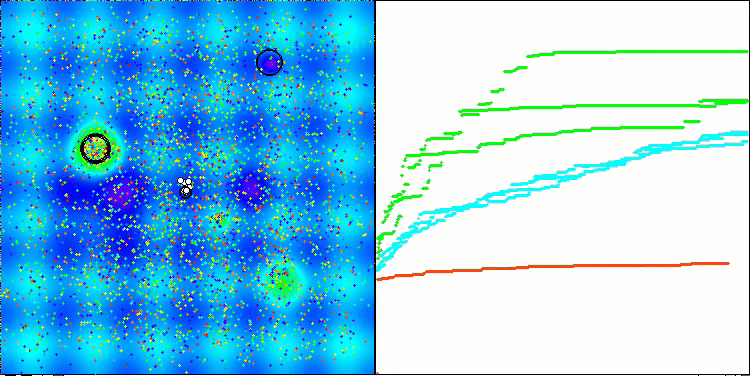
  ACSm2 na função de teste Hilly.

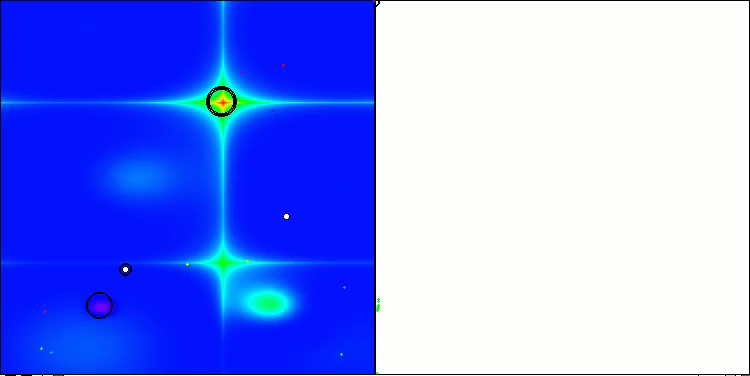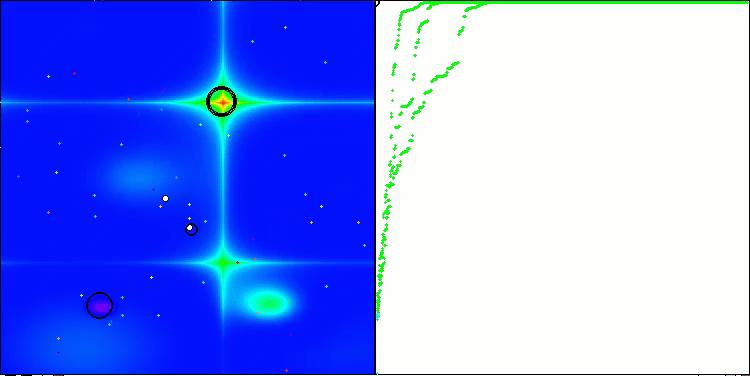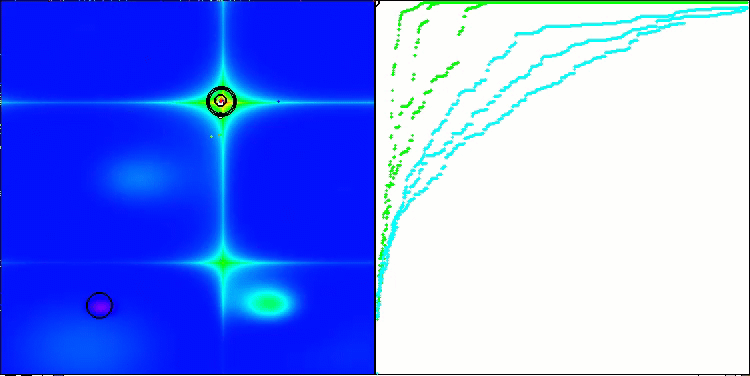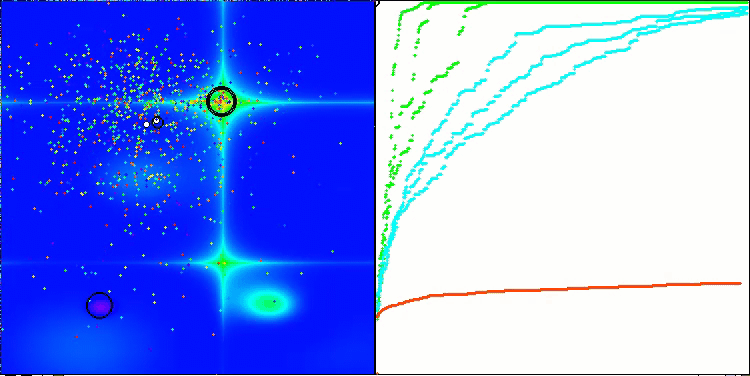
ACSm2 na função de teste Forest.

  ACSm2 na função de teste Megacity.

Coinsiderações finais

No geral, podem-se fazer as seguintes conclusões:

1. A primeira modificação do algoritmo ACS, com a adição de formas aumentadas das matrizes "A" e "B", melhorou a precisão das soluções, especialmente nas funções Hilly com 1000 variáveis e Forest com 50 e 1000 variáveis.

2. A segunda modificação, que altera a abordagem de preenchimento das matrizes "Predator" e "Prey" e utiliza comparações aleatórias para atualização das matrizes, mostrou uma melhoria significativa nos resultados em todas as funções de teste com 50 e 1000 variáveis, mas levou a uma maior dispersão de resultados na função Megacity com 10 variáveis.

3. A terceira modificação, focada no uso da adaptabilidade para a formação das populações "Predator" e "Prey", não atendeu às expectativas, apresentando um resultado geral ligeiramente inferior à versão básica do algoritmo, embora tenha melhorado a precisão da convergência em funções suaves com um pequeno número de variáveis.

Assim, cada modificação tem seus pontos fortes e fracos, e para o desenvolvimento futuro do algoritmo, é necessário considerar essas características para criar uma versão mais eficiente e universal do algoritmo ACS.

Possíveis direções para melhoria:

1. Modificação dos mecanismos de busca:

• Analisar os mecanismos de busca atuais utilizados no algoritmo e considerar a possibilidade de otimizá-los ainda mais.
• Investigar se é possível introduzir mecanismos adicionais, como passos adaptativos de busca, para aumentar a eficiência da busca.

2. Investigação de abordagens híbridas:

• Considerar a possibilidade de combinar o algoritmo atual com outros métodos de otimização, aproveitando os benefícios de diferentes abordagens. Por exemplo, pode-se tentar integrar elementos de algoritmos evolutivos ou de inteligência de enxame para aumentar a diversidade e a velocidade de convergência.

3. Análise e melhoria do mecanismo de interação entre as populações:

• Investigar como melhorar a maneira como as populações "A" e "B" interagem, para que complementem melhor uma à outra no processo de busca. Talvez valha a pena considerar esquemas mais complexos de troca de informações ou aprendizado conjunto entre as populações.

Figura 1. Graduação de cores das modificações do algoritmo para os respectivos testes em comparação com a versão básica. A cor branca destaca os resultados maiores ou iguais a 0.99.

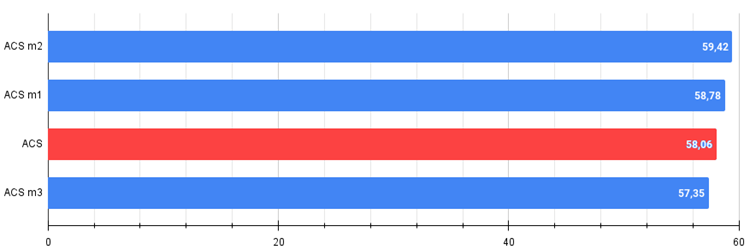
Figura 2. Histograma dos resultados das modificações do algoritmo (na escala de 0 a 100, quanto maior, melhor,

onde 100 é o resultado teórico máximo possível, o script para calcular a tabela de classificação está no arquivo anexado)

Vantagens e desvantagens gerais das versões modificadas do algoritmo de busca cooperativa artificial (ACS):

Vantagens:

1. Poucos parâmetros externos (apenas 1).
   
2. Boa convergência em diferentes tipos de funções.

Desvantagens:

1. Dispersão de resultados em funções com baixa dimensionalidade.
   

O artigo inclui um arquivo com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitas alterações foram feitas para melhorar as capacidades de busca. As conclusões e julgamentos apresentados nos artigos são baseados nos resultados dos experimentos realizados.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/pt/code/49355