Técnicas do MQL5 Wizard que você deve conhecer (Parte 23): CNNs

Introdução

Continuamos esta série em que analisamos ideias de aprendizado de máquina e estatísticas que podem ser benéficas para os traders, dado o ambiente de testes rápidos e prototipagem fornecido pelo MQL5 Wizard. O objetivo continua sendo abordar uma única ideia em um artigo e, para este, inicialmente pensei que levaria pelo menos 2 artigos. No entanto, parece que conseguimos encaixar tudo em um. Redes Neurais Convolucionais (CNNs), como o nome sugere, processam dados multidimensionais em convoluções graças aos kernels.

Esses kernels carregam os pesos da rede e, assim como os dados de entrada multidimensionais, geralmente estão em formato de matriz. Eles possuem dimensões menores em comparação com os dados de entrada, e ao iterar sobre a matriz de dados de entrada durante um feed forward, como veremos abaixo, cada iteração essencialmente percorre os dados de entrada. É esse ‘ciclo’ que dá o nome ‘convolucional’.

Portanto, neste artigo, vamos introduzir os principais passos envolvidos em uma CNN, construir uma classe simples em MQL5 que implemente esses passos, integrar essa classe em uma classe de sinal personalizada do MQL5 Wizard e, por fim, realizar testes com um Expert Advisor montado a partir dessa classe de sinal.

As CNNs são tipicamente redes neurais complexas cujas principais aplicações estão em processamento de vídeos e imagens, como vimos com GANs no artigo anterior. No entanto, diferentemente das GANs que são treinadas para identificar imagens reais e/ou sujeitos nas imagens a partir de falsificações, as CNNs tendem a funcionar mais como um classificador, dividindo os dados de entrada (que geralmente são pixels de imagem) em vários subgrupos de dados, onde cada subgrupo destina-se a capturar uma propriedade chave ou muito importante dos dados de entrada. Esses subgrupos produzidos são frequentemente chamados de mapas de características.

Os passos envolvidos na obtenção desses mapas de características são: Preenchimento, alimentação direta, ativação, agrupamento e, finalmente, se a rede for treinada, retropropagação. Vamos dar uma olhada em cada um desses passos abaixo com uma CNN muito simples de camada única. Por camada única, queremos dizer que os dados de entrada são processados através de uma única camada de kernels. Isso nem sempre é o caso com as CNNs, pois elas podem abranger várias camadas, de modo que cada um dos 4 passos mencionados acima de preenchimento, alimentação direta, ativação e agrupamento é repetido para cada camada. Em configurações de múltiplas camadas, a implicação é que, para cada mapa de características produzido por uma camada superior, existem outras propriedades componentes importantes nele que são divididas em novos mapas de características ao longo do processo.

Preenchimento

Isso marca o início de uma CNN e, independentemente de este passo ser incluído ou não, pode ser opcional. Então, o que é preenchimento? Bem, como o nome sugere, é simplesmente a adição de uma borda de dados ao longo das bordas dos dados de entrada. Essencialmente, os dados de entrada são preenchidos. Lembre-se de que os dados de entrada geralmente têm mais de uma dimensão; na verdade, são frequentemente bidimensionais, por isso uma representação em matriz é adequada. Imagens são compostas por pixels em um plano XY, então a classificação com uma CNN é direta.

Por que precisamos fazer o preenchimento? A necessidade surge da natureza da convolução com os kernels durante a etapa de alimentação direta. Os kernels, assim como os dados de entrada, também estão em formato de matriz. Eles carregam os pesos da rede. Normalmente, uma camada terá mais de um kernel, pois cada kernel é responsável por gerar um mapa de características específico.

O processo de multiplicar os pesos no kernel com os dados de entrada ocorre ao longo de uma iteração ou ciclo, ou o que é sinônimo de uma convolução. O produto final dessa multiplicação é uma matriz de mapa de características cujas dimensões são sempre menores que os dados de entrada. Portanto, o objetivo do preenchimento é que, caso o usuário deseje que o mapa de características tenha as mesmas dimensões dos dados de entrada brutos, será necessário adicionar bordas de dados extras aos dados de entrada.

fonte

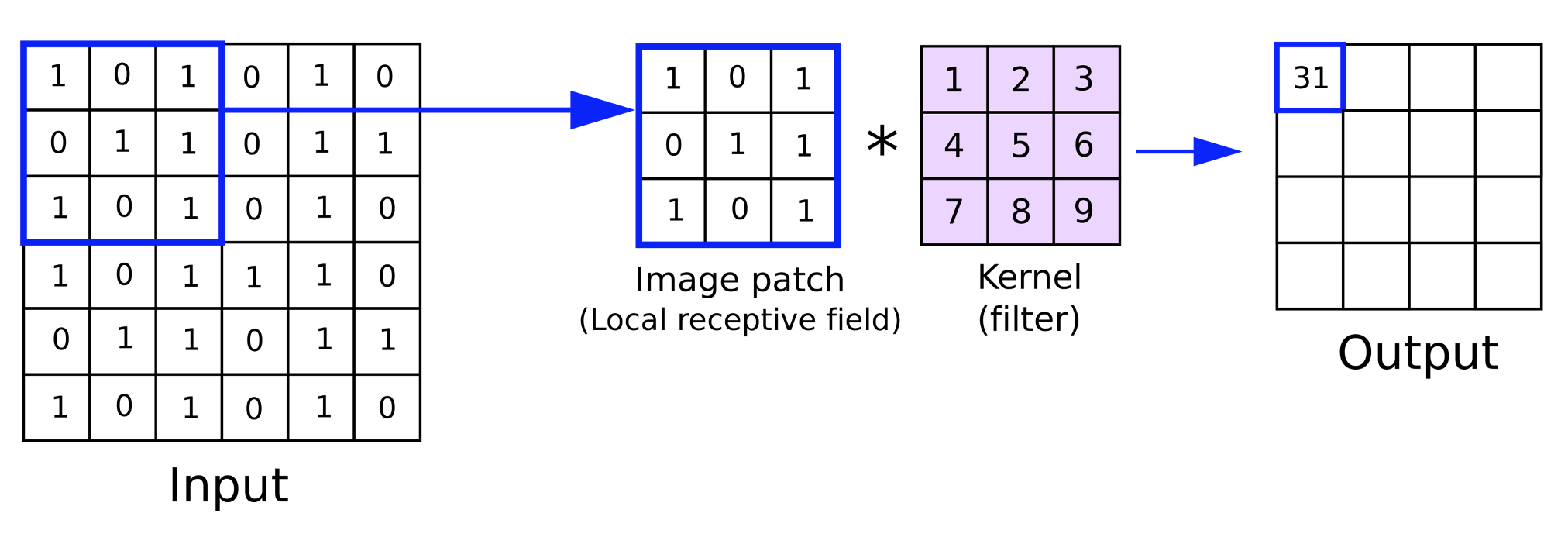
Para entender isso, se considerarmos uma matriz de dados de entrada de tamanho 6 x 6 e um kernel de pesos de tamanho 3 x 3, então uma multiplicação direta dos pesos resultará em uma matriz 4 x 4, conforme indicado acima. A fórmula para o tamanho da matriz de saída, dado o tamanho dos dados de entrada e o tamanho da matriz do kernel, é:

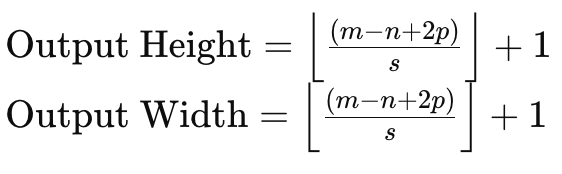
onde:

• m é a dimensão da matriz de dados de entrada,
• n é a dimensão do kernel de pesos,
• p é o tamanho do preenchimento,
• e s é o tamanho do passo.

Portanto, se precisarmos manter o tamanho de uma matriz de dados de entrada nos mapas de características, precisaríamos preencher a matriz de dados de entrada por uma quantidade que não considere apenas o tamanho da matriz de entrada e das matrizes do kernel, mas também a quantidade de passos a ser utilizada.

Existem principalmente 3 métodos de preenchimento. O primeiro é o preenchimento com zeros, onde 0s são adicionados ao longo da borda da matriz de entrada para corresponder à largura necessária. A segunda forma de preenchimento é o preenchimento de borda, onde os números na borda da matriz são repetidos ao longo da nova borda também para corresponder ao novo tamanho desejado. E, finalmente, existe o preenchimento refletido, onde os números na nova borda ampliada são obtidos de dentro da matriz de dados de entrada, com os números ao longo de sua borda atuando como uma linha de espelho.

<

fonte

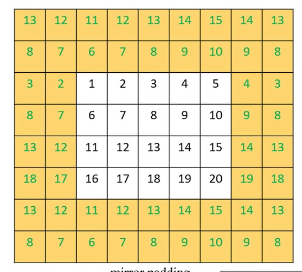
Uma vez que o preenchimento esteja completo, então a etapa de alimentação direta pode ser realizada. Esse preenchimento, porém, como mencionado, é opcional no sentido de que, se o usuário não exigir mapas de características de tamanho correspondente, ele pode ser totalmente ignorado. Por exemplo, considere uma situação em que uma CNN é destinada a examinar muitas imagens e extrair fotos de rostos humanos dentro dessas imagens.

Inevitavelmente, o mapa de características ou as imagens de saída de cada iteração terão menos pixels e, portanto, dimensões menores que a imagem de entrada, então, nesse caso, pode não haver razão para fazer um preenchimento inicial ou ampliação da imagem de entrada. Implementamos o preenchimento por meio desta listagem:

//+------------------------------------------------------------------+
//| Pad                                                              |
//+------------------------------------------------------------------+
void Ccnn::Pad()
{  if(!validated)
   {  printf(__FUNCSIG__ + " network invalid! ");
      return;
   }
   if(padding != PADDING_NONE)
   {  matrix _padded;
      _padded.Init(inputs.Rows() + 2, inputs.Cols() + 2);
      _padded.Fill(0.0);
      for(int i = 0; i < int(_padded.Cols()); i++)
      {  for(int j = 0; j < int(_padded.Rows()); j++)
         {  if(i == 0 || i == int(_padded.Cols()) - 1 || j == 0 || j == int(_padded.Rows()) - 1)
            {  if(padding == PADDING_ZERO)
               {  _padded[j][i] = 0.0;
               }
               else if(padding == PADDING_EDGE)
               {  if(i == 0 && j == 0)
                  {  _padded[j][i] = inputs[0][0];
                  }
                  else if(i == 0 && j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 1][0];
                  }
                  else if(i == int(_padded.Cols()) - 1 && j == 0)
                  {  _padded[j][i] = inputs[0][inputs.Cols() - 1];
                  }
                  else if(i == int(_padded.Cols()) - 1 && j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 1][inputs.Cols() - 1];
                  }
                  else if(i == 0)
                  {  _padded[j][i] = inputs[j - 1][i];
                  }
                  else if(j == 0)
                  {  _padded[j][i] = inputs[j][i - 1];
                  }
                  else if(i == int(_padded.Cols()) - 1)
                  {  _padded[j][i] = inputs[j - 1][inputs.Cols() - 1];
                  }
                  else if(j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 1][i - 1];
                  }
               }
               else if(padding == PADDING_REFLECT)
               {  if(i == 0 && j == 0)
                  {  _padded[j][i] = inputs[1][1];
                  }
                  else if(i == 0 && j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 2][1];
                  }
                  else if(i == int(_padded.Cols()) - 1 && j == 0)
                  {  _padded[j][i] = inputs[1][inputs.Cols() - 2];
                  }
                  else if(i == int(_padded.Cols()) - 1 && j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 2][inputs.Cols() - 2];
                  }
                  else if(i == 0)
                  {  _padded[j][i] = inputs[j - 1][1];
                  }
                  else if(j == 0)
                  {  _padded[j][i] = inputs[1][i - 1];
                  }
                  else if(i == int(_padded.Cols()) - 1)
                  {  _padded[j][i] = inputs[j - 1][inputs.Cols() - 2];
                  }
                  else if(j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 2][i - 1];
                  }
               }
            }
            else
            {  _padded[j][i] = inputs[j - 1][i - 1];
            }
         }
      }
      //
      Set(_padded, false);
   }
}

Para nossos propósitos como traders e não como cientistas de imagens, teremos uma matriz de dados de entrada com valores de indicadores. Esses valores de indicadores podem ser personalizados para uma ampla variedade de opções. No entanto, selecionamos lacunas de preços de fechamento de vários indicadores de médias móveis.

Feed forward (Convolução)

Uma vez que os dados de entrada estejam preparados, a multiplicação de pesos é realizada em toda a matriz de entrada para cada kernel na camada, a fim de produzir um mapa de características. Além da multiplicação de pesos, que gera uma matriz de tamanho menor, um viés é adicionado a cada valor da matriz. Esse viés, assim como os pesos correspondentes, é único para cada kernel.

Cada kernel possui os pesos e o viés que se especializam em extrair uma característica ou propriedade chave dos dados de entrada. Portanto, quanto mais características se deseja extrair, mais kernels serão empregados na rede. A alimentação é realizada pela função ‘Convolve’, e a listagem é fornecida aqui:

//+------------------------------------------------------------------+
//| Convolve through all kernels                                     |
//+------------------------------------------------------------------+
void Ccnn::Convolve()
{  if(!validated)
   {  printf(__FUNCSIG__ + " network invalid! ");
      return;
   }
// Loop through kernel at set padding_stride
   for (int f = 0; f < kernels; f++)
   {  bool _stop = false;
      int _stride_row = 0, _stride_col = 0;
      output[f].Fill(0.0);
      for (int g = 0; g < int(output[f].Cols()); g++)
      {  for (int h = 0; h < int(output[f].Rows()); h++)
         {  for (int i = 0; i < int(kernel[f].weights.Cols()); i++)
            {  for (int j = 0; j < int(kernel[f].weights.Rows()); j++)
               {  output[f][h][g] += (kernel[f].weights[j][i] * inputs[_stride_row + j][_stride_col + i]);
               }
            }
            output[f][h][g] += kernel[f].bias;
            _stride_col += padding_stride;
            if(_stride_col + int(kernel[f].weights.Cols()) > int(inputs.Cols()))
            {  _stride_col = 0;
               _stride_row += padding_stride;
               if(_stride_row + int(kernel[f].weights.Rows()) > int(inputs.Rows()))
               {  _stride_col = 0;
                  _stride_row = 0;
               }
            }
         }
      }
   }
}

Ativação

Após a convolução, as matrizes produzidas serão ativadas, semelhante à ativação em perceptrons multicamadas típicos. No processamento de imagens, porém, o propósito mais comum da ativação é introduzir no modelo a capacidade de mapear dados não lineares, de modo que relações mais complexas (por exemplo, equações quadráticas) possam ser capturadas. Algoritmos comuns de ativação são ReLU, leaky ReLU, Sigmoid e Tanh.

O ReLU é, sem dúvida, o algoritmo de ativação mais popularmente usado, pois lida melhor com os problemas de gradiente que desaparece. No entanto, enfrenta o problema dos neurônios mortos, que é mitigado pelo leaky ReLU. Um neurônio morto refere-se a situações em que as saídas da rede são atualizadas para valores constantes, independentemente das mudanças nas entradas. Isso pode ser um grande problema em redes que são inicializadas com pesos, e entradas negativas são fornecidas, então, as saídas permanecerão estáticas independentemente da variabilidade das entradas negativas. Isso ocorreria mesmo durante o treinamento, o que inevitavelmente levaria a pesos distorcidos. Haveria uma perda na capacidade representacional, tornando o modelo incapaz de representar padrões mais complexos. Na retropropagação, o fluxo de gradientes através da rede aconteceria com uma convergência mais lenta ou até uma completa estagnação.

O leaky ReLU, portanto, mitiga isso parcialmente, permitindo que um pequeno valor positivo, otimizável, denominado ‘alfa’, seja atribuído como um pequeno declive para entradas negativas, de forma que neurônios com valores negativos não morram, mas ainda contribuam para o processo de aprendizado. Um fluxo de gradientes mais suave na retropropagação também leva a um processo de treinamento mais estável e eficiente do que o ReLU típico.

Pooling

Depois que as imagens de características, que são as saídas da convolução, são ativadas, elas são analisadas em busca de ruído em um processo conhecido como pooling. Pooling é o processo de redução das dimensões dos mapas de características, em altura e largura. O objetivo do pooling é reduzir a carga computacional, diminuindo a quantidade de parâmetros com que a rede precisa lidar. O pooling também ajuda na invariância de translação, detectando propriedades chave de cada mapa de características com dados mínimos.

Existem predominantemente 3 tipos de pooling: max pooling, average pooling e global pooling. O max pooling escolhe o valor máximo em cada trecho da matriz de características em um ponto de convolução. E cada um dos pontos escolhidos é reunido em uma nova matriz, que será a matriz de pooling. Seus defensores argumentam que ele preserva a maioria das propriedades críticas do mapa de características agrupado, reduzindo a probabilidade de overfitting.

O average pooling calcula o valor médio de cada trecho durante a convolução e, assim como no max pooling, retorna esse valor para a matriz de pooling. O tamanho da matriz de pooling é influenciado não apenas pelo tamanho da janela de pooling e sua diferença em relação ao mapa de características, mas também pelo passo de pooling. Passos de pooling geralmente são usados com um valor maior que 1, o que inevitavelmente torna a matriz de pooling significativamente menor do que o mapa de características. Para este artigo, queremos manter as coisas simples, assumindo que seja uma introdução às CNNs, então estamos usando um passo de pooling igual a um. Os defensores do average pooling afirmam que ele é mais sutil e menos agressivo do que o max pooling e, portanto, é menos propenso a ignorar características críticas durante o pooling.

O terceiro tipo de pooling comumente usado em CNNs é o global pooling. Nesse tipo de pooling, nenhuma convolução é realizada. Em vez disso, o mapa de características inteiro é reduzido a um único valor, seja pela média do mapa de características ou selecionando o valor máximo. É um tipo de pooling que pode ser aplicado na camada final de CNNs multicamadas, onde um único valor é destinado para cada kernel.

O tamanho da janela de pooling e o tamanho do passo de pooling são os principais determinantes do tamanho dos dados agrupados. Passos maiores tendem a resultar em dados agrupados menores, enquanto o tamanho do mapa de características e o tamanho da janela de pooling são inversamente relacionados. Tamanhos menores de dados agrupados reduzem significativamente as ativações da rede e os requisitos de memória. Nosso pooling é implementado em MQL5 da seguinte forma:

//+------------------------------------------------------------------+
//| Pool                                                             |
//+------------------------------------------------------------------+
void Ccnn::Pool()
{  if(!validated)
   {  printf(__FUNCSIG__ + " network invalid! ");
      return;
   }
   if(pooling != POOLING_NONE)
   {  for(int f = 0; f < int(output.Size()); f++)
      {  matrix _pooled;
         if(output[f].Cols() > 2 && output[f].Rows() > 2)
         {  _pooled.Init(output[f].Rows() - 2, output[f].Cols() - 2);
            _pooled.Fill(0.0);
            for (int g = 0; g < int(_pooled.Cols()); g++)
            {  for (int h = 0; h < int(_pooled.Rows()); h++)
               {  if(pooling == POOLING_MAX)
                  {  _pooled[h][g] = DBL_MIN;
                  }
                  for (int i = 0; i < int(output[f].Cols()); i++)
                  {  for (int j = 0; j < int(output[f].Rows()); j++)
                     {  if(pooling == POOLING_MAX)
                        {  _pooled[h][g] = fmax(output[f][j][i], _pooled[h][g]);
                        }
                        else if(pooling == POOLING_AVERAGE)
                        {  _pooled[h][g] += output[f][j][i];
                        }
                     }
                  }
                  if(pooling == POOLING_AVERAGE)
                  {  _pooled[h][g] /= double(output[f].Cols()) * double(output[f].Rows());
                  }
               }
            }
            output[f].Copy(_pooled);
         }
      }
   }
}

Retropropagação (Evoluir)

A retropropagação, como em qualquer rede neural, é a etapa em que os pesos e viés da rede "aprendem" ao serem ajustados. Ela é realizada durante o processo de treinamento, e a frequência desse treinamento será determinada pelo modelo empregado. Para modelos financeiros usados por traders, alguns modelos podem ser programados para treinar suas redes uma vez por trimestre, por exemplo, para ajustar às últimas notícias de resultados de empresas, enquanto outros podem fazer o treinamento uma vez por mês, em datas após os principais lançamentos do calendário econômico. O ponto aqui é que sim, ter os pesos e viés corretos da rede é importante, mas talvez mais ainda é ter um regime de treinamento claro e pré-definido para atualizar esses pesos e viés.

Existem redes que podem ser treinadas uma única vez e usadas depois sem necessidade de mais treinamentos? Sim, isso é possível, embora improvável em muitos cenários. Portanto, o prudente é sempre ter um calendário de treinamento da rede se for intenção negociar com uma rede neural.

Os passos típicos envolvidos em qualquer retropropagação são sempre 3, a saber: calcular o erro, usar esse delta de erro para trabalhar os gradientes e, então, usar esses gradientes para atualizar os pesos e viés. Executamos todos esses três passos na função ‘Evolve’, cujo código é compartilhado abaixo:

//+------------------------------------------------------------------+
//| Evolve pass through the neural network to update kernel          |
//| and biases using gradient descent                                |
//+------------------------------------------------------------------+
void Ccnn::Evolve(double LearningRate = 0.05)
{  if(!validated)
   {  printf(__FUNCSIG__ + " network invalid! ");
      return;
   }
   
   for(int f = 0; f < kernels; f++)
   {  matrix _output_error = target[f] - output[f];
      // Calculate output layer gradients
      matrix _output_gradients;
      _output_gradients.Init(output[f].Rows(),output[f].Cols());
      for (int g = 0; g < int(output[f].Rows()); g++)
      {  for (int h = 0; h < int(output[f].Cols()); h++)
         {  _output_gradients[g][h] =  LeakyReLUDerivative(output[f][g][h]) * _output_error[g][h];
         }
      }
      
      // Update output layer kernel weights and biases
      int _stride_row = 0, _stride_col = 0;
      for (int g = 0; g < int(output[f].Cols()); g++)
      {  for (int h = 0; h < int(output[f].Rows()); h++)
         {  double _bias_sum = 0.0;
            for (int i = 0; i < int(kernel[f].weights.Cols()); i++)
            {  for (int j = 0; j < int(kernel[f].weights.Rows()); j++)
               {  kernel[f].weights[j][i] += (LearningRate * _output_gradients[_stride_row + j][_stride_col + i]); // output[f][_stride_row + j][_stride_col + i]);
                  _bias_sum += _output_gradients[_stride_row + j][_stride_col + i];
               }
            }
            kernel[f].bias += LearningRate * _bias_sum;
            _stride_col += padding_stride;
            if(_stride_col + int(kernel[f].weights.Cols()) > int(_output_gradients.Cols()))
            {  _stride_col = 0;
               _stride_row += padding_stride;
               if(_stride_row + int(kernel[f].weights.Rows()) > int(_output_gradients.Rows()))
               {  _stride_col = 0;
                  _stride_row = 0;
               }
            }
         }
      }
   }
}

Nossas saídas finais são matrizes e, por isso, os deltas de erro serão capturados em formato de matriz também. Uma vez que temos esses deltas de erro, então precisamos ajustá-los para seu produto de ativação, pois antes de chegar a esta camada final, eles foram ativados. E como esse ajuste para a ativação é realizado? Multiplicando os deltas de erro pela derivada da função de ativação.

Também tenha em mente que, embora os erros de saída e os gradientes de saída estejam em formato de matriz, esse processo precisa ser repetido para cada kernel. É por isso que envelopamos cada uma dessas operações em outro laço abrangente, cujo indexador é o inteiro ‘f’ e o tamanho máximo nunca excede a contagem de kernels. Nossas matrizes de saída, para a classe de CNN de teste que estamos apresentando neste artigo, são três. Elas fornecem mapas de tendência de alta, baixa e volatilidade para o ativo cujas lacunas de preço com as diversas médias móveis foram fornecidas como entrada na CNN. Essas lacunas de preço também estão em formato de matriz.

Como os valores de erro de saída e gradiente de saída estão em formato de matriz e já foram agrupados em uma etapa anterior destacada acima, seus tamanhos não correspondem ao tamanho das matrizes de pesos dos kernels. Isso inicialmente apresenta um desafio em determinar como usar os gradientes para ajustar os pesos dos kernels. A solução, no entanto, é bastante simples, pois segue a abordagem de convolução que aplicamos no feed forward, onde as matrizes de pesos dos kernels, de tamanhos diferentes da matriz de dados de entrada (e seu preenchimento), foram multiplicadas em ciclos de forma que, em cada ponto, um único valor fosse somado a partir de todos os produtos dos kernels na janela em foco e fossem colocados na matriz de saída.

Isso é feito com passos, e nosso passo para este teste é apenas um, pois deve coincidir com o passo usado no feed forward. Atualizar os viés, porém, é um pouco complicado, pois eles são apenas um único valor. No entanto, a solução é sempre somar os gradientes na matriz e multiplicar essa soma com o viés antigo (após ajustar com uma taxa de aprendizado).

Integração em uma Classe de Sinal

Para usar nossa classe de CNN dentro de um sinal personalizado, essencialmente precisamos definir duas coisas. Primeiro, que forma de dados de entrada vamos usar e, em segundo lugar, o tipo de dados de saída que esperamos nas matrizes de saída. As respostas para essas duas perguntas já foram sugeridas acima, pois os dados de entrada são lacunas de preço entre o preço de fechamento atual e muitos (25 por padrão) valores de preço de médias móveis. As muitas médias móveis são diferenciadas por seu período único, e as populamos na matriz de entrada através da função 'GetOutput', conforme destacado abaixo:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalCNN::GetOutput()
{  int _index = 5;
   matrix _inputs;
   vector _ma, _h, _l, _c;
   _inputs.Init(m_input_size, m_input_size);
   for(int g = 0; g < m_epochs; g++)
   {  for(int h = m_train_set - 1; h >= 0; h--)
      {  _inputs.Fill(0.0);
         _index = 0;
         for(int i = 0; i < m_input_size; i++)
         {  for(int j = 0; j < m_input_size; j++)
            {  if(_ma.CopyIndicatorBuffer(m_ma[_index].Handle(), 0, h, __KERNEL + 1))
               {  _inputs[i][j] = _c[0] - _ma[0];
                  _index++;
               }
            }
         }
         //
         
        ...

      }
   }

        ...
   
        ...

}

O que não é tão simples é o dado alvo em nossas matrizes de saída. Como mencionado acima, queremos obter mapas de tendência de alta ou baixa. E, para simplificar, eles deveriam ser apenas esses dois (e não incluir uma medida para saber se os mercados estão estáveis), mas o leitor pode modificar o código-fonte para resolver isso. Como estamos medindo isso, no entanto, é observando a ação do preço posterior para cada ponto de dados de entrada. Novamente, nosso ponto de dados pega leituras de indicadores para as quais escolhemos lacunas de preço de fechamento em uma matriz de preços de médias móveis, mas isso pode ser facilmente personalizado de acordo com sua preferência.

Agora, nossa medida escolhida de tendência de alta, que queremos capturar em uma matriz, em vez de um valor único, será as mudanças no preço máximo ao longo de diferentes intervalos. Da mesma forma, para capturar eventual tendência de baixa, após registrar um ponto de dados, registramos as mudanças nos preços mínimos ao longo de diferentes intervalos em uma matriz. Isso é codificado conforme mostrado abaixo:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalCNN::GetOutput()
{  
   ...

   for(int g = 0; g < m_epochs; g++)
   {  for(int h = m_train_set - 1; h >= 0; h--)
      {  _inputs.Fill(0.0);
         _index = 0;
         
        ...

         //
         _h.CopyRates(m_symbol.Name(), m_period, 2, h, __KERNEL + 1);
         _l.CopyRates(m_symbol.Name(), m_period, 4, h, __KERNEL + 1);
         _c.CopyRates(m_symbol.Name(), m_period, 8, h, __KERNEL + 1);
         //Print(" inputs are: \n", _inputs);
         CNN.Set(_inputs);
         CNN.Pad();
         //Print(" padded inputs are: \n", CNN.inputs);
         CNN.Convolve();
         CNN.Activate();
         CNN.Pool();
         // targets as eventual price changes with each matrix a proxy for bullishness, bearishness, or whipsaw action
         // implying matrices for eventual:
         // high price changes
         // low price changes
         // close price changes,
         // respectively
         //
         // price changes in each column are over 1 bar, 2 bar and 3 bars respectively
         // & price changes in each row are over different weightings of the applied price with other applied prices
         // so high is: highs only(H); (Highs + Highs + Close)/3 (HHC); and (Highs + Close)/3 (HC)
         // while low is: lows only(L); (Lows + Lows + Close)/3 (LLC); and (Lows + Close)/3 (LC)
         // and close is: closes only(C); (Highs + Lows + Close + Close)/3 (HLCC); and (Highs + Lows + Close)/3 (HLC)
         //
         // assumptions here are:
         // large values in highs mean bullishness
         // large values in lows mean bearishness
         // and small magnitude in close imply a whipsaw market
         matrix _targets[];
         ArrayResize(_targets, __KERNEL_SIZES.Size());
         for(int i = 0; i < int(__KERNEL_SIZES.Size()); i++)
         {  _targets[i].Init(__KERNEL_SIZES[i], __KERNEL_SIZES[i]);
            //
            for(int j = 0; j < __KERNEL_SIZES[i]; j++)
            {  if(i == 0)// highs for 'bullishness'
               {  _targets[i][j][0] = _h[j] - _h[j + 1];
                  _targets[i][j][1] = ((_h[j] + _h[j] + _c[j]) / 3.0) - ((_h[j + 1] + _h[j + 1] + _c[j + 1]) / 3.0);
                  _targets[i][j][2] = ((_h[j] + _c[j]) / 2.0) - ((_h[j + 1] + _c[j + 1]) / 2.0);
               }
               else if(i == 1)// lows for 'bearishness'
               {  _targets[i][j][0] = _l[j] - _l[j + 1];
                  _targets[i][j][1] = ((_l[j] + _l[j] + _c[j]) / 3.0) - ((_l[j + 1] + _l[j + 1] + _c[j + 1]) / 3.0);
                  _targets[i][j][2] = ((_l[j] + _c[j]) / 2.0) - ((_l[j + 1] + _c[j + 1]) / 2.0);
               }
               else if(i == 2)// close for 'whipsaw'
               {  _targets[i][j][0] = _c[j] - _c[j + 1];
                  _targets[i][j][1] = ((_h[j] + _l[j] + _c[j] + _c[j]) / 3.0) - ((_h[j + 1] + _l[j + 1] + _c[j + 1] + _c[j + 1]) / 3.0);
                  _targets[i][j][2] = ((_h[j] + _l[j] + _c[j]) / 2.0) - ((_h[j + 1] + _l[j + 1] + _c[j + 1]) / 2.0);
               }
            }
            //
            //Print(" targets for: "+IntegerToString(i)+" are: \n", _targets[i]);
         }
         CNN.Get(_targets);
         CNN.Evolve(m_learning_rate);
      }
   }
   
        ...

}

Nossa terceira matriz de saída, que também registra quão estáveis os mercados ficam após cada ponto de dados, é representada ao focar na magnitude das mudanças no preço de fechamento, novamente ao longo de diferentes intervalos, e os vários comprimentos desses intervalos correspondem aos tamanhos usados para medir tanto a tendência de alta quanto de baixa mencionadas acima. A captura desses dados-alvo em cada nova barra significa que nosso modelo está sendo treinado em cada nova barra, e novamente essa é apenas uma abordagem, já que pode-se optar por realizar esse treinamento com menos frequência, como mensal ou trimestralmente, conforme mencionado acima.

Após cada sessão de treinamento, precisamos fazer uma previsão sobre como será a perspectiva de tendência de alta e baixa, dados os pontos de dados atuais, e a parte do nosso código que lida com isso é compartilhada abaixo:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalCNN::GetOutput()
{  
        ...

        ...

   _index = 0;
   _h.CopyRates(m_symbol.Name(), m_period, 2, 0, __KERNEL + 1);
   _l.CopyRates(m_symbol.Name(), m_period, 4, 0, __KERNEL + 1);
   _c.CopyRates(m_symbol.Name(), m_period, 8, 0, __KERNEL + 1);
   for(int i = 0; i < m_input_size; i++)
   {  for(int j = 0; j < m_input_size; j++)
      {  if(_ma.CopyIndicatorBuffer(m_ma[_index].Handle(), 0, 0, __KERNEL + 1))
         {  _inputs[i][j] = _c[__KERNEL] - _ma[__KERNEL];
            _index++;
         }
      }
   }
   CNN.Set(_inputs);
   CNN.Pad();
   CNN.Convolve();
   CNN.Activate();
   CNN.Pool();
   double _long = 0.0, _short = 0.0;
   if(CNN.output[0].Median() > 0.0)
   {  _long = fabs(CNN.output[0].Median());
   }
   if(CNN.output[1].Median() < 0.0)
   {  _short = fabs(CNN.output[1].Median());
   }
   double _neutral = fabs(CNN.output[2].Median());
   if(_long+_short+_neutral == 0.0)
   {  return(0.0);
   }
   return((_long-_short)/(_long+_short+_neutral));
}

Uma matriz possui muitos pontos de dados, então a melhor abordagem escolhida para obter uma noção de tendência de alta ou baixa a partir das matrizes de saída é lendo os respectivos valores medianos de cada matriz. Portanto, para a matriz de alta, gostaríamos de obter um valor grande e positivo, enquanto para a matriz de baixa, gostaríamos de um valor muito negativo. Para nossa matriz de mercado estável, queremos a magnitude dessa mediana e, quanto menor for, mais estáveis os mercados são projetados para estar.

Portanto, o resultado da função ‘GetOutput’ será um valor de ponto flutuante que, se abaixo de 0,5, aponta para mais tendência de baixa adiante, ou se acima de 0,5, significa que temos uma perspectiva de alta. A partir dos testes realizados com uma CNN de camada única de matriz de entrada 5 x 5 com 3 kernels 3 x 3 que também utiliza preenchimento para ter matrizes de saída de tamanho 3 x 3 para o símbolo EURJPY no intervalo de tempo diário, obtivemos saídas muito próximas ao valor de 0,5, mais ou menos. Isso significava que, nesta implementação, qualquer valor acima de 0,5 era atribuído ao valor 100 na função de condição longa e qualquer valor abaixo de 0,5 era atribuído a 100 na função de condição curta.

Relatórios do Testador de Estratégia

A classe de sinal montada é integrada em um Expert Advisor via o MQL5 wizard, seguindo as diretrizes aqui e aqui, e ao testar no EURJPY para o ano de 2023 no intervalo de tempo diário, obtemos os seguintes resultados:

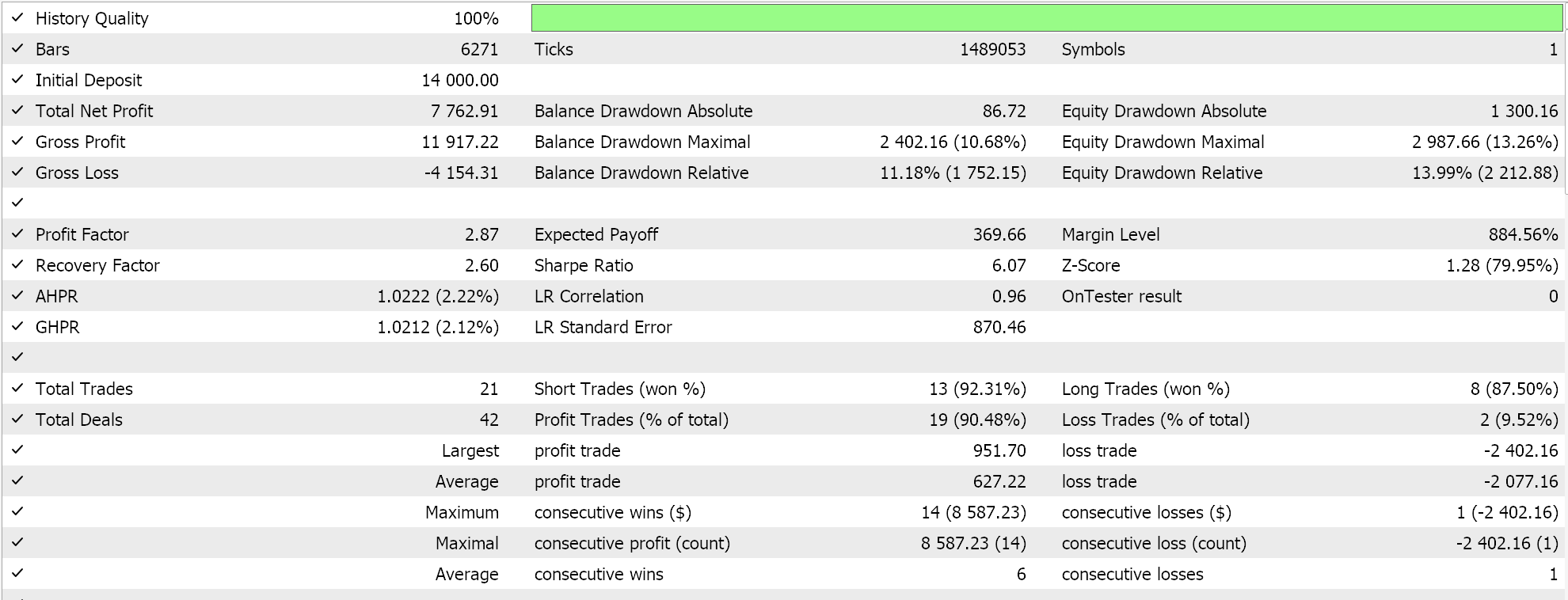
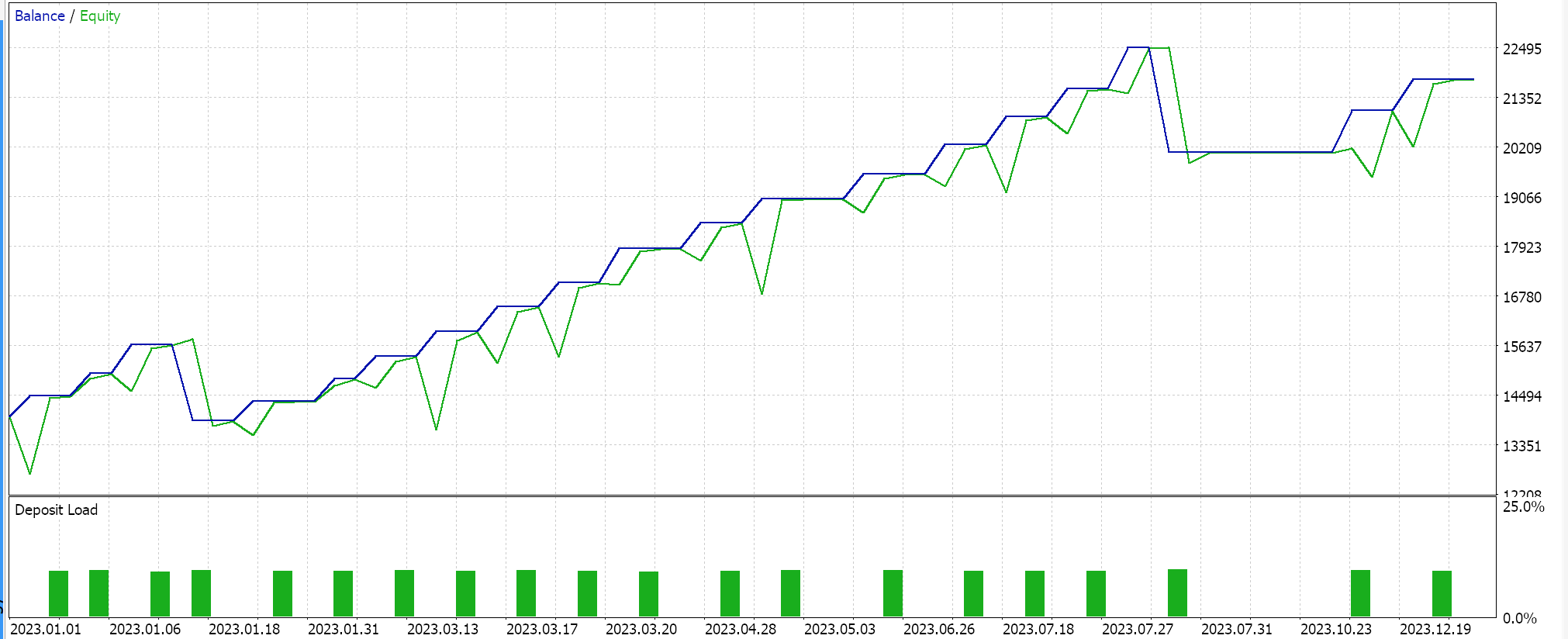
Esses resultados são de condições longas e curtas que são 0 ou 100, uma vez que o valor de saída da rede não está normalizado. Tentar normalizar os resultados da rede deve fornecer um resultado mais ‘sensível’, pois os limites de abertura e fechamento estarão abertos para ajuste fino.

Conclusão

Para resumir, analisamos as CNNs, um algoritmo de aprendizado de máquina que é frequentemente usado no processamento de imagens, através da ótica de um trader. Examinamos e codificamos seus principais passos de preenchimento, alimentação, ativação e pooling em um arquivo de classe MQL5 independente. Também abordamos o processo de treinamento, aprofundando-nos na retropropagação das CNNs, destacando o papel das convoluções em emparelhar matrizes de tamanhos desiguais. Este artigo apresentou uma CNN de camada única, então há muito terreno não abordado aqui que o leitor pode explorar, não apenas empilhando essa classe de camada única em um ou mais transformadores, mas até mesmo olhando para diferentes tipos de dados de entrada e conjuntos de dados de saída alvo.