Modificaciones más notables del algoritmo de búsqueda cooperativa artificial (Artificial Cooperative Search, ACSm)

Contenido

1. Introducción
2. Implementación del algoritmo
3. Resultados de las pruebas

1. Introducción

En el artículo anterior, conocimos un interesante y prometedor algoritmo de optimización conocido como Artificial Cooperative Search (ACS). Este algoritmo se inspira en las observaciones de la interacción y cooperación de los organismos vivos en la naturaleza, donde se unen para alcanzar objetivos comunes y obtener un beneficio mutuo. La idea básica de ACS es modelizar esas relaciones mutualistas entre «depredadores» y «presas» para optimizar problemas multidimensionales complejos.

Ahora que nos hemos familiarizado con la versión básica de ACS, intentaremos ampliar sus capacidades utilizando versiones modificadas del algoritmo. Estas versiones mejoradas de ACS utilizarán mecanismos adicionales inspirados en observaciones de ecosistemas naturales para mejorar la eficiencia en la búsqueda de soluciones óptimas.

El estudio de las versiones modificadas conocidas de ACS nos permitirá comprender mejor cómo los principios de cooperación y coexistencia mutuamente beneficiosa de los organismos vivos pueden adaptarse con éxito para resolver problemas complejos de optimización, y contribuirá a revelar nuevas perspectivas en el campo de la inteligencia artificial e inspirar nuevos avances en este apasionante ámbito.

2. Implementación del algoritmo

La primera y menor modificación de los ACS (algoritmos de búsqueda artificial cooperativa modificados) incluye dos cambios importantes:

1. Utilización de las formas aumentadas de las matrices A y B (poblaciones):
- En esta modificación, las matrices A y B tienen columnas adicionales. Cada fila de la matriz contiene N variables y una columna adicional que almacena el valor de la función calculado a partir de las N primeras variables. Esto facilita el seguimiento de los valores de las funciones y mejora la precisión de las soluciones.

2. Cambiar la forma de crear la matriz binaria M:
- En el algoritmo original, la matriz M se rellena con valores «0» y, a continuación, se seleccionan algunos elementos y se ponen a «1». Este cambio supone una pequeña mejora en la precisión de las soluciones, al menos para las funciones de prueba con las que se realizaron los experimentos.

Así pues, estos cambios en la primera y pequeña modificación del algoritmo ACS tienen como objetivo mejorar la precisión de las soluciones y la eficacia del algoritmo en la resolución de problemas de optimización. En lugar de añadir una columna adicional para almacenar los valores de fitness de los individuos, como sugieren los autores, utilizaremos el ya conocido campo «f» de la estructura de agentes que describe a los individuos de la población.

La segunda y significativa modificación del algoritmo ACS incluye los siguientes cambios que difieren de la versión original:

1. Cambiar el enfoque para rellenar las matrices Predator y Prey:
- En esta modificación, cada fila de las matrices A y B aumentadas se ordena por el valor de la función de aptitud. A continuación, se comparan las filas de las matrices A y B ordenadas y, en función de esta comparación, se determina qué filas irán a las matrices Depredador y Presa. Este enfoque permite seleccionar candidatos para la actualización en función de su mérito (valor de la característica) en lugar de una selección aleatoria.

2. Comparaciones aleatorias para actualizar las matrices A y B:
- Al final de cada iteración del bucle principal de esta modificación, las matrices A y B se actualizan mediante comparaciones aleatorias. Esto significa que ambas matrices tienen la misma probabilidad de actualizarse. Este enfoque permite que ambas poblaciones se actualicen por igual y mejora la diversidad en la búsqueda de la solución óptima.

Así, la segunda modificación del algoritmo ACS mejora la selección de candidatos y la actualización de las poblaciones A y B haciéndolas más eficientes y diversas en la búsqueda de la solución óptima. Difiere de la versión original del algoritmo en la forma en que se forman las poblaciones Predator y Prey y en el uso de comparaciones aleatorias para actualizar las matrices.

La tercera mayor modificación del algoritmo ACS representa un enfoque completamente diferente para la formación de las matrices Predator y Prey. Descripción detallada de los cambios introducidos en la tercera modificación:

1. Población:
- Esta modificación crea una nueva matriz de población que combina las matrices A y B aumentadas. La población contiene todas las filas de las matrices A y B. A continuación, se ordena por valores de la función de ajuste. Las primeras filas popSize en Pop se convierten en la población Predator, mientras que las últimas filas popSize se convierten en la población Prey.

2. Actualización de Predator y Prey:
- Tras formar las poblaciones Predator y Prey, el algoritmo sigue actualizándose en función de la adecuación de los individuos. Se da preferencia a las mejores soluciones seleccionadas como Predator, lo que ayuda a mejorar la precisión y la velocidad de convergencia del algoritmo.

3. Utilizando comparaciones aleatorias:
- De forma similar a la segunda modificación, al final de cada iteración del bucle principal, las matrices A y B se actualizan mediante comparaciones aleatorias. Este enfoque garantiza la igualdad de oportunidades de renovación de ambas poblaciones y fomenta la diversidad en la búsqueda de la solución óptima.

Así pues, la tercera modificación del algoritmo ACS se centra en el uso de la adecuación para formar las poblaciones Predator y Prey. Representa un enfoque más avanzado y eficaz para seleccionar candidatos y actualizar poblaciones mientras se busca una solución óptima.

Una vez revisadas las posibles modificaciones de la versión básica del algoritmo (ACS), estamos listos para pasar a la aplicación de la primera versión mejorada de este prometedor método de optimización. Nuestro objetivo es aumentar la eficacia en la búsqueda de soluciones óptimas. Paso a paso, introduciremos nuevos elementos en la estructura básica de ACS, analizando cuidadosamente su impacto en el rendimiento y la convergencia del algoritmo.

Empecemos a aplicar la primera versión modificada del algoritmo y exploremos su potencial. En cada versión posterior del algoritmo, las secciones del código que difieren de la versión anterior se indican en verde.

C_AO_ACSm1 descripción del código de clase:

1. C_AO_ACSm1 es una clase derivada de la clase base C_AO.
2. La clase tiene un constructor y un destructor públicos.
3. Los siguientes miembros de datos se inicializan en el constructor:

• ao_name, ao_desc y ao_link - filas descriptivas relativas al algoritmo
• popSize - tamaño de la población
• bioProbab - probabilidad de interacción biológica
• params - array de parámetros del algoritmo, en este caso tenemos dos parámetros: popSize y bioProbab.

4. SetParams() - establece los valores popSize y bioProbab en función de los parámetros de la matriz params.
5. Init() - toma como entrada los rangos y pasos de búsqueda, así como el número de épocas, y devuelve un valor lógico que indica el éxito de la inicialización.
6. Moving() y Revision() - métodos que contienen la lógica básica del algoritmo para mover y revisar los agentes.
7. Los miembros de datos privados incluyen matrices de estructuras de tipo S_AO_Agent y S_C, así como variables Key y phase utilizadas en el algoritmo.
8. ArrayShuffle() - método privado que baraja los elementos del array.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACSm1 : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ACSm1 () { }
  C_AO_ACSm1 ()
  {
    ao_name = "ACS";
    ao_desc = "Artificial Cooperative Search m1";
    ao_link = "https://www.mql5.com/ru/articles/15014";

    popSize   = 1;   //population size
    bioProbab = 0.9; //biological interaction probability

    ArrayResize (params, 2);

    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "bioProbab"; params [1].val = bioProbab;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    bioProbab = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double bioProbab; //biological interaction probability

  private: //-------------------------------------------------------------------
  S_AO_Agent A        [];
  S_AO_Agent B        [];
  S_AO_Agent Predator [];
  S_AO_Agent Prey     [];

  S_C M               [];

  int Key;
  int phase;

  void ArrayShuffle (double &arr []);
};
//——————————————————————————————————————————————————————————————————————————————

El método Init de la clase C_AO_ACSm1 realiza la inicialización del objeto:

1. Init() - declaración del método. Toma cuatro argumentos: rango de búsqueda mínimo «rangeMinP», rango de búsqueda máximo «rangeMaxP», paso de búsqueda «rangeStepP» y el número de épocas «epochsP», que es 0 por defecto.
2. if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false - llama a la función StandardInit, que realiza la inicialización estándar de la clase base. Si StandardInit devuelve false, el método Init termina inmediatamente y devuelve false.
3. En el bucle for (int i = 0; i < popSize; i++), cada elemento de las matrices A, B, Predator, Prey y M se inicializa mediante el método Init.
4. ArrayResize (A, popSize) y filas similares cambian el tamaño de las matrices A, B, Predator, Prey y M a popSize.
5. En el bucle anidado for (int j = 0; j < coords; j++), cada elemento c (coordenadas individuales) de cada objeto en las matrices A y B se inicializa utilizando un valor aleatorio en el rango dado.
6. phase = 0 establece phase en 0.
7. El método devuelve true si la inicialización se realiza correctamente.

El código se encarga de la configuración inicial y la preparación de los datos necesarios para el funcionamiento posterior del algoritmo. Crea matrices de objetos, inicializa sus valores y establece el estado inicial del algoritmo.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ACSm1::Init (const double &rangeMinP [], //minimum search range
                       const double &rangeMaxP  [], //maximum search range
                       const double &rangeStepP [], //step search
                       const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (A,        popSize);
  ArrayResize (B,        popSize);
  ArrayResize (Predator, popSize);
  ArrayResize (Prey,     popSize);

  ArrayResize (M,         popSize);

  for (int i = 0; i < popSize; i++)
  {
    A        [i].Init (coords);
    B        [i].Init (coords);
    Predator [i].Init (coords);
    Prey     [i].Init (coords);

    M        [i].Init (coords);
  }

  // Initialization
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      A [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      B [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
    }
  }

  phase = 0;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

El método Moving de la clase C_AO_ACSm1 implementa la lógica básica del movimiento de individuos en el algoritmo:

1. if (phase == 0) - aquí los individuos se copian de la población A a la matriz a (la matriz "а" se utiliza para pasar los individuos para el cálculo de la función de ajuste).

• Para cada elemento del bucle for (int i = 0; i < popSize; i++), se copian las coordenadas individuales de A a la matriz a.
• El valor de la variable phase se incrementa en 1 y se devuelve el método.

2. if (phase == 1) - aquí se asigna el ajuste a los individuos de la población A y se copian los individuos de la población B.

• Para cada elemento del bucle for (int i = 0; i < popSize; i++), el valor de ajuste de a[i].f se copia en A[i].f.
• A continuación, para cada elemento del bucle for (int i = 0; i < popSize; i++), se copian las coordenadas individuales de la matriz B a la matriz a para seguir calculando el ajuste de los individuos.
  
• El valor de fase se incrementa en 1 y se devuelve el método.

3. if (phase == 2) - aquí el ajuste se devuelve a los individuos de la población B.

• Para cada elemento del bucle for (int i = 0; i < popSize; i++), el valor de ajuste de a[i].f se copia en B[i].f.
  
• El valor de fase se incrementa en 1 y se ejecuta la lógica del algoritmo posterior.

4. Selección - aquí se realiza la selección.

• Si el valor aleatorio u.RNDprobab() es inferior a 0.5, por cada elemento del bucle for (int i = 0; i < popSize; i++), se copia el individuo A[i] en Predator[i], mientras que Key se pone a 1.
• De lo contrario, por cada elemento del bucle for (int i = 0; i < popSize; i++), se copia el individuo B[i] en Predator[i], mientras que Key se establece en 2.
• La selección de la matriz Prey se ejecuta de forma similar.

5. Permutación de presas - aquí las coordenadas se permutan aleatoriamente en cada individuo de la población Prey.

• Para cada individuo del bucle for (int i = 0; i < popSize; i++), se ejecuta ArrayShuffle (Prey[i].c) mezclando las coordenadas individuales (las coordenadas de cada individuo se mezclan por separado, mientras que las coordenadas entre individuos no se mezclan).

6. Mutation y Crossover - aquí se ejecutan la mutación y el cruce.

• El valor de R se calcula en función de un número aleatorio.
• La matriz binaria M se rellena con unos.
• Se realizan operaciones adicionales en la matriz M cambiando algunos de sus elementos a 0 o 1, dependiendo de la probabilidad bioProbab de interacción biológica.
• Para cada individuo del bucle for (int i = 0; i < popSize; i++), se realizan la mutación y el cruce, actualizando los valores de la matriz de población a.

7. Boundary control (Control de los límites) - bloque que realiza el control de límites, en el que los individuos de la población a coordenadas fuera del rango especificado de parámetros optimizados se sustituyen por valores aleatorios dentro del rango.

Este método implementa las operaciones básicas del algoritmo, como la selección, la mutación, el cruce y el control de límites, que se aplican a una población de individuos para encontrar la solución óptima.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm1::Moving ()
{
  //----------------------------------------------------------------------------
  if (phase == 0)
  {
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 1)
  {
    for (int i = 0; i < popSize; i++) A [i].f = a [i].f;
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 2)
  {
    for (int i = 0; i < popSize; i++) B [i].f = a [i].f;

    phase++;
  }

  //----------------------------------------------------------------------------
  // Selection
  if (u.RNDprobab () < 0.5)
  {
    for (int i = 0; i < popSize; i++)
    {
      Predator [i] = A [i];                                                       
    }

    Key = 1;
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      Predator [i] = B [i];                             
    }

    Key = 2;
  }

  if (u.RNDprobab () < 0.5)
  {
    for (int i = 0; i < popSize; i++)
    {
      Prey [i] = A [i];                                 
    }
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      Prey [i] = B [i];                                 
    }
  }

  // Permutation of Prey
  for (int i = 0; i < popSize; i++)
  {
    ArrayShuffle (Prey [i].c);
  }

  double R;

  if (u.RNDprobab () < 0.5)
  {
    R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0);
  }
  else R = 1 / MathExp (4 * MathRand () / 32767.0);

  // Fill binary matrix M with 0s
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      M [i].c [j] = 0;
    }
  }

  // Additional operations with matrix M
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    int sum = 0;

    for (int c = 0; c < coords; c++) sum += M [i].c [c];

    if (sum == coords)
    {
      int j = MathRand () % coords;
      M [i].c [j] = 0;
    }
  }

  // Mutation
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]);

      // Crossover
      if (M [i].c [j] > 0)
      {
        a [i].c [j] = Predator [i].c [j];
      }

      // Boundary control
      if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j])
      {
        a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      }
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

A continuación, consideremos el código del método Revision de la clase C_AO_ACSm1. Realiza las siguientes operaciones:

1. Comprueba si phase (fase de preparación de poblaciones) ya está completa fase >= 3. Si no se cumple esta condición, el método regresa sin realizar más acciones.

2. Actualiza la selección de Actualización de selección de los individuos:

• Para cada individuo de la población a, comprueba si su valor de ajuste f supera el valor correspondiente de la matriz Predator. En caso afirmativo, se actualiza el valor en Predator.
• En función del valor de la variable Key, los individuos de la población Predator se copian en la población A o B.

3. Determina el valor Ybest, que representa la mejor puntuación de aptitud, y su índice correspondiente Ibest dentro de la matriz Predator.

• Iterar sobre la matriz Predator, encontrar el valor máximo de ajuste y su índice.

4. Actualiza la fB mejor solución global:

• Si Ybest supera el mejor valor actual de fB, se actualiza fB, mientras que los elementos apropiados de la matriz a y cB se copian de la matriz Predator.

Este método actualiza la selección individual, determina la mejor solución y actualiza la mejor solución global dentro del algoritmo de optimización.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm1::Revision ()
{
  if (phase < 3) return;

  // Selection update
  for (int i = 0; i < popSize; i++)
  {
    double d = a [i].f;

    if (d > Predator [i].f)
    {                      
      Predator [i] = a [i];
    }                                    
  }

  if (Key == 1)
  {
    for (int i = 0; i < popSize; i++)
    {
      A [i] = Predator [i];
    }
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      B [i] = Predator [i];
    }
  }

  double Ybest = -DBL_MAX;
  int Ibest = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (Predator [i].f > Ybest)
    {
      Ybest = Predator [i].f;
      Ibest = i;
    }
  }

  if (Ybest > fB)
  {
    fB = Ybest;
    ArrayCopy (a [Ibest].c, Predator [Ibest].c);
    ArrayCopy (cB, Predator [Ibest].c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método ArrayShuffle de la clase C_AO_ACS se aplica en las tres modificaciones, además de realizar un barajado aleatorio de los elementos del array:

1. Define el tamaño del array «arr» mediante la función ArraySize.
2. Iterar sobre arr array en orden inverso, empezando por el último elemento.
3. Para cada elemento i, genera un índice aleatorio j de 0 a i.
4. Intercambia los elementos arr[i] y arr[j] utilizando la variable temporal tmp.

Como resultado, los elementos de la matriz arr se barajan aleatoriamente.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm1::ArrayShuffle (double &arr [])
{
  int n = ArraySize (arr);
  for (int i = n - 1; i > 0; i--)
  {
    int j = MathRand () % (i + 1);
    double tmp = arr [i];
    arr [i] = arr [j];
    arr [j] = tmp;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Ahora es el momento de analizar el código de la segunda modificación del algoritmo ACS. El código del método Moving de la clase C_AO_ACSm2 de acuerdo con los cambios:

1. Fase 0:

• Si la fase es igual a 0, cada individuo de la población a obtiene los valores de la población A.
• Se incrementa el valor de la fase y se devuelve el método.

2. Fase 1:

• Si la fase es 1, cada individuo de la población a obtiene valores de ajuste f en la población A.
• Cada individuo de la población a obtiene los valores de la población B.
• Se incrementa el valor de la fase y se devuelve el método.

3. Fase 2:

• Si la fase es 2, cada individuo de la población B obtiene «f» valores de ajuste de la población a.
• El valor de fase aumenta y continúa la lógica del algoritmo.

4. Selección:

• Para cada individuo de las poblaciones A y B, se comparan los valores de ajuste f.
• Si el valor de f en A supera a B, un individuo de A se copia en Predador, mientras que un individuo de B se copia en Prey. De lo contrario, es al revés (los individuos más aptos se designan como «depredadores» y los menos aptos se convierten en «presas»).

5. Permutación de presa:

• Las coordenadas de cada individuo de la población Prey se permutan utilizando la función ArrayShuffle.

6. Mutación y Cruce:

• R se define en función de un número aleatorio.
• La matriz binaria M se rellena con ceros.
• Se realizan operaciones adicionales en la matriz M, donde algunos elementos se ponen a 1 en función de la probabilidad bioProbab.

   Para cada individuo de la población a:

• Se realiza la mutación: a[i].c[j] se calcula como la suma de Predator[i].c[j] y el producto de R por la diferencia entre Prey[i].c[j] y Predator[i].c[j].
• Se realiza el cruce: si M[i].c[j] es igual a 1, a[i].c[j] se sustituye por Predator[i].c[j].
• Comprobación de límites: si a[i].c[j] está fuera de rangeMin[j] y rangeMax[j], se sustituye por un valor aleatorio dentro de este rango.

7. Comprobando coordenadas:

• Para cada individuo de la población a, se comprueban las coordenadas mediante la función SeInDiSp.
  

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm2::Moving ()
{
  //----------------------------------------------------------------------------
  if (phase == 0)
  {
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 1)
  {
    for (int i = 0; i < popSize; i++) A [i].f = a [i].f;
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 2)
  {
    for (int i = 0; i < popSize; i++) B [i].f = a [i].f;

    phase++;
  }

  //----------------------------------------------------------------------------
  // Selection                     
  for (int i = 0; i < popSize; i++)
  {                                
    if (A [i].f > B [i].f)         
    {                              
      Predator [i] = A [i];        
      Prey     [i] = B [i];        
    }                              
    else                           
    {                              
      Predator [i] = B [i];        
      Prey     [i] = A [i];        
    }                              
  }                                

  // Permutation of Prey
  for (int i = 0; i < popSize; i++)
  {
    ArrayShuffle (Prey [i].c);
  }

  double R;

  if (u.RNDprobab () < 0.5)
  {
    R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0);
  }
  else R = 1 / MathExp (4 * MathRand () / 32767.0);

  // Fill binary matrix M with 0s
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      M [i].c [j] = 0;
    }
  }

  // Additional operations with matrix M
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    int sum = 0;

    for (int c = 0; c < coords; c++) sum += M [i].c [c];

    if (sum == coords)
    {
      int j = MathRand () % coords;
      M [i].c [j] = 0;
    }
  }

  // Mutation
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]);

      // Crossover
      if (M [i].c [j] > 0)
      {
        a [i].c [j] = Predator [i].c [j];
      }

      // Boundary control
      if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j])
      {
        a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      }
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

No consideraré aquí el método Revision de la segunda modificación del algoritmo ya que ha permanecido intacto.

Pasemos a la tercera modificación. Se han realizado los siguientes cambios en la definición de la C_AO_ACSm3 tercera clase de modificación derivada de C_AO (clase base):

La lista de miembros de datos ha cambiado:

• bioProbab - probabilidad de interacción biológica.
• A[], B[], Predator[], Prey[], Pop[], pTemp[] - matrices que almacenan diferentes poblaciones de individuos.
• M[] - matriz que almacena datos adicionales asociados a los individuos.
• phase - fase actual del algoritmo.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACSm3 : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ACSm3 () { }
  C_AO_ACSm3 ()
  {
    ao_name = "ACS";
    ao_desc = "Artificial Cooperative Search m3";
    ao_link = "https://www.mql5.com/ru/articles/15014";

    popSize   = 10;   //population size
    bioProbab = 0.9; //biological interaction probability

    ArrayResize (params, 2);

    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "bioProbab"; params [1].val = bioProbab;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    bioProbab = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double bioProbab; //biological interaction probability

  private: //-------------------------------------------------------------------
  S_AO_Agent A        [];
  S_AO_Agent B        [];
  S_AO_Agent Predator [];
  S_AO_Agent Prey     [];
  S_AO_Agent Pop      [];
  S_AO_Agent pTemp    [];

  S_C M               [];

  int phase;

  void ArrayShuffle (double &arr []);
};
//——————————————————————————————————————————————————————————————————————————————

Se han realizado los siguientes cambios en el método de inicialización Init de la clase C_AO_ACSm3:

1. Se asigna memoria para las matrices A, B, Predator, Prey, Pop, pTemp y M de popSize o popSize * 2.

2. Cada elemento de las matrices A, B, Predator, Prey, Pop y M se inicializa mediante el método Init.

Los autores de la versión original del algoritmo no tienen una división de la lógica en fases. He añadido una división en fases para implementar el algoritmo en el estilo que he adoptado para todos los algoritmos de población. Esto era necesario porque el ACS utiliza un cálculo previo del ajuste del agente para las poblaciones А y B. Estas operaciones deben realizarse secuencialmente en los métodos.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ACSm3::Init (const double &rangeMinP [], //minimum search range
                       const double &rangeMaxP  [], //maximum search range
                       const double &rangeStepP [], //step search
                       const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (A,        popSize);
  ArrayResize (B,        popSize);
  ArrayResize (Predator, popSize);
  ArrayResize (Prey,     popSize);
  ArrayResize (Pop,      popSize * 2);
  ArrayResize (pTemp,    popSize * 2);

  ArrayResize (M,        popSize);

  for (int i = 0; i < popSize; i++)
  {
    A        [i].Init (coords);
    B        [i].Init (coords);
    Predator [i].Init (coords);
    Prey     [i].Init (coords);

    M        [i].Init (coords);
  }

  for (int i = 0; i < popSize * 2; i++) Pop [i].Init (coords);

  // Initialization
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      A [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      B [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
    }
  }

  phase = 0;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Ahora echemos un vistazo al código del método Moving dentro de la clase C_AO_ACSm3 de la tercera modificación. Los cambios han afectado a las siguientes áreas de código:

• Fusión de las poblaciones A y B en una única población Pop.
• Ordenar la población Pop por los valores de ajuste de los individuos.
• Rellenar las poblaciones Predator y Prey a partir de la matriz ordenada Pop donde la mejor mitad de la población se convierte en «depredadores» y la otra mitad en «presas», respectivamente.
• Rellenar la matriz binaria M con unos.
• Operaciones adicionales con la matriz M, en la que algunos elementos cambian a 0 o 1 dependiendo de un número aleatorio y de la probabilidad bioProbab de interacción biológica.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm3::Moving ()
{
  //----------------------------------------------------------------------------
  if (phase == 0)
  {
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 1)
  {
    for (int i = 0; i < popSize; i++) A [i].f = a [i].f;
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 2)
  {
    for (int i = 0; i < popSize; i++) B [i].f = a [i].f;

    phase++;
  }

  //----------------------------------------------------------------------------
  // Merge matrices A and B to create matrix Pop      
  for (int i = 0; i < popSize; i++)                   
  {                                                   
    Pop [i]           = A [i];                        
    Pop [i + popSize] = B [i];                        
  }                                                   
                                                      
  // Sort matrix Pop using column N as sort key values
  u.Sorting (Pop, pTemp, popSize * 2);                
                                                      
  // Populate Predator and Prey matrices              
  for (int i = 0; i < popSize; i++)                   
  {                                                   
    Predator [i] = Pop [i];                           
    Prey     [i] = Pop [i + popSize];                 
  }                                                   

  // Permutation of Prey
  for (int i = 0; i < popSize; i++)
  {
    ArrayShuffle (Prey [i].c);
  }

  double R;

  if (u.RNDprobab () < 0.5)
  {
    R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0);
  }
  else R = 1 / MathExp (4 * MathRand () / 32767.0);

  // Fill binary matrix M with 1s
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      M [i].c [j] = 1;                
    }
  }

  // Additional operations with matrix M
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 0;              
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        if (u.RNDprobab() < bioProbab)
        {                             
          M[i].c[j] = 1;              
        }                             
        else                          
        {                             
          M[i].c[j] = 0;              
        }                             
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    int sum = 0;

    for (int c = 0; c < coords; c++) sum += M [i].c [c];

    if (sum == coords)
    {
      int j = MathRand () % coords;
      M [i].c [j] = 0;
    }
  }

  // Mutation
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]);

      // Crossover
      if (M [i].c [j] > 0)
      {
        a [i].c [j] = Predator [i].c [j];
      }

      // Boundary control
      if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j])
      {
        a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      }
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Resultados de las pruebas

Hemos revisado y analizado cuidadosamente todas las versiones conocidas de este algoritmo. Ahora es el momento de centrarnos en sus resultados prácticos y en las conclusiones que podemos extraer. Me propongo detenerme en detalle en cómo afectó cada una de las modificaciones a la productividad, la precisión y la eficacia. Esto nos permitirá comprender mejor qué cambios han tenido más éxito y hacia dónde debemos avanzar a continuación.

La primera versión de la modificación mostró resultados aproximadamente comparables en la puntuación global, pero los resultados mejoraron significativamente en la función Hilly con 1000 variables y en la función Forest con 50 y 1000 variables.

ACS|Artificial Cooperative Search m1|1.0|0.7|
=============================
5 Hilly's; Func runs: 10000; result: 0.7130880902279995
25 Hilly's; Func runs: 10000; result: 0.7565145335137569
500 Hilly's; Func runs: 10000; result: 0.31899537529427235
=============================
5 Forest's; Func runs: 10000; result: 0.9999999999866176
25 Forest's; Func runs: 10000; result: 0.9555551824899264
500 Forest's; Func runs: 10000; result: 0.24186829565864398
=============================
5 Megacity's; Func runs: 10000; result: 0.6607692307692307
25 Megacity's; Func runs: 10000; result: 0.5038461538461539
500 Megacity's; Func runs: 10000; result: 0.13922307692307825
=============================
All score: 5.28986 (58.78%)

La segunda versión del algoritmo mostró una notable mejora de los resultados en todas las funciones de prueba con 50 y 1000 variables, pero los resultados empeoraron significativamente en Megacity con 10 variables (dispersión extremadamente grande de los resultados) en comparación con la versión básica. Esto indica que el movimiento en esta dirección es prometedor (aunque hay puntos controvertidos), y merece la pena seguir trabajando en nuevas modificaciones.

ACS|Artificial Cooperative Search m2|2.0|0.7|
=============================
5 Hilly's; Func runs: 10000; result: 0.7682797921658492
25 Hilly's; Func runs: 10000; result: 0.7664893907210706
500 Hilly's; Func runs: 10000; result: 0.31831672493319296
=============================
5 Forest's; Func runs: 10000; result: 0.9999997349437437
25 Forest's; Func runs: 10000; result: 0.9534110489423269
500 Forest's; Func runs: 10000; result: 0.24425762117784502
=============================
5 Megacity's; Func runs: 10000; result: 0.6176923076923077
25 Megacity's; Func runs: 10000; result: 0.5384615384615385
500 Megacity's; Func runs: 10000; result: 0.14057692307692446
=============================
All score: 5.34749 (59.42%)

Por desgracia, la tercera modificación, que parecía la más prometedora, no estuvo a la altura de las expectativas y mostró un resultado global algo peor que la versión básica del algoritmo. Aunque cabe destacar que los resultados sobre la función Hilly (suave) con 10 variables han mejorado notablemente. El algoritmo demuestra una mayor precisión de convergencia precisamente en funciones suaves con un número reducido de variables.

ACS|Artificial Cooperative Search m3|10.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.8836798635515516
25 Hilly's; Func runs: 10000; result: 0.715438105666966
500 Hilly's; Func runs: 10000; result: 0.3011611038405591
=============================
5 Forest's; Func runs: 10000; result: 0.9893902762645717
25 Forest's; Func runs: 10000; result: 0.7954795408759185
500 Forest's; Func runs: 10000; result: 0.21910399769909533
=============================
5 Megacity's; Func runs: 10000; result: 0.6315384615384615
25 Megacity's; Func runs: 10000; result: 0.49876923076923074
500 Megacity's; Func runs: 10000; result: 0.12683076923077044
=============================
All score: 5.16139 (57.35%)

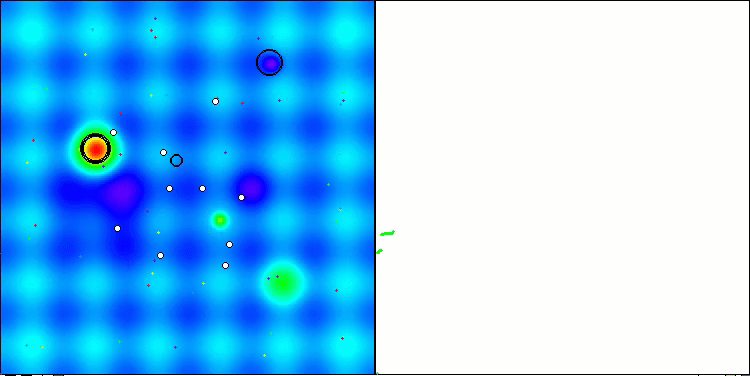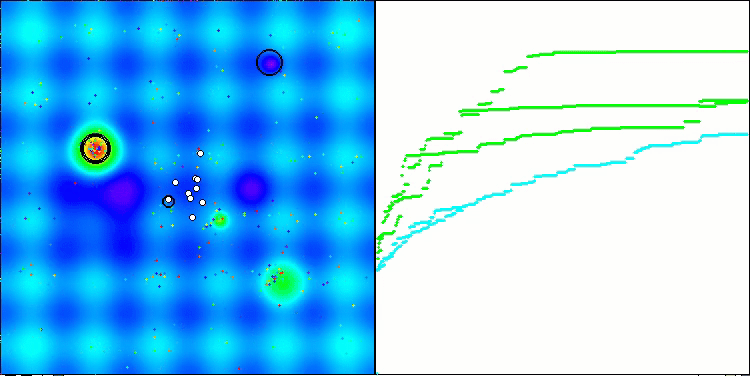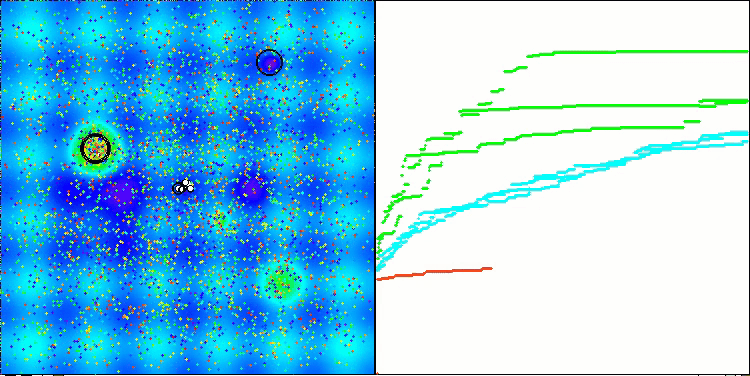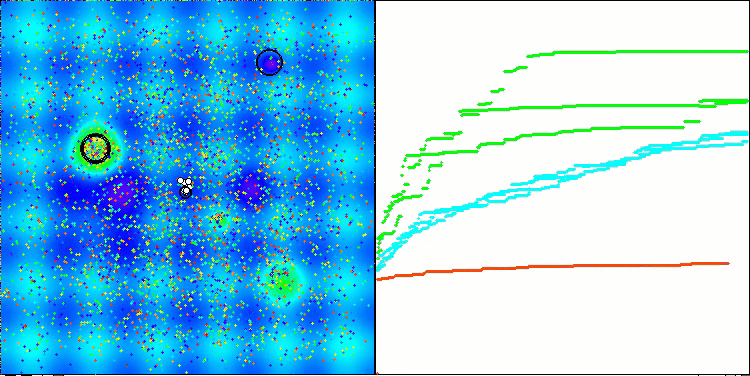
Visualización de la segunda modificación del algoritmo. Con un número reducido de variables, hay una gran diferencia en los resultados de las funciones Hilly y Megacity, mientras que el algoritmo es excelente en la función lisa y puntiaguda Forest.

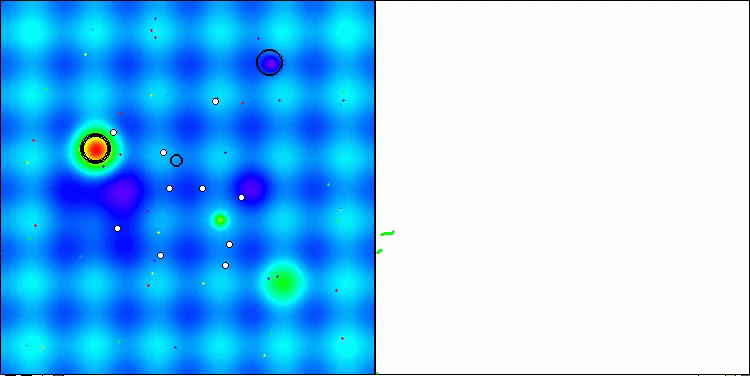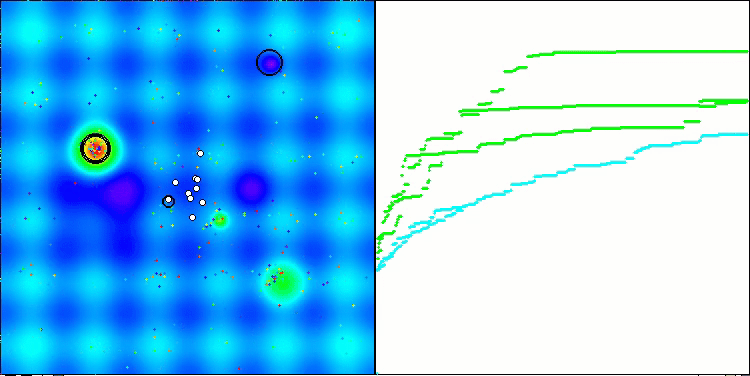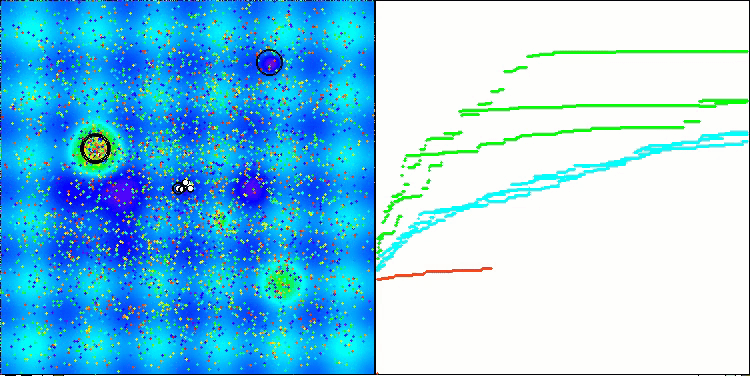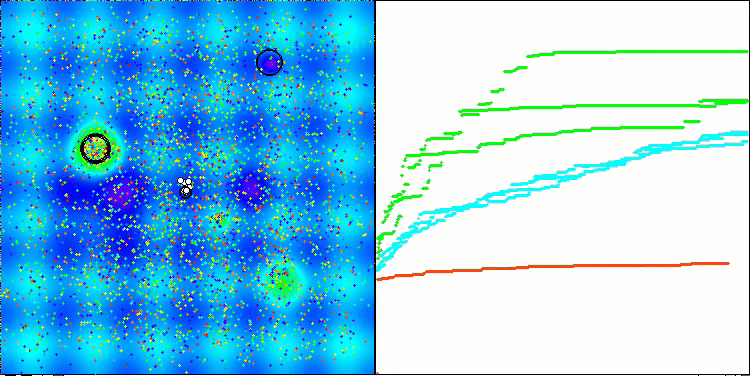
  ACSm2 en la función de prueba Hilly.

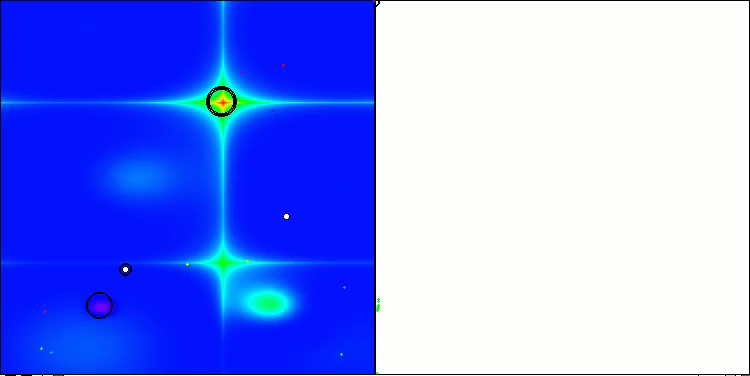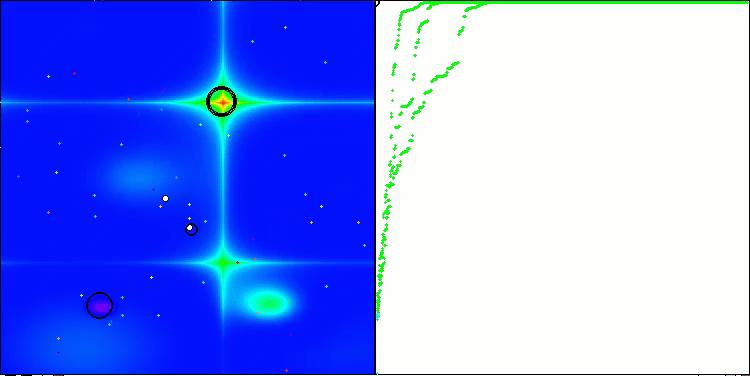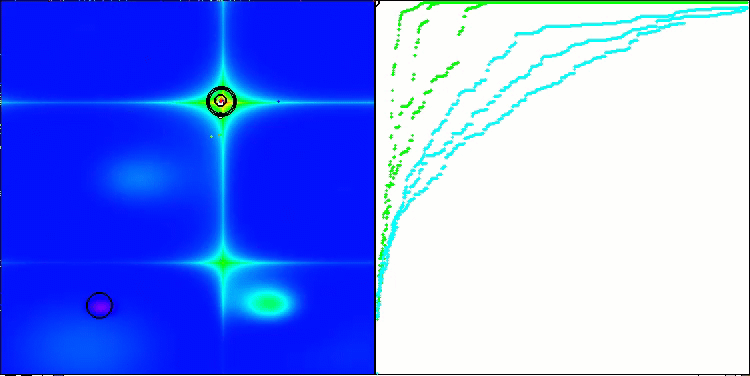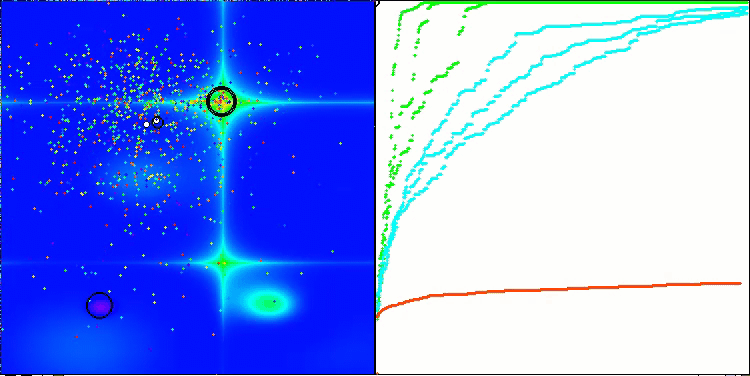
ACSm2 en la función de prueba Forest.

  ACSm2 en la función de prueba Megacity.

Resumen

Las conclusiones generales son las siguientes:

1. La primera modificación del algoritmo ACS, con la adición de formas aumentadas de las matrices A y B, mejoró la precisión de las soluciones, especialmente en funciones Hilly con 1000 variables y funciones Forest con 50 y 1000 variables.

2. La segunda modificación, que cambia el enfoque para rellenar las matrices Predator y Prey, utiliza comparaciones aleatorias para actualizar las matrices y mostró una notable mejora de los resultados en todas las funciones de prueba con 50 y 1000 variables, pero condujo a una mayor dispersión de los resultados en la función Megacity con 10 variables.

3. La tercera modificación, centrada en el uso del ajuste para formar las poblaciones Predator y Prey, no cumplió las expectativas, mostrando un resultado global algo peor que la versión básica del algoritmo, aunque mejoró la precisión de la convergencia en funciones suaves con un número reducido de variables.

Por lo tanto, cada modificación tiene sus propios puntos fuertes y débiles, y para un mayor desarrollo del algoritmo es necesario tener en cuenta estas características con el fin de crear una versión más eficiente y universal del algoritmo ACS.

Posibles áreas de mejora:

1. Modificación de los mecanismos de búsqueda:

• Analizar los mecanismos de búsqueda actuales utilizados en el algoritmo y considerar la posibilidad de optimizarlos aún más.
• Explorar si pueden introducirse mecanismos adicionales, como pasos de búsqueda adaptativos, para mejorar la eficacia de la búsqueda.

2. Exploración de enfoques híbridos:

• Considere la posibilidad de combinar el algoritmo actual con otros métodos de optimización para aprovechar los puntos fuertes de los distintos enfoques. Por ejemplo, podemos intentar integrar elementos de algoritmos evolutivos o métodos de inteligencia de enjambre para aumentar la diversidad y la velocidad de convergencia.

3. Análisis y mejora del mecanismo de interacción entre poblaciones:

• Descubra cómo se puede mejorar la forma en que interactúan las poblaciones A y B para que se complementen mejor durante la búsqueda. Puede que merezca la pena considerar estructuras más complejas de intercambio de información o aprendizaje cooperativo entre poblaciones.

Figura 1. Gradación cromática de las modificaciones del algoritmo según las pruebas pertinentes para su comparación con la versión básica. Los resultados superiores o iguales a 0,99 se resaltan en blanco

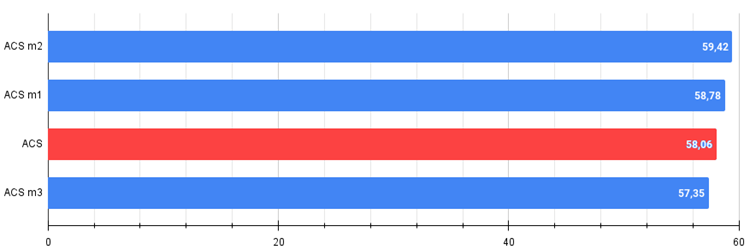
Figura 2. El histograma de los resultados de la modificación del algoritmo (en una escala de 0 a 100, cuanto más, mejor,

donde 100 es el resultado teórico máximo posible, el archivo contiene un script para calcular la tabla de cotizaciones)

Ventajas e inconvenientes generales de las versiones modificadas del algoritmo ACS:

Ventajas:

1. Número reducido de parámetros externos (sólo uno).
   
2. Buena convergencia en varios tipos de funciones.

Desventajas:

1. Dispersión de resultados en funciones de baja dimensión.
   

El artículo va acompañado de un archivo con las versiones actuales de los códigos de los algoritmos. El autor del artículo no se responsabiliza de la exactitud absoluta en la descripción de los algoritmos canónicos. Se han introducido cambios en muchos de ellos para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos.

• GitHub: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/ru/code/49355