
Ciência de Dados e Aprendizado de Máquina (Parte 03): Regressões Matriciais
Após um longo período de tentativas e erros, finalmente, o quebra-cabeça da regressão dinâmica múltipla está resolvido... continue lendo.
Se você prestou atenção nos dois artigos anteriores, notará que o grande problema que eu tive foi de programar modelos que pudessem lidar com mais variáveis independentes, em outras palavras, lidar dinamicamente com mais entradas pois quando se trata de criar estratégias, nós vamos lidar com centenas de dados, por isso nós queremos ter certeza de que os nossos modelos podem lidar com essa demanda.
Matriz
Para aqueles que pularam as aulas de matemática, uma matriz é um vetor retangular ou tabela de números ou outros objetos matemáticos organizados em linhas e colunas que são usados para representar um objeto matemático ou uma propriedade de tal objeto.
Por exemplo:
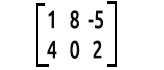
A maneira como nós lemos as matrizes é por linhas x colunas. A matriz acima é uma matriz 2x3 que significa 2 linhas, 3 colunas.
Não há dúvida de que as matrizes desempenham um papel importante na forma como os computadores modernos processam as informações e calculam grandes números, a principal razão pela qual eles são capazes de conseguir isso é porque os dados na matriz são armazenados na forma de vetores que os computadores podem ler e manipular. Então, vamos ver a sua aplicação no aprendizado de máquina.
Regressão linear
As matrizes permitem a realização de cálculos em álgebra linear. Portanto, o estudo das matrizes é uma grande parte da álgebra linear, então nós podemos usar as matrizes para fazer criar nossos modelos de regressão linear.
Como todos nós sabemos, a equação de uma reta é
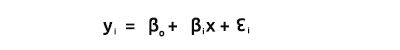
onde, ∈ são termos de erro, Bo e Bi são os coeficientes de interceptação em y e o coeficiente de inclinação respectivamente
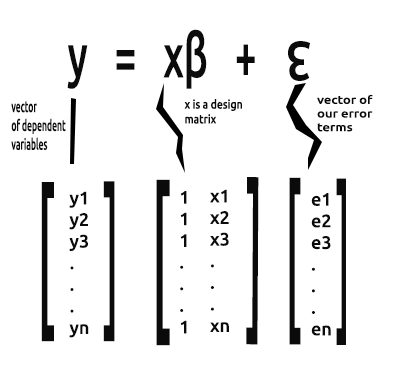
O que nós estamos interessados nesta série de artigos a partir de agora é a forma vetorial de uma equação. Aqui está ela
Esta é a formulação de uma regressão linear simples em forma de matriz.
Para um modelo linear simples (e outros modelos de regressão), geralmente, nós estamos interessados em encontrar os coeficientes de inclinação/estimadores dos mínimos quadrados ordinários.
O vetor Beta é um vetor contendo betas.
Bo e B1, como explicado a partir da equação
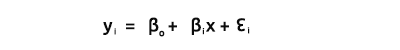
Nós estamos interessados em encontrar os coeficientes, pois eles são essenciais na construção de um modelo.
A fórmula para os estimadores dos modelos em forma vetorial é
Esta é uma fórmula muito importante para todos os nerds memorizarem. Nós discutiremos em breve como encontrar os elementos na fórmula.
O Produto de xTx fornecerá a matriz simétrica, pois o número de colunas em xT é o mesmo que o número de linhas em x, nós veremos isso mais tarde em ação.
Como dito anteriormente, x também é referido como a matriz de projeto, encontramos a seguir como a matriz será.
Matriz de Design
Como você pode ver, na primeira coluna, nós colocamos apenas os valores de 1 até o final de nossas linhas em um vetor matricial. Este é o primeiro passo para a preparação dos nossos dados para a regressão matricial, você verá as vantagens de fazer isso à medida que nós avançamos nos cálculos.
Tratamos esse processo na função Init() da nossa biblioteca.
void CSimpleMatLinearRegression::Init(double &x[],double &y[], bool debugmode=true) { ArrayResize(Betas,2); //since it is simple linear Regression we only have two variables x and y if (ArraySize(x) != ArraySize(y)) Alert("There is variance in the number of independent variables and dependent variables \n Calculations may fall short"); m_rowsize = ArraySize(x); ArrayResize(m_xvalues,m_rowsize+m_rowsize); //add one row size space for the filled values ArrayFill(m_xvalues,0,m_rowsize,1); //fill the first row with one(s) here is where the operation is performed ArrayCopy(m_xvalues,x,m_rowsize,0,WHOLE_ARRAY); //add x values to the array starting where the filled values ended ArrayCopy(m_yvalues,y); m_debug=debugmode; }
Até este ponto, ao exibimos os valores da matriz de design abaixo, é possível visualizar exatamente onde os valores preenchidos com o número 1 terminam em uma linha e onde os valores x começam.
[ 0] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 21] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
........
........
[ 693] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 714] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 735] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 4173.8 4179.2 4182.7 4185.8 4180.8 4174.6 4174.9 4170.8 4182.2 4208.4 4247.1 4217.4
[ 756] 4225.9 4211.2 4244.1 4249.0 4228.3 4230.6 4235.9 4227.0 4225.0 4219.7 4216.2 4225.9 4229.9 4232.8 4226.4 4206.9 4204.6 4234.7 4240.7 4243.4 4247.7
........
........
[1449] 4436.4 4442.2 4439.5 4442.5 4436.2 4423.6 4416.8 4419.6 4427.0 4431.7 4372.7 4374.6 4357.9 4381.6 4345.8 4296.8 4321.0 4284.6 4310.9 4318.1 4328.0
[1470] 4334.0 4352.3 4350.6 4354.0 4340.1 4347.5 4361.3 4345.9 4346.5 4342.8 4351.7 4326.0 4323.2 4332.7 4352.5 4401.9 4405.2 4415.8
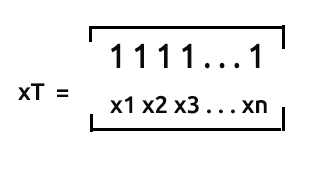
xT ou x transposto é um processo matricial na qual nós trocamos as linhas pelas colunas.
Isso significa que se nós multiplicarmos essas duas matrizes
Nós vamos pular o processo de transposição de uma matriz porque nós coletamos os nossos dados já na forma transposta, embora tenhamos que transpor novamente os valores de x para que possamos multiplicá-los pela matriz x já transposta.
A matriz nx2 que não é uma matriz transposta será semelhante a [1 x1 1 x2 1 ... 1 xn]. Vamos ver isso em ação.
Transpondo uma Matriz transposta de X
Nossa Matrix na forma transposta, que foi obtida de um arquivo csv ficará assim, quando impressa:
Transposed Matrix
[
[ 0] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
...
...
[ 0] 4174 4179 4183 4186 4181 4175 4175 4171 4182 4208 4247 4217 4226 4211 4244 4249 4228 4231 4236 4227 4225 4220 4216 4226
...
...
[720] 4297 4321 4285 4311 4318 4328 4334 4352 4351 4354 4340 4348 4361 4346 4346 4343 4352 4326 4323 4333 4352 4402 4405 4416
]
O processo de transposição de uma matriz transposta, nós só temos que trocar as linhas pelas colunas, sendo o mesmo processo oposto da transposição da matriz.
int tr_rows = m_rowsize, tr_cols = 1+1; //since we have one independent variable we add one for the space created by those values of one MatrixUnTranspose(m_xvalues,tr_cols,tr_rows); Print("UnTransposed Matrix"); MatrixPrint(m_xvalues,tr_cols,tr_rows);
As coisas ficam complicadas aqui.
Nós trocamos as colunas de uma matriz transposta em um local onde deveriam haver as linhas e as linhas em um local onde deveriam haver as colunas, a saída ao executar este trecho de código será:
UnTransposed Matrix [ 1 4248 1 4201 1 4352 1 4402 ... ... 1 4405 1 4416 ]
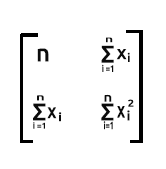
xT é uma matriz 2xn, x é uma nx2. A matriz resultante será uma matriz 2x2
Então, vamos trabalhar para ver como será o produto de sua multiplicação.
Atenção: para que a multiplicação de matrizes seja possível, o número de colunas da primeira matriz deve ser igual ao número de linhas da segunda matriz.
Veja as regras de multiplicação das matrizes neste link https://en.wikipedia.org/wiki/Matrix_multiplication.
A forma como a multiplicação é realizada nesta matriz é:
- Linha 1 multiplicado pela coluna 1
- Linha 1 multiplicado pela coluna 2
- Linha 2 multiplicado pela coluna 1
- Linha 2 multiplicado pela coluna 2
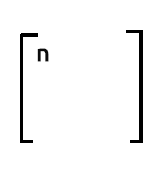
Das nossas matrizes a linha 1 multiplicada pela coluna1 terá uma saída equivalente a soma do produto da linha1 que contém os valores de um e o produto da coluna1 que também contém os valores de um, não há diferença de incrementar o valor um por um em cada iteração.
Nota:
Se você deseja saber o número de observações em seu conjunto de dados, você pode confiar no número do primeiro elemento da primeira coluna na saída de xTx.
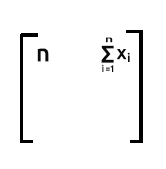
Linha 1 multiplicado pela coluna 2. Como a linha 1 contém os valores iguais a 1, quando nós somamos o produto da linha1 (que são valores iguais a 1) e a coluna2(que são valores iguais a x), a saída será a soma de x itens já que um não terá efeito na multiplicação.
Linha2 multiplicado pela coluna 1. A saída será a soma de x já que os valores iguais a 1 da linha2 não têm efeito quando eles multiplicam os valores de x da coluna 1.
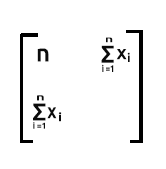
A última parte será a soma dos valores de x ao quadrado.
Uma vez que ele é a soma do produto da linha2, que contém os valores de x e da coluna2, que também contém os valores de x
Como você pode ver, a saída da matriz é uma matriz 2x2 neste caso.
Vamos ver como isso funciona no mundo real, usando o conjunto de dados do nosso primeiro artigo de Regressão linear https://www.mql5.com/en/articles/10459. Vamos extrair os dados e colocá-los em um vetor x para a variável independente e y para as variáveis dependentes.
//inside MatrixRegTest.mq5 script #include "MatrixRegression.mqh"; #include "LinearRegressionLib.mqh"; CSimpleMatLinearRegression matlr; CSimpleLinearRegression lr; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //double x[] = {651,762,856,1063,1190,1298,1421,1440,1518}; //stands for sales //double y[] = {23,26,30,34,43,48,52,57,58}; //money spent on ads //--- double x[], y[]; string file_name = "NASDAQ_DATA.csv", delimiter = ","; lr.GetDataToArray(x,file_name,delimiter,1); lr.GetDataToArray(y,file_name,delimiter,2); }
Eu importei a biblioteca CsimpleLinearRegression que nós criamos no primeiro artigo
CSimpleLinearRegression lr;
já que existem certas funções que nós podemos querer usar, como obter os dados para os vetores.
Vamos encontrar xTx
MatrixMultiply(xT,m_xvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols); Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5); //remember?? a saída da matriz será a linha1 e a col2 marcadas em vermelho
Se você prestar atenção ao vetor xT[], você pode ver que nós apenas copiamos os valores de x e os armazenamos no vetor xT[] apenas para esclarecimento, como eu disse anteriormente a maneira como coletamos os dados do nosso arquivo csv para um vetor usando a função GetDataToArray() nos fornece os dados que já estão transpostos.
Em seguida, nós multiplicamos o vetor xT[] com m_xvalues[] que agora não são transpostos, m_xvalues é o vetor definido globalmente para os nossos valores de x nesta biblioteca. Este é o nosso interior da função MatrixMultiply().
void CSimpleMatLinearRegression::MatrixMultiply(double &A[],double &B[],double &output_arr[],int row1,int col1,int row2,int col2) { //--- double MultPl_Mat[]; //where the multiplications will be stored if (col1 != row2) Alert("Matrix Multiplication Error, \n The number of columns in the first matrix is not equal to the number of rows in second matrix"); else { ArrayResize(MultPl_Mat,row1*col2); int mat1_index, mat2_index; if (col1==1) //Multiplication for 1D Array { for (int i=0; i<row1; i++) for(int k=0; k<row1; k++) { int index = k + (i*row1); MultPl_Mat[index] = A[i] * B[k]; } //Print("Matrix Multiplication output"); //ArrayPrint(MultPl_Mat); } else { //if the matrix has more than 2 dimensionals for (int i=0; i<row1; i++) for (int j=0; j<col2; j++) { int index = j + (i*col2); MultPl_Mat[index] = 0; for (int k=0; k<col1; k++) { mat1_index = k + (i*row2); //k + (i*row2) mat2_index = j + (k*col2); //j + (k*col2) //Print("index out ",index," index a ",mat1_index," index b ",mat2_index); MultPl_Mat[index] += A[mat1_index] * B[mat2_index]; DBL_MAX_MIN(MultPl_Mat[index]); } //Print(index," ",MultPl_Mat[index]); } ArrayCopy(output_arr,MultPl_Mat); ArrayFree(MultPl_Mat); } } }
Para ser honesto, esta multiplicação parece me confusa e feia, em especial quando usamos coisas como
k + (i*row2); j + (k*col2);
Relaxe, irmão! A maneira como eu manipulei esses índices é para que eles possam nos fornecer o índice em uma linha e coluna específica. Isso poderia ser facilmente compreensível se eu pudesse usar os vetores bidimensionais, por exemplo Matrix[linhas][colunas], que seria a Matrix[i][k], eu optei por não as usar pois os vetores multidimensionais têm limitações, então eu tive que encontrar um caminho. eu tenho o link de um código simples em c++ no final do artigo, que eu acho que ajudaria você a entender como eu fiz isso. Outra opção seria ler este blog para entender mais sobre isso https://www.programiz.com/cpp-programming/examples/matrix-multiplication.
A saída com sucesso da função xTx usando uma função MatrixPrint() será
Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5);
xTx [ 744.00000 3257845.70000 3257845.70000 14275586746.32998 ]
Como você pode ver o primeiro elemento em nosso vetor xTx, ele tem o número de observações para cada dado em nosso conjunto de dados, é por isso que preencher inicialmente a matriz de design com os valores iguais a 1 na primeira coluna é muito importante.
Agora vamos encontrar a inversa da matriz xTx.
Inversa da Matriz xTx
Para encontrar a inversa de uma matriz 2x2, nós primeiro trocamos o primeiro e o último elemento da diagonal, depois adicionamos os sinais negativos aos outros dois valores.
A fórmula é dada na imagem abaixo:
Para encontrar o determinante de uma matriz det(xTx)= Produto da primeira diagonal - Produto da segunda diagonal.
Aqui está o código em mql5 de como nós podemos encontrar a inversa
void CSimpleMatLinearRegression::MatrixInverse(double &Matrix[],double &output_mat[]) { // According to Matrix Rules the Inverse of a matrix can only be found when the // Matrix is Identical Starting from a 2x2 matrix so this is our starting point int matrix_size = ArraySize(Matrix); if (matrix_size > 4) Print("Matrix allowed using this method is a 2x2 matrix Only"); if (matrix_size==4) { MatrixtypeSquare(matrix_size); //first step is we swap the first and the last value of the matrix //so far we know that the last value is equal to arraysize minus one int last_mat = matrix_size-1; ArrayCopy(output_mat,Matrix); // first diagonal output_mat[0] = Matrix[last_mat]; //swap first array with last one output_mat[last_mat] = Matrix[0]; //swap the last array with the first one double first_diagonal = output_mat[0]*output_mat[last_mat]; // second diagonal //adiing negative signs >>> output_mat[1] = - Matrix[1]; output_mat[2] = - Matrix[2]; double second_diagonal = output_mat[1]*output_mat[2]; if (m_debug) { Print("Diagonal already Swapped Matrix"); MatrixPrint(output_mat,2,2); } //formula for inverse is 1/det(xTx) * (xtx)-1 //determinant equals the product of the first diagonal minus the product of the second diagonal double det = first_diagonal-second_diagonal; if (m_debug) Print("determinant =",det); for (int i=0; i<matrix_size; i++) { output_mat[i] = output_mat[i]*(1/det); DBL_MAX_MIN(output_mat[i]); } } }
A saída da execução deste bloco de código será
Diagonal already Swapped Matrix
[
14275586746 -3257846
-3257846 744
]
determinant =7477934261.0234375 Vamos imprimir a Inversa da Matriz para ver como ela fica
Print("inverse xtx"); MatrixPrint(inverse_xTx,2,2,_digits); //inverse of simple lr will always be a 2x2 matrix
A saída certamente será
[
1.9090281 -0.0004357
-0.0004357 0.0000001
]
Agora nós temos a inversa de xTx, vamos seguir em frente.
Encontrando xTy
Aqui nós multiplicamos xT[] com os valores de y[]
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //1 at the end is because the y values matrix will always have one column which is it Print("xTy"); MatrixPrint(xTy,tr_rows,1,_digits); //remember again??? how we find the output of our matrix row1 x column2
A saída certamente será
xTy
[
10550016.7000000 46241904488.2699585
]
Referência da fórmula
Agora que nós temos a inversa de xTx e xTy, vamos juntar as coisas.
MatrixMultiply(inverse_xTx,xTy,Betas,2,2,2,1); //inverse is a square 2x2 matrix while xty is a 2x1 Print("coefficients"); MatrixPrint(Betas,2,1,5); // for simple lr our betas matrix will be a 2x1
Mais detalhes sobre como nós chamamos a função.
A saída deste trecho de código será
coefficients
[
-5524.40278 4.49996
]
BAM !!! Este é o mesmo resultado sobre os coeficientes que nós conseguimos obter com o nosso modelo em na forma escalar, na Parte 01 desta série de artigos.
O número no primeiro índice do vetor Betas sempre será uma constante/ interseção em y. A razão pela qual nós conseguimos obtê-lo inicialmente é porque nós preenchemos a matriz de design com os valores iguais a 1 para a primeira coluna, novamente isso mostra o quão importante é esse processo. Ele deixa o espaço para que a interseção em y permaneça nessa coluna.
Agora, nós terminamos com a Regressão Linear Simples. Vamos ver como será a regressão múltipla. Preste muita atenção porque as coisas podem ficar complicadas.
Resolvido o quebra-cabeça da regressão dinâmica múltipla
O bom de construir os nossos modelos com base na matriz é que é fácil escalá-los sem ter que mudar muito o código quando se trata de construir o modelo. Uma mudança significativa que você notará na regressão múltipla é como a inversa de uma matriz é encontrada, esta é a parte mais difícil, eu passei muito tempo tentando descobri-la, detalharei mais tarde quando chegarmos a essa seção, mas por enquanto, vamos codificar as coisas que nós podemos precisar em nossa biblitoca MultipleMatrixRegression.
Nós poderíamos ter apenas uma biblioteca que pudesse lidar com a regressão simples e múltipla, deixando-nos apenas inserir os argumentos da função, mas eu decidi criar outro arquivo para esclarecer as coisas, pois o processo será quase o mesmo, desde que você tenha entendido os cálculos que nós realizamos na nossa seção de regressão linear simples que eu acabei de explicar.
Em primeiro lugar, vamos codificar as coisas básicas que nós podemos precisar em nossa biblioteca.
class CMultipleMatLinearReg { private: int m_handle; string m_filename; string DataColumnNames[]; //store the column names from csv file int rows_total; int x_columns_chosen; //Number of x columns chosen bool m_debug; double m_yvalues[]; //y values or dependent values matrix double m_allxvalues[]; //All x values design matrix string m_XColsArray[]; //store the x columns chosen on the Init string m_delimiter; double Betas[]; //Array for storing the coefficients protected: bool fileopen(); void GetAllDataToArray(double& array[]); void GetColumnDatatoArray(int from_column_number, double &toArr[]); public: CMultipleMatLinearReg(void); ~CMultipleMatLinearReg(void); void Init(int y_column, string x_columns="", string filename = NULL, string delimiter = ",", bool debugmode=true); };
Isto é o que acontece dentro da função Init()
void CMultipleMatLinearReg::Init(int y_column,string x_columns="",string filename=NULL,string delimiter=",",bool debugmode=true) { //--- pass some inputs to the global inputs since they are reusable m_filename = filename; m_debug = debugmode; m_delimiter = delimiter; //--- ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen); //--- if (m_debug) { Print("Init, number of X columns chosen =",x_columns_chosen); ArrayPrint(m_XColsArray); } //--- GetAllDataToArray(m_allxvalues); GetColumnDatatoArray(y_column,m_yvalues); // check for variance in the data set by dividing the rows total size by the number of x columns selected, there shouldn't be a reminder if (rows_total % x_columns_chosen != 0) Alert("There are variance(s) in your dataset columns sizes, This may Lead to Incorrect calculations"); else { //--- Refill the first row of a design matrix with the values of 1 int single_rowsize = rows_total/x_columns_chosen; double Temp_x[]; //Temporary x array ArrayResize(Temp_x,single_rowsize); ArrayFill(Temp_x,0,single_rowsize,1); ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //after filling the values of one fill the remaining space with values of x //Print("Temp x arr size =",ArraySize(Temp_x)); ArrayCopy(m_allxvalues,Temp_x); ArrayFree(Temp_x); //we no longer need this array int tr_cols = x_columns_chosen+1, tr_rows = single_rowsize; ArrayCopy(xT,m_allxvalues); //store the transposed values to their global array before we untranspose them MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //we add one to leave the space for the values of one if (m_debug) { Print("Design matrix"); MatrixPrint(m_allxvalues,tr_cols,tr_rows); } } }
Mais detalhes sobre o que foi feito
ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen);
Aqui, nós obtemos as x colunas que foram selecionadas (as variáveis independentes) ao chamar a função Init no TestScript, em seguida, armazenamos essas colunas no vetor global m_XColsArray, ter as colunas em um vetor tem as suas vantagens, pois em breve nós estaremos lendo elas para que nós possamos armazená-las na ordem correta para a matriz de todos os valores x (matriz de variáveis independentes)/matriz de design.
Nós também temos que garantir que todas as linhas em nossos conjuntos de dados sejam iguais, porque uma vez que haja uma diferença em apenas uma linha ou coluna, todos os cálculos falharão.
if (rows_total % x_columns_chosen != 0) Alert("There are variances in your dataset columns sizes, This may Lead to Incorrect calculations");
Em seguida, nós obtemos todos os dados das x colunas para uma matriz / matriz de design / vetor de todas as variáveis independentes (você pode optar por chamá-la por um desses nomes).
GetAllDataToArray(m_allxvalues);
Nós também queremos armazenar todas as variáveis dependentes em sua matriz.
GetColumnDatatoArray(y_column,m_yvalues);
Este é o passo crucial para preparar a matriz de design para os cálculos. Adicionamos os valores iguais a 1 na primeira coluna da nossa matriz de valores x, como dito anteriormente aqui.
{
//--- Refill the first row of a design matrix with the values of 1
int single_rowsize = rows_total/x_columns_chosen;
double Temp_x[]; //Temporary x array
ArrayResize(Temp_x,single_rowsize);
ArrayFill(Temp_x,0,single_rowsize,1);
ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //after filling the values of one fill the remaining space with values of x
//Print("Temp x arr size =",ArraySize(Temp_x));
ArrayCopy(m_allxvalues,Temp_x);
ArrayFree(Temp_x); //we no longer need this array
int tr_cols = x_columns_chosen+1,
tr_rows = single_rowsize;
MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //we add one to leave the space for the values of one
if (m_debug)
{
Print("Design matrix");
MatrixPrint(m_allxvalues,tr_cols,tr_rows);
}
} Desta vez, nós imprimimos a matriz não transposta ao inicializar a biblioteca.
Isso é tudo que nós precisamos na função Init por enquanto, vamos chamá-la em nosso multipleMatRegTestScript.mq5 (link no final do artigo)
#include "multipleMatLinearReg.mqh"; CMultipleMatLinearReg matreg; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- string filename= "NASDAQ_DATA.csv"; matreg.Init(2,"1,3,4",filename); }
A saída após a execução bem-sucedida do script será (esta é apenas uma visão geral):
Init, number of X columns chosen =3 "1" "3" "4" All data Array Size 2232 consuming 52 bytes of memory Design matrix Array [ 1 4174 13387 35 1 4179 13397 37 1 4183 13407 38 1 4186 13417 37 ...... ...... 1 4352 14225 47 1 4402 14226 56 1 4405 14224 56 1 4416 14223 60 ]
Encontrando xTx
Assim como nós fizemos na regressão simples. O processo é o mesmo aqui, nós pegamos os valores de xT que são os dados brutos de um arquivo csv e, então, multiplicamos pela matriz não transposta.
MatrixMultiply(xT,m_allxvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols);
A saída quando a matriz xTx for impressa será
xTx [ 744.00 3257845.70 10572577.80 36252.20 3257845.70 14275586746.33 46332484402.07 159174265.78 10572577.80 46332484402.07 150405691938.78 515152629.66 36252.20 159174265.78 515152629.66 1910130.22 ]
Legal, ela funciona como o esperado.
Inversa de xTx
Esta é a parte mais importante da regressão múltipla, você deve prestar muita atenção porque as coisas estão prestes a ficar complicadas, estamos prestes a nos aprofundar na matemática.
Quando nós estávamos encontrando a inversa de nossa xTx na parte anterior, nós estávamos encontrando a inversa de uma matriz 2x2, desta vez nós encontraremos a inversa de uma matriz 4x4 pois nós selecionamos 3 colunas como nossas variáveis independentes. Quando adicionamos os valores de uma coluna, teremos 4 colunas que nos levarão a uma matriz 4x4 ao tentar encontrar a sua inversa.
Nós não podemos mais usar o método que nós usamos anteriormente para encontrar a inversa desta vez, a verdadeira questão é porque?
Veja que não funciona encontrar a inversa de uma matriz usando o método determinante, que nós usamos anteriormente, quando as matrizes são enormes, você nem pode usá-la para encontrar a inversa de uma matriz 3x3.
Diversos métodos foram inventados por diferentes matemáticos para encontrar a inversa de uma matriz, uma delas é o clássico Método Adjunto mas pela minha pesquisa, a maioria desses métodos são difíceis de codificar, podendo ser confuso às vezes. Se você quiser obter mais detalhes sobre os métodos e como eles podem ser codificados, dê uma olhada neste post do blog - https://www.geertarien.com/blog/2017/05/15/different-methods-for-matrix-inversion/.
De todos os métodos, eu escolhi a eliminação de Gauss-Jordan pois eu descobri que ele é confiável, fácil de codificar e é facilmente escalável, há um ótimo vídeo https://www.youtube.com/watch?v=YcP_KOB6KpQ que explica bem a eliminação de Gauss Jordan, espero que ele possa ajudá-lo a entender o conceito.
Ok, então vamos codificar o método de Gauss-Jordan, se você achou o código difícil de entender, eu tenho um código em c++, o link do mesmo código e para o meu GitHub se encontram abaixo, isso pode te ajudar a entender como as coisas foram feitas.
void CMultipleMatLinearReg::Gauss_JordanInverse(double &Matrix[],double &output_Mat[],int mat_order) { int rowsCols = mat_order; //--- Print("row cols ",rowsCols); if (mat_order <= 2) Alert("To find the Inverse of a matrix Using this method, it order has to be greater that 2 ie more than 2x2 matrix"); else { int size = (int)MathPow(mat_order,2); //since the array has to be a square // Create a multiplicative identity matrix int start = 0; double Identity_Mat[]; ArrayResize(Identity_Mat,size); for (int i=0; i<size; i++) { if (i==start) { Identity_Mat[i] = 1; start += rowsCols+1; } else Identity_Mat[i] = 0; } //Print("Multiplicative Indentity Matrix"); //ArrayPrint(Identity_Mat); //--- double MatnIdent[]; //original matrix sided with identity matrix start = 0; for (int i=0; i<rowsCols; i++) //operation to append Identical matrix to an original one { ArrayCopy(MatnIdent,Matrix,ArraySize(MatnIdent),start,rowsCols); //add the identity matrix to the end ArrayCopy(MatnIdent,Identity_Mat,ArraySize(MatnIdent),start,rowsCols); start += rowsCols; } //--- int diagonal_index = 0, index =0; start = 0; double ratio = 0; for (int i=0; i<rowsCols; i++) { if (MatnIdent[diagonal_index] == 0) Print("Mathematical Error, Diagonal has zero value"); for (int j=0; j<rowsCols; j++) if (i != j) //if we are not on the diagonal { /* i stands for rows while j for columns, In finding the ratio we keep the rows constant while incrementing the columns that are not on the diagonal on the above if statement this helps us to Access array value based on both rows and columns */ int i__i = i + (i*rowsCols*2); diagonal_index = i__i; int mat_ind = (i)+(j*rowsCols*2); //row number + (column number) AKA i__j ratio = MatnIdent[mat_ind] / MatnIdent[diagonal_index]; DBL_MAX_MIN(MatnIdent[mat_ind]); DBL_MAX_MIN(MatnIdent[diagonal_index]); //printf("Numerator = %.4f denominator =%.4f ratio =%.4f ",MatnIdent[mat_ind],MatnIdent[diagonal_index],ratio); for (int k=0; k<rowsCols*2; k++) { int j_k, i_k; //first element for column second for row j_k = k + (j*(rowsCols*2)); i_k = k + (i*(rowsCols*2)); //Print("val =",MatnIdent[j_k]," val = ",MatnIdent[i_k]); //printf("\n jk val =%.4f, ratio = %.4f , ik val =%.4f ",MatnIdent[j_k], ratio, MatnIdent[i_k]); MatnIdent[j_k] = MatnIdent[j_k] - ratio*MatnIdent[i_k]; DBL_MAX_MIN(MatnIdent[j_k]); DBL_MAX_MIN(ratio*MatnIdent[i_k]); } } } // Row Operation to make Principal diagonal to 1 /*back to our MatrixandIdentical Matrix Array then we'll perform operations to make its principal diagonal to 1 */ ArrayResize(output_Mat,size); int counter=0; for (int i=0; i<rowsCols; i++) for (int j=rowsCols; j<2*rowsCols; j++) { int i_j, i_i; i_j = j + (i*(rowsCols*2)); i_i = i + (i*(rowsCols*2)); //Print("i_j ",i_j," val = ",MatnIdent[i_j]," i_i =",i_i," val =",MatnIdent[i_i]); MatnIdent[i_j] = MatnIdent[i_j] / MatnIdent[i_i]; //printf("%d Mathematical operation =%.4f",i_j, MatnIdent[i_j]); output_Mat[counter]= MatnIdent[i_j]; //store the Inverse of Matrix in the output Array counter++; } } //--- }
Ótimo, então vamos chamar a função e imprimir a inversa de uma matriz
double inverse_xTx[]; Gauss_JordanInverse(xTx,inverse_xTx,tr_cols); if (m_debug) { Print("xtx Inverse"); MatrixPrint(inverse_xTx,tr_cols,tr_cols,7); }
A saída certamente será,
xtx Inverse [ 3.8264763 -0.0024984 0.0004760 0.0072008 -0.0024984 0.0000024 -0.0000005 -0.0000073 0.0004760 -0.0000005 0.0000001 0.0000016 0.0072008 -0.0000073 0.0000016 0.0000290 ]
Lembre-se, para encontrar a inversa de uma matriz, ela deve ser uma matriz quadrada, é por essa razão que nós temos o argumento mat_order nas funções, que é igual ao número de linhas e colunas.
Encontrando xTy
Agora vamos encontrar o produto da Matriz de x transposta e Y. É o mesmo processo que nós fizemos antes.
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //remember!! the value of 1 at the end is because we have only one dependent variable y
Quando a saída é impressa, ela fica assim
xTy [ 10550016.70000 46241904488.26996 150084914994.69019 516408161.98000 ]
Legal, uma matriz 1x4 como esperado.
Referência da fórmula,
Agora que nós temos tudo o que nós precisamos para encontrar os coeficientes, vamos juntar tudo.
MatrixMultiply(inverse_xTx,xTy,Betas,tr_cols,tr_cols,tr_cols,1); A saída será (lembre-se novamente, o primeiro elemento de nossos coeficientes/ matriz Beta é uma constante ou, em outras palavras, a interseção em y):
Coefficients Matrix [ -3670.97167 2.75527 0.37952 8.06681 ]
Excelente! Agora, vamos executar em python para provar que estou errado.
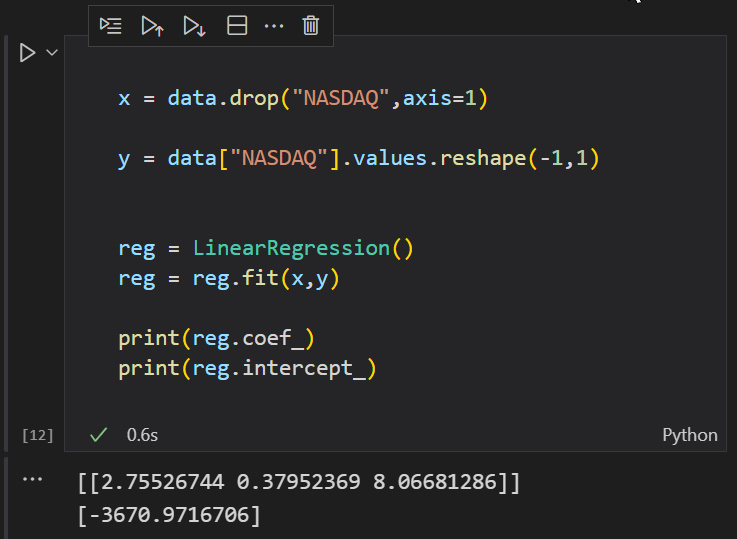
B A M duplo ! ! ! desta vez
Agora você tem vários modelos de regressão dinâmica possíveis em mql5, agora vamos ver onde tudo começou.
Tudo começou aqui
matreg.Init(2,"1,3,4",filename);
A ideia era ter uma entrada de string que pudesse nos ajudar a colocar um número ilimitado de variáveis independentes, e parece que em mql5 não há como ter *args e *kwargs das linguagens como python que podem nos permitir inserir muitos argumentos. Então, nossa única maneira de fazer isso era usar a string e, então, encontrar uma maneira de manipular o vetor para deixar apenas um único vetor contendo todos os nossos dados e mais tarde nós encontrarmos uma maneira de manipulá-los. Veja minha primeira tentativa sem sucesso para mais informações https://www.mql5.com/en/code/38894, a razão pela qual estou dizendo tudo isso é porque eu acredito que alguém possa seguir o mesmo caminho neste projeto ou em outro, estou apenas explicando o que funcionou para mim e o que não funcionou.
Pensamentos finais
Por mais legal que possa parecer que agora você pode ter quantas variáveis independentes quiser, lembre-se que existe um limite para qualquer coisa que tenha muitas variáveis independentes ou colunas de conjuntos de dados enormes, eles podem atingir os limites de cálculos de um computador. Como você acabou de ver os cálculos matriciais também podem resultar em um grande número durante os cálculos.
Adicionar variáveis independentes a um modelo de regressão linear múltipla sempre aumentará a quantidade de variância na variável dependente, que é normalmente expressa como r-quadrado, portanto, adicionar muitas variáveis independentes sem qualquer justificativa teórica pode resultar em um modelo sobreajustado.
Por exemplo, se nós tivéssemos construído um modelo como nós fizemos no primeiro artigo desta série, com base em apenas duas variáveis dependentes da NASDAQ e S&P500 sendo independentes, nossa precisão poderia ter sido superior a 95%, mas esse pode não ser o caso desta porque agora nós temos 3 independentes.
É sempre uma boa ideia verificar a precisão do seu modelo após a construção do mesmo, além disso, você deve verificar se existe uma correlação entre cada variável independente e o alvo antes de construir um modelo.
Sempre construa o modelo com base nos dados que provaram ter um forte relacionamento linear com a sua variável objetivo.
Obrigado por ler! Meu repositório do GitHub é encontrado aqui https://github.com/MegaJoctan/MatrixRegressionMQL5.git.
Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/10928
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Redes neurais de maneira fácil (Parte 15): Agrupamento de dados via MQL5
Redes neurais de maneira fácil (Parte 15): Agrupamento de dados via MQL5
 Como desenvolver um sistema de negociação baseado no indicador SAR Parabólico
Como desenvolver um sistema de negociação baseado no indicador SAR Parabólico
 Como desenvolver um sistema de negociação baseado no indicador OBV
Como desenvolver um sistema de negociação baseado no indicador OBV
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso

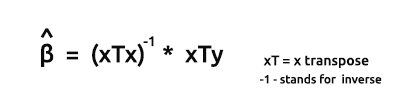
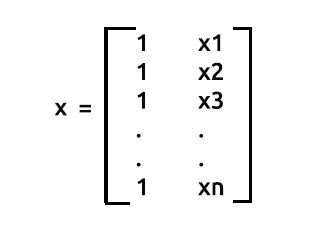
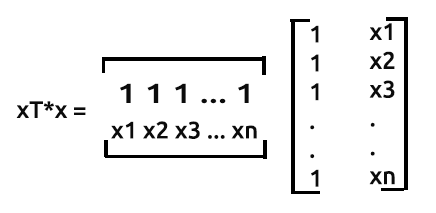

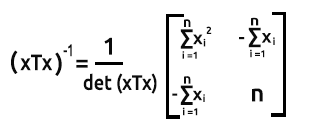
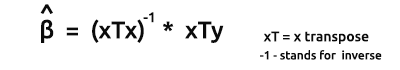
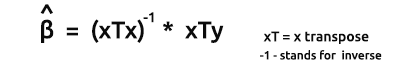
Foi publicado o novo artigo Data Science and Machine Learning part 03: Matrix Regressions:
Autor: Omega J Msigwa