Redes neurais de maneira fácil (Parte 90): Interpolação Frequencial de Séries Temporais (FITS)
Introdução
A análise de séries temporais desempenha um papel importante na tomada de decisões gerenciais no mercado financeiro. Os dados de séries temporais no setor financeiro são frequentemente complexos e dinâmicos, e seu processamento exige métodos eficazes.
Pesquisas recentes na análise de séries temporais levaram ao desenvolvimento de modelos e métodos sofisticados. No entanto, esses modelos geralmente exigem recursos computacionais significativos, tornando-os menos adequados para condições dinâmicas dos mercados financeiros. Ou seja, quando o tempo de decisão se torna parte de uma estratégia bem-sucedida.
Além disso, hoje em dia, um número crescente de decisões gerenciais é feito usando dispositivos móveis, que também possuem recursos limitados. Esse fato impõe requisitos adicionais aos modelos usados para essas decisões.
Nesse contexto, a representação de séries temporais no domínio da frequência pode oferecer uma forma mais eficiente e compacta de capturar padrões observados. Por exemplo, o uso de dados espectrais e a análise de frequências de alta amplitude podem ajudar a identificar características importantes.
Anteriormente, conhecemos o método FEDformer, que usa o domínio da frequência para encontrar padrões em séries temporais. Contudo, o Transformer utilizado não é uma das arquiteturas leves. Em vez de modelos complexos que exigem altos custos computacionais, o artigo "FITS: Modeling Time Series with 10k Parameters" apresentou o método de interpolação frequencial de séries temporais (Frequency Interpolation Time Series — FITS). Esta é uma solução compacta e eficaz para análise e previsão de séries temporais. O FITS utiliza a interpolação no domínio da frequência para expandir a janela do segmento temporal analisado, permitindo extrair eficientemente características temporais sem grandes custos de recursos computacionais.
Os autores do FITS destacam as seguintes vantagens de seu método:
- O FITS é um modelo leve com poucos parâmetros, tornando-o ideal para uso em dispositivos com recursos limitados.
- O FITS utiliza uma rede neural complexa para capturar informações de amplitude e fase do sinal, o que aumenta a eficiência na análise de dados de séries temporais.
1. Algoritmo FITS
A análise de séries temporais no domínio da frequência permite decompor o sinal em uma combinação linear de componentes sinusoidais sem perda de dados. Cada uma dessas componentes tem uma frequência, fase inicial e amplitude únicas. Enquanto a previsão de uma série temporal pode ser uma tarefa complexa, a previsão de componentes sinusoidais individuais é relativamente mais simples, pois envolve apenas o ajuste da fase da onda senoidal com base no deslocamento temporal. Essas ondas senoidais, ajustadas dessa maneira, são linearmente combinadas para obter os valores previstos da série temporal analisada.
Essa abordagem permite preservar eficientemente as características frequenciais da janela temporal analisada. Ao mesmo tempo, mantém-se a sequência semântica entre a janela temporal e o horizonte de previsão.
No entanto, a previsão de cada componente sinusoidal na área temporal pode ser bastante trabalhosa. Para resolver esse problema, os autores do método FITS propõem o uso do domínio complexo de frequência, que proporciona uma representação de dados mais compacta e informativa.
A Transformada Rápida de Fourier (FFT) transforma de maneira eficiente os sinais de séries temporais discretas da área temporal para o domínio complexo de frequência. Na análise de Fourier, o domínio complexo de frequência é representado como uma sequência em que cada componente de frequência é caracterizado por um número complexo. Esse número complexo reflete a amplitude e a fase do componente, fornecendo uma descrição completa. A amplitude do componente de frequência representa a magnitude, ou força, desse componente no sinal original da área temporal. Em contrapartida, a fase indica o deslocamento temporal ou o atraso introduzido por esse componente. Matematicamente, o número complexo associado à componente de frequência pode ser representado como um elemento exponencial complexo com amplitude e fase específicas:
![]()
onde X(f) — é o número complexo associado ao componente de frequência na frequência f,
|X(f)| é a amplitude do componente,
θ(f) é a fase do componente.
No plano complexo, o elemento exponencial pode ser representado como um vetor com comprimento igual à amplitude e ângulo correspondente à fase:
![]()
Dessa forma, o número complexo no domínio de frequência fornece uma maneira sucinta e elegante de representar a amplitude e a fase de cada componente de frequência na Transformada de Fourier.
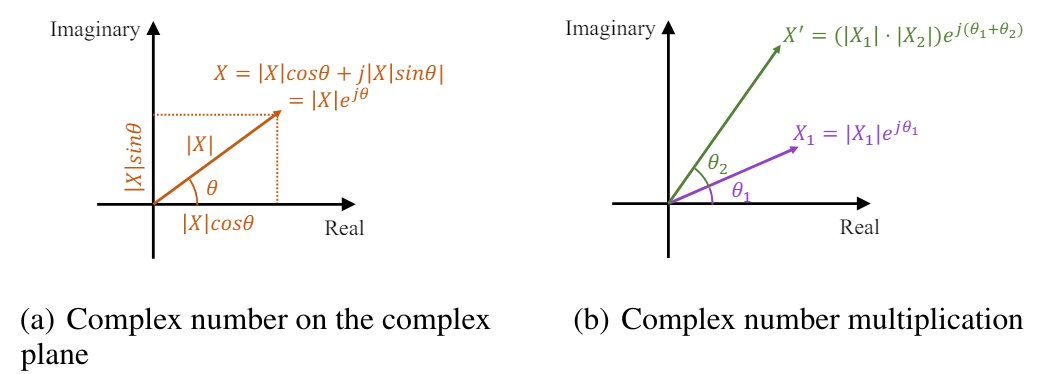
O deslocamento temporal de um sinal corresponde a um deslocamento de fase no domínio de frequência. No domínio das frequências complexas, esse deslocamento de fase pode ser expresso como a multiplicação de um elemento exponencial complexo unitário pela fase correspondente. O sinal deslocado mantém a amplitude |X(f)|, e a fase reflete um deslocamento linear no tempo.
Assim, o escalonamento da amplitude e o deslocamento de fase podem ser simultaneamente expressos como a multiplicação de números complexos.
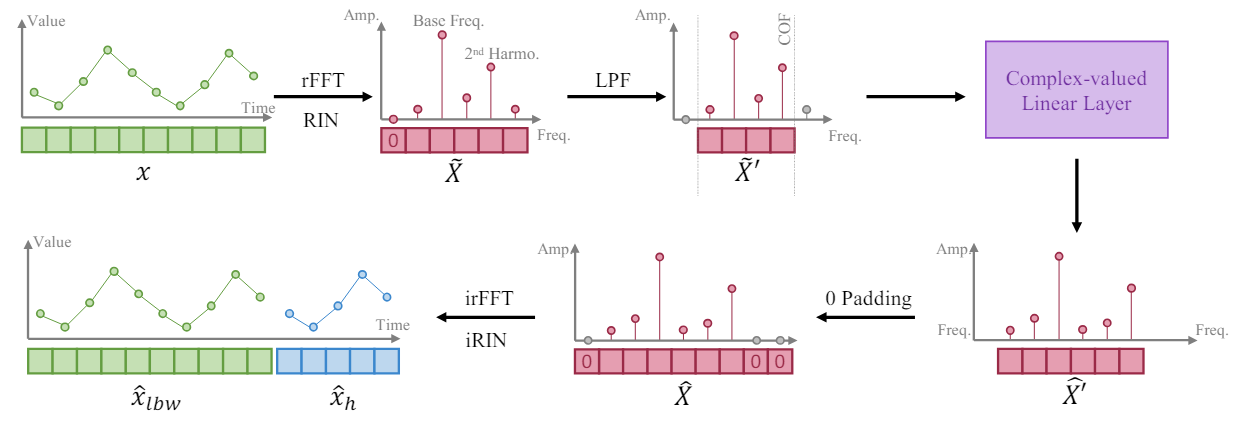
Baseando-se no fato de que uma série temporal mais longa proporciona maior resolução de frequência em sua representação no domínio de frequência, os autores do método FITS treinam o modelo para expandir o segmento da série temporal por meio da interpolação da representação frequencial da janela de dados originais. Eles sugerem o uso de uma única camada linear complexa para treinar essa interpolação. Como resultado, o modelo pode aprender o escalonamento da amplitude e o deslocamento de fase como multiplicações de números complexos durante o processo de interpolação. O algoritmo FITS utiliza a Transformada Rápida de Fourier para projetar os segmentos das séries temporais no domínio complexo de frequência. Após a interpolação, a representação frequencial é projetada de volta para a representação temporal usando a FFT inversa.
No entanto, a média de tais segmentos resultará em um componente muito grande com frequência zero em sua representação no domínio complexo de frequência. Para resolver esse problema, o sinal obtido é submetido a uma normalização reversível (RevIN), o que permite obter uma instância com média zero.
Além disso, os autores do método incorporam um filtro de baixas frequências (LPF) no FITS para reduzir o tamanho do modelo. O filtro de baixas frequências elimina eficazmente componentes de alta frequência acima de uma frequência de corte especificada, compactando a representação do modelo e mantendo, ao mesmo tempo, informações importantes das séries temporais.
Apesar de operar no domínio da frequência, o FITS é treinado no domínio temporal usando funções de perda padrão, como o erro médio quadrático (MSE) após a aplicação da Transformada Rápida de Fourier inversa. Isso garante uma abordagem universal, adaptada a diversas tarefas subsequentes de séries temporais.
Para tarefas de previsão, o FITS gera uma janela de análise retrospectiva juntamente com o horizonte de planejamento. Isso proporciona controle sobre a previsão e a análise retrospectiva, sendo recomendável que o modelo reconstrua com precisão a janela de análise retrospectiva. A análise apresentada no artigo dos autores mostra que a combinação da análise retrospectiva e da supervisão da previsão pode levar a um aumento de desempenho em certos cenários.
Para tarefas de reconstrução, o FITS subamostra o segmento original da série temporal com base em uma taxa de subamostragem específica. Em seguida, realiza a interpolação frequencial, o que permite restaurar o segmento subamostrado à sua forma original. Dessa forma, aplica-se um controle direto com funções de perda para garantir a reconstrução precisa do sinal.
Para controlar o comprimento do tensor de resultados do modelo, os autores introduzem a taxa de interpolação, denotada por 𝜂, que representa a razão entre o tamanho desejado do tensor de resultados do modelo e o tamanho correspondente do tensor dos dados originais.
É relevante observar que, ao aplicar o filtro de baixas frequências (LPF), o tamanho do tensor dos dados originais da nossa camada complexa corresponde à frequência de corte (COF) do LPF. Após a interpolação frequencial, a representação da frequência complexa é complementada com zeros até atingir o tamanho desejado do tensor de resultados. Antes da aplicação da FFT inversa, um zero adicional é introduzido como componente de frequência zero na representação.
O objetivo principal da inclusão do LPF no FITS é comprimir o volume do modelo sem perder informações relevantes. O LPF realiza isso ao descartar componentes de frequência acima de uma frequência de corte especificada (COF), resultando em uma representação mais concisa no domínio da frequência. O LPF mantém as informações pertinentes nas séries temporais, descartando componentes que ultrapassam as capacidades de aprendizado do modelo. Isso assegura a preservação de uma parte significativa do conteúdo relevante da série temporal original. Os experimentos conduzidos pelos autores mostram que o sinal filtrado apresenta distorções mínimas mesmo ao preservar apenas um quarto da representação original no domínio da frequência. Além disso, componentes de alta frequência filtrados pelo LPF geralmente contêm ruído, que, por sua natureza, não tem relevância para a modelagem eficaz de séries temporais.
A escolha da frequência de corte adequada (COF) continua sendo uma tarefa não trivial. Para abordar essa questão, os autores do FITS propõem um método baseado no conteúdo harmônico da frequência dominante. As harmônicas, que são múltiplos inteiros da frequência dominante, desempenham um papel importante na formação da forma do sinal da série temporal. Comparando a frequência de corte com essas harmônicas, conseguimos preservar os componentes de frequência relevantes, relacionados à estrutura e periodicidade do sinal. Essa abordagem utiliza a conexão intrínseca entre as frequências para extrair informações significativas, ao mesmo tempo em que suprime o ruído e componentes de alta frequência desnecessários.
A visualização feita pelos autores do FITS é apresentada abaixo.
2. Implementação com MQL5
Após entendermos os aspectos teóricos do método FITS, passamos à implementação prática das abordagens propostas utilizando MQL5.
Como de costume, utilizaremos as abordagens sugeridas, mas nossa implementação terá algumas diferenças em relação à visão original do algoritmo devido à especificidade da tarefa em questão.
2.1 Implementação da FFT
Do relato teórico apresentado, fica claro que o método baseia-se na Transformada Rápida de Fourier (FFT) direta e inversa. Com ela, primeiro transformamos o sinal analisado para o domínio das características de frequência e, em seguida, trazemos a sequência prevista de volta para a representação da série temporal. Nesse contexto, podemos destacar duas vantagens da Transformada Rápida de Fourier:
- a velocidade na execução das operações em comparação com outras transformações similares;
- a possibilidade de expressar a transformação inversa por meio da transformação direta.
Vale mencionar que, para nossa tarefa, precisamos implementar a FFT para séries temporais multidimensionais. Na prática, isso se traduz em aplicar a FFT a cada série temporal unitária da nossa sequência multidimensional.
Lembro que a maioria das operações matemáticas em nossas implementações é realizada no OpenCL. Isso nos permite distribuir a execução de inúmeras operações idênticas, com dados independentes, por diversos fluxos paralelos. Assim, conseguimos reduzir o tempo de execução das operações. As operações de Transformada Rápida de Fourier também serão executadas no lado do OpenCL. Em cada um dos fluxos paralelos, realizaremos a decomposição de uma série temporal unitária separada.
Estruturaremos o algoritmo das operações como um kernel FFT. Nos parâmetros do kernel, passaremos ponteiros para 4 arrays de dados. Usaremos dois arrays para os dados de entrada e dois para os resultados das operações. Um array armazenará a parte real do valor complexo (amplitude do sinal) e o outro a parte imaginária (sua fase).
No entanto, é importante observar que nem sempre forneceremos a parte imaginária do sinal como entrada para o kernel. Por exemplo, ao decompor a série temporal original, simplesmente não temos essa parte imaginária. Nessa situação, a solução é bastante simples: substituímos os dados ausentes por valores nulos. E, em vez de transmitir um buffer separado preenchido com zeros, criaremos apenas uma flag input_complex nos parâmetros do kernel.
Outro ponto a lembrar é que o algoritmo de Cooley-Tukey que usamos para a FFT funciona apenas para sequências cuja extensão é uma potência de 2. Essa condição impõe restrições consideráveis. No entanto, afirmo desde já que isso é apenas uma limitação na preparação do sinal a ser analisado. O método funciona perfeitamente se preenchermos os elementos ausentes da sequência com zeros. E, novamente, para evitar cópias excessivas de dados ao reformatar a série temporal, adicionaremos duas variáveis aos parâmetros do kernel: input_window e output_window. Na primeira, indicaremos o comprimento real da sequência a ser analisada, e na segunda, o tamanho do vetor de resultados da decomposição, que deve ser uma potência de 2. Ressalto que aqui estamos nos referindo aos tamanhos de uma sequência unitária.
Outro parâmetro, reverse, indica a direção da operação: transformação direta ou inversa.
__kernel void FFT(__global float *inputs_re, __global float *inputs_im, __global float *outputs_re, __global float *outputs_im, const int input_window, const int input_complex, const int output_window, const int reverse ) { size_t variable = get_global_id(0);
No corpo do kernel, primeiro definimos o identificador do fluxo, que nos indica qual sequência unitária está sendo analisada. Aqui também determinamos os deslocamentos nos buffers de dados e outras constantes necessárias.
const ulong N = output_window; const ulong N2 = N / 2; const ulong inp_shift = input_window * variable; const ulong out_shift = output_window * variable;
Na próxima etapa, reorganizamos os dados de entrada em uma ordem específica, o que permite otimizar um pouco o algoritmo FFT.
uint target = 0; for(uint position = 0; position < N; position++) { if(target > position) { outputs_re[out_shift + position] = (target < input_window ? inputs_re[inp_shift + target] : 0); outputs_im[out_shift + position] = ((target < input_window && input_complex) ? inputs_im[inp_shift + target] : 0); outputs_re[out_shift + target] = inputs_re[inp_shift + position]; outputs_im[out_shift + target] = (input_complex ? inputs_im[inp_shift + position] : 0); } else { outputs_re[out_shift + position] = inputs_re[inp_shift + position]; outputs_im[out_shift + position] = (input_complex ? inputs_im[inp_shift + position] : 0); } unsigned int mask = N; while(target & (mask >>= 1)) target &= ~mask; target |= mask; }
Em seguida, ocorre a transformação direta dos dados, realizada por meio de um sistema de laços aninhados. No laço externo, realizamos as iterações da FFT para segmentos de comprimento 2, 4, 8, ... n.
float real = 0, imag = 0; for(int len = 2; len <= (int)N; len <<= 1) { float w_real = (float)cos(2 * M_PI_F / len); float w_imag = (float)sin(2 * M_PI_F / len);
No corpo do laço, definimos o multiplicador para a rotação do argumento por uma unidade de comprimento de ciclo e organizamos um laço aninhado para iterar pelos blocos da sequência analisada.
for(int i = 0; i < (int)N; i += len) { float cur_w_real = 1; float cur_w_imag = 0;
Aqui declaramos as variáveis de rotação de fase atual e organizamos mais um laço aninhado para iterar pelos elementos dentro do bloco.
for(int j = 0; j < len / 2; j++) { real = cur_w_real * outputs_re[out_shift + i + j + len / 2] - cur_w_imag * outputs_im[out_shift + i + j + len / 2]; imag = cur_w_imag * outputs_re[out_shift + i + j + len / 2] + cur_w_real * outputs_im[out_shift + i + j + len / 2]; outputs_re[out_shift + i + j + len / 2] = outputs_re[out_shift + i + j] - real; outputs_im[out_shift + i + j + len / 2] = outputs_im[out_shift + i + j] - imag; outputs_re[out_shift + i + j] += real; outputs_im[out_shift + i + j] += imag; real = cur_w_real * w_real - cur_w_imag * w_imag; cur_w_imag = cur_w_imag * w_real + cur_w_real * w_imag; cur_w_real = real; } } }
No corpo do laço, modificamos primeiro os elementos analisados e, em seguida, alteramos o valor das variáveis de fase atual para a próxima iteração.
Vale destacar que a modificação dos elementos nos buffers é realizada "in-place", ou seja, sem alocação de memória adicional.
Após concluir as iterações do sistema de laços, verificamos o valor da flag reverse. E, caso seja realizada a transformação inversa, reorganizamos os dados no buffer de resultados. Nesse processo, os valores obtidos são divididos pelo número de elementos na sequência.
if(reverse) { outputs_re[0] /= N; outputs_im[0] /= N; outputs_re[N2] /= N; outputs_im[N2] /= N; for(int i = 1; i < N2; i++) { real = outputs_re[i] / N; imag = outputs_im[i] / N; outputs_re[i] = outputs_re[N - i] / N; outputs_im[i] = outputs_im[N - i] / N; outputs_re[N - i] = real; outputs_im[N - i] = imag; } } }
2.2 Combinação das partes real e imaginária da distribuição prevista
O kernel apresentado acima permite realizar a Transformada Rápida de Fourier direta e inversa, cobrindo assim nossas necessidades para esta questão. Mas há outro ponto no método FITS que merece atenção. Os autores utilizam uma rede neural complexa para a interpolação dos dados. Para um estudo mais detalhado sobre redes neurais complexas, recomendo a leitura do artigo A Survey of Complex-Valued Neural Networks. Nesta implementação, usaremos as classes existentes de camadas neurais que irão interpolar separadamente as partes real e imaginária, combinando-as posteriormente segundo a seguinte fórmula:
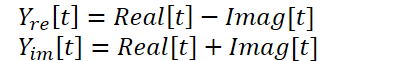
Para realizar essas operações, criaremos o kernel ComplexLayer. O algoritmo do kernel é bastante simples. Identificamos apenas o fluxo em duas dimensões, que nos indica a linha e a coluna das matrizes. Definimos os deslocamentos nos buffers de dados e executamos operações matemáticas não muito complexas.
__kernel void ComplexLayer(__global float *inputs_re, __global float *inputs_im, __global float *outputs_re, __global float *outputs_im ) { size_t i = get_global_id(0); size_t j = get_global_id(1); size_t total_i = get_global_size(0); size_t total_j = get_global_size(1); uint shift = i * total_j + j; //--- outputs_re[shift] = inputs_re[shift] - inputs_im[shift]; outputs_im[shift] = inputs_im[shift] + inputs_re[shift]; }
Da mesma forma, construímos o kernel de retropropagação do erro, ComplexLayerGradient, cujo código convido você a explorar por conta própria no anexo.
Com isso, encerramos o trabalho no lado OpenCL do programa.
2.3 Criação da classe do método FITS
Após concluir o trabalho com os kernels no programa OpenCL, avançamos para o programa principal, onde criaremos a classe CNeuronFITSOCL para implementar as abordagens propostas pelos autores do método FITS. Criamos a nova classe como uma derivada da classe base de camadas neurais CNeuronBaseOCL. A estrutura da nova classe é apresentada abaixo.
class CNeuronFITSOCL : public CNeuronBaseOCL { protected: //--- uint iWindow; uint iWindowOut; uint iCount; uint iFFTin; uint iIFFTin; //--- CNeuronBaseOCL cInputsRe; CNeuronBaseOCL cInputsIm; CNeuronBaseOCL cFFTRe; CNeuronBaseOCL cFFTIm; CNeuronDropoutOCL cDropRe; CNeuronDropoutOCL cDropIm; CNeuronConvOCL cInsideRe1; CNeuronConvOCL cInsideIm1; CNeuronConvOCL cInsideRe2; CNeuronConvOCL cInsideIm2; CNeuronBaseOCL cComplexRe; CNeuronBaseOCL cComplexIm; CNeuronBaseOCL cIFFTRe; CNeuronBaseOCL cIFFTIm; CBufferFloat cClear; //--- virtual bool FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false); virtual bool ComplexLayerOut(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im); virtual bool ComplexLayerGradient(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); public: CNeuronFITSOCL(void) {}; ~CNeuronFITSOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_out, uint count, float dropout, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual int Type(void) const { return defNeuronFITSOCL; } virtual void SetOpenCL(COpenCLMy *obj); virtual void TrainMode(bool flag); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); };
É fácil perceber que a estrutura da nova classe declara um número considerável de objetos de camadas neurais internas. Isso pode causar algum estranhamento diante da alegada simplicidade do modelo. Porém, devo destacar imediatamente que treinaremos apenas os parâmetros de 4 camadas neurais internas, que são responsáveis pela interpolação dos dados (cInsideRe* e cInsideIm*). As demais servem como buffers intermediários de dados, cuja função será compreendida durante a implementação dos métodos.
Também é importante observar a presença de 2 camadas CNeuronDropoutOCL. Nesta implementação, decidi abrir mão do uso do LPF, que envolve a definição de uma frequência de corte. Aqui, recordei os experimentos dos autores do método FEDformer, que ressaltam a eficácia da amostragem de um conjunto de características de frequência. Por isso, optei por utilizar a camada Dropout para zerar algumas características de frequência aleatórias.
Declaramos todos os objetos internos como estáticos, o que nos permite deixar o construtor e o destrutor da classe "vazios". A inicialização dos objetos e de todas as variáveis locais ocorre diretamente no método Init. Como de costume, os parâmetros do método incluem variáveis que definem de forma clara a estrutura necessária do objeto. Aqui vemos os tamanhos da janela da sequência unitária dos dados de entrada e de saída (window e window_out), o número de séries temporais unitárias (count) e a proporção de características de frequência a serem zeradas (dropout). Vale a pena notar que estamos construindo uma camada unificada, e os tamanhos das janelas, tanto dos dados de entrada quanto dos resultados, podem ser quaisquer números positivos, sem a necessidade de atender aos requisitos do algoritmo FFT. Lembro que o algoritmo mencionado requer que o tamanho dos dados de entrada seja uma potência de 2.
bool CNeuronFITSOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_out, uint count, float dropout, ENUM_OPTIMIZATION optimization_type, uint batch) { if(window <= 0) return false; if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * count, optimization_type, batch)) return false;
No corpo do método, fazemos primeiro um pequeno bloco de controle, onde verificamos o tamanho da janela dos dados de entrada (deve ser um número positivo) e chamamos o método homônimo da classe pai. Como você sabe, o método da classe pai implementa controles adicionais e a inicialização de objetos herdados.
Após a execução bem-sucedida do bloco de controle, salvamos os parâmetros obtidos em variáveis locais.
//--- Save constants
iWindow = window;
iWindowOut = window_out;
iCount = count;
activation=None;
Definimos os tamanhos dos tensores para a Transformada Rápida de Fourier (FFT) direta e inversa como as próximas potências de 2 maiores em relação aos parâmetros recebidos.
//--- Calculate FFT and iFFT size int power = int(MathLog(iWindow) / M_LN2); if(MathPow(2, power) != iWindow) power++; iFFTin = uint(MathPow(2, power)); power = int(MathLog(iWindowOut) / M_LN2); if(MathPow(2, power) != iWindowOut) power++; iIFFTin = uint(MathPow(2, power));
Em seguida, iniciamos o bloco de inicialização dos objetos internos. Os objetos cInputs* são usados como buffers dos dados de entrada para a FFT direta. Seu tamanho é o produto do tamanho da sequência unitária na entrada deste bloco e o número de sequências analisadas.
if(!cInputsRe.Init(0, 0, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cInputsIm.Init(0, 1, OpenCL, iFFTin * iCount, optimization, iBatch)) return false;
Os objetos cFFT* têm um tamanho semelhante e são usados para registrar os resultados da Transformada de Fourier direta.
if(!cFFTRe.Init(0, 2, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cFFTIm.Init(0, 3, OpenCL, iFFTin * iCount, optimization, iBatch)) return false;
Depois, declaramos os objetos Dropout. Não é difícil deduzir que eles terão o mesmo tamanho que os anteriores.
if(!cDropRe.Init(0, 4, OpenCL, iFFTin * iCount, dropout, optimization, iBatch)) return false; if(!cDropIm.Init(0, 5, OpenCL, iFFTin * iCount, dropout, optimization, iBatch)) return false;
Para a interpolação da sequência, utilizaremos um MLP (Perceptron Multicamadas) com uma camada oculta e a ativação tanh entre as camadas. Na saída do bloco, obtemos os dados conforme os requisitos do bloco da FFT inversa.
if(!cInsideRe1.Init(0, 6, OpenCL, iFFTin, iFFTin, 4*iIFFTin, iCount, optimization, iBatch)) return false; cInsideRe1.SetActivationFunction(TANH); if(!cInsideIm1.Init(0, 7, OpenCL, iFFTin, iFFTin, 4*iIFFTin, iCount, optimization, iBatch)) return false; cInsideIm1.SetActivationFunction(TANH); if(!cInsideRe2.Init(0, 8, OpenCL, 4*iIFFTin, 4*iIFFTin, iIFFTin, iCount, optimization, iBatch)) return false; cInsideRe2.SetActivationFunction(None); if(!cInsideIm2.Init(0, 9, OpenCL, 4*iIFFTin, 4*iIFFTin, iIFFTin, iCount, optimization, iBatch)) return false; cInsideIm2.SetActivationFunction(None);
Os resultados da interpolação serão combinados nos objetos cComplex*.
if(!cComplexRe.Init(0, 10, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cComplexIm.Init(0, 11, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false;
Conforme o método FITS, as sequências interpoladas passam pela Transformada de Fourier inversa, durante a qual as características de frequência são convertidas em uma série temporal. Os resultados dessa operação serão gravados nos objetos cIFFT.
if(!cIFFTRe.Init(0, 12, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cIFFTIm.Init(0, 13, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false;
Além disso, declararemos um buffer auxiliar de valores nulos para complementar os valores que estiverem faltando.
if(!cClear.BufferInit(MathMax(iFFTin, iIFFTin)*iCount, 0)) return false; cClear.BufferCreate(OpenCL); //--- return true; }
Após a inicialização bem-sucedida de todos os objetos internos, concluímos o método.
O próximo passo é implementar a funcionalidade da classe. Mas antes de prosseguir diretamente para os métodos de propagação direta e reversa, precisamos realizar um trabalho preparatório para implementar a funcionalidade de enfileiramento dos kernels criados anteriormente na fila de execução. O algoritmo para esses kernels é padronizado. E, neste artigo, analisaremos apenas o método de chamada do kernel da Transformada Rápida de Fourier CNeuronFITSOCL::FFT.
bool CNeuronFITSOCL::FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false) { uint global_work_offset[1] = {0}; uint global_work_size[1] = {iCount};
Nos parâmetros do método, passamos os ponteiros para 4 buffers de dados com os quais iremos trabalhar (2 de dados de entrada e 2 de resultados) e a flag de direção das operações.
No corpo do método, definimos o espaço de tarefas. Aqui, usamos um espaço unidimensional com base no número de sequências analisadas.
Em seguida, transmitimos os parâmetros ao kernel, começando pelos ponteiros para os buffers dos dados de entrada.
if(!OpenCL.SetArgumentBuffer(def_k_FFT, def_k_fft_inputs_re, inp_re.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FFT, def_k_fft_inputs_im, (!!inp_im ? inp_im.GetIndex() : inp_re.GetIndex()))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Vale destacar que permitimos a execução do kernel sem o buffer da parte imaginária do sinal. Como você deve se lembrar, para isso utilizamos a flag input_complex no kernel. No entanto, sem passar todos os parâmetros necessários ao kernel, ocorrerá um erro de execução. Portanto, caso não haja o buffer da parte imaginária, especificamos o ponteiro para o buffer da parte real do sinal e indicamos false para a flag correspondente.
if(!OpenCL.SetArgument(def_k_FFT, def_k_fft_input_complex, int(!!inp_im))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Em seguida, passamos os ponteiros para os buffers de resultados.
if(!OpenCL.SetArgumentBuffer(def_k_FFT, def_k_fft_outputs_re, out_re.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FFT, def_k_fft_outputs_im, out_im.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Os tamanhos das janelas dos dados de entrada e de resultados. O tamanho final é uma potência de 2. Note que calculamos os tamanhos das janelas em vez de usar constantes. Isso ocorre porque utilizaremos este método tanto para a transformação de Fourier direta quanto para a inversa, que operam com buffers diferentes e, portanto, com diferentes janelas de dados de entrada e resultados.
if(!OpenCL.SetArgument(def_k_FFT, def_k_fft_input_window, (int)(inp_re.Total() / iCount))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FFT, def_k_fft_output_window, (int)(out_re.Total() / iCount))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Por fim, transmitimos a flag que indica o uso do algoritmo de transformação inversa.
if(!OpenCL.SetArgument(def_k_FFT, def_k_fft_reverse, int(reverse))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
E colocamos o kernel na fila de execução.
if(!OpenCL.Execute(def_k_FFT, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
Em cada etapa, monitoramos o processo de execução das operações e retornamos um valor lógico que representa o sucesso das operações à função chamadora.
Os métodos CNeuronFITSOCL::ComplexLayerOut e CNeuronFITSOCL::ComplexLayerGradient, nos quais ocorre a chamada dos kernels de mesmo nome, são construídos de maneira semelhante. Convido você a estudá-los por conta própria no anexo.
Após concluirmos a preparação, passamos à construção do algoritmo de propagação para frente, descrito no método CNeuronFITSOCL::feedForward.
Nos parâmetros, o método recebe um ponteiro para o objeto da camada neural anterior, que nos fornece os dados de entrada. E no corpo do método, verificamos imediatamente o ponteiro recebido.
bool CNeuronFITSOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Aqui é importante mencionar que o método FITS prevê a normalização prévia dos dados. Assumimos que essa normalização é feita nas camadas neurais anteriores, e por isso omitimos essa etapa nesta classe.
Transformamos os dados recebidos para o domínio das características de frequência usando a Transformada Rápida de Fourier direta. Para isso, chamamos o método correspondente, cujo algoritmo foi detalhado anteriormente.
//--- FFT if(!FFT(NeuronOCL.getOutput(), NULL, cFFTRe.getOutput(), cFFTIm.getOutput(), false)) return false;
As características de frequência obtidas são diluídas usando as camadas Dropout.
//--- DropOut if(!cDropRe.FeedForward(cFFTRe.AsObject())) return false; if(!cDropIm.FeedForward(cFFTIm.AsObject())) return false;
Depois disso, interpolamos as características de frequência para o tamanho dos valores previstos.
//--- Complex Layer if(!cInsideRe1.FeedForward(cDropRe.AsObject())) return false; if(!cInsideRe2.FeedForward(cInsideRe1.AsObject())) return false; if(!cInsideIm1.FeedForward(cDropIm.AsObject())) return false; if(!cInsideIm2.FeedForward(cInsideIm1.AsObject())) return false;
Combinamos as interpolações separadas das partes real e imaginária do sinal.
if(!ComplexLayerOut(cInsideRe2.getOutput(), cInsideIm2.getOutput(), cComplexRe.getOutput(), cComplexIm.getOutput())) return false;
O sinal resultante é trazido de volta ao domínio temporal por meio da transformação inversa.
//--- iFFT if(!FFT(cComplexRe.getOutput(), cComplexIm.getOutput(), cIFFTRe.getOutput(), cIFFTIm.getOutput(), true)) return false;
Vale destacar que a série temporal prevista pode ser maior do que o tamanho da sequência que precisamos passar para a camada neural seguinte. Por isso, extrairemos apenas o bloco necessário da parte real do sinal.
//--- To Output if(!DeConcat(Output, cIFFTRe.getGradient(), cIFFTRe.getOutput(), iWindowOut, iIFFTin - iWindowOut, iCount)) return false; //--- return true; }
Lembramos de monitorar o processo de execução das operações em cada etapa. E, ao final de todas as iterações, retornamos o resultado lógico das operações realizadas para a função chamadora.
Após implementar a propagação, passamos a construir os métodos de retropropagação. Aqui, começamos pelo método que distribui o gradiente do erro a todos os objetos internos e para a camada anterior, conforme sua influência no resultado: CNeuronFITSOCL::calcInputGradients.
bool CNeuronFITSOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Nos parâmetros, o método recebe um ponteiro para o objeto da camada anterior, a quem devemos passar o gradiente do erro. E no corpo do método, verificamos imediatamente a validade do ponteiro recebido.
O gradiente do erro que recebemos da camada seguinte já está armazenado no buffer Gradient. No entanto, ele contém apenas a parte real do sinal e apenas até a profundidade de previsão definida. Precisamos do gradiente do erro tanto para a parte real quanto para a imaginária no horizonte completo do sinal proveniente da transformação inversa. Para gerar esses dados, baseamo-nos em duas suposições:
- Na saída do bloco da Transformada de Fourier inversa durante a propagação, esperamos obter os valores da série temporal discreta. Nesse caso, a parte real do sinal corresponde à série temporal desejada, enquanto a parte imaginária é (ou se aproxima de) "0". Consequentemente, o erro da parte imaginária é igual ao seu valor, mas com sinal oposto.
- Como não temos informações sobre a precisão dos valores previstos além do horizonte de planejamento definido, simplesmente ignoramos possíveis desvios e consideramos o erro como "0" para esses pontos.
//--- Copy Gradients if(!SumAndNormilize(cIFFTIm.getOutput(), GetPointer(cClear), cIFFTIm.getGradient(), 1, false, 0, 0, 0, -1)) return false;
if(!Concat(Gradient, GetPointer(cClear), cIFFTRe.getGradient(), iWindowOut, iIFFTin - iWindowOut, iCount)) return false;
Vale ressaltar que o gradiente do erro é representado como uma série temporal. Entretanto, como a previsão foi feita no domínio da frequência, também precisamos converter o gradiente do erro para o domínio da frequência. Essa operação requer a aplicação da Transformada Rápida de Fourier.
//--- FFT if(!FFT(cIFFTRe.getGradient(), cIFFTIm.getGradient(), cComplexRe.getGradient(), cComplexIm.getGradient(), false)) return false;
Distribuímos as características de frequência entre os dois MLPs responsáveis pelas partes real e imaginária.
//--- Complex Layer if(!ComplexLayerGradient(cInsideRe2.getGradient(), cInsideIm2.getGradient(), cComplexRe.getGradient(), cComplexIm.getGradient())) return false;
Em seguida, aplicamos o gradiente do erro através dos MLPs.
if(!cInsideRe1.calcHiddenGradients(cInsideRe2.AsObject())) return false; if(!cInsideIm1.calcHiddenGradients(cInsideIm2.AsObject())) return false; if(!cDropRe.calcHiddenGradients(cInsideRe1.AsObject())) return false; if(!cDropIm.calcHiddenGradients(cInsideIm1.AsObject())) return false;
Usamos a camada Dropout para propagar o gradiente do erro até a saída do bloco da Transformada de Fourier direta.
//--- Dropout if(!cFFTRe.calcHiddenGradients(cDropRe.AsObject())) return false; if(!cFFTIm.calcHiddenGradients(cDropIm.AsObject())) return false;
Agora, precisamos converter o gradiente do erro do domínio da frequência de volta para a série temporal. Realizamos essa operação por meio da transformação inversa.
//--- IFFT if(!FFT(cFFTRe.getGradient(), cFFTIm.getGradient(), cInputsRe.getGradient(), cInputsIm.getGradient(), true)) return false;
Por fim, passamos para a camada anterior apenas a parte necessária do gradiente do erro real.
//--- To Input Layer if(!DeConcat(NeuronOCL.getGradient(), cFFTIm.getGradient(), cFFTRe.getGradient(), iWindow, iFFTin - iWindow, iCount)) return false; //--- return true; }
Como sempre, monitoramos o processo de execução de todas as operações no corpo do método e, ao final, retornamos à função chamadora um valor lógico indicando a validade das operações realizadas.
Após a distribuição do gradiente do erro, segue o processo de atualização dos parâmetros do modelo, implementado no método CNeuronFITSOCL::updateInputWeights. Como já mencionado, entre os muitos objetos declarados na classe, apenas os parâmetros dos MLPs são treináveis. É justamente esses parâmetros que ajustaremos no método especificado.
bool CNeuronFITSOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!cInsideRe1.UpdateInputWeights(cDropRe.AsObject())) return false; if(!cInsideIm1.UpdateInputWeights(cDropIm.AsObject())) return false; if(!cInsideRe2.UpdateInputWeights(cInsideRe1.AsObject())) return false; if(!cInsideIm2.UpdateInputWeights(cInsideIm1.AsObject())) return false; //--- return true; }
A presença de vários objetos internos que não possuem parâmetros treináveis impacta também os métodos de manipulação de arquivos. Concordemos que não faz sentido salvar grandes quantidades de informações que não têm valor algum. Por isso, no método de salvamento de dados CNeuronFITSOCL::Save, chamamos primeiro o método homônimo da classe pai.
bool CNeuronFITSOCL::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false;
Em seguida, salvamos as constantes da arquitetura.
//--- Save constants if(FileWriteInteger(file_handle, int(iWindow)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iWindowOut)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iCount)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iFFTin)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iIFFTin)) < INT_VALUE) return false;
E então salvamos os objetos MLP.
//--- Save objects if(!cInsideRe1.Save(file_handle)) return false; if(!cInsideIm1.Save(file_handle)) return false; if(!cInsideRe2.Save(file_handle)) return false; if(!cInsideIm2.Save(file_handle)) return false;
Adicionamos também os objetos do bloco Dropout.
if(!cDropRe.Save(file_handle)) return false; if(!cDropIm.Save(file_handle)) return false; //--- return true; }
E pronto. Os outros objetos contêm apenas buffers de dados, cuja informação é relevante apenas durante um único ciclo de propagação para frente-inversa. Portanto, não os salvamos, economizando espaço em disco. No entanto, essa economia de espaço tem um custo: o algoritmo do método de carregamento de dados CNeuronFITSOCL::Load torna-se mais complexo.
bool CNeuronFITSOCL::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false;
Nesse método, começamos repetindo o processo de salvamento de maneira espelhada:
- Chamamos o método homônimo da classe pai.
- Carregamos as constantes, garantindo que não cheguemos ao fim do arquivo de dados inesperadamente.
//--- Load constants if(FileIsEnding(file_handle)) return false; iWindow = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iWindowOut = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iCount = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iFFTin = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iIFFTin = uint(FileReadInteger(file_handle)); activation=None;
- Lemos os parâmetros dos MLP e Dropout.
//--- Load objects if(!LoadInsideLayer(file_handle, cInsideRe1.AsObject())) return false; if(!LoadInsideLayer(file_handle, cInsideIm1.AsObject())) return false; if(!LoadInsideLayer(file_handle, cInsideRe2.AsObject())) return false; if(!LoadInsideLayer(file_handle, cInsideIm2.AsObject())) return false; if(!LoadInsideLayer(file_handle, cDropRe.AsObject())) return false; if(!LoadInsideLayer(file_handle, cDropIm.AsObject())) return false;
Em seguida, precisamos inicializar os objetos que estão faltando. Aqui, repetimos parte do código do método de inicialização da classe.
//--- Init objects if(!cInputsRe.Init(0, 0, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cInputsIm.Init(0, 1, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cFFTRe.Init(0, 2, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cFFTIm.Init(0, 3, OpenCL, iFFTin * iCount, optimization, iBatch)) return false; if(!cComplexRe.Init(0, 8, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cComplexIm.Init(0, 9, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cIFFTRe.Init(0, 10, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cIFFTIm.Init(0, 11, OpenCL, iIFFTin * iCount, optimization, iBatch)) return false; if(!cClear.BufferInit(MathMax(iFFTin, iIFFTin)*iCount, 0)) return false; cClear.BufferCreate(OpenCL); //--- return true; }
Com isso, finalizamos a descrição dos métodos do nosso novo classe CNeuronFITSOCL e seus algoritmos. O código completo dessa classe e de todos os seus métodos pode ser encontrado no anexo. Lá também estão todos os programas usados na elaboração deste artigo. Agora, passamos à descrição da arquitetura dos modelos treináveis.
2.4 Arquitetura das Modelos
O método FITS foi proposto para análise e previsão de séries temporais. E, acredito, você já percebeu que utilizaremos as abordagens propostas no Codificador de Estado do Ambiente. Sua arquitetura é descrita no método CreateEncoderDescriptions.
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
Nos parâmetros, o método recebe um ponteiro para um objeto de array dinâmico para armazenar a arquitetura do modelo criado. E no corpo do método, verificamos imediatamente a validade do ponteiro recebido. Se necessário, criamos uma nova instância do objeto de array dinâmico.
Como entrada para a modelo, como sempre, forneceremos os dados "brutos" que descrevem o estado atual do ambiente.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Os dados recebidos passam primeiro por uma camada de normalização em lote, o que permite padronizar os dados e aumentar a estabilidade do processo de aprendizado da modelo.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1000; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Nossos dados de entrada são uma série temporal multidimensional. Cada bloco de dados sequenciais contém diversos parâmetros que descrevem uma vela de dados históricos. No entanto, para analisar as sequências unitárias em nosso conjunto de dados, precisamos transpor o tensor recebido.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = HistoryBars; descr.window = BarDescr; if(!encoder.Add(descr)) { delete descr; return false; }
Neste ponto, consideramos a preparação concluída, e podemos prosseguir para a análise e previsão direta das séries temporais unitárias. Este processo é realizado no objeto da nossa nova classe.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFITSOCL; descr.count = BarDescr; descr.window = HistoryBars; descr.activation = None; descr.window_out = NForecast; if(!encoder.Add(descr)) { delete descr; return false; }
Vale destacar que implementamos quase todo o método FITS no corpo da nossa classe. E na saída da camada neural, já temos os valores previstos. Resta apenas transpor o tensor de valores previstos para a dimensionalidade dos resultados esperados.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = BarDescr; descr.window = NForecast; if(!encoder.Add(descr)) { delete descr; return false; }
E adicionar os parâmetros da distribuição estatística dos dados originais, que foram removidos anteriormente.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Como podemos observar, o modelo de análise e previsão dos estados futuros do ambiente é relativamente curto, como prometido pelos autores do método FITS. As alterações que fizemos na arquitetura da modelo não afetaram o volume nem o formato dos dados de entrada. Também não alteramos o formato dos resultados da modelo. Isso nos permite utilizar sem modificações as arquiteturas previamente criadas dos modelos Ator e Crítico. Além disso, podemos continuar utilizando os assessores de interação com o ambiente e de aprendizado das modelos, bem como os conjuntos de dados de treinamento já reunidos. A única coisa que precisamos ajustar é o ponteiro para a camada de representação latente do estado do ambiente.
#define LatentLayer 3
O código completo de todos os programas utilizados na elaboração deste artigo pode ser encontrado no anexo. Agora, seguimos para a etapa de teste dos resultados obtidos.
3. Testes
Familiarizamo-nos com o método FITS e realizamos um trabalho extenso para implementar as abordagens propostas em MQL5. Agora, chegou o momento de testar a eficácia dessa solução em dados históricos reais. Como anteriormente, treinaremos e testaremos o modelo em dados históricos do instrumento EURUSD no time frame H1. O treinamento foi realizado com dados de todo o ano de 2023. E a avaliação do modelo treinado será feita com os dados de janeiro de 2024.
O treinamento do modelo foi conduzido de forma semelhante ao processo descrito no artigo anterior. Primeiro, treinamos o Codificador do Estado do Ambiente para prever estados futuros. Em seguida, treinamos iterativamente a política de comportamento do Ator para maximizar a rentabilidade.
Como esperado, o modelo do Codificador revelou-se bastante leve. O processo de treinamento foi relativamente rápido e estável. Apesar do tamanho reduzido, o modelo apresentou resultados comparáveis ao modelo FEDformer discutido no artigo anterior. Vale destacar que o tamanho do modelo é quase 84 vezes menor.

Entretanto, na fase de treinamento da política do Ator, enfrentamos certa decepção. O modelo conseguiu gerar rentabilidade apenas em alguns trechos específicos dos dados históricos. No gráfico de saldo abaixo, vemos um crescimento acentuado na primeira década do mês. Porém, a segunda década mostra uma tendência de perda do saldo, com apenas algumas operações lucrativas. Já na terceira década, o número de operações lucrativas e não lucrativas aproxima-se do equilíbrio.

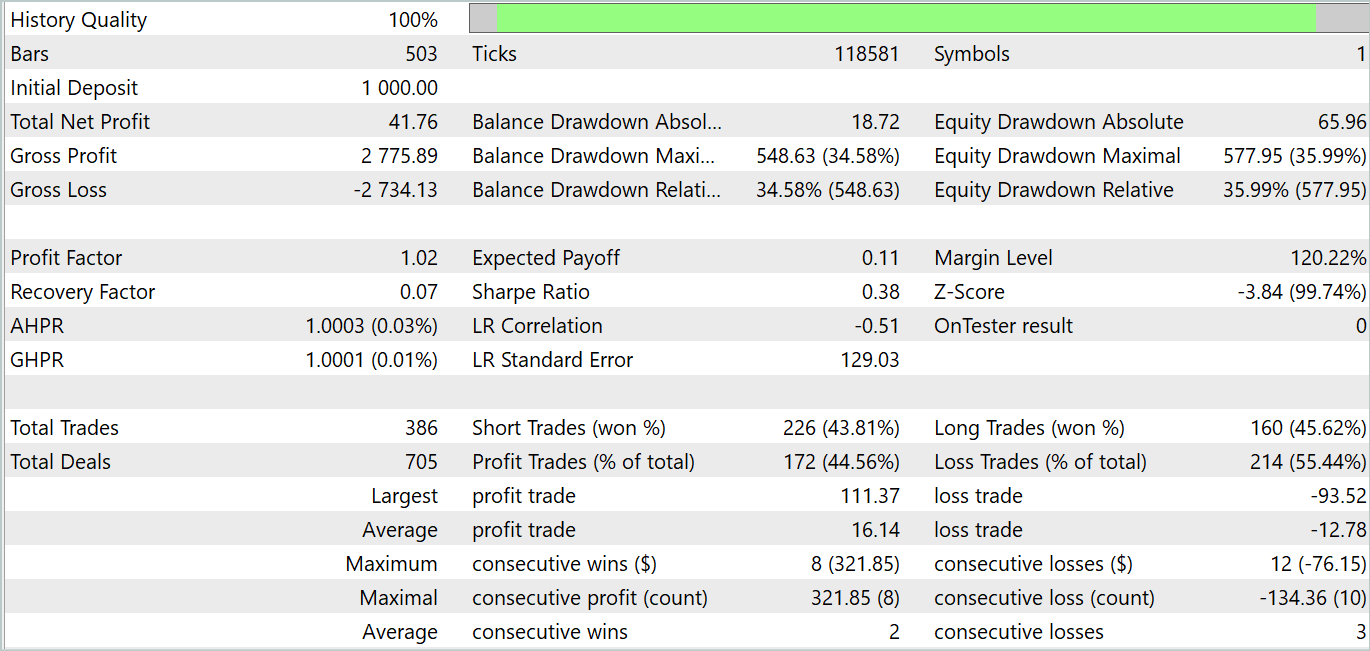
No geral, conseguimos um pequeno lucro no mês. Um ponto positivo é que o tamanho das operações lucrativas máximas e médias supera o das operações não lucrativas correspondentes. No entanto, a quantidade de operações lucrativas ficou abaixo de 50%, o que neutraliza a vantagem das operações médias lucrativas.
Podemos observar que os resultados dos testes corroboram parcialmente as conclusões feitas pelos autores do método FEDformer: devido à falta de uma periodicidade bem definida nos dados originais, DFT não é capaz de identificar o momento das mudanças de tendência.
Considerações finais
Neste artigo, apresentamos um novo método de análise e previsão de séries temporais, FITS. A principal característica desse método é o uso de análise e previsão no domínio das características de frequência. Ainda assim, graças à aplicação da Transformada Rápida de Fourier direta e inversa, trabalhamos com séries temporais discretas familiares tanto na entrada quanto na saída do modelo. Essa característica permite que a arquitetura leve proposta seja aplicada em várias áreas que exigem análise e previsão de séries temporais.
Na parte prática deste artigo, implementamos nossa visão das abordagens propostas utilizando MQL5. Treinamos e testamos os modelos com dados históricos reais. Infelizmente, os resultados dos testes não foram os desejados. Contudo, é importante frisar que esses resultados são específicos para a implementação apresentada. O uso do algoritmo original dos autores pode produzir resultados diferentes.
Links
- FITS: Modeling Time Series with 10k Parameters
- A Survey of Complex-Valued Neural Networks
- Outros artigos da série
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Advisor para coleta de exemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | Advisor para coleta de exemplos pelo método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | Advisor para treinamento de Modelos |
| 4 | StudyEncoder.mq5 | Expert Advisor | Advisor para treinamento do Codificador |
| 5 | Test.mq5 | Expert Advisor | Advisor para teste do modelo |
| 6 | Trajectory.mqh | Biblioteca de classes | Estrutura de descrição do estado do sistema |
| 7 | NeuroNet.mqh | Biblioteca de classes | Biblioteca de classes para criar a rede neural |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código para o programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/14913
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Simplificando a negociação com base em notícias (Parte 2): Gerenciando riscos
Simplificando a negociação com base em notícias (Parte 2): Gerenciando riscos
 Gerenciador de riscos para trading algorítmico
Gerenciador de riscos para trading algorítmico
 Desenvolvendo um sistema de Replay (Parte 74): Um novo Chart Trade (I)
Desenvolvendo um sistema de Replay (Parte 74): Um novo Chart Trade (I)
 Desenvolvendo um sistema de Replay (Parte 73): Uma comunicação inusitada (II)
Desenvolvendo um sistema de Replay (Parte 73): Uma comunicação inusitada (II)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso