Ganhe Vantagem em Qualquer Mercado (Parte V): Dados Alternativos FRED EURUSD

MetaTrader 5 — Exemplos | 6 agosto 2025, 11:42

Nesta série de artigos, nosso objetivo é ajudar você a navegar pelo cenário cada vez maior de dados financeiros alternativos. O investidor moderno, vivendo na era do big data, pode não dispor de recursos suficientes para decidir cuidadosamente quais conjuntos de dados alternativos deve incluir em seu processo de negociação. Buscamos fornecer as informações necessárias para que você tome uma decisão informada sobre quais datasets alternativos devem ser considerados e quais talvez seja melhor deixar de lado.

Visão Geral da Estratégia de Trading

Correlação é um princípio fundamental em uma abordagem analítica para finanças. Se dois ativos são correlacionados, então investidores que buscam diversificar seus portfólios ou maximizar sua exposição a movimentos esperados de preço podem usar inteligentemente essa métrica para construir seu portfólio.

O Federal Reserve mantém uma coleção de índices que servem como medidas resumidas do valor do dólar no mercado de câmbio estrangeiro. De todos os índices disponíveis, estávamos particularmente interessados no Nominal Broad Dollar Daily Index (NBDD). O índice foi estabelecido em janeiro de 2006 com valor de 100 pontos. No momento da redação deste artigo, o índice atingiu mínimas históricas de aproximadamente 86 pontos durante a recessão de 2008 e seu recorde máximo de cerca de 128 pontos em 2022. O índice está em tendência de alta desde o final de 2011 e atualmente está em torno de 121 pontos. Isso está bem próximo do seu recorde histórico.

No gráfico abaixo, sobrepomos o índice Broad Dollar e a taxa de câmbio do par EURUSD. É quase impossível ver qualquer relação material entre essas duas séries temporais. A taxa de câmbio do Dólar para o Euro está quase oculta como uma linha azul achatada na parte inferior do gráfico, enquanto o Broad Dollar Index é a linha vermelha claramente visível.

Dados FRED sem escala

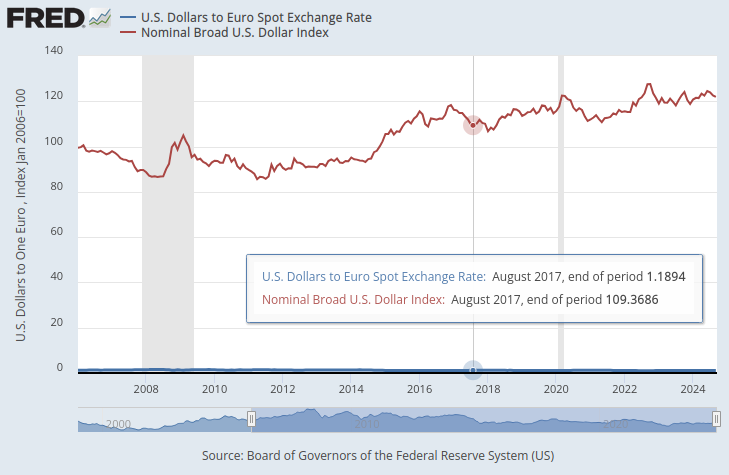
Fig 1: Taxa à vista Dólar para Euro & Broad Dollar Index

Se colocarmos ambas as séries temporais na mesma escala, um padrão óbvio surge. Vamos ajustar nosso eixo y para que registre a variação percentual nas séries temporais ao longo de 1 ano. Ao fazer isso, podemos observar claramente que o índice exibe uma correlação negativa quase perfeita com a taxa de câmbio EURUSD.

Dados FRED EURUSD

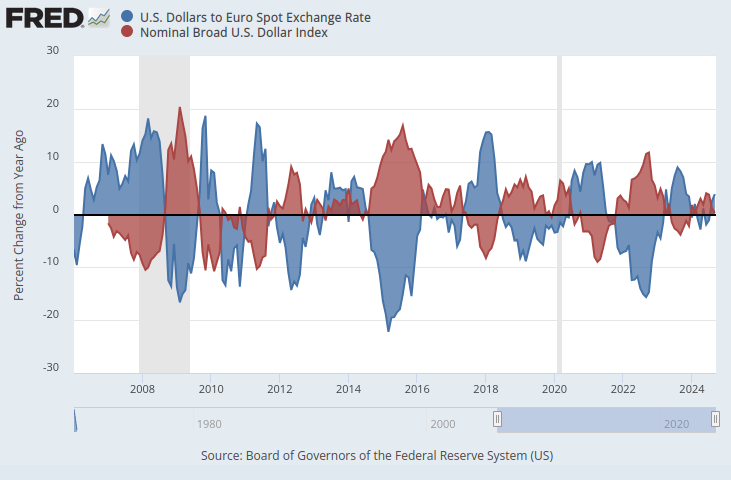
Fig 2: Taxa à vista Dólar para Euro & Broad Dollar Index em escala percentual

Vamos explorar a viabilidade de aprender, de forma algorítmica, uma estratégia de negociação que utilize esses conjuntos de dados para prever a taxa de câmbio futura do EURUSD. Dada a correlação negativa perfeita, pode haver alguma informação que nosso modelo consiga aprender sobre a taxa de câmbio, com base em indicadores macroeconômicos do Federal Reserve Economic Database (FRED).

Visão Geral da Metodologia

Para testar a validade de nossa hipótese, começamos obtendo as taxas históricas diárias de câmbio do EURUSD em nosso terminal MetaTrader 5 e mesclamos esses dados com 3 conjuntos de dados macroeconômicos recuperados pela API Python do FRED. Os 3 conjuntos de séries temporais FRED registravam:

Taxas de Juros de Títulos Americanos
Taxas de Inflação Esperada nos EUA
Broad Dollar Index

Isso nos permitiu criar 3 conjuntos de dados para construção do nosso modelo de IA:

Cotações de mercado OHLC convencionais.
Dados alternativos do FRED
Um superset dos dois primeiros.

Após a junção de todos os conjuntos de dados em questão e a conversão das escalas para replicar o que fizemos no site do FRED, observamos níveis de correlação entre os preços do EURUSD e o Broad Dollar Index próximos de -0,9. Isso é quase um score perfeito! Além disso, observamos a correlação entre o valor atual do Broad Dollar Index e o valor futuro (20 dias à frente) do fechamento do EURUSD em -0,7.

Ao visualizar, conseguimos separar as séries temporais de forma notável, com um nível de refinamento que dificilmente demonstramos antes nesta série de artigos. Parece que usar a variação percentual dos dados em janelas mais longas permite separar muito bem os dados. Nossos gráficos de dispersão 3D validaram ainda mais o quanto os dados estavam bem separados, permitindo identificar zonas de alta e baixa. Além disso, ao realizar scatter-plots no site oficial do FRED, foi possível observar claramente uma tendência nos dados. A tendência no gráfico de dispersão estava bem definida, mesmo sem utilizar nosso conjunto usual de ferramentas analíticas avançadas em Python. Isso nos deu confiança de que pode haver alguma informação compartilhada pelas duas séries temporais que nosso modelo possa aprender.

Dados FRED têm uma tendência

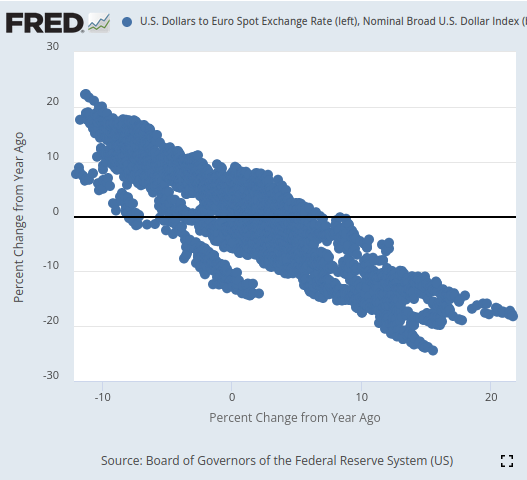
Fig 3: Visualização de um gráfico de dispersão dos dois conjuntos de dados de interesse

Por mais promissor que tudo isso pareça, nada disso se traduziu em melhora de desempenho na nossa capacidade de prever o valor futuro da taxa de câmbio EURUSD. Na verdade, nosso desempenho apenas piorou, e parece que tivemos melhores resultados usando o primeiro conjunto de dados que continha apenas as cotações normais de mercado.

Treinamos 3 Regressoras de Rede Neural Profunda (DNN) idênticas para aprender a relação entre nossos 3 conjuntos de dados e o alvo comum que todos compartilhavam. O primeiro modelo DNN produziu a menor taxa de erro. Além disso, nenhum de nossos algoritmos de seleção de variáveis se impressionou com qualquer um dos conjuntos de dados FRED selecionados para a análise. Mesmo assim, conseguimos ajustar os parâmetros do nosso modelo DNN usando o conjunto de treinamento, sem overfitting. Mesmo assim, conseguimos ajustar os parâmetros do nosso modelo DNN usando o conjunto de treinamento, sem overfitting. Utilizamos validação cruzada para séries temporais, sem embaralhamento aleatório, para tomar essas decisões no treinamento e validação.

Antes de exportarmos nosso modelo para o formato ONNX, inspecionamos os resíduos do modelo para garantir que ele estava em boas condições. Infelizmente, os resíduos observados estavam bem ruins, sugerindo que nosso modelo não conseguiu aprender de forma eficaz.

Por fim, exportamos nosso modelo para o formato ONNX e construímos um expert advisor integrado com IA usando Python e MQL5.

Buscando os Dados

Para começar, primeiro importamos as bibliotecas Python necessárias.

#Import the libraries we need
from   fredapi           import Fred
import seaborn           as sns
import numpy             as np
import pandas            as pd
import MetaTrader5       as mt5
import matplotlib.pyplot as plt

Em seguida, definimos nossas credenciais e quais séries temporais gostaríamos de buscar do FRED.

#Define important variables
fred_api                = "ENTER YOUR API KEY"
fred_broad_dollar_index = "DTWEXBGS"
fred_us_10y             = "DGS10"
fred_us_5y_inflation    = "T5YIFR"

Faça login no FRED.

#Login to fred
fred = Fred(api_key=fred_api)

Vamos buscar os dados de que precisamos.

#Fetch the data
dollar_index    = fred.get_series(fred_broad_dollar_index)
us_10y          = fred.get_series(fred_us_10y)
us_5y_inflation = fred.get_series(fred_us_5y_inflation)

Dar nomes às séries nos permitirá mesclá-las mais tarde.

#Name the series so we can merge the data
dollar_index.name    =  "Dollar Index"
us_10y.name          =  "Bond Interest"
us_5y_inflation.name =  "Inflation"

Preencha quaisquer valores ausentes com a média móvel.

#Fill in any missing values
dollar_index.fillna(dollar_index.rolling(window=5,min_periods=1).mean(),inplace=True)
us_10y.fillna(us_10y.rolling(window=5,min_periods=1).mean(),inplace=True)
us_5y_inflation.fillna(dollar_index.rolling(window=5,min_periods=1).mean(),inplace=True)

Antes de buscarmos os dados no nosso terminal MetaTrader 5, precisamos primeiro inicializá-lo.

#Initialize the terminal
mt5.initialize()

Verdadeiro

Gostaríamos de buscar 4 anos de dados históricos.

#Define how much data to fetch
amount = 365 * 4
#Fetch data
eur_usd = pd.DataFrame(mt5.copy_rates_from_pos("EURUSD",mt5.TIMEFRAME_D1,0,amount))
eur_usd

Converta a coluna de tempo do formato em segundos para datas reais.

#Convert the time column
eur_usd['time'] = pd.to_datetime(eur_usd.loc[:,'time'],unit='s')

Certifique-se de que a coluna de tempo seja o índice dos nossos dados.

#Set the column as the index
eur_usd.set_index('time',inplace=True)

Defina com quanto tempo de antecedência gostaríamos de fazer a previsão.

#Define the forecast horizon
look_ahead = 20

Vamos agora especificar nossos preditores e alvos.

#Define the predictors
predictors = ["open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"]
ohlc_predictors = ["open","high","low","close","tick_volume"]
fred_predictors = ["Dollar Index","Bond Interest","Inflation"]
target = "Target"
all_data = ["Target","open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"]
all_data_binary = ["Binary Target","open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"]

Mescle os dados.

#Merge our data
merged_data = eur_usd.merge(dollar_index,right_index=True,left_index=True)
merged_data = merged_data.merge(us_10y,right_index=True,left_index=True)
merged_data = merged_data.merge(us_5y_inflation,right_index=True,left_index=True)

Rotule os dados.

#Define the target
target         = merged_data.loc[:,"close"].shift(-look_ahead)
target.name    =  "Target"

Formate os dados para que exibam a variação percentual anual, assim como fizemos na análise do site do FRED.

#Convert the data to yearly percent changes
merged_data = merged_data.loc[:,predictors].pct_change(periods = 365) * 100
merged_data = merged_data.merge(target,right_index=True,left_index=True)
merged_data.dropna(inplace=True)
merged_data

Adicione um alvo binário para fins de visualização em gráficos.

#Add binary targets for plotting purposes
merged_data["Binary Target"] = 0
merged_data.loc[merged_data["close"] < merged_data["Target"],"Binary Target"] = 1

Redefina o índice dos dados.

#Reset the index
merged_data.reset_index(inplace=True,drop=True)
merged_data

Análise Exploratória dos Dados

Vamos começar recriando o gráfico que geramos no site do Federal Reserve de St. Louis, para validar que realizamos as etapas de pré-processamento conforme o esperado.

#Plotting our data set
plt.title("EURUSD Close Against FRED Broad Dollar Index")
plt.plot(merged_data.loc[:,"close"])
plt.plot(merged_data.loc[:,"Dollar Index"])

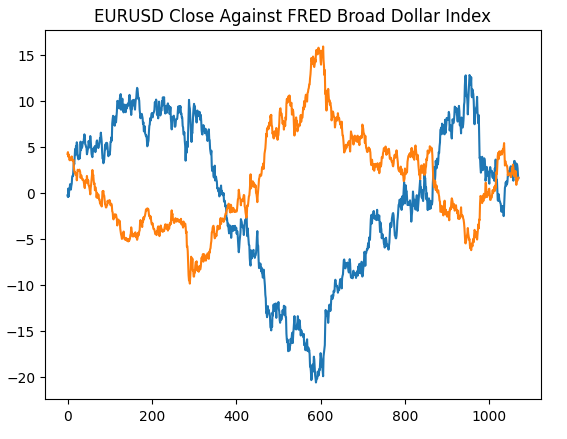
Fig 4: Recriando nossa observação do site do FRED em Python

Vamos agora analisar os níveis de correlação dentro do nosso conjunto de dados. Como podemos observar, o conjunto de dados de inflação possui os menores níveis de correlação dentre os 3 conjuntos alternativos de dados FRED que buscamos. No entanto, não obtivemos nenhuma melhoria de desempenho, mesmo que nossos outros 2 conjuntos alternativos de dados aparentassem ter tanto potencial.

#Exploratory data analysis
sns.heatmap(merged_data.loc[:,all_data].corr(),annot=True)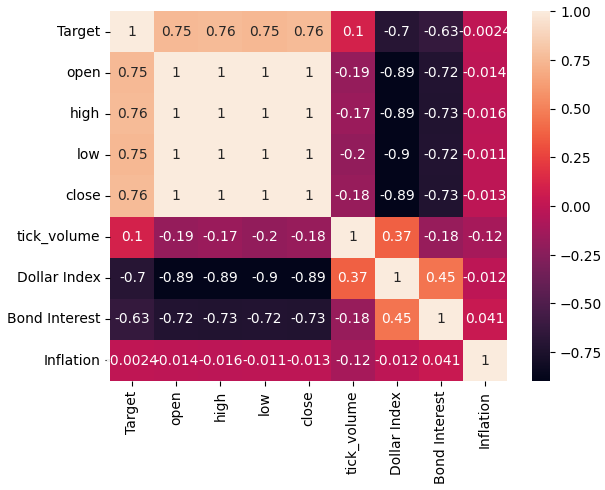

Fig 5: Nosso mapa de calor de correlação

Ao visualizar vários conjuntos de dados ao mesmo tempo, gráficos de pares (pair plots) podem nos ajudar a enxergar rapidamente as relações que podem existir entre todos os dados disponíveis. Podemos ver claramente que os pontos laranja e azul parecem estar notavelmente bem separados. Além disso, temos gráficos de estimativa de densidade do núcleo (KDE) ao longo da diagonal principal desse gráfico. Os gráficos KDE ajudam a visualizar a distribuição dos dados em cada coluna. O fato de observarmos duas formas de colinas que se sobrepõem apenas em uma pequena seção indica que, na maior parte, os dados estão bem separados.

sns.pairplot(merged_data.loc[:,all_data_binary],hue="Binary Target")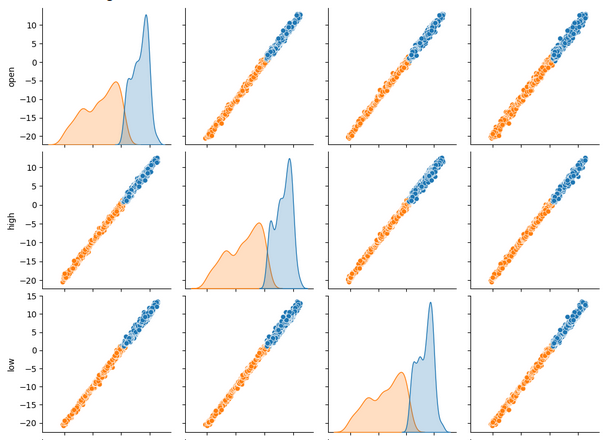

Fig 6: Visualizando nossos dados usando pair-plots

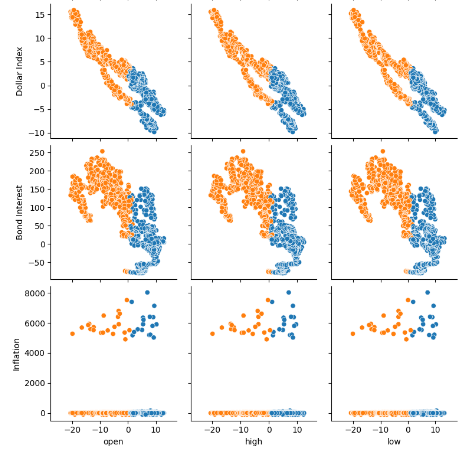
Fig 7: Visualizando nossos dados alternativos do FRED e sua relação com o par EURUSD

Agora, vamos criar gráficos de dispersão 3D usando o Broad Dollar Index e a Taxa de Juros de Títulos no eixo x e y, e o fechamento do EURUSD no eixo z. Os dados parecem formar 2 agrupamentos distintos, com pouca sobreposição. Isso naturalmente indicaria que pode existir uma fronteira de decisão que nosso modelo poderia aprender a partir dos dados. Lamentavelmente, acredito que não conseguimos expor isso de forma eficaz ao nosso modelo.

#Define the 3D Plot
fig = plt.figure(figsize=(7,7))
ax = plt.axes(projection="3d")
ax.scatter(merged_data["Dollar Index"],merged_data["Bond Interest"],merged_data["close"],c=merged_data["Binary Target"])
ax.set_xlabel("Dollar Index")
ax.set_ylabel("Bond Interest")
ax.set_zlabel("EURUSD close")

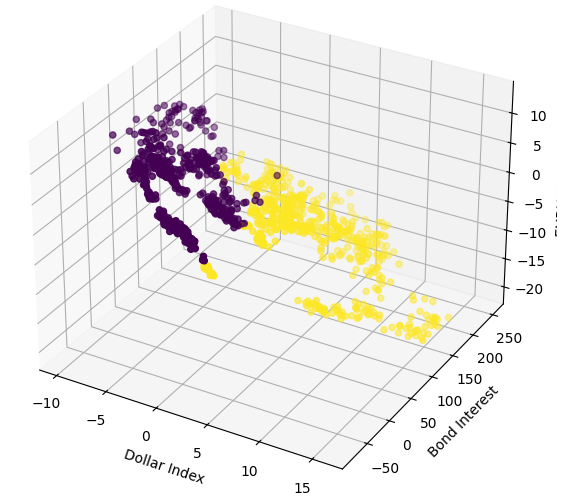
Fig 8: Visualizando nossos dados de mercado em 3D

Preparando os Dados para Modelagem

Vamos agora nos preparar para modelar os dados financeiros que temos, começando por definir as entradas do modelo e o alvo.

#Let's define our set of predictors
X = merged_data.loc[:,predictors]
y = merged_data.loc[:,"Target"]

Importando as bibliotecas necessárias.

#Import the libraries we need
from sklearn.model_selection import train_test_split

Agora, vamos particionar nossos dados nos 3 grupos definidos anteriormente.

#Partition the data
ohlc_train_X,ohlc_test_X,train_y,test_y = train_test_split(X.loc[:,ohlc_predictors],y,test_size=0.5,shuffle=False)
fred_train_X,fred_test_X,_,_            = train_test_split(X.loc[:,fred_predictors],y,test_size=0.5,shuffle=False)
train_X,test_X,_,_                      = train_test_split(X.loc[:,predictors],y,test_size=0.5,shuffle=False)

Crie um data frame para armazenar a acurácia de validação cruzada do nosso modelo.

#Prepare the dataframe to store our validation error
validation_error = pd.DataFrame(columns=["MT5 Data","FRED Data","ALL Data"],index=np.arange(0,5))

Modelagem dos Dados

Vamos importar as bibliotecas necessárias para modelar os dados.

#Let's cross validate our models
from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import cross_val_score

Defina as 3 redes neurais que descrevemos anteriormente.

#Define the neural networks
ohlc_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)
fred_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)
all_nn  = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)

Teste cada modelo.

#Let's obtain our cv score
ohlc_score = cross_val_score(ohlc_nn,ohlc_train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1)
fred_score = cross_val_score(fred_nn,fred_train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1)
all_score = cross_val_score(all_nn,train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1)

Armazene nossas pontuações de validação cruzada.

for i in np.arange(0,5):
    validation_error.iloc[i,0] = ohlc_score[i]
    validation_error.iloc[i,1] = fred_score[i]
    validation_error.iloc[i,2] = all_score[i]

Visualize o erro de validação.

#Our validation error
validation_error

Dados MetaTrader 5	Dados Alternativos FRED	Todos os Dados
-0.147973	-0.79131	-4.816608
-0.103913	-2.073764	-0.655701
-0.211833	-0.276794	-0.838832
-0.094998	-1.954753	-0.259959
-1.233912	-2.152471	-3.677273

Ao analisar o desempenho médio em todos os 5 folds, vemos que nossos dados de mercado convencionais do MetaTrader 5 podem ser nossa melhor aposta.

#Our mean performane across all groups
validation_error.mean()

Dados de Entrada	Erro Médio dos 5 Folds
MetaTrader 5	-0.358526
FRED	-1.449818
TODOS	-2.049675

Ao plotar o desempenho dos modelos, podemos observar que os dados do MetaTrader 5 apresentaram níveis de erro mais consistentes.

#Plotting our performance
validation_error.plot()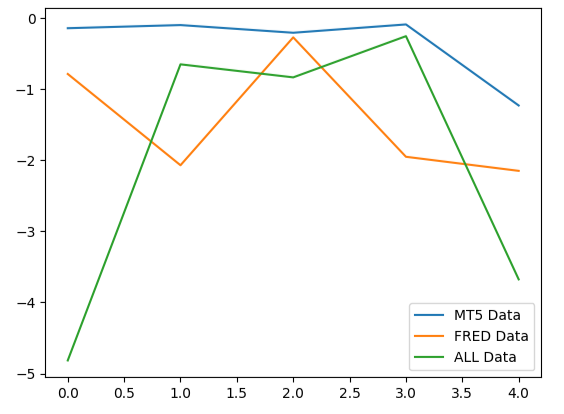

Fig 9: Visualizando os 3 diferentes níveis de erro produzidos pelos 3 conjuntos de dados disponíveis

O formato comprimido do boxplot de erro do MetaTrader 5 é desejável porque mostra que o modelo demonstra habilidade através de seu desempenho consistente.

#Creating box-plots of our performance
sns.boxplot(validation_error)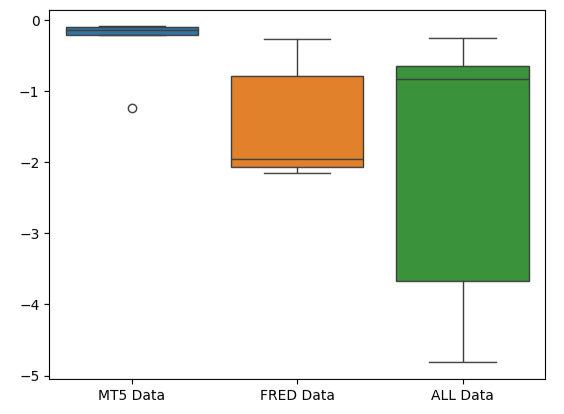

Fig 10: Visualizando as métricas de erro do modelo como boxplots

Importância das Variáveis

Vamos agora refletir sobre quais variáveis podem ser mais importantes para o nosso modelo DNN. Se os dados alternativos que selecionamos forem realmente úteis, isso será reconhecido por nossos algoritmos de importância de variáveis. Infelizmente, nossa análise sugere que a variação nos dados de mercado do MetaTrader 5 já explica o alvo razoavelmente bem por si só. Portanto, não havia informação adicional nas séries temporais do FRED que nosso modelo não pudesse deduzir a partir dos dados que já tinha.

Para começar, vamos importar as bibliotecas necessárias.

#Feature importance
from alibi.explainers import ALE, plot_ale

Os gráficos ALE (Accumulated Local Effects) ajudam a visualizar o efeito que cada entrada do modelo tem sobre o alvo. Gráficos ALE são populares por sua robustez ao explicar modelos treinados com dados altamente correlacionados, como os nossos. Métodos acadêmicos clássicos, como os gráficos de dependência parcial (Partial Dependency - PD), não são confiáveis ao explicar preditores com altos níveis de correlação. A especificação original do algoritmo pode ser lida no artigo científico completo de 2016 por Daniel W. Apley e Jingyu Zhu, disponível aqui.

Fig 11: Daniel W. Apley, co-criador do algoritmo ALE

Vamos ajustar o explicador ALE ao nosso Regressor DNN.

#Explaining our deep neural network
model = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)
model.fit(train_X,train_y)
dnn_ale = ALE(model.predict,feature_names=predictors,target_names=["Target"])

Agora podemos obter uma explicação sobre o efeito de cada preditor no alvo. Os gráficos ALE possuem uma interpretação visual intuitiva que os torna um bom ponto de partida. Resumidamente, se o gráfico ALE que obtemos é uma linha reta, isso significa que, do ponto de vista do nosso modelo DNN, o preditor em questão tem pouco ou nenhum efeito sobre o alvo. Da mesma forma, quanto mais afastado da linearidade for o gráfico ALE, mais o modelo aprendeu uma relação não-linear entre o alvo e o preditor.

O gráfico ALE do preço de abertura em relação ao alvo, no canto superior esquerdo da Fig 12, sugere que, à medida que o preço de abertura do EURUSD aumenta, o modelo aprendeu que o preço de fechamento futuro também irá aumentar. Observe como os gráficos ALE do preço de abertura e do preço de fechamento variam em direções opostas. Isso pode indicar que apenas esses dois preditores já explicam uma parcela significativa da variância do alvo.

#Obtaining the explanation
ale_X = X.to_numpy()
dnn_explanations = dnn_ale.explain(ale_X)
#Plotting feature importance
plot_ale(dnn_explanations,n_cols=3,fig_kw={'figwidth':8,'figheight':8},sharey=None)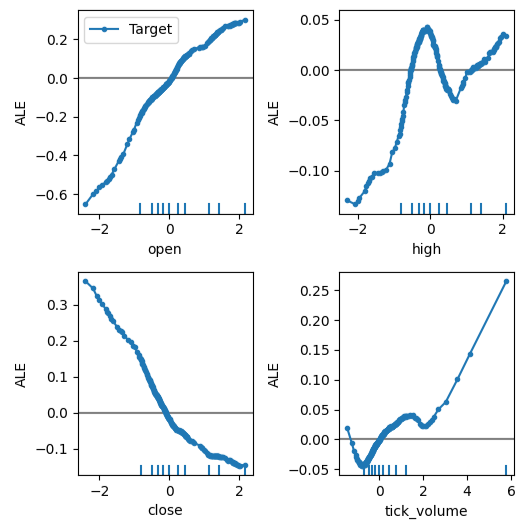

Fig 12: Visualizando nossos gráficos ALE nos dados de mercado do MetaTrader 5

Agora vamos realizar o forward-selection (seleção progressiva). O algoritmo começa com um modelo nulo e adiciona iterativamente 1 variável que mais melhora o desempenho do modelo, até que o desempenho não possa mais ser aumentado.

#Forward selection
from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from mlxtend.plotting import plot_sequential_feature_selection as plot_sfs

Inicializar o modelo.

#Reinitialize the model
all_nn  = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)

Agora precisamos especificar o objeto de forward-selection desejado. Vamos instruir esta instância do algoritmo a selecionar todas as variáveis que considerar importantes.

#Define the feature selector
sfs1 = SFS(all_nn,
           k_features=(1,X.shape[1]),
           forward=True,
           scoring='neg_mean_squared_error',
           cv=5,
           n_jobs=-1
          )

Nenhuma das séries temporais do FRED foi selecionada pelo algoritmo.

#Best features we identified
sfs1.k_feature_names_

('open', 'high', 'low')

Podemos visualizar o processo de seleção do algoritmo. Nosso gráfico mostra claramente que o desempenho do modelo diminuiu à medida que aumentamos o número de preditores no modelo.

#Fit the forward selection algorithm
fig1 = plot_sfs(sfs1.get_metric_dict(), kind='std_dev')

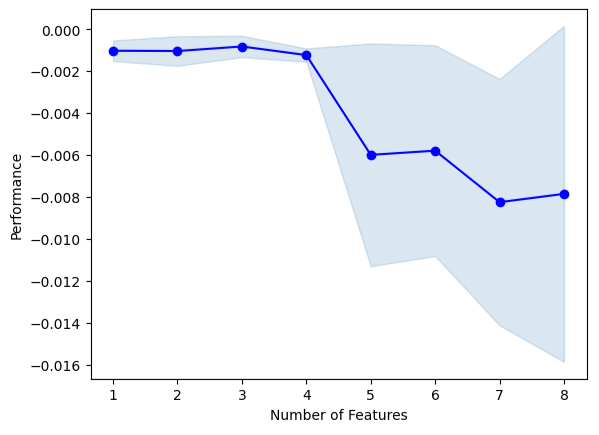
Fig 13: Visualizando o desempenho do modelo conforme adicionamos mais preditores iterativamente

Ajuste de Parâmetros

Vamos realizar o ajuste de parâmetros do nosso modelo DNN usando busca aleatória (random search). Primeiro, precisamos inicializar nosso modelo.

#Reinitialize the model
model  = MLPRegressor(max_iter=500)

Agora vamos definir os parâmetros a serem ajustados.

#Define the tuner
tuner = RandomizedSearchCV(
        model,
        {
        "activation" : ["relu","logistic","tanh","identity"],
        "solver":["adam","sgd","lbfgs"],
        "alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001],
        "tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "learning_rate":['constant','adaptive','invscaling'],
        "learning_rate_init":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "hidden_layer_sizes":[(10,20,40),(10,20,40,80),(5,10,20,100),(100,50,10),(20,20,10),(1,5,10,20),(20,10,5,1)],
        "early_stopping":[True,False],
        "warm_start":[True,False],
        "shuffle": [True,False]
        },
        n_iter=500,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

Ajuste o objeto de tuning.

#Fit the tuner
tuner.fit(train_X,train_y)

Vamos ver os melhores parâmetros que encontramos.

#The best parameters we found
tuner.best_params_

{'warm_start': False,
'tol': 1e-05,
'solver': 'lbfgs',
'shuffle': True,
'learning_rate_init': 0.01,
'learning_rate': 'invscaling',
'hidden_layer_sizes': (10, 20, 40, 80),
'early_stopping': True,
'alpha': 0.1,
'activation': 'relu'}

Otimização de Parâmetros Mais Profunda

Vamos buscar melhores parâmetros para o modelo utilizando a biblioteca SciPy. Podemos imaginar os processos de otimização como problemas de busca, quase como o jogo de esconde-esconde da infância. Veja, os parâmetros ideais para nosso modelo — aqueles que irão produzir a menor taxa de erro em dados ainda não vistos pelo modelo — estão escondidos no espaço infinito de valores possíveis que poderíamos atribuir a cada um dos nossos parâmetros contínuos.

Vamos importar as bibliotecas de que precisamos.

#Deeper optimization
from scipy.optimize import minimize
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import TimeSeriesSplit

Defina um objeto de divisão de séries temporais.

#Define the time series split object
tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)

Crie um data frame para retornar o custo atual e uma lista para armazenar o progresso do modelo para visualização.

#Create a dataframe to store our accuracy
current_error_rate = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"])
algorithm_progress = []

Agora vamos definir nossa função de custo. A biblioteca minimize do SciPy oferece diversos algoritmos para encontrar as entradas de qualquer função que resultem no menor valor de saída dessa função. Vamos usar a média do erro do modelo em 5 folds nos dados de treinamento como a métrica a ser minimizada, mantendo todos os outros parâmetros do DNN constantes.

#Define the objective function
def objective(x):
    #The parameter x represents a new value for our neural network's settings
    model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"],
                         early_stopping=tuner.best_params_["early_stopping"],
                         warm_start=tuner.best_params_["warm_start"],
                         max_iter=500,
                         activation=tuner.best_params_["activation"],
                         learning_rate=tuner.best_params_["learning_rate"],
                         solver=tuner.best_params_["solver"],
                         shuffle=tuner.best_params_["shuffle"],
                         alpha=x[0],
                         tol=x[1],
                         learning_rate_init=x[2]
                         )
    #Now we will cross validate the model
    for i,(train,test) in enumerate(tscv.split(train_X)):
        #Train the model
        model.fit(train_X.loc[train[0]:train[-1],:],train_y.loc[train[0]:train[-1]])
        #Measure the RMSE
        current_error_rate.iloc[i,0] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],:]))
    #Store the algorithm's progress
    algorithm_progress.append(current_error_rate.iloc[:,0].mean())
    #Return the Mean CV RMSE
    return(current_error_rate.iloc[:,0].mean())

Vamos definir os pontos iniciais para a rotina e especificar limites para os parâmetros. Para este problema, nosso único limite é que todos os parâmetros do modelo devem ser positivos.

#Define the starting point
pt = [tuner.best_params_["alpha"],tuner.best_params_["tol"],tuner.best_params_["learning_rate_init"]]
bnds = ((10.00 ** -100,10.00 ** 100),
        (10.00 ** -100,10.00 ** 100),
        (10.00 ** -100,10.00 ** 100))

Vamos usar o algoritmo Truncated Newton Constrained (TNC) para otimizar os parâmetros do nosso modelo. Os métodos de Newton truncado formam uma família de métodos adequados para resolver grandes problemas de otimização não linear sujeitos a restrições. A biblioteca SciPy nos fornece um wrapper para uma implementação em C deste algoritmo.

#Searching deeper for parameters
result = minimize(objective,pt,method="TNC",bounds=bnds)

Vamos verificar se o procedimento foi finalizado com sucesso.

#The result of our optimization
result

message: Linear search failed
success: False
status: 4
     fun: 0.001911232280110637
       x: [ 1.000e-100 1.000e-100 1.000e-100]
     nit: 0
     jac: [ 2.689e+06 9.227e+04 1.124e+05]
    nfev: 116

Parece que tivemos dificuldade em encontrar entradas ótimas, então vamos visualizar o desempenho do nosso procedimento de otimização.

#Store the optimal coefficients
optimal_weights = result.x
optima_y = min(algorithm_progress)
optima_x = algorithm_progress.index(optima_y)
inputs = np.arange(0,len(algorithm_progress))

#Plot the performance of our optimization procedure
plt.scatter(inputs,algorithm_progress)
plt.plot(optima_x,optima_y,'ro',color='r')
plt.axvline(x=optima_x,ls='--',color='red')
plt.axhline(y=optima_y,ls='--',color='red')
plt.xlabel("Iterations")
plt.ylabel("Training MSE")
plt.title("Minimizing Training Error")

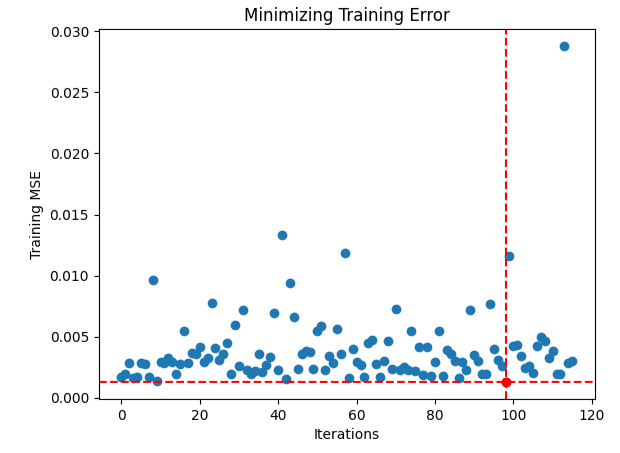
Fig 14: O ponto vermelho representa os valores ótimos estimados pelo nosso otimizador TNC

Testando Overfitting

Vamos inicializar nossos 3 modelos e ver se conseguimos treiná-los no conjunto de treinamento e superar o modelo padrão nos dados de teste. Lembre-se de que até aqui não utilizamos os dados de teste em nosso processo de decisão.

#Testing for overfitting
default_nn = MLPRegressor(max_iter=500)

#Randomized NN
random_search_nn = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"],
                         early_stopping=tuner.best_params_["early_stopping"],
                         warm_start=tuner.best_params_["warm_start"],
                         max_iter=500,
                         activation=tuner.best_params_["activation"],
                         learning_rate=tuner.best_params_["learning_rate"],
                         solver=tuner.best_params_["solver"],
                         shuffle=tuner.best_params_["shuffle"],
                         alpha=tuner.best_params_["alpha"],
                         tol=tuner.best_params_["tol"],
                         learning_rate_init=tuner.best_params_["learning_rate_init"]
                         )

#TNC NN
tnc_nn = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"],
                         early_stopping=tuner.best_params_["early_stopping"],
                         warm_start=tuner.best_params_["warm_start"],
                         max_iter=500,
                         activation=tuner.best_params_["activation"],
                         learning_rate=tuner.best_params_["learning_rate"],
                         solver=tuner.best_params_["solver"],
                         shuffle=tuner.best_params_["shuffle"],
                         alpha=result.x[0],
                         tol=result.x[1],
                         learning_rate_init=result.x[2]
                         )

Ajuste cada um dos modelos no conjunto de treinamento.

#Store the models in a list
models = [default_nn,random_search_nn,tnc_nn]

#Fit the models
for model in models:
    model.fit(train_X,train_y)

Crie um data frame para armazenar nossos níveis de erro de validação.

#Create a dataframe to store our validation error
validation_error = pd.DataFrame(columns=["Default","Randomized","TNC"],index=np.arange(0,5))

Teste cada modelo e registre sua pontuação.

#Let's obtain our cv score
default_score = cross_val_score(default_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1)
random_score = cross_val_score(random_search_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1)
tnc_score = cross_val_score(tnc_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1)

#Store the model error in a dataframe
for i in np.arange(0,5):
    validation_error.iloc[i,0] = default_score[i]
    validation_error.iloc[i,1] = random_score[i]
    validation_error.iloc[i,2] = tnc_score[i]

Vamos analisar o erro de validação.

#Let's see the validation error
validation_error

Modelo Padrão	Random Search	TNC
-0.362851	-0.029476	-0.054709
-0.323601	-0.053967	-0.087707
-0.064432	-0.024282	-0.026481
-0.121226	-0.019693	-0.017709
-0.064801	-0.012812	-0.016125

O cálculo do nosso desempenho médio em todos os 5 folds mostra claramente que o modelo ajustado via busca aleatória é nossa melhor opção.

#Our best performing model
validation_error.mean()

Modelo	Erro Médio de Validação
Modelo Padrão	-0.187382
Random Search	-0.028046
TNC	-0.040546

A criação de boxplots nos mostra rapidamente a extensão da variação de desempenho do modelo padrão. Nossos modelos customizados conseguiram operar dentro de uma faixa estreita de níveis de erro, o que aumenta nossa confiança nas escolhas de ajuste de parâmetros.

#Let's create box-plots
sns.boxplot(validation_error)

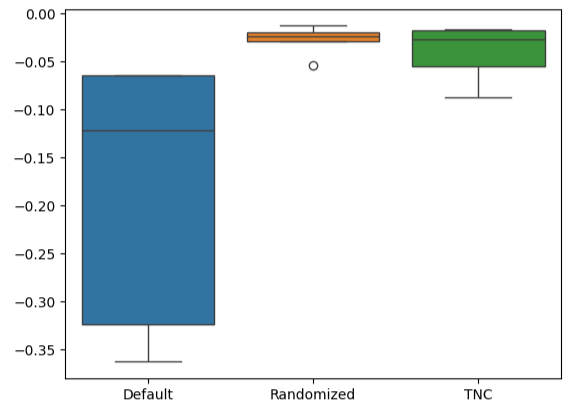
Fig 15: Visualizando o desempenho dos modelos em boxplots

A criação de gráficos de linhas com os dados de validação cruzada destaca a diferença entre o modelo padrão e nossos modelos ajustados. Podemos ver que há uma quantidade significativa de erro entre a linha azul (modelo padrão) e os demais gráficos coloridos.

#We can also visualize model performance through a line plot
validation_error.plot()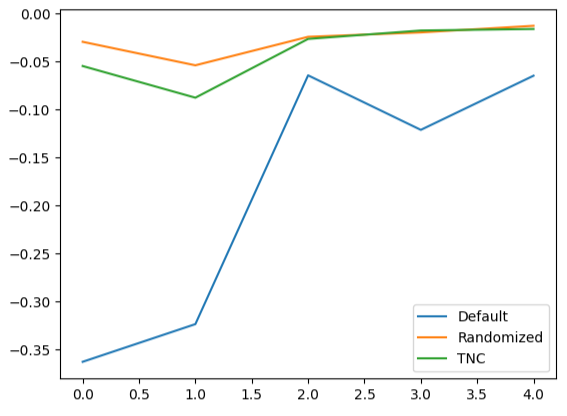

Fig 16: Plotando o desempenho dos diferentes modelos nos dados de teste em 5 folds

Análise dos Resíduos

Não podemos confiar cegamente em nosso modelo e colocá-lo em produção. Vamos tentar garantir que o modelo realmente aprendeu de forma eficaz, inspecionando os resíduos do modelo. Idealmente, um modelo que aproxima perfeitamente uma função terá resíduos formando uma linha reta. Ou seja, não há erro nas previsões do modelo. Além disso, isso também implica que a quantidade de erro na previsão do modelo não varia.

Consequentemente, quanto mais distante do ideal estiver o desempenho do modelo, maior será a distorção observada no gráfico de resíduos linear e estacionário. Os resíduos do nosso modelo apresentaram diferentes quantidades de erro, que por vezes estavam correlacionadas com a quantidade de erro anterior. Isso é motivo de atenção e pode, potencialmente, ser tratado transformando o preditor ou o alvo.

Vamos inicializar o modelo.

#Resdiuals analysis
model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"],
                         early_stopping=tuner.best_params_["early_stopping"],
                         warm_start=tuner.best_params_["warm_start"],
                         max_iter=500,
                         activation=tuner.best_params_["activation"],
                         learning_rate=tuner.best_params_["learning_rate"],
                         solver=tuner.best_params_["solver"],
                         shuffle=tuner.best_params_["shuffle"],
                         alpha=tuner.best_params_["alpha"],
                         tol=tuner.best_params_["tol"],
                         learning_rate_init=tuner.best_params_["learning_rate_init"]
                         )

Ajuste o modelo nos dados de treinamento e, em seguida, registre os resíduos usando os dados de teste.

#Fit the model
model.fit(train_X,train_y)

#Record the residuals
residuals = test_y - model.predict(test_X)

Nosso gráfico de resíduos estava longe do ideal, e talvez precisemos explorar outros passos de pré-processamento para lidar com isso.

#Residuals analysis
residuals.plot()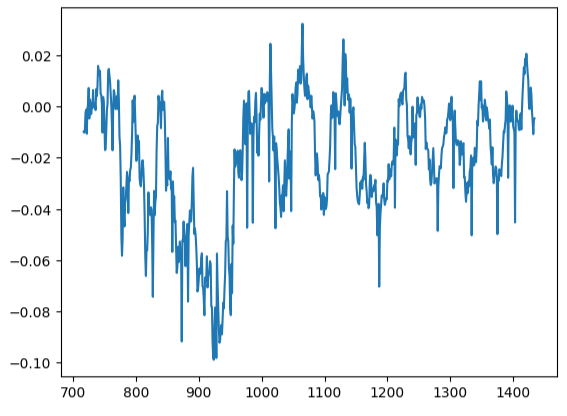

Fig 17: Visualizando os resíduos do nosso modelo nos dados de teste

Medir a autocorrelação é uma abordagem robusta para detectar possíveis regressões espúrias. Infelizmente, os resíduos do nosso modelo também falharam nesse teste, podendo indicar que melhorias adicionais podem ser obtidas se transformarmos melhor os preditores ou o alvo.

#Autocorrelation plot
from statsmodels.graphics.tsaplots import plot_acf
acf = plot_acf(residuals,lags=40)

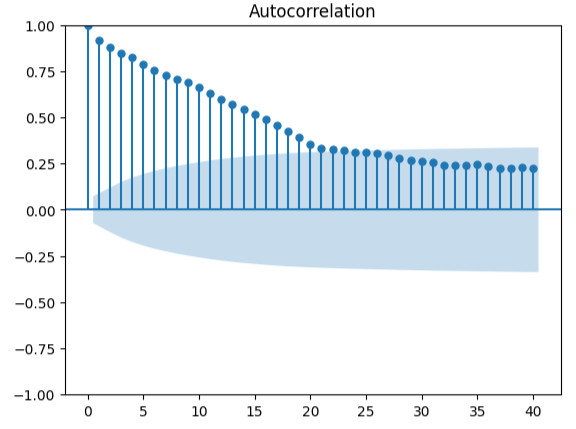
Fig 18: Visualizando os resíduos do nosso modelo

Preparando para Exportar para ONNX

Antes de exportarmos nossos dados para o formato ONNX, vamos primeiro armazenar os valores médios e os desvios padrão de cada coluna em um data frame. Observe que, como não obtivemos melhorias ao transformar os dados em variações percentuais, vamos usar os dados em sua forma original e usá-los para nossos cálculos de z-score.

#Prepare to convert the model to ONNX format
scale_factors = pd.DataFrame(columns=X.columns,index=["mean","std"])
for i in X.columns:
    scale_factors.loc["mean",i] = merged_data.loc[:,i].mean()
    scale_factors.loc["std",i]  = merged_data.loc[:,i].std()
    merged_data.loc[:,i] = (merged_data.loc[:,i] - scale_factors.loc["mean",i]) / scale_factors.loc["std",i]

scale_factors

Fig 19: Nosso data frame com nossos z-scores

Exporte os dados para o formato CSV.

#Save the scale factors to CSV format
scale_factors.to_csv("FRED EURUSD D1 scale factors.csv")

Exportando para ONNX

ONNX é um protocolo open-source que permite aos desenvolvedores criar e implantar modelos de machine learning em qualquer linguagem de programação que suporte a API ONNX. Primeiro, vamos importar as bibliotecas necessárias.

# Import the libraries we need
import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType

Inicialize o modelo, pela última vez.

#Initialize the model
model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"],
                         early_stopping=tuner.best_params_["early_stopping"],
                         warm_start=tuner.best_params_["warm_start"],
                         max_iter=500,
                         activation=tuner.best_params_["activation"],
                         learning_rate=tuner.best_params_["learning_rate"],
                         solver=tuner.best_params_["solver"],
                         shuffle=tuner.best_params_["shuffle"],
                         alpha=tuner.best_params_["alpha"],
                         tol=tuner.best_params_["tol"],
                         learning_rate_init=tuner.best_params_["learning_rate_init"]
                         )

Ajustar o modelo com todos os dados disponíveis.

# Fit the model on all the data we have
model.fit(merged_data.loc[:,predictors],merged_data.loc[:,target])

Defina o formato de saída do nosso modelo.

# Define the input type
initial_types = [("float_input",FloatTensorType([1,X.shape[1]]))]

Crie uma representação em grafo ONNX do nosso modelo.

# Create the ONNX representation
onnx_model = convert_sklearn(model,initial_types=initial_types,target_opset=12)

Salve o modelo ONNX.

# Save the ONNX model
onnx.save_model(onnx_model,"FRED EURUSD D1.onnx")

Visualizando Nosso Modelo no Netron

Visualizar nosso modelo nos ajudará a validar se ele foi criado conforme nossas especificações. Queremos validar se as formas de entrada e saída estão de acordo com nossas expectativas. Netron é uma biblioteca open-source para visualização de modelos de machine learning. Vamos importar a biblioteca para começar.

import netron

Agora podemos visualizar facilmente nosso Regressor DNN.

netron.start("FRED EURUSD D1.onnx")

Visualizando nossos Modelos ONNX

Fig 20: Visualizando nosso Regressor DNN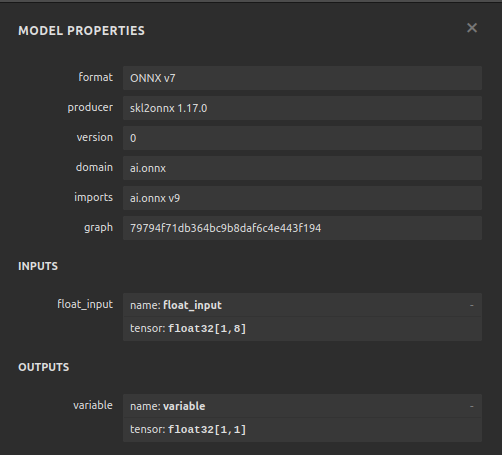

Nossas especificações do modelo

Fig 21: Visualizando as formas de entrada e saída do nosso modelo

Implementação em MQL5

O primeiro componente que precisamos integrar ao nosso Expert Advisor será o modelo ONNX. Vamos simplesmente incluir o arquivo ONNX como um recurso para nosso Expert Advisor.

//+------------------------------------------------------------------+
//|                                               FRED EURUSD AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Require the ONNX file                                            |
//+------------------------------------------------------------------+
#resource "\\Files\\FRED EURUSD D1.onnx" as const uchar onnx_buffer[];

Agora vamos carregar a biblioteca de operações de trade necessária para gerenciar nossas posições.

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include  <Trade/Trade.mqh>
CTrade Trade;

Criando variáveis globais que usaremos ao longo do programa.

//+------------------------------------------------------------------+
//| Define global variables                                          |
//+------------------------------------------------------------------+
long    model;
double  mean_values[5] = {1.1113568153310105,1.1152603484320558,1.1078179790940768,1.1114909337979093,65505.27177700349};
double  std_values[5]  = {0.05467420688685988,0.05413287747761819,0.05505429755411189,0.054630920048519924,26512.506288360997};
vectorf model_output   = vectorf::Zeros(1);
vectorf model_inputs   = vectorf::Zeros(8);
int     model_sate     = 0;
int     system_sate    = 0;
double  bid,ask;

Sempre que nosso modelo for carregado pela primeira vez, vamos tentar carregar o modelo ONNX e testar se está funcionando.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Load the ONNX model
   if(!load_onnx_model())
     {
      //--- We failed to load the ONNX model
      return(INIT_FAILED);
     }

//--- Test if we can get a prediction from our model
   model_predict();

//--- Eveything went fine
   return(INIT_SUCCEEDED);
  }

Se nosso modelo for removido do gráfico, também liberaremos os recursos que não estamos mais usando.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Release the resources we no longer need
   release_resources();
  }

Sempre que recebermos novos preços, atualizaremos as variáveis atribuídas para armazenar os preços atuais do mercado. Da mesma forma, se não houver posições abertas, seguiremos a indicação do nosso modelo. Por outro lado, se já tivermos posições abertas, permitiremos que nosso modelo nos alerte sobre possíveis reversões, e fecharemos as posições de acordo.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Update our bid and ask prices
   update_market_prices();

//--- Fetch an updated prediction from our model
   model_predict();

//--- If we have no trades, follow our model's directions.
   if(PositionsTotal() == 0)
     {
      //--- Our model is predicting price levels will appreciate
      if(model_sate == 1)
        {
         Trade.Buy(0.3,"EURUSD",ask,0,0,"FRED EURUSD AI");
         system_sate = 1;
        }
      //--- Our model is predicting price levels will deppreciate
      if(model_sate == -1)
        {
         Trade.Sell(0.3,"EURUSD",ask,0,0,"FRED EURUSD AI");
         system_sate = -1;
        }
     }

//--- Otherwise Manage our open positions
   else
     {
      if(system_sate != model_sate)
        {
         Alert("AI System Detected A Reversal! Closing All Positions on EURUSD");
         Trade.PositionClose("EURUSD");
        }
     }

  }
//+------------------------------------------------------------------+

Esta função atualizará as variáveis que acompanham os preços atuais do mercado.

//+------------------------------------------------------------------+
//| Update market prices                                             |
//+------------------------------------------------------------------+
void update_market_prices(void)
  {
   bid = SymbolInfoDouble(Symbol(),SYMBOL_BID);
   ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK);
  }

Agora vamos definir como nossos recursos devem ser liberados.

//+------------------------------------------------------------------+
//| Release the resources we no longer need                          |
//+------------------------------------------------------------------+
void release_resources(void)
  {
   OnnxRelease(model);
   ExpertRemove();
  }

Vamos definir a função responsável por criar nosso modelo ONNX a partir do buffer criado acima. Se esta função falhar em algum momento, retornará falso e interromperá o procedimento de inicialização.

//+------------------------------------------------------------------+
//| Create our ONNX model from the buffer we defined above           |
//+------------------------------------------------------------------+
bool load_onnx_model(void)
  {
//--- Create the ONNX model from the buffer we defined
   model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT);

//--- Validate the model was not illdefined
   if(model == INVALID_HANDLE)
     {
      //--- We failed to define our model
      Comment("We failed to create our ONNX model: ",GetLastError());
      return false;
     }

//---- Define the model I/O shape
   ulong input_shape[] = {1,8};
   ulong output_shape[] = {1,1};
//--- Validate our model's I/O shapes
   if(!OnnxSetInputShape(model,0,input_shape) || !OnnxSetOutputShape(model,0,output_shape))
     {
      Comment("Failed to define our model I/O shape: ",GetLastError());
      return(false);
     }
//--- Everything went fine!
   return(true);
  }

Esta é a função responsável por obter uma previsão do nosso modelo. A função primeiro buscará e normalizará as cotações de mercado do EURUSD, antes de chamar uma rotina responsável por ler nossos dados alternativos do FRED.

//+------------------------------------------------------------------+
//| This function will fetch a prediction from our model             |
//+------------------------------------------------------------------+
void model_predict(void)
  {
//--- Get the input data ready
   for(int i =0; i < 6; i++)
     {
      //--- The first 5 inputs will be fetched from the market
      matrix eur_usd_ohlc = matrix::Zeros(1,5);
      eur_usd_ohlc[0,0] = iOpen(Symbol(),PERIOD_D1,0);
      eur_usd_ohlc[0,1] = iHigh(Symbol(),PERIOD_D1,0);
      eur_usd_ohlc[0,2] = iLow(Symbol(),PERIOD_D1,0);
      eur_usd_ohlc[0,3] = iClose(Symbol(),PERIOD_D1,0);
      eur_usd_ohlc[0,4] = iTickVolume(Symbol(),PERIOD_D1,0);
      //--- Fill in the data
      if(i<4)
        {
         model_inputs[i] = (float)((eur_usd_ohlc[0,i] - mean_values[i])/ std_values[i]);
        }
      //--- We have to read in the fred alternative data
      else
        {
         read_fred_data();
        }
     }
  }
//+------------------------------------------------------------------+

Esta função irá ler nossos dados alternativos FRED do diretório MQL5\Files. Lembre-se de que o arquivo CSV será atualizado todos os dias pelo nosso script Python.

//+------------------------------------------------------------------+
//| This function will read in our FRED data                         |
//+------------------------------------------------------------------+
bool read_fred_data(void)
  {
//--- Read in the file
   string file_name = "FRED EURUSD ALT DATA.csv";

//--- Try open the file
   int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols).

//--- Check the result
   if(result != INVALID_HANDLE)
     {
      Print("Opened the file");
      //--- Store the values of the file

      int counter = 0;
      string value = "";
      while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end
        {
         if(counter > 20)   //if you aim to read 10 values set a break point after 10 elements have been read
            break;          //stop the reading progress

         value = FileReadString(result);
         Print("Counter: ");
         Print(counter);
         Print("Trying to read string: ",value);

         if(counter == 3)
           {
            model_inputs[5] = (float) value;
           }

         if(counter == 5)
           {
            model_inputs[6] = (float) value;
           }

         if(counter == 7)
           {
            model_inputs[7] = (float) value;
           }

         if(FileIsLineEnding(result))
           {
            Print("row++");
           }

         counter++;
        }

      //--- Show the input and Fred data
      Print("Input Data: ");
      Print(model_inputs);
      //---Close the file
      FileClose(result);
      //--- Store the model prediction
      OnnxRun(model,ONNX_DEFAULT,model_inputs,model_output);
      Comment("Model Forecast: ",model_output[0]);
      if(model_output[0] > iClose(Symbol(),PERIOD_D1,0))
        {
         model_sate = 1;
        }

      else
        {
         model_sate = -1;
        }

      //--- Everything went fine
      return(true);
     }

//--- We failed to find the file
   else
     {
      //--- Give the user feedback
      Print("We failed to find the file with the FRED data");
      return false;
     }

//--- Something went wrong
   return false;
  }

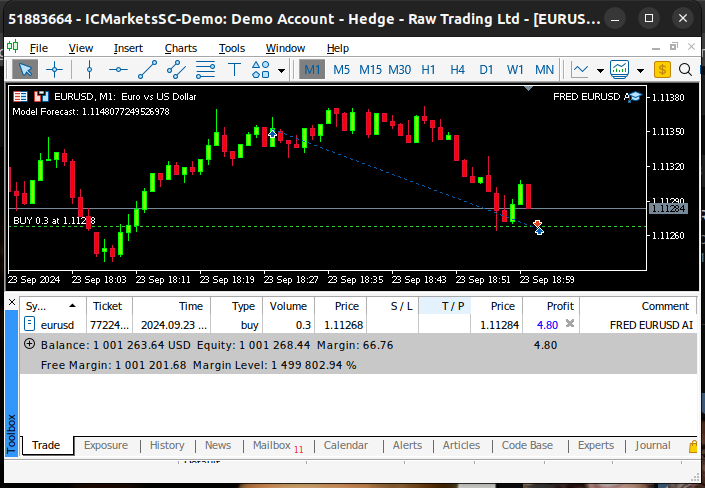
Fig 22: Testando nosso algoritmo em forward testing

Conclusão

Neste artigo, demonstramos que o Nominal Broad Daily Index pode não ser de grande ajuda na previsão do par EURUSD, ou, alternativamente, o ativo pode exigir mais transformações antes que a relação real possa ser aprendida de forma eficaz. Alternativamente, podemos considerar testar uma variedade maior de modelos para maximizar nossa chance de capturar bem a relação. Modelos como Support Vector Machines costumam ter bom desempenho em problemas que requerem o aprendizado de uma fronteira de decisão em espaço de alta dimensionalidade. Existem centenas de milhares de conjuntos de dados que ainda não exploramos. Mas, infelizmente, hoje não conseguimos obter vantagem sobre o restante do mercado.

Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/15949

Arquivos anexados |

Baixar como ZIP

FRED_EURUSD_AI.mq5 (8.61 KB)

FRED_EURUSD_D1.onnx (18.9 KB)

Alternative_Data_EURUSD.ipynb (2502.45 KB)

Fetch_Fred_Data.ipynb (3.75 KB)

Visualizing_The_Deep_Neural_Network.ipynb (1.31 KB)

Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

Outros artigos do autor

Ir para discussão

Exemplo de novo Indicador e LSTM Condicional

Este artigo explora o desenvolvimento de um Expert Advisor (EA) para trading automatizado que combina análise técnica com previsões de deep learning.

Adicionando um LLM personalizado a um robô investidor (Parte 5): Desenvolvimento e teste de uma estratégia de trading com LLM (II) - Configuração do LoRA

Os modelos de linguagem (LLMs) são uma parte importante da inteligência artificial que evolui rapidamente. E para aproveitar isso devemos pensar em como integrar LLMs avançados em nossa negociação algorítmica. Muitos acham desafiador ajustar esses modelos de acordo com suas necessidades, implantá-los localmente e, logo, aplicá-los à negociação algorítmica. Esta série de artigos explorará uma abordagem passo a passo para alcançar esse objetivo.

Está chegando o novo MetaTrader 5 e MQL5

Esta é apenas uma breve resenha do MetaTrader 5. Eu não posso descrever todos os novos recursos do sistema por um período tão curto de tempo - os testes começaram em 09.09.2009. Esta é uma data simbólica, e tenho certeza que será um número de sorte. Alguns dias passaram-se desde que eu obtive a versão beta do terminal MetaTrader 5 e MQL5. Eu ainda não consegui testar todos os seus recursos, mas já estou impressionado.

Ciência de dados e aprendizado de máquina (Parte 31): Aplicação de modelos CatBoost no trading

Os modelos de inteligência artificial CatBoost ganharam enorme popularidade na comunidade de aprendizado de máquina graças à sua precisão nas previsões, eficiência e resistência a conjuntos de dados fragmentados e complexos. Este artigo trata de como usar esses modelos no mercado Forex.