Redes neuronales: así de sencillo (Parte 91): Previsión en el dominio de la frecuencia (FreDF)
Introducción
Predecir las series temporales de precios futuros resulta fundamental en diversos escenarios de los mercados financieros. Y la mayoría de los métodos existentes actualmente se basan en la presencia de autocorrelación en los datos. En otras palabras, explotamos la presencia de una dependencia entre pasos temporales que existe tanto en los datos de origen como en los valores predichos.
Recientemente, los modelos basados en la arquitectura del Transformer que utilizan mecanismos de Self-Attention para estimar dinámicamente la autocorrelación han ido ganando popularidad. Al mismo tiempo, ha aumentado el interés por el uso del análisis de frecuencias en los modelos de previsión. Al representar la secuencia de datos de origen en el dominio de la frecuencia, podemos obviar la complejidad de la descripción de la autocorrelación, lo cual mejora la eficacia de diversos modelos.
Otro aspecto importante es la autocorrelación en la secuencia de valores predichos. Al fin y al cabo, está claro que los valores predichos forman parte de una serie temporal más amplia que incluye las secuencias analizadas y predichas. Por consiguiente, los valores predichos conservan las dependencias de los datos analizados. Pero este fenómeno suele ignorarse en los métodos modernos de previsión. En particular, los métodos más avanzados usan predominantemente el paradigma de Previsión Directa (Direct Forecast — DF), que genera previsiones multietapa de forma simultánea. Y esto supone implícitamente la independencia de los pasos en la secuencia de valores predichos. Dicho desajuste entre las hipótesis del modelo y las características de los datos provoca una calidad de previsión subóptima.
Una solución al problema indicado se propuso en el artículo "FreDF: Learning to Forecast in Frequency Domain". En él, los autores proponen un método de predicción directa mejorada en el dominio de la frecuencia (FreDF). Este método afina el paradigma DF alineando los valores predichos y la secuencia de etiquetas en el dominio de la frecuencia. Al pasar al dominio de la frecuencia, donde las bases son ortogonales e independientes, se reduce eficazmente la influencia de la autocorrelación. De esta forma, el FreDF sortea la discrepancia entre el supuesto de DF y la existencia de autocorrelación de etiquetas, al tiempo que conserva las ventajas del DF.
Los autores del método comprueban su eficacia en una serie de experimentos que demuestran una significativa superioridad del enfoque propuesto sobre los métodos más avanzados.
1. Algoritmo FreDF
El paradigma DF usa un modelo con varias salidas ɡθ para crear predicciones en T pasos Ŷ = ɡθ(X). Vamos a suponer que Yt es el t-ésimo paso Y, mientras que Yt(n) será la n-ésima observación de muestra. Los parámetros del modelo θ se optimizarán minimizando el error cuadrático medio (ECM):
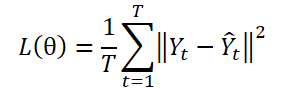
El paradigma DF calcula el error de predicción en cada paso de forma independiente, tratando cada elemento de la secuencia como una tarea individual. No obstante, este enfoque no tiene en cuenta la autocorrelación presente en Y, lo cual contradice la presencia de autocorrelación de etiquetas. Y, como consecuencia, provoca un desplazamiento o sesgo de la verosimilitud y a una desviación del principio de máxima verosimilitud durante el entrenamiento del modelo.
Una estrategia para superar esta limitación sería representar la secuencia de etiquetas en un dominio transformado formado por bases ortogonales. En concreto, esto se puede realizar eficazmente usando la transformada de Fourier, que proyecta la secuencia sobre bases ortogonales asociadas a distintas frecuencias. Transformando una secuencia de etiquetas en un dominio de frecuencia ortogonal, podemos reducir eficazmente la dependencia de la autocorrelación de las etiquetas.

donde i — es una unidad imaginaria definida como √(-1),
exp(•) — es la base de Fourier asociada a la frecuencia k, y es ortogonal para diferentes valores de k.
Debido a la ortogonalidad de la base, la representación de la secuencia de etiquetas en el dominio de la frecuencia evita la dependencia resultante de la autocorrelación en el dominio del tiempo. Esto pone de relieve el potencial del aprendizaje predictivo en el dominio de la frecuencia.
En el uso clásico de los enfoques DF, en la etiqueta temporal establecida n la secuencia histórica Xn se introduce en el modelo para generar pronósticos en T pasos designados como Ŷn=ɡθ(Xn). Y se calcula el error de predicción en el dominio temporal Ltmp.
Como complemento al enfoque canónico, los autores del método FreDF proponen transformar los valores predichos y etiquetar las secuencias en el dominio de la frecuencia. Entonces, el error de predicción en el dominio de la frecuencia se calcula usando la fórmula:

Aquí cada término sumatorio supone una matriz de números complejos A, |A| denota la operación de cálculo y suma del módulo de cada elemento de la matriz. Así, el módulo del número complejo a = ar + i ai se calcula como √(ar^2 + ai^2).
Obsérvese que, debido a las diferentes características numéricas de la secuencia de etiquetas en el dominio de la frecuencia, los autores del método FreDF no usan la forma de error cuadrático de pérdida (MSE), como es habitual para calcular el error de pérdida en el dominio del tiempo. En particular, los distintos componentes de frecuencia suelen tener magnitudes muy diferentes: las frecuencias más bajas poseen un volumen varios órdenes de magnitud mayor en comparación con las frecuencias más altas, lo cual hace que los métodos de pérdida cuadrática sean inestables.
Los errores de predicción en los dominios temporal y frecuencial se combinan usando un coeficiente α en el rango de valores [0,1], que controla la fuerza relativa de la alineación en el dominio frecuencial:
![]()
El FreDF evita el efecto de autocorrelación de los valores objetivo alineando los valores predichos generados y la secuencia de etiquetas en el dominio de la frecuencia. En este caso, además, se mantienen las ventajas de la DF, como la eficacia de la producción y la capacidad multitarea. Una propiedad notable del método FreDF es su compatibilidad con diversos modelos de predicción y transformación. Esta flexibilidad amplía enormemente las aplicaciones potenciales del FreDF.
A continuación le presentamos la visualización del método por parte del autor.
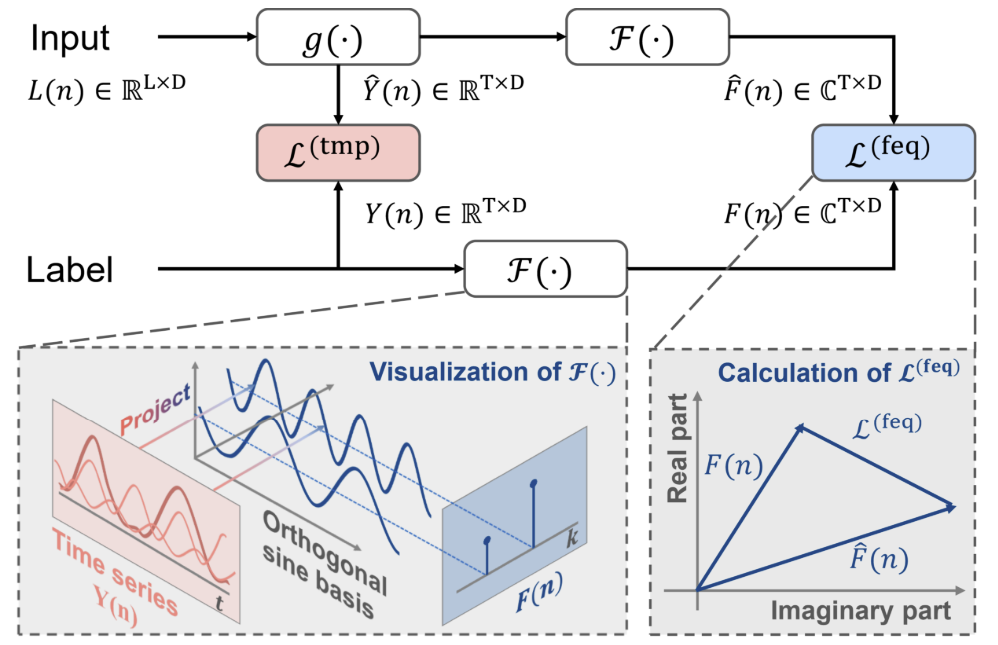
2. Implementación con MQL5
Tras analizar los aspectos teóricos del método FreDF propuesto, vamos a pasar a la parte práctica de nuestro artículo, donde haremos realidad nuestra visión del enfoque propuesto. A partir de la descripción teórica presentada anteriormente, podemos concluir que el enfoque propuesto esencialmente no introduce ninguna característica de diseño en la arquitectura del modelo. Además, no influye en el rendimiento del modelo durante su funcionamiento. Su efecto solo puede observarse durante el entrenamiento del modelo. Supongo que el método FreDF propuesto puede compararse con algún tipo de función de pérdida compleja, así que lo utilizaremos para entrenar un modelo cuyas etiquetas objetivo tengan dependencias de autocorrelación según nuestro conocimiento a priori.
Antes de proceder a la construcción de un nuevo objeto para aplicar los planteamientos propuestos, debemos señalar que los autores del método utilizan la transformada de Fourier para convertir los datos de las series temporales al dominio de la frecuencia. Debemos decir que el método FreDF es bastante flexible, y funciona bien con otros métodos de transformación de datos en un dominio ortogonal. Los autores del método realizan una serie de experimentos y demuestran su eficacia cuando se usan otras transformaciones. A continuación le presentamos los resultados de los experimentos anteriores.

Como podemos ver, los modelos que utilizan la transformada de Fourier muestran mejores resultados.
Querríamos llamar la atención de inmediato sobre el coeficiente α. Su valor de aproximadamente 0,8 parece óptimo según los resultados de los experimentos realizados. Cabe señalar que la predicción solo en el dominio de la frecuencia (utilizando α igual a 1) basada en los resultados de los mismos experimentos produce una disminución de la precisión del rendimiento del modelo.
De esto podemos concluir que, para obtener un modelo óptimo de predicción de series temporales, necesitaremos considerar tanto el dominio temporal como el frecuencial de la señal estudiada durante el proceso de entrenamiento. Las distintas representaciones nos permiten obtener más información sobre la señal y, en consecuencia, entrenar un modelo más eficaz.
Pero volvamos a nuestra implementación. Según los resultados experimentales de los autores del método, la transformada de Fourier permite entrenar modelos con un menor error de predicción. Recordemos que en el artículo anterior ya aplicamos la transformada rápida de Fourier directa e inversa. Así que en esta implementación podemos aprovechar estos avances.
Para implementar los enfoques FreDF, crearemos una nueva clase CNeuronFreDFOCL que heredará la funcionalidad básica de la clase básica de capas neuronales CNeuronBaseOCL. A continuación, mostraremos la estructura de la nueva clase.
class CNeuronFreDFOCL : public CNeuronBaseOCL { protected: uint iWindow; uint iCount; uint iFFTin; bool bTranspose; float fAlpha; //--- CBufferFloat cForecastFreRe; CBufferFloat cForecastFreIm; CBufferFloat cTargetFreRe; CBufferFloat cTargetFreIm; CBufferFloat cLossFreRe; CBufferFloat cLossFreIm; CBufferFloat cGradientFreRe; CBufferFloat cGradientFreIm; CBufferFloat cTranspose; //--- virtual bool FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false); virtual bool Transpose(CBufferFloat *inputs, CBufferFloat *outputs, uint rows, uint cols); virtual bool FreqMSA(CBufferFloat *target, CBufferFloat *forecast, CBufferFloat *gradient); virtual bool CumulativeGradient(CBufferFloat *gradient1, CBufferFloat *gradient2, CBufferFloat *cummulative, float alpha); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) { return true; } virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); public: CNeuronFreDFOCL(void) {}; ~CNeuronFreDFOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint count, float alpha, bool need_transpose = true, ENUM_OPTIMIZATION optimization_type = ADAM, uint batch = 1); virtual bool calcOutputGradients(CArrayFloat *Target, float &error); //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual int Type(void) const { return defNeuronFreDFOCL; } virtual void SetOpenCL(COpenCLMy *obj); };
En la estructura presentada de la nueva clase, podemos observar 2 características:
- los objetos internos solo están representados por búferes de datos y no existen capas internas;
- redefinición del método calcOutputGradients.
Aquí podemos añadir una característica implícita más, este objeto no contiene parámetros entrenables, lo cual resulta bastante raro. Y todas las características anteriores están relacionadas con el propósito de la clase: estamos creando una clase de una función de pérdida compleja, no una capa neuronal entrenable. Y el método calcOutputGradients de nuestra arquitectura de capas neuronales se encarga de calcular las desviaciones de los valores predichos respecto a los valores objetivo. Le sugiero familiarizarse con el propósito de los objetos internos y las variables en el proceso de implementación de métodos de clase.
Todos los objetos internos se han declarado estáticamente, lo cual nos permitirá dejar el constructor y el destructor de la clase "vacíos". En este caso, dejaremos al sistema el trabajo de limpieza de la memoria.
La inicialización de los objetos de clase se realiza en el método Init. Como es habitual, en los parámetros de este método transmitimos las constantes principales que definen la arquitectura de la clase. Aquí lo vemos:
- ventana de descripción de los elementos de los datos de origen (window),
- número de elementos de la secuencia (count),
- coeficiente de fuerza de alineación en el dominio de la frecuencia y del tiempo (alpha),
- bandera que indica la necesidad de transponer los datos para la conversión de frecuencia (need_transpose).
Lo primero que debemos decir es que planeamos utilizar este objeto en la salida del modelo. En consecuencia, la entrada serán los valores predichos generados por nuestro modelo. Los datos deben presentarse en un formato comparable al de los resultados predichos. También en este caso, los parámetros window y count se corresponden tanto con los valores predichos como con los valores objetivo. De este modo, podremos ofrecer al usuario la posibilidad de realizar la conversión de datos al dominio de la frecuencia en un plano diferente. Para ello hemos introducido el indicador need_transpose.
En este sentido, cabe citar los resultados de otros experimentos realizados por los autores del método. Estos comprobaron el rendimiento de los modelos comparando las características de frecuencia en series temporales unitarias de una secuencia multivariante (T), respecto a los pasos temporales individuales (D) y para una secuencia agregada (2D).

Los mejores resultados los ha obtenido el modelo con la representación de las características de frecuencia de la secuencia acumulativa total. Al mismo tiempo, la comparación de las características de frecuencia de los pasos temporales individuales ha resultado ser la oveja negra del experimento, mientras que el análisis de las características de frecuencia de las series temporales unitarias ha ocupado el honroso segundo puesto con un retraso insignificante respecto al líder.
En nuestra implementación, sin embargo, permitiremos que el usuario seleccione por sí mismo la medida para la conversión de frecuencia especificando el valor correspondiente de la bandera need_transpose. Para comparar las características de frecuencia bidimensionales, bastará con especificar el tamaño de toda la secuencia en el parámetro window, y para los demás parámetros especificar los siguientes valores:
- count: 1,
- need_transpose: false.
bool CNeuronFreDFOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint count, float Alpha, bool need_transpose = true, ENUM_OPTIMIZATION optimization_type = ADAM, uint batch = 1) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * count, optimization_type, batch)) return false;
En el cuerpo del método, primero llamamos al método homónimo de la clase padre y comprobamos el resultado de las operaciones. Permítanme recordarles que la clase padre implementa el conjunto mínimo requerido de controles, incluyendo el tamaño de la capa neuronal a crear. Como tamaño de la capa, especificamos el producto de las variables window y count. Obviamente, si especificamos un valor nulo en solo uno de ellos, todo el producto será igual a "0" y el método de la clase padre dará error.
Una vez ejecutado con éxito el método de la clase padre, almacenaremos los valores obtenidos en las variables locales.
bTranspose = need_transpose; iWindow = window; iCount = count; fAlpha = MathMax(0, MathMin(Alpha, 1)); activation = None;
Aquí debemos recordar que para la transformada rápida de Fourier necesitamos búferes de tamaño con grado 2. Ahora calculamos el tamaño de los búferes de datos:
//--- Calculate FFTsize uint size = (bTranspose ? count : window); int power = int(MathLog(size) / M_LN2); if(MathPow(2, power) != size) power++; iFFTin = uint(MathPow(2, power));
El siguiente paso consistirá en inicializar los búferes internos de datos. En primer lugar, inicializamos los búferes de características de frecuencia de los valores predichos. Utilizaremos un diseño de 2 búferes de datos. Uno para registrar los datos del componente real y otro para el componente imaginario.
//--- uint n = (bTranspose ? iWindow : iCount); if(!cForecastFreRe.BufferInit(iFFTin * n, 0) || !cForecastFreRe.BufferCreate(OpenCL)) return false; if(!cForecastFreIm.BufferInit(iFFTin * n, 0) || !cForecastFreIm.BufferCreate(OpenCL)) return false;
A continuación, crearemos búferes similares para las características de frecuencia de los valores objetivo:
if(!cTargetFreRe.BufferInit(iFFTin * n, 0) || !cTargetFreRe.BufferCreate(OpenCL)) return false; if(!cTargetFreIm.BufferInit(iFFTin * n, 0) || !cTargetFreIm.BufferCreate(OpenCL)) return false;
Vamos a escribir el error de predicción en los búferes cLossFreRe y cLossFreIm:
if(!cLossFreRe.BufferInit(iFFTin * n, 0) || !cLossFreRe.BufferCreate(OpenCL)) return false; if(!cLossFreIm.BufferInit(iFFTin * n, 0) || !cLossFreIm.BufferCreate(OpenCL)) return false;
Aquí cabe destacar la importancia de comparar ambos componentes de las características de frecuencia. Al fin y al cabo, para pronosticar correctamente las series temporales, nos importan tanto las amplitudes como las fases de las características de frecuencia de las series temporales.
Asimismo, debemos asegurarnos de crear búferes para registrar los gradientes de error al nivel de los valores predichos de las series temporales:
if(!cGradientFreRe.BufferInit(iFFTin * n, 0) || !cGradientFreRe.BufferCreate(OpenCL)) return false; if(!cGradientFreIm.BufferInit(iFFTin * n, 0) || !cGradientFreIm.BufferCreate(OpenCL)) return false;
Obviamente, para ahorrar memoria, podemos descartar los búferes cGradientFreRe y cGradientFreIm. Podemos sustituirlos fácilmente, por ejemplo, por los búferes cForecastFreRe y cForecastFreIm. Pero su presencia hace que el código resulte más legible, y la cantidad de memoria que utilizan en nuestro caso no es crítica.
Por último, crearemos un búfer temporal para registrar los valores transpuestos, si esto es necesario:
if(!cTranspose.BufferInit(iWindow * iCount, 0) || !cTranspose.BufferCreate(OpenCL)) return false; //--- return true; }
Tras inicializar los datos, normalmente se crea un método de pasada directa. Ya mencionamos antes que un objeto de esta clase no realiza operaciones con datos durante la explotación. Y como usted sabe, el método de pasada directa describe las operaciones del modo de funcionamiento del modelo. Parecería que podemos redefinir el método de pasada directa con "void", pero entonces la cuestión de la transferencia de datos se convertirá en un problema. Al mismo tiempo, nos gustaría minimizar el proceso de copiado de datos, porque la cantidad de datos puede variar y existe una "sobrecarga" añadida de organización del proceso. En este contexto, hemos creado un método de pasada directa tan sencillo como hemos podido. En él, solo comprobaremos si los punteros a los búferes de resultados de la capa actual y la anterior coinciden. De ser necesario, sustituiremos el puntero de la capa actual por el búfer de resultados de la capa anterior.
bool CNeuronFreDFOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL || !NeuronOCL.getOutput()) return false; if(NeuronOCL.getOutput() != Output) { Output.BufferFree(); delete Output; Output = NeuronOCL.getOutput(); } //--- return true; }
Así, el intercambio de punteros para un búfer sustituye al proceso de transferencia de datos independientemente de su tamaño. Tenga en cuenta que el control se realiza en cada pasada, y los búferes de datos se intercambian solo en la primera pasada.
Vamos a implementar ahora la funcionalidad principal de la clase para la pasada hacia atrás. Y aquí primero haremos un pequeño trabajo preparatorio. Para implementar completamente la funcionalidad requerida, crearemos 2 pequeños kernels en el lado OpenCL del programa.
Los autores del método FreDF recomiendan usar el MAE como función de pérdida al estimar los valores atípicos en el dominio de la frecuencia y observan una disminución de la estabilidad del entrenamiento cuando se utiliza el MSE. Recordemos que nuestra capa básica de neuronas CNeuronBaseOCL utiliza precisamente el MSE para determinar el gradiente de error. Y eso significa que necesitaremos crear un kernel para determinar el gradiente de error de los valores predichos utilizando el MAE. Desde un punto de vista matemático resulta bastante sencillo: basta con restar el vector de valores predichos del vector de etiquetas objetivo.
__kernel void GradientMSA(__global float *matrix_t, __global float *matrix_o, __global float *matrix_g ) { int i = get_global_id(0); matrix_g[i] = matrix_t[i] - matrix_o[i]; }
Tras determinar el gradiente de error en los dominios de la frecuencia y del tiempo, tendremos que combinar los gradientes de error utilizando el coeficiente de temperatura. Realizaremos esta funcionalidad en el kernel CumulativeGradient, cuya comprensión, a mi juicio, no resultará difícil.
__kernel void CumulativeGradient(__global float *gradient_freq, __global float *gradient_tmp, __global float *gradient_out, float alpha ) { int i = get_global_id(0); gradient_out[i] = alpha * gradient_freq[i] + (1 - alpha) * gradient_tmp[i]; }
Permítanme recordarles que para transformar los datos del dominio del tiempo al dominio de la frecuencia y viceversa, usaremos el algoritmo de la transformada rápida de Fourier que implementamos en el artículo anterior. Allí también encontrará una descripción del algoritmo utilizado y del método para poner el kernel en la cola de ejecución.
En este artículo, no nos detendremos en revisar los algoritmos de los métodos de colocación del kernel en la cola de ejecución. Todos siguen el mismo patrón, que hemos presentado muchas veces en los artículos de esta serie, incluido el anterior.
Vamos a analizar ahora el método CNeuronFreDFOCL::calcOutputGradients, que implementa la funcionalidad principal de nuestra clase. Como ya sabrá, la estructura de nuestros modelos en este método determinará el error de desviación de los valores predichos por el modelo respecto a las etiquetas objetivo. En los parámetros del método, obtenemos el puntero al búfer del valor objetivo. Y después de realizar las operaciones del método, debemos guardar el gradiente de error en el búfer correspondiente de la capa actual.
bool CNeuronFreDFOCL::calcOutputGradients(CArrayFloat *Target, float &error) { if(!Target) return false; if(Target.Total() < Output.Total()) return false;
En el cuerpo del método comprobamos la corrección del puntero recibido al búfer del valor de destino. Su tamaño deberá ser al menos tan grande como el tensor de resultados de nuestro modelo.
Como el búfer obtenido puede no tener su copia en el lado del contexto OpenCL, debemos crearlo allí para los cálculos posteriores. Sin embargo, para un uso más económico de los recursos del contexto OpenCL, podemos transferir los datos obtenidos al búfer de gradiente ya creado.
if(Target.Total() == Output.Total()) { if(!Gradient.AssignArray(Target)) return false; } else { for(int i = 0; i < Output.Total(); i++) { if(!Gradient.Update(i, Target.At(i))) return false; } } if(!Gradient.BufferWrite()) return false;
Y aquí hay 2 posibles desarrollos del escenario posterior. Si los tamaños del búfer de etiquetas de destino y del búfer de valores predichos son iguales, utilizaremos el método de copiado existente. De lo contrario, utilizaremos un ciclo para trasladar el número necesario de valores. Y en cualquier caso, después de copiar los datos, los trasladaremos a la memoria contextual OpenCL.
A continuación, los datos obtenidos se utilizarán para calcular las desviaciones tanto en el dominio del tiempo como en el de la frecuencia. Aquí vale la pena señalar que al calcular las desviaciones en el dominio del tiempo, el búfer de gradiente de error de nuestra capa será sobrescrito por las desviaciones calculadas con una pérdida completa de los valores objetivo obtenidos. Por lo tanto, antes de calcular las desviaciones en el dominio temporal, necesitaremos al menos descomponer la serie temporal obtenida de etiquetas objetivo en componentes de frecuencia.
Y aquí debemos recordar la posibilidad de descomponer las series temporales en características de frecuencia en dos dimensiones, cuya selección viene determinada por el valor de la bandera bTranspose. Si la bandera es true, primero transpondremos el búfer de resultados del modelo y luego lo descompondremos en características de frecuencia:
if(bTranspose) { if(!Transpose(Output, GetPointer(cTranspose), iWindow, iCount)) return false; if(!FFT(GetPointer(cTranspose), NULL, GetPointer(cForecastFreRe), GetPointer(cForecastFreIm), false)) return false;
Luego realizaremos operaciones similares para el tensor de etiquetas objetivo:
if(!Transpose(Gradient, GetPointer(cTranspose), iWindow, iCount)) return false; if(!FFT(GetPointer(cTranspose), NULL, GetPointer(cTargetFreRe), GetPointer(cTargetFreIm), false)) return false; }
Si el valor de la bandera bTranspose es false, realizaremos la descomposición de los valores objetivo y predichos en las características de frecuencia correspondientes sin transposición preliminar:
else { if(!FFT(Output, NULL, GetPointer(cForecastFreRe), GetPointer(cForecastFreIm), false)) return false; if(!FFT(Gradient, NULL, GetPointer(cTargetFreRe), GetPointer(cTargetFreIm), false)) return false; }
Una vez determinadas las características de frecuencia, podremos calcular las desviaciones tanto en el dominio temporal como en el de frecuencia sin temor a perder los valores objetivo.
if(!FreqMSA(GetPointer(cTargetFreRe), GetPointer(cForecastFreRe), GetPointer(cLossFreRe))) return false; if(!FreqMSA(GetPointer(cTargetFreIm), GetPointer(cForecastFreIm), GetPointer(cLossFreIm))) return false; if(!FreqMSA(Gradient, Output, Gradient)) return false;
Aquí cabe señalar que en el dominio de la frecuencia definimos desviaciones tanto en la parte real como en la imaginaria de las características de frecuencia. Después de todo, el valor del desfase resulta tan importante como la amplitud de la señal. Sin embargo, no podemos obtener directamente los gradientes de error en el dominio del tiempo y de la frecuencia. Al fin y al cabo, resulta evidente que los datos nos son comparables. Por lo tanto, primero debemos retornar los gradientes de error de las características de frecuencia al dominio temporal. Para ello, usaremos la transformada de Fourier inversa.
if(!FFT(GetPointer(cLossFreRe), GetPointer(cLossFreIm), GetPointer(cGradientFreRe), GetPointer(cGradientFreIm), true)) return false;
Después de conferir una forma comparable a los gradientes de error en el dominio del tiempo y de la frecuencia, conviene recordar que la medida de extracción de la características de frecuencia depende del valor de la bandera bTranspose. Por lo tanto, necesitamos convertir el gradiente de error al dominio de la frecuencia de acuerdo con el valor de la bandera. Y solo entonces podremos determinar el gradiente de error acumulado de nuestro modelo.
if(bTranspose) { if(!Transpose(GetPointer(cGradientFreRe), GetPointer(cTranspose), iCount, iWindow)) return false; if(!CumulativeGradient(GetPointer(cTranspose), Gradient, Gradient, fAlpha)) return false; } else if(!CumulativeGradient(GetPointer(cGradientFreRe), Gradient, Gradient, fAlpha)) return false; //--- return true; }
No se olvide de supervisar el proceso de las operaciones en cada paso. Y luego retornaremos el valor lógico de las operaciones realizadas al programa que realiza la llamada.
Tras determinar el gradiente de error de la salida del modelo, deberemos transmitirlo a la capa anterior. Como sabes, hemos implementado esta funcionalidad en el método CNeuronFreDFOCL::calcInputGradients, que obtiene en sus parámetros el puntero al objeto de la capa neuronal precedente.
Aquí conviene recordar que nuestra capa no contiene parámetros entrenables. En la pasada directa, realizamos un intercambio de búferes de datos, y mostramos los valores de la capa anterior como resultados. ¿Cuál es el objetivo de este método? Es muy simple. Solo tenemos que corregir el gradiente de error acumulativo calculado anteriormente para la función de activación de la capa anterior.
bool CNeuronFreDFOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false; //--- return DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), Gradient, NeuronOCL.Activation()); }
Bien, como nuestra clase no contiene parámetros entrenables, redefinimos el método updateInputWeights con un "stub vacío".
La ausencia de parámetros entrenables en la clase también impone una huella en los métodos de trabajo con archivos. Al fin y al cabo, no necesitamos almacenar objetos internos cuyos datos no tengan valor. Por lo tanto, al guardar los datos, solo llamaremos al método homónimo de la clase padre.
bool CNeuronFreDFOCL::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false;
Y almacenamos los valores de las variables que describen las características de diseño del objeto:
if(FileWriteInteger(file_handle, int(iWindow)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iCount)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(iFFTin)) < INT_VALUE) return false; if(FileWriteInteger(file_handle, int(bTranspose)) < INT_VALUE) return false; if(FileWriteFloat(file_handle, fAlpha) < sizeof(float)) return false; //--- return true; }
El algoritmo para restaurar un objeto a partir de un archivo de datos Load parece un poco más complicado. Aquí, en primer lugar, recuperamos los elementos de la clase padre:
bool CNeuronFreDFOCL::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false;
A continuación, cargamos los datos variables en el orden en que se han guardado, acordándonos de comprobar que se haya llegado al final del archivo de datos:
if(FileIsEnding(file_handle)) return false; iWindow = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iCount = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; iFFTin = uint(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; bTranspose = bool(FileReadInteger(file_handle)); if(FileIsEnding(file_handle)) return false; fAlpha = FileReadFloat(file_handle);
Luego inicializamos los objetos anidados según los parámetros de arquitectura de la clase cargada. La inicialización de objetos se realiza de manera similar al algoritmo de inicialización de una nueva instancia de una clase:
uint n = (bTranspose ? iWindow : iCount); if(!cForecastFreRe.BufferInit(iFFTin * n, 0) || !cForecastFreRe.BufferCreate(OpenCL)) return false; if(!cForecastFreIm.BufferInit(iFFTin * n, 0) || !cForecastFreIm.BufferCreate(OpenCL)) return false; if(!cTargetFreRe.BufferInit(iFFTin * n, 0) || !cTargetFreRe.BufferCreate(OpenCL)) return false; if(!cTargetFreIm.BufferInit(iFFTin * n, 0) || !cTargetFreIm.BufferCreate(OpenCL)) return false; if(!cLossFreRe.BufferInit(iFFTin * n, 0) || !cLossFreRe.BufferCreate(OpenCL)) return false; if(!cLossFreIm.BufferInit(iFFTin * n, 0) || !cLossFreIm.BufferCreate(OpenCL)) return false; if(!cGradientFreRe.BufferInit(iFFTin * n, 0) || !cGradientFreRe.BufferCreate(OpenCL)) return false; if(!cGradientFreIm.BufferInit(iFFTin * n, 0) || !cGradientFreIm.BufferCreate(OpenCL)) return false; if(bTranspose) { if(!cTranspose.BufferInit(iWindow * iCount, 0) || !cTranspose.BufferCreate(OpenCL)) return false; } else { cTranspose.BufferFree(); cTranspose.Clear(); } //--- return true; }
Con esto damos por concluida nuestra revisión de los métodos de la nueva clase CNeuronFreDFOCL. Podrá ver el código completo de esta clase en el archivo adjunto.
Tras construir la nueva clase de métodos, solemos proceder a describir la arquitectura de los modelos entrenados. Pero en este artículo, hemos construido una capa neuronal que no es del todo ordinaria. Más concretamente, vamos a implementar una función de pérdida compleja en forma de capa neuronal. Y esencialmente, podemos añadir el objeto creado anteriormente a uno de nuestros modelos previamente entrenados, entrenarlo de nuevo y ver cómo cambian los resultados. Para nuestros experimentos hemos elegido el modelo FEDformer, cuya arquitectura se describe aquí. Y le hemos añadido una nueva capa.
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- ........ ........ //--- layer 17 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Tengo que decir que después de pensarlo un poco, hemos decidido ampliar el experimento. Al fin y al cabo, los autores del método FreDF propusieron su algoritmo para considerar las dependencias en los resultados predichos. En general, también existe una correlación entre los parámetros individuales de los resultados de nuestro Actor. Por ejemplo, los volúmenes de las operaciones de compra y venta son mutuamente excluyentes, porque en un momento dado solo tenemos una posición abierta en una dirección. Los parámetros de Stop Loss y Take Profit determinan la fuerza del movimiento más probable. Como consecuencia, el Take Profit de una posición larga debería estar correlacionado en cierta medida con el Stop Loss de una posición corta y viceversa. Un razonamiento similar sugiere también dependencias en los valores predichos por el Crítico. ¿Y por qué no ampliamos el experimento también a los modelos anteriores? Vamos a ello. Añadimos una nueva capa a los modelos del Actor y el Crítico:
bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; } //--- Actor ......... ......... //--- layer 17 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NActions; descr.count = 1; descr.step = int(false); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- Critic ......... ......... //--- layer 17 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NRewards; descr.count = 1; descr.step = int(false); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
Obsérvese que en este caso estamos analizando las características de frecuencia de la secuencia completa de resultados en lugar de series unitarias individuales.
Nuestra aplicación de los planteamientos propuestos por el método FreDF no requiere ningún ajuste en el entrenamiento del modelo ni en los asesores de interacción con el entorno. Y esto significa que durante la comprobación de los resultados obtenidos podemos utilizar asesores expertos y muestras de entrenamiento recogidas previamente.
3. Simulación
Ya hemos trabajado lo suficiente para aplicar los enfoques propuestos por los autores del método FreDF utilizando herramientas MQL5. Ahora vamos a pasar a la fase final de nuestro trabajo: el entrenamiento y las pruebas del modelo.
Como hemos mencionado antes, utilizaremos el asesor experto previamente creado y los datos de entrenamiento previamente recopilados para entrenar los modelos. Permítanme recordarles que los modelos están entrenados con los datos históricos de EURUSD y el marco temporal H1 para todo el año 2023.
En primer lugar, entrenamos un modelo del Codificador de los estados del entorno. El modelo se entrena para predecir los estados del entorno posteriores a lo largo de un horizonte de planificación que viene determinado por la constante NPrevision. En nuestro experimento, son 12 velas consecutivas. La previsión se realiza en el contexto de todos los parámetros analizados de la descripción del estado del entorno.
#define NForecast 12 //Number of forecast
Durante el entrenamiento del Codificador, se observa una reducción del error de predicción en comparación con el modelo similar sin enfoques FreDF. Sin embargo, no hemos comparado gráficamente los resultados de las predicciones. Por ello, resulta difícil juzgar la calidad real de los valores predichos. Aquí conviene señalar que, por extraño que parezca, no pretendemos obtener las previsiones más exactas de todos los indicadores analizados. La cuestión es que el modelo del Actor se orienta por el espacio oculto del Codificador para decidir la acción óptima. Y el objetivo de la primera etapa de entrenamiento es obtener el espacio oculto más informativo del Codificador en el que se codificaría el movimiento de precios más probable.
Al igual que antes, el modelo del Codificador solo analiza los movimientos de precio, por lo que no es necesario actualizar la muestra de entrenamiento durante la primera fase del mismo.
En la segunda etapa de nuestro proceso de entrenamiento, buscamos la mejor política posible para las acciones de nuestro Actor. Y aquí ya podemos realizar un entrenamiento iterativo de los modelos del Actor y el Crítico que se alterne con la actualización de la muestra de entrenamiento.
Como resultado de varias iteraciones del entrenamiento de la política del Actor, hemos logrado obtener un modelo capaz de generar beneficios. Asimismo, hemos probado el rendimiento del modelo entrenado en el Simulador de Estrategias de MetaTrader 5 con datos históricos reales para enero de 2024. Al mismo tiempo, los parámetros de las pruebas se correspondían plenamente con los de la muestra de entrenamiento, incluidos el instrumento, el marco temporal y los parámetros de los indicadores analizados. Los resultados de la prueba se muestran en las siguientes capturas de pantalla.
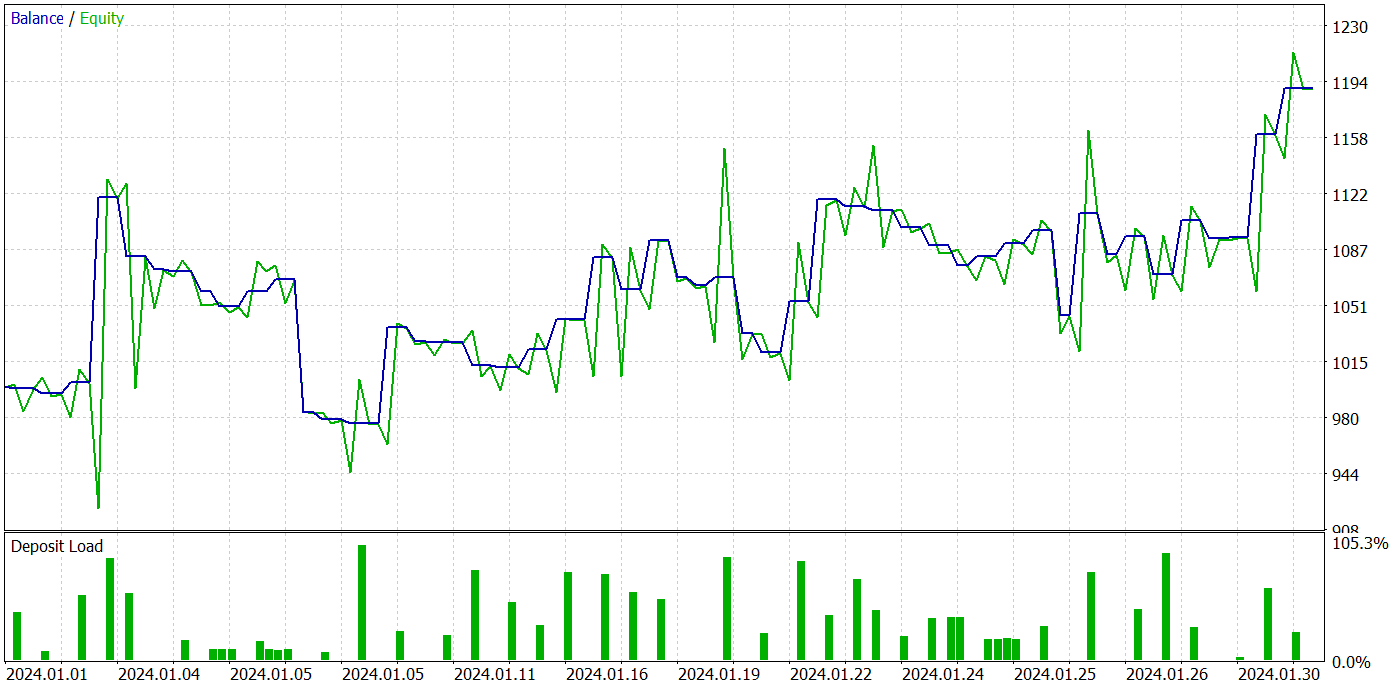
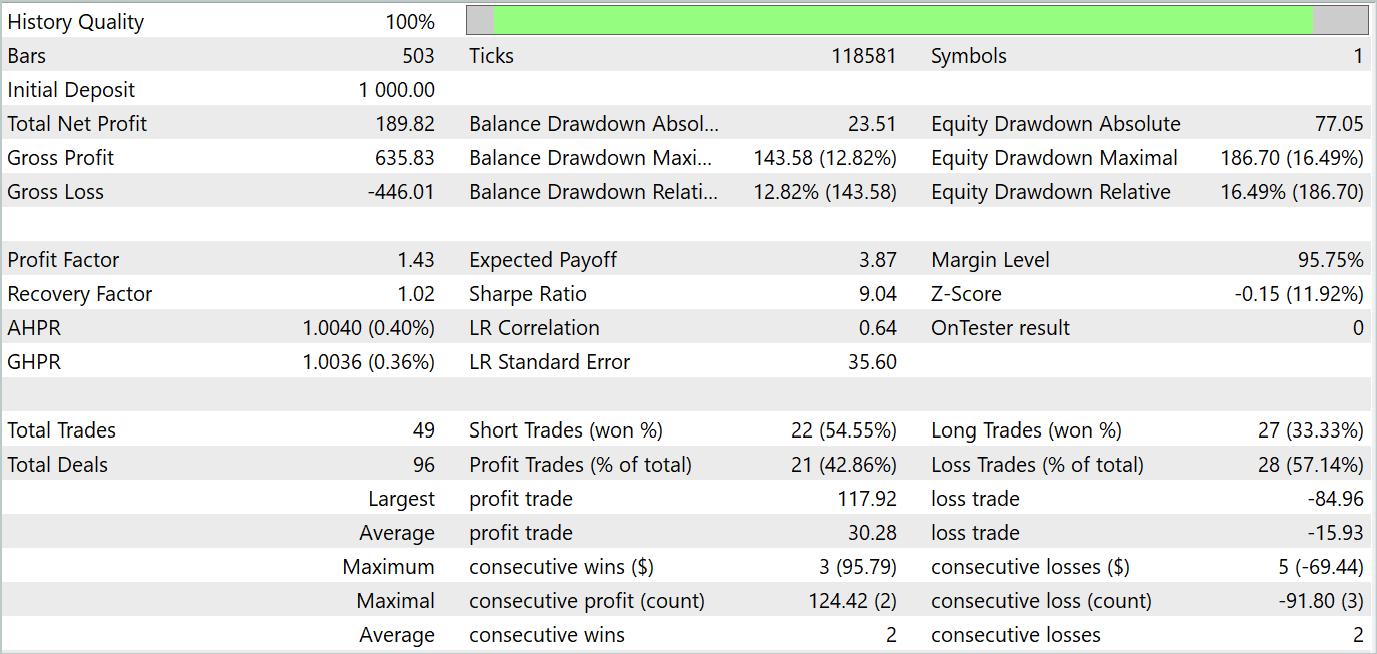
Según los resultados de la prueba, se observa una tendencia claramente pronunciada a aumentar el balance de la cuenta. Durante el periodo de prueba, el modelo ha realizado 49 transacciones, 21 de las cuales se han cerrado con beneficios. Sí, las posiciones rentables son menos de la mitad, pero la media de transacciones rentables es casi 2 veces superior a la media de transacciones perdedoras. Como consecuencia, el factor de beneficio del modelo en la muestra de prueba es de 1,43 y la rentabilidad mensual acumulada es de aproximadamente el 19%.
Conclusión
En este artículo, nos hemos familiarizado con el método FreDF, cuyo objetivo es mejorar la previsión de series temporales. Los autores del método han corroborado empíricamente que ignorar la autocorrelación en la secuencia de etiquetas provoca un sesgo de verosimilitud, así como peores predicciones en el paradigma DF actual. Además, hemos presentado una modificación sencilla pero eficaz del paradigma actual de DF que considera la autocorrelación igualando las predicciones y las secuencias de etiquetas en el dominio de la frecuencia. El método FreDF es compatible con diversos modelos de predicción y transformación, lo cual lo hace flexible y versátil.
En la parte práctica del artículo, hemos implementado nuestra visión de los enfoques propuestos usando MQL5. Asimismo, hemos complementado el modelo FEDformer previamente establecido con los enfoques propuestos y lo hemos entrenado. Los resultados de las pruebas del modelo entrenado nos permiten juzgar la eficacia de los enfoques propuestos, ya que la adición de FreDF nos permite aumentar la eficacia del modelo, en igualdad de condiciones.
Cabe destacar la flexibilidad del método FreDF, que permite su uso eficaz con una gama bastante amplia de modelos existentes.
Enlaces
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de Modelos |
| 4 | StudyEncoder.mq5 | Asesor | Asesor de entrenamiento del Codificador |
| 5 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 6 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 7 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/14944
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Vectores y valores propios: Análisis exploratorio de datos en MetaTrader 5
Vectores y valores propios: Análisis exploratorio de datos en MetaTrader 5
 Creación de un EA limitador de reducción diaria en MQL5
Creación de un EA limitador de reducción diaria en MQL5
 Desarrollo de un robot en Python y MQL5 (Parte 2): Selección, creación y entrenamiento de modelos, simulador personalizado en Python
Desarrollo de un robot en Python y MQL5 (Parte 2): Selección, creación y entrenamiento de modelos, simulador personalizado en Python
 Algoritmo de cerradura de código (Сode Lock Algorithm, CLA)
Algoritmo de cerradura de código (Сode Lock Algorithm, CLA)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso