MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português
preview
ニューラルネットワークが簡単に（第91回）：周波数領域予測(FreDF)

ニューラルネットワークが簡単に（第91回）：周波数領域予測(FreDF)

MetaTrader 5 — 例 | 18 11月 2024, 10:29
120 0
Dmitriy Gizlyk
Dmitriy Gizlyk

はじめに

将来の価格の時系列を予測することは、多様な金融市場のシナリオにおいて極めて重要です。現在存在する多くの予測手法は、データ内に見られる自己相関を活用しています。すなわち、入力データと予測結果の間に時間的な相関関係が存在する点を利用しているのです。

近年、注目を集めているモデルの1つに、動的な自己相関推定に自己アテンション(self-attention)メカニズムを組み込んだTransformerアーキテクチャに基づくものがあります。また、予測モデルにおける周波数分析への関心も高まっています。入力データのシーケンスを周波数領域で表現することにより、自己相関の複雑さを回避し、さまざまなモデルの効率を向上させることが可能になります。

さらに重要なのは、予測結果のシーケンス内における自己相関です。予測値は、分析対象のシーケンスおよび予測されたシーケンスを含む、より大きな時系列の一部を構成しています。そのため、予測値は分析データとの相関関係を維持する必要があります。しかしながら、現代の予測手法では、この点がしばしば見過ごされています。特に、現在主流となっている「直接予測(DF)」パラダイムでは、複数の予測ステップを一度に生成する際に、各ステップの予測値が独立していると暗黙的に仮定されています。この仮定がデータの特性と一致しない場合、予測結果の質が最適化されない原因となります。

この問題の解決策の1つとして、「FreDF:Learning to Forecast in Frequency Domain」という論文で提案された方法が挙げられます。この論文の著者は、周波数ゲイン(FreDF)を用いた直接予測手法を提案しました。この方法では、予測値とラベルのシーケンスを周波数領域で整列させることにより、DFパラダイムを再定義しています。周波数領域に移行することで、基底が直交かつ独立した形になり、自己相関の影響を効果的に軽減することができます。これにより、FreDFは、DFに関する仮定とラベルの自己相関の存在との不整合を解消しつつ、DFの利点を保持することを可能にしています。

この手法の著者は一連の実験を通じて、提案した手法が現代の予測方法に比べて大幅に優れていることを実証しました。


1. FreDFアルゴリズム

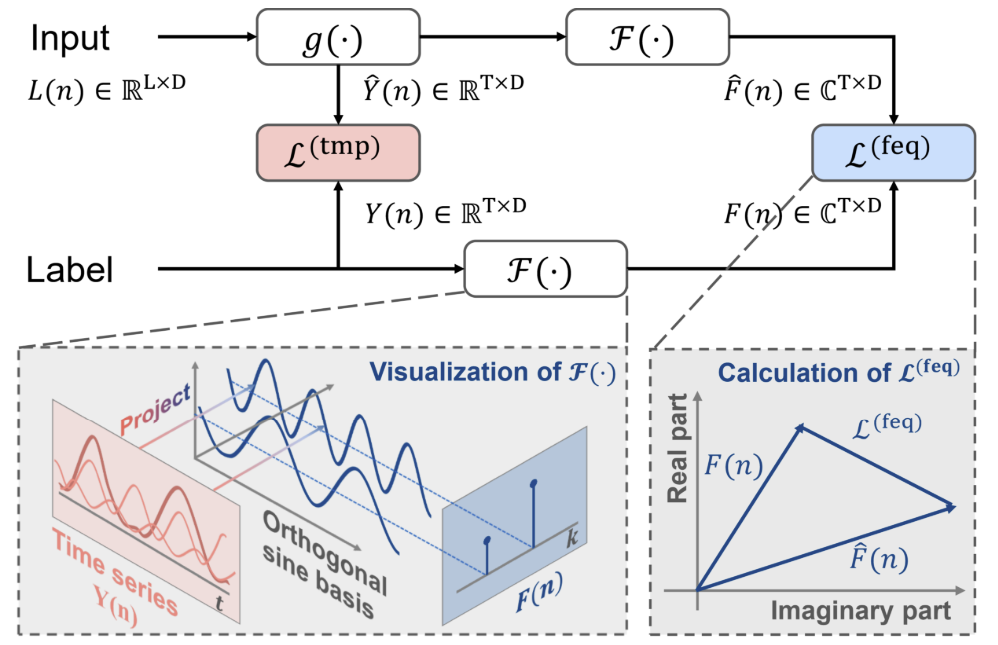
DFパラダイムでは、Tステップの予測Ŷ = ɡθ(X)を生成するために、複数出力モデルɡθを使用します。ここで、Ytは時系列Yのt番目のステップを、Yt(n)はそのn番目のサンプル観測値を指します。モデルパラメータθは、平均二乗誤差(MSE)を最小化することによって最適化されます。

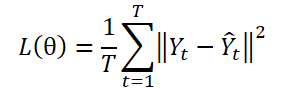
DFパラダイムでは、シーケンスの各要素を個別のタスクとして扱い、各ステップで予測誤差を独立して計算します。しかし、このアプローチでは、Y内の自己相関が無視され、ラベルの自己相関の存在と矛盾してしまいます。その結果、モデルの訓練中に尤度に偏りが生じ、最大尤度原理から外れてしまいます。

この制約を克服するための1つの方法は、ラベルシーケンスを直交基底によって形成された変換領域で表現することです。特に、フーリエ変換を使用してシーケンスを異なる周波数に関連付けられた直交基底に投影することで、効果的にこの問題を解決できます。ラベルシーケンスを直交周波数領域に変換することにより、ラベルの自己相関への依存を減少させることが可能になります。

ここで、iは虚数単位（√(-1)として定義）
exp(•)は周波数kに関連付けられたフーリエ基底を示します。これらの基底は異なるk値に対して直交性を持ちます。

基底の直交性により、ラベルシーケンスの周波数領域表現は、時間領域での自己相関から生じる依存関係を回避します。これにより、周波数領域での予測学習の有効性が強調されます。

従来のDFアプローチでは、特定のタイムスタンプnにおいて、履歴シーケンスXnがモデルに入力され、Ŷn=ɡθ(Xn)と表記されるTステップの予測が生成されます。その後、時間領域Ltmpで予測誤差が計算されます。

一方、FreDF法の著者は、従来のアプローチに加えて、予測値とラベルのシーケンスを周波数領域に変換することを提案しています。周波数領域での予測誤差は、次の式を用いて計算されます。

ここで、合計の各項は複素数行列Aの要素を示します。|A|は、行列の各要素に対する絶対値の計算を表し、複素数a = ar + i aiの係数は√(ar^2 + ai^2)として計算されます。

周波数領域におけるラベルシーケンスには異なる数値特性があるため、FreDF法の著者は、一般的な二乗損失(MSE)を時間領域の損失計算に使用していないことに注意する必要があります。具体的には、異なる周波数成分は通常、非常に異なるスケールを持ちます。低周波数は高周波数に比べて数桁大きい値を持つため、この差が原因で二乗損失法が不安定になることがあります。

そのため、時間領域と周波数領域の予測誤差は、値が[0,1]の範囲に収まる係数αを使用して組み合わせられ、周波数領域の正規化強度を調整します。

FreDFは、生成された予測値とラベルのシーケンスを周波数領域で調整することにより、目標値の自己相関の影響を回避します。これにより、DFの利点である効率的な出力やマルチタスク機能も保持されます。FreDFの注目すべき特徴は、さまざまな予測モデルや変換との高い互換性です。この柔軟性により、FreDFの潜在的な適用範囲は大幅に拡大します。

以下は、著者によるこの手法の視覚化です。


2. MQL5での実装

提案されたFreDFの理論的な側面を検討した後、この記事の実践的な部分に進み、このアプローチを実装します。上記の理論的説明から、提案されたアプローチはモデルアーキテクチャに特定の設計機能を追加しないと結論できます。さらに、この方法の効果はモデルの実際の動作には現れず、その効果は、モデルの訓練プロセス中にのみ確認できます。提案されたFreDF法は、複雑な損失関数に匹敵する可能性が高いです。したがって、この方法を使用することで、目標ラベルに自己相関の依存関係があると予想されるモデルを訓練することができます。

新しいオブジェクトを構築して提案されたアプローチを実装する前に、この方法の著者がデータを時系列から周波数領域に変換するためにフーリエ変換を使用したことに注目する価値があります。FreDF法は非常に柔軟であり、データを直交領域に変換する他の方法と組み合わせてもうまく機能します。実際、著者は他の変換方法を使用した場合でも有効であることを証明するために一連の実験をおこなっています。その結果を以下に示します。

ご覧の通り、フーリエ変換を使用するモデルは、より優れた結果を示しています。

特に注目すべきは係数αです。実験結果に基づくと、最適な値は約0.8であることがわかります。同じ実験結果から、予測が周波数領域でのみおこなわれる場合（αを1に設定）には、モデルの精度が低下することも確認されています。

これらの結果から、最適な時系列予測モデルを得るためには、訓練プロセスにおいて、対象とする信号の時間領域と周波数領域の両方を考慮することが重要であると結論できます。異なる表現を用いることで、信号に関するより多くの情報を取得でき、より効率的なモデルの訓練が可能となります。

さて、実装に戻りましょう。この手法の著者がおこなった実験結果によると、フーリエ変換を使用することで、より小さな予測誤差を得られることが示されています。前回の記事では、すでに直接および逆高速フーリエ変換を実装したので、これらの開発を新しい実装に活用することができます。

FreDFアプローチを実装するために、ニューラル層の基底クラスであるCNeuronFreDFOCLから主な機能を継承し、新しいクラスCNeuronBaseOCLを作成します。この新しいクラスの構造を以下に示します。

class CNeuronFreDFOCL   :  public CNeuronBaseOCL
  {
protected:
   uint              iWindow;
   uint              iCount;
   uint              iFFTin;
   bool              bTranspose;
   float             fAlpha;
   //---
   CBufferFloat      cForecastFreRe;
   CBufferFloat      cForecastFreIm;
   CBufferFloat      cTargetFreRe;
   CBufferFloat      cTargetFreIm;
   CBufferFloat      cLossFreRe;
   CBufferFloat      cLossFreIm;
   CBufferFloat      cGradientFreRe;
   CBufferFloat      cGradientFreIm;
   CBufferFloat      cTranspose;
   //---
   virtual bool      FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, 
                         CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false);
   virtual bool      Transpose(CBufferFloat *inputs, CBufferFloat *outputs, uint rows, uint cols);
   virtual bool      FreqMSA(CBufferFloat *target, CBufferFloat *forecast, CBufferFloat *gradient);
   virtual bool      CumulativeGradient(CBufferFloat *gradient1, CBufferFloat *gradient2, 
                                        CBufferFloat *cummulative, float alpha);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)   {  return true;   }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronFreDFOCL(void)   {};
                    ~CNeuronFreDFOCL(void)   {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint count, float alpha, bool need_transpose = true, 
                          ENUM_OPTIMIZATION optimization_type = ADAM, uint batch = 1);
   virtual bool      calcOutputGradients(CArrayFloat *Target, float &error);
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual int       Type(void)        const                      {  return defNeuronFreDFOCL; }
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

新しいクラスの構造には、2つの注目すべき特徴があります。

  • 内部オブジェクトはデータバッファのみで表現され、内部層は存在しない。
  • calcOutputGradientsメソッドはオーバーライドされる。

ここで、もう1つの暗黙的な特徴として挙げられるのは、このオブジェクトには訓練可能なパラメータが含まれていない点です。これは非常に珍しい特徴であり、これらすべての特徴はクラスの目的に密接に関連しています。具体的には、訓練可能なニューラルネットワーク層ではなく、複雑な損失関数を扱うクラスを作成しているためです。また、ニューラルネットワークのアーキテクチャで使用されるcalcOutputGradientsメソッドは、予測値と目標値の偏差を計算する役割を担っています。メソッドの実装を進めることで、内部オブジェクトと変数の目的が明確になっていきます。

すべてのオブジェクトは静的に宣言されているため、クラスのコンストラクタとデストラクタは「空」のままで問題ありません。メモリの解放に関連するすべての操作は、システム自体によっておこなわれます。

クラスオブジェクトはInitメソッドで初期化されます。このメソッドには、クラスのアーキテクチャを定義するための主要な定数が渡されます。具体的には、次のようなパラメータが含まれます。

  • 入力データの1つの要素を記述するwindow
  • シーケンス内の要素数のcount
  • 周波数領域と時間領域の均等化の力のalpha係数
  • データを転置して周波数領域に変換する必要がある場合に示すneed_transposeフラグ

このオブジェクトはモデルの出力に使用されます。したがって、入力データはモデルによって生成された予測値であり、目標結果と一致する形式で提供される必要があります。windowとcountのパラメータは、予測値と目標値の両方に対応します。さらに、データを異なる平面で表現された周波数領域に変換する機能も提供しています。これがneed_transposeフラグが導入された理由です。

次に、この方法の著者らが行った他の実験結果に触れたいと思います。著者は、多変量シーケンスにおける単位時系列(TT)、個々の時間ステップ(D)、およびシーケンス全体(2D)の周波数特性を比較し、モデルのパフォーマンスをテストしました。

最も優れた結果は、一般的な集約シーケンスの周波数特性を表すモデルによって得られました。個々の時間ステップの周波数特性を比較するアプローチは、実験のアウトサイダーであることが判明しました。単位時系列の周波数特性を分析する手法は、わずかに劣る結果となり、2番目に良いパフォーマンスを示しました。

私たちの実装では、ユーザーに周波数変換の測定を選択する機能を提供しています。この機能は、対応するneed_transposeフラグ値を指定することで実現できます。2次元の周波数特性を比較するためには、windowパラメータでシーケンス全体のサイズを指定し、残りのパラメータに次の値を使用します。

  • count： 1
  • need_transpose：false

bool CNeuronFreDFOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                           uint window, uint count, float Alpha, bool need_transpose = true, 
                           ENUM_OPTIMIZATION optimization_type = ADAM, uint batch = 1)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * count, optimization_type, batch))
      return false;

メソッド本体では、まず親クラスの関連するメソッドを呼び出して、その操作の結果を確認します。ここで、親クラスはニューラル層のサイズなど、必要なコントロールを実装しています。層のサイズは、変数windowとcountの積として指定されます。当然のことながら、これらのいずれかにゼロ値が指定されると、積全体が「0」になり、親クラスのメソッドは失敗します。

親クラスメソッドが正常に実行された場合、得られた値はローカル変数に保存されます。

   bTranspose = need_transpose;
   iWindow = window;
   iCount = count;
   fAlpha = MathMax(0, MathMin(Alpha, 1));
   activation = None;

前に見たように、高速フーリエ変換には2の累乗のサイズのバッファが必要です。データバッファのサイズを計算してみましょう。

//--- Calculate FFTsize
   uint size = (bTranspose ? count : window);
   int power = int(MathLog(size) / M_LN2);
   if(MathPow(2, power) != size)
      power++;
   iFFTin = uint(MathPow(2, power));

次のステップは、内部データバッファを初期化することです。まず、予測値の周波数応答バッファを初期化します。2つのデータバッファ設計が使用されます。1つは実数成分のデータを格納し、もう1つは虚数成分のデータを格納します。

//---
   uint n = (bTranspose ? iWindow : iCount);
   if(!cForecastFreRe.BufferInit(iFFTin * n, 0) || !cForecastFreRe.BufferCreate(OpenCL))
      return false;
   if(!cForecastFreIm.BufferInit(iFFTin * n, 0) || !cForecastFreIm.BufferCreate(OpenCL))
      return false;

次に、目標値の周波数特性に対して同様のバッファを作成します。

   if(!cTargetFreRe.BufferInit(iFFTin * n, 0) || !cTargetFreRe.BufferCreate(OpenCL))
      return false;
   if(!cTargetFreIm.BufferInit(iFFTin * n, 0) || !cTargetFreIm.BufferCreate(OpenCL))
      return false;

予測誤差をバッファcLossFreeReとcLossFreeに書き込みます。

   if(!cLossFreRe.BufferInit(iFFTin * n, 0) || !cLossFreRe.BufferCreate(OpenCL))
      return false;
   if(!cLossFreIm.BufferInit(iFFTin * n, 0) || !cLossFreIm.BufferCreate(OpenCL))
      return false;

周波数特性の振幅と位相の両方を比較することの重要性に注目してください。時系列を正確に予測するためには、これらの周波数特性が両方とも重要であることを理解する必要があります。

また、予測された時系列値における誤差勾配を記録するためのバッファも必要です。

   if(!cGradientFreRe.BufferInit(iFFTin * n, 0) || !cGradientFreRe.BufferCreate(OpenCL))
      return false;
   if(!cGradientFreIm.BufferInit(iFFTin * n, 0) || !cGradientFreIm.BufferCreate(OpenCL))
      return false;

メモリを節約するために、バッファcGradientFreeReとcGradientFreeImを除外することができます。これらは、たとえばバッファcForecastFreeReおよびcForecastFreeImに簡単に置き換えることができますが、それらが存在すると、コードはより読みやすくなります。また、ここでの場合、使用されるメモリの量は重要ではありません。

最後に、必要に応じて転置された値を書き込むための一時バッファを作成します。

      if(!cTranspose.BufferInit(iWindow * iCount, 0) || !cTranspose.BufferCreate(OpenCL))
         return false;
//---
   return true;
  }

データの初期化後、次にフィードフォワードパスメソッドを作成します。このクラスのオブジェクトは、操作中にデータ操作を実行しないことは既に述べました。フィードフォワードメソッドは、モデルの動作モードを記述する役割を果たします。このメソッドを「ダミー」として再定義することも可能ですが、その場合、データがどのように転送されるのかが問題になります。データのボリュームが異なる場合や、プロセスの編成により「オーバーヘッドコスト」が発生する可能性があるため、常にデータコピーのプロセスを最小限に抑えたいと考えています。この文脈では、フィードフォワードパスメソッドを可能な限りシンプルに保ちます。このメソッドでは、現在の層と前の層の結果バッファへのポインタの対応を確認します。そして、必要に応じて、現在の層のポインタを前の層の結果バッファに置き換えます。

bool CNeuronFreDFOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL || !NeuronOCL.getOutput())
      return false;
   if(NeuronOCL.getOutput() != Output)
     {
      Output.BufferFree();
      delete Output;
      Output = NeuronOCL.getOutput();
     }
//---
   return true;
  }

したがって、データの転送は量に関係なくおこなわれるのではなく、1つのバッファへのポインタを置き換えることで効率化されます。ここで重要なのは、制御がパスごとにおこなわれ、データバッファが最初のパスでのみ置き換えられる点です。

次に、バックプロパゲーションパスのクラスに必要な主な機能を実装します。まずは、実装に向けた準備作業を進めましょう。完全な実装には、OpenCLプログラム側で2つの小さなカーネルを作成する必要があります。

FreDF法の著者は、周波数領域での偏差を推定する際に損失関数としてMAE（平均絶対誤差）を使用することを推奨しています。また、MSE（平均二乗誤差）を使用すると、訓練の安定性が低下する可能性があることも指摘されています。ニューラル層の基底クラスCNeuronBaseOCLは、誤差勾配を計算する際にMSEを使用していることを思い出してください。そのため、MAEを使用して予測誤差勾配を決定するカーネルを作成する必要があります。数学的には、この処理は非常に簡単で、予測値のベクトルから目標ラベルのベクトルを引くだけです。

__kernel void GradientMSA(__global float *matrix_t,
                          __global float *matrix_o,
                          __global float *matrix_g
                         )
  {
   int i = get_global_id(0);
   matrix_g[i] = matrix_t[i] - matrix_o[i];
  }

周波数領域と時間領域で誤差勾配を決定した後、温度係数を使用して誤差勾配を組み合わせる必要があります。この機能をCumulativeGradientカーネルに実装してみましょう。これは非常に簡単に理解できると思います。

__kernel void CumulativeGradient(__global float *gradient_freq,
                                 __global float *gradient_tmp,
                                 __global float *gradient_out,
                                 float alpha
                                )
  {
   int i = get_global_id(0);
   gradient_out[i] = alpha * gradient_freq[i] + (1 - alpha) * gradient_tmp[i];
  }

時間領域から周波数領域へ、そしてその逆にデータを変換する際には、前回の記事で実装した高速フーリエ変換アルゴリズムを使用することを思い出してください。その記事では、使用するアルゴリズムやカーネルを実行キューに配置する方法について詳述しました。

ここでは、カーネルを実行キューに配置するアルゴリズムについては触れません。これらの手順はすべて同じ方法に従っており、前回の記事を含み、本連載内で既に何度か説明されています。

クラスの主な機能を実装するCNeuronFreDFOCL::calcOutputGradientsメソッドについて考えてみましょう。このメソッドは、モデルの構造に基づき、目標ラベルから予測値の偏差を算出します。メソッドのパラメータには、目標値を含むバッファへのポインタが渡されます。メソッドの操作後には、誤差勾配を現在の層の対応するバッファに保存する必要があります。

bool CNeuronFreDFOCL::calcOutputGradients(CArrayFloat *Target, float &error)
  {
   if(!Target)
      return false;
   if(Target.Total() < Output.Total())
      return false;

メソッド本体では、受け取った目標値バッファへのポインタの正当性を確認します。また、そのサイズがモデルの結果テンソルよりも大きい必要があります。

受信したバッファは、OpenCLコンテキスト側に自分自身のコピーを持っていない可能性があるため、後続の計算のためにその場所にコピーを作成する必要があります。しかし、OpenCLコンテキストのリソースを効率的に使用するために、取得したデータはすでに作成された勾配バッファに転送されます。

   if(Target.Total() == Output.Total())
     {
      if(!Gradient.AssignArray(Target))
         return false;
     }
   else
     {
      for(int i = 0; i < Output.Total(); i++)
        {
         if(!Gradient.Update(i, Target.At(i)))
            return false;
        }
     }
   if(!Gradient.BufferWrite())
      return false;

ここでは、2つの方法で展開できます。目標ラベルと予測値バッファのサイズが等しい場合は、既存のコピーメソッドを使用します。それ以外の場合、必要な数の値を転送するためにループを使用します。どちらの場合も、データをコピーした後、それをOpenCLコンテキストメモリに転送します。

取得したデータは、時間領域と周波数領域の両方で偏差を計算するために使用されます。時間領域で偏差を計算する際、層の誤差勾配バッファは計算された偏差で上書きされ、取得した目標値は完全に失われることに注意してください。したがって、時間領域で偏差を計算する前に、少なくとも取得した目標ラベルの時系列を周波数成分に分解する必要があります。

時系列は2次元の周波数特性に分解されます。使用される方法は、bTransposeフラグの値によって決まります。フラグがtrueに設定されている場合、最初にモデルの結果バッファを転置し、その後周波数応答に分解します。

   if(bTranspose)
     {
      if(!Transpose(Output, GetPointer(cTranspose), iWindow, iCount))
         return false;
      if(!FFT(GetPointer(cTranspose), NULL, GetPointer(cForecastFreRe), GetPointer(cForecastFreIm), false))
         return false;

目標ラベルテンソルに対しても同様の操作を実行します。

      if(!Transpose(Gradient, GetPointer(cTranspose), iWindow, iCount))
         return false;
      if(!FFT(GetPointer(cTranspose), NULL, GetPointer(cTargetFreRe), GetPointer(cTargetFreIm), false))
         return false;
     }

bTransposeフラグの値がfalseの場合、予備的な転置をおこなわずに、目標値と予測値を対応する周波数特性に分解します。

   else
     {
      if(!FFT(Output, NULL, GetPointer(cForecastFreRe), GetPointer(cForecastFreIm), false))
         return false;
      if(!FFT(Gradient, NULL, GetPointer(cTargetFreRe), GetPointer(cTargetFreIm), false))
         return false;
     }

周波数特性が決定されると、目標値を失うことを心配することなく、時間領域と周波数領域の両方で偏差を計算できます。

   if(!FreqMSA(GetPointer(cTargetFreRe), GetPointer(cForecastFreRe), GetPointer(cLossFreRe)))
      return false;
   if(!FreqMSA(GetPointer(cTargetFreIm), GetPointer(cForecastFreIm), GetPointer(cLossFreIm)))
      return false;
   if(!FreqMSA(Gradient, Output, Gradient))
      return false;

周波数領域では、周波数応答の実数部と虚数部の両方で偏差を決定することが重要です。なぜなら、位相シフトの値は信号の振幅と同じくらい重要だからです。しかし、時間領域と周波数領域の誤差勾配を直接近似することはできません。データが比較できないためです。したがって、最初に周波数応答誤差の勾配を時間領域に戻す必要があります。この処理には、逆フーリエ変換を使用します。

   if(!FFT(GetPointer(cLossFreRe), GetPointer(cLossFreIm), GetPointer(cGradientFreRe), GetPointer(cGradientFreIm), true))
      return false;

時間領域と周波数領域の誤差勾配が比較可能な形式に変換されました。周波数特性抽出の測定は、bTransposeフラグの値に依存しています。そのため、フラグ値に応じて周波数領域の誤差勾配を適切に変換する必要があります。これにより、初めてモデルの累積誤差勾配を正確に決定することができます。

   if(bTranspose)
     {
      if(!Transpose(GetPointer(cGradientFreRe), GetPointer(cTranspose), iCount, iWindow))
         return false;
      if(!CumulativeGradient(GetPointer(cTranspose), Gradient, Gradient, fAlpha))
         return false;
     }
   else
      if(!CumulativeGradient(GetPointer(cGradientFreRe), Gradient, Gradient, fAlpha))
         return false;
//---
   return true;
  }

各ステップで結果を制御することを忘れないでください。演算の論理値が呼び出し元に返されます。

モデルの出力で誤差勾配を決定した後、それを前の層に渡す必要があります。この機能は、前のニューラル層のオブジェクトへのポインタをパラメータとして受け取るCNeuronFreDFOCL::calcInputGradientsメソッドで実装します。

この層には訓練可能なパラメータが含まれていないことに留意してください。フィードフォワードパス中に、データバッファを置き換え、前の層の値を結果として表示しています。この方法の目的はとても簡単です。先に計算した累積誤差勾配を前の層の活性化関数に適切に調整することです。

bool CNeuronFreDFOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;
//---
   return DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), Gradient, NeuronOCL.Activation());
  }

クラスには訓練可能なパラメータが含まれていないため、updateInputWeightsメソッドを「空のスタブ」で再定義します。

クラスに実行可能なパラメータが存在しないことも、ファイル操作方法に影響します。内部オブジェクトが無関係であるため、保存する必要がありません。そのため、データを保存する際には、親クラスの同名のメソッドのみを呼び出します。

bool CNeuronFreDFOCL::Save(const int file_handle)
  {
   if(!CNeuronBaseOCL::Save(file_handle))
      return false;

オブジェクトの設計上の特徴を記述する変数の値を保存します。

   if(FileWriteInteger(file_handle, int(iWindow)) < INT_VALUE)
      return false;
   if(FileWriteInteger(file_handle, int(iCount)) < INT_VALUE)
      return false;
   if(FileWriteInteger(file_handle, int(iFFTin)) < INT_VALUE)
      return false;
   if(FileWriteInteger(file_handle, int(bTranspose)) < INT_VALUE)
      return false;
   if(FileWriteFloat(file_handle, fAlpha) < sizeof(float))
      return false;
//---
   return true;
  }

データファイルからオブジェクトを復元するための読み込みアルゴリズムは、もう少し複雑に見えます。ここではまず親クラスの要素を復元します。

bool CNeuronFreDFOCL::Load(const int file_handle)
  {
   if(!CNeuronBaseOCL::Load(file_handle))
      return false;

次に、変数データを保存された順序で読み込みし、データファイルの終わりに達したかどうかを忘れずに確認します。

   if(FileIsEnding(file_handle))
      return false;
   iWindow = uint(FileReadInteger(file_handle));
   if(FileIsEnding(file_handle))
      return false;
   iCount = uint(FileReadInteger(file_handle));
   if(FileIsEnding(file_handle))
      return false;
   iFFTin = uint(FileReadInteger(file_handle));
   if(FileIsEnding(file_handle))
      return false;
   bTranspose = bool(FileReadInteger(file_handle));
   if(FileIsEnding(file_handle))
      return false;
   fAlpha = FileReadFloat(file_handle);

次に、クラスアーキテクチャの読み込まれたパラメータに従って、ネストされたオブジェクトを初期化する必要があります。これらのオブジェクトは、新しいクラスインスタンスを初期化するアルゴリズムと同様に初期化されます。

   uint n = (bTranspose ? iWindow : iCount);
   if(!cForecastFreRe.BufferInit(iFFTin * n, 0) || !cForecastFreRe.BufferCreate(OpenCL))
      return false;
   if(!cForecastFreIm.BufferInit(iFFTin * n, 0) || !cForecastFreIm.BufferCreate(OpenCL))
      return false;
   if(!cTargetFreRe.BufferInit(iFFTin * n, 0) || !cTargetFreRe.BufferCreate(OpenCL))
      return false;
   if(!cTargetFreIm.BufferInit(iFFTin * n, 0) || !cTargetFreIm.BufferCreate(OpenCL))
      return false;
   if(!cLossFreRe.BufferInit(iFFTin * n, 0) || !cLossFreRe.BufferCreate(OpenCL))
      return false;
   if(!cLossFreIm.BufferInit(iFFTin * n, 0) || !cLossFreIm.BufferCreate(OpenCL))
      return false;
   if(!cGradientFreRe.BufferInit(iFFTin * n, 0) || !cGradientFreRe.BufferCreate(OpenCL))
      return false;
   if(!cGradientFreIm.BufferInit(iFFTin * n, 0) || !cGradientFreIm.BufferCreate(OpenCL))
      return false;
   if(bTranspose)
     {
      if(!cTranspose.BufferInit(iWindow * iCount, 0) || !cTranspose.BufferCreate(OpenCL))
         return false;
     }
   else
     {
      cTranspose.BufferFree();
      cTranspose.Clear();
     }
//---
   return true;
  }

これで、新しいCNeuronFreDFOCLクラスのメソッドの説明は終了です。このクラスの完全なコードは添付ファイルで確認できます。

新しいクラスのメソッドを構築した後、通常は訓練可能なモデルアーキテクチャの説明に進みます。しかし、この記事では、かなり珍しいニューラル層を構築しました。この層は、ニューラル層の形式で複雑な損失関数を実装したものです。したがって、ここで作成したオブジェクトを、以前訓練したモデルの1つに追加し、再訓練をおこない、結果がどのように変化するかを確認できます。私の実験では、FEDformerモデルを選択しました。このモデルのアーキテクチャについては、こちらで説明されています。次に、この新しい訓練を追加してみましょう。

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
........
........
//--- layer 17
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = BarDescr;
   descr.count =  NForecast;
   descr.step = int(true);
   descr.probability = 0.8f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

しばらく考えた後、実験を拡張することにしました。FreDF法の著者は、予測結果の依存関係を活用する独自のアルゴリズムを提案しています。実際、Actorの結果における個々のパラメータ間にも依存関係が存在します。たとえば、買い取引と売り取引のボリュームは相互に排他的であり、これはポジションが任意の時点で1方向しか持てないためです。また、ストップロスとテイクプロフィットのパラメーターは、最も可能性の高い今後の動きの強さを決定します。そのため、ロングポジションのテイクプロフィットはショートポジションのストップロスと相関しており、その逆も同様です。このような推論を基に、予測されたCritic値の依存関係も示唆できます。それでは、前述のモデルに実験を拡張してみましょう。言うよりも早く実行します。ActorモデルとCriticモデルに新しい層を追加してみましょう。

bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!critic)
     {
      critic = new CArrayObj();
      if(!critic)
         return false;
     }
//--- Actor
.........
.........
//--- layer 17
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = NActions;
   descr.count =  1;
   descr.step = int(false);
   descr.probability = 0.8f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- Critic
.........
.........
//--- layer 17
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = NRewards;
   descr.count =  1;
   descr.step = int(false);
   descr.probability = 0.8f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

この場合、個々の単位系列ではなく、結果のシーケンス全体の周波数特性を分析していることに注意してください。

FreDF法によって提案されたアプローチを実装する際、モデルの訓練や環境とのやり取りに使用されるエキスパートアドバイザー(EA)の調整は必要ありません。つまり、テストのために事前に準備されたEAと訓練データセットを使用して取得した結果を評価できます。   


3.テスト

FreDFの著者が提案したアプローチをMQL5を使用して実装するために、かなりの作業をおこなってきました。次は、作業の最終段階である訓練とテストに進みます。

前述のように、以前に作成したEAと事前に収集した訓練データを使用してモデルを訓練します。この記事では、2023年のH1時間枠でEURUSD商品の履歴データを使用してモデルを訓練します。

まず、環境状態Encoderのモデルを訓練します。このモデルは、NForecast定数によって決まる計画期間にわたって環境の将来の状態を予測するように訓練されます。実験では、12本の後続のローソク足を使用しました。予測は、環境の状態を記述するすべての分析されたパラメータのコンテキストで生成されます。

#define        NForecast               12            //Number of forecast

エンコーダの訓練過程で、FreDFアプローチを使用しない同様のモデルと比較して予測誤差が減少していることがわかります。ただし、予測結果のグラフィカルな比較はおこないませんでした。そのため、予測値の実際の品質を判断することは難しいです。奇妙に思えるかもしれませんが、ここで注目すべき点は、分析されたすべての指標の最も正確な予測を得ることがここでの目標ではないということです。Actorモデルは、エンコーダの潜在空間を使用して最適なアクションを決定します。訓練の最初の段階の目標は、最も可能性の高い今後の価格変動をエンコードする、エンコーダの最も有益な潜在空間を取得することです。

これまでと同様に、エンコーダモデルは価格変動のみを分析するため、訓練の最初の段階では訓練セットを更新する必要はありません。

学習プロセスの第2段階では、最適なActor行動方策を検索します。ここでは、ActorモデルとCriticモデルの反復訓練を実行し、訓練データセットの更新を交互におこないます。

Actor方策訓練を数回繰り返した結果、利益を生み出すことができるモデルを得ることができました。2024年1月の実際の履歴データを使用して、MetaTrader 5ストラテジーテスターで訓練済みモデルのパフォーマンスをテストしました。テストパラメータは、分析された指標の商品、時間枠、パラメータなど、訓練データセットのパラメータと完全に一致していました。テスト結果は以下のスクリーンショットに示されています。 

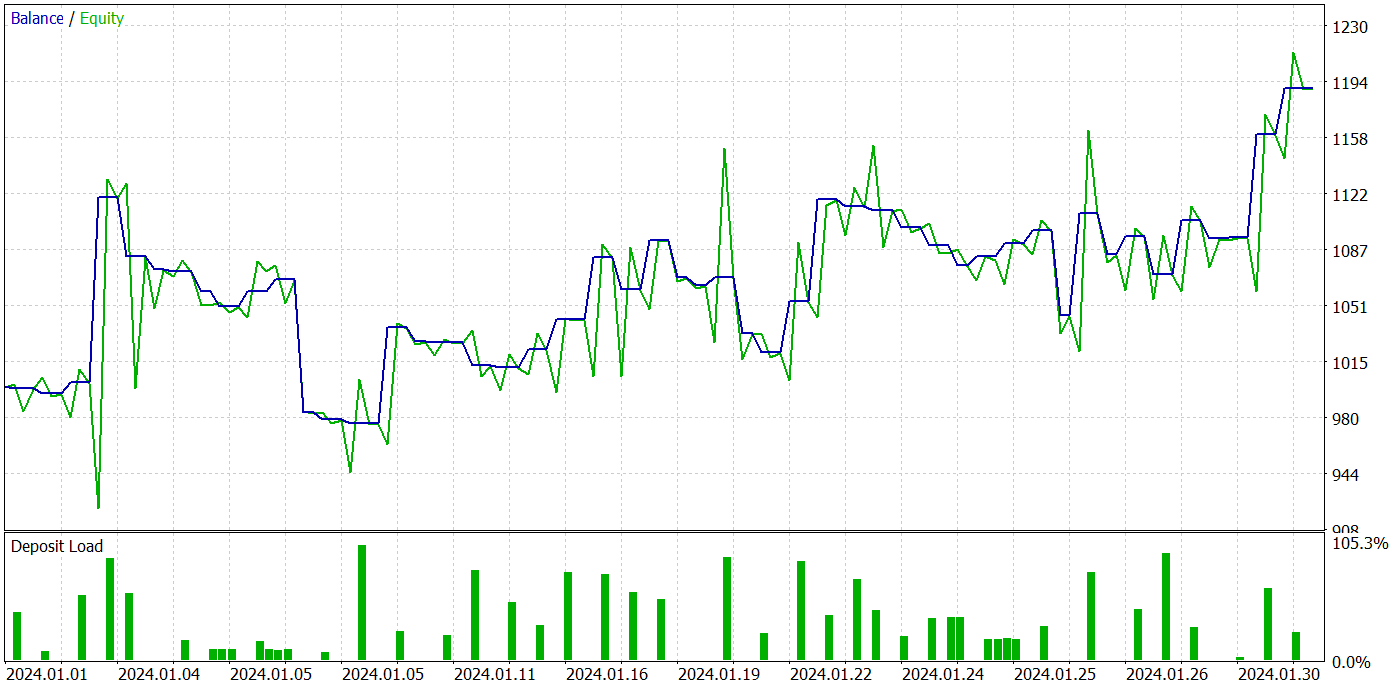
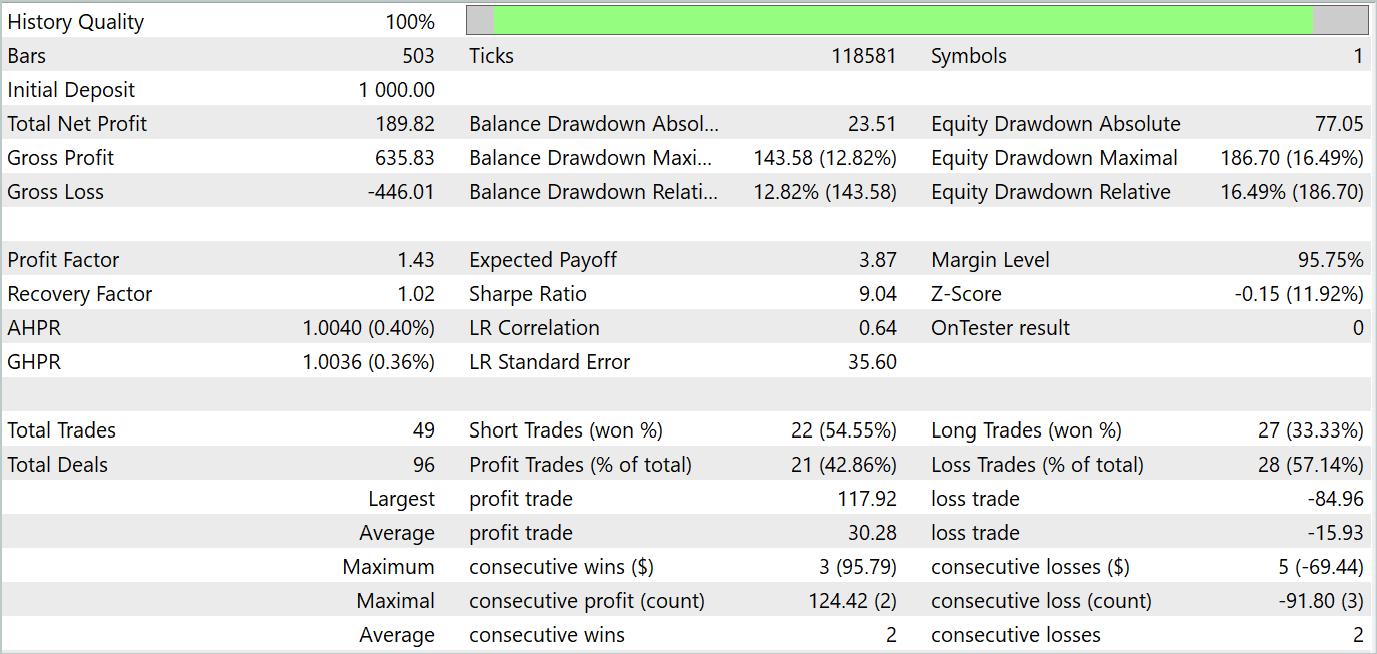
テスト結果から、口座残高が明らかに増加傾向にあることがわかります。テスト期間中、モデルは49件の取引を実行し、そのうち21件は利益を出して終了しました。確かに、利益を上げたポジションは半分以下でした。ただし、利益を出した取引の平均額は、損失を出した取引の平均額のほぼ2倍です。その結果、テストデータセットでのモデルの利益率は1.43で、その月の総収入は約19%です。


結論

この記事では、時系列予測を改善するためのFreDF法について説明しました。この手法の著者は、ラベル付きシーケンスの自己相関を無視すると、現在のDFパラダイムにおいて尤度が偏り、予測の品質が低下することを経験的に実証しました。著者は、周波数領域で予測とラベルシーケンスを合わせることで、自己相関を考慮するという、DFパラダイムへのシンプルで効果的な修正を提案しています。FreDF法は、さまざまな予測モデルや変換と互換性があり、非常に柔軟で多用途な手法です。

実践的な部分では、MQL5言語で提案されたアプローチを実装し、以前に作成したFEDformerモデルにこのアプローチを追加して訓練を実施しました。その後、訓練されたモデルをテストしました。テスト結果では、すべての条件が同じ場合にFreDFを追加することでモデルの効率が向上したことが示され、提案されたアプローチの有効性が裏付けられました。

FreDF法の柔軟性が非常に高く、既存のさまざまなモデルに効果的に組み込むことができる点が重要です。

参照文献


記事で使用されているプログラム

# 名前 種類 詳細
1 Research.mq5 EA コレクションEAの例
2 ResearchRealORL.mq5
 EA
 Real-ORL法による事例収集のためのEA
3 Study.mq5 EA モデル訓練EA
4 StudyEncoder.mq5 EA
 エンコード訓練EA
5 Test.mq5 EA モデルをテストするEA
6 Trajectory.mqh クラスライブラリ システム状態記述の構造体
7 NeuroNet.mqh クラスライブラリ ニューラルネットワークを作成するためのクラスのライブラリ
8 NeuroNet.cl コードベース OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/14944

添付されたファイル |
ZIPをダウンロード
MQL5.zip (1240.5 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
リプレイシステムの開発（第51回）：物事は複雑になる(III) リプレイシステムの開発（第51回）：物事は複雑になる(III)
この記事では、MQL5プログラミングの分野で最も難解な問題の1つである、チャートIDを正しく取得する方法と、オブジェクトがチャートにプロットされない場合がある理由について解説します。ここで提供される資料は教育目的のみに使用されるべきです。いかなる状況においても、提示された概念を学習し習得する以外の目的でアプリケーションを閲覧することは避けてください。
PSAR、平均足、ディープラーニングを組み合わせて取引に活用する PSAR、平均足、ディープラーニングを組み合わせて取引に活用する
このプロジェクトでは、ディープラーニングとテクニカル分析の融合を探求し、FXの取引戦略を検証します。EUR/USDの動きを予測するために、PSAR、SMA、RSIのような伝統的な指標とともにONNXモデルを採用し、迅速な実験のためにPythonスクリプトを使用します。MetaTrader 5のスクリプトは、この戦略をライブ環境に導入し、ヒストリカルデータとテクニカル分析を使用して、情報に基づいた取引決定をおこないます。バックテストの結果は、積極的な利益追求よりもリスク管理と着実な成長に重点を置いた、慎重かつ一貫したアプローチを示しています。
ニューラルネットワークが簡単に（第92回）：周波数および時間領域における適応的予測 ニューラルネットワークが簡単に（第92回）：周波数および時間領域における適応的予測
FreDF法の著者は、周波数領域と時間領域を組み合わせた予測の利点を実験的に確認しました。しかし、重みハイパーパラメータの使用は、非定常時系列には最適ではありません。この記事では、周波数領域と時間領域における予測の適応的組み合わせの方法について学びます。
MQL5で取引管理者パネルを作成する（第3回）：ビジュアルスタイリングによるGUIの強化(I) MQL5で取引管理者パネルを作成する（第3回）：ビジュアルスタイリングによるGUIの強化(I)
この記事では、MQL5を使用して、取引管理パネルのグラフィカルユーザーインターフェイス(GUI)を視覚的にスタイル設定することに焦点を当てます。MQL5で利用できるさまざまなテクニックと機能について説明します。これらのテクニックと機能により、インターフェイスのカスタマイズと最適化が可能になり、魅力的な外観を維持しながらトレーダーのニーズを満たすことができます。