
Operações baseadas em ângulos para traders
Introdução
Operações baseadas em ângulos têm sido utilizadas no trading há muito tempo. A principal vantagem dessas operações é a simplicidade na construção dos ângulos e sua clareza. Um exemplo marcante de operações baseadas em ângulos são as ferramentas de Gann.
Parece que já sabemos tudo sobre ângulos. Mas vou tentar olhar para os ângulos de uma perspectiva diferente. Vamos tentar lembrar das coisas bem esquecidas para obter algo completamente novo.
Construindo o primeiro ângulo
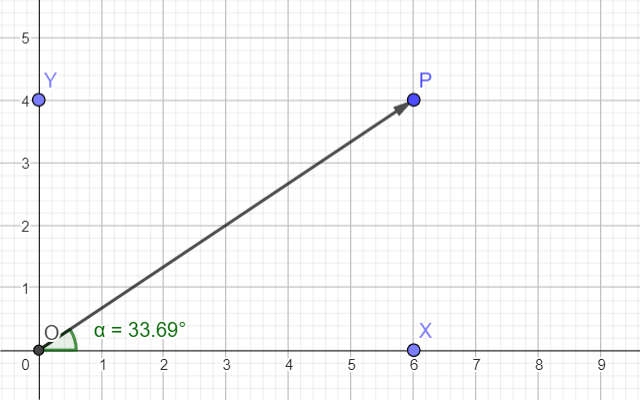
O ângulo é uma das formas geométricas mais simples. Desenhar duas linhas a partir de um ponto - o que poderia ser mais simples? Uma das linhas frequentemente representa o eixo das abscissas.
Neste caso, o valor do ângulo é muito fácil de calcular usando as coordenadas do ponto P.
Como o ângulo é uma quantidade adimensional, ambos os eixos devem ter os mesmos valores. Se você medir metros ao longo de um eixo e quilogramas ao longo do outro, obterá algum tipo de relação entre eles, mas não um ângulo.
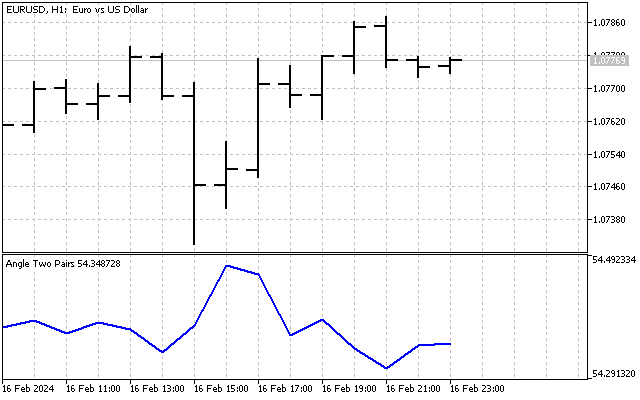
Vamos tentar implementar a operação baseada em ângulos como um indicador. Vou criar o seguinte indicador: diferentes pares de moedas serão exibidos ao longo dos eixos X e Y. Então, um ângulo pequeno corresponderá a um preço alto para o primeiro par de moedas e a um preço baixo para o segundo. Consequentemente, um ângulo grande indicará que o preço do segundo símbolo é mais alto do que o primeiro. Em outras palavras, nosso indicador futuro determinará o estado de sobrecompra/sobrevenda de um par de moedas em relação a outro. Não é uma má ideia para o trading de pares.
A primeira dificuldade que encontramos é que temos valores diferentes em diferentes eixos (por exemplo, peguei EURUSD e USDJPY). Podemos superar essa dificuldade facilmente dividindo o preço de cada instrumento pelo valor do ponto.
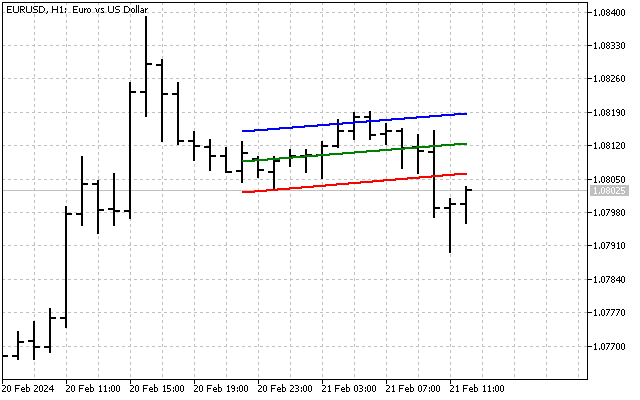
Assim, resolvemos imediatamente dois problemas - em ambos os eixos teremos valores comparáveis (preço expresso em pontos), além disso, a escala nesses eixos será a mesma. É assim que nosso indicador se parece.
À primeira vista, o indicador parece bastante trivial. Seu valor flutua em torno de algum valor médio, e a diferença entre o máximo e o mínimo do indicador é de apenas 2-3 graus. Mas não vamos tirar conclusões precipitadas. Talvez possamos melhorar esse indicador e torná-lo mais informativo.
Um pequeno lembrete. A medida angular mais comum que usamos na vida cotidiana é o grau. Para cálculos matemáticos, a medida em radianos é mais frequentemente usada. A transição de uma medida em graus para uma medida em radianos e vice-versa é realizada de acordo com as seguintes equações:
Em outras palavras, converter graus em radianos e vice-versa é simplesmente multiplicar por algum fator de escala. No entanto, se você precisar exibir informações numericamente, é preferível usar graus. 45° definitivamente parece melhor do que 0,78539 rad.
Ângulos e distribuição normal
Ao estudar processos reais, os pesquisadores usam várias distribuições de probabilidade de variáveis aleatórias. A mais popular é a distribuição normal.
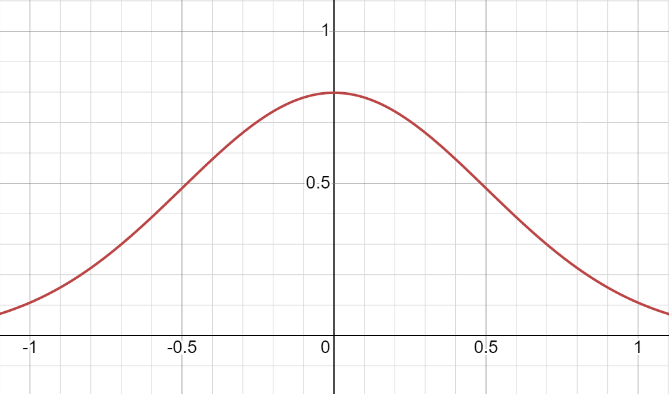
Vamos relembrar algumas de suas propriedades. Seu gráfico é uma linha em forma de sino. Os extremos dessa linha vão para o infinito.
Vamos realizar mentalmente a seguinte operação. Começaremos a dobrar lentamente o eixo X em um círculo. Ao fazer isso, seguiremos a seguinte regra - quanto mais nos afastarmos do centro, mais forte será a dobra. Se formos pacientes o suficiente, o eixo X se transformará em um círculo. A própria linha da distribuição normal será distorcida e, como resultado, obteremos a distribuição normal envolvida.
A primeira diferença entre uma distribuição normal regular e uma distribuição envolvida é que -∞ se mapeia para -180°, e +∞ se mapeia para +180°. Mas esse não é nosso objetivo. O principal objetivo da distribuição normal envolvida é lidar com valores angulares. A equação da distribuição normal envolvida é assim:
Como podemos ver, a distribuição envolvida usa tanto a média quanto o desvio padrão. Tudo como na distribuição normal usual. A soma parece bastante perturbadora, mas lidaremos facilmente com essas infinitudes ao trabalhar com dados reais.
Vamos pegar nosso indicador e aplicar a distribuição normal envolvida a ele.
Primeiro, precisamos determinar a média de todos os ângulos que ocorrem na história. No nosso caso, encontrar a média não será difícil - a soma usual e a divisão pelo número de observações. Mas, geralmente falando, a média angular precisa ser procurada de maneira um pouco diferente. Imagine que você precisa encontrar a média de dois ângulos - 10° e 350°. A abordagem usual dá a resposta de 180°. Essa resposta está errada. A média deles é zero.
Para obter a resposta correta em qualquer situação, teremos que fazer o seguinte: primeiro precisamos encontrar as somas dos seno e cosseno de todos os ângulos. Divida a primeira soma pela segunda e obtenha o tangente do ângulo médio.
Agora, encontrar o valor do ângulo médio não será difícil. Mas há uma pequena condição aqui também. Se todos os ângulos estiverem entre -90° e +90°, podemos usar a função MathArctan. Se os ângulos ultrapassarem esses limites, devemos definitivamente usar a função mais universal MathArctan2.
Assim, o ângulo médio será igual a:
Depois de estimarmos o valor do ângulo médio, podemos começar a estimar o desvio padrão. Para isso, podemos usar o método Yamartino. Primeiro, precisamos encontrar a quantidade auxiliar:
Já fornece uma estimativa bastante precisa do desvio padrão, mas também pode ser melhorado:
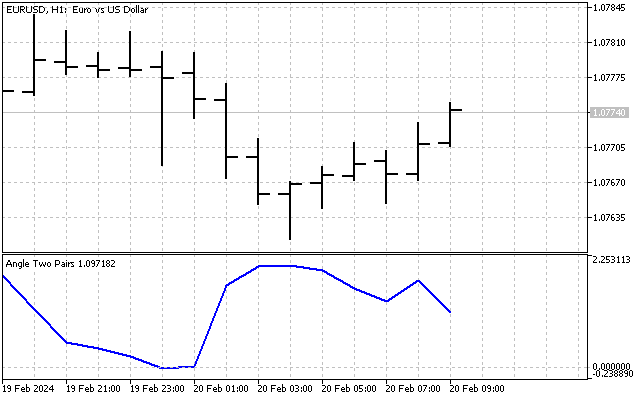
Agora, vamos fazer mudanças no nosso indicador. Vamos calcular suas leituras da seguinte forma: primeiro, encontraremos a diferença entre os ângulos atuais e médios, e depois compararemos essa diferença com o desvio padrão. Como resultado, obteremos uma imagem assim.
O indicador nos permite determinar com mais precisão os níveis de sobrecompra/sobrevenda, e seu análogo mais próximo é o indicador CCI.
Ângulos e função linear
Lidamos com ângulos para o mesmo tipo de dados. É possível aplicar operações angulares a uma tendência? A resposta é não, já que estamos lidando com tipos diferentes de dados - temos tempo em um eixo e preço no outro.
Bem, a resposta está correta, mas mesmo assim errada. Vamos relembrar a função linear. Ela descreve uma relação linear entre duas variáveis independentes e é dada pela equação:
Onde está o ângulo aqui? Ele está oculto na razão k. Essa razão é igual ao tangente do ângulo de inclinação da linha em relação ao eixo X.
Vamos tentar usar essa função para descrever uma tendência. A equação da função linear para traders ficará assim:
Neste caso, a razão k receberá outra interpretação - ela mostra a mudança média de preço por unidade de tempo. Mais uma pequena observação: eu inseri o tempo na equação. Mas em cálculos reais, é muito mais fácil usar índices em vez de tempo. rimeiro, feriados e fins de semana afetarão muito a precisão dos cálculos. E segundo, usar índices torna as equações (e os cálculos) muito mais simples. O único requisito para esses índices é que eles devem aumentar da esquerda para a direita.
Agora vamos olhar para maneiras de estimar parâmetros de tendência linear. Primeiro de tudo, podemos usar o método dos mínimos quadrados (LSM). Deixe-me lembrar que, em vez de tempo, eu uso índices cujos valores variam de 0 a n-1.
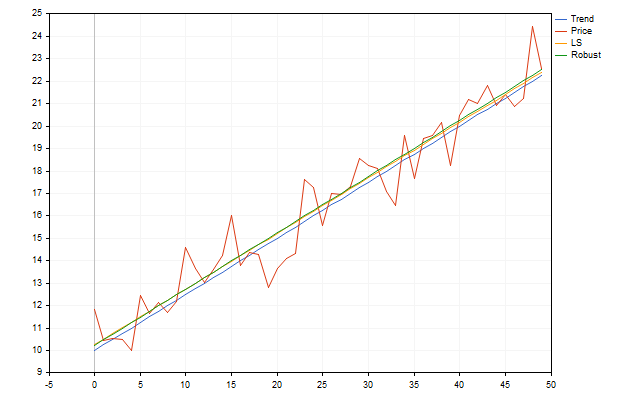
as há maneiras mais confiáveis de avaliar esses parâmetros. Por exemplo, podemos usar a estimativa de Theil-Sen. Vamos ver como essa avaliação pode funcionar em um cenário do mundo real. Vamos pegar uma tendência com os parâmetros k=0,25 e b=10. Adicione um pouco de ruído na forma de desvios distribuídos aleatoriamente. Usando os pontos resultantes, tentaremos encontrar os parâmetros da tendência inicial. Como resultado, obteremos algo assim.
À primeira vista, parece que o método robusto não fornece muita vantagem. Mas isso é apenas porque os erros no nosso modelo de tendência foram distribuídos de forma igual e de acordo com a lei normal. Os preços reais podem não atender a esse critério. Então o método de Theil-Sen funcionará muito melhor e pode fornecer um pouco mais de informações. É a estimativa robusta que usarei no futuro.
Então, vamos ver como você pode estimar os parâmetros de uma tendência linear usando o método de Theil-Sen. Primeiro, precisamos fazer o parâmetro k. Ele será igual à mediana de todas as possíveis diferenças da forma:
O valor mediano pode ser encontrado da seguinte forma. Primeiro, escreva todos os valores em um array. Depois classifique. A mediana será igual ao valor localizado no centro do array.
Agora podemos começar a estimar o parâmetro b. Para isso, precisamos encontrar a mediana de todos os valores possíveis:
Entendemos a teoria, então é hora de passar para a prática. Vamos ver quais possibilidades o uso da estimativa de Theil-Sen nos abre.
Estimativa de Theil-Sen e indicadores
Depois de estimar os parâmetros da tendência, ficamos com dois arrays de dados. Vamos ver se podemos usar esses arrays de outra maneira.
Então, avaliamos os parâmetros da tendência e até construímos sua linha. Agora podemos construir um canal dentro do qual ocorre o movimento de preços. Para fazer isso, primeiro precisamos avaliar o quão longe os preços se desviam da linha de tendência.
Vamos usar o array que usamos ao estimar o parâmetro b. Para estimar a variação, precisamos encontrar a mediana da variação absoluta. Ou seja, primeiro, para cada elemento do array, encontramos o valor absoluto da diferença com o parâmetro b. Então, resta encontrar a mediana dos valores obtidos. Essa mediana fornecerá uma estimativa robusta do desvio padrão.
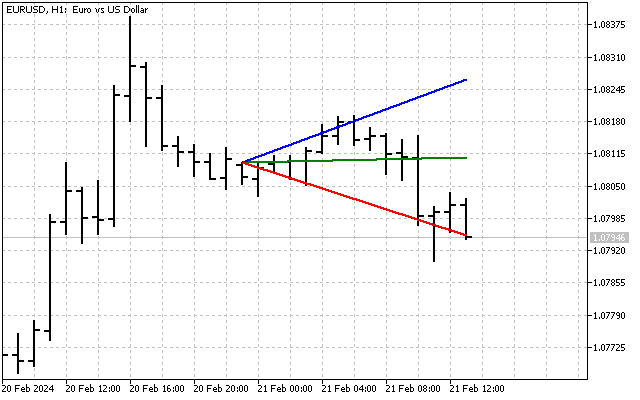
Conhecendo o desvio padrão, podemos construir um canal de tendência. Por exemplo, é assim que se parece um canal com 6 desvios padrão de largura.
Este indicador é essencialmente semelhante às Bollinger Bands. Além disso, as linhas do canal de tendência podem ser usadas como níveis de suporte e resistência.
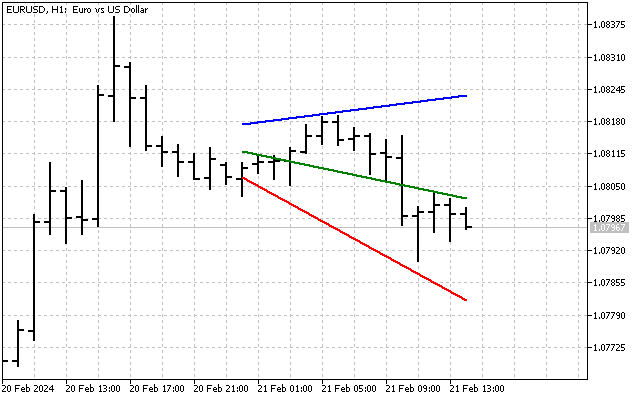
Além disso, podemos construir um leque de linhas de tendência. Todos os cálculos são realizados da mesma forma que na construção de um canal. A única diferença é que precisamos pegar o parâmetro k e o array correspondente. É assim que se parece um leque com um intervalo de 1 desvio por ângulo.
Claro, podemos combinar um canal e um leque. Para fazer isso, primeiro construímos as linhas do canal. Depois aplicamos o leque a elas. Como resultado, obteremos algo assim.
Assim, o uso de métodos robustos nos permitiu obter uma linha de tendência e três indicadores adicionais que podem ser usados na análise técnica.
Considerações adicionais
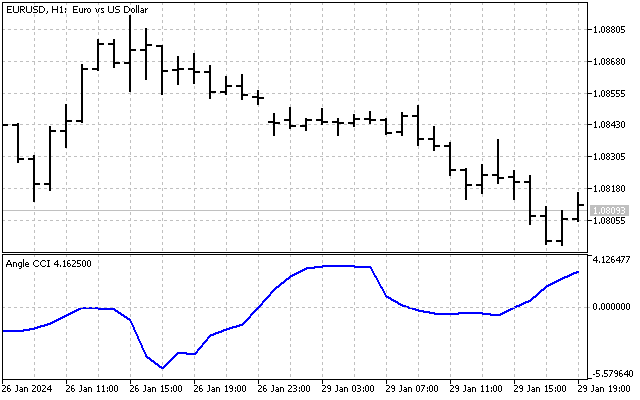
As operações baseadas em ângulos podem ser usadas não apenas para construir tendências e ângulos. Vamos relembrar o indicador CCI já mencionado no artigo. E se fizermos um indicador semelhante, usando ângulos de tendência em vez de preços?
Então, poderemos avaliar as mudanças de tendência com base no histórico. É assim que nosso indicador ficará.
Todos os indicadores técnicos podem ser convertidos para trabalhar com valores angulares. Com esses ajustes, podemos descobrir novas formas de análise técnica.
Conclusão
Os seguintes programas foram usados ao escrever este artigo.
| Nome | Tipo | Descrição |
|---|---|---|
| Angle Two Pairs | Indicador |
|
| LS vs Robust | Script | Comparar LSM e estimativa de Theil-Sen |
| Estimador de Theil–Sen | Indicador |
|
| Angle CCI | Indicador |
|
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/14326
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Multibot no MetaTrader (Parte II): Modelo dinâmico aprimorado
Multibot no MetaTrader (Parte II): Modelo dinâmico aprimorado
 Usando algoritmos de otimização para configurar parâmetros de EA em tempo real
Usando algoritmos de otimização para configurar parâmetros de EA em tempo real
 Rede neural na prática: Pseudo Inversa (II)
Rede neural na prática: Pseudo Inversa (II)
 Construindo e testando sistemas de negociação com o Canal Keltner
Construindo e testando sistemas de negociação com o Canal Keltner
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
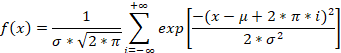
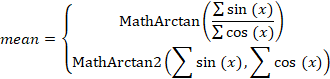
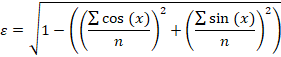
Os ângulos de Gunn fizeram meus olhos lacrimejarem).
Em primeiro lugar, não estou desenhando esses cantos.
Eles aparecerão facilmente por conta própria se o eixo vertical for continuado mais adiante.
Em segundo lugar, usarei o desvio padrão como a unidade vertical e o preço médio como o eixo. O resultado é algo parecido com isto.
Em vez de um quadrado, temos um retângulo. E os cantos mostram (aproximadamente) os limites do movimento de preço browniano.
Bem.
abordagem interessante
Em vez de um quadrado, temos um retângulo. E os cantos mostram (aproximadamente) os limites do movimento browniano de preços.
????? quando o movimento browniano e alguns de seus limites são alguma coisa, mas não um retângulo :-)) Esse é o tipo de matemática que deveria "voar pelos dentes". Como a tabuada de multiplicação.
Uma figura bem próxima de um losango é obtida a partir da volatilidade sazonal (dia-semana-mês-trimestre). E isso acabará sendo uma "decifração" dos ângulos e grades de Gana sem quadrados místicos e torções na tabela. Você pode deduzir estatisticamente
um robô de negociação com base no princípio semelhante ao da sua captura de tela:
Outra maneira de obter ângulos fora do preço. Graças ao vovô Gunn.
Outra maneira de obter ângulos fora do preço. Graças ao vovô Gunn.
valor de ângulo estranho
Outra maneira de obter ângulos fora do preço. Graças ao vovô Gunn.
A caixa (modelo) é muito mais conveniente, pois você obtém os níveis de preço e de tempo (cortes) de uma só vez. E, em um dia, é mais preciso fazer a quadratura do movimento passado, obtendo-se o menor erro nos cálculos.