
角度ベースの取引
はじめに
角度ベースの操作は、非常に長い間、取引で使用されてきました。これらの操作の主な利点は、角度の構成が単純であることと、その明快さです。角度ベースの操作の顕著な例は、ギャンツールです。
角度に関することはすべて、すでに知られているように思えますが、違った角度から見てみようと思います。まったく新しいものを手に入れるために、忘れ去られた古いものを思い出してみましょう。
最初の角度を作成する
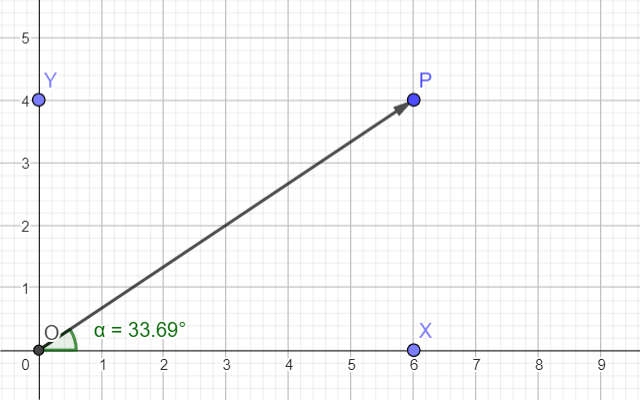
角度は最も単純な幾何学的図形の1つです。1点から2本の線を引く。これ以上簡単なことがあるでしょうか。線の1つは、多くの場合、横軸を表します。
この場合、角度値は P点座標を使用して簡単に計算できます。
角度は無次元量なので、両軸は同じ値を持つはずです。一方の軸に沿ってメートルを測り、もう一方の軸に沿ってキログラムを測ったならば、両者の間に何らかの関係は得られるが、角度は得られません。
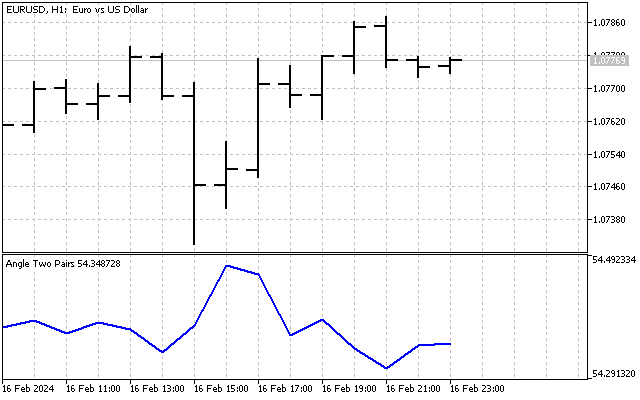
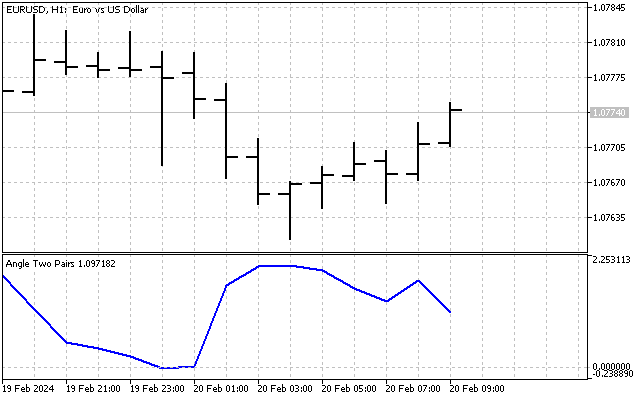
角度を使用した操作を指標として実装してみましょう。Xと Y軸に沿って異なる通貨ペアを表示する指標を作成します。その場合、角度が小さければ、1つ目の通貨ペアは高値、2つ目の通貨ペアは安値となります。従って、角度が大きければ、2つ目の銘柄の価格が1つ目の銘柄より高いことを示します。言い換えれば、将来の指標は、ある通貨ペアが他の通貨ペアに対して買われ過ぎか売られ過ぎかを判断します。ペア取引には悪くないアイデアです。
最初に遭遇する困難は、異なる軸に異なる値があることです(例えば、EURUSDとUSDJPY)。各商品の価格をポイント値で割ることで、この難題は簡単に克服できます。
両方の軸で同等の値(価格はポイントで表される)を持ち、さらにこれらの軸のスケーリングは同じになります。この指標は次のようになります。
一見すると、この指標は些細に思えます。その値はある平均値を中心に変動し、指標の最大値と最小値の差はわずか2~3度です。しかし、早合点は禁物です。おそらく、この指標を改善し、より有益なものにできるでしょう。
少し思い出してください。日常生活で最もよく使われる角度の尺度は度です。数学の計算では、ラジアン尺度が最もよく使用されます。度数からラジアンの移行、およびその逆は、以下の式に従っておこなわれます。
言い換えれば、度数をラジアンに変換することも、その逆も、単にあるスケーリング係数を掛けるだけです。しかし、情報を数値で表示する必要がある場合は、度数を使用するのが望ましいです。45°の方が0.78539radより確実に良く見えます。
角度と正規分布
現実のプロセスを研究するとき、研究者は確率変数のさまざまな確率分布を使用します。最もポピュラーなものは正規分布です。
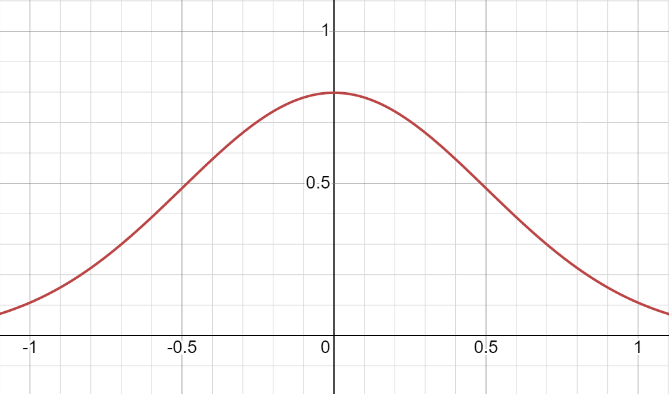
その特性をいくつか思い出してみましょう。グラフは釣鐘型です。この線の両端は無限大まで続いています。
次のような操作を頭の中でおこなってみましょう。ゆっくりとX軸を円形に折りたたみ始めます。これを実行する際、中心から離れるほど折り目が強くなるというルールに従います。十分に辛抱すれば、X軸は円になります。正規分布の線そのものが歪み、その結果、ラップされた正規分布(英語)が得られることになります。
通常の正規分布とラップされた分布の最初の違いは、-∞が-180°に、+∞が+180°に対応することです。ただし、これは私たちの目的ではありません。ラップされた正規分布の主な目的は、角度値を扱うことです。ラップされた正規分布の式は次のようになります。
見てわかるように、ラップされた分布は平均と標準偏差の両方を使用しています。すべてが通常の正規分布と同じです。総和はかなり不安なものに見えますが、実際のデータを扱う際には、このような無限大に簡単に対処できるでしょう。
この指標にラップされた正規分布を適用してみましょう。
まず、履歴で起こったすべての角度の平均を求める必要があります。私たちの場合、平均を求めることは難しいことではありません。通常の合計と観測数による除算です。しかし、一般的に言えば、角度平均は少し違った見方をする必要があります。10°と350°の2つの角度の平均を求める必要があるとしましょう。通常のアプローチでは180度という答えが出ます。この答えは間違っています。平均はゼロです。
どのような状況でも正しい答えを得るためには、次のようにしなければなりません。まず、すべての角度の正弦 余弦の和を求める必要があります。最初の和を2番目の和で割って、中間の角の正接を求めます。
さて、平均角の値を求めるのは難しいことではありません。しかし、ここにも小さな条件があります。すべての角度が-90°から+90°の間にある場合、MathArctan関数を使用することができます。角度がこれらの制限を超える場合は、より普遍的なMathArctan2関数を使用するべきです。
したがって、平均角度は次のようになります。
平均角度の値が推定できたら、標準偏差の推定に取りかかりましょう。これにはYamartino法(英語)を使用できます。まず、補助量を求める必要があります。
これはすでに標準偏差のかなり正確な推定値を提供していますが、改善することもできます。
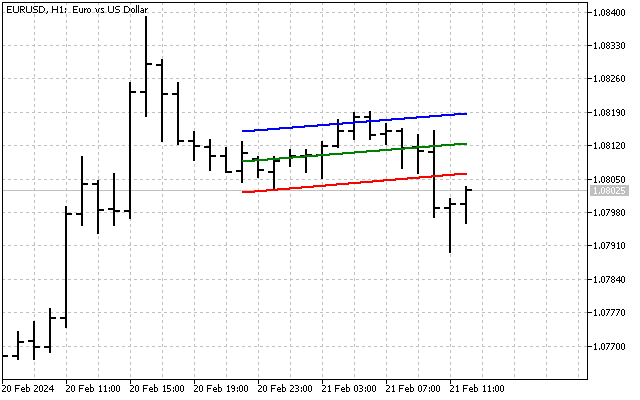
では、指標に変更を加えましょう。まず、現在の角度と平均角度の差を求め、この差を標準偏差と比較します。その結果、このようになります。
この指標は、買われすぎ/売られすぎのレベルをより正確に判断することができます。これに最も近い類似指標はCCI指標です。
角度と一次関数
同じ種類のデータに対して角度を扱いました。トレンドに角度操作を加えることは可能でしょうか。答えは「いいえ」です。片方の軸には時間、もう片方には価格という、異なるデータのタイプがあるからです。
まあ、正解ですが、それでも間違っています。一次関数を思い出してみましょう。これは2つの独立変数間の線形関係を表し、次の式で与えられます。
角度は、kの比率に隠されています。この比率は、X軸に対する線の傾斜角度の接線に等しくなります。
この関数を使用してトレンドを表現してみましょう。トレーダーの一次関数方程式は次のようになります。
この場合kの比率は別の解釈を受けることになります。単位時間あたりの平均価格変動です。もう1つ小さなノートです。方程式に時間を入力しましたが、実際の計算では、時間の代わりに指数を使用する方がはるかに簡単です。まず、休日や週末は計算の精度に大きく影響します。次に、インデックスを使用することで方程式(と計算)がよりシンプルになります。これらの指標の唯一の条件は、左から右へ増加することです。
次に、線形トレンドパラメータを推定する方法を見てみましょう。まず、最小二乗法(LSM)を使用することができます。時間の代わりに、0からn-1までさまざまな値を持つインデックスを使用していることを思い出してください。
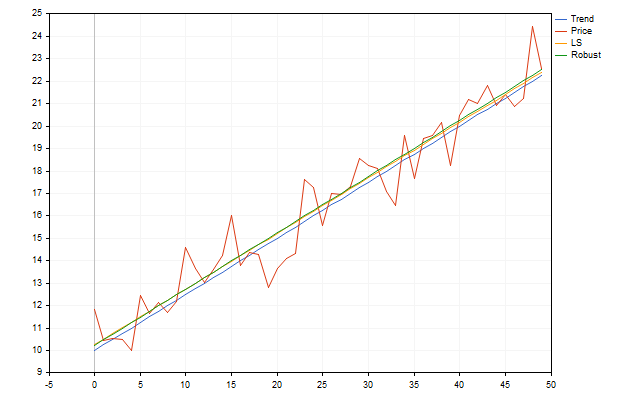
しかし、これらのパラメータを評価するには、もっと信頼できる方法があります。例えば、titlehttps://en.wikipedia.org/wiki/Theil%E2%80%93Sen_estimatortitleTheil-Sen推定量 (英語)の使用です。この評価が実際の現場でどのように機能するか見てみましょう。k=0.25およびb=10のパラメータでトレンドを見てみましょう。 そこにランダムに分布する偏差という形で、少しノイズを加えます。得られたポイントを使用して、初期トレンドのパラメータを求めてみます。その結果、次のようになります。
一見すると、このロバストな手法にはあまり利点がないように見えますが、これは、私たちのトレンドモデルの誤差が正規の法則に従って均等に分布していたからに他なりません。実際の価格はこの基準を満たさない可能性があります。それなら、Theil-Sen法の方がずっとうまくいくだろうし、もう少し情報が得られるかもしれません。これは、今後私が使用するロバストな推定量です。
それでは、Theil-Sen法を用いて線形トレンドのパラメータを推定する方法を見てみましょう。まず kパラメータを作成する必要があります。これは、すべての可能な差からの、次の形式の中央値に等しくなります。
中央値は次のようにして求めることができます。まず、すべての値を配列に書き込みます。そして、並び替えます。中央値は、配列の中心に位置する値に等しくなります。
次にbパラメータの推定を開始します。そのためには、すべての可能な値の中央値を見つける必要があります。
理論は理解できたので、次は実践です。Theil-Sen推定量を使用することでどんな可能性が開けるか見てみましょう。
Theil-Sen推定量と指標
トレンドパラメータを推定した後、2つのデータ配列が残ります。これらの配列を他の方法で使えないか試してみましょう。
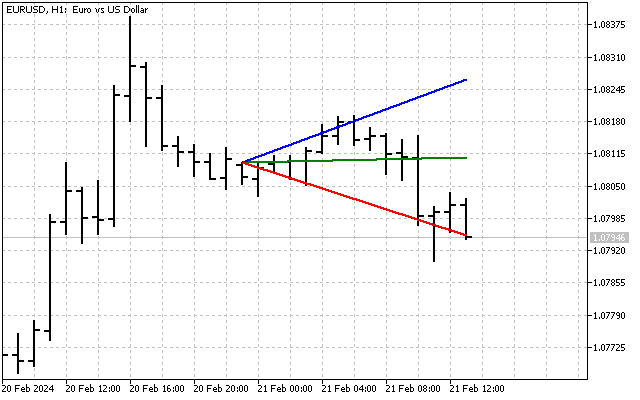
トレンドのパラメータを評価し、そのラインまで構築しました。これで、値動きが発生するチャネルを構築することができます。そのためにはまず、価格がトレンドラインからどの程度乖離しているかを評価する必要があります。
bパラメータを推定するときに使用した配列を使用してみましょう。偏差を推定するためには、中央値絶対偏差(英語)を求める必要があります。つまり、まず、配列の各要素について、bパラメータとの差の絶対値 を求めます。あとは、得られた値の中央値を求めるだけです。この中央値から標準偏差を推定することができます。
標準偏差を知ることで、トレンドチャネルを構築することができます。たとえば、6標準偏差幅のチャンネルはこんな感じです。
この指標は、基本的にボリンジャーバンドに似ています。さらに、トレンドチャネルラインは、支持線と抵抗線として使用することができます。
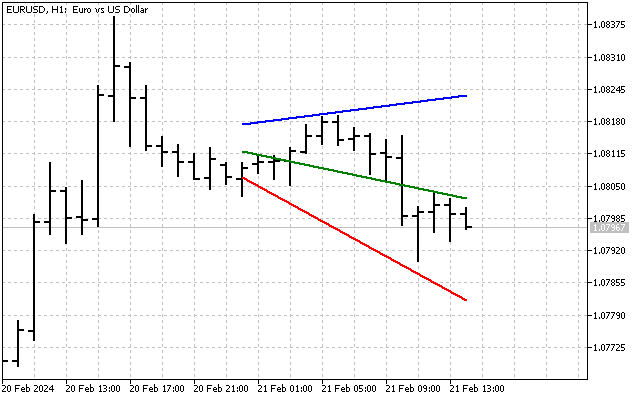
それに、トレンドラインのファンを作成することもできます。すべての計算は、チャネルを作成するときと同じようにおこなわれます。唯一の違いは kパラメータと対応する配列を取る必要があることです。角度によって1偏差の範囲を持つファンはこのように見えます。
もちろん、チャンネルとファンを組み合わせることもできます。そのために、まずチャンネルラインを作成します。次にファンを適用します。その結果、次のようになります。
このように、ロバストな手法を使用することで、トレンドラインと、テクニカル分析に使用できる3つの追加指標を得ることができました。
その他の考慮事項
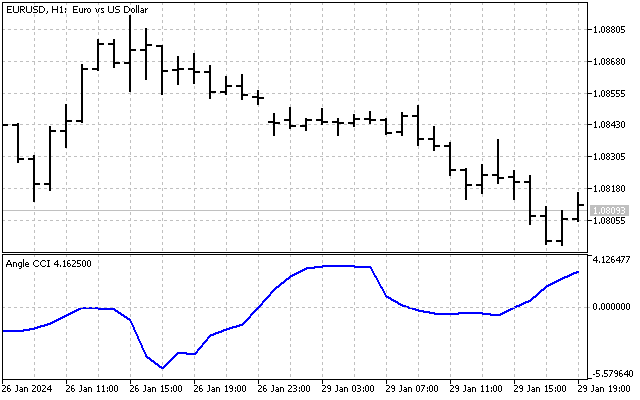
角度ベースの演算は、トレンドや角度を構成するためだけに使用できるわけではありません。記事の中ですでに触れたCCI指標を思い出してみましょう。価格ではなく、トレンド角度を使用して同じような指標を作ったらどうでしょうか。
そうすれば、トレンドの変化を履歴に基づいて評価できるようになります。指標はこのようになります。
すべてのテクニカル指標は、角度値で動作するように変換することができます。これらの微調整によって、テクニカル分析の新しい方法を発見することができます。
結論
この記事を書くにあたり、以下のプログラムを使用しました。
| 名前 | 種類 | 詳細 |
|---|---|---|
| Angle Two Pairs | 指標 |
|
| LS vs Robust | スクリプト | LSMとTheil-Sen推定量を比較 |
| Theil–Sen estimator | 指標 |
|
| Angle CCI | 指標 |
|
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/14326
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 効率的な最適化のバックボーンとしての母集団アルゴリズムの基本クラス
効率的な最適化のバックボーンとしての母集団アルゴリズムの基本クラス
 MetaTraderのMultibot(第2回):動的テンプレートの改良
MetaTraderのMultibot(第2回):動的テンプレートの改良
 ニューラルネットワークが簡単に(第78回):Transformerを用いたデコーダなしの物体検出器(DFFT)
ニューラルネットワークが簡単に(第78回):Transformerを用いたデコーダなしの物体検出器(DFFT)
 多通貨エキスパートアドバイザーの開発(第4回):仮想注文の保留と状況の保存
多通貨エキスパートアドバイザーの開発(第4回):仮想注文の保留と状況の保存
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
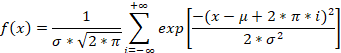
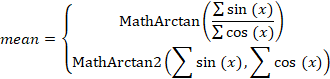
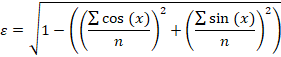
ガンのアングルは私の目を潤ませた)。
まず第一に、私はこのコーナーを描いていない。
縦軸をさらに続ければ簡単に解決する。
次に、標準偏差を縦軸の単位とし、中央値を軸とする。結果はこのようになる。
正方形の代わりに長方形になります。そして、角はブラウン的な値動きの境界を(おおよそ)示している。
なるほど。
興味深いアプローチ
正方形の代わりに長方形になる。そして、角は(おおよそ)ブラウン的な値動きの境界を示して いる。
ブラウン運動とその境界のいくつかは何かであるが、長方形ではない:-))。これは「歯が浮く」ような数学だ。掛け算表のように。
季節変動(日-週-月-四半期)から、ひし形にかなり近い図形が得られる。そしてそれは、神秘的な正方形や表をひねることなく、ガーナの角度や格子を「解読」することになる。あなたは統計的に
あなたのスクリーンショットと同様の原理で取引するロボットを統計的に推論することができる:
価格から角度を得るもう一つの方法。ガン爺さんに感謝。
価格から角度を得るもう一つの方法。ガン爺さんに感謝。
奇妙な角度値
価格から角度を得るもう一つの方法。ガン爺さんに感謝。
ボックス(テンプレート)は、価格と時間レベル(カットオフ)の両方が一度に得られるので、はるかに便利です。そして、1日以内に過去の動きを四則演算するのが最も正確で、計算の誤差が最小になる。