Rede neural na prática: Pseudo Inversa (II)

Introdução

Olá pessoal, e sejam bem-vindos a mais um artigo sobre Rede Neural. 

No artigo anterior Rede neural na prática: Pseudo Inversa (I), mostrei como poderíamos usar uma chamada presente na biblioteca do MQL5, a fim de conseguir computar a pseudo inversa. Porém, o método presente na biblioteca do MQL5. Assim como presente em diversas linguagens de programação, visam computar a pseudo inversa, quando estamos usando matrizes. Ou no mínimo um tipo de estrutura que possa de alguma forma se assemelhar a uma matriz.

Pois bem, mesmo que naquele artigo tenha sido mostrado, como seria feita a multiplicação de duas matrizes. E até mesmo a fatoração a fim de conseguir obter o determinante de qualquer matriz. Que é importante para que saibamos se uma matriz pode ou não ser invertida. Ainda faltou implementar uma outra fatoração. Isto para que você, meu caro leitor, consiga compreender como a fatoração a fim de conseguir os valores da pseudo inversa são feitos. Tal fatoração é conseguir gerar a inversa de uma matriz.

Talvez você esteja pensando: Mas e quanto a transposta? Bem, no artigo anterior mostrei como você poderia fazer a fatoração, de forma a simular a multiplicação de uma matriz por sua transposta. Não sendo de fato um problema fazer tal operação.

No entanto, este cálculo que nos falta implementar, que é justamente obter a matriz inversa. Não é algo que de fato quero mostrar. Não que seja complicado de implementar. Mas sim por que não vejo necessidade de mostrar ele. Isto por conta do fato, de que estes artigos visam terem como objetivo serem didáticos. E não para mostrar como implementar esta ou aquela funcionalidade. Pensando nisto, pensei em fazer algo um pouco diferente neste artigo. Em vez de mostrar como implementar a fatoração para conseguir a inversa de uma matriz. Vamos focar em como fatorar a pseudo inversa, com os dados que estamos usando desde os primórdios. Ou seja, não faz sentido, montar e mostrar como fatorar algo de forma genérica. Se podemos fazer a mesma coisa de forma especializada. E melhor, será algo que você, meu caro leitor, conseguirá entender muito mais do por que da coisas funcionarem. Do que se fosse feita toda uma lógica para se criar uma fatoração genérica. Como foi mostrado no artigo anterior. Onde aquelas funções são genérica. Mas podemos tornar o cálculo muito mais rápido se fizemos as coisas de forma específica. Então para entender melhor este conceito, vamos a um novo tópico.

Por que generalizar, se podemos especializar os procedimentos

O título que está sendo usado neste tópico, é no mínimo controverso, ou em muitos casos, algo que muitos não entendem. Geralmente, muitos dos programadores gostam mesmo é de criar as coisas de forma que elas sejam bastante genéricas. Ou no mínimo pensam que ao fazer algo que seja genérico, terão em suas mãos algo bem mais útil, e que será rápido na maior parte das vezes. Mas em geral, na maior parte das vezes, procuram criar algo que conseguirá funcionar em qualquer tipo de cenário. Bem, a questão da generalização, em alguns casos, nos gera um custo, que não precisamos pagar. Isto por que, se o objetivo a ser alcançado pode ser conseguido, por meio de algo que seja feito em um procedimento especializado. Por que generalizar? Neste caso, a generalização, não nos promove nenhum beneficio que justifique a sua existência.

Se você pensa que estou falando um monte de besteiras. Vamos pensar um pouco e você irá entender a dimensão do que estou querendo explicar. Para entender melhor, quero que pense e responda a seguinte questão:

Oque é um computador? Por que ele tem tantos componentes e tantas coisas nele? Por que de tempos em tempos, aparece um novo hardware em substituição a um software?

Bem, se você tem menos de 40 anos, ou nasceu depois dos anos de 1990, e não procurou estudar tecnologias antigas. Talvez o que eu vá lhe dizer, possa parecer um verdadeiro absurdo. Mas em meados dos anos 70 até perto da primeira metade dos anos 80. Computadores não eram como são hoje. Para que você tenha uma noção. Jogos eletrônicos, eram inteiramente programados em hardware. Usando transistores, resistores, capacitores e por ai vai. Não existiam jogos que usavam software. Era tudo na base do hardware. Agora pense na dificuldade de fazer um jogo, mesmo do tipo PONG, usando somente componentes eletrônicos. As pessoas de fato eram muito boas no que faziam. Não era para qualquer um.

Porém, justamente por conta que tudo tinha que ser feito com componentes discretos, como são conhecidos os transistores, resistores e capacitores no meio eletrônico. As coisas eram feitas de forma muito mais lenta e tinham que ser simples. Mas quando surgiu os primeiros kits para montar, fosse um Z80 ou mesmo um 6502. A coisa começou a mudar. Pois tais processadores, que ainda podem ser conseguidos atualmente, ajudaram muito que o software tomasse força. Era muito mais simples e rápido, programar um cálculo via software. Do que fazer o mesmo cálculo via hardware. Com isto começou a era do software. Mas do que isto teria haver com o tema de redes neurais e com o que estamos implementando? Calma, meu caro leitor, já vamos chegar lá.

O simples fato, de podermos programar, algo relativamente complexo, via instruções simples. Tornou o computador algo realmente interessante de ser usado. Muitas coisas primeiro são desenvolvidas em termos de software. Sendo bastante genéricas. O fato de que isto possa acontecer, torna o desenvolvimento de novas soluções algo tão rápido que muitas vezes é difícil de acompanhar. Tanto que muito do que vemos sendo colocados em GPUs (placas de vídeo) primeiro nascem em software. E são refinados ao extremo, até que fique simples o suficiente para que possa ser pensado uma hipótese de colocar a coisa em hardware. E é neste ponto em que mora a questão que é tema deste tópico. Podemos generalizar as coisas. Mas fazer isto as torna lentas, não de serem implementadas. Mas de serem executadas. Já que precisamos sempre ficar testando para ver se não está sendo gerados erros estranhos, durante a execução das fatorações. Porém, se colocarmos a coisa de forma especializada, podemos testar elas com menos frequência. Assim conseguimos tentar fazer com que elas sejam executadas de forma mais rápida.

Bem, mas por que desta preocupação, se estamos lidando com quatro valores no banco de dados? Esta é a questão meu caro leitor. Primeiro criamos um sistema que consiga trabalhar, com poucos dados e depois escalamos para uma quantidade cada vez maior. Chega um momento, em que temos um tempo de execução que começa a deixar de compensar. Neste momento, surge a necessidade de um hardware especializado para efetuar aquele mesmo tipo de cálculo, que antes era feito via software. Assim surge as novas tecnologias em temos de hardware.

Se você tem acompanhado o desenvolvimento de hardware, deve ter notado que ele tende a se dirigir para algumas tecnologias. Mas por que? O motivo é justamente este. A solução via software passa a ser mais cara que a mesma solução via hardware. Então antes que você decida comprar uma nova GPU, apenas por conta que ela é anunciada com alguma coisa que acelere os cálculos para redes neurais. Você, meu caro leitor e entusiasta, deve saber como explorar da melhor forma possível o hardware, que você já tem. E para fazer isto, precisamos de um cálculo que não seja do tipo genérico. Mas sim um cálculo que seja especializado em fazer algo. E no nosso caso atual, queremos promover o cálculo da pseudo inversa. Por isto, ficou decidido que em vez de criar um artigo com um cálculo genérico para conseguir mostrar como fatorar a pseudo inversa. Faremos a implementação de um cálculo um pouco mais especializado. Sem bem, que ele não estará otimizado. Visto que o objetivo é ser didático e não eficiente em termos de poder de computação. E quando digo isto, estou me referindo a forma como as coisas serão feitas. Ou seja, não pretendo a procurar um ponto de poder computacional, em que se torne necessário a implementação da fatoração em uma modelagem vai hardware especializado. Que é justamente o que acontece, quando uma nova tecnologia de hardware surge.

Muito tem se falando em placas de vídeo, ou mesmo processadores, com capacidades de cálculo, para redes neurais. Mas você, meu caro leitor, sabe se este tipo de abordagem, é ou não o que você precisa de fato? Bem, para saber responder isto, você precisa saber o que está acontecendo em termos de software. Então vamos ao próximo tópico, onde vermos o que estará sendo implementado em termos de software.

Pseudo inversa, uma proposta para abordagem

Muito bem, acredito que você, meu caro leitor, tenha conseguido entender o tópico anterior. Então vamos pensar o seguinte: No nosso banco de dados. Cada informação pode ser visualizada em um gráfico de duas coordenadas. Sendo um X e um Y usados para tentarmos criar algum tipo de relação matemática entre as informações. Ok, isto tem sido explorado deste o começo desta pequena sequência. O fato de podermos usar uma regressão linear, ajuda bastante no que precisaremos implementar em temos de código. Já mostrei em artigos anteriores, como fazer o cálculo escalar a fim de conseguir encontrar o coeficiente angular e o ponto de intersecção. Isto nos permitindo criar a equação mostrada abaixo.

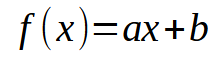
Nesta os pontos procurados são os valores de < a > e < b >. Porém existe uma outra forma, além da já mostrada. Esta envolve fatorações de matrizes. Basicamente o que precisaremos implementar é uma pseudo inversa. O cálculo para fazer isto é visto logo abaixo.

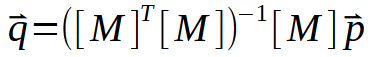
Aqui, os valores para as constantes < a > e < b > estão no vetor < q >. Assim a matriz M deverá sofrer uma pequena sequência de fatorações até que se consiga gerar o vetor < q >. Mas a parte interessante não é vista nesta imagem acima, e sim na imagem abaixo.

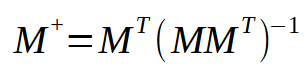
Esta imagem é justamente o que precisamos implementar. Já que ela é a representação do que acontece na pseudo inversa. Veja que o resultado é uma matriz, que recebe um nome especial de pseudo inversa. Está como você pode ver na imagem anterior é multiplicada por um vetor < p > dando origem assim ao vetor < q >. E este vetor < q > é o resultado que queremos encontrar.

No artigo anterior e no começo deste, falei que a função pseudo inversa, é implementada em bibliotecas de forma a usar matrizes para isto. Mas aqui, não estamos usando matrizes. Estamos usando um similar a elas, que são os arrays. Ok, neste ponto temos um problema, cuja solução é: Transformarmos o array em uma matriz, ou implementar a pseudo inversa para usar arrays. Devido ao fato de querer mostrar como o cálculo é implementado. Vamos para a segunda abordagem. Ou seja, implementar a pseudo inversa. O cálculo para isto é visto no fragmento logo abaixo.

01. //+------------------------------------------------------------------+
02. matrix __PInv(const double &A[])
03. {
04.     double M[], T[4], Det;
05. 
06.     ArrayResize(M, A.Size() * 2);
07.     M[0] = M[1] = 0;
08.     M[3] = (double)A.Size();
09.     for (uint c = 0; c < M[3]; c++)
10.     {
11.         M[0] += (A[c] * A[c]);
12.         M[2] = (M[1] += A[c]);
13.     }
14.     Det = (M[0] * M[3]) - (M[1] * M[2]);
15.     T[0] = M[3] / Det;
16.     T[1] = T[2] = -(M[1] / Det);
17.     T[3] = M[0] / Det;
18.     ZeroMemory(M);
19.     for (uint c = 0; c < A.Size(); c++)
20.     {
21.         M[(c * 2) + 0] = (A[c] * T[0]) + T[1];
22.         M[(c * 2) + 1] = (A[c] * T[2]) + T[3];
23.     }
24. 
25.     matrix Ret;
26.     Ret.Init(A.Size(), 2);
27.     for (uint c = 0; c < A.Size(); c++)
28.     {
29.         Ret[c][0] = M[(c * 2) + 0];
30.         Ret[c][1] = M[(c * 2) + 1];
31.     }
32. 
33.     return Ret;
34. }
35. //+------------------------------------------------------------------+

Este fragmento, mostrado acima, faz tudo o trabalho para nos. Parece algo bizarramente complicado. Mas não tem nada de complicado. Na verdade ele é bem simples e direto. Aqui recebemos um vetor em formato de array, com diversos valores do tipo double. Poderíamos usar outro tipo. Mas é bom que você meu caro leitor, comece a se acostumar em usar valores double de agora em diante. O motivo será entendido em breve. Depois que todas as fatorações forem executadas, iremos ter como retorno uma matriz de valores do tipo double.

Agora preste atenção: O array que estamos aplicando é do tipo singelo. Mas mesmo assim ele será tratado como se fosse uma matriz com duas colunas. Mas como isto é possível? Bem, vamos entender isto, antes de vermos como usar este código.

Na linha seis, criamos uma matriz que terá tantas linhas quanto for o número de elementos no array. Mas esta matriz terá duas colunas. Diferente do array que terá internamente apenas uma coluna. Agora nas linhas sete e oito, iniciamos a matriz M, de uma forma bem específica. Para entender veja a imagem abaixo.

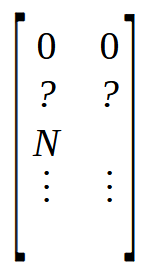
Observe que as duas primeiras posições estão como zero. Seguida de duas outras posições com sinal de interrogação. Já que não sabemos o real valor que está ali. Mas logo depois temos uma posição com o valor N. Este valor é o tamanho do array. Mas por que estou colocando o tamanho do array na matriz? O motivo é simples. É mais rápido para procurar o valor em uma posição conhecida, do que procurar o mesmo valor em uma função. E como precisamos de quatro posições livres no começo da matriz, coloco o tamanho do array na posição indicada como N. Isto é que está sendo feito nas linhas sete e oito.

Muito bem, olhando na imagem antes do fragmento, vemos que a primeira coisa a ser feita é multiplicar uma matriz por sua transposta. Mas aqui não temos nenhuma matriz ainda. Tudo que temos é um vetor, ou melhor dizendo um array. Então como faremos a tal multiplicação? Simples, para isto usaremos o laço presente na linha nove. Mas o que é isto? Você ficou doido. Isto não faz sentido nenhum. O que você está tentando fazer? Bem, vamos entender olhando a imagem abaixo.

Um array, nada mais é do que uma coleção de valores, que aqui estão sendo representados de a0 até an. Se você visualizar a coisa não como um array, mas sim como uma matriz poderá ver uma matriz de uma coluna ou uma linha. Dependendo é claro da forma como os dados estiverem sido organizados. Ok, se você efetuar uma operação entre uma matriz de uma coluna por uma outra de uma linha, encontrará um valor escalar, e não uma matriz. Lembre-se de que a fórmula da pseudo inversa, faz primeiro a multiplicação entre uma matriz e sua transposta. Mas podemos subentender este array mostrado acima, como algo visto na imagem abaixo.

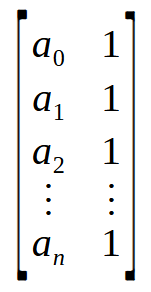
Uau, agora sim, temos a matriz que precisamos. Assim ao multiplicar uma matriz n x 2 por sua transposta, temos uma matriz 2 x 2 como resultado. Ou seja, conseguimos transformar um vetor, ou melhor um array em uma matriz 2 x 2. E é isto que o laço for da linha nove está fazendo. Multiplicando uma matriz por sua transposta, e colocando o resultado no topo da matriz que declaramos na linha seis.

Agora precisamos encontrar a matriz inversa desta que acabamos de construir. Em uma matriz 2 x 2, a forma mais rápida e simples de encontrar a inversa é via determinante. Note o seguinte fato, não precisamos de uma forma genérica para encontrar a matriz inversa ou o determinante. Tal pouco precisamos de uma forma genérica para multiplicar a matriz por sua transposta. Podemos fazer tudo de forma direta, já que resumimos tudo em uma matriz 2 x 2, tornando assim o trabalho muito mais simples e rápido. Desta maneira, para encontrarmos o determinante, usamos a linha 14. Pronto, agora já podemos procurar a matriz inversa. Este cálculo da matriz inversa, que de forma genérica seria muito lento, é feito de forma extremamente rápido, pelo simples fato de termos feito algumas escolhas. Então nas linhas 15 a 17, geramos a inversa na matriz que conseguimos via array. Agora está quase tudo pronto. A próxima coisa a ser feita, e limpar a matriz M, isto é feito na linha 18. Agora preste atenção. A matriz T contém a matriz inversa e o array A contem os valores dos quais queremos fatorar a pseudo inversa. Tudo que falta ser feito, é multiplicar um pelo outro e colocar o resultado na matriz M. O detalhe é que a matriz T é do tipo 2 x 2, e o array pode ser visto como uma matriz n x 2. Assim teremos como resultado uma matriz n x 2, que contém justamente os valores da pseudo inversa.

Esta fatoração é feita no laço da linha 19. Já na linha 21 e 22, colocamos os valores dentro da matriz M. E ai está o resultado da pseudo inversa. Este cálculo que estou mostrando pode ser portado para dentro de um bloco em OpenCL, usando assim as capacidades da GPU para calcular a regressão linear de um banco de dados bem grande. Em alguns casos usar a CPU faria com que os cálculos demorassem alguns minutos, mas jogando todo o trabalho para a GPU, seria muito mais rápido de ser feito. Está é a tal otimização da qual mencionei no começo deste artigo.

Tudo que nos resta fazer é colocar o resultado do array M para dentro de uma matriz. Isto é feito entre as linhas 25 e 31. Mas o que se encontra dentro de M já é resultado desejado. No anexo, vou deixar um código para que você veja como as coisas funcionam. Assim poderá comparar com o que é mostrado no código do artigo anterior. Só que nem tudo é perfeito. Note que não estou fazendo nenhum teste dentro desta função. Isto por que, mesmo ela sendo didática. A ideia aqui é que ela se pareça com algo que pode ser implementado em termos de hardware. E neste caso os testes seriam feitos de outra maneira, nos poupando assim tempo de processamento.

Muito bem, mas isto não responde a uma pergunta: Como esta PInv pode conseguir gerar de forma muito rápida a regressão linear? Bem, para responder isto, vamos ver um novo tópico.

Velocidade máxima

No tópico anterior, vimos como com base em um array, poderíamos gerar o cálculo da pseudo inversa. Mas podemos acelerar ainda mais as coisas. De forma que não teremos como retorno o valor da pseudo inversa, e sim o da regressão linear. E para fazer isto, precisaremos mudar um pouco. Na verdade só um pouco o código visto no tópico anterior. Mas esta mudança já será suficiente para que possamos usar a velocidade total da GPU, ou mesmo de uma CPU dedicada, para procurar os fatores da equação linear. Lembrando que os fatores procurados são, o coeficiente angular e o ponto de intersecção. O novo fragmento pode ser visto logo abaixo.

01. //+------------------------------------------------------------------+
02. void Straight_Function(const double &Infos[], double &Ret[])
03. {
04.     double M[], T[4], Det;
05.     uint n = (uint)(Infos.Size() / 2);
06. 
07.     if (!ArrayIsDynamic(Ret))
08.     {
09.         Print("Response array must be of the dynamic type...");
10.         Det = (1 / MathAbs(0));
11.     }
12.     ArrayResize(M, Infos.Size());
13.     M[0] = M[1] = 0;
14.     M[3] = (double)(n);
15.     for (uint c = 0; c < n; c++)
16.     {
17.         M[0] += (Infos[c * 2] * Infos[c * 2]);
18.         M[2] = (M[1] += Infos[c * 2]);
19.     }
20.     Det = (M[0] * M[3]) - (M[1] * M[2]);
21.     T[0] = M[3] / Det;
22.     T[1] = T[2] = -(M[1] / Det);
23.     T[3] = M[0] / Det;
24.     ZeroMemory(M);
25.     for (uint c = 0; c < n; c++)
26.     {
27.         M[(c * 2) + 0] = (Infos[c * 2] * T[0]) + T[1];
28.         M[(c * 2) + 1] = (Infos[c * 2] * T[2]) + T[3];
29.     }
30.     ArrayResize(Ret, 2);
31.     ZeroMemory(Ret);
32.     for (uint c = 0; c < n; c++)
33.     {
34.         Ret[0] += (Infos[(c * 2) + 1] * M[(c * 2) + 0]);
35.         Ret[1] += (Infos[(c * 2) + 1] * M[(c * 2) + 1]);
36.     }
37. }
38. //+------------------------------------------------------------------+

Observe que neste fragmento de código acima, já temos um teste sendo feito. Este visa verificar se o array de retorno é do tipo dinâmico. Caso não seja, a aplicação deverá ser encerrada. E este encerramento se dá na linha 10. No artigo anterior, expliquei o que esta linha significa, na dúvida, leia o mesmo para mais detalhes. Fora isto, quase todo o código continua funcionando da mesma maneira que foi visto no tópico anterior. Isto até a linha 30, onde as coisas começa a ir em outra direção. Mas vamos voltar um pouco as coisas. Ao olhar este código, você pode estar estranhando o que está acontecendo aqui, já que a multiplicação da transposta com a matriz, ou melhor dizendo array as coisas estão um tanto quanto diferentes. Assim como também a multiplicação da matriz inversa com a matriz original a fim de conseguir calcular a pseudo inversa.

Mas o que significa esta coisa que estamos vendo neste fragmento? Bem, isto que parece ser algo extremamente complicado, nada mais é do que uma matriz de pontos. Para entender, veja a imagem abaixo.

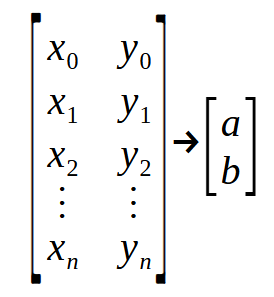
Observe que temos uma "matriz" entrando e uma "matriz" saindo. Na declaração na linha dois, o parâmetro Infos, é a primeira matriz vista na imagem acima, e Ret é a segunda matriz da imagem. Os valores < a > e  < b >, são os que estamos procurando para criar a equação da reta. Agora preste bastante atenção. Como cada uma das linhas da matriz da esquerda representa um ponto no gráfico. Os valores pares são onde estão os valores usados na função vista no tópico anterior. Já os valores nas posições ímpares, são os que representam os vetores na fórmula vista no começo deste artigo. Ou seja, o vetor < p >.

Como esta função vista no começo deste tópico, recebe todos os pontos no gráfico e retorna a equação da regressão linear. Precisamos de alguma forma separar as coisas. E a forma de fazer isto é ligando tudo entre valores pares e ímpares. Por isto, parece tão diferente este código do código visto no tópico anterior. Mas eles não são diferentes isto até que a linha 30 seja alcançada. Neste ponto, temos algo que não fazemos no código anterior. Aqui pegamos o resultado da pseudo inversa, que se encontra na matriz M, e multiplicamos pelos vetores que estão na parte ímpar do parâmetro Infos. Resultando assim no vetor Ret, que nada mais é do que as constantes necessárias para se criar a equação de reta, ou regressão linear, como queira.

Se você fizer a mesma coisa, usando os valores que serão retornados pela função PInv vista no artigo anterior. Terá o mesmo resultado visto neste fragmento mostrado acima. Com uma única diferença, que é justamente o fato de que o código mostrado neste fragmento, pode vir a ser o que será usado para se construir um hardware dedicado para cálculos em redes neurais. Fazendo assim, surgir uma nova tecnologia para ser colocado em processadores. Onde a indústria pode dizer que um dado processador ou circuito contem mecanismos de inteligência artificial ou rede neural. Mas não é nada demais, ou algo que possa ser de grande novidade. Apenas construirão em hardware, algo que era feito em software. Tornando assim o genérico em algo especializado.

Considerações finais

Muito bem, meus caros leitores e entusiastas. Com tudo que foi visto até este momento, considero finalizado o assunto sobre tudo que se precisa saber sobre redes neurais e inteligência artificial. Apesar de que, até este momento, tudo que foi visto, se refere ao uso, não de uma rede neural, mas sim de usar e construir um único neurônio. Já que temos apenas um único cálculo sendo feito. No caso da rede neural, temos um conjunto destes mesmos cálculos simples sendo feitos, mas em escala um pouco maior. Mesmo que você, neste momento, não consiga entender este fato. Uma rede neural, nada mais é do que implementar uma arquitetura de grafo. Onde cada nó representa um neurônio, ou função de regressão linear. E dependendo dos resultados calculados, teremos uma ou outra direção sendo seguida.

Sei que parece desmotivador, e até mesmo bobo pensar em uma rede neural desta forma. Mas esta é a verdade. Não tem nada de mágico ou fantástico por trás do assunto. Por mais que a mídia, ou pessoas que não entendem ou estudam o assunto queiram passar. Qualquer coisa feita por uma máquina, não passa de simples cálculos matemáticos. Se você entender estes cálculos, conseguirá entender uma rede neural. E digo mais, conseguirá entender como simular comportamentos de seres vivos. Não que seres vivos sejam máquinas orgânicas. Se bem que em alguns casos podemos pensar assim. Mas isto é outra conversa para os mais próximos de mim.

O que desejo para você, meu caro e estimado leitor. É que você entendendo o que seria uma rede neural no seu aspecto mais simples. Ou seja, usando apenas um único neurônio. Que é justamente o que acontece até este momento.

Nos próximos artigos, que ainda não sei como serão. Iremos tratar de organizar este único neurônio em termos de uma pequena rede. Isto para que ele consiga aprender algo. Como não quero mostrar nada relacionado a mercado financeiro usando tais coisas. Não espere ver isto no futuro. Pelo menos não da minha parte. Quero que você entenda, aprenda e consiga saber explicar por sua própria experiência, o que é e como uma rede neural consegue aprender. E para fazer isto, será preciso que você experimente um sistema suficientemente simples.

Então aguarde uma sequência sobre este tema. Vou pensar em algo legal para mostrar a você. Algo que seja realmente interessante de ser mostrado. Nos anexos você tem os códigos para poder começar a estudar como um único neurônio funciona.