
Operaciones angulares para tráders
Introducción
Las operaciones angulares en el trading se utilizan desde hace mucho tiempo. La principal ventaja de estas operaciones es la sencillez del trazado de ángulos y la visibilidad de dichas operaciones. Un buen ejemplo de operaciones angulares son las herramientas de Gunn.
Parece que ya sabemos todo sobre los ángulos, pero hoy intentaremos ver los ángulos desde otro ángulo (disculpen la tautología). Asimismo, trataremos de refrescar viejos conocimientos para conseguir algo completamente nuevo.
Construyendo el primer ángulo
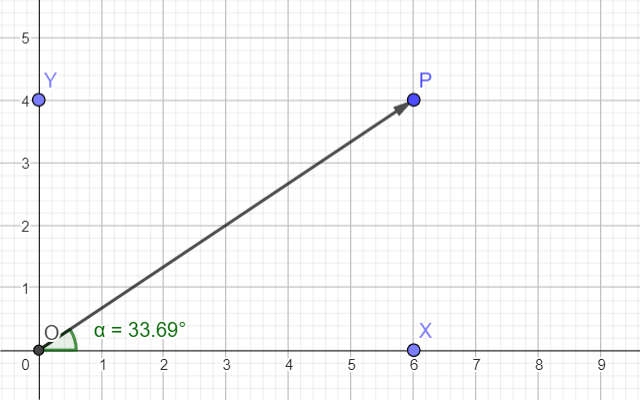
Un ángulo es una de las figuras geométricas más sencillas. Dibujar dos líneas a partir de un punto: ¿qué puede haber más sencillo? Además, una de las líneas suele ser el eje de abscisas.
En este caso, la magnitud del ángulo se puede calcular de forma muy sencilla a través de las coordenadas del punto P.
Como el ángulo es una magnitud adimensional, ambos ejes deberán tener los mismos valores. Si tenemos metros en un eje y kilogramos en el otro, obtendremos alguna relación entre ellos, pero no un ángulo.
Vamos a intentar plasmar una operación angular en forma de indicador. Crearemos un indicador como este: en los ejes X e Y se mostrarán los precios de diferentes pares de divisas. Entonces, un ángulo pequeño se corresponderá con un precio alto para el primer par de divisas y con un precio bajo para el segundo. Por consiguiente, un ángulo grande indicará que el precio del segundo símbolo es superior al precio del primero. Es decir, nuestro futuro indicador determinará la sobrecompra/sobreventa de un par de divisas con respecto al otro. Para el comercio de pares, no es una mala idea.
La primera dificultad a la que nos enfrentamos es que tenemos diferentes valores en diferentes ejes (hemos tomado EURUSD y USDJPY para el ejemplo). Superaremos esta dificultad de forma fácil y sencilla, dividiendo el precio de cada instrumento por el valor del pip.
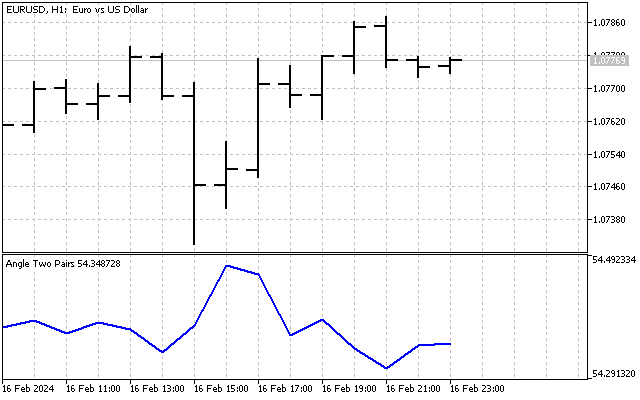
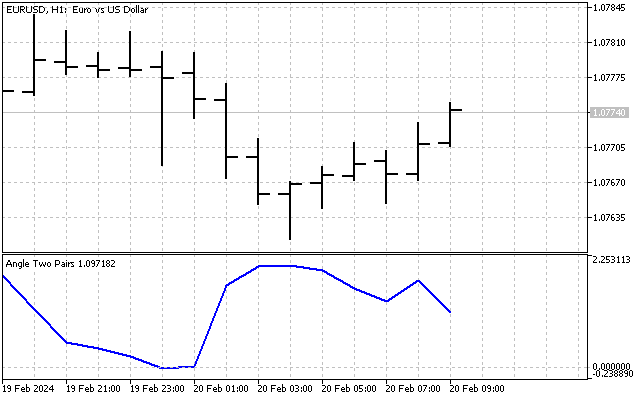
Así resolveremos dos problemas a la vez: tendremos valores comparables en ambos ejes (precio expresado en puntos) y, además, la escala de dichos ejes será la misma. Y este será el aspecto de nuestro indicador.
A primera vista, el indicador parece bastante trivial. Su valor fluctúa en torno a algún valor medio, y la diferencia entre el máximo y el mínimo del indicador es de solo 2-3 grados. Sin embargo, no debemos sacar conclusiones prematuras. Quizá podamos mejorar este indicador y hacerlo más informativo.
Un pequeño recordatorio. La medida angular más común que usamos en la vida ordinaria es el grado. Y para los cálculos matemáticos, la medida más usada es el radián. El paso de la medida en grados a la medida en radianes y viceversa se efectúa con la ayuda de fórmulas:
Es decir, la conversión de grados a radianes y viceversa consiste simplemente en multiplicar por algún factor de escala. No obstante, si necesitamos mostrar la información de forma numérica, los grados serán preferibles. Estará de acuerdo en que 45° queda mejor que 0,78539 rad. Esencialmente es lo mismo, pero el primer valor parece más claro.
Ángulos y distribución normal
Al estudiar procesos del mundo real, los investigadores usan distintas distribuciones de probabilidad de variables aleatorias. La distribución más conocida es la distribución normal.
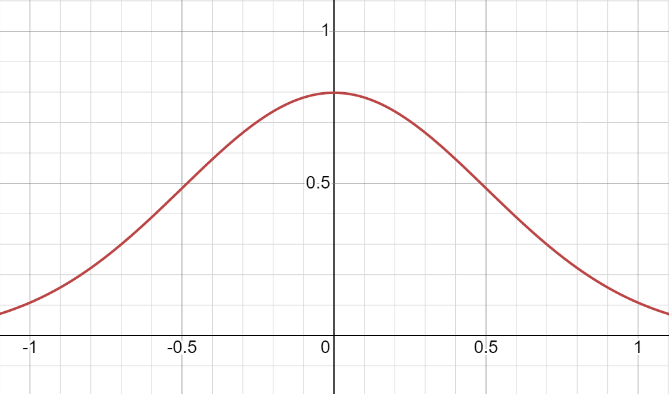
Recordemos algunas propiedades de la distribución normal. Su gráfico es una línea en forma de campana, mientras que los extremos de esta línea llegan hasta el infinito.
Haremos esta operación mentalmente. Vamos a empezar a reducir lentamente el eje X en una circunferencia. Al hacerlo, seguiremos esta regla: cuanto más nos alejemos del centro, más fuerte será la curvatura. Si tenemos paciencia, el eje X se convertirá en una circunferencia. La propia línea de distribución normal se distorsionará, y como resultado tendremos una distribución normal envuelta.
La primera diferencia entre la distribución normal y la distribución envuelta será que -∞ se asignará a -180° y +∞ a +180°. Pero eso no era lo que pretendíamos. El objetivo principal de la distribución normal envuelta consiste en manejar magnitudes angulares. La fórmula de la distribución normal envuelta es la siguiente:
Como vemos, la distribución envuelta utiliza tanto la media como la desviación típica. Es como una distribución normal. Resumir resulta un poco intimidante, pero cuando trabajamos con datos reales podemos manejar fácilmente estos infinitos.
Ahora tomaremos nuestro indicador y le aplicaremos una distribución normal envuelta.
Primero tendremos que determinar la media de todos los ángulos encontrados en la historia. En nuestro caso, no será muy difícil hallar la media: consistirá en la suma habitual y la división por el número de observaciones. Pero, en general, la media angular deberá buscarse de forma un poco diferente. Imagina que necesita hallar la media de dos ángulos, de 10° y 350°. El enfoque convencional dará una respuesta de 180°. Y esa respuesta será errónea. La respuesta correcta: su media es cero.
Para obtener la respuesta correcta en cualquier situación deberemos hacer lo siguiente: primero tendremos que encontrar las sumas de los senos y cosenos de todos los ángulos. Dividiendo la primera suma por la segunda, obtendremos la tangente del ángulo medio.
Ahora, encontrar el valor del ángulo medio no resultará difícil. No obstante, aquí hay una pequeña condición. Si todos los ángulos se encuentran entre -90° y +90°, podremos utilizar la función MathArctan. Si los ángulos sobrepasan estos límites, deberemos utilizar una función más universal, MathArctan2.
Así, el ángulo medio será igual a:
Una vez estimado el valor del ángulo medio, podremos proceder a estimar la desviación típica. Para ello podemos usar el método de Yamartino. Primero tendremos que encontrar la magnitud auxiliar:
Esta ya ofrece una estimación bastante precisa de la desviación típica, pero también puede mejorarse:
Ahora, haremos algunos cambios en nuestro indicador. Calcularemos sus lecturas de la siguiente manera: primero hallaremos la diferencia entre los ángulos actual y medio, y después compararemos dicha diferencia con la desviación típica. Como resultado, tendremos una imagen como esta.
Este indicador permite determinar con mayor precisión los niveles de sobrecompra/sobreventa, y su análogo más cercano será el indicador CCI.
Ángulos y función lineal
Ya nos hemos aclarado con los ángulos para los datos uniformes. ¿Se pueden aplicar operaciones angulares a una tendencia? La respuesta es que no, porque estamos tratando con diferentes tipos de datos: tenemos el tiempo en un eje y el precio en el otro.
Bueno, la respuesta es correcta, pero equivocada. Vamos a recordar la función lineal. Esta describe una relación lineal entre dos variables independientes y viene dada por una ecuación:
Podríamos preguntarnos: ¿y dónde está aquí el ángulo? Pues el ángulo se oculta en el coeficiente k. Este coeficiente es igual a la tangente del ángulo de inclinación de la recta con respecto al eje X.
Vamos a intentar aplicar esta función para describir una tendencia. La ecuación de la función lineal para los tráders tendrá este aspecto:
En este caso, el coeficiente k tendrá otra interpretación: mostrará la variación media del precio por unidad de tiempo. Una pequeña nota más: hemos puesto el tiempo en la fórmula, es lo más académico y correcto, pero, en los cálculos reales, resulta mucho más fácil utilizar índices en lugar de tiempo. En primer lugar, los días festivos y los fines de semana afectarán en gran medida a la exactitud de los cálculos, y en segundo lugar, el uso de índices simplificará mucho las fórmulas (y los cálculos). El único requisito para estos índices será que deben aumentar de izquierda a derecha.
Veamos ahora cómo estimar los parámetros de una tendencia lineal. En primer lugar, podemos utilizar el método de los mínimos cuadrados (LSM). Recordemos que, en lugar de tiempo, usaremos índices cuyos valores varían de 0 a n-1.
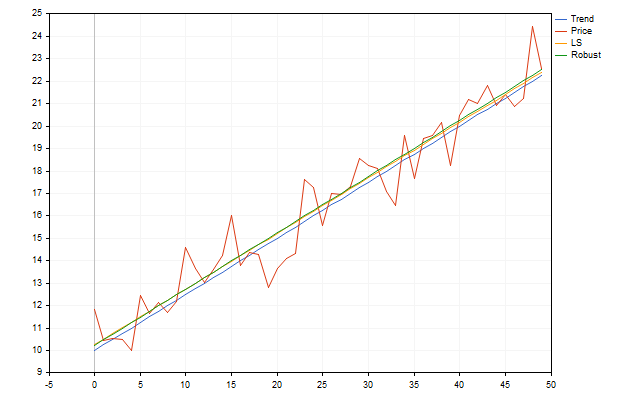
Pero existen formas más fiables de estimar estos parámetros. Por ejemplo, podemos usar la estimación de Theil-Sen. Veamos cómo puede funcionar dicha estimación en el mundo real. Tomaremos una tendencia con los parámetros k=0.25 y b=10. Luego le añadiremos algo de ruido, en forma de valores atípicos distribuidos aleatoriamente. A partir de los puntos resultantes, trataremos de hallar los parámetros de la tendencia inicial. El resultado será una imagen como ésta.
A primera vista, parece que el método robusto no ofrece muchas ventajas. Sin embargo, esto se debe únicamente a que los errores de nuestro modelo de tendencia se han distribuido de forma equitativa y normal. Los precios reales pueden no cumplir este criterio. Entonces el método Theil-Sen funcionará mucho mejor, además de que podrá dar un poco más de información. Es la estimación robusta que utilizaremos en lo sucesivo.
Así pues, veamos cómo podemos estimar los parámetros de una tendencia lineal usando el método de Theil-Sen. Primero deberemos encontrar el parámetro k. Será igual a la mediana de todas las diferencias posibles del tipo:
El valor de la mediana se puede hallar de la siguiente forma. En primer lugar, escribiremos todos los valores en un array. Luego lo clasificaremos. La mediana será igual al valor que se encuentra en el centro del array.
Ahora podremos proceder a la estimación del parámetro b. Para ello, deberemos hallar la mediana de todos los valores posibles:
Una vez superada la teoría, es hora de pasar a la práctica. Veamos las posibilidades que nos ofrece la estimación de Theil-Sen.
Estimación e indicadores de Theil-Sen
Tras estimar los parámetros de tendencia, nos han quedado dos arrays de datos. Veamos si podemos usarlos de alguna otra forma.
Así pues, hemos estimado los parámetros de la tendencia e incluso hemos trazado su línea. Ahora podremos construir un canal dentro del cual se producirá el movimiento del precio. Para ello, primero tendremos que evaluar cuánto se desvían los precios respecto a la línea de tendencia.
Así, tomaremos el array con el que hemos estimado el valor del parámetro b. Para estimar la desviación necesitaremos encontrar la mediana de la desviación absoluta. Es decir, primero, para cada elemento del array hallaremos el valor absoluto de la diferencia con el parámetro b. Después nos quedará hallar la mediana de los valores obtenidos. Esta mediana ofrecerá una estimación sólida de la desviación típica.
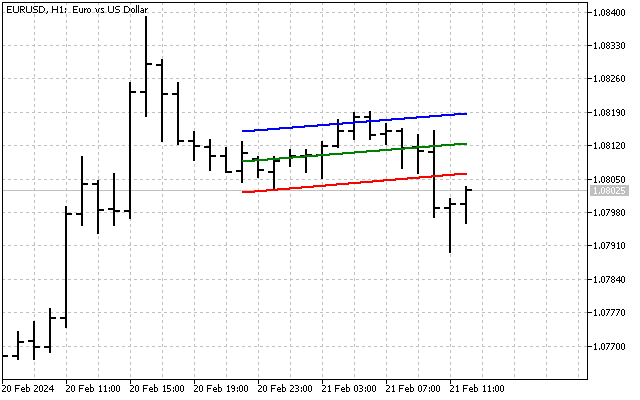
Y conociendo la desviación típica, podremos construir un canal de tendencia. Por ejemplo, este será el aspecto de un canal con una anchura de 6 desviaciones estándar.
En esencia, este indicador será similar a las Bandas de Bollinger. Además, las líneas del canal de tendencia pueden usarse como líneas de apoyo y resistencia.
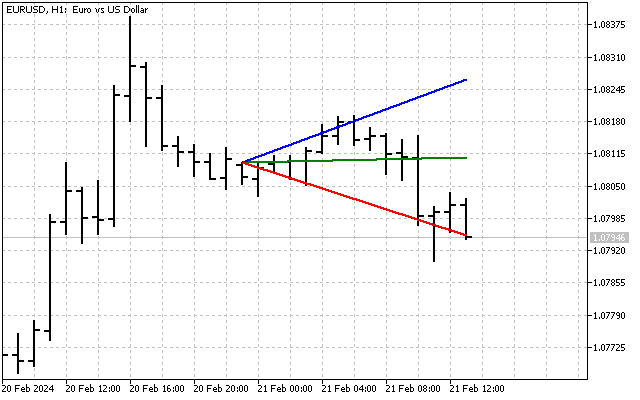
Asimismo, podremos construir un abanico de líneas de tendencia. Todos los cálculos se realizarán de la misma manera que al construir un canal. La única diferencia es que deberemos tomar el parámetro k y el array correspondiente. Este será el aspecto de un abanico con una desviación de 1 ángulo.
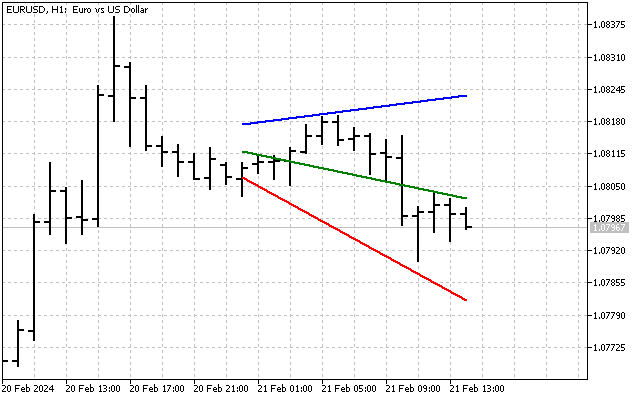
Bueno, y por supuesto, podremos combinar el canal y el abanico. Para ello, primero construimos las líneas del canal. Y luego aplicaremos el abanico a esas líneas. El resultado será una imagen como ésta.
Así, la aplicación de métodos robustos nos ha permitido obtener una línea de tendencia y tres indicadores adicionales que pueden utilizarse en el análisis técnico.
Algunas palabras más
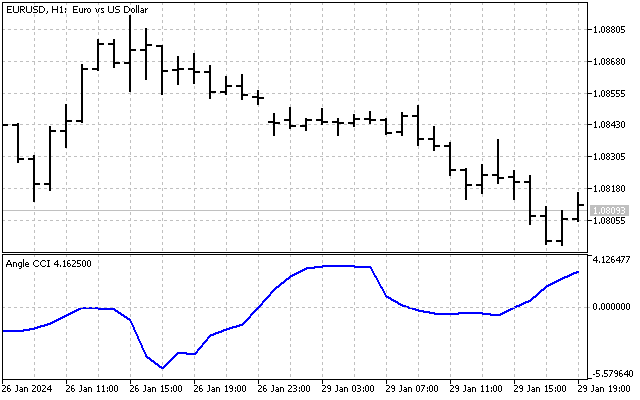
Las operaciones angulares pueden utilizarse no solo para trazar tendencias y ángulos. Tomemos el indicador CCI ya mencionado en el artículo. ¿Qué pasará si hacemos un indicador similar, pero utilizando como datos de entrada ángulos de tendencia, en lugar de precios?
Entonces podremos evaluar los cambios de tendencia a partir de la historia. Y así es como se verá nuestro indicador.
Todos los indicadores técnicos pueden rehacerse para trabajar con valores angulares. Con estos rediseños, podremos descubrir nuevas formas de análisis técnico.
Conclusión
En la redacción de este artículo hemos utilizado los siguientes programas.
| Nombre | Tipo | Descripción |
|---|---|---|
| Angle Two Pairs | Indicador |
|
| LS vs Robust | Script | Compara los resultados de la estimación ISC y Theil-Sen |
| Theil–Sen estimator | Indicador |
|
| Angle CCI | Indicador |
|
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/14326
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Operar con noticias de manera sencilla (Parte 1): Creando una base de datos
Operar con noticias de manera sencilla (Parte 1): Creando una base de datos
 Aprendizaje automático y Data Science (Parte 20): Elección entre LDA y PCA en tareas de trading algorítmico en MQL5
Aprendizaje automático y Data Science (Parte 20): Elección entre LDA y PCA en tareas de trading algorítmico en MQL5
 Desarrollo de asesores expertos autooptimizables en MQL5
Desarrollo de asesores expertos autooptimizables en MQL5
 Introducción a MQL5 (Parte 6): Guía para principiantes sobre las funciones de matriz en MQL5 (II)
Introducción a MQL5 (Parte 6): Guía para principiantes sobre las funciones de matriz en MQL5 (II)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
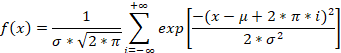
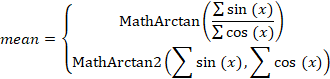
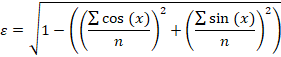
Los ángulos de Gunn me hicieron llorar).
En primer lugar, no estoy dibujando estos ángulos.
Se resolverán fácilmente si el eje vertical se continúa más allá.
En segundo lugar, utilizaré la desviación típica como unidad vertical y el precio medio como eje. El resultado es algo como esto.
En lugar de un cuadrado, tenemos un rectángulo. Y las esquinas muestran (aproximadamente) los límites del movimiento browniano de los precios.
Bueno.
enfoque interesante
En lugar de un cuadrado, obtenemos un rectángulo. Y las esquinas muestran (aproximadamente) los límites del movimiento browniano de los precios.
????? cuando el movimiento browniano y algunos de sus límites son algo, pero no un rectángulo :-)) Este es el tipo de matemáticas que deberían "volar de los dientes". Como la tabla de multiplicar.
A partir de la volatilidad estacional (día-semana-mes-trimestre) se obtiene una cifra bastante cercana a un rombo. Y resultará ser un "desciframiento" de los ángulos y cuadrículas de Ghana sin cuadrados místicos ni retorcimiento de la tabla. Se puede deducir estadísticamente
un robot de comercio en el principio similar a su captura de pantalla:
Otra forma de sacar ángulos del precio. Gracias al abuelo Gunn.
Otra forma de sacar ángulos del precio. Gracias al abuelo Gunn.
extraño valor de ángulo
Otra forma de sacar ángulos del precio. Gracias al abuelo Gunn.
El recuadro (plantilla) es mucho más conveniente, porque se obtienen a la vez los niveles de precio y tiempo (cut-offs). Y dentro de un día es más preciso cuadratura el movimiento pasado, se obtiene el menor error en los cálculos.