
交易者基于角度的操作
概述
基于角度的操作在交易中应用已久。这些操作的主要优点是构造角度的简单性和清晰度。江恩工具就是基于角度操作的一个明显示例。
关于角度的一切似乎都已众所周知,不过,我会尝试从不同的角度看问题。让我们试着记住那些被遗忘的旧事物,以便获得全新的东西。
构建第一个角
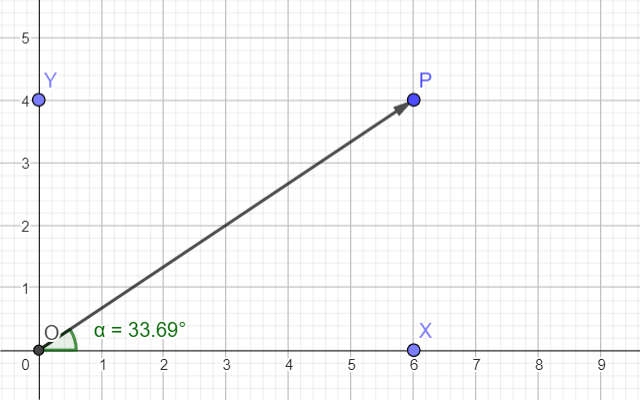
角是最简单的几何图形之一。从一点出发画两条线 - 还有比这更简单的吗?其中一条线最常代表横坐标轴。
在这种情况下,使用 P 点坐标计算角度值。
由于角度是一个无量纲的量,因此两个轴应具有相同的值。如果你沿着一个轴测量米,沿着另一个轴衡量千克,那么你会得到它们之间的某种关系,但不是角度。
让我们尝试将基于角度的操作作为指标来实现。我将制作以下指标:不同的货币对将沿着 X 和 Y 轴显示。那么,小角度将对应于第一个货币对的价格高而第二个货币对的价格低。对应地,大角度表示第二个交易品种的价格高于第一个交易品种。换句话说,我们的未来指标将确定一种货币对相对于另一种货币对的超买/超卖状态。对于配对交易来说,这不失为一个好主意。
我们遇到的第一个困难是在不同的坐标轴上有不同的值(例如,我取的是 EURUSD 和 USDJPY)。我们可以用每个工具的价格除以点值,从而轻松克服这一困难。
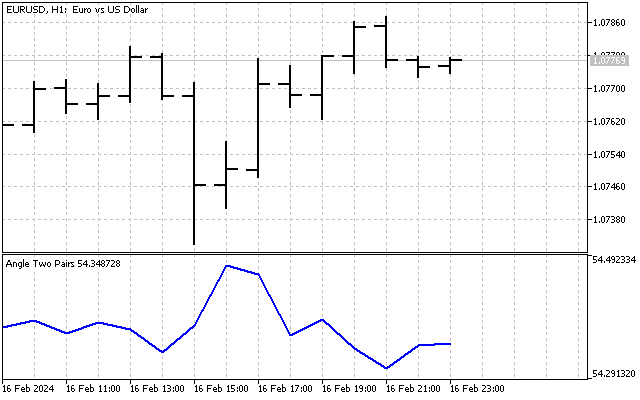
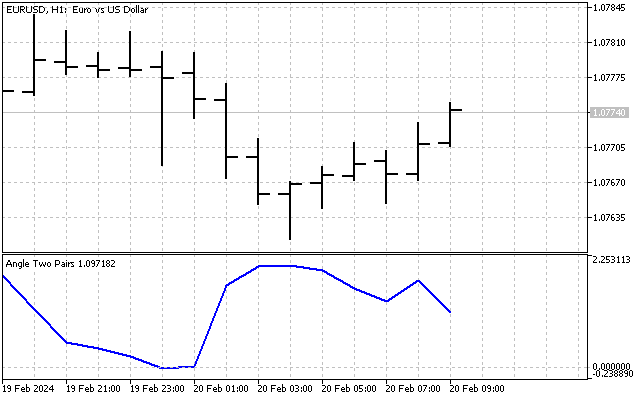
这样,我们就立刻解决了两个问题 - 在两个坐标轴上,我们都可以得到可比的数值(价格以点表示),而且这些坐标轴上的刻度也是相同的。这就是我们的指标。
乍一看,这个指标似乎相当微弱。其值在某个平均值附近波动,指标的最大值和最小值之间的差值仅为2-3度。但我们不要过早下结论。也许我们可以改进这一指标,使其更有信息量。
小小提醒一下,我们在日常生活中最常用的角度度量单位是 "度"。在数学计算中,最常用的是弧度。从度到弧度的转换,以及从弧度到度的转换,都是根据以下公式进行的:
换句话说,将度数转换为弧度,反之亦然,只不过是乘以某个比例系数而已。但是,如果需要用数字显示信息,则最好使用度数。45° 绝对比 0.78539 弧度好看。
角度和正态分布
在研究实际过程时,研究人员会使用各种随机变量的概率分布。最常见的是正态分布。
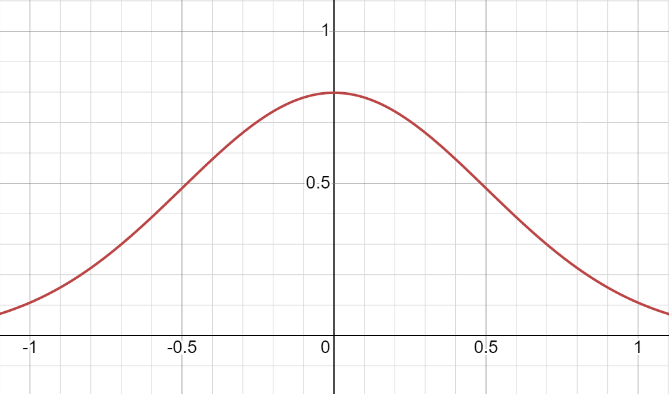
让我们回顾一下它的一些特性。它的图形是一条钟形线,这条线的两端一直延伸到无穷远。
让我们在头脑中执行以下操作。我们将开始慢慢折叠轴线 X 轴慢慢折成一个圆。在此过程中,我们要遵循以下规则 - 离中心越远,折叠的力度就越大。如果我们有足够的耐心,X 轴会变成一个圆。正态分布线本身会被扭曲,结果我们会得到包裹正态分布。
常规正态分布与包裹正态分布的第一个区别是,-∞ 映射到 -180° ,而 +∞ 映射到 +180° 。但这不是我们的目标。包裹正态分布的主要目的是处理角度值。包裹正态分布的方程是这样的:
我们可以看到,包裹分布同时使用了均值和标准差。一切都像通常的正态分布一样。这个总和看起来非常令人不安,但我们在处理实际数据时会很容易应对这些无穷大。
让我们将我们的指标应用包裹正态分布。
首先,我们需要确定历史上所有角度的平均值。在我们的例子中,求平均值并不困难 - 通常是求和,然后除以观察数。但一般来说,角平均值需要用不同的方法来寻找。想象一下,您需要求 10° 和 350° 两个角的平均值。按照通常的方法,答案是 180°。这个答案是错误的,其平均值为零。
要在任何情况下得到正确答案,我们都必须这样做:首先,我们需要求出所有角的正弦和余弦之和。用第一个和除以第二个和,得到中角正切。
现在,找出角度的平均值就不难了。但这里也有一个小条件。如果所有角度都在 -90° 和 +90° 之间,那么我们可以使用 MathArctan 函数。如果角度超出了这些限制,我们肯定应该使用更通用的 MathArctan2 函数。
因此,平均角度将等于:
估算出平均角度值后,我们就可以开始估算标准偏差了。为此,我们可以使用 Yamartino 方法。首先,我们需要找到辅助量:
它已经对标准偏差做出了相当准确的估计,但还可以加以改进:
现在,让我们对指标进行修改。我们将按以下方法计算其读数:首先,我们将找出当前角度和平均角度之间的差值,然后将该差值与标准偏差进行比较。因此,我们会得到这样一张图片。
该指标能让我们更准确地判断超买/超卖水平,与之最接近的指标是 CCI 指标。
角和线性函数
我们已经处理过同类数据的角度问题。是否可以对趋势进行角度运算?答案是否定的,因为我们处理的是不同类型的数据 - 一个轴是时间,另一个轴是价格。
嗯,这个答案是正确的,但也是错误的。让我们回顾一下线性函数。它描述了两个自变量之间的线性关系,由以下等式给出:
角度在哪里呢?它隐藏在 k 比值中。这个比值等于直线斜角的切线相对于 X 的正切值。
让我们试着用这个函数来描述一种趋势。交易者的线性函数方程将如下所示:
在这种情况下 k比值会有另一种解释 - 它显示单位时间内的平均价格变化。还有一个小注意点:我在方程式中输入了时间。但在实际计算中,使用索引而不是时间要容易得多。首先,节假日和周末会大大影响计算的准确性。其次,使用索引可以使方程(和计算)变得更加简单。对这些索引的唯一要求是,它们应从左向右递增。
现在让我们来看看估算线性趋势参数的方法。首先,我们可以使用最小二乘法(LSM)。让我提醒大家,我使用的不是时间,而是数值从 0 到 n-1 不等的索引。
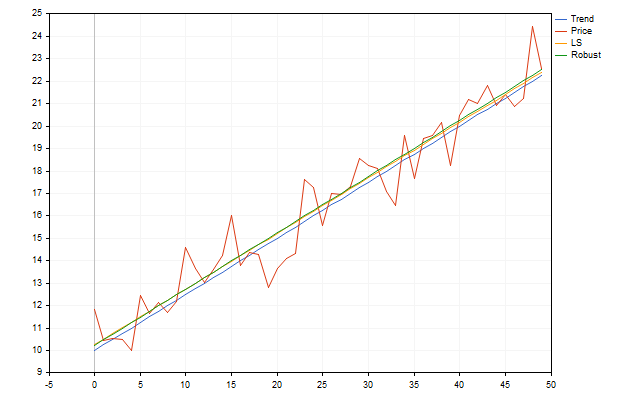
但有更可靠的方法来评估这些参数。例如,我们可以使用Theil-Sen(泰尔-森)估算。让我们来看看这种估算在现实世界中是如何运作的。让我们选择参数 k = 0.25 和 b = 10 的一个趋势,以随机分布偏差的形式给它添加一点噪音。利用得到的点,我们将尝试找到初始趋势的参数。我们会得到这样的结果。
乍一看,稳健的方法似乎没有提供太多优势。但这只是因为我们的趋势模型中的误差是均匀分布的,并且符合正态律。实际价格可能不符合这一标准。这样,Theil-Sen 方法就会好用得多,也能提供更多信息。这是我未来将使用的稳健估算方法。
因此,让我们来看看如何使用 Theil-Sen 方法估计线性趋势的参数。首先,我们需要得到 k 参数。它等于所有可能差值的中位值:
中位值的计算方法如下。首先,将所有数值写入数组。然后进行排序。中值等于位于数组中心的值。
现在我们可以开始估算 b 参数。为此,我们需要找出所有可能值的中位数:
我们已经弄懂了理论,现在是时候开始实践了。让我们看看使用 Theil-Sen 估算值会给我们带来哪些可能性。
Theil-Sen 估算和指标
在估算出趋势参数后,我们还剩下两个数据数组。让我们看看能否以其他方式使用这些数组。
因此,我们评估了趋势参数,甚至构建了趋势线。现在,我们可以建立一个价格波动的通道。为此,我们首先需要评估价格偏离趋势线的程度。
让我们使用估算 b 参数时使用的数组。为了估算偏差,我们需要找到绝对中位差。也就是说,首先,对于数组中的每个元素,我们都要找出与 b 参数差的绝对值。然后找出所得数值的中位数。这一中位数将给出标准偏差的可靠估计值。
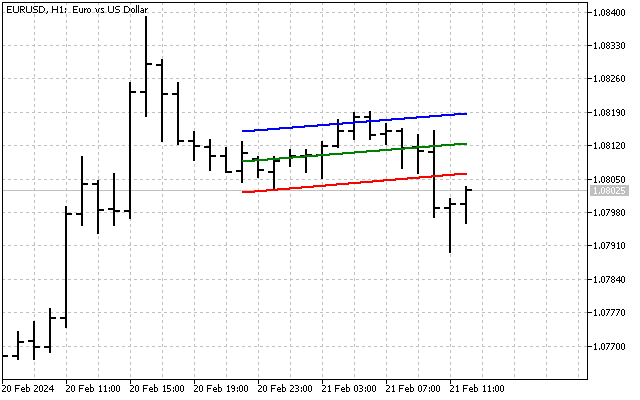
知道了标准偏差,我们就可以建立一个趋势通道。例如,宽度为 6 个标准差的通道看起来就是这样。
该指标与布林带基本相似。此外,趋势通道线还可用作支撑位和阻力位。
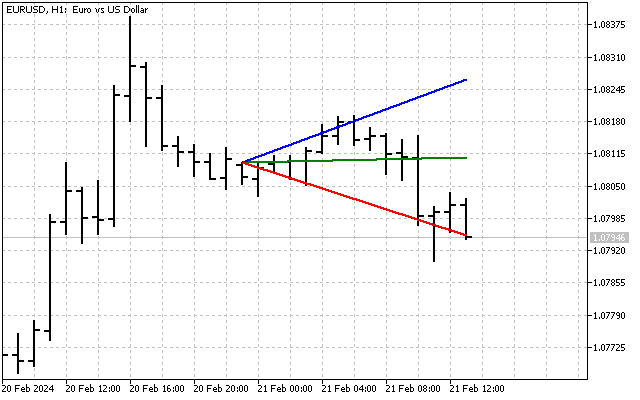
此外,我们还可以建立一个趋势线扇形。所有计算的方法与建造通道时相同。唯一不同的是,我们需要使用 k 参数和相应的数组。这就是角度偏差范围为 1 的扇形的样子。
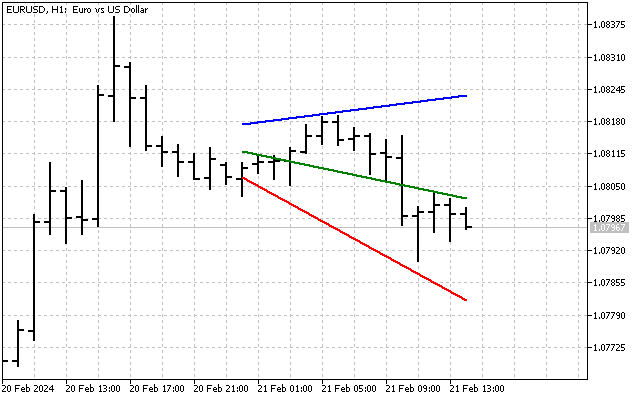
当然,我们可以将通道和扇形结合起来。为此,我们首先要建立通道线。然后,我们将扇形应用在它们身上。我们会得到这样的结果。
因此,通过使用稳健方法,我们获得了一条趋势线和另外三个可用于技术分析的指标。
其他考虑因素
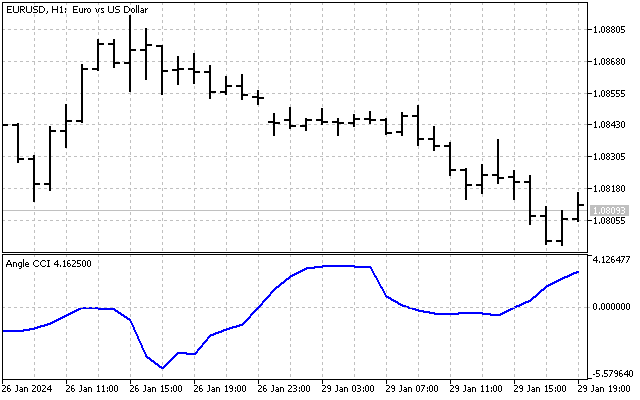
基于角度的操作不仅可以用于构建趋势和角度。让我们回顾一下文章中提到的 CCI 指标。如果我们使用趋势角度而不是价格来制作类似的指标呢?
然后,我们就能根据历史记录评估趋势变化。这就是我们的指标看起来的样子。
所有技术指标都可以转换为角度值。通过这些调整,我们可以发现新的技术分析方法。
结论
撰写本文时使用了以下程序。
| 名称 | 类型 | 描述 |
|---|---|---|
| Angle Two Pairs | 指标 |
|
| LS vs Robust | 脚本 | 比较 LSM 和 Theil-Sen 估算值 |
| Theil–Sen estimator | 指标 |
|
| Angle CCI | 指标 |
|
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/14326
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 改编版 MQL5 网格对冲 EA(第 II 部分):制作一款简单的网格 EA
改编版 MQL5 网格对冲 EA(第 II 部分):制作一款简单的网格 EA
 您应当知道的 MQL5 向导技术(第 10 部分):非常规 RBM
您应当知道的 MQL5 向导技术(第 10 部分):非常规 RBM
 开发回放系统(第 43 部分):Chart Trade 项目(II)
开发回放系统(第 43 部分):Chart Trade 项目(II)
 MQL5 简介(第 4 部分):掌握结构、类和时间函数
MQL5 简介(第 4 部分):掌握结构、类和时间函数
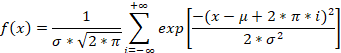
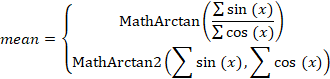
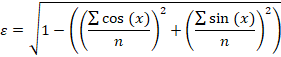
冈恩的角度让我的眼睛湿润了)。
首先,这些角不是我画的。
如果将纵轴继续延伸,它们会很容易自行解决。
其次,我将使用标准差作为垂直单位,中位数价格作为坐标轴。结果是这样的
我们得到的不是一个正方形,而是一个长方形。四角(近似)显示了布朗价格运动的边界。
好吧。
有趣的方法
我们得到的 不是一个正方形,而是一个长方形。四角(近似) 显示了布朗价格运动的边界。
????? 当布朗运动及其某些边界是某种东西时,但不是矩形:-))这种数学应该 "一飞冲天"。比如乘法表。
从季节波动(日-周-月-季)中可以得到一个非常接近菱形的数字。这将是对加纳角和网格的 "破译",而不需要神秘的正方形和扭曲的表格。您可以从统计学角度推断出
与您的截图类似的机器人交易原理:
另一种从价格中获取角度的方法。感谢冈恩爷爷。
另一种从价格中获取角度的方法。感谢冈恩爷爷。
奇怪的角度值
另一种从价格中获取角度的方法。感谢冈恩爷爷。
方框(模板)更方便,因为您可以同时获得价格和时间水平(截点)。而在一天之内,对过去的走势进行四分法计算是最准确的,可以获得最小的计算误差。