
Guia Prático Estatística do Trader: Hipóteses
Introdução
Qualquer trader disposto a criar o seu próprio sistema de negociação se tornará um analista, mais cedo ou mais tarde. Eles estão permanentemente tentando encontrar as tendências do mercado e testando idéias de negociação. O teste de uma idéia pode ser baseado em abordagens diferentes - desde uma busca dos melhores valores para os parâmetros no modo de otimização do Strategy Tester até pesquisas científicas de mercado (as vezes pseudo científica).
Neste artigo, eu sugiro a consideração de uma hipótese estatística - um instrumento de análise estatística para a investigação e verificação da inferência. Vamos testar várias hipóteses e exemplos com o pacote Statistica e com a biblioteca de análise numérica ALGLIB MQL5.
1. O Conceito de Hipótese
Existem várias definições sobre o conceito "hipótese estatística". Alguns deles envolvem uma suposição sobre as propriedades estatísticas do objeto ou fenômeno em questão.
Uma hipótese estatística é uma suposição sobre leis probabilísticas em que um fenômeno em questão se adere.
Outras definições apontam que as propriedades estatísticas devem ser conectadas com alguma variável ou parâmetro de distribuição aleatória desta distribuição.
A hipótese estatística é uma suposição sobre parâmetros da distribuição estatística ou do princípio distributivo de uma variável aleatória.
Na literatura sobre estatística matemática, a noção de "hipótese" é interpretada da segunda maneira. Então, podemos distinguir:
- Hipótese Paramétrica (Hipótese sobre os valores dos parâmetros de distribuição ou sobre o valor comparativo dos parâmetros de duas distribuições);
- Hipótese Não Paramétrica (Hipótese sobre o tipo da distribuição de valor aleatório).
Na próxima seção, vamos discutir um método de verificação de hipóteses.
2. Testando as Hipóteses. Teoria
A hipótese a ser testada é chamada de hipótese nula (Н0). Uma hipótese concorrente (Н1) é a sua alternativa. Ela esta do outro lado da moeda de Н0, ou seja, ela logicamente não admite a hipótese nula.
Imagine que há uma população de dados sobre o Stop Loss de algum sistema de negociação. Vamos indicar duas hipóteses formando uma base para o teste.
Н0 - valor médio do Stop Loss igual a 30 pontos;
Н1 - valor médio do Stop Loss diferente de 30 pontos.
Variantes de aceitação e rejeição das hipóteses:
- Н0 é verdade e é aceito;
- Н0 é falso e é rejeitado em favor de Н1;
- Н0 é verdade, mas é rejeitado em favor de Н1;
- Н0 é falso, mas é aceitável.
As duas últimas variantes estãa ligadas aos erros.
Agora, o valor do nível de significância deve ser especificado. Ela é a probabilidade de que a hipótese alternativa será aceita desde que a hipótese verdadeira seja a nula (terceira variante). Esta probabilidade é preferível ser minimizada.
No nosso caso tal erro ocorrerá se assumirmos que Stop Loss médio não é igual a 30 pontos, mesmo que ele realmente seja.
Normalmente, o nível de significância (α) é igual a 0.05. Isso significa que o valor estatístico do teste da hipótese nula pode povoar a região crítica em não mais que cinco casos em cada 100.
Em nosso caso, o valor da estatística de teste serão avaliados em um gráfico clássico (Fig.1).
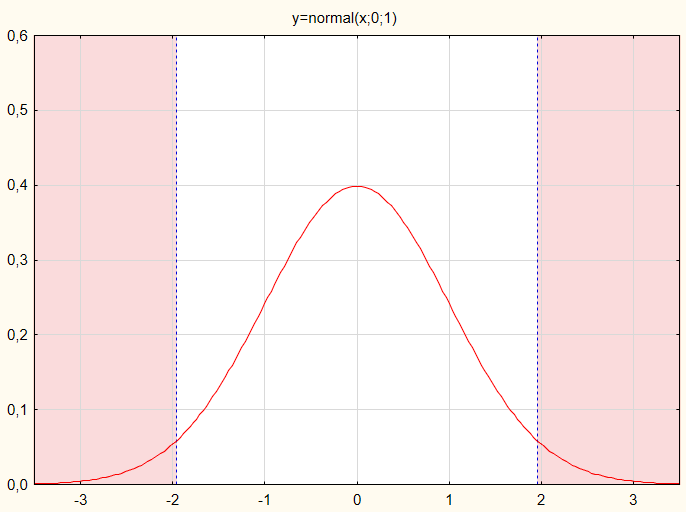
Fig.1. Distribuição do valor estatístico do teste pela lei de probabilidade normal
Para a hipótese nula ser aceita, os valores do teste estatístico não devem chegar às zonas vermelhas. Para efeitos de exemplo, vamos supor que os valores do teste estatístico são distribuídos normalmente.
Cada teste tem sua própria fórmula para calcular o valor estatístico de teste.
A variante 4 implica que existe um erro do segundo tipo (β). No nosso caso, tal erro ocorrerá se presumirmos que o Stop Loss médio seja igual a 30 pontos e não igual a este número de pontos.
3. Exemplos Estatísticos de Teste de hipóteses
A fonte de dados utilizados para os exemplos são armazenados no arquivo DATA.XLS.
3.1. Teste Simples de Dependência
Imagine a seguinte situação. Assuma que exista um sistema de negociação gerando uma população de negociações. Vamos pegar uma amostra de negócios rentáveis com um volume de 100 unidades. Os dados de origem estão na planilha "Profits".
A estatística descritiva da amostra Profits após a exclusão dos casos periféricas são apresentados na Tabela 1:
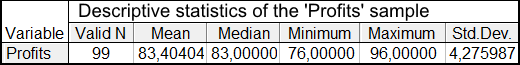
Tabela 1. Estatísticas da amostra Profits
O histograma da amostra tem o seguinte aspecto (Fig.2).
Fig.2. O histograma da amostra Profits
O valor médio é de 83.4 pontos e a mediana é de 83 pontos.
O que vai acontecer se o ponto de entrada no mercado for alterado em alguns pontos? Por exemplo, uma ordem limite melhorando o preço de entrada pode ser colocada após o sinal de negociação aparecer.
Como isso vai afetar os resultados? Esta questão pode ser respondida com hipóteses estatísticas.
No pacote Statistica nós verificamos formalmente se as amostras não foram retiradas de uma população:
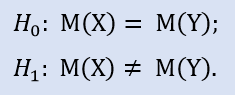
Se mudamos o preço de entrada por 15 pontos, nos devemos receber a amostra NewProfits. Idealmente, a imagem resultante tem o seguinte aspecto (Figura 3).
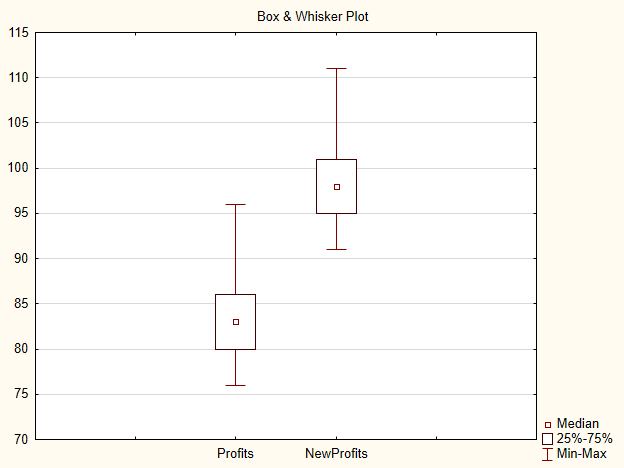
Fig.3. Gráfico para as amostras Profits e NewProfits
A probabilidade de que a hipótese alternativa seja aceita é alta já que as medianas das amostras se diferem.
Este cenário, no entanto, vai ser difícil de obter, porque pode não haver preços melhores no mercado. No meu caso, a segunda amostra foi composta por 84 negociações após o preço de entrada ser alterado. As outras 15 negociações simplesmente não foram executadas. Esta amostra corrigida será nomeada de NewProfitsReal.
Na plotagem do tipo "box-and-whisker" não há muita diferença entre as duas amostras.
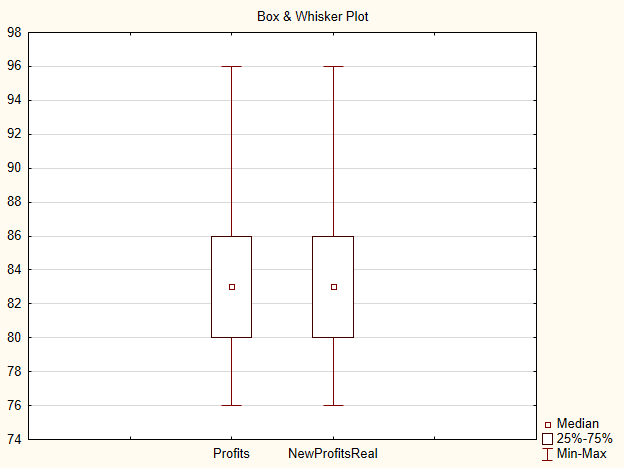
Fig.4. Plotagem das amostras Profits e NewProfitsReal
Vamos conduzir o teste não paramétrico de Wilcoxon, conhecido como Wilcoxon signed-rank test, para a amostra conectada.
Os resultados estão na Tabela 2:

Tabela 2. Os resultados do teste de Wilcoxon para as amostras Profits e NewProfitsReal
O nível de significância é muito alto, o que favorece a hipótese nula.
Dessa forma, podemos dizer que a mudança do ponto de entrada não influenciou no rendimento do sistema. Isto é, em termos relativos. Em termos absolutos, o sistema acabou sendo menos rentável por causa dos pontos de entrada não atendidos.
O Teste de Wilcoxon pode ser realizado por meio da programação em MQL5. Embora ele comparar a mediana da distribuição com o valor especificado de m, esta diferença não é significativa.
Vamos verificar:
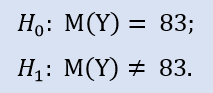
A biblioteca ALGLIB contém o seguinte procedimento: CAlglib::WilcoxonSignedRankTest(). Ele dá um resultado para três tipos de teste: dois lados, do lado esquerdo e do lado direito.
O Script test_profits.mq5 fornece um exemplo deste cálculo Na aba "Experts" temos os seguintes resultados para a amostra NewProfitsReal:
OO 0 12:04:08.814 test_profits (EURUSD.e,H1) p-value for the two-sided test: 0.7472 HD 0 12:04:08.814 test_profits (EURUSD.e,H1) p-value for the left-sided test: 0.6285 CM 0 12:04:08.814 test_profits (EURUSD.e,H1) p-value for the right-sided test: 0.3736
O teste do lado esquerdo tem o seguinte aspecto:
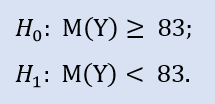
Aqui verificamos a alternativa de que a mediana da amostra NewProfitsReal possa ser superior ou igual a 83. A probabilidade do erro em rejeitar H0 é de 0.63. Portanto H0 é aceito.
O teste do lado direito tem o seguinte aspecto:
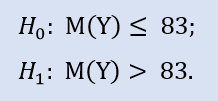
Neste teste, nós verificamos a alternativa de que a mediana da amostra NewProfitsReal possa ser inferior ou igual a 83. A probabilidade do erro em rejeitar H0 é igual a 0.37. Portanto H0 é aceito.
3.2. Testando Amostras Independentes
Vamos supor que temos que verificar a rapidez com que as diferentes corretoras processam as ordens de negociação e se existe uma diferença entre as corretores em relação ao tempo de execução das ordens de negociação.
Assim, há duas amostras de dados para a análise. Cada amostra continha inicialmente 50 observações. Depois de eliminar os casos extremos, 48 observações foram deixados na primeira amostra (corretora А), e 49 observações na segunda (corretora B). Os dados podem ser encontrados na planilha "ExecutionTime".
Vamos verificar:
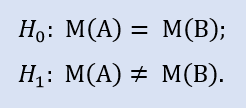
Vamos representar os índices de amostra em uma imagem (Fig.5). De acordo com a plotagem, os valores das medianas diferem entre si, embora que, não sejam de forma significativa.
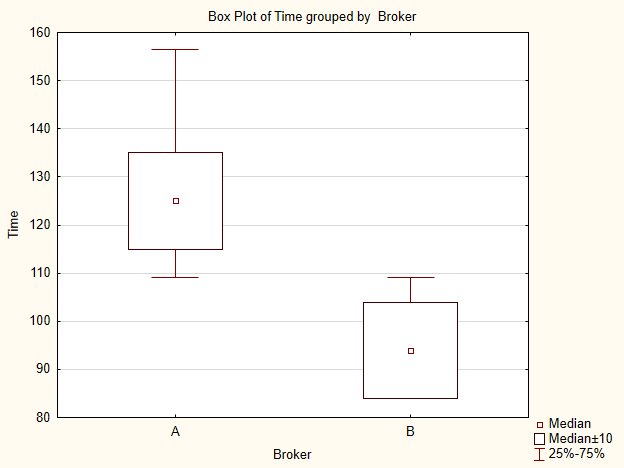
Fig.5. Plotagem das amostras de dados das corretores A e B
Já que nós não sabemos o a que distribuição cada amostra pertence, nós vamos referir-se a testes não paramétricos para comparação.
Por exemplo, vamos realizar o teste Mann - Whitney U-test (Tabela 3). Acredita-se que esta seja a mais informativa.

Tabela 3. Resultados de Mann — Whitney U-test para as amostras de dados das corretoras A e B
Conclusão: os resultados dos testes são diferentes e, portanto, as hipóteses nulas sobre a igualdade de amostras são rejeitadas a favor de Н1.
Mann — Whitney U-test pode ser conduzido por meio da programação MQL5. Na biblioteca ALGLIB há o procedimento CAlglib:: MannWhitneyUTest(). Ele dá um resultado para três tipos de teste: dois lados, do lado esquerdo e do lado direito.
O Script test_time_execution.mq5 fornece o exemplo de cálculo. Na aba "Expert" há o seguinte resultado que pode ser utilizado para comparar as amostras:
MR 0 12:55:08.577 test_time_execution (EURUSD.e,H1) p-value for the two sided test: 0.0001 QF 0 12:55:08.577 test_time_execution (EURUSD.e,H1) p-value for the left-sided test: 1.0000 PF 0 12:55:08.577 test_time_execution (EURUSD.e,H1) p-value for the right-sided test: 0.0001
O teste do lado esquerdo tem o seguinte aspecto:
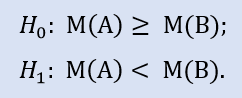
A hipótese nula é de que a mediana da amostra de dados da corretora A possa ser maior ou igual à mediana da amostra de dados da corretora B. A alternativa é a sua rejeição. Probabilidade de erro em rejeitar H0 é de 1.0. Portanto H0 é aceito.
O teste do lado direito tem o seguinte aspecto:
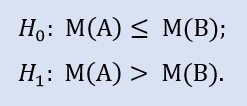
A hipótese nula é de que a mediana da amostra de dados da corretora A possa ser menor ou igual à mediana da amostra de dados da corretora B. A alternativa é a sua rejeição.
Probabilidade de erro em rejeitar H0 é de 0.0. Portanto H0 é rejeitado em favor de Н1.
3.3. Teste de Correlação
Imagine um portfólio de estratégias. O objetivo é reduzir o número de estratégias neste portfólio.
O critério de escolha será o seguinte: se duas estratégias são as mesmas em comparação com a série de Stop Loss, então, uma das estratégias será removida do portfólio. Tomemos duas amostras com dados de Stop Loss de dois sistemas diferentes. Premissas: os sistemas reagem a entrada do mercado da mesma forma e reagem a saída do mercado de forma diferente.
Vamos usar o teste de correlação de Spearman (Spearman's Rank-Order). Existem três amostras na planilha do arquivo de daos "Correlation".
Verifique se o coeficiente de correlação é igual a zero:
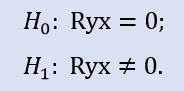
A comparação do par de amostras Stops1-Stops2 dará o resultado a seguir (Tabela 4).

Tabela 4. Correlação de Spearman para as amostras Stops1 e Stops2
Neste caso, a hipótese nula sobre a ausência de conexão entre os elementos das amostras não podem ser rejeitadas a favor da alternativa. Por isso, ela é aceita.
A plotagem na Fig.6 mostra que os dados não formam qualquer configuração perceptível. Os dados são espalhados na plotagem plana.
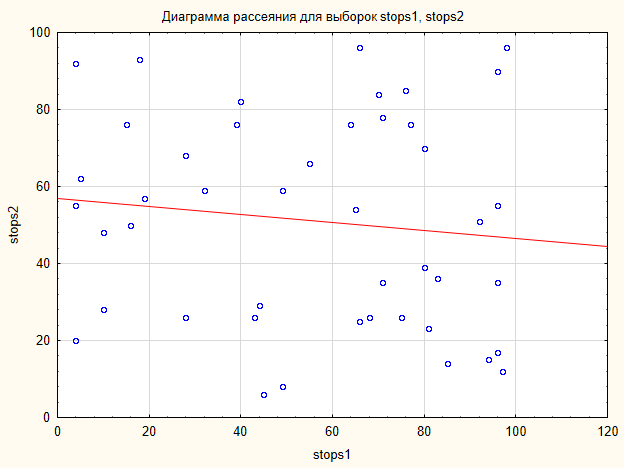
Fig.6. Gráfico de dispersão para as amostras Stops1 e Stops2
Os resultados da relação entre a verificação das amostras Stops1-Stops3 são mostradas na Tabela 5:
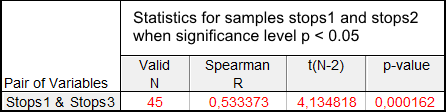
Tabela 5. Resultados do teste de correlação Spearman para as amostras Stops1 e Stops3
Neste caso, a hipótese nula pode ser rejeitada já que a probabilidade de erro é muito baixa.
Por isso, a alternativa sobre uma relação existente é aceito. A relação tem o seguinte aspecto (Fig.7).
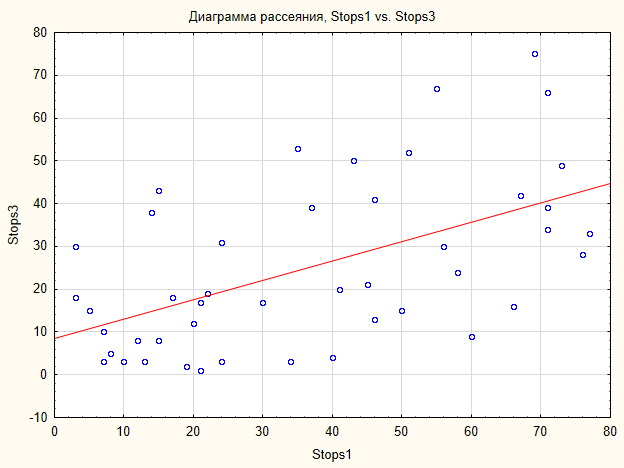
Fig.7. Gráfico de dispersão para as amostras Stops1 e Stops3
Confirme o resultado com o código em MQL5. O arquivo test_correlation.mq5 contém um exemplo de cálculo.
A biblioteca ALGLIB contém o procedimento CAlglib::SpearmanRankCorrelationSignificance(), que implementa o teste de significância do coeficiente de correlação de Spearman.
O diário contém os seguintes registros:
OO 0 12:57:43.545 test_correlation (EURUSD.e,H1) ---===Samples Stops1 and Stops2===--- GO 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the two-sided test: 0.9840 KK 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the left-sided test: 0.4920 JJ 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the right-sided test: 0.5080 DM 0 12:57:43.545 test_correlation (EURUSD.e,H1) HJ 0 12:57:43.545 test_correlation (EURUSD.e,H1) ---===Samples Stops1 and Stops3===--- NS 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the two-sided test: 0.0002 RO 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the left-sided test: 0.9999 FG 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the right-sided test: 0.0001
O teste do lado esquerdo tem o seguinte aspecto:
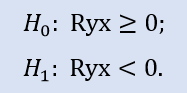
Neste teste a hipótese nula é de que exista uma correlação entre as variáveis não negativas (isto é, a correlação é zero, ou negativa), é verificada.
O teste do lado esquerdo mostra que para o par de amostras Stops1-Stops2, a hipótese nula é aceita. O teste do lado esquerdo mostra que para o par de amostras Stops1-Stops3 a hipótese nula é aceita também. A questão lógica a se perguntar é "Por que não há conexão entre as amostras Stops1-Stops2 e há uma entre Stops1-Stops3? "A razão está na declaração de vericação que é "maior ou igual a zero". No primeiro caso, "igual a zero" é importante para H0, já no segundo caso é "superior a zero".
O teste do lado direito tem o seguinte aspecto:
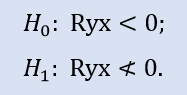
Aqui, a hipótese nula do que é uma correlação negativa foi verificada.
Para o par de amostras Stops1-Stops2, o teste do lado direito mostra que a hipótese nula é aceita. Para o par de amostras Stops1-Stops3 o teste do lado direito mostra que a hipótese nula é rejeitada.
Um último comentário. O teste revelou que existe uma relação probabilística positiva entre as amostras Stops1-Stops3. A força desta ligação é média. Portanto, cabe ao trader decidir se irá rejeitar a estratégia 1 ou 3.
Conclusão
Neste artigo eu tentei mostrar em exemplos como as variáveis quantitativas podem ser avaliados através da estatística matemática. Espero que os desenvolvedores iniciantes achem este artigo útil para seus futuros sistemas de negociação. Eu espero também que a série de artigos sobre a utilização dos métodos matemáticos sobre estatística continue.
Os arquivos da biblioteca ALGLIB devem ser baixados separadamente.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/1240
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Redes Neurais Simples e Econômica - Conecte o NeuroPro com o MetaTrader 5
Redes Neurais Simples e Econômica - Conecte o NeuroPro com o MetaTrader 5
 Princípios da Precificação da Bolsa Tomando como Exemplo o Mercado de Derivativos da Bolsa de Moscou (MOEX)
Princípios da Precificação da Bolsa Tomando como Exemplo o Mercado de Derivativos da Bolsa de Moscou (MOEX)
 Gráfico Líquido
Gráfico Líquido
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Esse é um paradoxo interessante. Onde posso obter mais informações sobre isso?
Paradoxo interessante. Onde posso obter mais informações sobre ele?
Esclareça o que você quer dizer com ambiente ergódico .Seu artigo me dá uma dupla impressão.
Além disso. Neste fórum, o próprio fato de perguntar sobre a avaliação hipotética dos resultados é muito importante. O fórum está cheio de pessoas que desenham uma mashka e presumem que esse é o caso, em vez de uma mashka no intervalo.
Menos.
Concordo totalmente com Reshetov. Tudo o que você disse refere-se a séries estacionárias ou próximas a elas, ou seja, séries com pouca alteração de mo e variância ao longo do tempo. Mas não existem séries desse tipo nos mercados financeiros, e toda a aplicação de estatísticas nos mercados financeiros gira em torno da estacionariedade das séries temporais. Os exemplos mais famosos são ARIMA, ARCH e todos os demais.
Sua série aleatória, cujo histograma é mostrado na Fig. 2, mostra que a série tem uma relação fraca com a série estacionária, é distorcida e tem caudas significativamente diferentes. Isso é especialmente bem visto em relação à curva perfeitamente normal desenhada por você. Dessa forma, seu raciocínio não se aplica de forma alguma ao seu exemplo. Este é apenas uma ilustração dos pensamentos de Reshetov.
PS. O conceito mais perigoso e desprezível da estatística é a correlação. É melhor não mencioná-lo de forma alguma.
...Tudo o que você disse se refere a séries estacionárias ou próximas a elas, ou seja, séries com pouca alteração de mo e variância ao longo do tempo. E não existem tais séries nos mercados financeiros, e toda a aplicação de estatísticas nos mercados financeiros gira em torno da estacionariedade das séries temporais. Os exemplos mais famosos são ARIMA, ARCH e todos os demais.
Sua série aleatória, cujo histograma é mostrado na Fig. 2, mostra que a série tem uma relação fraca com a série estacionária, é distorcida e tem caudas significativamente diferentes. Isso é especialmente bem visto em relação à curva perfeitamente normal desenhada por você. Dessa forma, seu raciocínio não se aplica de forma alguma ao seu exemplo. Este aqui é uma ilustração dos pensamentos de Reshetov.
Obrigado por sua opinião!
Vou apresentar meus contra-argumentos.
A estacionariedade é uma característica de uma série temporal. A Figura 2 é uma série de variação. O artigo não fala sobre séries temporais! Embora eu concorde que o tempo é uma característica útil.....
Pelo que entendi, ergodicidade significa uma certa estabilidade do sistema em estudo....
Portanto, gostaria de observar um ponto importante. Se o sistema, vamos falar de uma série temporal financeira, não for estacionário, ainda assim podemos usar a econometria para encontrar um modelo estável (por exemplo, GARCH) que descreva o comportamento do modelo. E nisso eu vejo a constância do sistema - comportamento de acordo com o modelo.... mas com a condição de que há alguma probabilidade de o sistema "quebrar" o modelo...
Obrigado por sua opinião!
Aqui estão meus contra-argumentos.
A estacionariedade é uma característica de uma série temporal. A Figura 2 é uma série de variação. O artigo não fala sobre séries temporais! Embora eu concorde que o tempo é uma característica útil.....
Pelo que entendi, ergodicidade significa uma certa estabilidade do sistema em estudo....
Portanto, gostaria de observar um ponto importante. Se o sistema, vamos falar de uma série temporal financeira, não for estacionário, ainda assim podemos usar a econometria para encontrar um modelo estável (por exemplo, GARCH) que descreva o comportamento do modelo. E nisso eu vejo a constância do sistema - comportamento de acordo com o modelo.... mas com a condição de que haja alguma probabilidade de o sistema "quebrar" o modelo.....
Há alguns anos, publiquei um artigo aqui no site no qual fundamentei uma ideia que é completamente inaceitável para a maioria das pessoas. A saber.
Existem muitos indicadores. Todo mundo acha que se um indicador é desenhado, ele é o mesmo - afinal, vemos exatamente isso. Ao mesmo tempo, não ocorre à maioria das pessoas que o que vemos na realidade pode não existir! O motivo é banal. Se pegarmos a regressão correspondente ao indicador, podemos facilmente descobrir que alguns de seus coeficientes têm intervalos de confiança tão amplos que é impossível falar sobre o valor de tal coeficiente, e se descartarmos esse coeficiente defeituoso, o padrão do indicador será completamente diferente. Quando se diz: existe a verdade, existe a falsidade e existe a estatística, isso se refere a essa circunstância triste e pouco usual - nada é confiável, inclusive os intervalos de confiança.
É por isso que abandonei os modelos paramétricos e me envolvi em modelos baseados em aprendizado de máquina. Não há problemas com a estacionariedade, mas os problemas com o excesso de treinamento estão em plena glória.
E gostei do artigo.
Sim, as observações de San Sanych e Reshetov são legítimas - se o sistema (ou sistema) comparado alterar seus parâmetros, os resultados do teste serão inúteis.
Mas a própria demonstração da aplicação dos métodos é agradável. Isso é raro no Forex!
Eu diria outra coisa, como uma pessoa que aplica métodos semelhantes exatamente para preços de cotação. É possível verificar antecipadamente se o ambiente é homogêneo (em duas grandes amostras independentes) e, em seguida, confiar nos resultados do teste de hipótese com um certo grau de tranquilidade. Isso também pode ser feito graças aos mesmos testes.