トレーダーの統計的クックブック：仮説
2 105
0
はじめに
積極的に独自のトレーディングシステムを作成しようとするトレーダーはだれも遅かれ早かれ分析家になっていきます。そういう人達は永遠にマーケットトレンドを探し、トレーディングのアイデアを検証しようとしています。アイデアを検証することは異なるアプローチで行えます。－ストラテジーテスタの最適化モードで行う最良のパラメータ値の通常検索から科学的（疑似科学的なこともありますが）なマーケットリサーチまで。
本稿では統計的仮説について考察することを提案します。－検索と推論検索の統計的解析手段です。Statistica パッケージによってさまざまな仮説と移植された数値解析ライブラリ ALGLIB MQL5 を例を用いて検証します。
1. 仮説のコンセプト
『統計的仮説』の定義は複数あります。いくつかは対象のオブジェクトや現象の統計的特性を扱います。
統計的仮説は問題の減少が従う確率論的法則についての仮定です。
別の定義は統計的特性は一部のランダム変数の分布またはこの分布のパラメータに関連する必要があると指摘します。
統計的仮説は統計分布のパラメータまたはランダム変数の分布原則に従った仮定です。
数理統計学の文献では、『仮説』の概念は後者のように解釈されています。われわれは以下のように区別します。
- パラメトリック仮説（分布パラメータ値または2つの分布のパラメータ値比較にについての仮説）
- ノンパラメトリック仮説（ランダム変数分布のタイプについての仮説）
次のセクションでは仮説検定方法についてお話します。
2. 仮説の検定理論
検定される仮説は null 仮説（Н0）と呼ばれます。比較する仮説（Н1）はその対立です。それは Н0 のコインの反対側にあります。すなわちそれは理論的に仮説を否定するものです。
なんらかのトレーディングシステムのストップロスデータの母集団があるとイメージします。検定の基盤を作成して2とおりの仮説を述べようとしています。
Н0 – 30 ポイントの平均的ストップロス値
Н1 – 30ポイントではない平均的ストップロス値
仮定受け入れと拒絶のバリアンス：
- Н0 は真で受け入れ
- Н0 は誤りで Н1 を指示して拒絶
- Н0 は真であるが Н1 を指示して拒絶
- Н0 は誤りであるが受け入れ
最後の2つのバリアントはエラーにつながります。
ここで優位レベル値が指定されます。真の仮説が null 仮説である（3番目のバリアント）一方で、それは対立仮説が受け入れられる確率です。この確率は最小限に抑えることが好ましいです。
われわれの場合、平均のストップロスが30ポイントではないと仮定する場合、実際には30ポイントであったとしても、そのエラーは発生します。
通常有意性レベル（α）は0.05 です。それは null 仮説の検定統計値は100 の内 5 件より大きくない臨界領域を追加する可能性があることを意味しています。
われわれの場合、検定統計値は古いタイプのチャートで評価されます（図1）。
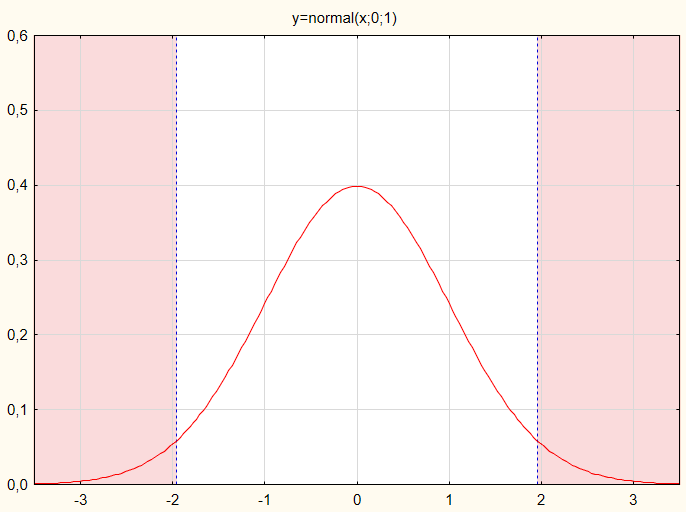
図1 正規確率法則による検定統計値分布
仮説が受け入れられるには、検定統計値が赤いゾーンに入らないことです。例として、検定統計値が正規に分布されると仮定します。
検定はどれもみな検定統計値を計算するために独自の式を持ちます。
バリアント4は2番目のタイプ（β）にエラーがあることを示しています。われわれの場合、平均でのストップロスが30ポイントで、それがそのポイント数に等しくなければそのエラーが発生します。
3. 統計的仮説検定例
例い用いられているソースデータは Data.xls ファイルに保存されています。
3.1. 依存サンプル検定
次の状況をイメージします。ディールの母集団を作るトレーディングシステムがあるとします。100 ユニットのボリュームで収益性あるディールのサンプルを採ります。ソースデータは『収益』シートにあります。
表1の範囲外のケースを削除したあとの収益 サンプルの 記述統計
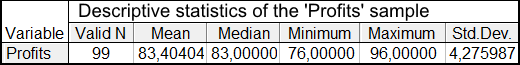
表1 収益サンプルの統計
以下がサンプルのヒストグラムです（図2）。
図2 収益のサンプルヒストグラム
平均値は83.4 ポイントで中央値は 83 ポイントです。
マーケットエントリーポイントが数ポイント変化したら何がおこるのでしょうか？たとえば、トレードシグナルが表示されたあとにエントリー価格を上げる指値注文が出される可能性があります。
これは結果にどう影響するのでしょうか？この疑問は統計的仮説で回答することができます。
Statistica パッケージでわれわれはサンプルが母集団から取られていなかったか正式に確認します。
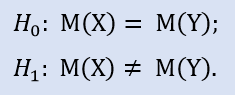
エントリー価格を15ポイント変えれば、NewProfits サンプルを取得します。理想的には結果の絵は以下のようなものとなります（図3）。
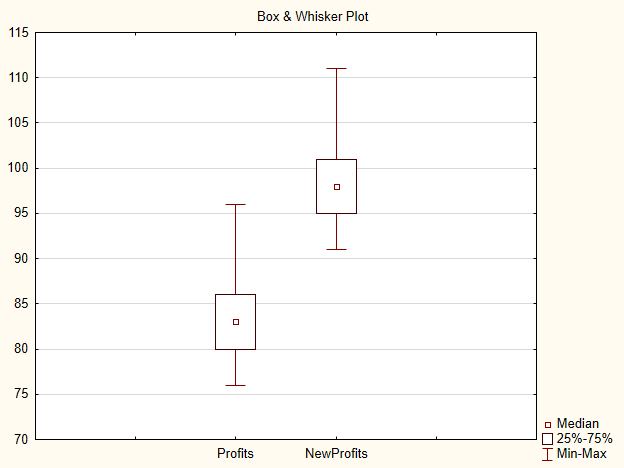
図3 収益とNewProfits サンプルのチャート
対立仮説が受け入れられる確率は、サンプルの中央値が変わると高くなります。
ただ、マーケットではこれ以上によい価格はないので、この絵を取得するのは困難です。私の場合は、エントリー価格が変わったあと、2番目のサンプル84ディールでした。その他15件のディールは行われませんでした。この修正済みサンプルはNewProfitsRealと名前を付けます。
箱ひげ図タイプでは、2件のサンプルの間に大きな違いはありません。
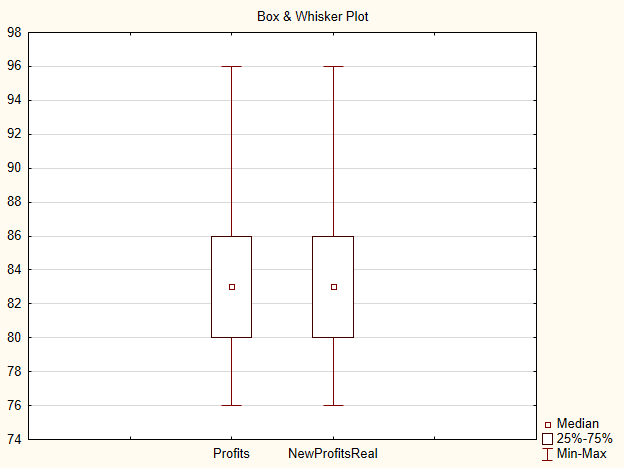
図4 収益とNewProfitsReal サンプルのプロット
関連するサンプルに対してノンパラメトリックなウィルコクソンの符号順位検定を行います。
表2がその結果です。
表2 収益とNewProfitsReal サンプルに対するウィルコクソン検定結果
有意レベルはひじょうに高いものとなっています。それは null 仮説を支持するものです。
このようにエントリーポイントの変化がシステム収量に影響を与えなかったと言えます。それは相対的な条件です。絶対的条件では、不足しているエントリーポイントのためシステムは収益性が下がります。
ウィルコクソン検定は MQL5 ではプログラム で行うことが可能です。それは分布の中央値を指定の値 m と比較しますが、この差は有意ではありません。
確認します。
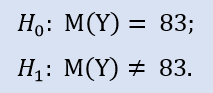
ALGLIB ライブラリには次のプロシージャが入っています：CAlglib::WilcoxonSignedRankTest()。それは3種類の検定タイプに対する結果を提供します：両側、左側、右側です。
スクリプト test_profits.mq5 によりこの計算の例を提示します。『エキスパート』のジャーナルにはNewProfitsReal サンプルに対する以下の結果があります。
OO 0 12:04:08.814 test_profits (EURUSD.e,H1) p-value for the two-sided test: 0.7472 HD 0 12:04:08.814 test_profits (EURUSD.e,H1) p-value for the left-sided test: 0.6285 CM 0 12:04:08.814 test_profits (EURUSD.e,H1) p-value for the right-sided test: 0.3736
左側検定は次の形式をとります。
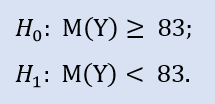
ここで対立仮説のチェックをします。というもの NewProfitsReal サンプルの中央値は83よりも大きい可能性があるためです。H0 拒否時のエラー確率は 0.63 です。よって H0 は受け入れられます。
以下は右側仮説です。
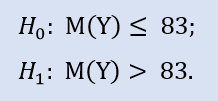
この検証では、NewProfitsReal サンプルの中央値が83以下であることを対立仮説でチェックします。H0 拒否時のエラー確率は 0.37 です。よって H0 は受け入れられます。
3.2. 独立サンプルの検定
異なるブローカーがどのくらい迅速にトレード注文を処理するか、トレード注文の実行に関してブローカー間で差があるかどうか確認する必要があるとします。
よって解析にはソースデータのサンプルが2つあります。どのサンプルも最初は50の観測を持っていました。範囲外のケースを削除したのち、最初のサンプル（ブローカーA）には観測が48残り、次のサンプル（ブローカーB）には49残りました。データは "ExecutionTime" シートにあります。
確認します。
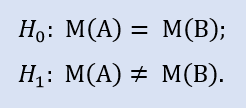
画像でサンプルインデックスを提示します（図5）。プロットによると、大きくはありませんが中央値は異なります。
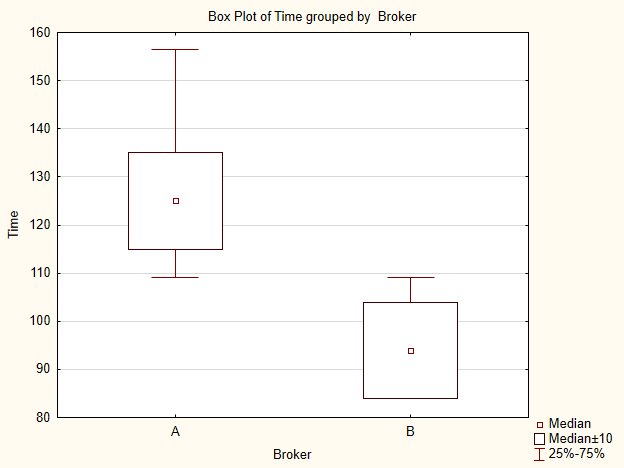
図5 ブローカーA および B のデータサンプルに対するプロット
各サンプルがどの分布に属するか判らないため、比較にノンパラメトリック検証を採用します。
たとえば、マン－ホイットニー U 検定を行います（表3）。それはもっとも有益であると思われているものです。
表3 ブローカーA および B のデータサンプルに対するマン－ホイットニー U 検定結果
結論：検証結果は異なり、そのためサンプルの同等性についての null 仮説は Н1 支持の下拒否されます。
マン－ホイットニー U 検定はMQL5 ではプログラム で行うことが可能です。ALGLIBライブラリには CAlglib:: MannWhitneyUTest() プロシージャが入っています。それは3種類の検定タイプに対する結果を提供します：両側、左側、右側です。
スクリプト test_time_execution.mq5 によりこの計算の例を提示します。『エキスパート』のジャーナルにはサンプル比較に使用できる以下の結果があります。
MR 0 12:55:08.577 test_time_execution (EURUSD.e,H1) p-value for the two sided test: 0.0001 QF 0 12:55:08.577 test_time_execution (EURUSD.e,H1) p-value for the left-sided test: 1.0000 PF 0 12:55:08.577 test_time_execution (EURUSD.e,H1) p-value for the right-sided test: 0.0001
左側検定は次の形式をとります。
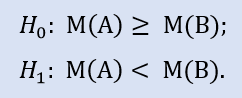
仮説はブローカーAサンプルの中央値がブローカーBサンプルの中央値以上であるというものです。対立仮説はその否定です。H0 拒否時のエラー確率は 1.0 です。よって H0 は受け入れられます。
以下は右側仮説です。
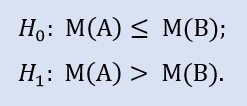
仮説はブローカーAサンプルの中央値がブローカーBサンプルの中央値以下であるというものです。対立仮説はその否定です。
H0 拒否時のエラー確率は 0.0 です。よって Н1 支持の下 H0 は拒否されます。
3.3. 相関関係検定
戦略のポートフォリオを想像します。目標はポートフォリオ内の戦略数を減らすことです。
選択基準は以下です。ストップロス系列を比較するとき2つの戦略が同じであれば、そのうちの1つはポートフォリオから消去される。2件の異なるシステムからストップロスデータを持つサンプルを2つ採ります。仮定：マーケットエントリーでシステムは同じように反応し、エグジットでは違った反応をする。
スピアマンの順位相関試験を使用します。データファイルの『相関関係』シートにはサンプルが3件あります。
相関係数がゼロかどうか確認します。
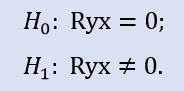
収益サンプルの統計
表4 サンプルStops1 および Stops2 につていのスピアマンの順位相関試験
この場合サンプルエレメント間の関連のない null 仮説は対立仮説を指示する下で拒否されることはありません。よってそれは受け入れられます。
図6のプロットはデータが目立つコンフィギュレーションをなにも形成しないことを示しています。データはプロット面にちらばっています。
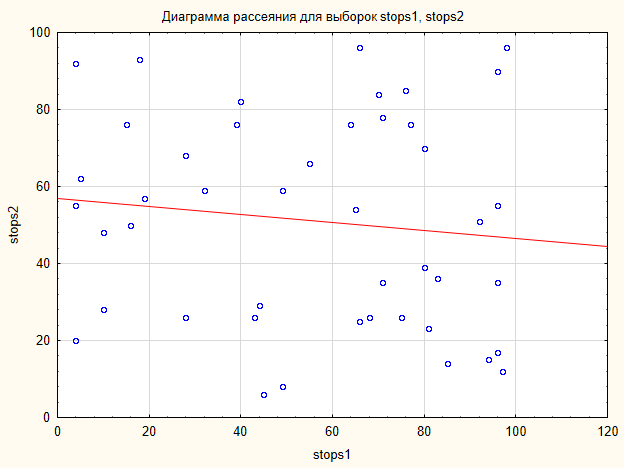
図6 サンプルStops1 と Stops2 に対する散布図
サンプルStops1-Stops3 間での関係チェックの結果は表5に示されています。
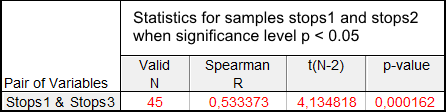
表5 サンプルStops1 および Stops3 につていのスピアマンの順位相関試験結果
この場合、エラー可能性がひじょうに低いためnull 仮説は拒否される可能性があります。
よって関係存在についての対立仮説が受け入れられます。以下が関係の表示です（図7）。
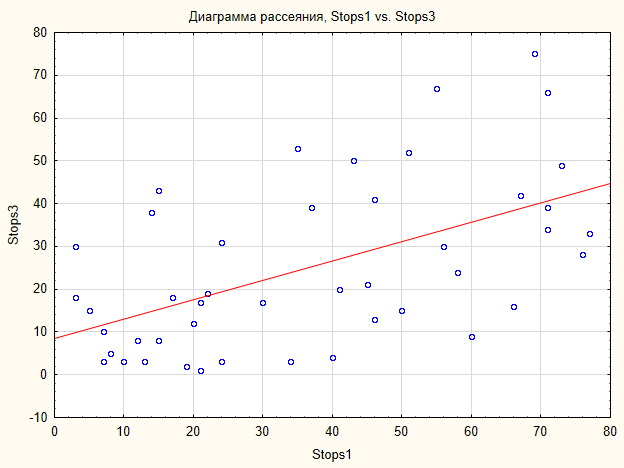
図7 サンプルStops1 と Stops3 に対する散布図
MQL5のコードで結果を確認します。test_correlation.mq5には計算例が入っています。
ALGLIB ライブラリにはプロシージャ CAlglib::SpearmanRankCorrelationSignificance()があります。それはスピアマンの順位相関係数の有意性についての検証を実装します。
ジャーナルには以下のレコードが入っています。
OO 0 12:57:43.545 test_correlation (EURUSD.e,H1) ---===Samples Stops1 and Stops2===--- GO 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the two-sided test: 0.9840 KK 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the left-sided test: 0.4920 JJ 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the right-sided test: 0.5080 DM 0 12:57:43.545 test_correlation (EURUSD.e,H1) HJ 0 12:57:43.545 test_correlation (EURUSD.e,H1) ---===Samples Stops1 and Stops3===--- NS 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the two-sided test: 0.0002 RO 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the left-sided test: 0.9999 FG 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the right-sided test: 0.0001
左側検定は次の形式をとります。
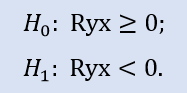
この検定では変数間に非負の相関がある（相関はゼロ、または負）とする null 仮説が検証されます。
左側検定はサンプルペアStops1-Stops2,に対してゼロ仮説が受け入れられることを示します。左側検定はサンプルペアStops1-Stops3に対してもゼロ仮説が受け入れられることを示します。質問すべき論理的疑問は「 Stops1-Stops2 サンプル間には関連がなく、Stops1-Stops3間にはあるのか？」というものです。理由は確認のステートメントが『ゼロ以上である』ためです。前者のケースでは H0 にとって『ゼロに等しい』が重要で、後者では『ゼロより大きい』が重要です。
以下は右側仮説です。
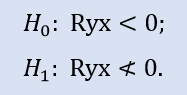
ここでは負の相関であるものの null 仮説が確認されます。
サンプルペア Stops1-Stops2について右側検定は null 仮説が受け入れられることを示しています。サンプルペア Stops1-Stops3 について右側検定は null 仮説が拒否されることを示しています。
最後に一言。検定によりサンプル Stops1-Stops3間には正の確率的関連があることが明らかとなりました。この関連の強さは平均です。よって戦略 1 か 3 を拒否するかどうかはトレーダー次第です。
おわりに
本稿では定量変数が数理統計学を用いて評価可能であることを例を挙げて示そうとしました。初心者開発者の方に将来のトレーディングシステムのために本稿が有用であると思っていただけるのを願っています。また数理統計学の手法を利用することに関する記事シリースが続行していければいいと思います。
ALGLIB ライブラリのファイルは個別にダウンロードする必要があります。
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/1240
オブジェクト指向アプローチによる EA モードのプログラミング
MQL5 プログラミングの基礎：ターミナルのグローバル変数
モスクワ証券取引所のデリバティブ市場を例にとった取り引き価格の原則
リキッドチャート
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索