Statistik-Cookbook für Händler: Hypothesen
520
0
Einleitung
Jeder Händler, der sein eigenes Handelssystem erzeugen will, wird früher oder später auch zu einem Analysten, da er ja ständig versucht, Markttrends zu finden und Handelskonzepte zu testen. Das Testen eines Konzepts kann auf verschiedenen Ansätzen beruhen - von der üblichen Suche nach den besten Parameterwerten im Optimierungsmodus des Strategietesters bis hin zu wissenschaftlicher (oder manchmal nur pseudo-wissenschaftlicher) Marktforschung.
Ich schlage in diesem Beitrag die Betrachtung von statistischer Hypothese vor - einem statistischen Analyseinstrument zur Recherche und Überprüfung entsprechender Rückschlüsse. Wir werden im Folgenden verschiedene Hypothesen im Statistica-Paket und der übertragenen numerischen Analyse-Library ALGLIB MQL5 anhand von Beispielen testen.
1. Das Konzept der Hypothese
Für das Konzept der "statistischen Hypothese" gibt es mehrere Definitionen, wovon einige mit einer Vermutung über die statistischen Eigenschaften des Objekts oder des Phänomens, das gerade untersucht wird, arbeiten.
Eine statistische Hypothese ist eine Annahme über die Wahrscheinlichkeitsgesetze, denen ein entsprechendes Phänomen folgt.
Andere Definitionen heben darauf ab, dass statistische Eigenschaften mit der Verteilung einer gewissen zufälligen Variable oder mit Parametern dieser Verteilung verknüpft sein müssen.
Eine statistische Hypothese ist die Vermutung hinsichtlich Parametern statistischer Verteilung oder des Prinzips der zufälligen Verteilung von Variablen.
In der Fachliteratur zu mathematischer Statistik, wird der Begriff "Hypothese" auf die zweite Art und Weise interpretiert. Daher können wir also unterscheiden:
- Parametrische Hypothese (Hypothese über die Werte der Verteilungsparameter oder über den Vergleichswert der Parameter zweier Verteilungen);
- Nicht-Parametrische Hypothese (Hypothese über die Art der zufälligen Verteilung von Werten).
Im nächsten Abschnitt. besprechen wir die Methode zur Überprüfung einer Hypothese.
2. Hypothesen testen. Theorie
Die Hypothese, die getestet werden soll, heißt Null-Hypothese (Н0). Eine konkurrierende Hypothese (Н1) ist ihre Alternative. Sie befindet sich auf der Rückseite der "Н0-Münze", lehnt also logischerweise die Null-Hypothese ab.
Stellen wir uns nun vor, es gibt eine Datenpopulation zu den Stop Losses irgendeines Handelssystems. Wir geben also zwei Hypothesen an, die die Grundlage für unseren Test bilden.
Н0 – durchschnittlicher Wert des Stop Loss ist gleich 30 Punkte;
Н1 – durchschnittlicher Wert des Stop Loss ist nicht gleich 30 Punkte.
Die Varianten der Akzeptanz und Ablehnung der Hypothesen:
- Н0 ist wahr und akzeptiert;
- Н0 ist falsch und wird zugunsten von Н1 abgelehnt;
- Н0 ist wahr, wird aber zugunsten von Н1 abgelehnt;
- Н0 ist falsch, wird aber akzeptiert.
Die letzten zwei Varianten hängen mit Fehlern zusammen.
Nun muss der Wert der Bedeutung festgelegt werden: er besteht in der Wahrscheinlichkeit, dass die alternative Hypothese akzeptiert wird, wohingegen die wahre Hypothese die Null-Hypothese ist (dritte Variante). Diese Wahrscheinlichkeit soll möglichst gering gehalten werden.
In unserem Fall passiert so ein Fehler, wenn wir davon ausgehen, dass der Stop Loss im Durchschnitt nicht gleich 30 Punkte ist, selbst wenn er dies in Wirklichkeit ist.
Meistens ist der Grad der Bedeutung (α) = 0,05. Das bedeutet, dass der statistische Testwert der Null-Hypothese den kritischen Bereich nur in maximal 5 Fällen von 100 möglichen, "füllen" kann.
Für uns heißt das: der statistische Testwert wird auf einem klassischen Chart bewertet (Abb. 1).
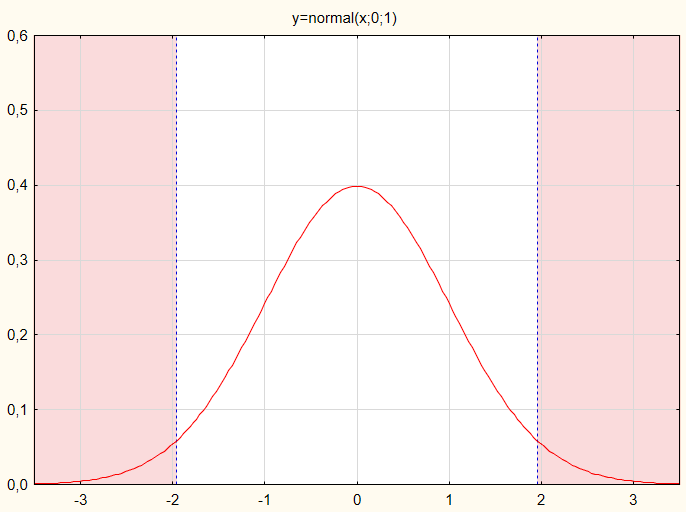
Abb. 1 Abb. 1 Verteilung des statistischen Testwerts per normalem Wahrscheinlichkeitsgesetz
Damit die Null-Hypothese akzeptiert werden kann, dürfen die statistischen Testwerte nicht in die roten Bereichr gelangen. Nehmen wir für unser Beispiel daher an, dass die statistischen Testwerte normal verteilt sind.
Jeder Test hat seine eigene Formel, mit der der statistische Testwert berechnet wird.
Variante 4 lässt darauf schließen, dass ein Fehler des zweiten Typs vorhanden ist (β). In unserem Fall passiert so ein Fehler, wenn wir annehmen, dass der Stop Loss im Durchschnitt gleich 30 Punkte ist und er dies eben nicht ist.
3. Beispiele von Tests statistischer Hypothesen
Die für diese Beispiele verwendeten Quelldaten sind in der Datei Data.xls gespeichert.
3.1 Testen abhängiger Stichproben
Stellen Sie sich mal folgende Situation vor: Angenommen, es gibt ein Handelssystem, das eine Population an Abschlüssen erzeugt. Nehmen wir eine Stichprobe gewinnbringender Abschlüsse mit dem Volumen 100 Einheiten. Die Quelldaten befinden sich im "Profits"-Blatt.
Tabelle 1 zeugt die beschreibende Statistik der Profits-Stichprobe nach dem Löschen der abgelegenen Fälle:
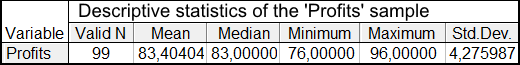
Tabelle 1 Statistik der Profits-Stichprobe
Das Stichproben-Histogramm sieht so aus (Abb. 2).
Abb. 2 Das Profits-Stichproben-Histogramm
Der Mittelwert beträgt 83,4 Punkte und der Zentralwert liegt bei 83 Punkten.
Was geschieht, wenn sich der Markteinstiegspunkt um einige Punkte verändert? Nachdem das Handelssignal erscheint, kann z.B. eine Limit Order platziert werden, die den Einstiegskurs verbessert.
Wie wirkt sich das auf die Ergebnisse aus? Diese Frage kann man mit statistischen Hypothesen beantworten.
Im Statistica-Paket prüfen wir formal, ob die Stichproben nicht aus einer Population entnommen wurden:
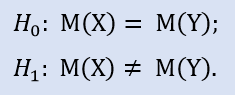
Wenn wir den Einstiegskurs um 15 Punkte ändern, erhalten wir die NewProfits-Stichprobe. Im Idealfall sollte das Ergebnis folgendermaßen aussehen (Abb. 3).
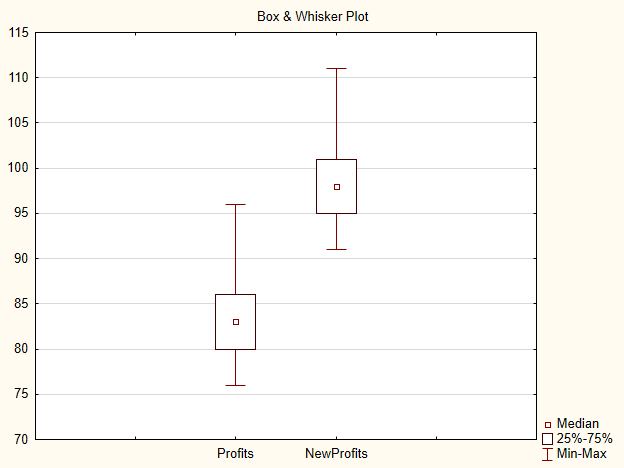
Abb. 3 Abb. 3 Chart für die Stichproben 'Profits' und 'NewProfits'
Die Wahrscheinlichkeit, dass die alternative Hypothese akzeptiert wird ist hoch, da die Zentralwerte der Stichproben unterschiedlich sind.
Dieses Bild erhält man jedoch nur schwer, da es gut sein kann, dass es auf dem Markt keine besseren Kurse gibt. In meinem Fall hat die zweite Stichprobe nach Änderung des Einstiegskurses 84 Abschlüsse enthalten. Die anderen 15 Abschlüsse wurden schlicht nicht ausgeführt. Diese berichtigte Stichprobe nennen wir nun NewProfitsReal.
Auf der grafischen "Box-und-Whisker" Darstellung lässt sich zwischen beiden Stichproben kein großer Unterschied feststellen.
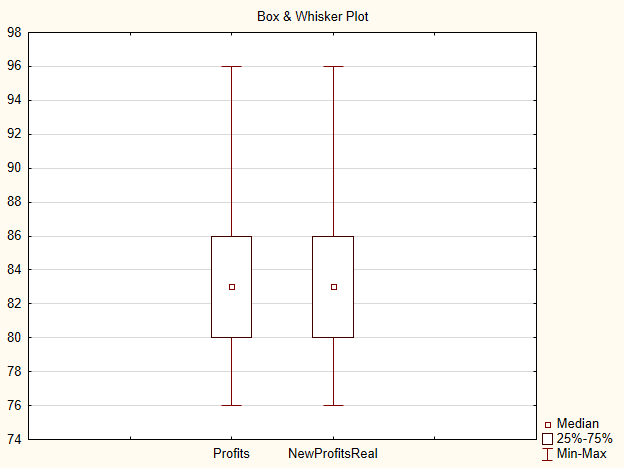
Abb. 4 Grafische Darstellung für die Stichproben 'Profits' und 'NewProfits'
Führen wir nun für eine verknüpfte Stichprobe einen nicht-parameterischen Wilcoxon Signed Rank Test durch.
Tabelle 2 enthält die Ergebnisse:
Tabelle 2 Wilcoxon Testergebnisse für die Stichproben 'Profits' und 'NewProfits'
Der Grad der Bedeutung ist ziemlich hoch, was eindeutig für die Null-Hypothese spricht.
Auf diese Weise können wir also sagen, dass sich die Änderung des Einstiegspunkts nicht auf den Ertrag des Systems ausgewirkt hat - zumindest in relativer Hinsicht. In absoluter Hinsicht jedoch, hat sich das System, aufgrund fehlender Einstiegspunkte als weniger gewinnbringend erwiesen.
Der Wilcoxon Test kann in MQL5 programmatisch durchgeführt werden. Obwohl er den Zentralwert der Verteilung mit dem spezifizierten Wert 'm' umfasst, ist der Unterschied nicht signifikant.
Prüfen wir also nach:
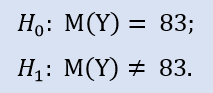
Die ALGLIB-Library enthält das folgende Verfahren: CAlglib::WilcoxonSignedRankTest() und liefert uns ein Ergebnis für drei Testarten: beidseitig, links und rechts.
Das Script test_profits.mq5 liefert ein Beispiel dieser Berechnung. Das "Experts" Logbuch enthält die folgenden Ergebnisse für die NewProfitsReal Stichprobe:
OO 0 12:04:08.814 test_profits (EURUSD.e,H1) p-value for the two-sided test: 0.7472 HD 0 12:04:08.814 test_profits (EURUSD.e,H1) p-value for the left-sided test: 0.6285 CM 0 12:04:08.814 test_profits (EURUSD.e,H1) p-value for the right-sided test: 0.3736
Der linke Test hat die Form von:
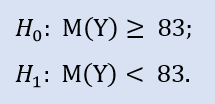
Hier prüfen wir die Alternative, dass der Zentralwert der NewProfitsReal Stichprobe größer oder gleich 83 sein kann. Fehlerwahrscheinlichkeit bei Ablehnung von H0 = 0,63. H0 kann also akzeptiert werden.
Der rechte Test sieht so aus:
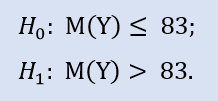
In diesem Test prüfen wir die Alternative, dass der Zentralwert der NewProfitsReal Stichprobe kleiner oder gleich 83 sein kann. Fehlerwahrscheinlichkeit bei Ablehnung von H0 = 0,37. H0 kann also akzeptiert werden.
3.2 Testen unabhängiger Stichproben
Nehmen wir nun an, wir müssen überprüfen, wie schnell unterschiedliche Makler Handelsorders verarbeiten und ob es zwischen den Maklern in Bezug auf die Ausführungszeit der Handelsorders irgendwelche Unterschiede gibt.
Es gibt also zwei Stichproben an Quelldaten für unsere Analyse. Jede Stichprobe enthielt ursprünglich 50 Beobachtungen. Nachdem abgelegene Fälle gelöscht wurden, verblieben in der ersten Stichprobe noch 48 Beobachtungen (Makler А), und in der zweiten 49 (Makler B). Die Daten befinden sich im "ExecutionTime"-Blatt.
Wir überprüfen:
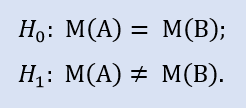
Stellen wir die Stichprobe-Indices als Bild dar (Abb. 5). Wie wir anhand der grafischen Darstellung sehen, unterschieden sich die Zentralwerte zwar, jedoch nicht signifikant.
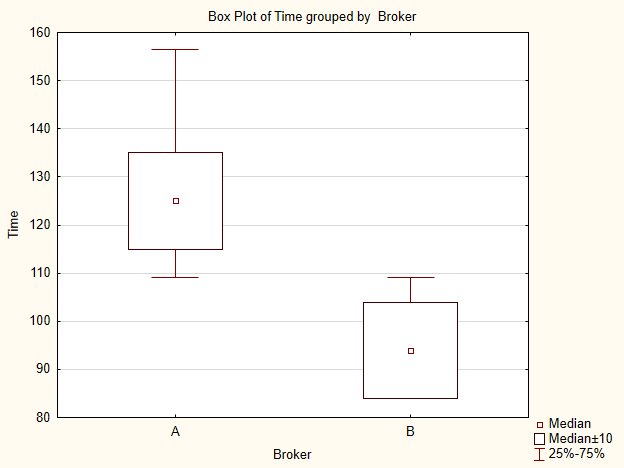
Abb. 5 Grafische Darstellung der Datenstichproben von Makler A und Makler B
Da wir nicht wissen, zu welcher Verteilung jede Stichprobe gehört, ziehen wir zum Vergleich nichtparametrische Tests heran, z.B.
den Mann — Whitney U-Test (Tabelle 3). Er gilt als der, mit dem man die meisten Informationen erhält.
Tabelle 3 Mann — Whitney U-Testergebnisse für die Datenstichproben von Makler A und Makler B
Schlussfolgerung: Die Testergebnisse weichen voneinander ab, und daher wird die Null-Hypothese bzgl. Gleichheit der Stichproben zugunsten von Н1 abgelehnt.
Der Mann — Whitney U-Test kann in MQL5 programmatisch durchgeführt werden. In der ALGLIB-Library findet sich das CAlglib:: MannWhitneyUTest()-Verfahren. Es liefert uns ein Ergebnis für drei Testarten: beidseitig, links und rechts.
Das Script test_time_execution.mq5 liefert ein Beispiel dieser Berechnung. Das "Expert" Logbuch enthält das folgende Ergebnis, das zum Vergleich der Stichproben verwendet werden kann:
MR 0 12:55:08.577 test_time_execution (EURUSD.e,H1) p-value for the two sided test: 0.0001 QF 0 12:55:08.577 test_time_execution (EURUSD.e,H1) p-value for the left-sided test: 1.0000 PF 0 12:55:08.577 test_time_execution (EURUSD.e,H1) p-value for the right-sided test: 0.0001
Der linke Test hat die Form von:
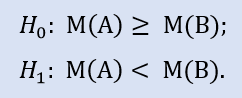
Die Null-Hypothese ist, dass der Zentralwert der Datenstichprobe von Makler A größer oder gleich dem Zentralwert der Datenstichprobe von Makler B sein kann. Die Alternative ist ihre Ablehnung. Fehlerwahrscheinlichkeit bei Ablehnung von H0 = 1,0. H0 kann also akzeptiert werden.
Der rechte Test sieht so aus:
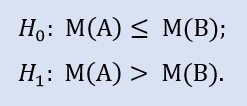
Die Null-Hypothese ist, dass der Zentralwert der Datenstichprobe von Makler A kleiner oder gleich dem Zentralwert der Datenstichprobe von Makler B sein kann. Die Alternative ist die Ablehnung.
Fehlerwahrscheinlichkeit bei Ablehnung von H0 = 0,0. Daher wird H0 zugunsten von Н1 abgelehnt.
3.3 Testen der Zusammenhang
Stellen Sie sich ein Portfolio an Strategien vor. Das Ziel ist, die Zahl der Strategien im Portfolio zu verringern.
Das Auswahlkriterium ist folgendes: wenn sich zwei Strategien beim Vergleich der Stop Loss-Reihen als identisch erweisen, wird eine der beiden Strategien aus dem Portfolio entfernt. Dazu nehmen wir zwei Stichproben mit Stop Loss-Daten verschiedener Systeme. Annahme: Systeme reagieren bei Markteinstieg gleich und bei Marktaustritt unterschiedlich.
Wir arbeiten mit dem Spearmans Rank-Order Correlation-Test. Im "Correlation"-Blatt der Datendatei finden wir drei Stichproben
Wir prüfen nach, ob der Korrelationskoeffizient = "0" ist:
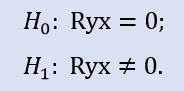
Vergleich des Stichprobenpaars Stops1-Stops2 liefert uns folgendes Ergebnis (Tabelle 4).
Tabelle 4 Spearmans Rank-Order Correlation-Test für die Stops1 und Stops2 Stichproben
In diesem Fall kann die Null-Hypothese über das Nichtvorhandensein einer Verbindung zwischen Elementen der Stichproben nicht zugunsten der Alternative abgelehnt werden. Daher wird sie also akzeptiert.
Die grafische Darstellung in Abb. 6 zeigt, dass die Daten keine deutliche Konfiguration bilden. Die Daten werden grafisch auf der Ebene als Punktwolke dargestellt.
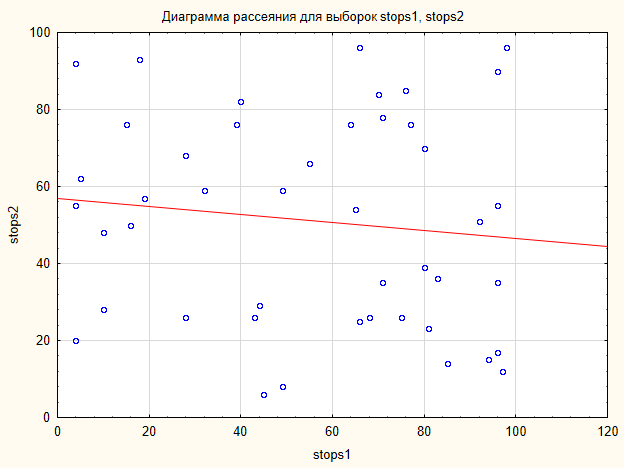
Abb. 6 Punktwolke für die Stops1 und Stops2 Stichproben
Tabelle 5 zeigt die Ergebnisse der Prüfung der Beziehung zwischen den Stops1-Stops3 Stichproben:
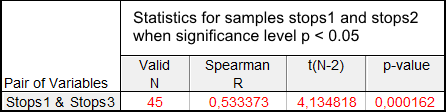
Tabelle 5 Ergebnisse des Spearmans Rank-Order Correlation-Test für die Stops1 und Stops3 Stichproben
In diesem Fall kann die Null-Hypothese abgelehnt werden, da die Wahrscheinlichkeit eines Fehlers ziemlich gering ist.
Daher wird die Alternative über eine bestehende Beziehung akzeptiert. Die Beziehung sieht so aus (Abb. 7).
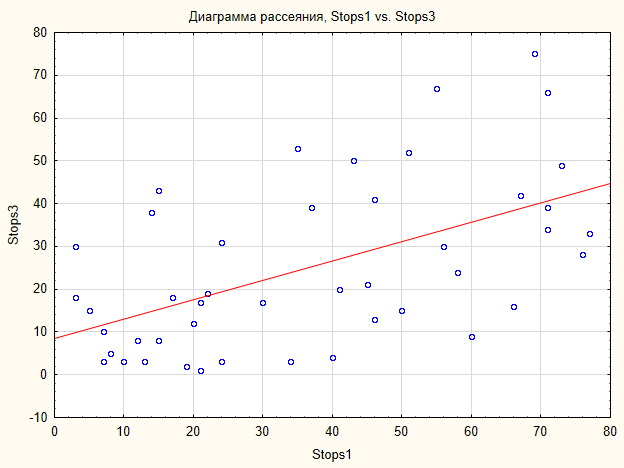
Abb. 7 Punktwolke für die Stops1 und Stops3 Stichproben
Das Ergebnis wird mit dem Code in MQL5 bestätigt. Die Datei test_correlation.mq5 enthält ein Berechnungsbeispiel.
Die ALGLIB-Library enthält das CAlglib::SpearmanRankCorrelationSignificance()-Verfahren, das den Test der Bedeutung des Spearmans Rank-Order Korrelationskoeffizienten implementiert.
Das Logbuch enthält die folgenden Einträge:
OO 0 12:57:43.545 test_correlation (EURUSD.e,H1) ---===Samples Stops1 and Stops2===--- GO 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the two-sided test: 0.9840 KK 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the left-sided test: 0.4920 JJ 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the right-sided test: 0.5080 DM 0 12:57:43.545 test_correlation (EURUSD.e,H1) HJ 0 12:57:43.545 test_correlation (EURUSD.e,H1) ---===Samples Stops1 and Stops3===--- NS 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the two-sided test: 0.0002 RO 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the left-sided test: 0.9999 FG 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the right-sided test: 0.0001
Der linke Test hat die Form von:
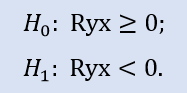
In diesem Test wird die Null-Hypothese verifiziert - nämlich, dass es eine nicht-negative Korrelation zwischen Variablen gibt (also der Zusammenhang ist entweder "0" oder negativ) .
Der linke Test zeigt, dass für das Stops1-Stops2 Stichprobenpaar die Null-Hypothese akzeptiert wird. Der linke Test zeigt, dass auch für das Stops1-Stops3 Stichprobenpaar die Null-Hypothese akzeptiert wird. Stellt sich die logische Frage: "Warum gibt es keine Korrelation zwischen den Stops1-Stops2 Stichproben, aber eine zwischen den Stops1-Stops3 Stichproben?" Das liegt daran, weil die Aussage in der Prüfung lautete: "größer oder gleich "0". Im ersten Fall ist "gleich 0" wichtig für H0; im zweiten Fall ist es "größer als 0".
Der rechte Test sieht so aus:
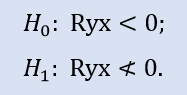
Hier wird die Null-Hypothese geprüft, was denn eine negative Korrelation ist.
Für das Stops1-Stops2 Stichprobenpaar zeigt der rechte Test, dass die Null-Hypothese akzeptiert wird. Für das Stops1-Stops3 Stichprobenpaar zeigt der rechte Test, dass die Null-Hypothese abgelehnt wird.
Eine letzte Bemerkung. Der Test bewies, dass es zwischen den Stops1-Stops3 Stichproben eine positive, wahrscheinliche Korrelation gibt Die Stärke dieser Verknüpfung ist ihr Durchschnitt. Daher bleibt es dem Händler überlassen, ob er Strategie 1 oder 3 ablehnt.
Fazit
Ich habe in diesem Beitrag anhand von Beispielen zu zeigen versucht, das quantitative Variablen mit Hilfe mathematischer Statistik bewertet werden können. Ich hoffe, dass dieser Beitrag für Programmierneulinge für ihre zukünftigen Handelssysteme hilfreich ist. Des Weiteren hoffe ich auch, dass die Beitragsreihe über den Einsatz von Methoden der mathematischen Statistik fortgeführt wird.
Die Dateien der ALGLIB-Library müssen nicht extra heruntergeladen werden.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/1240
Grundlagen der Programmierung in MQL5: Globale Variablen des Terminals
Programmierung von EA-Modi mit Hilfe des Objekt-orientierten Ansatzes
Liquid-Chart
Bidirektionaler Handel und Absicherung von Positions in MetaTrader 5 mit Hilfe des HedgeTerminal Panels - Teil 1
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.