Статистические рецепты для трейдера - Гипотезы
6 309
6
Введение
Любой трейдер, у которого есть желание создать свою торговую систему, рано или поздно превращается в аналитика. Он пытается найти закономерности на рынке и проверить ту или иную торговую идею. Тестирование идеи может основываться на разных подходах, начиная от обычного поиска лучших значений параметров в режиме оптимизации Тестера стратегий, заканчивая научными (а иногда и псевдонаучными) исследованиями рыночных данных.
В данной статье я предлагаю рассмотреть такой инструмент статистического анализа для исследования и проверки выводов, как статистическая гипотеза. Попробуем на примерах протестировать различные гипотезы с помощью пакета Statistica и портированной библиотеки численного анализа ALGLIB MQL5.
1. Гипотеза, понятие
Есть несколько определений понятия "статистическая гипотеза". Некоторые из них просто касаются предположения о статистических свойствах изучаемого объекта или явления.
Статистическая гипотеза – это предположительное суждение о вероятностных закономерностях, которым подчиняется изучаемое явление.
Другие указывают, что эти свойства должны быть связаны с распределением некоторой случайной величины или параметрами этого распределения.
Статистическая гипотеза – это предположение относительно параметров статистического распределения или закона распределения случайной величины.
В профильной литературе по математической статистике понятие "гипотеза" чаще всего трактуется по второму варианту. Тогда бывают:
- Параметрическая гипотеза (гипотеза о значениях параметров распределения или о сравнительной величине параметров двух распределений);
- Непараметрическая гипотеза (гипотеза о виде распределения случайной величины).
В следующем разделе познакомимся с методикой проверки гипотез.
2. Проверка гипотез, теория
Гипотеза, которую нужно проверить, называется нулевой (Н0). Для нее подбирают альтернативу – конкурирующую гипотезу (Н1). Она является обратной стороной медали для Н0, т.е. логически отрицает нулевую гипотезу.
Представьте, что имеется совокупность данных по стоп-лоссам некоторой торговой системы. Сформируем пару гипотез, образующих базис для проверки.
Н0 – среднее значение стоп-лосса равно 30 пунктов;
Н1 – среднее значение стоп-лосса не равно 30 пунктов.
Варианты принятия-отвержения гипотез:
- верна Н0, и она принимается;
- не верна Н0, и она отвергается в пользу Н1;
- верна Н0, но она отвергается в пользу Н1;
- не верна Н0, но она принимается.
Последние 2 варианта связаны с ошибками.
Теперь нужно выбрать значение уровня значимости. Это вероятность того, что будет принята альтернативная гипотеза, тогда как верной окажется нулевая (третий вариант). Естественно, что эту вероятность желательно минимизировать.
В нашем примере такая ошибка случится, если сочтем, что стоп-лосс в среднем не равен 30 пп при условии, что он действительно равен этому числу пунктов.
Как правило, значение уровня значимости (α) равно 0,05. То есть, не более чем в 5 случаях из 100 допускается попадание значение критерия проверки нулевой гипотезы в критическую область.
В нашем примере оценивать критерий будем по хрестоматийному графику (рис.1).
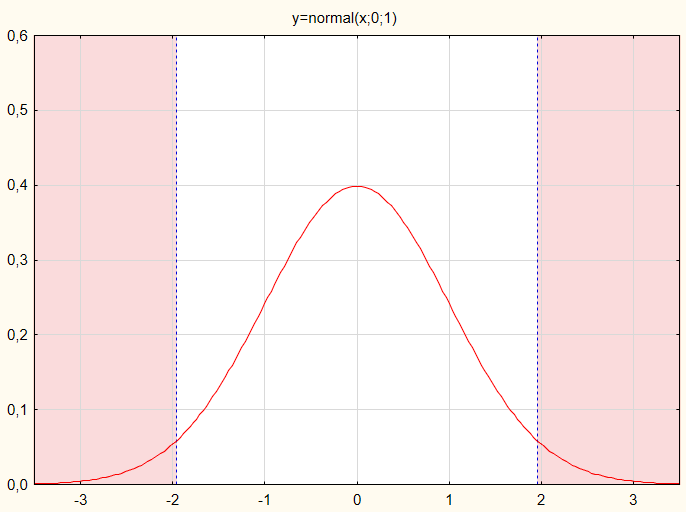
Рис.1. Распределение критерия по нормальному закону
Чтобы нулевая гипотеза была принята, критерий не должен попасть в красные зоны. Для целей примера допустим, что сам критерий распределен нормально.
Для каждого статистического теста есть своя формула, по которой рассчитывается критерий.
Вариант 4 подразумевает, что имеет место ошибка второго рода (β). В нашем примере такая ошибка случится, если сочтем, что стоп-лосс в среднем равен 30 пп при условии, что он действительно не равен этому числу пунктов.
3. Проверка гипотез, примеры
Все исходные данные, используемые для примеров, находятся в файле Data.xls.
3.1. Проверка зависимых выборок
Представим следующую ситуацию. Допустим, есть торговая система, которая генерирует некоторую совокупность торговых сделок. Составим выборку из прибыльных сделок объемом 100 единиц. Исходные данные находятся в листе "Profits".
Описательная статистика выборки Profits после удаления выбросов представлена в табл.1:
Табл.1. Статистика выборки Profits
Гистограмма выборки выглядит следующим образом (рис.2).
Рис.2. Гистограмма для выборки Profits
Среднее значение выборки равно 83,4 пп, медиана – 83 пп.
Что если немного изменить точку входа в рынок на несколько пунктов? Например после появления торгового сигнала можно выставлять лимитный ордер, улучшающий цену входа.
Как поменяются результаты? На этот вопрос можно ответить с помощью статистических гипотез.
В пакете Statistica формально проверяем, не извлечены ли выборки из одной генеральной совокупности:
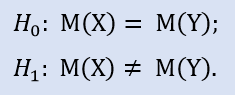
Изменим цену входа на 15 пунктов, получим выборку NewProfits. В идеале должна получиться такая картинка (рис.3).
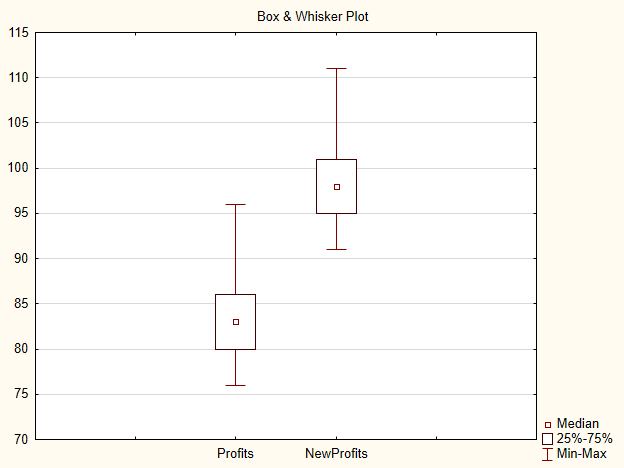
Рис.3. График для выборок Profits и NewProfits
Высока вероятность, что будет принята альтернативная гипотеза, т.к. медианы выборок отличаются.
Но такую картину вряд ли удастся получить, т.к. рынок может не дать лучшие цены. В моем случае, при изменении цены входа, во вторую выборку попало 84 сделки. А другие 15 сделок просто не были совершены. Назовем эту скорректированную выборку NewProfitsReal.
На графике типа "ящик с усами" нет практически никакой разницы между выборками.
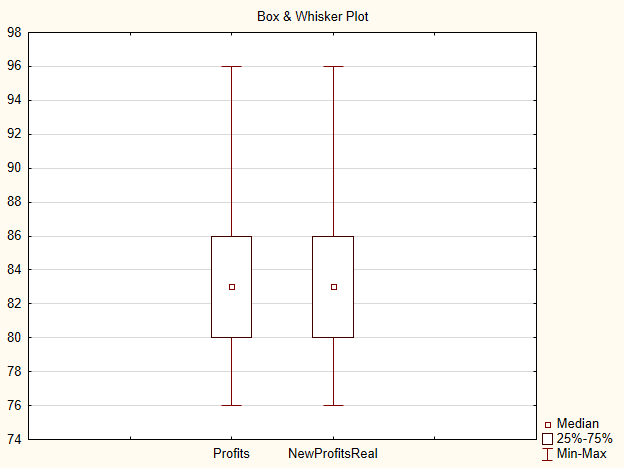
Рис.4. График для выборок Profits и NewProfitsReal
Проведем непараметрический тест по критерию Уилкоксона для связных выборок.
Результаты представлены в табл.2:
Табл.2. Результаты теста по критерию Уилкоксона для выборок Profits, NewProfitsReal
Уровень значимости очень высокий, что свидетельствует в пользу принятия нулевой гипотезы.
Таким образом, можно сделать вывод о том, что изменение точки входа не повлияло на доходность системы. Это в относительном смысле. В абсолютном же выражении, из-за пропущенных точек входа, система оказалась менее прибыльной.
Интересно, что в MQL5 программным образом тоже можно провести тест Уилкоксона. Правда он сравнивает медиану распределения с заданным значением m. Но это отличие непринципиальное.
Формально проверяем:
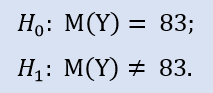
В библиотеке ALGLIB есть такая процедура: CAlglib::WilcoxonSignedRankTest(). Она сразу же дает результат для 3 видов теста: двухстороннего, левостороннего и правостороннего.
В скрипте test_profits.mq5 есть пример расчета. В журнале "Эксперты" увидим следующие результаты для выборки NewProfitsReal:
OO 0 12:04:08.814 test_profits (EURUSD.e,H1) p-значение для двухстороннего теста: 0.7472 HD 0 12:04:08.814 test_profits (EURUSD.e,H1) p-значение для левостороннего теста: 0.6285 CM 0 12:04:08.814 test_profits (EURUSD.e,H1) p-значение для правостороннего теста: 0.3736
Левосторонний тест имеет форму:
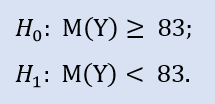
Здесь проверяем альтернативу, что медиана выборки NewProfitsReal может быть больше или равна 83. Вероятность ошибки при отвержении H0 равна 0,63. Поэтому H0 принимается.
Правосторонний тест имеет форму:
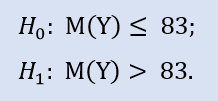
Здесь проверяем альтернативу, что медиана выборки NewProfitsReal может быть меньше или равна 83. Вероятность ошибки при отвержении H0 равна 0,37. Поэтому H0 принимается.
3.2. Проверка независимых выборок
Допустим, что нужно проверить, как быстро обрабатываются торговые приказы у различных брокеров, и есть ли отличие между брокерами относительно времени исполнения торгового приказа.
Итак, для целей анализа были созданы 2 выборки исходных данных. В каждой выборке изначально находилось 50 наблюдений. После удаления выбросов в первой выборке (брокер А) осталось 48 наблюдений, во второй (брокер B) – 49 наблюдений. Данные находятся в листе "ExecutionTime".
Формально проверяем:
Визуализируем показатели выборок (Рис.5). Судя по графику, значения медиан хотя и несильно, но отличаются.
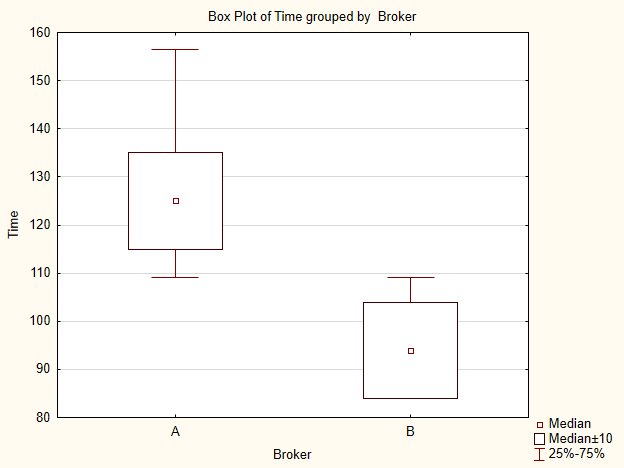
Рис.5. График для выборок данных брокера A и B
Поскольку мы априори не знаем, к какому распределению относится каждая выборка, то обратимся к непараметрическим тестам для сравнения.
Например, воспользуемся U-критерием Манна-Уитни (табл.3). Среди непараметрических он считается одним из самых мощных.
Табл.3. Результаты теста по U-критерию Манна-Уитни для выборок данных брокера A и B
Вывод – есть отличие по тестам, нулевая гипотеза о равенстве выборок отвергается в пользу Н1.
В MQL5 программным образом тоже можно провести тест Манна-Уитни. В библиотеке ALGLIB есть процедура CAlglib:: MannWhitneyUTest(). Она сразу же дает результат для 3 видов теста: двухстороннего, левостороннего и правостороннего.
В скрипте test_time_execution.mq5 есть пример расчета. В журнале "Эксперты" увидим следующие результаты для сравнения выборок:
MR 0 12:55:08.577 test_time_execution (EURUSD.e,H1) p-значение для двухстороннего теста: 0.0001 QF 0 12:55:08.577 test_time_execution (EURUSD.e,H1) p-значение для левостороннего теста: 1.0000 PF 0 12:55:08.577 test_time_execution (EURUSD.e,H1) p-значение для правостороннего теста: 0.0001
Левосторонний тест имеет форму:
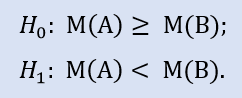
Нулевая гипотеза - медиана выборки данных брокера A может быть больше или равна медиане выборки данных брокера B. Альтернатива – ее отрицание. Вероятность ошибки при отвержении H0 равна 1,0. Поэтому H0 принимается.
Правосторонний тест имеет форму:
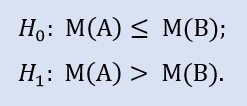
Нулевая гипотеза - медиана выборки данных брокера A может быть меньше или равна медиане выборки данных брокера B. Альтернатива – ее отрицание.
Вероятность ошибки при отвержении H0 равна 0,0. Поэтому H0 отвергается в пользу Н1.
3.3. Проверка корреляции
Представьте, что имеется некоторый портфель стратегий. Задача заключается в том, чтобы сократить число этих стратегий в портфеле.
Критерий для решения может быть таким: если при сравнении серий стоп-лоссов две стратегии окажутся одинаковыми, то одну стратегию из портфеля убираем. Для исследования возьмем две выборки, представляющие данные по стоп-лоссам двух различных торговых систем. Допущение: системы одинаково реагируют на вход в рынок, но по-разному реагируют на выход из него.
Воспользуемся тестом ранговой корреляции Спирмена. В файле данных, лист "Correlation", есть 3 выборки.
Формально проверяем, равно ли нулю значение коэффициента корреляции:
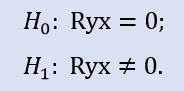
Если сравнить пару выборок Stops1-Stops2, то получим такие результаты (табл.4).
Табл.4. Результаты теста ранговой корреляции Спирмена для выборок Stops1, Stops2
Здесь нулевую гипотезу об отсутствии связи между элементами выборок в пользу альтернативы отвергнуть нельзя. Значит, она принимается.
На графике (рис.6) можно заметить, что данные не образуют какую-то заметную конфигурацию. Они скорее рассеяны по всей плоскости графика.
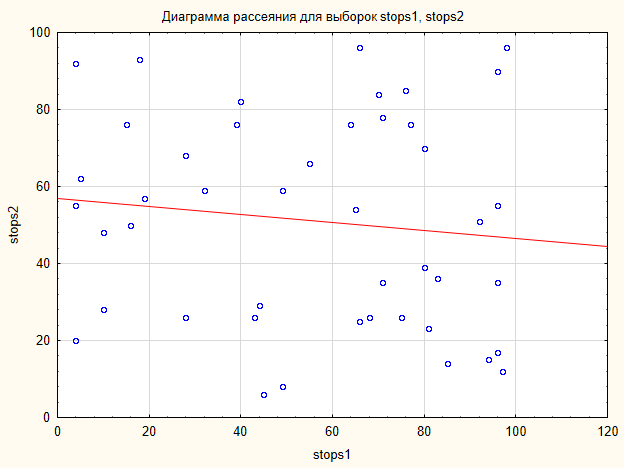
Рис.6. Диаграмма рассеяния для выборок Stops1, Stops2
Результаты проверки связи между выборками Stops1-Stops3 приведены в табл.5:
Табл.5 Результаты теста ранговой корреляции Спирмена для выборок Stops1, Stops3
Здесь нулевую гипотезу можно отвергнуть – слишком низкая вероятность ошибки.
Значит, принимается альтернатива о наличии связи. Визуально зависимость выглядит так (рис.7).
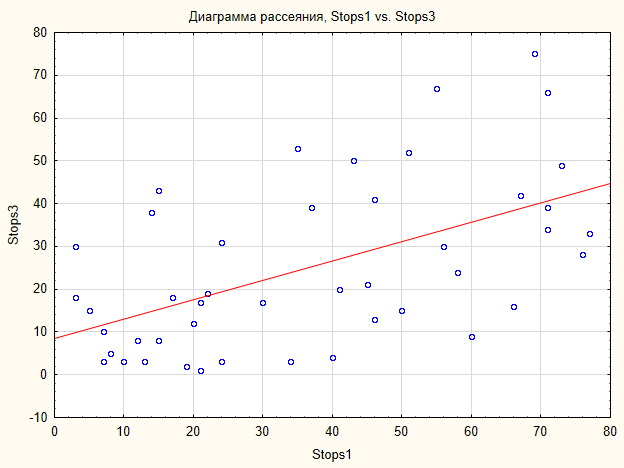
Рис.7. Диаграмма рассеяния для выборок Stops1, Stops3
Подтвердим результаты кодом в MQL5. В скрипте test_correlation.mq5.есть пример расчета.
В самой библиотеке ALGLIB имеется процедура CAlglib::SpearmanRankCorrelationSignificance(), которая реализует тест на значимость коэффициента ранговой корреляции Спирмена
В журнале появятся такие записи:
OO 0 12:57:43.545 test_correlation (EURUSD.e,H1) ---===Выборки Stops1 и Stops2===--- GO 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-значение для двухстороннего теста: 0.9840 KK 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-значение для левостороннего теста: 0.4920 JJ 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-значение для правостороннего теста: 0.5080 DM 0 12:57:43.545 test_correlation (EURUSD.e,H1) HJ 0 12:57:43.545 test_correlation (EURUSD.e,H1) ---===Выборки Stops1 и Stops3===--- NS 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-значение для двухстороннего теста: 0.0002 RO 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-значение для левостороннего теста: 0.9999 FG 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-значение для правостороннего теста: 0.0001
Левосторонний тест имеет форму:
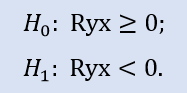
Здесь проверяется нулевая гипотеза о том, что между переменными имеется неотрицательная корреляция (т.е. либо нулевая корреляция, либо положительная).
Для пары выборок Stops1-Stops2 левосторонний тест показал, что нулевая гипотеза принимается. Для пары выборок Stops1-Stops3 левосторонний тест показал, что нулевая гипотеза тоже принимается. Почему так, если между выборками Stops1-Stops2 связи нет, а между выборками Stops1-Stops3 связь есть? Причина в том, что проверяется утверждение "больше или равно нулю". В первом случае на стороне H0 играет "равно нулю", а во втором – "больше".
Правосторонний тест имеет форму:
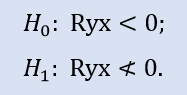
Здесь проверяется нулевая гипотеза о том, что есть отрицательная корреляция.
Для пары выборок Stops1-Stops2 правосторонний тест показал, что нулевая гипотеза принимается. Для пары выборок Stops1-Stops3 правосторонний тест показал, что нулевая гипотеза отвергается.
И еще одно замечание. В ходе теста было выявлено, что между выборками Stops1-Stops3 есть положительная вероятностная связь. Но сила этой связи носит скорее средний характер. Поэтому решение об отказе от стратегии 1 или 3 в портфеле остается за трейдером.
Заключение
В своей статье я попытался на примерах показать, что можно рассуждать и делать выводы о количественных параметрах с использованием аппарата математической статистики. Надеюсь, материал статьи будет полезен для начинающих разработчиков своих будущих, а главное, осмысленных торговых систем. Также надеюсь, что серия статей об использовании методов математической статистики будет продолжена.
Файлы библиотеки ALGLIB нужно скачать отдельно.
Основы биржевого ценообразования на примере срочной секции Московской биржи
Оптимизировать оптимизацию: несколько простых идей
Программируем режимы работы советника с помощью ООП
Третье поколение нейросетей: "Глубокие нейросети"
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Интересный парадокс. Где можно об этом узнать поподробнее?
Интересный парадокс. Где можно об этом узнать поподробнее?
Уточните, что подразумеваете под эргодичной средой.От Вашей статьи двоякое впечатление.
Плюс. На данном форуме очень важной является сама по себе постановка вопроса о гипотетичной оценке результатов. На форуме полно людей, которые рисуют машку и считают, что это так и есть, а не машка в интервале.
Минус.
Полностью согласен с Решетовым. Все, что Вы рассказали - это относится к стационарным рядам или близким к ним - т.е. рядам, у которых с течением времени мало меняется мо и дисперсия. А таких рядов на финансовых рынках не бывает и все применение статитстики на финансовых рынках вертится вокруг стационарности временных рядов. Наиболее известные примеры: ARIMA, ARCH и все остальное.
Ваш случайный ряд, гистограмма которого приведена на рис.2, говорит о том, что ряд имеет слабое отношение к стационарному, он скошен и имеет существенно разные хвосты. Особенно это хорошо видно по отношению к нарисованной Вами идеально нормальной кривой. В силу этого все Ваши рассуждения ВООБЩЕ не применимы к Вашему примеру. Этот как раз является иллюстрацией мыслей Решетова.
ПС. Самое опасно и подлое понятие в статистике - это корреляция. Лучше вообще ее не упоминать.
...Все, что Вы рассказали - это относится к стационарным рядам или близким к ним - т.е. рядам, у которых с течением времени мало меняется мо и дисперсия. А таких рядов на финансовых рынках не бывает и все применение статитстики на финансовых рынках вертится вокруг стационарности временных рядов. Наиболее известные примеры: ARIMA, ARCH и все остальное.
Ваш случайный ряд, гистограмма которого приведена на рис.2, говорит о том, что ряд имеет слабое отношение к стационарному, он скошен и имеет существенно разные хвосты. Особенно это хорошо видно по отношению к нарисованной Вами идеально нормальной кривой. В силу этого все Ваши рассуждения ВООБЩЕ не применимы к Вашему примеру. Этот как раз является иллюстрацией мыслей Решетова.
Спасибо за мнение!
Приведу свои контраргументы.
Стационарность - это характеристика временного ряда. На рис.2 вариационный ряд. О временных рядах речь в статье не идёт! Хотя согласен с тем, что время - это полезная характеристика...
Насколько понимаю, под эргодичностью подразумевается некоторая стабильность изучаемой системы...
Так вот, хотелось бы заметить важный момент. Если система, пусть говорим о временном финансовом ряде, не является стационарной, всё равно с помощью эконометрики можем подобрать устойчивую модель (например GARCH), описывающую поведение модели. И в этом вижу постоянство системы - поведение согласно модели... но с условием, что есть какая-то вероятность, что система "поломает" модель...
Спасибо за мнение!
Приведу свои контраргументы.
Стационарность - это характеристика временного ряда. На рис.2 вариационный ряд. О временных рядах речь в статье не идёт! Хотя согласен с тем, что время - это полезная характеристика...
Насколько понимаю, под эргодичностью подразумевается некоторая стабильность изучаемой системы...
Так вот, хотелось бы заметить важный момент. Если система, пусть говорим о временном финансовом ряде, не является стационарной, всё равно с помощью эконометрики можем подобрать устойчивую модель (например GARCH), описывающую поведение модели. И в этом вижу постоянство системы - поведение согласно модели... но с условием, что есть какая-то вероятность, что система "поломает" модель...
Когда-то, несколько лет назад я опубликовал здесь на сайте статью, в которой обосновывал одну совершенно не приемлемую для большинства мысль. А именно.
Полно индикаторов. При этом все считают, что если индикатор нарисовать, то оно так и есть - ведь мы вот это самое и видим. При этом большинству не приходит в голову, что ТО, что мы видим в действительности может не существовать! Причина банальна. Если взять соответствующую индикатору регрессию, то запросто может оказаться, что несколько ее коэффициенты имеют столь широкие доверительные интервалы, что говорить о величине такого коэффициента вообще нельзя, а если выкинуть такой дефектный коэффициент, то рисунок индикатора будет совсем другой. Когда говорят: есть, правда, есть ложь, а есть статистика, то имеется ввиду именно это грустное и очень не привычное обстоятельство - ничему верить нельзя, включая доверительные интервалы.
Именно поэтому ушел из параметрических моделей и занялся моделями на базе машинного обучения. Там нет проблем со стационарностью, но проблемы с переобученностью во всей красе.
А мне статья понравилась.
Да, замечания Сан Саныча и Решетова законны - если сравниваемые системы (или система) поменяет свои параметры, то результаты теста будут бесполезны.
Но сама демонстрация применения методов радует. Для Форекса это редкость!
Я бы сказал еще кое-что, как человек, применяющий похожие методы именно для цен котировок. Можно заранее проверить, является ли среда гомогенной (на двух независимых больших по объему выборках), а затем уже с известной долей спокойствия довериться результатам проверки гипотезы. Это тоже возможно сделать благодаря тем же самым тестам.