Redes Neurais Simples e Econômica - Conecte o NeuroPro com o MetaTrader 5

MetaTrader 5 — Integração | 28 maio 2015, 09:50

3 186

ds2

Sobre o NeuroPro

O programa NeuroPro foi escrito em um dos institutos russos em 1998, sendo ainda relevante nos dias de hoje.

Ele é executado de forma eficiente no Windows XP, Vista e Windows 7. Eu não posso dizer como ele funciona nas versões mais novas do Windows, já que eu não testei nelas.

Sobre o NeuroPro

Fig. 1. Sobre o NeuroPro

A versão 0.25 é gratuita e pode ser encontrada em muitos sites pela Internet. O NeuroPro pode criar redes neurais em multi camadas com a função de ativação do tipo sigmóide. Se você só começou a aprender as redes neurais agora, você não precisará de mais recursos nesta fase. Deve-se ter em mente que a interface do NeuroPro está em russo e não foi traduzido para outros idiomas.

Uma rede neural pode ser treinada em um array de dados e, em seguida, testada em outro. Isto é uma característica essencial para os traders, pois ela permite compreender rapidamente se a estrutura da rede selecionada está propensa a overfitting e se ele pode negociar de forma consistente fora dos dados históricos, ou seja, em uma conta real.

Aqueles que gostam de ir mais a fundo, têm a oportunidade de ver os pesos da rede neural, bem como quais são as entradas de rede que mais influenciam no resultado das operações de rede. Os iniciantes não precisam disso, podendo pular esta parte do programa. Esta informação é útil para os traders experientes que procuram o Santo Graal, pois isto lhe permite assumir qual padrão foi identificado pela rede neural e ver onde eles podem continuar a sua pesquisa.

Fora disso, não há recursos significativos no NeuroPro, exceto as várias configurações e utilitários úteis, como o minimizador da estrutura da rede. Essas seções de menu não são de uso obrigatórios, assim, os novatos não precisam complicar as coisas, podendo usar somente as configurações padrão.

Do ponto de vista de um trader, o NeuroPro tem apenas uma desvantagem - a ausência de integração com o MetaTrader 5. Na verdade, este artigo é dedicado principalmente no carregamento dos dados do mercado e indicador do MetaTrader 5 para o NeuroPro e depois transformar a rede neural recebida em um Expert em MQL5.

Avançando o tema, eu posso dizer que a rede neural que nós vamos criar com o NeuroPro será convertido com todos os pesos do neurônio em um script em MQL5 (ao contrário do sistema de incluir DLL´s como em qualquer outro programa de rede neural). Isso vai garantir um trabalho rápido e o uso mínimo de recursos do computador. Isso é uma clara vantagem de usar NeuroPro. Ele pode ser usado para a criação de quaisquer estratégias de negociação, até mesmo de escalpelamento com a exigência de que o Expert tome decisões quase que instantaneamente.

Estratégia de Negociação

Neste artigo não vamos considerar escalpelamento porque o processo de criação, treinamento e teste de Experts de escalpelamento possuem um monte de peculiaridades e vai além deste artigo.

Para fins educacionais vamos criar um Expert simples para o tempo gráfico H1, pelo popular par de moeda EURUSD. Então, vamos deixar nosso Expert analisar as últimas 24 barras, ou seja, o comportamento de mercado no último dia, prever a direção do movimento dos preços na hora seguinte e, em seguida, negociar com base nessa informação.

Como carregar dados do MetaTrader para o NeuroPro

Formato de Dados Suportados

NeuroPro lê os dados apenas nos formatos de DBMS (tabelas DBMS Paradox) e DBF (tabelas DBMS FoxPro e dBase). DBF é o formato mais comum no mundo e se você é um programador experiente, você deve ter se deparado com ela muitas vezes. Nós vamos usar este formato também.

O algoritmo da transferência de dados no NeuroPro é o seguinte:

escrever um script para o MetaTrader, carregar os dados necessários para um arquivo de texto no formato CSV dividindo os dados com vírgulas;
com o uso de programas especiais, converter CSV em DBF;
abrir o DBF no NeuroPro.

Carregar os Dados do MetaTrader

Ao escrever um script de carregamento de dados, algumas nuances devem ser levadas em conta:

o nome de campo dos dados em DBF não pode ser maior do que 11 símbolos, além disso, alguns conversores cortam o campo para 10. É por isso que os nomes de campo não deve ser maiores do que 10 símbolos;
em redes neurais com um grande número de entrada de barras, os nomes de campo são geralmente do tipo "BarN", onde N é um número seqüencial da barra. No nosso caso, haverá 24 campos e os nomes, consequentemente, vão variar de "Bar1" a "Bar24". Eu recomendo, embora não seja obrigatório, escrever os nomes de tais campos como "Bar___N__" (nos três primeiros subtraços e, em seguida, dois). Mais abaixo, quando estaremos escrevendo o Expert, você vai ver o porquê.

Abaixo está um script pronto para a nossa estratégia de teste (que também está anexado a este artigo):

#property script_show_inputs
//+------------------------------------------------------------------+
input string    Export_FileName  = "NeuroPro\\data.csv"; // File for export (in the "MQL5/Files" folder)
input int       Export_Bars_Skip = 0;                    // Number of historical bars to skip before export
input int       Export_Bars      = 5000;                 // Number of lines for export
//+------------------------------------------------------------------+
const int inputlen=24;    // Number of past bars analyzed by the trading strategy
//+------------------------------------------------------------------+
void OnStart()
  {
   //--- create a file
   int file=FileOpen(Export_FileName,FILE_WRITE|FILE_CSV|FILE_ANSI,',');

   if(file!=INVALID_HANDLE)
     {
      //--- write the data header
      string row="date";
      for(int i=0; i<=inputlen; i++)
        {
         if(StringLen(row)) row+=",";
         //========================================================
         // Note! 
         // In the Expert substitute underscores for [].
         // A field name in the DBase format is no longer than 11 symbols. Calc reduces it down to 10.
         // Maximum number of fields in the DBase format is 128-512, depending on the version.
         //========================================================
         StringConcatenate(row,row,"Bar___",i,"__");
        }
      FileWrite(file,row);

      //--- copy required data from history
      MqlRates rates[],rate;
      int count=Export_Bars+inputlen;
      if(CopyRates(Symbol(),Period(),1+Export_Bars_Skip,count,rates)<count)
        {
         Print("Error! Insufficient historical data for exporting required data.");
         return;
        }
      ArraySetAsSeries(rates,true);

      //--- write down the data      
      for(int bar=0; bar<Export_Bars; bar++)
        {
         row="";
         //--- closing price of the 1st bar will be the zero level for normalization of others
         double zlevel=rates[bar+1].close; 
         for(int i=0; i<=inputlen; i++)
           {
            if(StringLen(row)) row+=",";
            rate=rates[bar+i];
            if(i==0) row+=TimeToString(rate.time,TIME_DATE || TIME_MINUTES)+",";
            row+=DoubleToString(rate.close-zlevel,Digits());
           }
         FileWrite(file,row);
        }
      FileClose(file);
      Print("Data export successfully completed.");
     }
   else Print("Error! Failed to create a file for data export. ",GetLastError());
  }

Agora vamos lançá-lo no terminal. Após a conclusão bem-sucedida, ele irá imprimir uma mensagem correspondente na aba Expert.

O arquivo de dados criado pelo script contém aproximadamente o seguinte.

Na primeira seqüência existem os nomes dos campos da tabela; em seguida, siga as strings com os valores desses campos divididos por vírgula:

date,Bar___0__,Bar___1__,Bar___2__,Bar___3__,Bar___4__,Bar___5__,Bar___6__,Bar___7__,Bar___8__,Bar___9__,Bar___10__,Bar___11__,Bar___12__,Bar___13__,Bar___14__,Bar___15__,Bar___16__,Bar___17__,Bar___18__,Bar___19__,Bar___20__,Bar___21__,Bar___22__,Bar___23__,Bar___24__
2014.09.25,-0.0008,0.0000,-0.0005,-0.0014,0.0007,0.0035,0.0035,0.0036,0.0047,0.0052,0.0050,0.0046,0.0046,0.0047,0.0049,0.0052,0.0049,0.0053,0.0055,0.0056,0.0067,0.0056,0.0097,0.0105,0.0113
2014.09.25,0.0005,0.0000,-0.0009,0.0012,0.0040,0.0040,0.0041,0.0052,0.0057,0.0055,0.0051,0.0051,0.0052,0.0054,0.0057,0.0054,0.0058,0.0060,0.0061,0.0072,0.0061,0.0102,0.0110,0.0118,0.0123
2014.09.25,0.0009,0.0000,0.0021,0.0049,0.0049,0.0050,0.0061,0.0066,0.0064,0.0060,0.0060,0.0061,0.0063,0.0066,0.0063,0.0067,0.0069,0.0070,0.0081,0.0070,0.0111,0.0119,0.0127,0.0132,0.0130
2014.09.25,-0.0021,0.0000,0.0028,0.0028,0.0029,0.0040,0.0045,0.0043,0.0039,0.0039,0.0040,0.0042,0.0045,0.0042,0.0046,0.0048,0.0049,0.0060,0.0049,0.0090,0.0098,0.0106,0.0111,0.0109,0.0122

Conversão de CSV para DBF

Há muitas maneiras de fazê-lo.

Microsoft Excel, versões anteriores a de 2007. Ele pode abrir os arquivos CSV e também salvar os dados no formato DBF. Tenha em mente que as versões muito antigas do Excel acomodam apenas 65.535 strings. Dizendo isto, esta capacidade, geralmente, é suficiente para negociação já que um volume desse pode caber 10 anos de histórico no tempo H1;
Microsoft Excel, versões de 2007 e posterior. Não está disponível nos mesmos para salvar em em DBF. Um add-on enriquecendo o Excel com esta funcionalidade pode ser encontrado na Internet;
Microsoft Access (programa do pacote Microsoft Office para trabalhar com bases de dados). A tabela pode ser criada em uma base de dados por meio da importação a partir de um arquivo de texto (CSV) e, em seguida, exportá-lo para DBF;
Conversores CSV-DBF. Há um monte deles, é possível encontrar diferentes marcas pela internet, no entanto, a maioria delas são pagos;
Calc do pacote gratuito OpenOffice. Calc é quase um análogo completo do Excel. Ele pode abrir arquivos CSV e salvá-los em DBF.

Todos os métodos acima são intuitivos e deve ser bastante fácil de usar.

Eu irei efetuar uma conversão em uma das maneiras listadas. Vou usar o último, pois o NeuroPro é um programa gratuito e livre, a idéia por trás de Calc é a mais próxima dele. Você pode baixar o OpenOffice a partir do web site oficial - http://www.openoffice.org/.

O processo de conversão.

Inicie o Calc. Abra o nosso arquivo de dados com a extensão CSV.
Calc irá lançar o assistente de reconhecimento de dados.
Especifique nos parâmetros do assistente que os campos devem ser separados por vírgulas.

Outro ponto importante aqui é o separador de inteiro e partes fracionárias do número. De acordo com as configurações no meu computador ("Iniciar" > "Painel de controle" > "Linguagem e padrões regionais"), o ponto é usado como separador. Em nosso arquivo CSV também usamos ponto. Para o Calc ler os números corretamente, um separador tem de ser especificado também. Isso pode ser feito selecionando o idioma requerido nas configurações do assistente de conversão. Escolha uma das variantes da língua Inglesa já que o ponto é um separador padrão de lá.

As configurações corretas do assistente são mostradas na imagem:

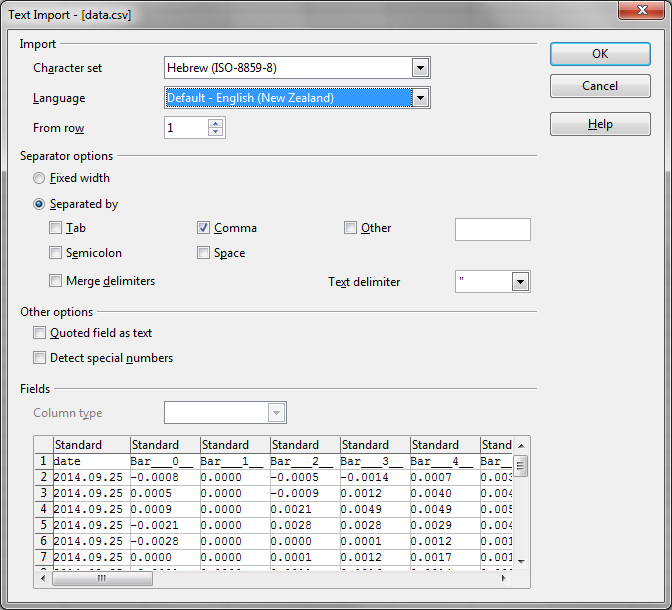
Fig. 2. Configuração do assistente de importação do arquivo CSV

Dica: para pular a seleção do idioma a cada conversão de arquivo CSV, é possível ser configurado como um idioma padrão nas configurações do Calc: menu "Ferramentas" > "Opções" e, em seguida, como destacado em verde na imagem:

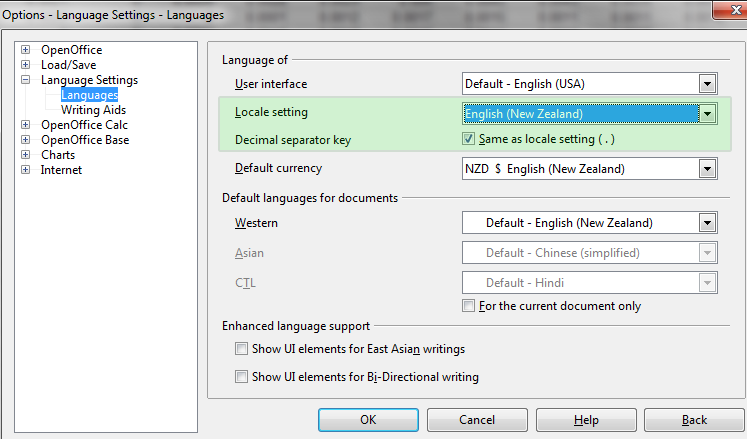
Fig. 3. Configuração Local no Calc

4) Assim, o arquivo CSV e submetido e os dados são automaticamente colocados nas colunas:

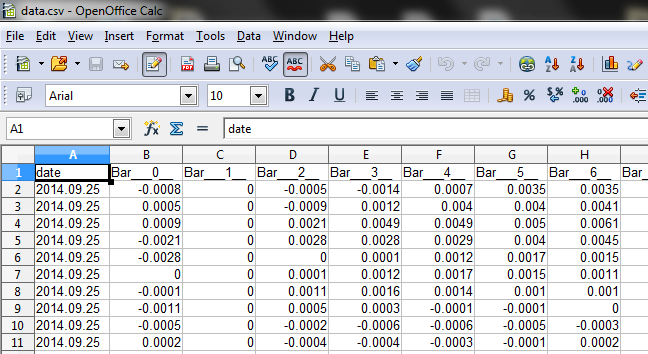
Fig. 4. Arquivo CSV aberto com sucesso

5) Para os dados a serem escritos corretamente no formato DBF seu tipo e precisão precisam ser especificados.

Para isso, todas as colunas com números devem ser realçados e atribuído as propriedades correspondentes como destacado em verde na imagem:

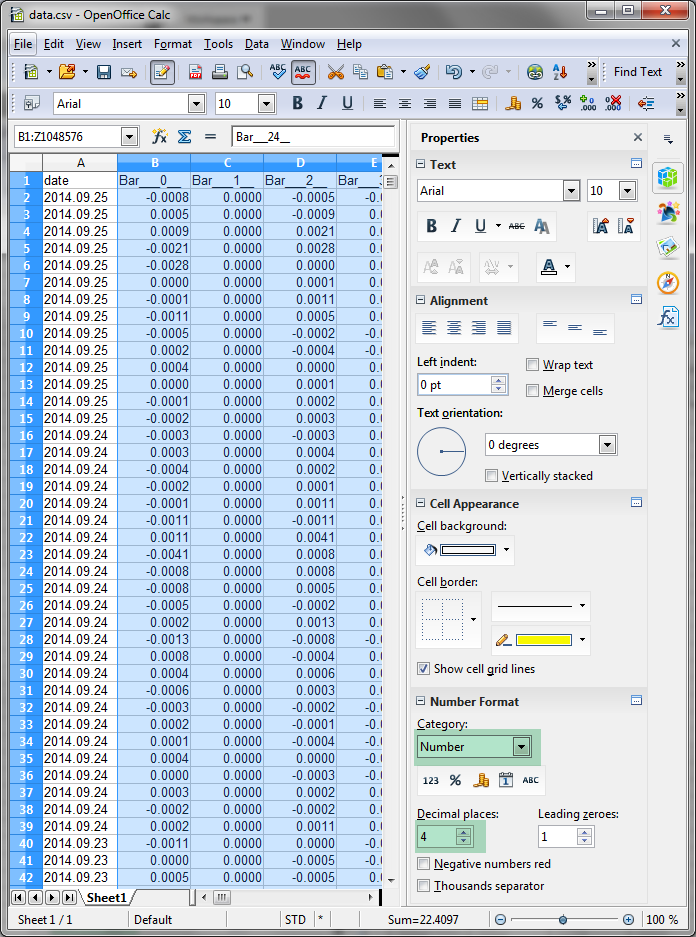
Fig. 5. Configurando as colunas com números

6) Salve em DBF: menu "Arquivo" > "Salvar como". Na janela de diálogo, selecione o tipo de arquivo "dBase (*.dbf)":

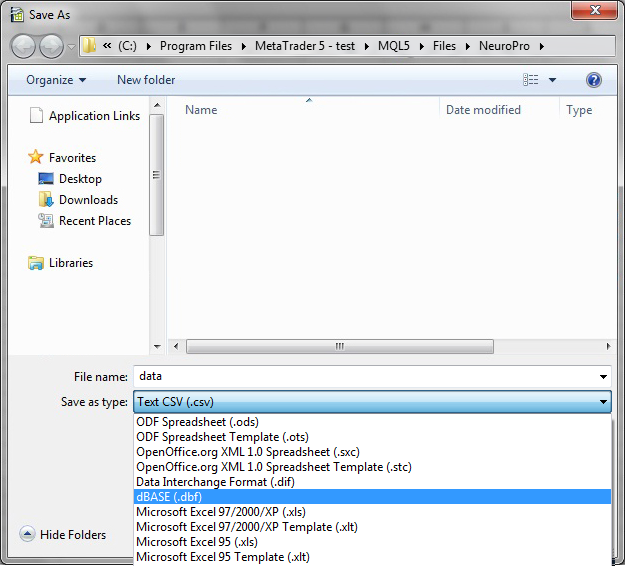
Fig. 6. Diálogo para salvar um arquivo no formato DBF

Em seguida, pressione "Salvar".

7) Calc irá pedir para confirmar o formato selecionado:

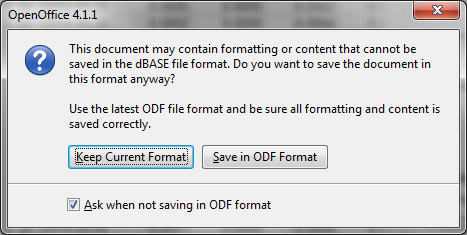
Fig. 7. Calc sugere salvar um arquivo no formato padrão ODF em vez de DBF

Confirmar a escolha pressionando o botão "Manter formato atual".

8) Calc irá perguntar qual a codificação utilizada para os dados de texto no arquivo DBF. Uma vez que não há tais dados em nosso exemplo e dados de texto é impossível para usar em redes neurais de qualquer maneira, você poderá especificar qualquer um:

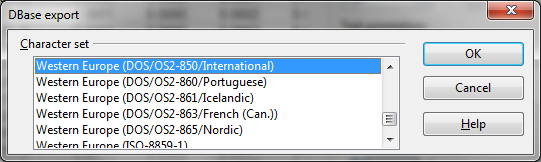
Fig. 8. Selecionando a codificação de texto do arquivo

Agora temos um arquivo com a extensão DBF que contém os dados recebidos do MetaTrader, necessários para a rede neural.

Como Criar e Treinar uma Rede Neural no NeuroPro

1) Inicie o NeuroPro.

2) Crie um projeto de trabalho: menu "Arquivo" > "Criar":

Fig. 9. Criado um projeto vazio

3) Na janela do projeto pressione o botão "Abrir arquivo de dados" e abra o arquivo DBF na caixa de diálogo que apareceu:

Fig. 10. O arquivo DBF aberto para usar com uma futura rede neural

4) Na janela de projeto, clique em "Nova rede". Na janela aberta há duas guias. Nós vamos preencher primeiro a guia "Entradas e saídas".

Especifique no campo "Bar___0__" que ele será o neurônio de saída da rede. O resto dos campos "Bar___N__" serão designados para ser entradas:

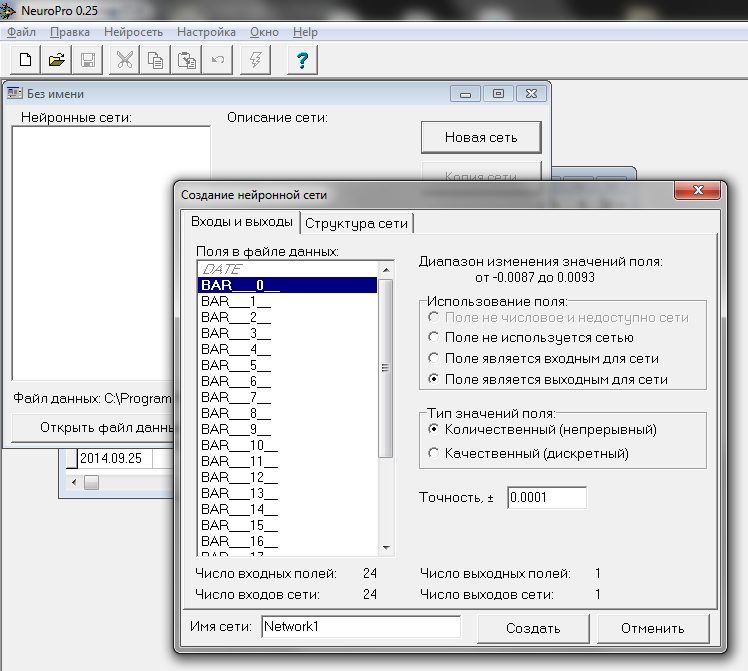
Fig. 11. Configuração das entradas e saídas da rede neural

Nós também podemos especificar a precisão necessária para o neurônio de saída. Em Forex é um ponto, ou seja, no nosso caso, é de 0,0001.

5) Agora nós vamos para a aba "Estrutura de Rede". Aqui, podemos especificar o número de camadas intermediárias (excluindo as camadas de entrada e saída) e o número de neurônios em cada um deles. Neste exemplo particular de aprendizagem, vamos criar três camadas, cada uma contendo 20 neurônios:

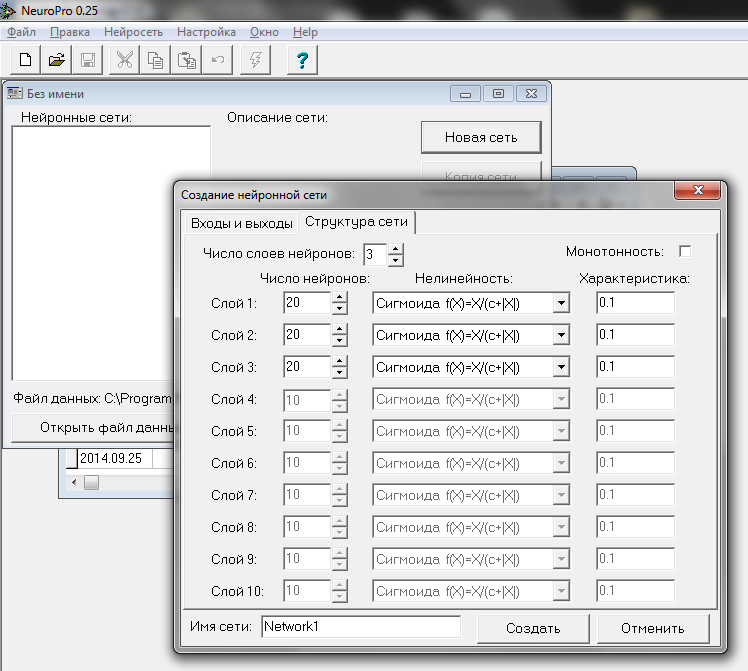
Fig. 12. Configuração das camadas da rede neural

6) Pressione o botão "Criar" e a rede estará pronta para usar:

Fig. 13. Uma nova rede neural recém configurada apareceu no projeto

7) Vá para o menu "Rede Neural" > "Verificação", para ver como uma nova e inexperiente rede está lidando com a produção de previsões de preços.

Como os resultados dos testes mostraram, esta rede neural não treinada previu um preço com uma precisão especificada (com o erro não superior a 1 ponto) em menos de 5% dos casos. Em média, um erro de previsão de preço foi de cerca de 10 pontos:

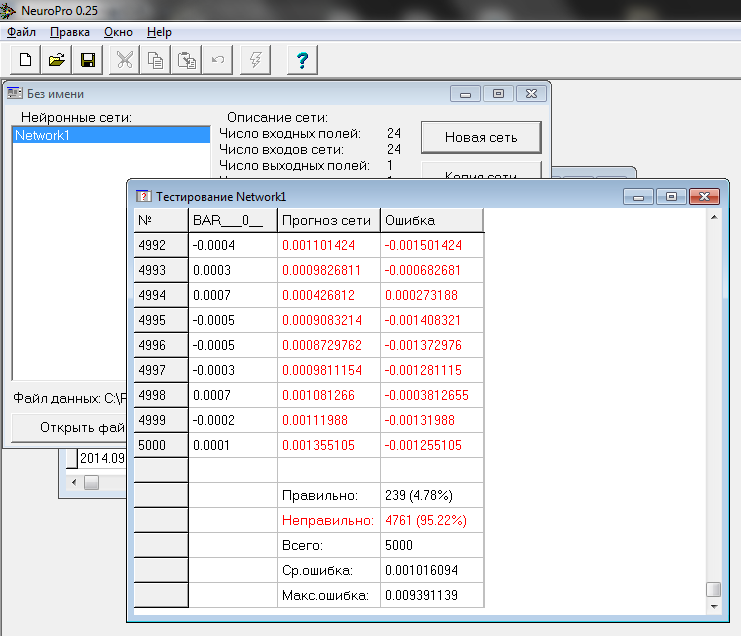
Fig. 14. Estatísticas da precisão das previsões da rede neural destreinada

8) Agora, temos de treinar a rede com base em nossos dados.

Mais uma vez, vá para a janela do projeto e pressione: "rede neural" > "Formação" no menu. Um indicador de progresso de aprendizagem irá aparecer. Espere até o fim do processo:

Fig. 15. Indicador do processo de aprendizagem da rede neural

9) Volte para a janela do projeto e vá para "Rede neural" > "Verificação".

A rede melhorou significativamente: sua previsão de preço foi preciso em 16% dos casos, e o erro de previsão média foi de 4 pontos:

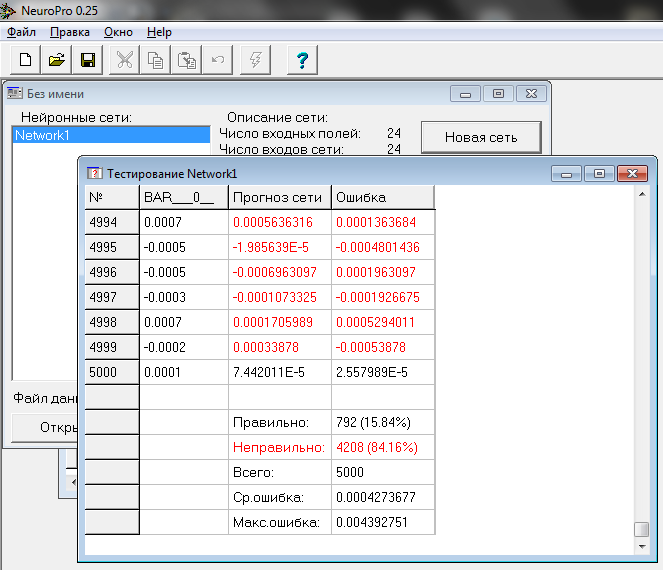
Fig. 16. Estatísticas da precisão das previsões de uma rede treinada

A rede aprendeu algumas coisas. Vamos transferi-la para o MetaTrader.

Como transferir uma Rede Neural do NeuroPro para o MetaTrader 5

O NeuroPro não sabe nada sobre o MetaTrader 5, não podendo passar de uma rede neural diretamente para ele. Eu tenho trabalhado em uma maneira semi-automática de converter uma rede neural em um fragmento de código em MQL5.

Ao contrário de muitos outros programas de rede neural, o NeuroPro pode mostrar a estrutura da rede neural em uso como um texto. Ela é um conjunto de fórmulas que descrevem sequencialmente todas as transformações de dados a partir do momento de entrada até a saída da rede. A fórmulas incluem todas as camadas, cada neurônio, cada conexão com os valores peso das conexões já substituídas (treinado).

Para vê-lo, vá para o Menu "Rede neural" > "Verbalização". No nosso caso, as fórmulas são as seguintes:

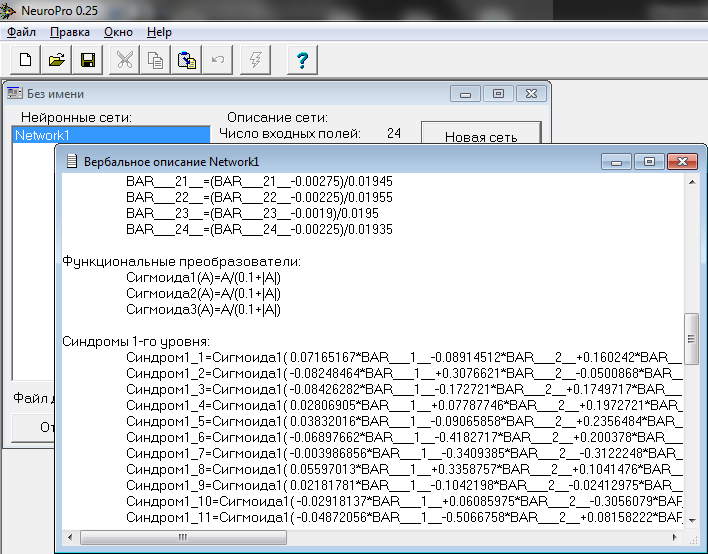
Fig. 17. Fórmulas que determinam o trabalho da rede neural treinada

Na verdade, o conjunto destas fórmulas podem ser consideradas como um código fonte de um programa escrito numa linguagem de programação abstrata. Tudo o que precisamos fazer é modificar este código para sua sintaxe corresponde em MQL5. Estas mudanças podem ser feitas em qualquer editor de texto. Para automatizar parcialmente esse processo, eu recomendo usar um editor que pode executar uma substituição em massa de frases. Isso pode ser feito em: Word, sua versão gratuita Writer (a partir do pacote OpenOffice), Excel, Calc e até mesmo o Bloco de Notas do Windows.

Tenho certeza que você poderá mudar essas fórmulas para um código em MQL5 sozinho, no entanto, eu vou compartilhar minha experiência na otimização deste processo para que você possa fazê-lo mais rapidamente.

No meu exemplo vou usar o bloco de notas do Windows 7.

1) Então, nós temos um projeto aberto no NeuroPro com a rede neural treinada. Vamos para "Rede neural" > "verbalização", onde abrirá uma janela com as fórmulas (veja a imagem acima).

2) Salve o conteúdo desta janela no: menu "Arquivo" > "Salvar como".

3) Agora abra este arquivo no bloco de notas.

4) Chame a função de substituição frase: menu "Editar" > "Substituir".

Lista de substituições a ser feito:

O que substituir	Substituir com	Comentário
___	[	subtraço triplo
__	]	subtraço duplo
--	- -	dois menos (dedução de um número negativo nas fórmulas) estão divididos por um espaço porque um sinal de menos duas vezes em MQL (bem como em outros idiomas semelhantes a C) pode ter um duplo sentido, o que leva a um erro de compilação
Sigmoid	Sigmoid	traduza os nomes da função para o latim (lembre-se, o programa está em Russo. Não há necessidade de fazê-lo, pois o MetaEditor suporta cirílico também)
Syndrom	Syndrome	traduza os nomes das variáveis para o latim (novamente, não há nenhum ponto em fazer isso já que o MetaEditor suporta cirílico também)

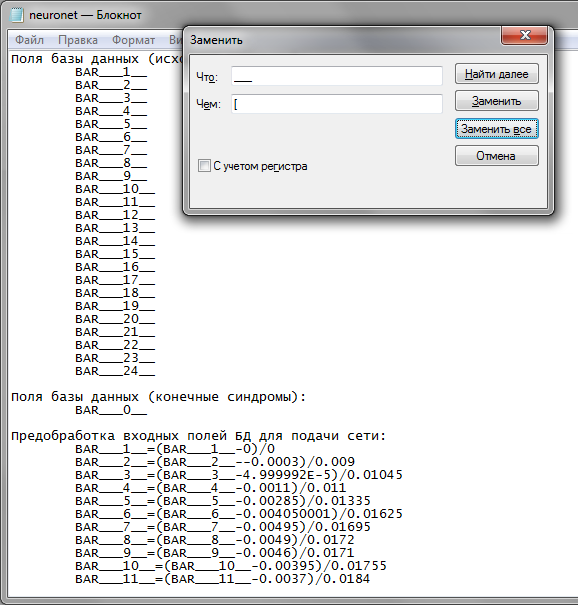
Fig. 18. Substitua o subtraço triplo com colchetes

Use o botão "Substituir tudo" para realizar a substituição.

Agora você entende que eu chamei os campos de preços "BAR___N__" para serem capazes de substituir rapidamente os subtraços para colchetes, ou seja, apresentam todas as entradas de rede como um array.

É mais fácil de declarar um array e preenchê-lo com os dados de preços da série do que um número de variáveis individuais.

5) Como mencionei antes, a enumeração de todas as entradas e saídas tem de ser alterada para declarar um array:

Antes	Depois
Campos da base de dados (sintomas iniciais): BAR[1] BAR[2] BAR[3] BAR[4] BAR[5] BAR[6] BAR[7] BAR[8] BAR[9] BAR[10] BAR[11] BAR[12] BAR[13] BAR[14] BAR[15] BAR[16] BAR[17] BAR[18] BAR[19] BAR[20] BAR[21] BAR[22] BAR[23] BAR[24] Campos da base de dados (síndromes finais): BAR[0]	double BAR [25];

Antes

Depois

Campos da base de dados (sintomas iniciais):

BAR[1]

BAR[2]

BAR[3]

BAR[4]

BAR[5]

BAR[6]

BAR[7]

BAR[8]

BAR[9]

BAR[10]

BAR[11]

BAR[12]

BAR[13]

BAR[14]

BAR[15]

BAR[16]

BAR[17]

BAR[18]

BAR[19]

BAR[20]

BAR[21]

BAR[22]

BAR[23]

BAR[24]

Campos da base de dados (síndromes finais):

BAR[0]

double BAR [25];

6) As funções de ativação do neurônio devem parecer como funções do programa MQL5:

Antes	Depois
Sigmoid1(A)=A/(0.1+\|A\|) Sigmoid2(A)=A/(0.1+\|A\|) Sigmoid3(A)=A/(0.1+\|A\|)	double Sigmoid1 (double A) { return A/(0.1 + MathAbs(A)); } double Sigmoid2 (double A) { return A/(0.1 + MathAbs(A)); } double Sigmoid3 (double A) { return A/(0.1 + MathAbs(A)); }

Antes

Depois

Sigmoid1(A)=A/(0.1+|A|)

Sigmoid2(A)=A/(0.1+|A|)

Sigmoid3(A)=A/(0.1+|A|)

double Sigmoid1 (double A)
{
  return A/(0.1 + MathAbs(A));
}

double Sigmoid2 (double A)
{
  return A/(0.1 + MathAbs(A));
}

double Sigmoid3 (double A)
{
  return A/(0.1 + MathAbs(A));
}

7) De acordo com as regras MQL5, um ponto e vírgula deve ser colocado no final de todas as fórmulas, os comentários devem ser escritos corretamente (ou excluído) e o tipo de declaração deve ser adicionado a todas as variáveis inicializadas.

No nosso caso, o tipo não foi declarado, apenas para os nomes de neurônios nas camadas intermediárias. Nós vamos usar a substituição de texto em massa novamente, em vez de introduzir a palavra "double" manualmente por 60 vezes. Precisamos destacar o início de uma string com um nome do neurônio (a margem no início da cadeia tem que ser destacado também porque os nomes dos neurônios também serão usados na parte direita das fórmulas e a palavra "double" não precisará ser inserido ali):

Fig. 19. Destacando o texto para a substituição

Depois de copiar a parte destacada do texto, insira-o na caixa de diálogo de substituição de texto para substituir com o mesmo texto e a palavra "double", acrescentada a ele:

Fig. 20. Adicione otipo do nome às variáveis

Não se esqueça de pressionar o botão "Substituir tudo".

8) O NeuroPro tem um pequeno bug. Se vocÊ introduzir um valor constante para a rede neural, em seguida, no formato de texto a fórmula de normalização desta entrada conterá uma divisão por zero. No nosso caso a "BAR___1__" é como uma entrada. Ela sempre tem zeros porque é o ponto de referência para a nossa normalização das barras.

Idealmente, "BAR___1__" não deve ser introduzida na rede neural como entradas com valores constantes que não influenciam a previsão de qualquer maneira. No entanto, se o valor for uma entrada, a fórmula produzida por NeuroPro terá de ser ajustada. Para evitar mensagens de erro do compilador, a "BAR___1__" terá de ser substituída com o valor que seja permanentemente de entrada aqui. No nosso caso, é zero:

Antes	Depois
BAR[1]=(BAR[1]-0)/0;	BAR[1]=0;

9) Há um outro bug muito insignificante (o desenvolvedor do NeuroPro não achou que uma descrição de texto de uma rede neural seria usada como um código de programa e, portanto, não a verificou com cuidado).

Na última fórmula no final há um parêntese de fechamento extra. Este erro é muito pequeno, mas ele confunde o compilador MetaEditor. Ele não vai apontar para o parêntese extra nessa cadeia, mas ele não vai demorar para pegar um colchete em outra parte do programa. Por favor, tenha em mente que você pode corrigi-lo quando se deparar com isso.

Antes	Depois
BAR[0]=((BAR[0]*0.0180000001564622)+0.000599999912083149)/2);	BAR[0]=((BAR[0]*0.0180000001564622)+0.000599999912083149)/2;

As operações descritas nesta seção levam apenas alguns minutos se praticada regularmente. Não há necessidade de lembrar a lista ao pé da letra. Na seguinte compilação do MetaEditor, ele irá apontar as partes não corrigidos do código como erros.

Finalmente, depois de trazer todas as fórmulas para o formato MQL5, tudo o que precisamos fazer é transferir o código resultante do bloco de notas para o MetaEditor e adicionar o restante do código necessário para o Expert. Certamente, se você usa regularmente as redes neurais criadas no NeuroPro, esta etapa será fácil. Você simplesmente irá substituir a rede neural anterior do Expert existente com um novo código MQL5 de uma rede neural a partir do bloco de notas. Isto irá levar um minuto, literalmente.

O código final do Expert, totalmente pronto para trabalhar no MetaTrader 5 (você também poderá baixar este código de aplicação deste artigo):

input double    Lots = 0.1;        // Deal volume
input double    MinPrognosis = 0;  // Open deals with a forecast more promising than the current one
//+------------------------------------------------------------------+
const int inputlen=24; // Number of past bars analyzed by the trading strategy
//+------------------------------------------------------------------+
double Sigmoid1(double A)
  {
   return A/(0.1 + MathAbs(A));
  }
//+------------------------------------------------------------------+
double Sigmoid2(double A)
  {
   return A/(0.1 + MathAbs(A));
  }
//+------------------------------------------------------------------+
double Sigmoid3(double A)
  {
   return A/(0.1 + MathAbs(A));
  }
//+------------------------------------------------------------------+
double CalcNeuroNet()
  {
//--- get current quotes for neural network
   MqlRates rates[],rate;
   CopyRates(Symbol(),Period(),0,inputlen+1,rates);
   ArraySetAsSeries(rates,true);

//--- neural network inputs
   double BAR[512]; // 512 - maximum permissible number of fields in the DBF format

//--- fill the array of the neural network input data
//--- closing price of the 1st bar will be the zero level for normalization of others
   double zlevel=rates[1].close; 

   for(int bar=0; bar<=inputlen; bar++)
     {
      rate=rates[bar];
      BAR[bar]=rate.close-zlevel;
     }

//==============================================
// Calculate the neural network with NeuroPro formulas
//==============================================

//--- preprocessing of the data base input fields for training the network:
   BAR[1]=0;//(BAR[1]-0)/0;
   BAR[2]=(BAR[2]- -0.0003)/0.009;
   BAR[3]=(BAR[3]-4.999992E-5)/0.01045;
   BAR[4]=(BAR[4]-0.0011)/0.011;
   BAR[5]=(BAR[5]-0.00285)/0.01335;
   BAR[6]=(BAR[6]-0.004050001)/0.01625;
   BAR[7]=(BAR[7]-0.00495)/0.01695;
   BAR[8]=(BAR[8]-0.0049)/0.0172;
   BAR[9]=(BAR[9]-0.0046)/0.0171;
   BAR[10]=(BAR[10]-0.00395)/0.01755;
   BAR[11]=(BAR[11]-0.0037)/0.0184;
   BAR[12]=(BAR[12]-0.0034)/0.0188;
   BAR[13]=(BAR[13]-0.0029)/0.0194;
   BAR[14]=(BAR[14]-0.002499999)/0.0196;
   BAR[15]=(BAR[15]-0.00245)/0.01935;
   BAR[16]=(BAR[16]-0.00275)/0.01925;
   BAR[17]=(BAR[17]-0.0028)/0.0194;
   BAR[18]=(BAR[18]-0.002950001)/0.01965;
   BAR[19]=(BAR[19]-0.002649999)/0.01965;
   BAR[20]=(BAR[20]-0.002699999)/0.0197;
   BAR[21]=(BAR[21]-0.00275)/0.01945;
   BAR[22]=(BAR[22]-0.00225)/0.01955;
   BAR[23]=(BAR[23]-0.0019)/0.0195;
   BAR[24]=(BAR[24]-0.00225)/0.01935;

//--- syndromes of the 1st level:
   double Syndrome1_1=Sigmoid1( 0.07165167*BAR[1]-0.08914512*BAR[2]+0.160242*BAR[3]-0.1136391*BAR[4]+0.01358515*BAR[5]+0.3755009*BAR[6]-0.1433693*BAR[7]+0.224411*BAR[8]+0.03298632*BAR[9]-0.2551045*BAR[10]-0.1418581*BAR[11]+0.007130164*BAR[12]-0.08727393*BAR[13]-0.2567087*BAR[14]+0.1118081*BAR[15]+0.73848*BAR[16]+0.05880548*BAR[17]-0.1544689*BAR[18]+0.192913*BAR[19]-0.1743894*BAR[20]-0.2184512*BAR[21]-0.2290305*BAR[22]+0.3946579*BAR[23]-0.02947071*BAR[24]-0.08091708 );
   double Syndrome1_2=Sigmoid1( -0.08248464*BAR[1]+0.3076621*BAR[2]-0.0500868*BAR[3]-0.6526818*BAR[4]+0.04266862*BAR[5]+0.581119*BAR[6]-0.0356447*BAR[7]+0.0292943*BAR[8]-0.3660156*BAR[9]-0.3244759*BAR[10]+0.05519342*BAR[11]+0.2419113*BAR[12]-0.2178954*BAR[13]+0.4037299*BAR[14]-0.1593139*BAR[15]+0.3567515*BAR[16]+0.08094382*BAR[17]-0.01788837*BAR[18]-0.379636*BAR[19]+0.6658992*BAR[20]-0.1899142*BAR[21]+0.02259956*BAR[22]+0.767949*BAR[23]-0.5380562*BAR[24]-0.06307755 );
   double Syndrome1_3=Sigmoid1( -0.08426282*BAR[1]-0.172721*BAR[2]+0.1749717*BAR[3]-0.07916483*BAR[4]-0.0523758*BAR[5]+0.1935233*BAR[6]+0.01627235*BAR[7]+0.1254414*BAR[8]-0.1101555*BAR[9]-0.02285305*BAR[10]-0.14389*BAR[11]+0.1788775*BAR[12]-0.007144043*BAR[13]+0.1925385*BAR[14]-0.08001231*BAR[15]-0.2021703*BAR[16]+0.08694438*BAR[17]+0.3090158*BAR[18]-0.3330302*BAR[19]+0.2519112*BAR[20]-0.2170611*BAR[21]-0.2216277*BAR[22]+0.09618518*BAR[23]+0.049888*BAR[24]-0.06465426 );
   double Syndrome1_4=Sigmoid1( 0.02806905*BAR[1]+0.07787746*BAR[2]+0.1972721*BAR[3]-0.247464*BAR[4]-0.008635854*BAR[5]-0.1975036*BAR[6]-0.0652089*BAR[7]-0.1276176*BAR[8]-0.3386112*BAR[9]-0.103951*BAR[10]+0.08352495*BAR[11]-0.1821419*BAR[12]-0.05604611*BAR[13]-0.05922695*BAR[14]-0.1670811*BAR[15]+0.002476109*BAR[16]-0.03657883*BAR[17]-0.09295338*BAR[18]+0.2500353*BAR[19]-0.03980102*BAR[20]+0.1059941*BAR[21]-0.4037244*BAR[22]-0.08735184*BAR[23]+0.1546644*BAR[24]+0.1966186 );
   double Syndrome1_5=Sigmoid1( 0.03832016*BAR[1]-0.09065858*BAR[2]+0.2356484*BAR[3]-0.2436682*BAR[4]+0.09812659*BAR[5]+0.09220826*BAR[6]+0.434221*BAR[7]-0.005478878*BAR[8]-0.1657191*BAR[9]-0.2605299*BAR[10]+0.3523667*BAR[11]+0.3595579*BAR[12]+0.3402678*BAR[13]-0.3346431*BAR[14]+0.1215327*BAR[15]-0.1869196*BAR[16]+0.07256371*BAR[17]-0.09229603*BAR[18]-0.09961994*BAR[19]+0.2491707*BAR[20]+0.3703756*BAR[21]+0.1369175*BAR[22]+0.0560869*BAR[23]-0.007567503*BAR[24]-0.01722363 );
   double Syndrome1_6=Sigmoid1( -0.06897662*BAR[1]-0.4182717*BAR[2]+0.200378*BAR[3]-0.4152234*BAR[4]-0.2081593*BAR[5]+0.3120443*BAR[6]-0.1582431*BAR[7]+0.1900958*BAR[8]+0.002503331*BAR[9]+0.02297609*BAR[10]+0.03145982*BAR[11]+0.1816629*BAR[12]+0.1854629*BAR[13]-0.1660063*BAR[14]+0.3112128*BAR[15]-0.4799304*BAR[16]-0.100519*BAR[17]-0.1523588*BAR[18]+0.07141552*BAR[19]+0.2336634*BAR[20]+0.01279082*BAR[21]-0.2179644*BAR[22]+0.4898897*BAR[23]-0.1818153*BAR[24]-0.1783737 );
   double Syndrome1_7=Sigmoid1( -0.003986856*BAR[1]-0.3409385*BAR[2]-0.3122248*BAR[3]+0.5656545*BAR[4]+0.07564658*BAR[5]+0.07956024*BAR[6]+0.1820322*BAR[7]-0.05595554*BAR[8]+0.1027963*BAR[9]+0.2596273*BAR[10]+0.1156801*BAR[11]+0.04490443*BAR[12]+0.1426405*BAR[13]+0.06763341*BAR[14]-0.03249188*BAR[15]-0.1912978*BAR[16]-0.2003477*BAR[17]-0.2413947*BAR[18]+0.3188735*BAR[19]-0.2899658*BAR[20]+0.06846272*BAR[21]+0.08726751*BAR[22]-0.2134383*BAR[23]-0.436768*BAR[24]+0.08075105 );
   double Syndrome1_8=Sigmoid1( 0.05597013*BAR[1]+0.3358757*BAR[2]+0.1041476*BAR[3]-0.334706*BAR[4]-0.07069201*BAR[5]+0.06152828*BAR[6]+0.1577689*BAR[7]+0.1737777*BAR[8]-0.7711719*BAR[9]-0.2970988*BAR[10]+0.06691784*BAR[11]+0.0528774*BAR[12]+0.06260363*BAR[13]+0.2449201*BAR[14]-0.3098814*BAR[15]+0.06859511*BAR[16]+0.1355444*BAR[17]-0.15844*BAR[18]+0.2791151*BAR[19]-0.412524*BAR[20]+0.228981*BAR[21]-0.4042732*BAR[22]+0.197847*BAR[23]+0.477078*BAR[24]-0.2478239 );
   double Syndrome1_9=Sigmoid1( 0.02181781*BAR[1]-0.1042198*BAR[2]-0.02412975*BAR[3]+0.1485616*BAR[4]+0.07645424*BAR[5]-0.02779776*BAR[6]-0.1519209*BAR[7]-0.1878287*BAR[8]+0.1637603*BAR[9]+0.248636*BAR[10]+0.2032469*BAR[11]-0.03869069*BAR[12]+0.02014448*BAR[13]-0.2079489*BAR[14]+0.08846121*BAR[15]+0.1025348*BAR[16]+0.01593455*BAR[17]-0.4964754*BAR[18]+0.1635097*BAR[19]-0.04561989*BAR[20]-0.0662128*BAR[21]-0.2423395*BAR[22]+0.2898602*BAR[23]+0.03824728*BAR[24]-0.07471437 );
   double Syndrome1_10=Sigmoid1( -0.02918137*BAR[1]+0.06085975*BAR[2]-0.3056079*BAR[3]-0.5144019*BAR[4]-0.1966296*BAR[5]+0.04413594*BAR[6]+0.03249943*BAR[7]+0.08405613*BAR[8]-0.08797813*BAR[9]+0.06621616*BAR[10]-0.2226632*BAR[11]-0.1000158*BAR[12]+0.0106046*BAR[13]-0.1383344*BAR[14]+0.05141285*BAR[15]-0.1009147*BAR[16]-0.1503479*BAR[17]+0.2877283*BAR[18]-0.2209365*BAR[19]+0.1310906*BAR[20]-0.1188305*BAR[21]-0.002668453*BAR[22]+0.1106755*BAR[23]+0.3884961*BAR[24]+0.0006983803 );
   double Syndrome1_11=Sigmoid1( -0.04872056*BAR[1]-0.5066758*BAR[2]+0.08158222*BAR[3]+0.2647052*BAR[4]+0.3632542*BAR[5]+0.4538754*BAR[6]-0.1346472*BAR[7]+0.16742*BAR[8]+0.2974689*BAR[9]+0.3446769*BAR[10]-0.2784187*BAR[11]+0.2461497*BAR[12]-0.166853*BAR[13]-0.4296628*BAR[14]+0.7343794*BAR[15]+0.2154892*BAR[16]-0.4086125*BAR[17]-0.6446049*BAR[18]-0.5614476*BAR[19]-0.593914*BAR[20]+0.5039462*BAR[21]+0.113933*BAR[22]+0.3599374*BAR[23]-0.5517*BAR[24]+0.1249064 );
   double Syndrome1_12=Sigmoid1( -0.09035824*BAR[1]-0.2619464*BAR[2]+0.5151641*BAR[3]+0.08415102*BAR[4]+0.007849894*BAR[5]-0.3585253*BAR[6]-0.3458216*BAR[7]-0.006490127*BAR[8]+0.1933572*BAR[9]+0.1655464*BAR[10]-0.2591909*BAR[11]+0.2810482*BAR[12]-0.3552095*BAR[13]+0.1032239*BAR[14]-0.2380441*BAR[15]-0.6082169*BAR[16]-0.3652177*BAR[17]+0.4065064*BAR[18]-0.1538232*BAR[19]-0.03332642*BAR[20]+0.06235149*BAR[21]-0.08935639*BAR[22]-0.2274701*BAR[23]+0.2350571*BAR[24]-0.1009272 );
   double Syndrome1_13=Sigmoid1( -0.05370994*BAR[1]+0.2999545*BAR[2]-0.2855853*BAR[3]+0.1123754*BAR[4]+0.2561198*BAR[5]-0.2846766*BAR[6]+0.008345681*BAR[7]+0.1896221*BAR[8]-0.1973753*BAR[9]+0.3510076*BAR[10]+0.4492245*BAR[11]-0.09004608*BAR[12]+0.002758034*BAR[13]+0.03157447*BAR[14]+0.02175433*BAR[15]-0.399723*BAR[16]-0.2736914*BAR[17]+0.1198452*BAR[18]+0.2808644*BAR[19]-0.06968442*BAR[20]-0.5771574*BAR[21]+0.3748633*BAR[22]-0.2721373*BAR[23]-0.2329663*BAR[24]+0.07683773 );
   double Syndrome1_14=Sigmoid1( 0.094418*BAR[1]+0.2155959*BAR[2]-0.4787674*BAR[3]+0.3605456*BAR[4]+0.06799955*BAR[5]+0.607367*BAR[6]-0.3518007*BAR[7]+0.1633829*BAR[8]+0.3040094*BAR[9]+0.3707297*BAR[10]+0.02556368*BAR[11]-0.0885786*BAR[12]-0.3713907*BAR[13]-0.2014098*BAR[14]-0.289242*BAR[15]-0.09950806*BAR[16]-0.5361071*BAR[17]+0.4154459*BAR[18]+0.02827369*BAR[19]-0.04972957*BAR[20]-0.1700879*BAR[21]+0.2973098*BAR[22]-0.2097459*BAR[23]-0.0422597*BAR[24]+0.2318914 );
   double Syndrome1_15=Sigmoid1( 0.02161242*BAR[1]+0.5484816*BAR[2]+0.002152426*BAR[3]-0.3017516*BAR[4]+0.02010602*BAR[5]-0.8008425*BAR[6]-0.2985114*BAR[7]+0.5151479*BAR[8]+0.1572166*BAR[9]-0.04494689*BAR[10]+0.2529401*BAR[11]-0.02046412*BAR[12]-0.05892481*BAR[13]-0.1359019*BAR[14]-0.2005993*BAR[15]+0.03077302*BAR[16]+0.745619*BAR[17]-0.4197147*BAR[18]-0.1354882*BAR[19]-0.6034228*BAR[20]-0.04950687*BAR[21]-0.1093793*BAR[22]-0.46851*BAR[23]+0.2340346*BAR[24]-0.1910115 );
   double Syndrome1_16=Sigmoid1( 0.06201033*BAR[1]+0.2311719*BAR[2]-0.6587076*BAR[3]-0.1937433*BAR[4]-0.3063492*BAR[5]+0.0458253*BAR[6]+0.2621455*BAR[7]-0.3292437*BAR[8]-0.07124191*BAR[9]+0.03962434*BAR[10]-0.03539502*BAR[11]+0.1602975*BAR[12]+0.1252141*BAR[13]-0.1939677*BAR[14]-0.3524359*BAR[15]-0.02675135*BAR[16]-0.1550312*BAR[17]+0.2015329*BAR[18]-0.1383009*BAR[19]+0.3079963*BAR[20]+0.06971535*BAR[21]-0.2415089*BAR[22]-0.03791533*BAR[23]+0.01494107*BAR[24]+0.01395546 );
   double Syndrome1_17=Sigmoid1( -0.03211073*BAR[1]-0.2057187*BAR[2]-0.2208917*BAR[3]+0.1034868*BAR[4]+0.003785761*BAR[5]-0.1510143*BAR[6]-0.04637882*BAR[7]-0.01963908*BAR[8]-0.3622932*BAR[9]+0.03135398*BAR[10]-0.1296021*BAR[11]-0.2571803*BAR[12]+0.02485986*BAR[13]-0.05831699*BAR[14]+0.2441404*BAR[15]+0.4313999*BAR[16]-0.05117986*BAR[17]-0.06832605*BAR[18]-0.01433043*BAR[19]-0.3331767*BAR[20]-0.09270683*BAR[21]+0.1077102*BAR[22]+0.0517161*BAR[23]+0.1463209*BAR[24]+0.08033083 );
   double Syndrome1_18=Sigmoid1( -0.01044874*BAR[1]+0.8255618*BAR[2]-0.3581862*BAR[3]+0.2379437*BAR[4]-0.05247816*BAR[5]+0.3858318*BAR[6]-0.04216846*BAR[7]+0.2305764*BAR[8]-0.2754549*BAR[9]+0.1255125*BAR[10]-0.1954638*BAR[11]+0.04934186*BAR[12]-0.08713531*BAR[13]+0.08193728*BAR[14]-0.01578137*BAR[15]+0.04301662*BAR[16]-0.01941852*BAR[17]+0.0321704*BAR[18]-0.4490997*BAR[19]-0.2165072*BAR[20]+0.5094138*BAR[21]-0.08077756*BAR[22]-0.1167052*BAR[23]+0.008337143*BAR[24]-0.1847742 );
   double Syndrome1_19=Sigmoid1( 0.07863438*BAR[1]+0.6541001*BAR[2]-0.0287532*BAR[3]-0.07992863*BAR[4]-0.1936443*BAR[5]+0.2021953*BAR[6]+0.5814793*BAR[7]+0.1076662*BAR[8]-0.2505759*BAR[9]-0.1958519*BAR[10]+0.2982949*BAR[11]-0.130183*BAR[12]-0.2418064*BAR[13]-0.03213368*BAR[14]-0.1050228*BAR[15]-0.04116086*BAR[16]+0.1059578*BAR[17]-0.09407587*BAR[18]+0.2511382*BAR[19]+0.03090675*BAR[20]-0.2050715*BAR[21]+0.07968493*BAR[22]-0.1085312*BAR[23]-0.3073632*BAR[24]+0.1479857 );
   double Syndrome1_20=Sigmoid1( 0.01779699*BAR[1]+0.1517631*BAR[2]+0.1832252*BAR[3]+0.4329565*BAR[4]-0.1528609*BAR[5]-0.2424133*BAR[6]+0.1942621*BAR[7]+0.1390828*BAR[8]-0.3387062*BAR[9]+0.3891163*BAR[10]+0.3485644*BAR[11]+0.06489421*BAR[12]-0.01458877*BAR[13]-0.1127466*BAR[14]+0.1122861*BAR[15]-0.1973242*BAR[16]+0.4340822*BAR[17]-0.633949*BAR[18]+0.1276167*BAR[19]+0.2476585*BAR[20]-0.4445719*BAR[21]+0.6248969*BAR[22]-0.2169943*BAR[23]-0.501359*BAR[24]-0.1358235 );

//--- syndromes of the 2nd level:
   double Syndrome2_1=Sigmoid2( 0.2332734*Syndrome1_1-0.2002641*Syndrome1_2-0.03174414*Syndrome1_3-0.3868614*Syndrome1_4-0.1933812*Syndrome1_5-0.2366997*Syndrome1_6+0.3920829*Syndrome1_7+0.1015497*Syndrome1_8-0.1333193*Syndrome1_9+0.05584235*Syndrome1_10-0.2983295*Syndrome1_11+0.1034668*Syndrome1_12-0.4040487*Syndrome1_13-0.2103508*Syndrome1_14-0.2480657*Syndrome1_15-0.1906435*Syndrome1_16+0.2692898*Syndrome1_17+0.2760854*Syndrome1_18-0.1738693*Syndrome1_19-0.1861307*Syndrome1_20-0.07152162 );
   double Syndrome2_2=Sigmoid2( -0.1242675*Syndrome1_1+0.05587832*Syndrome1_2+0.1567961*Syndrome1_3+0.1077346*Syndrome1_4-0.2112047*Syndrome1_5+0.04008683*Syndrome1_6-0.1716478*Syndrome1_7+0.3083204*Syndrome1_8-0.1864694*Syndrome1_9+0.08867304*Syndrome1_10-0.06801239*Syndrome1_11-0.1810985*Syndrome1_12-0.05133555*Syndrome1_13+0.2981661*Syndrome1_14-0.01543425*Syndrome1_15-0.1859617*Syndrome1_16+0.027973*Syndrome1_17-0.1715439*Syndrome1_18-0.1249511*Syndrome1_19+0.5925598*Syndrome1_20-0.279602 );
   double Syndrome2_3=Sigmoid2( -0.4745722*Syndrome1_1-0.1248492*Syndrome1_2-0.1128288*Syndrome1_3+0.1485692*Syndrome1_4-0.3948999*Syndrome1_5+0.2633227*Syndrome1_6-0.2046695*Syndrome1_7-0.03632757*Syndrome1_8+0.259578*Syndrome1_9-0.07442582*Syndrome1_10+0.06552354*Syndrome1_11-0.2452848*Syndrome1_12-0.1599011*Syndrome1_13+0.1749917*Syndrome1_14-0.07113215*Syndrome1_15-0.1524421*Syndrome1_16+0.3606906*Syndrome1_17+0.3524929*Syndrome1_18+0.1315838*Syndrome1_19+0.1981817*Syndrome1_20+0.0126604 );
   double Syndrome2_4=Sigmoid2( -0.3605324*Syndrome1_1+0.2803221*Syndrome1_2+0.07412126*Syndrome1_3+0.2101911*Syndrome1_4-0.1933928*Syndrome1_5-0.2068641*Syndrome1_6+0.1302721*Syndrome1_7+0.04962961*Syndrome1_8+0.2879501*Syndrome1_9-0.04214102*Syndrome1_10-0.02194729*Syndrome1_11-0.0501424*Syndrome1_12+0.007969459*Syndrome1_13+0.1151657*Syndrome1_14+0.04063402*Syndrome1_15+0.1461606*Syndrome1_16-0.07482237*Syndrome1_17-0.3319329*Syndrome1_18+0.2494595*Syndrome1_19-0.09345333*Syndrome1_20-0.1831799 );
   double Syndrome2_5=Sigmoid2( -0.03081687*Syndrome1_1-0.419345*Syndrome1_2-0.01301429*Syndrome1_3+0.008855551*Syndrome1_4+0.2869771*Syndrome1_5+0.06881366*Syndrome1_6-0.1612982*Syndrome1_7-0.491662*Syndrome1_8+0.04266098*Syndrome1_9-0.7546657*Syndrome1_10+0.0472151*Syndrome1_11-0.5099863*Syndrome1_12+0.1196823*Syndrome1_13+0.2611973*Syndrome1_14-0.0241531*Syndrome1_15-0.5843646*Syndrome1_16+0.08374172*Syndrome1_17+0.041931*Syndrome1_18-0.181801*Syndrome1_19+0.6314354*Syndrome1_20+0.2967799 );
   double Syndrome2_6=Sigmoid2( 0.2783457*Syndrome1_1+0.05858535*Syndrome1_2+0.03348543*Syndrome1_3-0.09202126*Syndrome1_4+0.09466362*Syndrome1_5-0.01946918*Syndrome1_6-0.008507644*Syndrome1_7+0.1967683*Syndrome1_8-0.1593684*Syndrome1_9+0.2202749*Syndrome1_10-0.2754305*Syndrome1_11-0.08108314*Syndrome1_12+0.1606592*Syndrome1_13+0.03723634*Syndrome1_14+0.3494412*Syndrome1_15-0.139782*Syndrome1_16+0.03641316*Syndrome1_17-0.1216527*Syndrome1_18-0.2194063*Syndrome1_19+0.3015033*Syndrome1_20-0.1307777 );
   double Syndrome2_7=Sigmoid2( -0.1451617*Syndrome1_1-0.1851998*Syndrome1_2-0.2149245*Syndrome1_3-0.05804037*Syndrome1_4-0.03970402*Syndrome1_5+2.506166E-6*Syndrome1_6+0.223578*Syndrome1_7-0.1718342*Syndrome1_8+0.001228896*Syndrome1_9-0.03911417*Syndrome1_10+0.3167912*Syndrome1_11+0.2213001*Syndrome1_12-0.3518667*Syndrome1_13-0.6146168*Syndrome1_14-0.1061097*Syndrome1_15-0.3044312*Syndrome1_16-0.04269538*Syndrome1_17-0.1753355*Syndrome1_18+0.1989161*Syndrome1_19-0.3667244*Syndrome1_20+0.2514035 );
   double Syndrome2_8=Sigmoid2( -0.1430153*Syndrome1_1-Syndrome1_2+0.02704678*Syndrome1_3+0.09941091*Syndrome1_4+0.07057924*Syndrome1_5-0.3370984*Syndrome1_6+0.1565579*Syndrome1_7-0.6226992*Syndrome1_8-0.4750121*Syndrome1_9+0.0914355*Syndrome1_10+0.7518402*Syndrome1_11-0.3350138*Syndrome1_12-0.3099903*Syndrome1_13+0.01266479*Syndrome1_14-0.7965527*Syndrome1_15-0.1753905*Syndrome1_16-0.1435609*Syndrome1_17+0.1683903*Syndrome1_18+0.1800467*Syndrome1_19+0.02699256*Syndrome1_20+0.3138063 );
   double Syndrome2_9=Sigmoid2( -0.2611458*Syndrome1_1-0.03994129*Syndrome1_2-0.2299157*Syndrome1_3+0.3549923*Syndrome1_4-0.001759748*Syndrome1_5-0.1117837*Syndrome1_6+0.03037107*Syndrome1_7+0.2023677*Syndrome1_8+0.2628252*Syndrome1_9+0.09683131*Syndrome1_10+0.2576693*Syndrome1_11-0.06357097*Syndrome1_12-0.2162403*Syndrome1_13-0.2190126*Syndrome1_14-0.1675369*Syndrome1_15-0.2458067*Syndrome1_16-0.06660707*Syndrome1_17-0.2096998*Syndrome1_18+0.2432118*Syndrome1_19+0.06210691*Syndrome1_20+0.1555794 );
   double Syndrome2_10=Sigmoid2( 0.1120118*Syndrome1_1-0.09789048*Syndrome1_2-0.1146162*Syndrome1_3-0.02268722*Syndrome1_4-0.4754501*Syndrome1_5+0.1567527*Syndrome1_6+0.4281512*Syndrome1_7+0.1428995*Syndrome1_8+0.4317052*Syndrome1_9-0.1987304*Syndrome1_10-0.3471439*Syndrome1_11-0.2485701*Syndrome1_12+0.2200699*Syndrome1_13-0.1804247*Syndrome1_14+0.5553524*Syndrome1_15+0.004284344*Syndrome1_16-0.5408193*Syndrome1_17-0.2304406*Syndrome1_18+0.2462995*Syndrome1_19+0.1687378*Syndrome1_20+0.480715 );
   double Syndrome2_11=Sigmoid2( 0.2892572*Syndrome1_1+0.2819389*Syndrome1_2-0.2116477*Syndrome1_3-0.1031269*Syndrome1_4-0.2198152*Syndrome1_5-0.2882532*Syndrome1_6-0.7462316*Syndrome1_7+0.7820893*Syndrome1_8-0.05574411*Syndrome1_9-0.1144354*Syndrome1_10-0.1073154*Syndrome1_11+0.5092962*Syndrome1_12-0.07017706*Syndrome1_13-0.5550667*Syndrome1_14-0.5170746*Syndrome1_15-0.1299864*Syndrome1_16+0.03325708*Syndrome1_17-0.5107772*Syndrome1_18+0.04024922*Syndrome1_19+0.1836878*Syndrome1_20+0.0346345 );
   double Syndrome2_12=Sigmoid2( -0.10614*Syndrome1_1+0.06027444*Syndrome1_2+0.08108542*Syndrome1_3-0.1568731*Syndrome1_4+0.1509192*Syndrome1_5-0.1630516*Syndrome1_6+0.01426157*Syndrome1_7+0.02186926*Syndrome1_8+0.1099893*Syndrome1_9-0.02269597*Syndrome1_10-0.04576464*Syndrome1_11-0.161096*Syndrome1_12-0.1901706*Syndrome1_13-0.02513908*Syndrome1_14+0.1317106*Syndrome1_15-0.06866668*Syndrome1_16+0.1083753*Syndrome1_17+0.1449683*Syndrome1_18+0.006118122*Syndrome1_19+0.1255394*Syndrome1_20-0.3822223 );
   double Syndrome2_13=Sigmoid2( -0.01638931*Syndrome1_1+0.1172011*Syndrome1_2-0.1022018*Syndrome1_3+0.1098846*Syndrome1_4+0.3456185*Syndrome1_5-0.276273*Syndrome1_6-0.1697723*Syndrome1_7-0.1394644*Syndrome1_8+0.0530486*Syndrome1_9+0.04139024*Syndrome1_10-0.02131393*Syndrome1_11+0.1144992*Syndrome1_12-0.1791101*Syndrome1_13+0.124498*Syndrome1_14+0.2169005*Syndrome1_15+0.06764794*Syndrome1_16+0.3542189*Syndrome1_17+0.0647957*Syndrome1_18+0.01778502*Syndrome1_19-0.0183728*Syndrome1_20-0.09863564 );
   double Syndrome2_14=Sigmoid2( 0.1046498*Syndrome1_1+0.1199886*Syndrome1_2-0.3787079*Syndrome1_3+0.568437*Syndrome1_4-0.09216721*Syndrome1_5-0.07998162*Syndrome1_6-0.1422648*Syndrome1_7-0.220407*Syndrome1_8+0.00417607*Syndrome1_9+0.2042087*Syndrome1_10+0.2614584*Syndrome1_11+0.04491196*Syndrome1_12+0.1860093*Syndrome1_13-0.1642074*Syndrome1_14+0.3918036*Syndrome1_15+0.05427575*Syndrome1_16-0.0002294437*Syndrome1_17+0.008295977*Syndrome1_18-0.2818146*Syndrome1_19-0.3877438*Syndrome1_20+0.03536745 );
   double Syndrome2_15=Sigmoid2( -0.1754033*Syndrome1_1-0.0528489*Syndrome1_2-0.1744897*Syndrome1_3+0.1113354*Syndrome1_4+0.1185713*Syndrome1_5-0.0231303*Syndrome1_6+0.006316248*Syndrome1_7-0.08525342*Syndrome1_8+0.1568578*Syndrome1_9+0.2965699*Syndrome1_10+0.2781587*Syndrome1_11+0.2391527*Syndrome1_12-0.08555941*Syndrome1_13-0.2362186*Syndrome1_14+0.1128907*Syndrome1_15-0.04770778*Syndrome1_16-0.0139725*Syndrome1_17+0.1079882*Syndrome1_18-0.09141354*Syndrome1_19+0.3320866*Syndrome1_20-0.3015116 );
   double Syndrome2_16=Sigmoid2( 0.1962015*Syndrome1_1+0.0192374*Syndrome1_2-0.1578716*Syndrome1_3+0.03360523*Syndrome1_4+0.04818176*Syndrome1_5+0.2462966*Syndrome1_6-0.2103649*Syndrome1_7+0.01318523*Syndrome1_8-0.09349868*Syndrome1_9+0.08476428*Syndrome1_10-0.06272572*Syndrome1_11+0.2246324*Syndrome1_12+0.2539908*Syndrome1_13-0.2059217*Syndrome1_14-0.08641216*Syndrome1_15-0.09780023*Syndrome1_16+0.0005770256*Syndrome1_17-0.2842666*Syndrome1_18-0.05383059*Syndrome1_19-0.2822465*Syndrome1_20+0.2277268 );
   double Syndrome2_17=Sigmoid2( 0.5981864*Syndrome1_1+0.5172131*Syndrome1_2-0.2310352*Syndrome1_3-0.1814138*Syndrome1_4-0.2148922*Syndrome1_5+0.562911*Syndrome1_6+0.5865576*Syndrome1_7-0.2790301*Syndrome1_8-0.3841165*Syndrome1_9+0.3223535*Syndrome1_10+0.2096305*Syndrome1_11+0.08284206*Syndrome1_12+0.7050048*Syndrome1_13+0.4129859*Syndrome1_14+0.2116682*Syndrome1_15+0.2213966*Syndrome1_16-0.1637594*Syndrome1_17+0.1191863*Syndrome1_18-0.6626714*Syndrome1_19-0.9127383*Syndrome1_20-0.1505798 );
   double Syndrome2_18=Sigmoid2( -0.008298698*Syndrome1_1-0.1847953*Syndrome1_2-0.1930849*Syndrome1_3-0.1005524*Syndrome1_4+0.0737519*Syndrome1_5+0.04218475*Syndrome1_6-0.422835*Syndrome1_7+0.06019862*Syndrome1_8-0.2056148*Syndrome1_9+0.3398327*Syndrome1_10-0.2526269*Syndrome1_11-0.06098709*Syndrome1_12-0.1447722*Syndrome1_13-0.05216306*Syndrome1_14-0.09496115*Syndrome1_15+0.2071376*Syndrome1_16+0.03088453*Syndrome1_17-0.521363*Syndrome1_18-0.06449924*Syndrome1_19-0.4105364*Syndrome1_20+0.3204305 );
   double Syndrome2_19=Sigmoid2( -0.1376712*Syndrome1_1-0.0153131*Syndrome1_2+0.04377801*Syndrome1_3+0.08896239*Syndrome1_4+0.03197494*Syndrome1_5-0.02259021*Syndrome1_6+0.008662836*Syndrome1_7-0.1961185*Syndrome1_8-0.0720102*Syndrome1_9+0.05738823*Syndrome1_10-0.004060962*Syndrome1_11-0.3752605*Syndrome1_12+0.02065136*Syndrome1_13+0.1263955*Syndrome1_14-0.05906902*Syndrome1_15+0.4029721*Syndrome1_16-0.159444*Syndrome1_17-0.1619136*Syndrome1_18+0.3338208*Syndrome1_19-0.0656369*Syndrome1_20+0.1602566 );
   double Syndrome2_20=Sigmoid2( -0.003900121*Syndrome1_1+0.3159288*Syndrome1_2+0.2550703*Syndrome1_3+0.05409481*Syndrome1_4+0.06660215*Syndrome1_5-0.1948439*Syndrome1_6-0.370153*Syndrome1_7+0.5337713*Syndrome1_8-0.06716464*Syndrome1_9+0.550526*Syndrome1_10+0.4723933*Syndrome1_11+0.09457724*Syndrome1_12+0.5613732*Syndrome1_13+0.3709611*Syndrome1_14-0.07680532*Syndrome1_15-0.5097623*Syndrome1_16+0.4023384*Syndrome1_17+0.2330064*Syndrome1_18-0.09448317*Syndrome1_19+0.2668969*Syndrome1_20-0.2110061 );

//--- syndromes of the 3rd level:
   double Syndrome3_1=Sigmoid3( -0.05101856*Syndrome2_1-0.04933448*Syndrome2_2+0.03248681*Syndrome2_3-0.05835526*Syndrome2_4-0.01888579*Syndrome2_5-0.07940733*Syndrome2_6-0.04341835*Syndrome2_7-0.07906266*Syndrome2_8+0.2054683*Syndrome2_9+0.1553352*Syndrome2_10-0.07296721*Syndrome2_11-0.01849408*Syndrome2_12-0.07505544*Syndrome2_13+0.08666297*Syndrome2_14-0.2001411*Syndrome2_15+0.07931387*Syndrome2_16+0.1598745*Syndrome2_17+0.01308129*Syndrome2_18+0.159161*Syndrome2_19+0.1903208*Syndrome2_20+0.0190388 );
   double Syndrome3_2=Sigmoid3( 0.0643296*Syndrome2_1+0.3451192*Syndrome2_2-0.1247545*Syndrome2_3+0.03276825*Syndrome2_4+0.303136*Syndrome2_5+0.03152885*Syndrome2_6+0.1118743*Syndrome2_7-0.3860323*Syndrome2_8-0.08593427*Syndrome2_9-0.2664599*Syndrome2_10+0.213205*Syndrome2_11-0.0977626*Syndrome2_12-0.2923501*Syndrome2_13-0.3133417*Syndrome2_14-0.1915279*Syndrome2_15+0.4333939*Syndrome2_16+0.02110274*Syndrome2_17+0.5802879*Syndrome2_18+0.03386912*Syndrome2_19+0.08908307*Syndrome2_20+0.06071822 );
   double Syndrome3_3=Sigmoid3( -0.08613513*Syndrome2_1+0.1200513*Syndrome2_2+0.3818525*Syndrome2_3-0.09603316*Syndrome2_4-0.2353039*Syndrome2_5-0.1816488*Syndrome2_6+0.002517342*Syndrome2_7-0.2414117*Syndrome2_8+0.2011739*Syndrome2_9-0.3057347*Syndrome2_10-0.4593749*Syndrome2_11-0.2228307*Syndrome2_12+0.03512295*Syndrome2_13+0.4402955*Syndrome2_14-0.1967632*Syndrome2_15+0.07873345*Syndrome2_16+0.1981131*Syndrome2_17-0.2677957*Syndrome2_18+0.1719814*Syndrome2_19-0.474854*Syndrome2_20+0.01101439 );
   double Syndrome3_4=Sigmoid3( 0.02534361*Syndrome2_1+0.1845266*Syndrome2_2+0.149674*Syndrome2_3-0.1454014*Syndrome2_4+0.00701888*Syndrome2_5+0.08219463*Syndrome2_6+0.05163066*Syndrome2_7-0.1836077*Syndrome2_8+0.1429968*Syndrome2_9+0.518382*Syndrome2_10-0.00966637*Syndrome2_11-0.1674386*Syndrome2_12+0.1387497*Syndrome2_13+0.1385897*Syndrome2_14-0.01148864*Syndrome2_15+0.3751494*Syndrome2_16-0.08906862*Syndrome2_17-0.06286599*Syndrome2_18+0.2061662*Syndrome2_19-0.07524439*Syndrome2_20-0.08077133 );
   double Syndrome3_5=Sigmoid3( 0.3856083*Syndrome2_1-0.01700347*Syndrome2_2-0.1044575*Syndrome2_3+0.111998*Syndrome2_4-0.5157402*Syndrome2_5-0.05508286*Syndrome2_6-0.3101066*Syndrome2_7-0.5261913*Syndrome2_8-0.05983765*Syndrome2_9+0.1723307*Syndrome2_10-0.2564277*Syndrome2_11+0.06385356*Syndrome2_12-0.07245655*Syndrome2_13+0.1154206*Syndrome2_14-0.3492871*Syndrome2_15+0.136372*Syndrome2_16+0.3627071*Syndrome2_17-0.3074959*Syndrome2_18+0.4425845*Syndrome2_19-0.9329191*Syndrome2_20+0.01476912 );
   double Syndrome3_6=Sigmoid3( 0.5246867*Syndrome2_1-0.2347829*Syndrome2_2+0.01062111*Syndrome2_3+0.2374777*Syndrome2_4-0.02361662*Syndrome2_5+0.1804156*Syndrome2_6+0.07669501*Syndrome2_7-0.142881*Syndrome2_8+0.2566245*Syndrome2_9+0.1024709*Syndrome2_10-0.04695484*Syndrome2_11-0.004103919*Syndrome2_12+0.3340242*Syndrome2_13-0.3702791*Syndrome2_14+0.1852374*Syndrome2_15+0.02175477*Syndrome2_16+0.09901489*Syndrome2_17-0.1502062*Syndrome2_18+0.3814779*Syndrome2_19-0.06319473*Syndrome2_20+0.2657273 );
   double Syndrome3_7=Sigmoid3( 0.1613003*Syndrome2_1-0.2738772*Syndrome2_2-0.03304096*Syndrome2_3+0.3934855*Syndrome2_4+0.3955218*Syndrome2_5-0.3004892*Syndrome2_6+0.1339742*Syndrome2_7+0.09475601*Syndrome2_8+0.03064043*Syndrome2_9-0.7264652*Syndrome2_10-0.4579849*Syndrome2_11-0.1183059*Syndrome2_12+0.2197721*Syndrome2_13-0.08493897*Syndrome2_14+0.2115426*Syndrome2_15-0.07834542*Syndrome2_16-0.3884689*Syndrome2_17-0.101394*Syndrome2_18+0.1002519*Syndrome2_19-0.07787764*Syndrome2_20+0.3529212 );
   double Syndrome3_8=Sigmoid3( -0.3544801*Syndrome2_1+0.03471621*Syndrome2_2-0.2373467*Syndrome2_3-0.2836286*Syndrome2_4+0.01646966*Syndrome2_5+0.06978795*Syndrome2_6-0.03310004*Syndrome2_7+0.01844743*Syndrome2_8+0.05259214*Syndrome2_9-0.05343668*Syndrome2_10+0.3971725*Syndrome2_11-0.08770485*Syndrome2_12-0.2040168*Syndrome2_13+0.1109144*Syndrome2_14-0.06249888*Syndrome2_15-0.5860764*Syndrome2_16+0.1217078*Syndrome2_17+0.2471277*Syndrome2_18-0.03716509*Syndrome2_19-0.1908655*Syndrome2_20+0.03838157 );
   double Syndrome3_9=Sigmoid3( 0.1542789*Syndrome2_1+0.3505224*Syndrome2_2+0.06042741*Syndrome2_3+0.08956298*Syndrome2_4-0.03655836*Syndrome2_5-0.3083843*Syndrome2_6+0.2483124*Syndrome2_7-0.1132483*Syndrome2_8-0.3571556*Syndrome2_9-0.04335312*Syndrome2_10+0.005499069*Syndrome2_11+0.371572*Syndrome2_12-0.1199554*Syndrome2_13+0.1160574*Syndrome2_14-0.01656827*Syndrome2_15+0.09481092*Syndrome2_16-0.07926448*Syndrome2_17+0.3847227*Syndrome2_18+0.1039986*Syndrome2_19-0.02874756*Syndrome2_20-0.2311832 );
   double Syndrome3_10=Sigmoid3( -0.5099882*Syndrome2_1-0.2619184*Syndrome2_2+0.2441412*Syndrome2_3-0.02311796*Syndrome2_4+0.004243354*Syndrome2_5-0.04681544*Syndrome2_6+0.1402575*Syndrome2_7-0.03166823*Syndrome2_8-0.2629028*Syndrome2_9-0.03275445*Syndrome2_10-0.311464*Syndrome2_11+0.3158014*Syndrome2_12-0.04689252*Syndrome2_13+0.1556217*Syndrome2_14-0.02266529*Syndrome2_15-0.15192*Syndrome2_16+0.02253294*Syndrome2_17+0.04638374*Syndrome2_18-0.4847055*Syndrome2_19-0.0543578*Syndrome2_20-0.4383866 );
   double Syndrome3_11=Sigmoid3( 0.09181526*Syndrome2_1-0.009475656*Syndrome2_2+0.08283823*Syndrome2_3+0.06638021*Syndrome2_4-0.04110251*Syndrome2_5+0.03041244*Syndrome2_6-0.2266526*Syndrome2_7+0.3537511*Syndrome2_8+0.2091044*Syndrome2_9-0.2312607*Syndrome2_10-0.01409533*Syndrome2_11-0.06294888*Syndrome2_12+0.1980267*Syndrome2_13+0.07864135*Syndrome2_14-0.01312789*Syndrome2_15+0.02964603*Syndrome2_16-0.1720168*Syndrome2_17-0.01523064*Syndrome2_18+0.07354444*Syndrome2_19+0.1534344*Syndrome2_20+0.04784121 );
   double Syndrome3_12=Sigmoid3( -0.01962976*Syndrome2_1-0.1254692*Syndrome2_2+0.01237085*Syndrome2_3-0.006583595*Syndrome2_4-0.06446695*Syndrome2_5-0.1581757*Syndrome2_6-0.01416831*Syndrome2_7+0.08909909*Syndrome2_8+0.02427519*Syndrome2_9+0.06101634*Syndrome2_10-0.07296847*Syndrome2_11-0.02960677*Syndrome2_12+0.1195403*Syndrome2_13+0.007260199*Syndrome2_14-0.005008513*Syndrome2_15+0.07686368*Syndrome2_16-0.1097991*Syndrome2_17+0.02348211*Syndrome2_18-0.01508969*Syndrome2_19+0.06078456*Syndrome2_20+0.1424098 );
   double Syndrome3_13=Sigmoid3( -0.1845686*Syndrome2_1-0.1120369*Syndrome2_2+0.1346949*Syndrome2_3+0.2425685*Syndrome2_4+0.1310953*Syndrome2_5-0.1957272*Syndrome2_6+0.2163845*Syndrome2_7+0.04189415*Syndrome2_8+0.05685329*Syndrome2_9-0.1108158*Syndrome2_10-0.04702755*Syndrome2_11-0.2698838*Syndrome2_12+0.05045844*Syndrome2_13+0.1487544*Syndrome2_14+7.648221E-5*Syndrome2_15-0.04902162*Syndrome2_16+0.3119571*Syndrome2_17-0.2076546*Syndrome2_18+0.1465537*Syndrome2_19+0.2386554*Syndrome2_20+0.09121808 );
   double Syndrome3_14=Sigmoid3( 0.015057*Syndrome2_1-0.07630379*Syndrome2_2+0.10373*Syndrome2_3-0.01276504*Syndrome2_4+0.01637872*Syndrome2_5+0.1570177*Syndrome2_6+0.02290879*Syndrome2_7+0.1426407*Syndrome2_8-0.3037595*Syndrome2_9-0.1183627*Syndrome2_10-0.05010238*Syndrome2_11-0.06874149*Syndrome2_12+0.0325584*Syndrome2_13-0.1127614*Syndrome2_14+0.1010367*Syndrome2_15+0.2743505*Syndrome2_16+0.02752565*Syndrome2_17-0.01011515*Syndrome2_18-0.1072115*Syndrome2_19-0.1723324*Syndrome2_20-0.1862434 );
   double Syndrome3_15=Sigmoid3( -0.0602835*Syndrome2_1+0.1044827*Syndrome2_2-0.03398157*Syndrome2_3+0.1103081*Syndrome2_4-0.2517793*Syndrome2_5-0.1388755*Syndrome2_6+0.1680355*Syndrome2_7+0.08541053*Syndrome2_8+0.2264198*Syndrome2_9+0.1319854*Syndrome2_10+0.2397746*Syndrome2_11+0.04893836*Syndrome2_12+0.07067535*Syndrome2_13+0.03666123*Syndrome2_14-0.2249698*Syndrome2_15+0.1039975*Syndrome2_16+0.03130547*Syndrome2_17+0.1295152*Syndrome2_18-0.1380298*Syndrome2_19-0.2716908*Syndrome2_20+0.3049682 );
   double Syndrome3_16=Sigmoid3( 0.006898584*Syndrome2_1+0.172121*Syndrome2_2+0.08287619*Syndrome2_3-0.2843233*Syndrome2_4+0.3360839*Syndrome2_5-0.06360124*Syndrome2_6+0.08605669*Syndrome2_7+0.1303328*Syndrome2_8+0.176666*Syndrome2_9+0.3064248*Syndrome2_10+0.03492442*Syndrome2_11-0.1337793*Syndrome2_12+0.2166045*Syndrome2_13+0.1651906*Syndrome2_14-0.2159452*Syndrome2_15-0.02087162*Syndrome2_16-0.1321865*Syndrome2_17+0.02330898*Syndrome2_18-0.1607926*Syndrome2_19+0.100959*Syndrome2_20+0.3113509 );
   double Syndrome3_17=Sigmoid3( 0.2484581*Syndrome2_1+0.07501616*Syndrome2_2-0.2955785*Syndrome2_3-0.06893355*Syndrome2_4-0.110545*Syndrome2_5+0.009258383*Syndrome2_6-0.04150206*Syndrome2_7-0.1581711*Syndrome2_8-0.1503464*Syndrome2_9-0.1641756*Syndrome2_10+0.2800875*Syndrome2_11+0.1470316*Syndrome2_12+0.08529772*Syndrome2_13-0.07939056*Syndrome2_14+0.1105667*Syndrome2_15-0.003909521*Syndrome2_16-0.1663841*Syndrome2_17+0.1384012*Syndrome2_18-0.2260507*Syndrome2_19-0.1310463*Syndrome2_20+0.03011392 );
   double Syndrome3_18=Sigmoid3( 0.2167049*Syndrome2_1+0.1083723*Syndrome2_2+0.03713056*Syndrome2_3-0.07394339*Syndrome2_4-0.08689396*Syndrome2_5+0.1893489*Syndrome2_6-0.004869457*Syndrome2_7+0.06987588*Syndrome2_8-0.1505099*Syndrome2_9+0.1717843*Syndrome2_10+0.07792218*Syndrome2_11+0.02835098*Syndrome2_12+0.03617713*Syndrome2_13+0.1599271*Syndrome2_14-0.1617647*Syndrome2_15-0.04720658*Syndrome2_16+0.004165665*Syndrome2_17-0.1073883*Syndrome2_18+0.06164433*Syndrome2_19+0.01017194*Syndrome2_20-0.1073146 );
   double Syndrome3_19=Sigmoid3( 0.1966043*Syndrome2_1-0.06785608*Syndrome2_2-0.02568222*Syndrome2_3+0.2323583*Syndrome2_4-0.1949882*Syndrome2_5-0.0180097*Syndrome2_6-0.1995831*Syndrome2_7-0.3007537*Syndrome2_8+0.03133066*Syndrome2_9-0.3836962*Syndrome2_10+0.8646971*Syndrome2_11-0.04459784*Syndrome2_12+0.1127359*Syndrome2_13+0.3645059*Syndrome2_14+0.3924035*Syndrome2_15+0.2070317*Syndrome2_16-0.1975317*Syndrome2_17+0.249992*Syndrome2_18-0.1090982*Syndrome2_19+0.9234442*Syndrome2_20+0.0260936 );
   double Syndrome3_20=Sigmoid3( -0.1054238*Syndrome2_1+0.01094678*Syndrome2_2+0.1854347*Syndrome2_3-0.03105933*Syndrome2_4-0.1428708*Syndrome2_5+0.1660853*Syndrome2_6-0.0540761*Syndrome2_7+0.08364562*Syndrome2_8+0.01462638*Syndrome2_9+0.05958234*Syndrome2_10+0.05540805*Syndrome2_11+0.1415959*Syndrome2_12-0.2088391*Syndrome2_13-0.02437577*Syndrome2_14+0.03789431*Syndrome2_15+0.1342704*Syndrome2_16+0.02136465*Syndrome2_17+0.1529594*Syndrome2_18-0.2515772*Syndrome2_19-0.009984408*Syndrome2_20-0.02554057 );

//--- final syndromes:
   BAR[0]=0.377357*Syndrome3_1-0.1995524*Syndrome3_2+0.44664*Syndrome3_3-0.2634062*Syndrome3_4-0.1150927*Syndrome3_5-0.3349093*Syndrome3_6-0.3639574*Syndrome3_7+0.2705039*Syndrome3_8+0.5313437*Syndrome3_9+0.2664694*Syndrome3_10+0.1713557*Syndrome3_11+0.1208919*Syndrome3_12-0.4120659*Syndrome3_13+0.3021899*Syndrome3_14+0.4149051*Syndrome3_15+0.7103375*Syndrome3_16+0.1180793*Syndrome3_17-0.2354599*Syndrome3_18-0.1013937*Syndrome3_19+0.3054902*Syndrome3_20+0.03919306;

//--- postprocessing of the final syndromes:
   BAR[0]=((BAR[0]*0.0180000001564622)+0.000599999912083149)/2;

   return (BAR[0]);
  }
//+------------------------------------------------------------------+

double Prognosis;

//+------------------------------------------------------------------+
#include <Trade\Trade.mqh>
//+------------------------------------------------------------------+
void OnTick()
  {
//--- receive a price forecast from a neural network
   Prognosis=CalcNeuroNet();
//--- perform necessary trade actions
   Trade();
  }
//+------------------------------------------------------------------+
void Trade()
  {
   //--- close an opened position if it does not fit the forecast
   if(PositionSelect(_Symbol))
     {
      long type=PositionGetInteger(POSITION_TYPE);
      bool close=false;
      if((type == POSITION_TYPE_BUY)  && (Prognosis <= 0)) close = true;
      if((type == POSITION_TYPE_SELL) && (Prognosis >= 0)) close = true;
      if(close)
        {
         CTrade trade;
         trade.PositionClose(_Symbol);
        }
     }

   //--- if there are no positions, then open by the forecast
   if((Prognosis!=0) && (!PositionSelect(_Symbol)))
     {
      CTrade trade;
      if(Prognosis >  MinPrognosis) trade.Buy (Lots);
      if(Prognosis < -MinPrognosis) trade.Sell(Lots);
     }
  }

Testando

Lance o Expert sobre o mesmo período que você forneceu os dados para treinamento da rede neural. Gostaria de lembrar que este Expert foi escrito para EURUSD, H1 (o tempo de aprendizagem é quase que 10 meses).

Não há nenhum ponto eme entrar em um negócio quando a previsão do lucro é de um valor comparável com o spread. O Expert tem um filtro interno para tal caso. Defina o parâmetro de entrada MinPrognosis em 0,0005.

A constante do volume de negociação é de 0,1 lote.

Recebemos os seguintes resultados:

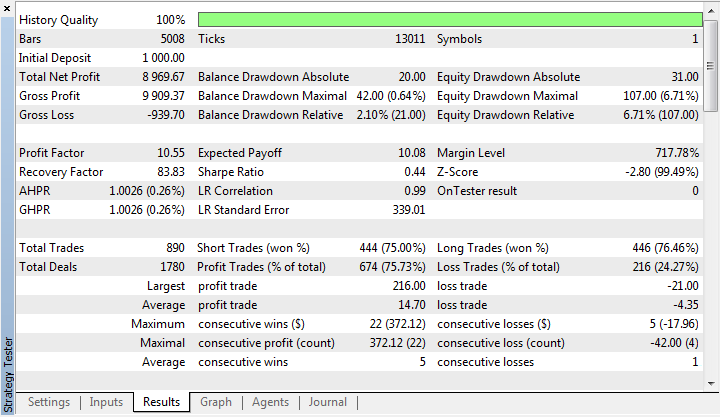
Fig. 21. Estatísticas do teste do Expert Advisor no MetaTester

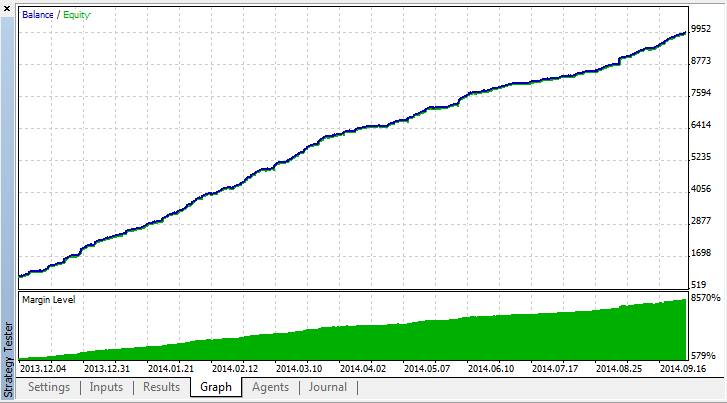
Fig. 22. Gráfico do saldo após o Expert Advisor ser testado no MetaTester

O crescimento constante do saldo mostra que todas as etapas de desenvolvimento do Expert de rede neural foram implementadas corretamente.

Deve-se ter em mente que o lucro em um período de tempo quando o Expert estava aprendendo não garante lucro fora desse intervalo. A criação de verdadeiros Experts de redes neurais rentáveis requerem um conhecimento aprofundado do princípio operacional da rede neural e uma experiência significativa em negociação. Neste artigo eu mostrei como usar uma ferramenta de rede neural e agora cabe a você para torná-la eficiente.

Conclusão

NeuroPro é um programa único. Tivemos a oportunidade de ver que uma rede neural pode ser transitada do NeuroPro para um Expert em MetaTrader 5 em minutos usando apenas as ferramentas em mãos.

Um monte de outros programas de rede neural não possuem essa vantagem. É por isso que o NeuroPro é altamente recomendado.

Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/830

Arquivos anexados |

Baixar como ZIP

NeuroPro_allOS.zip (7824.54 KB)

neuropro-export.mq5 (5.78 KB)

neuropro.mq5 (68.46 KB)

Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

Outros artigos do autor

Ir para discussão

Freelance MQL5.com: Fonte de Renda dos Desenvolvedores (Infográfico)

Por ocasião do quarto aniversário do Serviço Freelance MQL5, nós preparamos uma infográfico demonstrando os resultados do serviço durante todo o tempo de sua existência. Os números falam por si mesmo: mais de 10.000 pedidos no valor total de 600 mil dólares foram executados até a presente data, enquanto que 3.000 clientes e 300 desenvolvedores já utilizaram o serviço.

Guia Prático Estatística do Trader: Hipóteses

Este artigo considera a hipótese - uma das idéias básicas da estatística. Várias hipóteses são examinadas e verificadas através de exemplos usando métodos matemáticos da estatística. Os dados reais são generalizados usando métodos não-paramétricos. O pacote Statistica e a bilbioteca de análise numérica ALGLIB MQL5 são usadas para o processamento de dados.

Construindo uma Aplicação Interativa para exibir feeds RSS no MetaTrader 5

Neste artigo vamos ver a possibilidade de criar um aplicativo para a exibição de feeds RSS. O artigo irá mostrar como os aspectos da Biblioteca Padrão podem ser utilizados para a criação de programas interativos para o MetaTrader 5.

Princípios da Precificação da Bolsa Tomando como Exemplo o Mercado de Derivativos da Bolsa de Moscou (MOEX)

Este artigo descreve a teoria de precificação cambial e das especificidades da Câmara de Compensação (Clearing) do Mercado de Derivativos da Bolsa de Moscou (MOEX). Este é um artigo abrangente para iniciantes que querem obter uma primeira experiência na negociação de derivativos cambial, bem como para os traders experientes do mercado forex que estão considerando a negociação em plataforma centralizada da bolsa de valores.