Artigo publicado Statistical Recipes for Traders - Hypotheses (Receitas estatísticas para traders):
- Há três tipos de mentiras: inocentes, descaradas e estatísticas © Mark Twain
- "Paradoxo de Bleek: realizamos vários experimentos e calculamos a probabilidade da hipótese nula para cada um deles. Embora todos os resultados estatísticos dos experimentos individuais tenham sido "bem-sucedidos", ou seja, a hipótese nula de cada um tenha sido rejeitada com probabilidade p < n, após a meta-análise, obtemos o resultado oposto: p > n.
- Antes de aplicar a estatística em uma área específica, é necessário ter certeza de que estamos lidando com um ambiente ergódico. Caso contrário, isso se tornará um jogo de números com uma aparência inteligente.
- "Paradoxo de Bleck: realizamos vários experimentos e calculamos a probabilidade da hipótese nula para cada um deles. Apesar do fato de que todos os resultados estatísticos de experimentos individuais foram "bem-sucedidos", ou seja, a hipótese nula para cada um deles foi rejeitada com probabilidade p < n, após a meta-análise obtemos o resultado oposto: p > n.
Esse é um paradoxo interessante. Onde posso obter mais informações sobre isso?
Paradoxo interessante. Onde posso obter mais informações sobre ele?
Seu artigo me dá uma dupla impressão.
Além disso. Neste fórum, o próprio fato de perguntar sobre a avaliação hipotética dos resultados é muito importante. O fórum está cheio de pessoas que desenham uma mashka e presumem que esse é o caso, em vez de uma mashka no intervalo.
Menos.
Concordo totalmente com Reshetov. Tudo o que você disse refere-se a séries estacionárias ou próximas a elas, ou seja, séries com pouca alteração de mo e variância ao longo do tempo. Mas não existem séries desse tipo nos mercados financeiros, e toda a aplicação de estatísticas nos mercados financeiros gira em torno da estacionariedade das séries temporais. Os exemplos mais famosos são ARIMA, ARCH e todos os demais.
Sua série aleatória, cujo histograma é mostrado na Fig. 2, mostra que a série tem uma relação fraca com a série estacionária, é distorcida e tem caudas significativamente diferentes. Isso é especialmente bem visto em relação à curva perfeitamente normal desenhada por você. Dessa forma, seu raciocínio não se aplica de forma alguma ao seu exemplo. Este é apenas uma ilustração dos pensamentos de Reshetov.
PS. O conceito mais perigoso e desprezível da estatística é a correlação. É melhor não mencioná-lo de forma alguma.
...Tudo o que você disse se refere a séries estacionárias ou próximas a elas, ou seja, séries com pouca alteração de mo e variância ao longo do tempo. E não existem tais séries nos mercados financeiros, e toda a aplicação de estatísticas nos mercados financeiros gira em torno da estacionariedade das séries temporais. Os exemplos mais famosos são ARIMA, ARCH e todos os demais.
Sua série aleatória, cujo histograma é mostrado na Fig. 2, mostra que a série tem uma relação fraca com a série estacionária, é distorcida e tem caudas significativamente diferentes. Isso é especialmente bem visto em relação à curva perfeitamente normal desenhada por você. Dessa forma, seu raciocínio não se aplica de forma alguma ao seu exemplo. Este aqui é uma ilustração dos pensamentos de Reshetov.
Obrigado por sua opinião!
Vou apresentar meus contra-argumentos.
A estacionariedade é uma característica de uma série temporal. A Figura 2 é uma série de variação. O artigo não fala sobre séries temporais! Embora eu concorde que o tempo é uma característica útil.....
Pelo que entendi, ergodicidade significa uma certa estabilidade do sistema em estudo....
Portanto, gostaria de observar um ponto importante. Se o sistema, vamos falar de uma série temporal financeira, não for estacionário, ainda assim podemos usar a econometria para encontrar um modelo estável (por exemplo, GARCH) que descreva o comportamento do modelo. E nisso eu vejo a constância do sistema - comportamento de acordo com o modelo.... mas com a condição de que há alguma probabilidade de o sistema "quebrar" o modelo...
Obrigado por sua opinião!
Aqui estão meus contra-argumentos.
A estacionariedade é uma característica de uma série temporal. A Figura 2 é uma série de variação. O artigo não fala sobre séries temporais! Embora eu concorde que o tempo é uma característica útil.....
Pelo que entendi, ergodicidade significa uma certa estabilidade do sistema em estudo....
Portanto, gostaria de observar um ponto importante. Se o sistema, vamos falar de uma série temporal financeira, não for estacionário, ainda assim podemos usar a econometria para encontrar um modelo estável (por exemplo, GARCH) que descreva o comportamento do modelo. E nisso eu vejo a constância do sistema - comportamento de acordo com o modelo.... mas com a condição de que haja alguma probabilidade de o sistema "quebrar" o modelo.....
Há alguns anos, publiquei um artigo aqui no site no qual fundamentei uma ideia que é completamente inaceitável para a maioria das pessoas. A saber.
Existem muitos indicadores. Todo mundo acha que se um indicador é desenhado, ele é o mesmo - afinal, vemos exatamente isso. Ao mesmo tempo, não ocorre à maioria das pessoas que o que vemos na realidade pode não existir! O motivo é banal. Se pegarmos a regressão correspondente ao indicador, podemos facilmente descobrir que alguns de seus coeficientes têm intervalos de confiança tão amplos que é impossível falar sobre o valor de tal coeficiente, e se descartarmos esse coeficiente defeituoso, o padrão do indicador será completamente diferente. Quando se diz: existe a verdade, existe a falsidade e existe a estatística, isso se refere a essa circunstância triste e pouco usual - nada é confiável, inclusive os intervalos de confiança.
É por isso que abandonei os modelos paramétricos e me envolvi em modelos baseados em aprendizado de máquina. Não há problemas com a estacionariedade, mas os problemas com o excesso de treinamento estão em plena glória.
E gostei do artigo.
Sim, as observações de San Sanych e Reshetov são legítimas - se o sistema (ou sistema) comparado alterar seus parâmetros, os resultados do teste serão inúteis.
Mas a própria demonstração da aplicação dos métodos é agradável. Isso é raro no Forex!
Eu diria outra coisa, como uma pessoa que aplica métodos semelhantes exatamente para preços de cotação. É possível verificar antecipadamente se o ambiente é homogêneo (em duas grandes amostras independentes) e, em seguida, confiar nos resultados do teste de hipótese com um certo grau de tranquilidade. Isso também pode ser feito graças aos mesmos testes.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Novo artigo Guia Prático Estatística do Trader: Hipóteses foi publicado:
Este artigo considera a hipótese - uma das idéias básicas da estatística. Várias hipóteses são examinadas e verificadas através de exemplos usando métodos matemáticos da estatística. Os dados reais são generalizados usando métodos não-paramétricos. O pacote Statistica e a bilbioteca de análise numérica ALGLIB MQL5 são usadas para o processamento de dados.
Qualquer trader disposto a criar o seu próprio sistema de negociação se tornará um analista, mais cedo ou mais tarde. Eles estão permanentemente tentando encontrar as tendências do mercado e testando idéias de negociação. O teste de uma idéia pode ser baseado em abordagens diferentes - desde uma busca dos melhores valores para os parâmetros no modo de otimização do Strategy Tester até pesquisas científicas de mercado (as vezes pseudo científica).
Neste artigo, eu sugiro a consideração de uma hipótese estatística - um instrumento de análise estatística para a investigação e verificação da inferência. Vamos testar várias hipóteses e exemplos com o pacote Statistica e com a biblioteca de análise numérica ALGLIB MQL5.
2. Testando as Hipóteses. Teoria
A hipótese a ser testada é chamada de hipótese nula (Н0). Uma hipótese concorrente (Н1) é a sua alternativa. Ela esta do outro lado da moeda de Н0, ou seja, ela logicamente não admite a hipótese nula.
Imagine que há uma população de dados sobre o Stop Loss de algum sistema de negociação. Vamos indicar duas hipóteses formando uma base para o teste.
Н0 - valor médio do Stop Loss igual a 30 pontos;
Н1 - valor médio do Stop Loss diferente de 30 pontos.
Variantes de aceitação e rejeição das hipóteses:
As duas últimas variantes estãa ligadas aos erros.
Agora, o valor do nível de significância deve ser especificado. Ela é a probabilidade de que a hipótese alternativa será aceita desde que a hipótese verdadeira seja a nula (terceira variante). Esta probabilidade é preferível ser minimizada.
No nosso caso tal erro ocorrerá se assumirmos que Stop Loss médio não é igual a 30 pontos, mesmo que ele realmente seja.
Normalmente, o nível de significância (α) é igual a 0.05. Isso significa que o valor estatístico do teste da hipótese nula pode povoar a região crítica em não mais que cinco casos em cada 100.
Em nosso caso, o valor da estatística de teste serão avaliados em um gráfico clássico (Fig.1).
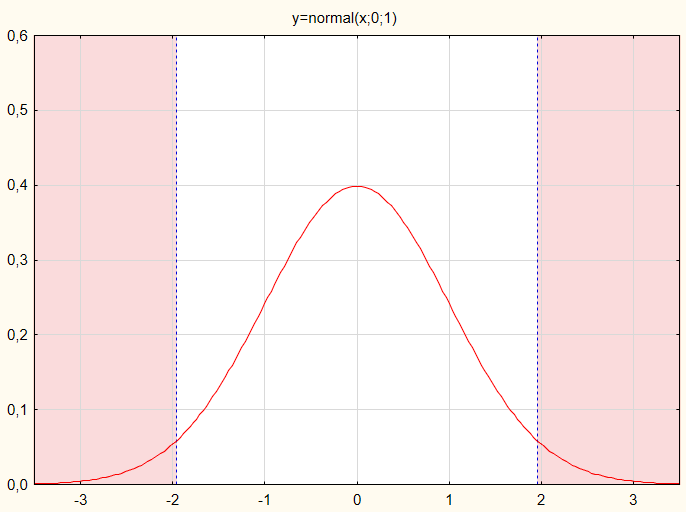
Fig.1. Distribuição do valor estatístico do teste pela lei de probabilidade normalAutor: Dennis Kirichenko