ニューラルネットワークが簡単に(第6回): ニューラルネットワークの学習率を実験する

目次

• イントロダクション
• 1. 問題点
• 2. 実験1
• 3. 実験2
• 4. 実験3
• 結論
• レファレンス
• 記事内で使用しているプログラム

イントロダクション

以前の記事では、完全接続パーセプトロン、畳み込みネットワーク、リカレントネットワークの動作原理と実装方法を検討しました。 すべてのネットワークを学習するためにグラディエントディセントを使用しました。 この方法によれば、各ステップでネットワーク予測誤差を求め、誤差が小さくなるように加重を調整します。 ただし、各ステップでの誤差を完全に排除するのではなく、加重を調整して誤差を小さくするだけです。 したがって、その全長に沿ってトレーニングセットを密接に繰り返すような加重を見つける必要があります。 学習率は、各ステップでの誤差最小化速度を担当します。

1. 問題点

学習率選択の問題点とは？ 学習率の選択に関連する基本的な疑問点を概説してみましょう。

1. 1に等しいレート（または近い値）を使って、すぐに誤差を補正することができないのはなぜでしょうか？
。 この場合、直近の状況にニューラルネットワークを過剰にトレーニングすることになります。 その結果、ヒストリーを無視して最新のデータのみで更なる判断をすることになります。

2. それを承知の上で、サンプル全体の値の平均化を可能にするような小さなレートで何が問題なのでしょうか？
このアプローチの最初の問題は、ニューラルネットワークのトレーニング期間です。 ステップが小さすぎると、そのようなステップが多く必要になります。 それには時間とリソースが必要です。

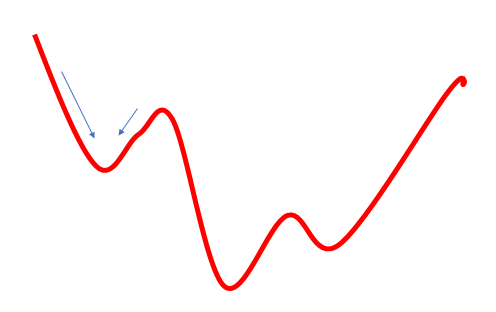
このアプローチの2つ目の問題点は、ゴールまでの道のりが必ずしもスムーズではないということです。 谷があったり、丘があったりします。 あまりにも小さなステップで動くと、そのような値のどれかにはまってしまい、グローバルな最小値と誤って判断してしまうことがあります。 この場合、ゴールに到達することはありません。 重量の更新式にモメンタムを使用することで部分的に解決できますが、でも問題は存在します。

3. 一定距離の値を平均化して局所的な最小値を回避するような、大きなレートで何が問題なのでしょうか？
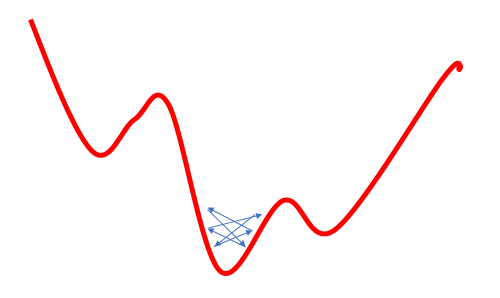
学習率を上げることで局所的な最小値の問題を解決しようとする試みは、別の問題につながります。大きな学習率を使用すると、加重の次の更新でその変化が必要なものよりも大きくなり、結果としてグローバルな最小値を飛び越えることになるため、しばしばエラーを最小化することができません。 さらに戻すと、また似たような状況になります。 その結果、グローバル最小値付近で揺れることになります。

よく知られている問題で、これはよく考察されていますが、学習率の選択に関する明確な推奨事項は見つかりませんでした。 誰もが経験的に特定のタスクごとにレートを選択することを提案しています。 他の著者は、上記のリスク3を最小化するために、学習プロセスの間にレートを徐々に減少させることを提案しています。

この論文では、学習率の異なる1つのニューラルネットワークをトレーニングし、このパラメータがニューラルネットワーク全体のトレーニングに与える影響を見るために、実験を行うことを提案します。    

2. 実験1

便宜上、CNeuronBaseOCLクラスのeta変数をグローバル変数にしてみましょう。

double   eta=0.01;
#include "NeuroNet.mqh"

and

class CNeuronBaseOCL    :  public CObject
  {
protected:
   ........
   ........
//---
   //const double      eta;

さて、異なる学習率パラメータ(0,1; 0,01; 0,001)を持つExpert Advisorのコピーを3つ作成します。 また、初期学習率を0.01とし、10エポックごとに10回ずつ減らしていく第4のEAを作成します。 これを行うには、Train関数のトレーニングループに以下のコードを追加します。

         if(discount>0)
            discount--;
         else
           {
            eta*=0.1;
            discount=10;
           }

4つのEAはすべて1つのターミナルで同時に起動されました。 この実験では、以前のEAテストのパラメータを使用しました：シンボルEURUSD、タイムフレームH1、20著書の連続したローソク足のデータをネットワークに投入し、過去2年間のヒストリーを使用してトレーニングを行います。 トレーニングサンプルは約12.4千本。

すべてのこのEAは、ゼロ値を除いて、-1から1までのランダムな加重で初期化されました。

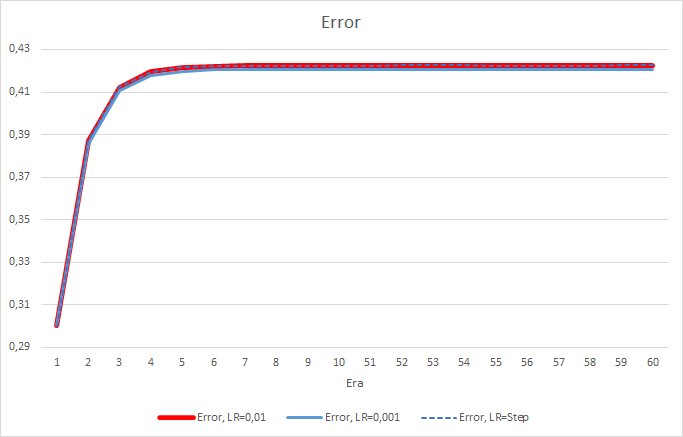
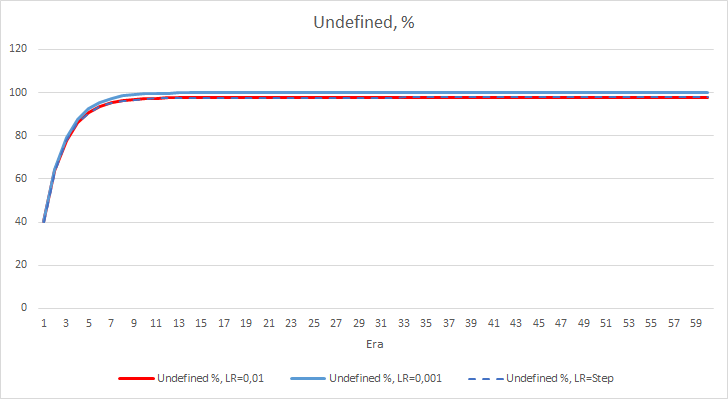
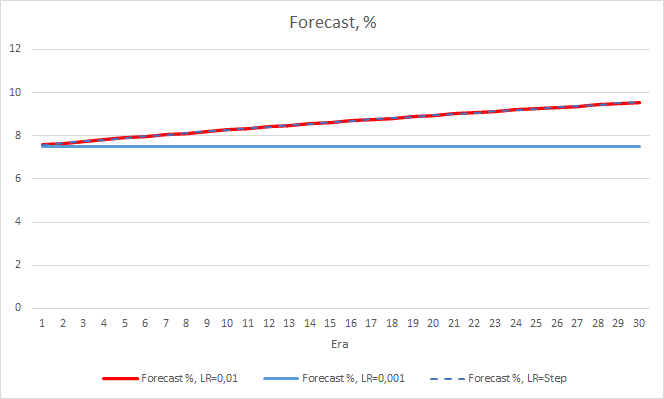
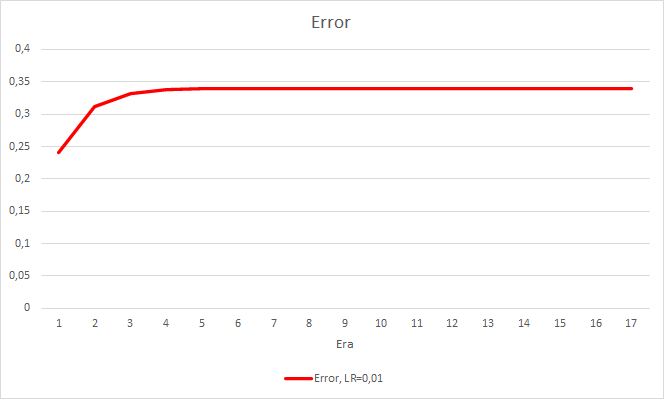
残念ながら、学習率が0.1に等しいEAは1に近い誤差を示したため、チャートには表示されません。 他のEAの学習ダイナミクスは、以下のチャートに示されています。

5エポック後、すべてのEAの誤差は0.42のレベルに達し、残りの時間は変動し続けました。 学習率が0.001に等しいEAの誤差はわずかに小さくなっています。 小数点第3位（他の2つのEAの0.422に対して0.420）に差が現れました。

学習率を変化させたEAの誤差軌跡は、学習係数0.01のEAの誤差線に追従します。 最初の10エポックではかなり期待できますが、レートが下がっても偏差はありません。

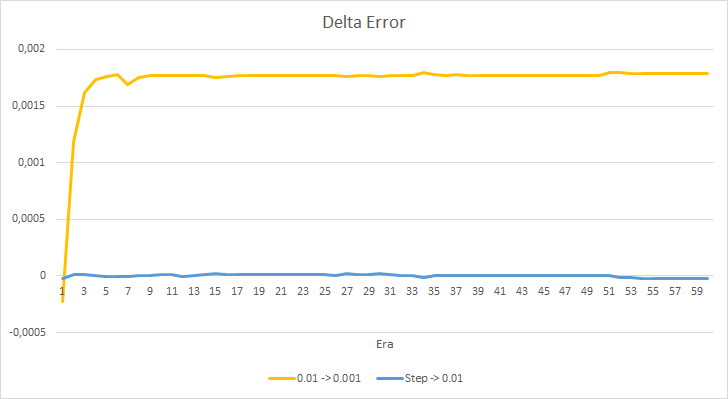
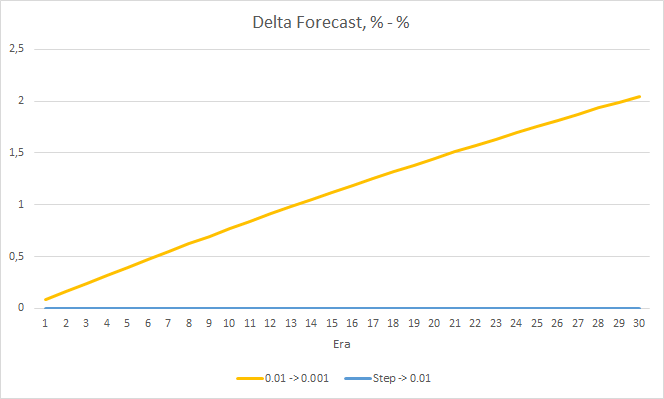
上記のEAの誤差の差をもう少し詳しく見てみましょう。 実験のほぼ全期間を通じて、学習率が0.01と0.001で一定のEAの誤差の差は0.0018前後で変動していました。 さらに、10エポックごとにEAの学習率を下げてもほとんど影響はなく、0.01（初期学習率に相当）のEAからの偏差は0前後で変動します。

得られた誤差値から、本実施例では学習率0.1が適用できないことがわかります。 0.01以下の学習率を使用しても、約42％の誤差で同様の結果が得られます。

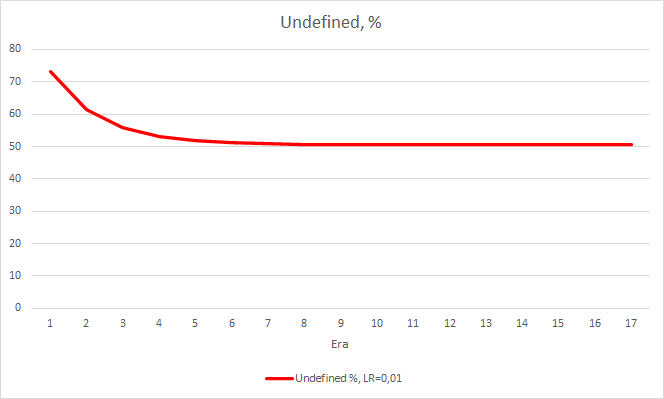
ニューラルネットワークの統計的な誤差はかなりはっきりします。 EAの性能にどのような影響があるのでしょうか？ 見逃したフラクタルの数を確認してみましょう。 残念ながら、すべてのEAは実験で悪い結果を示しました。 さらに、学習率0.01のEAでは約2.5%のフラクタルが決定されるのに対し、学習率0.001のEAでは100%のフラクタルをスキップしています。 52回目以降、学習率0.01のEAでは、フラクタルのスキップ数が減少するトレンドが見られました。 変動率のあるEAではそのようなトレンドは見られませんでした。 

   

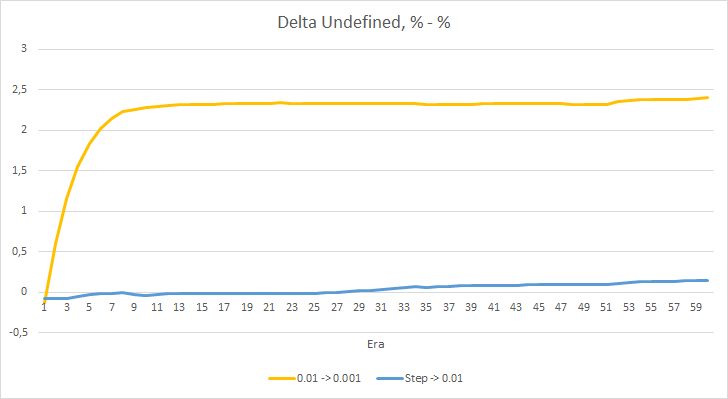
フラクタルパーセンテージデルタの欠落チャートも、学習率0.01でEAに有利な差が徐々に拡大していることがわかります。

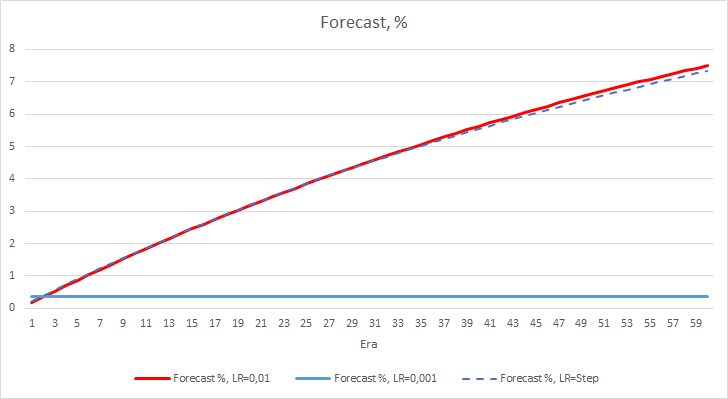
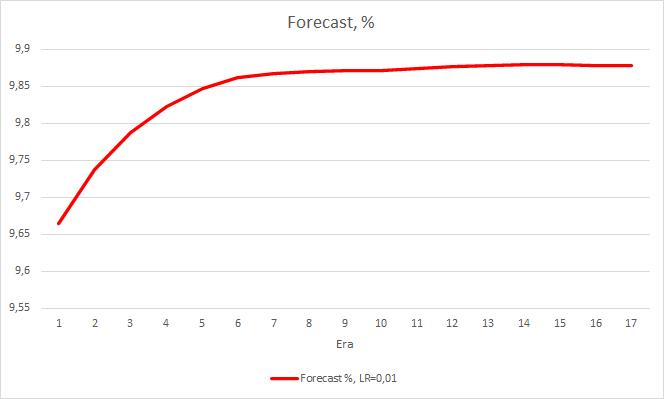
ニューラルネットワークの性能インジケータを2つ考えてみましたが、今のところ学習率の低いEAの方が誤差は小さいですが、フラクタルを見逃してしまいます。 では、3つ目の値を確認してみましょう。"予測されたフラクタルの「ヒット」です。

下のチャートは、学習率0.01のEAと動的に減少するEAの学習における「ヒット率」の成長を示します。 学習率が低下すると変動成長率が低下します。 学習率0.001のEAでは「ヒット率」が0前後で止まっていましたが、フラクタルの100%を見逃しているので当然のことです。 

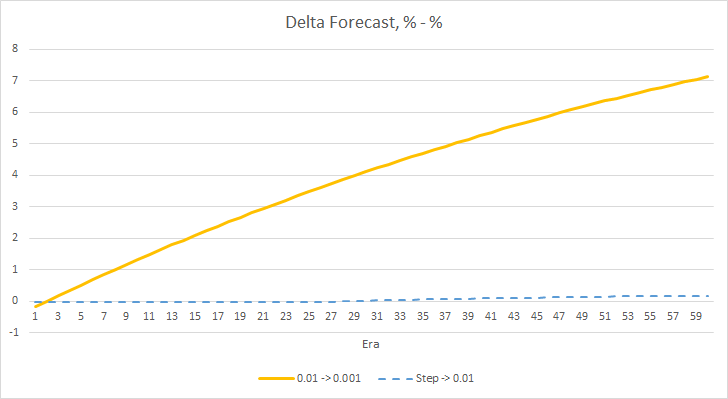
上記の実験では、問題内での最適な学習率またはニューラルネットワークのトレーニングは0.01に近いことがわかります。 学習率が徐々に低下してもプラスにはなりませんでした。 おそらく、10エポックの時よりも減らす回数を少なくすると、レート低下の効果が違ってくるのではないでしょうか。 おそらく、100エポック、1000エポックの方が結果が良いのではないでしょうか。 しかし、これは実験的に検証する必要があります。

3. 実験2

最初の実験では、ニューラルネットワークの加重行列をランダムに初期化しました。 したがって、すべてのEAは異なる初期状態を持っていました。 実験結果へのランダム性の影響を排除するために、前回の実験で得られた加重行列に学習率0.01のEAを3つのEAすべてに負荷をかけ、さらに30エポック分の学習を継続します。

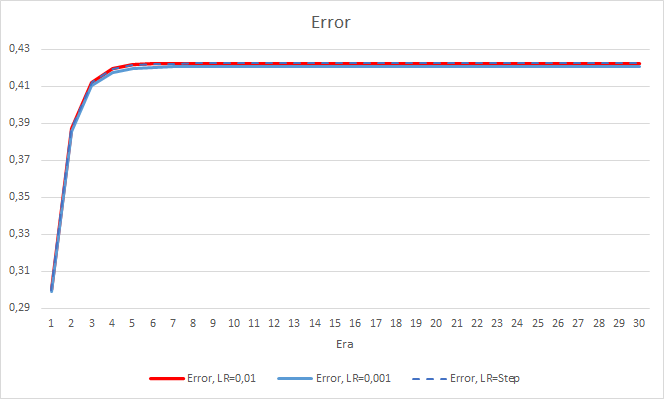
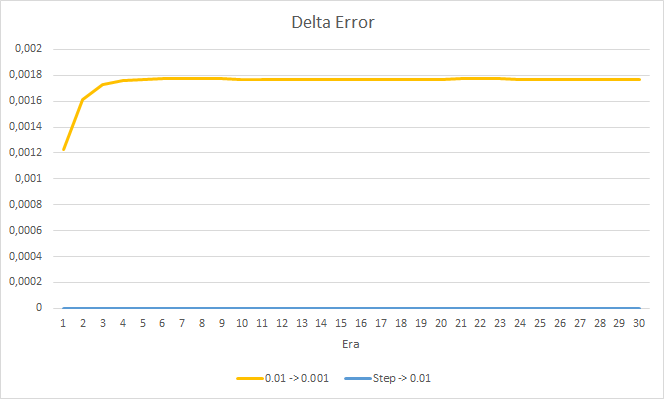
新しいトレーニングでは、以前に得られた結果を確認することができます。 3つのEAすべてで0.42前後の平均的な誤差が見られます。 学習率が最も低いEA（0.001）では、再び誤差がやや小さくなっていました（差は同じ0.0018）。 学習率が徐々に低下していく効果は実質的に0に等しいです。

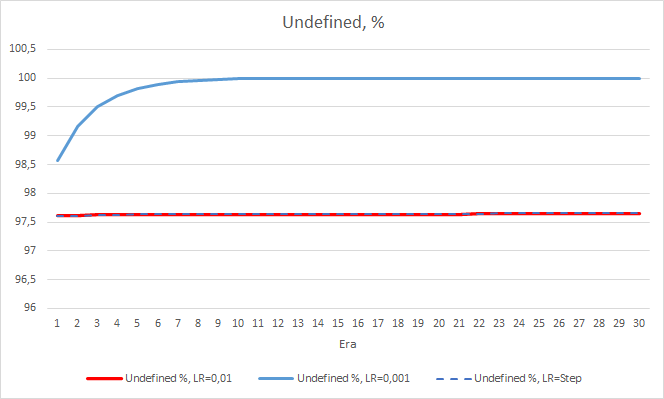
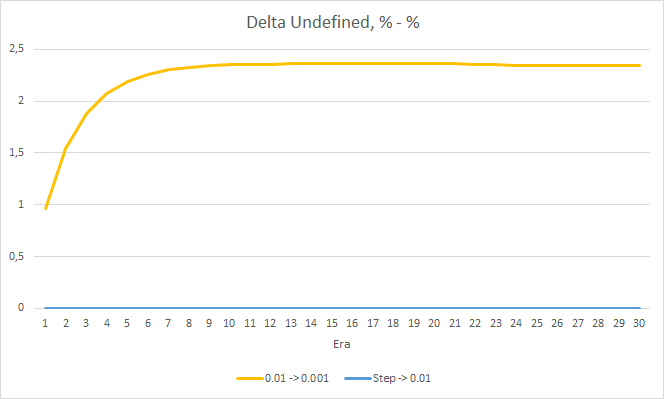
フラクタルの見逃し率については、先に得られた結果を再確認しました。 学習係数の低いEAは10エポックで100％に近づきました。 他の２つのＥＡは97.6%です。 学習率が徐々に低下していく効果は実質的に0に等しいです。  

学習率0.001のEAの「ヒット」率は、徐々に伸び続けています。 学習率が徐々に低下しても、この値には影響しません。 

 

4. 実験3

実験3は、この記事の本題から少し逸脱します。 そのアイデアは、最初の2つの実験の間に生まれました。 ということで、シェアすることにしました。 ニューラルネットワークのトレーニングを観察しているうちに、フラクタルが存在しない確率は60～70％前後で変動し、50％を下回ることはほとんどないことに気がつきました。 フラクタルの出現確率、売買は20～30％程度です。 トレンドの内側にあるローソク足よりも、チャート上のフラクタルの方がはるかに少ないので、ごく自然なことです。 このように、ニューラルネットワークは過剰にトレーニングされており、上記の結果が得られます。 フラクタルはほぼ100％が外れ、レアなものしか捉えられません。  

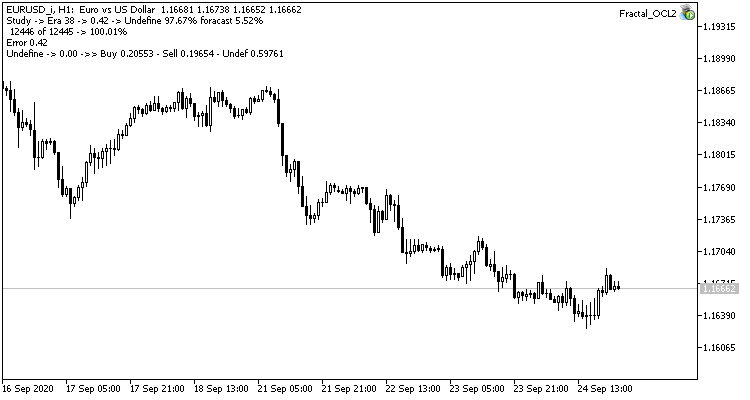
この問題を解決するために、サンプルの凹凸をわずかに補正することにしました。基準値にフラクタルがない場合、ネットワークを学習する際に1の代わりに0.5を指定しました。

            TempData.Add((double)buy);
            TempData.Add((double)sell);
            TempData.Add((double)((!buy && !sell) ? 0.5 : 0));

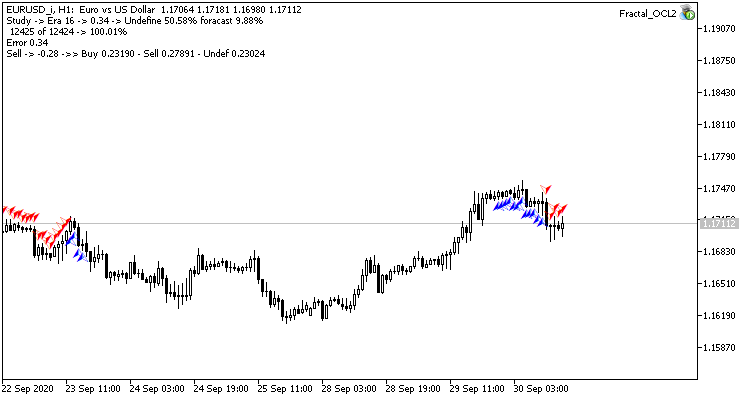
このステップで良い効果が得られました。 学習率0.01、過去の実験で得られた加重行列を用いて実行したエキスパートアドバイザは、5回の学習で約0.34の誤差安定化を示しました。 ミスフラクタルのシェアが51％に減少し、ヒット率が9.88％に上昇しました。 EAがグループ内のシグナルを生成し、したがって、特定のゾーンを示していることをチャートから見ることができます。 明らかに、このアイデアには追加の開発とテストが必要です。 しかし、この結果は、このアプローチがかなり有望であることを示唆します。 

結論

この記事では3つの実験を実施しました。 最初の2つの実験では、ニューラルネットワークの学習率を正しく選択することの重要性が示されました。 学習率は、ニューラルネットワーク全体の学習結果に影響を与えます。 しかし、学習率を選択するための明確なルールは現在のところありません。 よって、実際には実験的に選ぶ必要があるでしょう。

実験３では、非標準的なアプローチで問題を解くことで結果が改善されることが示されています。 しかし、各ソリューションの応用は実験的に確認する必要があります。

レファレンス

1. ニューラルネットワークを簡単に
2. ニューラルネットワークが簡単に(その2）. ネットワークの学習とテスト
3. ニューラルネットワークが簡単に（その3）. 畳み込みネットワーク
4. ニューラルネットワークが簡単に（その4）。リカレントネットワーク
5. ニューラルネットワークが簡単に（その5）．OpenCLでのマルチスレッド計算

記事内で使用しているプログラム

#	名前	タイプ	詳細
1	Fractal_OCL1.mq5	EA	OpenCL技術を使用した分類ニューラルネットワーク（出力層に3つのニューロン）を持つエキスパート・アドバイザー 学習率 = 0.1
2	Fractal_OCL2.mq5	エキスパートアドバイザ	OpenCL技術を使用した分類ニューラルネットワーク（出力層に3つのニューロン）を持つEA学習率 = 0.01
3	Fractal_OCL3.mq5	EA	OpenCL技術を用いた分類ニューラルネットワーク（出力層に3つのニューロン）を使用したEA学習率 = 0.001
4	Fractal_OCL_step.mq5	エキスパートアドバイザ	OpenCL技術を用いた分類ニューラルネットワーク（出力層に3つのニューロン）を用いたEA学習率は10エポックごとに0.01から10倍に減少
5	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
6	NeuroNet.cl	コードベース	OpenCL プログラムコードライブラリ